Как найти интегралы используя интегрирование по частям - Сайт, где вы сможете решить свои вопросы

Интегрирование по частям

Пусть U(x) и V(x) – дифференцируемые функции. Тогда d(U(x)V(x)) = U(x)dV(x) + V(x)dU(x). Поэтому U(x)dV(x) = d(U(x)V(x)) – V(x)dU(x). Вычисляя интеграл от обеих частей последнего равенства, с учетом того, что ∫d(U(x)V(x))=U(x)V(x)+C, получаем соотношение

называемое формулой интегрирования по частям. Понимают его в том смысле, что множество первообразных, стоящее в левой части, совпадает со множеством первообразных, получаемых по правой части.

Решение онлайн
Видеоинструкция

С помощью данного онлайн-калькулятора можно вычислять интегралы по частям. Решение сохраняется в формате Word.

Также рекомендуется изучить сервис вычисление интегралов онлайн

Примеры

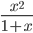≡ x^2/(x+2)

cos²(2x+π) ≡ (cos(2*x+pi))^2

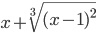≡ x+(x-1)^(2/3)

Применение метода интегрирования по частям

В связи с особенностями нахождения определенных величин, формулу интегрирования по частям очень часто используют в следующих задачах:

Математическое ожидание непрерывной случайной величины. Формула для нахождения математического ожидания и дисперсии непрерывной случайной величины включает в себя два сомножителя: функцию полинома от x и плотность распределения f(x).
Разложение в ряд Фурье. При разложении необходимо определять коэффициенты, которые находятся интегрированием от произведения функции f(x) и тригонометрической функции cos(x) или sin(x).

Типовые разложения по частям

Вид интеграла	Разложения на части
`∫P_n(x)cos(ax)dx`, `∫P_n(x)sin(ax)dx`, `∫P_n(x)e^axdx`, где `P_n(x)` – некоторый полином (многочлен) степени `n`	`U(x)=P_n(x)`, `dV(x)=cos(ax)dx`
`∫ln(P(x))dx`	`U=ln(P(x))`; `dV=dx`
`∫arcsin(ax)dx`	`U=arcsin(ax)`; `dV=dx`
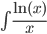	`U=ln(x)`; `dV=dx/x`

При использовании формулы интегрирования по частям нужно удачно выбрать U и dV, чтобы интеграл, полученный в правой части формулы находился легче. Положим в первом примере U=e^x, dV=xdx. Тогда dU=e^xdx, 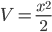и Вряд ли интеграл ∫x²e^xdx можно считать проще исходного.

Иногда требуется применить формулу интегрирования по частям несколько раз, например, при вычислении интеграла ∫x²sin(x)dx.

Интегралы ∫e^axcos(bx)dx и ∫e^axsin(bx)dx называются циклическими и вычисляются с использованием формулы интегрирования по частям два раза.

Пример №1. Вычислить ∫xe^xdx.

Положим U=x, dV=e^xdx. Тогда dU=dx, V=e^x. Поэтому ∫xe^xdx=xe^x-∫e^xdx=xe^x-e^x+C.

Пример №2. Вычислить ∫xcos(x)dx.

Полагаем U=x, dV=cos(x)dx. Тогда dU=dx, V=sin(x) и ∫xcos(x)dx=xsin(x) - ∫sin(x)dx = xsin(x)+cos(x)+C

Пример №3. ∫(3x+4)cos(x)dx

Решение:

Ответ: (3x+4)sin(x)+3cos(x)+C

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

Метод интегрирования по частям используется тогда, когда нужно упростить имеющийся неопределенный интеграл или свести его к табличному значению. Чаще всего он применяется в случае наличия показательных, логарифмических, прямых и обратных тригонометрических формул и их сочетаний в подынтегральном выражении.

Основная формула, необходимая для использования этого метода, выглядит так:

∫f(x)dx=∫u(x)d(v(x))=u(x)v(x)-∫v(x)d(u(x))

Она означает, что нам нужно сначала представить выражение под интегралом в качестве произведения функции u(x) и дифференциала функции v(x). После этого мы вычисляем значение функции v(x) каким-либо методом (чаще всего применяется метод непосредственного интегрирования), а полученные выражения подставляем в указанную формулу, сводя исходный интеграл к разности u(x)v(x)-∫v(x)d(u(x)). Полученный в итоге интеграл также можно взять, используя любой метод интегрирования.

Рассмотрим задачу, в которой нужно найти множество первообразных функции логарифма.

Пример 1

Вычислите неопределенный интеграл ∫ln(x)dx.

Решение

Используем метод интегрирования по частям. Для этого берем ln(x) как функцию u(x), а остаток подынтегрального выражения – как d(v(x)). В итоге получаем, что ln(x)dx=u(x)d(v(x)), где u(x)=ln(x), d(v(x))=dx.

Дифференциалом функции u(x) является d(u(x))-u'(x)dx=dxx, а функция v(x) может быть представлена как v(x)=∫d(v(x))=∫dx=x

Важно: константа C при вычислении функции v(x) будет считаться равной 0.

Подставим то, что у нас получилось, в формулу интегрирования по частям:

∫ln(x)dx=u(x)v(x)-∫v(x)d(u(x))==ln(x)·x-∫x·dxx=ln(x)·x-∫dx=ln(x)·x-x+C1==x(ln(x)-1)+C

где C=-C1

Ответ: ∫ln(x)dx=x(ln(x)-1)+C.

Наиболее сложным в применении данного метода является выбор, какую именно часть исходного выражения под интегралом взять в качестве u(x), а какую – d(v(x)).

Разберем несколько стандартных случаев.

Если у нас в условии стоят интегралы вида ∫Pn(x)·eaxdx, ∫Pn(x)·sin(ax)dx либо ∫Pn(x)·cos(ax)dx, где a является коэффициентом, а Pn(x) – многочленом степени n, то в качестве функции u(x) нужно взять именно Pn(x).

Пример 2

Найдите множество первообразных функции f(x)=(x+1)·sin(2x).

Решение

Мы можем взять по частям неопределенный интеграл ∫(x+1)·sin(2x)dx. Берем x+1 в качестве u(x) и sin(2x)dx в качестве d(v(x)), то есть d(u(x)) = d(x+1) = dx.

Используя непосредственное интегрирование, получим:

v(x)=∫sin(2x)dx=-12cos(2x)

Подставляем в формулу интегрирования по частям:

∫(x+1)·sin(2x)dx=u(x)v(x)-∫v(x)d(u(x))==(x+1)·-12cos(2x)-∫-12cos(2x)dx==-12(x+1)·cos(2x)+12∫cos(2x)·d(x)==-12(x+1)·cos(2x)+14sin(2x)+C

Ответ: ∫(x+1)·sin(2x)dx=-12(x+1)·cos(2x)+14sin(2x)+C.

Пример 3

Вычислите неопределенный интеграл ∫(x2+2x)exdx.

Решение

Берем многочлен второго порядка x2+2x в качестве u(x) и d(v(x))-exdx.

∫x2+2xexdx=u(x)=x2+2x, d(v(x))=exdxd(u(x))=(2x+2)dx, v(x)=∫exdx=ex==u(x)v(x)-∫v(x)d(u(x))=(x2+2x)ex-∫(2x+2)exdx

К тому, что у нас получилось, надо опять применить метод интегрирования по частям:

∫(2x+2)exdx=(x2+2x)ex-∫2x+2exdx==u(x)=(2x+2), d(v(x))=exdxd(u(x))=2dx, v(x)=∫exdx=ex==(x2+2x)ex-(2x+2)ex-∫v(x)d(u(x))==(x2+2x)ex-(2x+2)ex-∫2exdx==(x2+2x-2x-2)ex+2∫exdx=(x2-2)ex+2ex+C=x2ex+C

Ответ: ∫(x2+2x)exdx=x2ex+C.

Пример 4

Вычислите интеграл ∫x3cos13xdx.

Решение

Согласно методу интегрирования по частям, берем u(x)=x3 и d(v(x))=cos13xdx.

В таком случае d(u(x))=3x2dx и v(x)=∫cos13xdx=3sin13x.

Теперь подставим полученные выражения в формулу:

∫x3cos13xdx=u(x)v(x)-∫v(x)d(u))==x33sin13x-∫3x23sin13xdx==3x3sin13x-9∫x2sin13xdx

У нас получился неопределенный интеграл, который опять же нужно взять по частям:

∫x3cos13xdx=3x3sin13x-9∫x2sin13xdx==u(x)=x2, d(v(x))=sin13xdxd(u(x))=2xdx, v(x)=∫sin13xdx=-3cos13x==3x3sin13x-9-3x2cos13x-∫-3cos13x·2xdx==3x3sin13x+27×2·cos13x-54∫xcos13xdx

Выполняем частичное интегрирование еще раз:

∫x3cos13xdx=3x3sin13x+27×2·cos13x-54∫xcos13xdx==u(x)=x, d(v(x))=cos13xdxd(u(x))=dx, v(x)=∫cos13xdx=3sin13x==3x3sin13x+27x2cos13x-543xsin13x-∫3sin13xdx==3×3-162xsin13x+27x2cos13x+162∫sin13xdx==(3×3-162x)sin13x+27x2cos13x-486cos13x+C==(3×3-162x)sin13x+(27×2-486)cos13x+C

Ответ: ∫x3cos13xdx=(3×3-162x)sin13x+(27×2-486)cos13x+C.

Если же у нас в условии стоят интегралы вида ∫Pn(x)·ln(ax)dx, ∫Pn(x)·arcsin(ax)dx,∫Pn(x)·arccos(ax)dx, ∫Pn(x)·arctg(ax)dx, ∫Pn(x)·arcctg(ax)dx

то нам следует брать в качестве u(x) функции arctg(ax), arcctg(x), ln(ax), arcsin(ax), arcos(ax).

Пример 5

Вычислите множество первообразных функции (x+1)ln(2x).

Решение

Принимаем ln(2x) в качестве u(x), а (x+1)dx – в качестве d(v(x)). Получаем:

d(u(x))=(ln(2x))’dx=12x(2x)’dx=dxxv(x)=∫(x+1)dx=x22+x

Подставим эти выражения в формулу:

∫(x+1)ln(2x)dx=u(x)v(x)-∫v(x)d(u(x))==x22+xln2x-∫x22+xdxx==x22+xln(2x)-∫x2+1dx=x22+xln2x-12∫xdx-∫dx==x22+xln(2x)-x24-x+C

Ответ: ∫(x+1)ln(2x)dx=x22+xln(2x)-x24-x+C.

Пример 6

Вычислите неопределенный интеграл ∫x·arcsin(2x)dx.

Решение

Решаем, какую часть взять за u(x), а какую – за d(v(x)). Согласно правилу, приведенному выше, в качестве первой функции нужно взять arcsin(2x), а d(v(x)) = xdx. Получим:

d(u(x))=(arcsin(2x)’dx=2x’dx1-(2x)2=2dx1-(2x)2, v(x)=∫xdx=x22

Подставляем значения в формулу:

∫x·arcsin(2x)dx=u(x)v(x)-∫v(x)d(u(x))==x22arcsin(2x)-∫x22-2dx1-(2x)2=x22arcsin(2x)-∫x2dx1-4×2

В итоге мы пришли к следующему равенству:

∫x·arcsin(2x)dx=x22arcsin(2x)-∫x2dx1-4×2

Теперь вычислим получившийся в итоге интеграл ∫x2dx1-4×2:

∫x2dx1-4×2=∫x2dx414-x2=12∫x2dx14-x2=-12∫-x2dx14-x2==-12∫14-x2-1414-x2dx=-1214-x2dx+18∫dx14-x2==-12∫14-x2dx+18arcsin(2x)

Здесь можно применить метод интегрирования по частям и получить:

∫x2dx1-4×2=-12∫14-x2dx+18arcsin(2x)==u(x)=14-x2, d(v(x))=dxd(u(x))=14-x2’dx214-x2=-xdx14-x2, v(x)=∫dx=x==-12u(x)v(x)-∫v(x)d(u(x))+18arcsin(2x)==-12×14-x2-∫-x2dx14-x2+18arcsin(2x)==-12×14-x2-12∫x2dx14-x2+18arcsin(2x)==-12×14-x2-∫x2dx1-4×2+18arcsin(2x)

Теперь наше равенство выглядит так:

∫x2dx1-4×2=-12×14-x2-∫x2dx1-4×2+18arcsin(2x)

Мы видим, что интеграл справа аналогичен тому, что получился слева. Переносим его в другую часть и получаем:

2∫x2dx1-4×2=-12×14-x2+18arcsin(2x)+C1⇒x2dx1-4×2=-14×14-x2+116arcsin(2x)+C2x2dx1-4×2=-18×14-x2+116arcsin(2x)+C2

где C2=C12

Вернемся к исходным переменным:

∫x·arcsin(2x)dx=x22arcsin(2x)-∫x2dx1-4×2==x22arcsin(2x)–18×1-4×2+116arcsin(2x)+C2==12×2-18arcsin(2x)+18×1-4×2+C

где С=-С2

Ответ: ∫x·arcsin(2x)dx=12×2-18arcsin(2x)+18×1-4×2+C.

Если же у нас в задаче стоит интеграл вида ∫ea·x·sin(bx)dx либо ∫ea·x·cos(bx)dx, то в качестве u(x) может быть выбрана любая функция.

Пример 7

Вычислите неопределенный интеграл ∫ex·sin(2x)dx.

Решение

∫exsin(2x)dx=u(x)=sin(2x), d(v(x))=exdxd(u(x))=2cos(2x)dx, v(x)=∫exdx=ex==u(x)v(x)-∫v(x)d(u(x))=sin(2x)ex-∫ex·2cos2xdx==sin(2x)ex-2∫excos(2x)dx=u(x)=cos(2x), d(v(x))=exdxd(u(x))=-2sin(2x)dx, v(x)=∫exdx=ex==sin(2x)ex-2cos(2x)ex-∫(ex(-2sin(2x)dx))==sin(2x)ex=2cos(2x)ex-4∫exsin(2x)dx

В итоге у нас получится:

∫exsin(2x)dx=sin(2x)ex-2cos(2x)ex-4∫exsin(2x)dx

Мы видим одинаковые интегралы слева и справа, значит, можем привести подобные слагаемые:

5∫exsin(2x)dx=sin(2x)ex-2cos(2x)ex⇒∫exsin(2x)dx=15sin(2x)ex-25cos(2x)ex+C

Ответ: ∫exsin(2x)dx=15sin(2x)ex-25cos(2x)ex+C

Этот способ решения является стандартным, и справа нередко получается интеграл, который идентичен исходному.

Мы рассмотрели наиболее типовые задачи, в которых можно точно определить, какую часть выражения взять за d(v(x)), а какую за u(x). В остальных случаях это приходится определять самостоятельно.

Также советуем вам ознакомиться с материалом, посвященным основным методам интегрирования.

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Уважаемые студенты!
Срочно заказать решение своих задач можно здесь всего за 10 минут.

Интегрирование по частям

Интегрирование по частям – метод для решения интегралов от произведения двух элементарных функций. Одна из них легко дифференцируема, а другая интегрируема. Работает техника для неопределенных и определенных интегралов.

Формула для неопределенного интеграла:

$$ int udv = uv – int vdu $$

Формула для определенного интеграла:

$$ int limits_{a}^{b} udv = uv bigg |_{a}^{b} – int limits_{a}^{b} vdu $$

Рассмотрим на практике примеры решения интегрирования по частям, которые часто предлагаются преподавателями на контрольных работах. Обратите внимание ещё раз на то, что под значком интеграла стоит произведение двух функций. Это как признак того, что для решения подойдет данный метод.

Пример 1

Найти интеграл $ int xe^xdx $

Решение

Видим, что подынтегральная функция состоит из двух функций, одна из которых при дифференцировании моментально превращается в единицу, а другая легко интегрируется. Для решения интеграла используем метод интегрирования по частям. Положим, $ u = x rightarrow du=dx $, а $ dv = e^x dx rightarrow v=e^x $

Подставляем найденные значения в первую формулу интегрирования и получаем

$$ int xe^x dx = xe^x – int e^x dx = xe^x – e^x + C. $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ int xe^x dx = xe^x – e^x + C $$

Пример 2

Найти интеграл $ int xcos x dx $

Решение

В качестве неизвестных функций $ u $ и $ v $ возьмем следующие: $ u=x rightarrow du=dx $ и $ dv = cos x dx rightarrow v = sin x $.

Подставим функции $ u $ и $ v $ в первую формулу

$$ int x cos x dx = x sin x – int sin x dx = x sin x + cos x + C. $$

Ответ

$$ int x cos x dx = x sin x + cos x + C $$

Пример 3

Вычислить интеграл $ int limits_1 ^e xln x dx $

Решение

В данном задании имеем интеграл с пределами, а поэтому будем применять формулу для определенного интеграла. Введём обозначения

$$ u = ln x rightarrow du = frac{dx}{x}, text{a за } dv = xdx rightarrow v = frac{x^2}{2}. $$

Осталось подставить это в формулу

$$ int limits_1 ^e xln x dx = frac{x^2}{2} ln x bigg |_1 ^e – int limits_1 ^e frac{x^2}{2}frac{dx}{x} = frac{e^2}{2} – 0 – frac{1}{2} int limits_1 ^e xdx = $$

$$ =frac{e^2}{2} – frac{1}{2} frac{x^2}{2}bigg |_1 ^e = frac{e^2}{2} – frac{1}{2}(frac{e^2}{2} – frac{1}{2}) = frac{e^2}{2} – frac{e^2}{4} + frac{1}{4} = frac{e^2+1}{4} .$$

Ответ

$$ int limits_0 ^1 x ln x dx = frac{e^2+1}{4} $$

Пример 4

Вычислить интеграл $ int limits_0 ^1 (x+5) 3^x dx $

Решение

По аналогии с предыдущими решенными примерами разберемся какую функцию без проблем интегрировать, какую дифференцировать. Обращаем внимание, что если продифференцировать $ (x+5) $, то произойдет автоматическое преобразования этого выражения в единицу, что нам будет “на руку”. Поэтом поступаем так

$$ u=x+5 rightarrow du=dx, dv=3^x dx rightarrow v=frac{3^x}{ln3} .$$

Теперь все неизвестные функции стали найдены и могут быть поставлены во вторую формулу

$$ int limits_0 ^1 (x+5) 3^x dx = (x+5) frac{3^x}{ln 3} bigg |_0 ^1 – int limits_0 ^1 frac{3^x dx}{ln 3} = $$

$$ = frac{18}{ln 3} – frac{5}{ln 3} – frac{3^x}{ln^2 3}bigg| _0 ^1 = frac{13}{ln 3} – frac{3}{ln^2 3}+frac{1}{ln^2 3} = frac{13}{ln 3}-frac{4}{ln^2 3}. $$

Ответ

$$ intlimits_0 ^1 (x+5)3^x dx = frac{13}{ln 3}-frac{4}{ln^2 3} $$

Источник

Пусть
и– непрерывно дифференцируемые функции.
На основании формулы дифференциала
произведения имеем

Отсюда

Интегрируя,
получим:

или окончательно

(4)

Формула (4) называется формулой
интегрирования по частям.

Выведенная формула показывает, что
интеграл
приводится к интегралу,
который может оказаться более простым,
чем исходный, или даже табличным. Сущность
метода интегрирования по частям вполне
соответствует его названию. Дело в том,
что при вычислении интеграла этим
методом подынтегральное выражениепредставляется в виде произведения
множителейuиdv.
При этом dx обязательно входит в
dv. В результате получается, что заданный
интеграл находится по частям: сначала
находим,
а затем.

Пример 1.

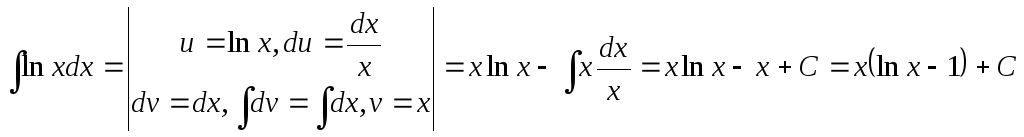В представленном примере, как и в
дальнейших, вертикальными черточками
отделены вспомогательные записи. Отметим
также, что в качестве vможно взять любую функцию видаx+C,гдеС– постоянная. Мы взялиv=x,
т.е.С=0.

Пример
2.
.

Пример
3.

Пример 4.

Иногда для вычисления
интеграла формулу интегрирования по
частям приходится применять несколько
раз.

Пример
5.

Таким образом, интеграл
вычислен двукратным интегрированием
по частям.

Пример 6.

Если бы выражение
u
и dv
мы выбрали иначе, т.е.
,
то получили бы,
откуда,
и пришли бы к интегралу более сложному,
чем исходный, т.к. степень сомножителя
при тригонометрической функции повысилась
на единицу.

Приведенный пример показывает, что при
вычислении интегралов методом
интегрирования по частям главным
является разумное разбиение подынтегрального
выражения на множители uиdv. Общих установок
по этому вопросу не имеется. Однако, для
некоторых типов интегралов сделать это
возможно.

а) В интегралах вида

где
P(х)
– многочлен относительно x,
а –
некоторое число, полагают u=P(x),
а остальные сомножители за
.

Пример 7.
Найти
.


Положим
,,
тогда,.
Следовательно,



б) В интегралах вида

полагают

а
остальные сомножители – заu.

Пример 8.
Найти
.

Следовательно,

Вычислим отдельно последний интеграл:

Итак,
.

Отметим, что на
практике важно научиться применять
формулу (4), не выписывая по возможности
в стороне выражения для функций u
и v.

Так, решение приведенного примера может
быть представлено в виде:



=.

Возвращение к исходному интегралу

Формула интегрирования
по частям применима и для нахождения
интегралов вида
и,
гдеа
и b
– числа. При
нахождении этих интегралов она применяется
последовательно два раза, причем оба
раза за u
выбирается либо показательная функция,
либо тригонометрическая. После
двукратного интегрирования по частям
получается линейное уравнение относительно
искомого интеграла.

Пример 9.
Найти I
=.


Положим
,.
Тогда,.

Следовательно,
I
=.

Для вычисления
интеграла
снова
применим интегрирование по частям.
Положим,.
Тогда,.

Таким образом,

I==.

Так как в правой части стоит искомый
интеграл, то, перенося его в левую часть,
получим:

Отсюда получаем окончательный результат:

=.

Применим изложенный
метод к вычислению еще двух, часто
используемых в приложении, интегралов.

Пример
10. Найти
I
=.


Положим
,.
Тогда,.
Следовательно,

(*)

Так
как
,
то

(см.
лекция 2, п.2б, пример 20).

Подставив
полученное выражение в равенство (*),
будем иметь

Таким
образом,
.

Пример
11. Найти

,(а0)


Положим
,,
откуда,.
Следовательно,

или

Отсюда получаем:
.

Соседние файлы в предмете Высшая математика

Источник

Простое объяснение принципов решения интегралов функций с использованием метода интегрирования по частям и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения интегралов функций с использованием метода интегрирования по частям

Для нахождения интегралов функций с использованием метода интегрирования по частям используется формула интегрирования по частям, свойства интеграла, а также таблица интегралов.

Формула интегрирования по частям:

Таблица основных интегралов

Примеры решений интегралов функций с использованием метода интегрирования по частям

Задача

Вычислить интеграл:

$[int xe^{x}dx]$

Решение

Обозначим:

$[u = x, dv = e^{x}dx, du = dx, v = e^{x}]$

Применяя формулу интегрирования по частям

получаем:

$[int xe^{x}dx = xe^{x} - int e^{x}dx = xe^{x} - e^{x} + C = e^{x}(x -1) + C]$

Ответ

$[int xe^{x}dx = e^{x}(x -1) + C]$

Задача

Вычислить интеграл:

Решение

Обозначим:

Применяя формулу интегрирования по частям

получаем:

Ответ

Задача

Вычислить интеграл:

Решение

Обозначим:

$[u = ln{x}, dv = dx, du = frac{dx}{x}, v = x]$

Применяя формулу интегрирования по частям

, получаем:

$[int ln{x}dx = xln{x} - int xfrac{dx}{x} = xln{x} - int dx = xln{x} - x + C = x(ln{x} - 1) + C]$

Ответ

Задача

Вычислить интеграл:

Решение

Обозначим:

$[u = arctg{x}, dv = dx, du = frac{dx}{1 + x^{2}}, v = x]$

Применяя формулу интегрирования по частям

получаем:

$[int arctg{x}dx = x arctg{x} - int frac{x}{1 + x^{2}}dx = x arctg{x} - frac{1}{2}ln{(1 + x^{2})} + C]$

Ответ

$[int arctg{x}dx = x arctg{x} - frac{1}{2}ln{(1 + x^{2})} + C]$

Задача

Вычислить интеграл:

Решение

Обозначим:

$[u = arcsin{x}, dv = dx, du = frac{dx}{sqrt{1 - x^{2}}}, v = x]$

Применяя формулу интегрирования по частям

получаем:

$[int arcsin{x}dx = xarcsin{x} - int frac{x}{sqrt{1 - x^{2}}}dx = xarcsin{x} + sqrt{1 - x^{2}} + C]$

Ответ

$[int arcsin{x}dx = xarcsin{x} + sqrt{1 - x^{2}} + C]$

Задача

Вычислить интеграл:

Решение

Обозначим:

Применяя формулу интегрирования по частям

получаем:

Ответ

Задача

Вычислить интеграл:

$[int x^{3}ln{x}dx]$

Решение

Обозначим:

$[u = ln{x}, dv = x^{3}dx, du = frac{dx}{x}, v = frac{x^{4}}{4}]$

Применяя формулу интегрирования по частям

получаем:

$[int x^{3}ln{x}dx = ln{x}frac{x^{4}}{4} - int frac{x^{4}}{4}frac{dx}{x}]$

$[ln{x}frac{x^{4}}{4} - frac{1}{4}int x^{3}dx = ln{x}frac{x^{4}}{4} - frac{1}{4}frac{x^{4}}{4} + C = frac{x^{4}ln{x}}{4} - frac{x^{4}}{16} + C]$

Ответ

$[int x^{3}ln{x}dx = frac{x^{4}ln{x}}{4} - frac{x^{4}}{16} + C]$

Задача

Вычислить интеграл:

$[int frac{xarcsin{x}}{sqrt{1 - x^{2}}}dx]$

Решение

Обозначим:

$[u = arcsin{x}, dv = frac{xdx}{sqrt{1 - x^{2}}}, du = frac{dx}{sqrt{1 - x^{2}}}, v = -sqrt{1 - x^{2}}]$

Применяя формулу интегрирования по частям

получаем:

$[int frac{xarcsin{x}}{sqrt{1 - x^{2}}}dx = -sqrt{1 - x^{2}}arcsin{x} - int frac{-sqrt{1 - x^{2}}}{sqrt{1 - x^{2}}}dx]$

$[int frac{xarcsin{x}}{sqrt{1 - x^{2}}}dx = -sqrt{1 - x^{2}}arcsin{x} + x + C]$

Ответ

$[int frac{xarcsin{x}}{sqrt{1 - x^{2}}}dx = -sqrt{1 - x^{2}}arcsin{x} + x + C]$

Задача

Вычислить интеграл:

$[int frac{ln{x}}{x^{2}}dx]$

Решение

Обозначим:

$[u = ln{x}, dv = frac{dx}{x^{2}}, du = frac{dx}{x}, v = -frac{1}{x}]$

Применяя формулу интегрирования по частям

получаем:

$[int frac{ln{x}}{x^{2}}dx = -frac{ln{x}}{x} - int -frac{dx}{x^{2}} = -frac{ln{x}}{x} - frac{1}{x} + C]$

Ответ

$[int frac{ln{x}}{x^{2}}dx = -frac{ln{x}}{x} - frac{1}{x} + C]$

Задача

Вычислить интеграл:

Решение

Обозначим:

Применяя формулу интегрирования по частям

получаем:

Ответ

Источник

Интегрирование по частям

Применение метода интегрирования по частям

Типовые разложения по частям

Интегрирование по частям

Алгоритм решения интегралов функций с использованием метода интегрирования по частям

Примеры решений интегралов функций с использованием метода интегрирования по частям

Вам также может понравиться

Если потерялся карта как можно найти

Жди меня как найти по имени

Как найти дерево гинзо в игре

Добавить комментарий Отменить ответ