Вычислить первообразные функции мы можем не всегда, но задача на дифференцирование может быть решена для любой функции. Именно поэтому единого метода интегрирования, который можно использовать для любых типов вычислений, не существует.
В рамках данного материала мы разберем примеры решения задач, связанных с нахождением неопределенного интеграла, и посмотрим, для каких типов подынтегральных функций подойдет каждый метод.
Метод непосредственного интегрирования
Основной метод вычисления первообразной функции – это непосредственное интегрирование. Это действие основано на свойствах неопределенного интеграла, и для вычислений нам понадобится таблица первообразных. Прочие методы могут лишь помочь привести исходный интеграл к табличному виду.
Вычислите множество первообразных функции f(x)=2x+32·5x+43.
Решение
Для начала изменим вид функции на f(x)=2x+32·5x+43=2x+32·5x+413.
Мы знаем, что интеграл суммы функций будет равен сумме этих интегралов, значит:
∫f(x)dx=∫32·5x+43=2x+32·5x+413dx=∫32·5x+413dx
Выводим за знак интеграла числовой коэффициент:
∫f(x)dx=∫2xdx+∫32(5x+4)13dx==∫2xdx+23·∫(5x+4)13dx
Чтобы найти первый интеграл, нам нужно будет обратиться к таблице первообразных. Берем из нее значение ∫2xdx=2xln 2+C1
Чтобы найти второй интеграл, потребуется таблица первообразных для степенной функции ∫xp·dx=xp+1p+1+C, а также правило ∫fk·x+bdx=1k·F(k·x+b)+C.
Следовательно, ∫f(x)dx=∫2xdx+32·∫5x+413dx==2xln 2+C1+32·320·(5x+4)43+C2==2xln2+940·5x+443+C
У нас получилось следующее:
∫f(x)dx=∫2xdx+32·∫5x+413dx==2xln 2+C1+32·320·(5x+4)43+C2==2xln 2+940·5x+443+C
причем C=C1+32C2
Ответ: ∫f(x)dx=2xln 2+940·5x+443+C
Непосредственному интегрированию с применением таблиц первообразных мы посвятили отдельную статью. Рекомендуем вам ознакомиться с ней.
Метод подстановки
Такой метод интегрирования заключается в выражении подынтегральной функции через новую переменную, введенную специально для этой цели. В итоге мы должны получить табличный вид интеграла или просто менее сложный интеграл.
Этот метод очень полезен, когда нужно интегрировать функции с радикалами или тригонометрические функции.
Вычислите неопределенный интеграл ∫1x2x-9dx.
Решение
Добавим еще одну переменную z=2x-9. Теперь нам нужно выразить x через z:
z2=2x-9⇒x=z2+92⇒dx=dz2+92=z2+92’dz=12·2zdz=zdz
Далее подставляем полученные выражения в исходный интеграл и получаем:
∫dxx2x-9=∫zdzz2+92·z=2∫dzz2+9
Берем таблицу первообразных и узнаем, что 2∫dzz2+9=23arctgz3+C.
Теперь нам нужно вернуться к переменной x и получить ответ:
23arctgz3+C=23arctg2x-93+C
Ответ: ∫1x2x-9dx=23arctg2x-93+C.
Если нам приходится интегрировать функции с иррациональностью вида xm(a+bxn)p, где значения m, n, p являются рациональными числами, то важно правильно составить выражение для введения новой переменной. Подробнее об этом читайте в статье, посвященной интегрированию иррациональных функций.
Как мы говорили выше, метод подстановки удобно использовать, когда требуется интегрировать тригонометрическую функцию. Например, с помощью универсальной подстановки можно привести выражение к дробно рациональному виду.
Этот метод объясняет правило интегрирования ∫f(k·x+b)dx=1k·F(k·x+b)+C.
Добавляем еще одну переменную z=k·x+b. У нас получается следующее:
x=zk-bk⇒dx=dzk-bk=zk-bk’dz=dzk
Теперь берем получившиеся выражения и добавляем их в интеграл, заданный в условии:
∫f(k·x+b)dx=∫f(z)·dzk=1k·∫f(z)dz==1k·Fz+C1=F(z)k+C1k
Если же мы примем C1k=C и вернемся к исходной переменной x, то у нас получится:
F(z)k+C1k=1k·Fkx+b+C
Метод подведения под знак дифференциала
Это метод основывается на преобразовании подынтегрального выражения в функцию вида f(g(x))d(g(x)). После этого мы выполняем подстановку, вводя новую переменную z=g(x), находим для нее первообразную и возвращаемся к исходной переменной.
∫f(g(x))d(g(x))=g(x)=z=∫f(z)d(z)==F(z)+C=z=g(x)=F(g(x))+C
Чтобы быстрее решать задачи с использованием этого метода, держите под рукой таблицу производных в виде дифференциалов и таблицу первообразных, чтобы найти выражение, к которому надо будет приводится подынтегральное выражение.
Разберем задачу, в которой нужно вычислить множество первообразных функции котангенса.
Вычислите неопределенный интеграл ∫ctg xdx.
Решение
Преобразуем исходное выражение под интегралом с помощью основных тригонометрических формул.
ctg xdx=cos sdxsin x
Смотрим в таблицу производных и видим, что числитель можно подвести под знак дифференциала cos x·dx=d(sin x), значит:
ctg xdx=cos xdxsin x=dsin xsin x, т.е. ∫ctg xdx=∫dsin xsin x.
Допустим, что sin x=z, в таком случае ∫dsin xsin x=∫dzz. Согласно таблице первообразных, ∫dzz=lnz+C. Теперь вернемся к исходной переменной ∫dzz=lnz+C=lnsin x+C.
Все решение в кратком виде можно записать так:
∫сtg xdx=∫cos xdxsin x=∫dsin xsin x=sin x=t==∫dtt=lnt+C=t=sin x=lnsin x+C
Ответ: ∫сtg xdx=lnsin x+C
Метод подведения под знак дифференциала очень часто используется на практике, поэтому советуем вам прочесть отдельную статью, посвященную ему.
Метод интегрирования по частям
Этот метод основывается на преобразовании подынтегрального выражения в произведение вида f(x)dx=u(x)·v’xdx=u(x)·d(v(x)), после чего применяется формула ∫u(x)·d(v(x))=u(x)·v(x)-∫v(x)·du(x). Это очень удобный и распространенный метод решения. Иногда частичное интегрирование в одной задаче приходится применять несколько раз до получения нужного результата.
Разберем задачу, в которой нужно вычислить множество первообразных арктангенса.
Вычислите неопределенный интеграл∫arctg(2x)dx.
Решение
Допустим, что u(x)=arctg(2x), d(v(x))=dx, в таком случае:
d(u(x))=u'(x)dx=arctg(2x)’dx=2dx1+4x2v(x)=∫d(v(x))=∫dx=x
Когда мы вычисляем значение функции v(x), прибавлять постоянную произвольную С не следует.
Далее используем формулу интегрирования по частям и получаем:
∫arctg(2x)dx=u(x)·v(x)-∫v(x)d(u(x))==x·arctg(2x)-∫2xdx1+4×2
Получившийся интеграл вычисляем, используя метод подведения под знак дифференциала.
Поскольку ∫arctg(2x)dx=u(x)·v(x)-∫v(x)d(u(x))=x·arctg(2x)-∫2xdx1+4×2, тогда 2xdx=14d(1+4×2).
Значит
∫arctg(2x)dx=x·arctg(2x)-∫2xdx1+4×2==x·arctg(2x)-14ln1+4×2+C1==x·arctg(2x)-14ln1+4×2+C
Ответ: ∫arctg(2x)dx=x·arctg(2x)-14ln1+4×2+C.
Главная сложность применения такого метода – это необходимость выбирать, какую часть брать за дифференциал, а какую – за функцию u(x). В статье, посвященной методу интегрирования по частям, даны некоторые советы по этому вопросу, с которыми следует ознакомиться.
Если нам требуется найти множество первообразных дробно рациональной функции, то нужно сначала представить подынтегральную функцию в виде суммы простейших дробей, а потом интегрировать получившиеся дроби. Подробнее см. статью об интегрировании простейших дробей.
Если мы интегрируем степенное выражение вида sin7x·dx или dx(x2+a2)8, то нам будут полезны рекуррентные формулы, которые могут постепенно понижать степень. Они выводятся с помощью последовательного многократного интегрирования по частям. Советуем прочитать статью «Интегрирование с помощью рекуррентных формул.
Подведем итоги. Для решения задач очень важно знать метод непосредственного интегрирования. Другие методы (подведение под знак дифференциала, подстановка, интегрирование по частям) также позволяют упростить интеграл и привести его к табличному виду.
Интегрирование подстановкой (внесение под знак дифференциала). Первая часть.
Сначала немного поговорим о постановке задачи в общем виде, а затем перейдём к примерам интегрирования подстановкой. Допустим, в нас есть некий интеграл $int g(x) ; dx$. Однако в таблице интегралов нужной формулы нет, да и разбить заданный интеграл на несколько табличных не удаётся (т.е. непосредственное интегрирование отпадает). Однако задача будет решена, если нам удастся найти некую подстановку $u=varphi(x)$, которая сведёт наш интеграл $int g(x) ; dx$ к какому-либо табличному интегралу $int f(u) ; du=F(u)+C$. После применения формулы $int f(u) ; du=F(u)+C$ нам останется только вернуть обратно переменную $x$. Формально это можно записать так:
$$int g(x) ; dx=|u=varphi(x)|=int f(u) ; du=F(u)+C=F(varphi(x))+C.$$
Проблема в том, как выбрать такую подстановку $u$. Для этого понадобится знание, во-первых, таблицы производных и умение её применять для дифференцирования сложных функций, а во-вторых, таблицы неопределенных интегралов. Кроме того, нам будет крайне необходима формула, которую я запишу ниже. Если $y=f(x)$, то:
$$
begin{equation}
dy=y’dx
end{equation}
$$
Т.е. дифференциал некоторой функции равен производной этой функции, умноженной на дифференциал независимой переменной. Это правило очень важно, и именно оно позволит применять метод подстановки. Здесь же укажем пару частных случаев, которые получаются из формулы (1). Пусть $y=x+C$, где $C$ – некая константа (число, попросту говоря). Тогда, подставляя в формулу (1) вместо $y$ выражение $x+C$, получим следующее:
$$ d(x+C)=(x+C)’ dx $$
Так как $(x+C)’=x’+C’=1+0=1$, то указанная выше формула станет такой:
$$ d(x+C)=(x+C)’ dx=1cdot dx=dx.$$
Запишем полученный результат отдельно, т.е.
$$
begin{equation}
dx=d(x+C)
end{equation}
$$
Полученная формула означает, что прибавление константы под дифференциалом не изменяет оный дифференциал, т.е. $dx=d(x+10)$, $dx=d(x-587)$ и так далее.
Рассмотрим еще один частный случай для формулы (1). Пусть $y=Cx$, где $C$, опять-таки, является некоторой константой. Найдем дифференциал этой функции, подставляя в формулу (1) выражение $Cx$ вместо $y$:
$$ d(Cx)=(Cx)’dx $$
Так как $(Cx)’=Ccdot (x)’=Ccdot 1=C$, то записанная выше формула $d(Cx)=(Cx)’dx$ станет такой: $d(Cx)=Cdx$. Если разделить обе части этой формулы на $C$ (при условии $Cneq 0$), то получим $frac{d(Cx)}{C}=dx$. Этот результат можно переписать в несколько иной форме:
$$
begin{equation}
dx=frac{1}{C}cdot d(Cx);;;(Cneq 0)
end{equation}
$$
Полученная формула говорит о том, что умножение выражения под дифференциалом на некую ненулевую константу требует введения соответствующего множителя, компенсирующего такое домножение. Например, $dx=frac{1}{5} d(5x)$, $dx=-frac{1}{19} d(-19x)$.
В примерах №1 и №2 формулы (2) и (3) будут рассмотрены подробно.
Замечание относительно формул
В данной теме будут использоваться как формулы 1-3, так и формулы из таблицы неопределённых интегралов, которые тоже имеют свои номера. Чтобы не было путаницы, условимся о следующем: если в теме встречается текст “используем формулу №1”, то означает он буквально следующее “используем формулу №1, расположенную на этой странице“. Если нам понадобится формула из таблицы интегралов, то это будем оговаривать каждый раз отдельно. Например, так: “используем формулу №1 из таблицы интегралов”.
И ещё одно небольшое примечание
Перед началом работы с примерами рекомендуется ознакомиться с материалом, изложенным в предыдущих темах, посвящённых понятию неопределённого интеграла и непосредственному интегрированию. Изложение материала в этой теме опирается на сведения, указанные в упомянутых темах.
Пример №1
Найти $int frac{dx}{x+4}$.
Решение
Если мы обратимся к таблице неопределённых интегралов, то не сможем найти формулу, которая точно соответствует интегралу $int frac{dx}{x+4}$. Наиболее близка к этому интегралу формула №2 таблицы интегралов, т.е. $int frac{du}{u}=ln|u|+C$. Проблема в следующем: формула $int frac{du}{u}=ln|u|+C$ предполагает, что в интеграле $int frac{du}{u}$ выражения в знаменателе и под дифференциалом должны быть одинаковы (и там и там расположена одна буква $u$). В нашем случае в $int frac{dx}{x+4}$ под дифференциалом находится буква $x$, а в знаменателе – выражение $x+4$, т.е. налицо явное несоответствие табличной формуле. Попробуем “подогнать” наш интеграл под табличный. Что произойдёт, если под дифференциал вместо $x$ подставить $x+4$? Для ответа на этот вопрос применим формулу №1, подставив в неё выражение $x+4$ вместо $y$:
$$ d(x+4)=(x+4)’dx $$
Так как $(x+4)’=x’+(4)’=1+0=1$, то равенство $ d(x+4)=(x+4)’dx $ станет таким:
$$ d(x+4)=1cdot dx=dx $$
Итак, $dx=d(x+4)$. Честно говоря, этот же результат можно было получить, просто подставив в формулу №2 вместо константы $C$ число $4$. В дальнейшем мы так и будем делать, а на первый раз разобрали процедуру получения равенства $dx=d(x+4)$ подробно. Но что даёт нам равенство $dx=d(x+4)$?
А даёт оно нам следующий вывод: если $dx=d(x+4)$, то в интеграл $int frac{dx}{x+4}$ вместо $dx$ можно подставить $d(x+4)$, причём интеграл от этого не изменится:
$$ int frac{dx}{x+4}=int frac{d(x+4)}{x+4}$$
Сделали мы это преобразование лишь для того, чтобы полученный интеграл стал полностью соответствовать табличной формуле $int frac{du}{u}=ln|u|+C$. Чтобы такое соответствие стало совсем явным, заменим выражение $x+4$ буквой $u$ (т.е. сделаем подстановку $u=x+4$):
$$ int frac{dx}{x+4}=int frac{d(x+4)}{x+4}=|u=x+4|=int frac{du}{u}=ln|u|+C.$$
По сути, задача уже решена. Осталось лишь вернуть переменную $x$. Вспоминая, что $u=x+4$, получим: $ln|u|+C=ln|x+4|+C$. Полное решение без пояснений выглядит так:
$$ int frac{dx}{x+4}=int frac{d(x+4)}{x+4}=|u=x+4|=int frac{du}{u}=ln|u|+C=ln|x+4|+C.$$
Ответ: $int frac{dx}{x+4}=ln|x+4|+C$.
Пример №2
Найти $int e^{3x} dx$.
Решение
Если мы обратимся к таблице неопределённых интегралов, то не сможем найти формулу, которая точно соответствует интегралу $int e^{3x} dx$. Наиболее близка к этому интегралу формула №4 из таблицы интегралов, т.е. $int e^u du=e^u+C$. Проблема в следующем: формула $int e^u du=e^u+C$ предполагает, что в интеграле $int e^u du$ выражения в степени числа $e$ и под дифференциалом должны быть одинаковы (и там и там расположена одна буква $u$). В нашем случае в $int e^{3x} dx$ под дифференциалом находится буква $x$, а в степени числа $e$ – выражение $3x$, т.е. налицо явное несоответствие табличной формуле. Попробуем “подогнать” наш интеграл под табличный. Что произойдёт, если под дифференциал вместо $x$ подставить $3x$? Для ответа на этот вопрос применим формулу №1, подставив в неё выражение $3x$ вместо $y$:
$$ d(3x)=(3x)’dx $$
Так как $(3x)’=3cdot (x)’=3cdot 1=3$, то равенство $d(3x)=(3x)’dx$ станет таким:
$$ d(3x)=3dx $$
Разделив обе части полученного равенства на $3$, будем иметь: $frac{d(3x)}{3}=dx$, т.е. $dx=frac{1}{3}cdot d(3x)$. Вообще-то, равенство $dx=frac{1}{3}cdot d(3x)$ можно было получить, просто подставив в формулу №3 вместо константы $C$ число $3$. В дальнейшем мы так и будем делать, а на первый раз разобрали процедуру получения равенства $dx=frac{1}{3}cdot d(3x)$ подробно.
Что нам дало полученное равенство $dx=frac{1}{3}cdot d(3x)$? Оно означает, что в интеграл $int e^{3x} dx$ вместо $dx$ можно подставить $frac{1}{3}cdot d(3x)$, причём интеграл от этого не изменится:
$$ int e^{3x} dx= int e^{3x} cdotfrac{1}{3} d(3x) $$
Вынесем константу $frac{1}{3}$ за знак интеграла и заменим выражение $3x$ буквой $u$ (т.е. сделаем подстановку $u=3x$), после чего применим табличную формулу $int e^u du=e^u+C$:
$$ int e^{3x} dx= int e^{3x} cdotfrac{1}{3} d(3x)=frac{1}{3}cdot int e^{3x} d(3x)=|u=3x|=frac{1}{3}cdotint e^u du=frac{1}{3}cdot e^u+C.$$
Как и в предыдущем примере, нужно вернуть обратно исходную переменную $x$. Так как $u=3x$, то $frac{1}{3}cdot e^u+C=frac{1}{3}cdot e^{3x}+C$. Полное решение без комментариев выглядит так:
$$ int e^{3x} dx= int e^{3x} cdotfrac{1}{3} d(3x)=frac{1}{3}cdot int e^{3x} d(3x)=|u=3x|=frac{1}{3}cdotint e^u du=frac{1}{3}cdot e^u+C=frac{1}{3}cdot e^{3x}+C.$$
Ответ: $ int e^{3x} dx= frac{1}{3}cdot e^{3x}+C$.
Пример №3
Найти $int (3x+2)^2 dx$.
Решение
Для нахождения данного интеграла применим два способа. Первый способ состоит в раскрытии скобок и непосредственном интегрировании. Второй способ заключается в применении метода подстановки.
Первый способ
Так как $(3x+2)^2=9x^2+12x+4$, то $int (3x+2)^2 dx=int (9x^2+12x+4)dx$. Представляя интеграл $int (9x^2+12x+4)dx$ в виде суммы трёх интегралов и вынося константы за знаки соответствующих интегралов, получим:
$$
int (9x^2+12x+4)dx=int 9x^2 dx+int 12x dx+int 4 dx=9cdot int x^2 dx+12cdot int x dx+4cdot int 1 dx
$$
Чтобы найти $int x^2 dx$ подставим $u=x$ и $alpha=2$ в формулу №1 таблицы интегралов: $int x^2 dx=frac{x^{2+1}}{2+1}+C=frac{x^3}{3}+C$. Аналогично, подставляя $u=x$ и $alpha=1$ в ту же формулу из таблицы, будем иметь: $int x^1 dx=frac{x^{1+1}}{1+1}+C=frac{x^2}{2}+C$. Так как $int 1 dx=x+C$, то:
$$
9cdot int x^2 dx+12cdot int x dx+4cdot int 1 dx=9cdotfrac{x^3}{3}+12cdot frac{x^2}{2}+4cdot x+C=3x^3+6x^2+4x+C.
$$
Полное решение без пояснений таково:
$$
int (9x^2+12x+4)dx=int 9x^2 dx+int 12x dx+int 4 dx=9cdot int x^2 dx+12cdot int x dx+4cdot int 1 dx=\
=9cdotfrac{x^3}{3}+12cdot frac{x^2}{2}+4cdot x+C=3x^3+6x^2+4x+C.
$$
Второй способ
Скобки раскрывать не будем. Попробуем сделать так, чтобы под дифференциалом вместо $x$ появилось выражение $3x+2$. Это позволит ввести новую переменную и применить табличную формулу. Нам нужно, чтобы под дифференциалом возник множитель $3$, посему подставляя в формулу №3 значение $C=3$, получим $d(x)=frac{1}{3}d(3x)$. Кроме того, под дифференциалом не хватает слагаемого $2$. Согласно формуле №2 прибавление константы под знаком дифференциала не меняет оный дифференциал, т.е. $frac{1}{3}d(3x)=frac{1}{3}d(3x+2)$. Из условий $d(x)=frac{1}{3}d(3x)$ и $frac{1}{3}d(3x)=frac{1}{3}d(3x+2)$ имеем: $dx=frac{1}{3}d(3x+2)$.
Отмечу, что равенство $dx=frac{1}{3}d(3x+2)$ можно получить и иным способом:
$$
d(3x+2)=(3x+2)’dx=((3x)’+(2)’)dx=(3cdot x’+0)dx=3cdot 1 dx=3dx;\
dx=frac{1}{3}d(3x+2).
$$
Используем полученное равенство $dx=frac{1}{3}d(3x+2)$, подставив в интеграл $int (3x+2)^2 dx$ выражение $frac{1}{3}d(3x+2)$ вместо $dx$. Константу $frac{1}{3}$ вынесем за знак получившегося интеграла:
$$
int (3x+2)^2 dx=int (3x+2)^2 cdot frac{1}{3}d(3x+2)=frac{1}{3}cdot int (3x+2)^2 d(3x+2).
$$
Дальнейшее решение состоит в осуществлении подстановки $u=3x+2$ и применении формулы №1 из таблицы интегралов:
$$
frac{1}{3}cdot int (3x+2)^2 d(3x+2)=|u=3x+2|=frac{1}{3}cdot int u^2 du=frac{1}{3}cdot frac{u^{2+1}}{2+1}+C=frac{u^3}{9}+C.
$$
Возвращая вместо $u$ выражение $3x+2$, получим:
$$
frac{u^3}{9}+C=frac{(3x+2)^3}{9}+C.
$$
Полное решение без пояснений таково:
$$
int (3x+2)^2 dx=frac{1}{3}cdot int (3x+2)^2 d(3x+2)=|u=3x+2|=\
=frac{1}{3}cdot int u^2 du=frac{u^3}{9}+C=frac{(3x+2)^3}{9}+C.
$$
Предвижу пару вопросов, поэтому попробую сформулировать их дать ответы.
Вопрос №1
Что-то тут не сходится. Когда мы решали первым способом, что получили, что $int (9x^2+12x+4)dx=3x^3+6x^2+4x+C$. При решении вторым путём, ответ стал таким: $int (3x+2)^2 dx=frac{(3x+2)^3}{9}+C$. Однако перейти от второго ответа к первому не получается! Если раскрыть скобки, то получаем следующее:
$$
frac{(3x+2)^3}{9}+C=frac{27x^3+54x^2+36x+8}{9}+C=frac{27x^3}{9}+frac{54x^2}{9}+frac{36x}{9}+frac{8}{9}+C=3x^3+6x^2+4x+frac{8}{9}+C.
$$
Ответы не совпадают! Откуда взялась лишняя дробь $frac{8}{9}$?
Ответ
Этот вопрос говорит о том, что Вам стоит обратиться к предыдущим темам. Почитать тему про понятие неопределённого интеграла (уделив особое внимание вопросу №2 в конце страницы) и непосредственному интегрированию (стоит обратить внимание на вопрос №4). В указанных темах этот вопрос освещается подробно. Если уж совсем коротко, то интегральная константа $C$ может быть представлена в разных формах. Например, в нашем случае переобозначив $C_1=C+frac{8}{9}$, получим:
$$
3x^3+6x^2+4x+frac{8}{9}+C=3x^3+6x^2+4x+C_1.
$$
Посему никакого противоречия нет, ответ может быть записан как в форме $3x^3+6x^2+4x+C$, так и в виде $frac{(3x+2)^3}{9}+C$.
Вопрос №2
Зачем было решать вторым способом? Это же лишнее усложнение! Зачем применять кучу лишних формул, чтобы найти ответ, который первым способом получается в пару действий? Всего-то и нужно было, что скобки раскрыть, применив школьную формулу.
Ответ
Ну, во-первых, не такое уж это и усложнение. Когда вы разберётесь в методе подстановки, то решения подобных примеров станете делать в одну строчку:
$$int (3x+2)^2 dx=frac{1}{3}cdot int (3x+2)^2 d(3x+2)=frac{(3x+2)^3}{9}+C.$$
Однако давайте взглянем на этот пример по-иному. Представьте, что нужно вычислить не $int (3x+2)^2 dx$, а $int (3x+2)^{200} dx$. При решении вторым способом придётся лишь чуток подправить степени и ответ будет готов:
$$
int (3x+2)^{200} dx=frac{1}{3}cdot int (3x+2)^{200} d(3x+2)=|u=3x+2|=\
=frac{1}{3}cdot int u^{200} du=frac{u^{201}}{603}+C=frac{(3x+2)^{201}}{603}+C.
$$
А теперь представьте, что этот же интеграл $int (3x+2)^{200} dx$ требуется взять первым способом. Для начала нужно будет раскрыть скобку $(3x+2)^{200}$, получив при этом сумму в двести одно слагаемое! А потом каждое слагаемое ещё и проинтегрировать придётся. Поэтому вывод тут такой: для больших степеней метод непосредственного интегрирования не годится. Второй способ, несмотря на кажущуюся сложность, более практичен.
Пример №4
Найти $int sin2x dx$.
Решение
Решение этого примера проведём тремя различными способами.
Первый способ
Заглянем в таблицу интегралов. Ниболее близка к нашему примеру формула №5 из этой таблицы, т.е. $int sin u du=-cos u+C$. Чтобы подогнать интеграл $int sin2x dx$ под вид $int sin u du$, воспользуемся формулой №3, внеся множитель $2$ под знак дифференциала. Собственно, мы это делали уже в примере №2, так что обойдёмся без подробных комментариев:
$$
int sin 2x dx=left|dx=frac{1}{2}cdot d(2x) right|=int sin 2x cdotfrac{1}{2}d(2x)=\
=frac{1}{2} int sin 2x d(2x)=|u=2x|=frac{1}{2} int sin u du=-frac{1}{2}cos u+C=-frac{1}{2}cos 2x+C.
$$
Ответ: $int sin2x dx=-frac{1}{2}cos 2x+C$.
Второй способ
Для решения вторым способом применим простую тригонометрическую формулу: $sin 2x=2sin xcos x$. Подставим вместо $sin 2x$ выражение $2 sin x cos x$, при этом константу $2$ вынесем за знак интеграла:
$$
int sin 2x dx=int 2 sin xcos x dx=2cdotint sin xcos x dx
$$
Какова цель такого преобразования? В таблице интеграла $int sin xcos x dx$ нет, но мы можем немного препобразовать $int sin xcos x dx$, чтобы он стал больше походить на табличный. Для этого найдем $d(cos x)$, используя формулу №1. Подставим в упомянутую формулу $cos x$ вместо $y$:
$$
d(cos x)=(cos x)’dx=-sin x dx.
$$
Так как $d(cos x)=-sin x dx$, то $sin x dx=-d(cos x)$. Так как $sin x dx=-d(cos x)$, то мы можем в $int sin xcos x dx$ вместо $sin x dx$ подставить $-d(cos x)$. Значение интеграла при этом не изменится:
$$
2cdotint sin xcos x dx=2cdotint cos x cdot (-d(cos x))=-2intcos x d(cos x)
$$
Говоря иными словами, мы внесли под дифференциал $cos x$. Теперь, сделав подстановку $u=cos x$, мы сможем применить формулу №1 из таблицы интегралов:
$$
-2intcos x d(cos x)=|u=cos x|=-2int u du=-2cdot frac{u^2}{2}+C=-u^2+C=-cos^2x+C.
$$
Ответ получен. Вообще, можно не вводить букву $u$. Когда вы приобретёте достаточный навык в решении подобного рода интегралов, то необходимость в дополнительных обозначениях отпадёт. Полное решение без пояснений таково:
$$
int sin 2x dx=2cdotint sin xcos x dx=|sin x dx=-d(cos x)|=-2intcos x d(cos x)=|u=cos x|=\
=-2int u du=-2cdot frac{u^2}{2}+C=-u^2+C=-cos^2x+C.
$$
Ответ: $int sin2x dx=-cos^2x+C$.
Третий способ
Для решения третьим способом применим ту же тригонометрическую формулу: $sin 2x=2sin xcos x$. Подставим вместо $sin 2x$ выражение $2 sin x cos x$, при этом константу $2$ вынесем за знак интеграла:
$$
int sin 2x dx=int 2 sin xcos x dx=2cdotint sin xcos x dx
$$
Найдем $d(sin x)$, используя формулу №1. Подставим в упомянутую формулу $sin x$ вместо $y$:
$$
d(sin x)=(sin x)’dx=cos x dx.
$$
Итак, $d(sin x)=cos x dx$. Из полученного равенства следует, что мы можем в $int sin xcos x dx$ вместо $cos x dx$ подставить $d(sin x)$. Значение интеграла при этом не изменится:
$$
2cdotint sin xcos x dx=2cdotint sin x cdot d(sin x)
$$
Говоря иными словами, мы внесли под дифференциал $sin x$. Теперь, сделав подстановку $u=sin x$, мы сможем применить формулу №1 из таблицы интегралов:
$$
2intsin x d(sin x)=|u=sin x|=2int u du=2cdot frac{u^2}{2}+C=u^2+C=sin^2x+C.
$$
Ответ получен. Полное решение без пояснений имеет вид:
$$
int sin 2x dx=2cdotint sin xcos x dx=|cos x dx=d(sin x)|=2cdotint sin x cdot d(sin x)=|u=sin x|=\
=2int u du=2cdot frac{u^2}{2}+C=u^2+C=sin^2x+C.
$$
Ответ: $int sin2x dx=sin^2x+C$.
Возможно, что после прочтения этого примера, особенно трёх различных (на первый взгляд) ответов, возникнет вопрос. Рассмотрим его.
Вопрос №3
Погодите. Ответы должны совпадать, но они отличаются! В примере №3 различие было всего-то в константе $frac{8}{9}$, но здесь даже внешне ответы не похожи: $-frac{1}{2}cos 2x+C$, $-cos^2x+C$, $sin^2x+C$. Неужели всё дело опять в интегральной константе $C$?
Ответ
Да, дело именно в этой константе. Давайте сведём все ответы к одной форме, после чего это различие в константах станет совсем явным. Начнём с $-frac{1}{2}cos 2x+C$. Используем простое тригонометрическое равенство: $cos 2x=1-2sin^2 x$. Тогда выражение $-frac{1}{2}cos 2x+C$ станет таким:
$$
-frac{1}{2}cos 2x+C=-frac{1}{2}cdot(1-2sin^2 x)+C=-frac{1}{2}+frac{1}{2}cdot 2sin^2x+C=sin^2 x+C-frac{1}{2}.
$$
Теперь поработаем со вторым ответом, т.е. $-cos^2x+C$. Так как $cos^2 x=1-sin^2x$, то:
$$
-cos^2x+C=-(1-sin^2x)+C=-1+sin^2x+C=sin^2x+C-1
$$
Три ответа, которые мы получили в примере №4, стали такими: $sin^2 x+C-frac{1}{2}$, $sin^2x+C-1$, $sin^2x+C$. Полагаю, теперь видно, что отличаются они друг от друга лишь некоторым числом. Т.е. дело опять оказалось в интегральной константе. Как видите, небольшое различие в интегральной константе способно, в принципе, сильно изменить внешний вид ответа, – но от этого ответ не перестанет быть правильным. К чему я веду: если в сборнике задач вы увидите ответ, не совпадающий с вашим, то это вовсе не означает, что ваш ответ неверен. Возможно, что вы просто пришли к ответу иным способом, чем предполагал автор задачи. А убедиться в правильности ответа поможет проверка, основанная на определении неопределённого интеграла. Например, если интеграл $int sin2x dx=-frac{1}{2}cos 2x+C$ найден верно, то должно выполняться равенство $left( -frac{1}{2}cos 2x+Cright)’=sin 2x$. Вот и проверим, правда ли, что производная от $left( -frac{1}{2}cos 2x+Cright)$ равна подынтегральной функции $sin 2x$:
$$
left( -frac{1}{2}cos 2x+Cright)’=left( -frac{1}{2}cos 2xright)’+C’=-frac{1}{2}cdot(cos 2x)’+0=\
=-frac{1}{2}cdot (-sin 2x)cdot (2x)’=-frac{1}{2}cdot (-sin 2x)cdot 2=sin 2x.
$$
Проверка пройдена успешно. Равенство $left( -frac{1}{2}cos 2x+Cright)’=sin 2x$ выполнено, поэтому формула $int sin2x dx=-frac{1}{2}cos 2x+C$ верна. В примере №5 также осуществим проверку результата, дабы убедиться в его правильности. Наличие проверки не является обязательным, хотя в некоторых типовых расчётах и контрольных работах требование проверять результат присутствует.
Метод замены переменной или метод подстановки. Этот метод заключается во введении новой переменной интегрирования (то есть делается подстановка). При этом заданный интеграл приводится к новому интегралу, который является табличным или с помощью преобразований его можно свести к табличному.
|
Пусть требуется вычислить интеграл |
. Сделаем подстановку |
. |
||
|
Тогда |
и интеграл принимает вид: |
∫ ( ) |
, |
|
|
или |
||||
|
, т.е в подынтегральном выражении должна находиться некоторая |
||||
|
функция |
. После решения интеграла |
делаем |
||
|
∫ ( ) и её производная |
обратную подстановку t = x.
Общее правило: за t обозначаем саму функцию (а не её производную).
Находим dt следующим образом:
1)записываем формулу подстановки: ϕ(t) = f(x);
2)заключаем функции в скобки со знаком производной и домножаем на dx и dt
соответственно: (ϕ(t))’dt =(f(x))’dx;
3)берем производные и выражаем dx через dt.
Например подстановка: t2 = (2x-1) → ( t2)’ dt = (2x-1)’dx → 2tdt = 2dx →
→ dx = tdt Запомните это.
Пример 15.
Найти интеграл 
Сделаем замену переменной: 
, далее приведем интеграл к табличному виду и решим
его. В конце решения делаем обратную замену.
Пример 16
Найти интеграл 
.
Упростим подынтегральную функцию, а потом сделаем замену переменной: 
Пример 17
Найти неопределенный интеграл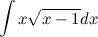 
Введем замену 
Заменим интеграл суммы на сумму интегралов и вынесем постоянные коэффициенты.
Полученные интегралы находим как интегралы от степенной функции:
Делая обратную замену, окончательно получим
Пример 18
Найти неопределенный интеграл 
Введем замену 
и полученный интеграл находим как интеграл от степенной функции:
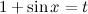
Сделаем обратную замену
Пример 19
Найти неопределенный интеграл 
Введем замену и полученный интеграл находим как интеграл от обратной функции:
Выполним обратную замену
Пример 20
Найти неопределенный интеграл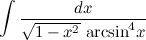 
Введем замену и полученный интеграл находим как интеграл от степенной функции:
Выполним обратную замену и окончательно получим:
Точное нахождение первообразной (или интеграла) произвольных функций — процедура более сложная, чем «дифференцирование», то есть нахождение производной. Зачастую, выразить интеграл в элементарных функциях невозможно.
Непосредственное интегрирование[править | править код]
Непосредственное интегрирование — метод, при котором интеграл, путём тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла, приводится к одному или нескольким интегралам элементарных функций.
Метод замены переменной (метод подстановки)[править | править код]
Метод интегрирования подстановкой заключается в введении новой переменной интегрирования. При этом, заданный интеграл приводится к интегралу элементарной функции, или к нему сводящемуся.
Общих методов подбора подстановок не существует — умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 
Сделаем подстановку 
где 
— функция, имеющая непрерывную производную.
Тогда 
и на основании свойства инвариантности формулы интегрирования
неопределенного интеграла получаем формулу интегрирования подстановкой:
Этот метод также называют методом подведения под знак дифференциала и записывают следующим образом: функция вида 
интегрируется следующим образом:
Пример: Найти 
Решение: Пусть 
, тогда 
.
Вообще различные подстановки часто используются для вычисления интегралов, содержащих радикалы. Другим примером может служить подстановка Абеля
применяемая для вычисления интегралов вида
где m натуральное число[1]. Иногда применяются подстановки Эйлера. См. также об интегрировании дифференциального бинома ниже.
Интегрирование некоторых тригонометрических функций[править | править код]
Пусть требуется проинтегрировать выражение 
, где R является рациональной функцией от двух переменных. Такой интеграл удобно вычислять методом подстановки:
Частный случай этого правила:
Выбор подстановки производится следующим образом:
Пример: 
.
Решение: Пусть 
; тогда 
и 
, где C — любая константа.
Интегрирование дифференциального бинома[править | править код]
Для вычисления интеграла от дифференциального бинома
где a, b — действительные числа, a m, n, p — рациональные числа, также применяется метод подстановки в следующих трёх случаях:
В остальных случаях, как показал П. Л. Чебышёв в 1853 году, этот интеграл не выражается в элементарных функциях[4].
Интегрирование по частям[править | править код]
Интегрирование по частям — применение следующей формулы для интегрирования:
Или:
В частности, с помощью n-кратного применения этой формулы находится интеграл
где 
— многочлен 
-й степени.
Пример: Найти интеграл 
.
Решение: Чтобы найти данный интеграл применим метод интегрирования по частям, для этого будем полагать, что 
и 
, тогда согласно формуле интегрирования по частям получаем 
Интегрирование рациональных дробей[править | править код]
Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.
Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.
Всякую правильную рациональную дробь 
, знаменатель которой разложен на множители
можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:
где 
— некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.
Пример: 
Решение: Разложим подынтегральное выражение на простейшие дроби:
Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями:
Следовательно
Тогда
Теперь легко вычислить исходный интеграл
Интегрирование элементарных функций[править | править код]
Для нахождения первообразной от элементарной функций в виде элементарной функции (или определения того, что первообразная не является элементарной) был разработан алгоритм Риша. Он полностью или частично реализован во многих системах компьютерной алгебры.
См. также[править | править код]
- Символьное интегрирование
- Формулы Фруллани
- Универсальная тригонометрическая подстановка
- Подстановки Эйлера
Примечания[править | править код]
- ↑ Виноградова И. А., Олехник С. Н., Садовничий В. А. Задачи и упражнения по математическому анализу. Книга 1. — 2-е изд. — М.: Высшая школа, 2000. — С. 213.
- ↑ 1 2 См. обоснование в книге: И. М. Уваренков, М. З. Маллер. Курс математического анализа. — М.: Просвещение, 1966. — Т. 1. — С. 459-460.
- ↑ См. обоснование в книге: В. А. Ильин, Э. Г. Позняк. Основы математического анализа. — 2-е изд. — М.: Наука, 1967. — С. 219. — (Курс высшей математики и математической физики).
- ↑ P. Tchebichef. Sur l’intégration des différentielles irrationnelles (фр.) // Journal de mathématiques pures et appliquées (англ.) (рус. : magazine. — 1853. — Vol. XVIII. — P. 87—111.
Ссылки[править | править код]
- Wolfram Integrator — вычисление интегралов онлайн с помощью системы Mathematica
- Mathematical Assistant on Web — символьные вычисления онлайн
- Онлайн Калькулятор Интегралов
Содержание:
- Примеры решения интегралов данным методом
- Следствия из метода интегрирования заменой переменной
Суть данного метода заключается в том, что в рассмотрение вводится новая переменная интегрирования или, что тоже
самое, делается подстановка. После этого заданный в условии интеграл сводится либо к
табличному интегралу, либо к нему сводящемуся.
Если в неопределенном интеграле $int f(x) d x$ сделать
подстановку $x=phi(t)$, где функция
$phi(t)$ – функция с непрерывной первой производной, то тогда
$d x=d(phi(t))=phi^{prime}(t) d t$ и согласно
свойству 6 неопределенного интеграла имеем, что:
$int f(x) d x=int f(phi(t)) phi^{prime}(t) d t$
Эта формула называется формулой замены переменной в неопределенном интеграле.
Замечание
После нахождения интеграла по новой переменной $t$
необходимо вернуться к первоначальной переменной $x$.
Замечание
В некоторых случаях целесообразно делать подстановку $t=g(x)$, тогда
$int f(g(x)) g^{prime}(x) d x=int f(t) d t$
Примеры решения интегралов данным методом
Пример
Задание. Найти интеграл
$int x e^{x^{2}} d x$
Решение. Сделаем замену переменной: $x^{2}=t$,
далее приведем интеграл к табличному виду и решим его. В конце решения делаем обратную замену.
$$begin{array}{c||l||l}
& x^{2}=t & \
& dleft(x^{2}right)=d t & \
int x e^{x^{2}} d x=int e^{x^{2}} cdot x d x & 2 x d x=d t & =int e^{t} cdot frac{d t}{2}= \
& x d x=frac{d t}{2}
end{array}$$
$=frac{1}{2} int e^{t} d t=frac{1}{2} cdot e^{t}+C=frac{e^{x^{2}}}{2}+C$
Ответ. $int x e^{x^{2}} d x=frac{e^{x^{2}}}{2}+C$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти интеграл
$int frac{x^{2}+x ln x}{x^{2}} d x$
Решение. Упростим подынтегральную функцию, а потом сделаем замену переменной:
$ln x=t$
$int frac{x^{2}+x ln x}{x^{2}} d x=intleft(frac{x^{2}}{x^{2}}+frac{x ln x}{x^{2}}right) d x=intleft(1+frac{ln x}{x}right) d x=$
$$=int d x+int frac{ln x}{x} d xleft|begin{array}{l}
ln x=t \
frac{d x}{x}=d t
end{array}right|=x+int t d t=x+frac{t^{2}}{2}+C=$$
$=x+frac{(ln x)^{2}}{2}+C=x+frac{ln ^{2} x}{2}+C$
Ответ. $int frac{x^{2}+x ln x}{x^{2}} d x=x+frac{ln ^{2} x}{2}+C$
Следствия из метода интегрирования заменой переменной
Используя метод подстановки, можно получить следующие соотношения для некоторых интегралов,
которые рационально использовать уже в конечном виде, а не каждый раз производить вычисления:
$int frac{d x}{x+a}left|_{d x=t}^{x+a=t}right|=int frac{d t}{t}=ln |t|+C=ln |x+a|+C$
то есть
$int frac{d x}{x+a}=ln |x+a|+C$
Аналогично можно показать, что
$int e^{k x+b} d x=frac{1}{k} e^{k x+b}+C$
$int cos (k x+b) d x=frac{1}{k} sin (k x+b)+C$
$int sin (k x+b) d x=-frac{1}{k} cos (k x+b)+C$
Подобные соотношения можно было вывести и с использованием
метода внесения под дифференциал.
Читать дальше: метод интегрирования по частям.
