Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Электромагнитные волны могут вызывать разные эффекты, например, вызывать отклонение стрелки гальванометра, который соединен с детектором, накаливать нить лампы, включенной в диполь. Это все говорит о том, что электромагнитные волны переносят энергию.
К энергетическим характеристика электромагнитной волны отнесем:
- Энергию волны.
- Объемную плотность энергии.
- Вектор потока электромагнитной энергии.
- Интенсивность.
Энергия электромагнитных волн
Предположим, что в поле электромагнитной волны расположена площадка $S$ (рис.1).
Рисунок 1. Площадка, расположенная в поле электромагнитной волны. Автор24 — интернет-биржа студенческих работ

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определим, какая энергия ($W$) переносится электромагнитной волной сквозь эту площадку за малое время ∆t. Построим на основании площадки $S$ параллелепипед, с ребрами параллельными скорости перемещения волны $vec{v}$. Пусть длины ребер параллелепипеда будут равны $vDelta{}t$. Объем выделенного параллелепипеда будет:
$Delta{}V=SvDelta{}tcos{alpha{} left(1right),}$
где α – угол между нормалью к площадке $S$ и направлением вектора скорости движения волны. Поскольку за время $Delta{}t$ волна пробегает расстояние $vDelta{}t$, то через выделенную нами площадь пройдет искомая нами энергия $W$, которая заключена внутри параллелепипеда.
$W=wDelta{}V=wSvDelta{}tcos{alpha{} left(2right),}$
где $w $ – объемная плотность энергии.
Электромагнитная волна имеет две составляющие, которые обладают энергией – это переменное электрическое и магнитное поля, поэтому объемную плотность нашей волны мы запишем как:
$w=frac{epsilon{}{epsilon{}}_0}{2}E^2+frac{mu{}{mu{}}_0}{2}H^2left(3right).$
«Интенсивность электромагнитой волны» 👇
Мы знаем, что напряженности полей в электромагнитной волне связывает уравнение:
$sqrt{epsilon{}{epsilon{}}_0}E=sqrt{mu{}{mu{}}_0}Hleft(4right),$
откуда следует, что мы можем написать:
$w=epsilon{}{epsilon{}}_0E^2=mu{}{mu{}}_0H^2=sqrt{epsilon{}mu{}}sqrt{{epsilon{}}_0{mu{}}_0}EHleft(5right).$
Принимая во внимание, что скорость распространения электромагнитной волны в веществе можно представить как:
$v=frac{1}{sqrt{epsilon{}mu{}{epsilon{}}_0{mu{}}_0}}left(6right),$
учитывая формулу (5) из выражения (2) следует, что искомая энергия равна:
$W=sqrt{epsilon{}mu{}}sqrt{{epsilon{}}_0{mu{}}_0}EHSfrac{1}{sqrt{epsilon{}mu{}{epsilon{}}_0{mu{}}_0}}Delta{}tcos{alpha{}=EHSDelta{}tcos{alpha{}}left(7right).}$
Вектор потока электромагнитной энергии
Энергия, которая проходит сквозь площадку $S$ за единицу времени равна:
$P_n=EHScos{alpha{}}left(8right),$
где $ P_n=Pcos{alpha{}}$ – вектора $vec{P}$ на направление нормали к площадке.
$vec{P}$ – вектор потока электромагнитной энергии или вектор Умова – Пойнтинга.
Определение 1
Поток электромагнитной энергии определяют как вектор, перпендикулярный $vec{E}$ ⃗и $vec{H}$, совпадающий по направлению с вектором скорости движения волны, равный: $$vec{P}=left[vec{E}vec{H}right]left(9right).$$
Так, распространение энергии в электромагнитном поле можно характеризовать с помощью потока энергии (вектора Умова – Пойнтинга). Направление данного вектора указывает направление движения энергии.
Если представить себе линии, касательные к которым в любой точке совпадают с направление вектора $vec{P}$, то получим линии вектора потока энергии, указывающие пути, по которым распространяется энергия, рассматриваемого нами поля. С другой стороны, в оптике, линии по которым перемещается энергия, называют лучами. Поскольку видимый свет – это электромагнитные волны, то лучи света – это линии вектора потока энергии этих волн.
Интенсивность
Определение 2
Интенсивностью электромагнитной волны ($I$) считают скалярную физическую величину, равную энергии, которую переносит электромагнитная волна в единицу времени через единичную площадку поверхности, нормальной к направлению по которому эта волна распространяется.
Из определения 1 следует, что величина интенсивности связана с модулем вектора Умова – Пойнтинга.
$I=leftlangle{}vec{P}rightrangle{}=frac{1}{T}leftvert{}int_0^TPdtrightvert{}left(10right).$
Выражение (10) означает, что интенсивность электромагнитной волны равна средней по времени величине модуля вектора Умова – Пойнтинга.
Учитывая формулу (9) можно сказать, что:
$I=leftlangle{}EHrightrangle{} left(11right),$
интенсивность электромагнитной волны можно найти как среднюю величину произведения модулей векторов напряженностей полей.
Интенсивность плоской электромагнитной волны
Допустим, что плоская монохроматическая волна распространяется в вакууме по оси X. Это означает, что напряженности этой волны можно записать при помощи уравнений:
$E=E_0sin{left(omega{}t-kxright),}$
$H=H_0sin{left(omega{}t-kxright) left(12right),}$
где $k=frac{2pi{}}{lambda{}}$ .
Мгновенная величина вектора Умова – Пойнтинга равна:
$P=EH=E_0H_0{sin}^2left(omega{}t-kxright)left(13right).$
От полученной в (13) величины мы должны взять среднее по времени:
$I=leftlangle{}vec{P}rightrangle{}=frac{1}{T}leftvert{}int_0^TPdtrightvert{}=frac{E_0H_0}{2}left(14right).$
Наша волна распространяется в вакууме ($epsilon{}=1; mu{}=1$) и
$sqrt{{epsilon{}}_0}E=sqrt{{mu{}}_0}Hleft(15right),$
Окончательно имеем:
$I=sqrt{frac{{epsilon{}}_0}{{mu{}}_0}}frac{E_0^2}{2} left(16right).$
Выражение (16) показывает, что интенсивность плоской, линейно поляризованной волны пропорциональна квадрату амплитуды напряженности поля.
- Для произвольной плоской волны в однородной среде при отсутствии поглощения интенсивность электромагнитной волны постоянна.
- В стоячей электромагнитной волне интенсивность равна нулю.
- Для сферической электромагнитной волны в среде без поглощения интенсивность волны изменяется только в зависимости от расстояния от ее центра ($r$) и можно считать, что:
$I=frac{const}{r^2}left(17right).$
Интенсивность электромагнитной волны, втекающей в поверхность проводника с постоянным током
Допустим, что у нас имеется длинный цилиндрический проводник радиуса $r$ плотность постоянного тока в котором $j$ (рис.2).
Рисунок 2. Проводник. Автор24 — интернет-биржа студенческих работ
При этом электрическое и магнитное поля имеют направления, указанные на рисунке, следовательно, вектор Умова – Пойнтинга направлен внутрь проводника, нормально к его боковой поверхности. Это говорит нам о том, что энергия постоянно втекает в проводник из окружающей его среды.
Согласно закону Ома:
$E=rho{}j left(18right), $
где $rho{}$ – удельная плотность проводника.
Напряженность магнитного поля у поверхности длинного прямого проводника:
$H=frac{I}{2pi{}r}=frac{jr}{2}left(20right).$
Модуль вектора Умова – Пойнтинга равен:
$P=EH=rho{}jfrac{jr}{2}=rho{}rfrac{j^2}{2}left(21right).$
Мы получили, что интенсивность электромагнитной волны:
$I=P=rho{}rfrac{j^2}{2} left(22right).$
Замечание 1
Указанный выше пример говорит о том, что электромагнитная энергия входит в проводник через его боковую поверхность, а не по оси.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

Как уже упоминалось в начале этой главы, переменное электрическое поле порождает переменное магнитное поле, а переменное магнитное поле порождает переменное электрическое поле. Поэтому, если заряды будут двигаться с ускорением, то появится одновременно электрическое и магнитное поле, то есть будет излучаться электромагнитная волна, распространяющаяся в пространстве со скоростью света.
17.1. Уравнение волны. Интенсивность электромагнитной волны
Уравнение плоской электромагнитной волны имеет такой же вид, как и для механической волны, см. п. 4.4. Так, для компоненты электрического поля1
|
E(x, t) = E0 sin(ωt – kx), |
(17.1) |
υ |
|||||
|
где E0 – амплитуда колебаний напряженности электри- |
|||||||
|
E |
|||||||
|
ческого |
поля; ω – циклическая частота |
волны; |
|||||
|
k = ω = |
2π |
– волновое число; λ – длина волны. Длина |
|||||
|
υ |
λ |
Х |
|||||
|
волны λ связана с частотой ν и скоростью распро- |
|||||||
|
λ |
|||||||
|
странения волны υ соотношением (4.11) λ = υ/ν. |
B |
||||||
|
Векторы B и E не только меняются по величине |
Рис. 17.1. |
||||||
|
с циклической частотой ω, но еще и движутся (бегут) |
|||||||
со скоростью υ вдоль оси Х, рис. 17.1. Поэтому такую волну называют бегущей. Электромагнитные волны распространяются со скоростью света. В вакууме скорость света υ = с = 3·108 м/с, в какой-либо среде скорость света меньше этого значения (υ < с). В металлах электромагнитные волны не распространяются, так как металлы сильно отражают эти волны, а частично прошедшую волну полностью поглощают (переменное электрическое и магнитное поле прошедшей волны возбуждает в металле токи, энергия которых переходит в тепло).
Уравнение (17.1) описывает плоскую волну. Для сферических и других волн волновое уравнение несколько другое. Все электромагнитные волны
поперечные (колебания векторов B и E происходят в плоскостях, перпендикулярных направлению распространения волны, рис. 17.1).
Энергия электромагнитной волны складывается из энергии электрического и магнитного полей. Соответственно и объемная плотность энергии:
|
w = w |
+ w = |
εE2 |
+ |
B2 |
. |
|
|
8πk |
8πk μ |
|||||
|
эл |
м |
1
Здесь мы воспользовались выражениями для объемной плотности энергии электрического (13.19) и магнитного (15.11) полей.
В плоской бегущей электромагнитной волне электрическая энергия в любой момент равна магнитной2, то есть wэл = wм. Поэтому
1Для компоненты магнитного поля уравнение аналогичное.
2Это следует из уравнений Максвелла для электромагнитного поля.
111
|
w = 2w |
= |
εE2 |
= |
εE2 |
sin2 (ωt − kx). |
|
4πk |
0 |
||||
|
эл |
4πk |
Это значение объемной плотности энергии в любой момент времени (мгновенное значение). Для нахождения потока энергии нам понадобится ее усредненное значение. Как и в случае нахождения средней мощности переменного тока, см. п. 16.2, усредним это выражение по времени (периоду колебаний
T = 2π/ω):
|
1 |
T |
εE2 |
T |
εE 2 |
T |
εE 2 |
|
|
wср = |
∫w(t)dt = |
0 |
∫sin2 (ωt − kx)dt = |
0 |
∫(1 − cos(2(ωt − kx)))dt = |
8πk0 . |
|
|
T |
4πkT |
8πkT |
|||||
|
0 |
0 |
0 |
Тогда плотность потока электромагнитной энергии или интенсивность электромагнитной волны определяется из формулы (4.12), где энергия равна1 wсрV = wср Sx = wср Sυt,
|
J = υw = |
υεE2 |
(17.2) |
|
0 . |
||
|
ср |
8πk |
|
Таким образом, как и в случае механических волн, интенсивность электромагнитной волны пропорциональна квадрату ее амплитуды.
17.2. Шкала электромагнитных волн
Хорошо известно, что все окружающее нас пространство пронизано электромагнитными волнами. Радиоантенны, Солнце, далекие звезды испускают электромагнитные волны, которые в зависимости от длины волны носят разные названия: радиоволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновское и γ-излучение.
Так, радиоволны излучаются электронами, ускоренно движущимися в антенне радиопередатчика. Эти волны проходят большие расстояния, попадают в антенну радиоприемника и приводят в движение электроны в ней. В приемнике это движение электронов особым образом преобразуется в звуковой или видеосигнал. Испускание радиоволн далекими галактиками и звездными системами обусловлено ускоренным движением заряженных частиц в магнитных полях этих объектов.
В таблице приведены названия и краткая характеристика основных диапазонов электромагнитных волн (длина волны идет в сторону убывания).
|
Электромагнитная волна |
Длина волны, м |
||
|
Радиоволны |
> 10–4 |
||
|
Инфракрасное излучение (излучают нагретые тела) |
10–4 – 7,6·10–7 |
||
|
Видимый свет (излучают атомы при переходе электронов на более низ- |
7,6·10–7 – 4·10–7 |
||
|
кие энергетические уровни) |
|||
|
Ультрафиолетовое излучение (излучают атомы при переходе электронов |
4·10–7 – 10–8 |
||
|
на более низкие энергетические уровни) |
|||
1 Объем мысленного цилиндра или прямоугольного параллелепипеда с площадью основания S и высотой x, вырезанного в пространстве, где распространяется волна V = Sx = Sυt.
112

|
Электромагнитная волна |
Длина волны, м |
|
Рентгеновское излучение (излучают электроны при резком торможении, |
10–8 – 10–11 |
|
например, в рентгеновской трубке) |
|
|
Гамма-излучение (возникает при переходе ядра на более низкий энерге- |
< 10–11 |
|
тический уровень) |
Приведенная шкала электромагнитных волн довольно приближенная. На самом деле некоторые диапазоны сильно перекрываются, так как волны одной и той же длины могут образовываться в разных процессах. Так, наиболее коротковолновое ультрафиолетовое излучение перекрывается длинноволновым рентгеновским. Диапазоны рентгеновского и γ-излучения тоже перекрываются.
17.3. Принципы радиосвязи
В радиовещании пользуются частотами, лежащими приблизительно в пределах от 0,1 до 100 МГц, чему соответствуют длины волн от 3 км до 3 м. Для решения специальных задач, где существенна точная направленность излучения, применяют дециметровые, сантиметровые и даже миллиметровые волны (частоты выше 100 МГц).
В современных радиотехнических устройствах радиоволны излучаются антеннами, к которым присоединен генератор электрических колебаний, рис. 17.2, а). При этом в антеннах, представляющих собой металлические проводники, возбуждаются вынужденные колебания тока. Эти колебания и порождают электромагнитные волны с соответствующими частотами.
|
Генератор |
Детектор |
|
а) Передатчик |
б) Приемник |
Рис. 17.2.
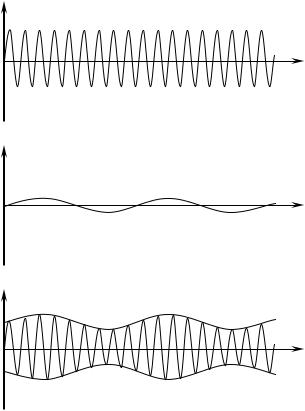
Синусоидальная электромагнитная волна содержит очень мало информации: направление на источник излучения, воспринимаемая частота и интенсивность. Для передачи различной информации, например, звукового или видеосигнала, необходимо видоизменить электромагнитную волну в соответствии с этими сигналами: синусоидальная волна высокой частоты (несущая частота) изменяется низкочастотными сигналами. Такое изменение называется модуляцией, а сами волны – модулированными. Модуляция заключается в изменении амплитуды, частоты или фазы колебаний и в зависимости от изменяемой характеристики называется амплитудной, частотной или фазовой модуляцией. Наиболее простая для понимания – амплитудная модуляция.
Для получения амплитудно-модулированной волны используются устройства, перемножающие сигналы. Рассмотрим процесс перемножения математически на примере радиостанции. Если из студии радиостанции не произво-
113
|
I |
дится передача, то колебания тока в |
|
|
передающей антенне или отсутствуют, |
||
|
или синусоидальны: |
||
|
t |
I = I0 sinωt, |
|
|
где ω – несущая частота, рис. 17.3, а). |
||
|
а) |
Во время передачи (речь, музыка) эти |
|
|
колебания преобразуются в |
||
|
f |
||
|
I = I0(1 + f(t))sinωt, |
||
|
где вид функции f(t) зависит от формы |
||
|
t |
передаваемого (модулирующего) сиг- |
|
|
нала, причем | f(t)| < 1. Она называется |
||
|
б) |
модулирующей функцией. Простейшая |
|
|
модулирующая функция соответствует |
||
|
I |
передаче чистого музыкального тона с |
|
|
какой-либо частотой Ω. В этом случае |
||
|
f(t) = α sin Ωt, рис. 17.3, б). Частота Ω |
||
|
t |
называется частотой модуляции, а по- |
|
|
стоянная α – глубиной модуляции. |
||
|
в) |
Тогда модулированное колеба- |
|
|
ние имеет вид |
||
|
Рис. 17.3. |
I = I0(1 + αsinΩt)sinωt, |
|
|
рис. 17.3, в). Несущий сигнал можно |
модулировать разными частотами, передавая таким образом разнородную информацию. При этом вид сигнала будет гораздо сложнее.
Итак, передатчик излучает модулированные электромагнитные волны, а приемник их воспринимает. Для приема электромагнитных волн также применяют антенны, рис. 17.2, б). Приемная антенна, в которой возникают вынужденные высокочастотные колебания, совместно с контуром настраивается в резонанс. Так как колебания в приемном контуре сравнительно невелики, то используется усиление. В приемнике происходит обратный процесс – демодуляция – выделение из принятого сигнала модулирующих частот, которые и несут разнородную информацию. Демодуляция происходит в детекторе.
Радиоволны используются не только для передачи речи, музыки и изображений с обычными бытовыми целями, но и для сообщения количественной информации о различных параметрах систем (радиотелеметрия). Кроме этого, электромагнитные волны применяют для определения положения объектов (спутников, самолетов, боевых ракет, автомобилей и др.) в пространстве (радиолокация), для вождения кораблей и самолетов (радионавигация) и других целей.
Вопросы к лекции 17
1.Укажите основные характеристики электромагнитной волны. От чего зависит ее интенсивность?
2.Почему диэлектрики хорошо пропускают электромагнитные волны, а металлы – нет?
3.Какие типы электромагнитных волн вы знаете? Как они возникают?
4.Как осуществляется радиосвязь? Что такое модуляция?
114
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
Конкурс “Я иду на урок”
Проф. В. В.
Майер,
< varaksina_ei@list.ru >, ГГПИ им. В.Г.Короленко, г. Глазов, Удмуртская Респ.
Интенсивность, давление и импульс электромагнитной волны
Урок 5-й из серии уроков на тему «Электромагнитные волны». См. № 24/08; 2, 4, 6/09
Цели обучения: ввести и сформировать понятия интенсивности, давления и импульса электромагнитной волны; теоретически и экспериментально обосновать эти понятия.
Цели развития: совершенствовать критичность мышления, умения рассуждать по аналогии; способности применять теоретические знания для объяснения физических явлений.
Цели воспитания: развивать волевые, мотивационные и толерантные характеристики личности.
Дидактические средства:
- Мякишев Г.Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений / Г.Я.Мякишев, Б.Б.Буховцев. – М.: Просвещение, 2004.
- Касьянов В.А. Физика. 11 кл.: Учебн. для 11 кл. общеобразоват. учеб. заведений. – М.: Дрофа, 2002.
- Электронная версия опорного конспекта урока; видеофрагменты демонстрационных опытов.
- Комплект для изучения электромагнитных волн (выпускается ЗАО НПК «Компьютерлинк»), вольтметр, миллиамперметр, регулируемый источник напряжения.
5.1. Введение
Учитель. Сегодня мы продолжим знакомство с важнейшими характеристиками электромагнитной волны как материального объекта. Перенос энергии волной характеризуется специальной величиной, которая называется интенсивностью. Электромагнитная волна, падая на препятствие, оказывает на него давление. При этом препятствие приобретает импульс, следовательно, импульсом обладает само электромагнитное излучение. Давление и импульс доступной нам электромагнитной волны ничтожно малы, поэтому мы не сможем измерить их в учебных опытах. Однако мы сумеем объяснить их существование и оценить значения соответствующих величин.
5.2. Интенсивность электромагнитной волны
Учитель. Вспомните, как математически записывается гармоническая волна и как выражается её энергия.
Учащиеся. Уравнение для напряжённости электрического поля в гармонической электромагнитной волне имеет вид 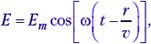 где
где

а плотность её энергии:
ω = ε0εE2. (5.2)
Учитель. Произведение плотности энергии на скорость волны называется поверхностной плотностью потока энергии j = ωυ.
Учащиеся. Неужели мы должны запомнить этот длинный термин?!
Учитель. Нет, конечно. Но авторы школьных учебников почему-то очень любят его, поэтому, если вы хотите получить высшее образование, познакомиться с этим термином и его фамильярным вариантом «плотность потока энергии», хочешь-не хочешь, а запомнить придётся.
Учащиеся. Тогда нужно по крайней мере понять, откуда он взялся.
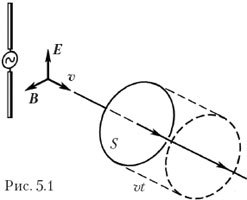
Учитель. Волна, проходящая по нормали через площадку S за время t, занимает объём V = sυt (рис. 5.1). Так как плотность энергии равна энергии в единице объёма: ω = W/V, – то поверхностную плотность потока энергии можно записать в виде:

Отношение энергии волны W ко времени t, в течение которого она проходит через поверхность, называется потоком энергии. А отношение потока энергии к площади поверхности, через которую он проходит, естественно назвать поверхностной плотностью потока энергии.
Учащиеся. Теперь понятно, что это просто энергия, переносимая волной за единицу времени через единицу площади, или мощность излучения, проходящая через единицу площади.
Учитель. Выясните, как зависит поверхностная плотность потока энергии электромагнитной волны от её частоты.
Учащиеся. Из формул (5.1), (5.2) и (5.3) получаем:
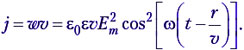
Так как косинус здесь получился в квадрате, то поверхностная плотность потока энергии электромагнитной волны колеблется с частотой, в два раза превышающей частоту волны. Как измерить эту величину?
Учитель. Измеряют не мгновенное, а среднее по времени значение плотности потока энергии, которое называют интенсивностью волны. Вы хорошо знаете, что среднее значение квадрата косинуса равно 1/2. Подставляя его в предыдущую формулу и учитывая выражения для Em (5.1) и для 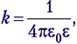 после небольших преобразований можно получить, что интенсивность гармонической волны равна
после небольших преобразований можно получить, что интенсивность гармонической волны равна
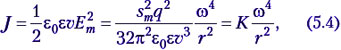
где K – постоянный коэффициент. Проанализируйте этот результат.
Учащиеся. Из формулы (5.4) следует, что интенсивность электромагнитной волны, испускаемой гармоническим осциллятором, при прочих равных условиях пропорциональна четвёртой степени её частоты и обратно пропорциональна квадрату расстояния, пройденного волной.
Учитель. Дайте ещё один вариант определения интенсивности волны и качественно объясните, почему интенсивность электромагнитной волны пропорциональна четвёртой степени её частоты.
Учащиеся. Интенсивность волны есть средняя по времени энергия Wcр, проходящая через единицу площади за единицу времени:

Значит, интенсивность пропорциональна энергии волны J ~ Wcр. А энергия пропорциональна квадрату напряжённости электрического поля Wcр ~Em2. В свою очередь напряжённость электрического поля пропорциональна ускорению излучающего волну заряда Em ~ am, а ускорение пропорционально квадрату частоты колебаний заряда am ~ ω2. Отсюда следует, что интенсивность пропорциональна четвёртой степени частоты:
J ~ Wcр ~ Em2 ~ am2 ~ ω4. (5.6)
Учитель. Уточните, какие значения напряжённости и ускорения вы имеете в виду.
Учащиеся. Мы говорим об амплитуде напряжённости электрического поля Em электромагнитной волны и амплитуде ускорения am гармонически колеблющегося заряда.
Учитель. А почему интенсивность обратно пропорциональна квадрату расстояния?
Учащиеся. Потому, что напряжённость электрического поля электромагнитной волны, созданной колеблющимся зарядом, обратно пропорциональна расстоянию до заряда, а интенсивность волны пропорциональна квадрату напряжённости.
5.3. Экспериментальное исследование излучения диполя
Учитель. На опыте исследуем зависимость интенсивности электромагнитной волны от расстояния до излучающего вибратора. Для этого рядом с лампой приёмного диполя (2,5 В; 0,15 А) расположим точно такую же лампу накаливания, через амперметр подключим её к регулируемому источнику постоянного напряжения и параллельно этой эталонной лампе включим вольтметр. Установим расстояние между излучающим и приёмным диполями 10 см и, регулируя напряжение источника, добьёмся, чтобы яркость эталонной лампы стала равна яркости приёмной (рис. 5.2, а). Тогда можно утверждать, что в эталонной лампе выделяется та же мощность, что и в приёмной. Вычислите её.

Учащиеся. Приборы показывают, что сила тока и напряжение на эталонной лампе соответственно равны I1 = 0,111 А и U1 = 1,8 В, значит, искомая мощность P1 = U1 I1 = 0,20 Вт.
Учитель. Теперь удалим приёмный диполь на расстояние 20 см от излучающего, повторим измерения и сделаем выводы.
Учащиеся. Получилось I2 = 0,087 А и U2 = 1,2 В (рис. 5.2, б), поэтому P2 = U2 I2 = 0,10 Вт. Отношение P1 / P2 равно двум, а не четырём, как следовало ожидать! Неужели в теории ошибка?
Учитель. Прежде чем менять теорию, посмотрим соответствуют ли её исходным данным условия эксперимента. Вспомним, при рассмотрении распространения энергии от излучающего диполя мы молчаливо предполагали, что она во все стороны излучается одинаково. Иначе говоря, мы допускали, что диполь является изотропным источником. В таком случае электромагнитная энергия равномерно распределяется по сферической поверхности. Так как площадь сферы S = 4πr2 пропорциональна квадрату её радиуса, то мощность, приходящаяся на единицу площади, т.е. интенсивность волны, обратно пропорциональна квадрату расстояния.
Учащиеся. Нужно исследовать, как излучает диполь по разным направлениям, и тогда сделать вывод об интенсивности излучения.
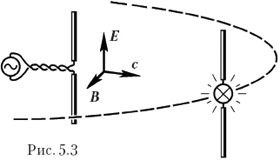
Учитель. Параллельно излучающему диполю располагаю приёмный так, чтобы яркость его лампы стала максимальной, и перемещаю его по окружности с центром в центре излучающего диполя (рис. 5.3). Сделайте вывод из результата эксперимента.
Учащиеся. Во всех точках окружности лампа приёмного диполя горит с одинаковым накалом. Значит, во всех направлениях, перпендикулярных излучающему диполю, интенсивность электромагнитной волны одинакова.
Учитель. Теперь я перемещаю и поворачиваю приёмный диполь в плоскости, проходящей через излучающий диполь (рис. 5.4). Делаю это так, чтобы приёмный диполь, двигаясь по окружности с центром в излучающем диполе, был направлен по касательной к этой окружности. Что вы наблюдаете и к какому выводу приходите?
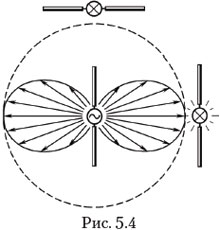
Учащиеся. Лампа горит всё слабее по мере того, как приёмный диполь поворачивается относительно излучающего. Значит, соединённый с генератором диполь даёт максимум излучения в направлении, перпендикулярном диполю, и совершенно не излучает в направлении самого диполя.
Учитель. Если в полярной системе координат построить график зависимости интенсивности электромагнитной волны от угла между диполем и направлением излучения, то получится диаграмма направленности полуволнового диполя, подобная показанной на рис. 5.4 (длина стрелок пропорциональна интенсивности). Вернитесь теперь к опыту, в котором мы измеряли зависимость интенсивности электромагнитной волны от расстояния, и попробуйте объяснить его результат.
Учащиеся. Проделанный только что опыт показывает, что диполь не является изотропным источником электромагнитной волны: излучение распространяется в основном в плоскости, перпендикулярной излучающему диполю и проходящей через его центр. Значит, излучаемая энергия вблизи диполя приходится не на сферическую, а на цилиндрическую поверхность. Площадь боковой поверхности цилиндра пропорциональна его радиусу. Поэтому и интенсивность излучения диполя обратно пропорциональна не квадрату расстояния, а просто расстоянию до источника.
Учитель. Заметьте, что и приёмник не является изотропным: его чувствительность также зависит от направления, под которым на него падает волна. В теоретической модели мы полагали источник и приёмник точечными и изотропными. Нетрудно сообразить, что условия этой модели будут выполнены, если расстояние между источником и приёмником значительно превышает их размеры.
5.4. Давление и импульс электромагнитной волны
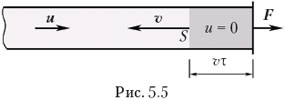
Учитель. Опыты показывают, что электромагнитная волна переносит энергию, значит, падая на препятствия, она должна оказывать на них давление. Корректно вывести соответствующую формулу довольно сложно, поэтому воспользуемся гидродинамической аналогией. Представьте, что по трубе, площадь сечения которой S со скоростью u течёт вода (рис. 5.5). Плотность энергии в движущейся воде очевидно равна ω = W/V = mu2/(2V) = ρu2/2, где ρ – плотность воды. Внезапно отверстие трубы перекрывают заслонкой. Что при этом происходит?
Учащиеся. Вода возле заслонки останавливается и сжимается. Фронт сжатия распространяется со скоростью перемещения упругой деформации υ навстречу движущейся воде. Скорость υ – это скорость упругой волны или скорость звука в воде.
Учитель. Верно. Применим к рассматриваемому явлению закон сохранения импульса. За небольшое время τ заслонкой останавливается объём воды Sυτ массой ρSυτ, который передаёт заслонке импульс ρSυτu. При этом на заслонку действует сила F, импульс которой равен Fτ. Приравнивая два последних выражения, после сокращения на время τ получаем равенство ρSυu = F. Отсюда давление внезапно остановленного потока воды равно P = F/S = ρuυ.
Учащиеся. Но скорость звука в воде равна 1500 м/с, неужели так сильно растёт давление?
Учитель. Именно так, и это явление называется гидродинамическим ударом. К слову сказать, его теорию создал наш соотечественник Н.Е.Жуковский. Но не будем отвлекаться. Допустим, что вода в трубе течёт со скоростью упругой волны u = υ. Что отсюда следует?
Учащиеся. Тогда возникающее давление равно P = ρuυ = ρu2. Так как плотность энергии в текущей воде ω = ρu2/2, то мы должны заключить, что давление при внезапной остановке воды составляет P = 2ω.
Учитель. Вы только что нашли формулу для давления, которое оказывает на полностью отражающее препятствие падающая на него нормально упругая волна. Но если эта формула справедлива для упругих волн, то почему бы не предположить, что она будет справедлива и для электромагнитных?
Учащиеся. Тогда можно считать, что электромагнитная волна оказывает на отражающее её препятствие или зеркало давление, равное удвоенной плотности энергии падающей волны. Если волна распространяется в вакууме, то её скорость υ = c и с учётом выражения для интенсивности J = ωcрυ = ωcрс. (5.5) имеем:
P = 2ωcр = 2J/c. (5.7)
Учитель. Поскольку электромагнитная волна оказывает давление, она должна обладать импульсом. Попробуйте найти формулу для импульса электромагнитного излучения. Для этого рассмотрите отражение короткого всплеска электромагнитного излучения от зеркала.
Учащиеся. Если импульс электромагнитной волны p, то при полном отражении её от зеркала за время t изменение импульса составляет 2p. Зеркало за то же время t получает импульс Ft = PSt = 2p. Так как давление P = 2J/c (5.7), то, подставляя это выражение в предыдущую формулу, получаем, что импульс электромагнитной волны p = J/c · St.
Учитель. Ещё раз вспоминая выражение для интенсивности J = Wcр / St (5.5), получаем
p = Wcр/с. (5.8)
Таким образом, импульс электромагнитной волны, распространяющейся в вакууме, равен средней по времени энергии волны, делённой на скорость света в вакууме.
5.5. Почему электромагнитная волна оказывает давление?
Учитель. Нам теперь нужно установить физическую причину, по которой электромагнитная волна оказывает давление. Напротив излучающего диполя я располагаю приёмный с лампой накаливания. Докажите, что в электромагнитном поле на диполь действует сила в направлении распространения волны.
Учащиеся. Под действием электрического поля волны электроны в приёмном диполе приходят в колебательное движение. При этом по диполю идёт переменный электрический ток, о чём свидетельствует свечение лампы. Но откуда берётся сила?
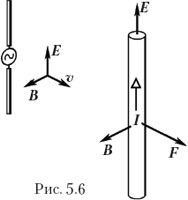
Учитель. Не забывайте, что в электромагнитной волне помимо электрического имеется магнитное поле.
Учащиеся. Тогда понятно! На ток в проводнике со стороны магнитного поля действует сила Ампера (рис. 5.6). Чтобы определить её направление, применим правило левой руки. Получается, что сила F на диполь действует в направлении распространения электромагнитной волны. В следующий полупериод переменного тока в диполе направление индукции сменится на противоположное, но направление силы Ампера не изменится.
Учитель. Вычисления, которые мы проводить не будем, показывают, что среднее по времени значение действующей на электроны силы Лоренца, которая приходится на единицу площади отражающего проводника, в точности совпадает с выражением (5.7). Поэтому гидродинамическая аналогия (рис. 5.5), использованная нами в теоретической модели, вполне уместна.
5.6. Заключение
Учитель. Что нового вы узнали на этом уроке? Чему вы научились? Что произвело на вас наибольшее впечатление?
Учащиеся. Мы узнали, что такое интенсивность, давление и импульс электромагнитной волны, а также, как они связаны друг с другом. Выяснили, как интенсивность зависит от частоты и расстояния, проходимого волной. Научились экспериментально определять интенсивность электромагнитного излучения. Очень интересна аналогия между течением воды и распространением волны. Убедительны опыты, в которых определяется пространственное распределение интенсивности электромагнитного излучения диполя.
Учитель. Как обычно, домашнее задание даётся тем, кому интересно его выполнять, или тем, кто хочет повторить пройденное, узнать новое, углубить свои знания и умения. Материал для выполнения задания вы найдёте в учебниках физики и в электронной версии опорного конспекта урока.
Статья подготовлена при поддержке банка лекций www.Siblec.Ru. Если Вы решили приобрести или расширить свои знания в разных областях науки и техники, то оптимальным решением станет зайти на сайт www.Siblec.Ru. Перейдя по ссылке: «лекции по физике», вы сможете, не потратив много времени, получить доступ к лекциям по физике и по другим научным дисциплинам. Банк лекций www.Siblec.Ru постоянно обновляется, поэтому вы всегда сможете найти свежий и актуальный материал.
- Дайте определение поверхностной плотности потока излучения. Что понимают под точечным источником электромагнитного излучения? Как плотность потока излучения зависит от частоты и расстояния до источника? [Г.Я.Мякишев, § 50; В.А.Касьянов, § 49.]
- Что такое интенсивность электромагнитной волны? Как зависит интенсивность от частоты волны? По какому закону убывает интенсивность электромагнитной волны, испускаемой точечным источником? [Г.Я.Мякишев, § 50; В.А.Касьянов, § 49.]
- Как определяются давление и импульс электромагнитной волны? В чём суть опытов П.Н.Лебедева по определению давления света? [Г.Я.Мякишев, § 92; В.А.Касьянов, § 50.]
- Сделайте вывод формулы (5.4) для интенсивности гармонической электромагнитной волны. [ОК.]
- Как экспериментально доказать, что излучающий диполь не является изотропным источником электромагнитной волны? [ОК.]
- Мощность излучения точечного изотропного источника электромагнитной волны 2 Вт. Чему равна интенсивность на расстоянии 1 м от источника?
- В некоторой области интенсивность электромагнитного излучения составляет 1 Вт/м2. Чему равны напряжённость электрического и индукция магнитного полей в этой области?
Продолжение
следует
Вспомним, что волна — это колебания, распространяющиеся в пространстве. Механическая волна представляет собой колебания, распространяющиеся в вещественной среде. Тогда электромагнитная волна — это электромагнитные колебания, которые распространяются в электромагнитном поле.
Как появляются и распространяются электромагнитные волны
Представьте себе неподвижный точечный заряд. Пусть его окружают еще много таких зарядов. Тогда он будет действовать на них с некоторой кулоновской силой (и они на него). А теперь представьте, что заряд сместился. Это приведет к изменению расстояния по отношению к другим зарядам, а, следовательно, и к изменению сил, действующих на них. В результате они тоже сместятся, но с некоторым запаздыванием. При этом начнут смещаться и другие заряды, которые взаимодействовали с ними. Так распространяется электромагнитные взаимодействия.
Теперь представьте, что заряд не просто сместился, а он начал быстро колебаться вдоль одной прямой. Тогда по характеру движения он будет напоминать шарик, подвешенный к пружине. Разница будет только в том, что колебания заряженных частиц происходят с очень высокой частотой.
Вокруг колеблющегося заряда начнет периодически изменяться электрическое поле. Очевидно, что период изменений этого поля, будет равен периоду колебаний заряда. Периодически меняющееся электрическое поле будет порождать периодически меняющееся магнитное поле. Это магнитное поле, в свою очередь, будет создавать переменное электрическое поле, но уже на большем расстояние от заряда, и т.д. В результате появления взаимно порождаемых полей в пространстве, окружающем заряд, возникает система взаимно перпендикулярных, периодически меняющихся электрических и магнитных полей. Так образуется электромагнитная волна, которая распространяется от колеблющегося заряда во все стороны.
Электромагнитная волна не похожа на те возмущения вещественной среды, которые вызывают механические волны. Посмотрите на рисунок. На нем изображены векторы напряженности →E и магнитной индукции →B в различных точках пространства, лежащих на оси Oz, в фиксированный момент времени. Никаких гребней и впадин среды при этом не появляется.
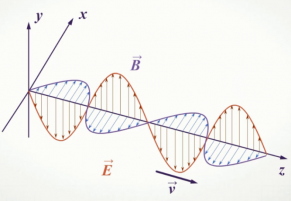
В каждой точке пространства электрические и магнитные пол меняются во времени периодически. Чем дальше расположена точка от заряда, тем позднее ее достигнут колебания полей. Следовательно, на разных расстояниях от заряда колебания происходят с различными фазами. Колебания векторов →E и →B в любой точке совпадают по фазе.
Определение
Длина электромагнитной волны — расстояние между двумя ближайшими точками, в которых колебания происходят в одинаковых фазах.
Длина электромагнитной волны обозначается как λ. Единица измерения — м (метр).
Обратите внимание на рисунок выше. Векторы магнитной индукции и напряженности поля, являющиеся периодически изменяющимися величинами, в любой момент времени перпендикулярны направлению распространения волны. Следовательно, электромагнитная волна — поперечная волна.
Условия возникновения электромагнитных волн
Электромагнитные волны излучаются только колеблющимися заряженными частицами. При этом важно, чтобы скорость их движения постоянно менялась, т.е. чтобы они двигались с ускорением.
Наличие ускорения — главное условие возникновения электромагнитных волн.
Электромагнитное поле может излучаться не только колеблющимся зарядом, но и заряженной частицей, перемещающейся с постоянно меняющейся скоростью. Интенсивность электромагнитного излучения тем больше, чем больше ускорение, с которым движется заряд.
Представим заряд, движущийся с постоянной скоростью. Тогда создаваемые им электрическое и магнитное поля будут сопровождать его как шлейф. Только при ускорении заряда поля «отрываются» от частицы и начинают самостоятельное существование в форме электромагнитных волн.
Это интересно!
Впервые существование электромагнитных волн предположил Максвелл, который посчитал, что они должны распространяться со скоростью света. Но экспериментально они были обнаружены лишь спустя 10 лет после смерти ученого. Их открыл Герц. Он же подтвердил, что скорость распространения электромагнитных волн равна скорости света: c = 300 000 км/с.
Плотность потока электромагнитного излучения
Излученные электромагнитные волны несут с собой энергию. Рассмотрим поверхность площадью S, через которую электромагнитные волны переносят энергию.
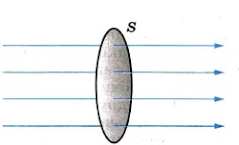
На рисунке выше прямые линии указывают направления распространения электромагнитных волн. Это лучи — линии, перпендикулярные поверхностям, во всех точках которых колебания происходят в одинаковых фазах. Такие поверхности называются волновыми поверхностями.
Определение
Плотность потока электромагнитного излучения, или интенсивность волны — отношение электромагнитной энергии ΔW, проходящей за время Δt через перпендикулярную лучам поверхность площадью S, к произведению площади S на время Δt.
Плотность потока электромагнитного излучения обозначается как I. Единица измерения — Вт/м2 (ватт на квадратный метр). Поэтому плотность потока электромагнитного излучения фактически представляет собой мощность электромагнитного излучения, проходящего через единицу площади поверхности.
Численно плотность потока электромагнитного излучения определяется формулой:
I=ΔWSΔt
Выразим I через плотность электромагнитной энергии и скорость ее распространения с. Выберем поверхность площадью S, перпендикулярную лучам, и построим на ней как на основании цилиндр с образующей cΔt (см. рисунок ниже).
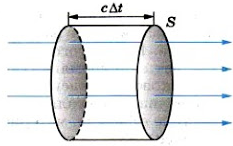
Объем цилиндра: ΔV = ScΔt. Энергия электромагнитного поля внутри цилиндра равна произведению плотности энергии на объем: ΔW = wcΔtS. Вся эта энергия за время Δt пройдет через правое основание цилиндра. Поэтому получаем:
I=wcΔtSSΔt=wc
Следовательно, плотность потока электромагнитного излучения равна произведению плотности электромагнитной энергии на скорость ее распространения.
Определение
Плотность электромагнитной энергии — энергия электромагнитного излучения в единице объема. Обозначается как w. Единица измерения — Дж/м3.
Пример №1. Плотность потока излучения равна 6 мВт/м2. Найти плотность энергии электромагнитной волны.
I=wc
Отсюда:
w=Ic=6·10−33·108=2·10−11 (Джм3)
Точечный источник излучения
Источники излучения электромагнитных волн могут быть весьма разнообразными. Простейшим является точечный источник.
Точечный источник — источник излучения, размеры которого много меньше расстояния, на котором оценивается его действие.
Предполагается, что точечный источник посылает электромагнитные волны по всем направлениям с одинаковой интенсивностью. В действительности таких источников не существует. Но за такие источники излучения можно принять звезды, так как расстояние между ними существенно больше размеров самих звезд.
Энергия, которую переносят электромагнитные волны, с течением времени распределяется по все большей и большей поверхности. Поэтому энергия, передаваемая через поверхность единичной площадки за единицу времени, т. е. плотность потока излучения, уменьшается по мере удаления от источника.
Поместим точечный источник в центр сферы радиусом R. Площадь поверхности сферы S = 4πR2. Если считать, что источник по всем направлениям за время Δt излучает суммарную энергию ΔW, получим:
I=ΔWSΔt=ΔW4πΔt·1R2
Плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника.
Пример №2. Плотность потока электромагнитного излучения на расстоянии 5 метров от точечного источника составляет 20 мВт/м2. Найти плотность потока электромагнитного излучения на расстоянии 10 метров от этого источника.
Расстояние по условию задачи увеличилось вдвое. Так как плотность потока излучения от точечного источника убывает обратно пропорционально квадрату расстояния до источника, при увеличении расстояния вдвое интенсивность излучения уменьшится в 4 раза. То есть, она станет равной 5 мВт/м2.
Зависимость плотности потока излучения от частоты
Напряженность электрического поля и магнитная индукция электромагнитной волны пропорциональны ускорению заряда. Ускорение при гармонических колебаниях пропорционально квадрату частоты. Поэтому напряженность электрического поля и магнитная индукция также пропорциональны квадрату частоты:
E~a~ω2, B~a~ω2
Плотность энергии электрического поля пропорциональна квадрату напряженности поля. Энергия магнитного поля, как это можно показать, пропорциональна квадрату магнитной индукции. Полная плотность энергии электромагнитного поля равна сумме плотностей энергий электрического и магнитного полей. Поэтому плотность потока излучения I пропорциональна:
I~w
~(E2+B2)
Вспомним, что:
E~ω2, B~ω2
Тогда:
I~ω4
Плотность потока излучения пропорциональна четвертой степени частоты. Так, при увеличении частоты колебаний зарядов в 2 раза энергия, излучаемая ими, возрастает в 16 раз. При увеличении частоты в 3 раза, энергия излучения увеличивается в 81 раз, и т.д.
Пример №3. Частота электромагнитной волны уменьшилась в 4 раза. Найти, во сколько раз изменилась плотность потока излучения.
Так как плотность потока излучения пропорциональна четвертой степени частоты, мы можем найти плотность потока излучения путем извлечения корня из числа 4 дважды:
4√4=√√4=√2≈1,4
Плотность потока излучения уменьшилась в 1,4 раза.
Свойства электромагнитных волн
Современные радиотехнические устройства позволяют провести очень наглядные опыты по наблюдению свойств электромагнитных волн. При этом лучше всего пользоваться волнами сантиметрового диапазона. Эти волны излучаются специальным генератором сверхвысокой частоты (СВЧ). Электрические колебания генератора модулируют звуковой частотой. Принятый сигнал после детектирования подается на громкоговоритель.
| Свойство 1 — Поглощение электромагнитных волн | |
 |
Если расположить рупоры друг против друга и добиться хорошей слышимости звука в громкоговорители, а затем поместить между ними диэлектрик, звук будет менее громким. |
| Свойство 2 — Отражение электромагнитных волн | |
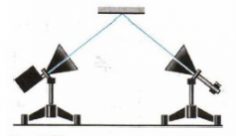 |
Если диэлектрик заменить металлической пластиной, то звук перестанет быть слышимым. Волны не достигают приемника вследствие отражения. Отражение происходит под углом, равным углу падения, как и в случае световых и механических волн. Чтобы убедиться в этом, рупоры располагают под одинаковыми углами к большому металлическому листу. Звук исчезнет, если убрать лист или повернуть его. |
| Свойство 3 — Преломление электромагнитных волн | |
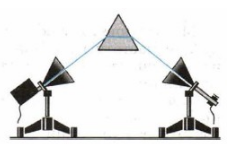 |
Электромагнитные волны изменяют свое направление (преломляются) на границе диэлектрика. Это можно обнаружить с помощью большой треугольной призмы из парафина. Рупоры располагают под углом друг к другу, как и при демонстрации отражения. Металлический лист заменяют затем призмой. Убирая призму или поворачивая ее, наблюдают исчезновение звука. |
| Свойство 4 — Поперечность электромагнитных волн | |
 |
Поместим между генератором и приемником решетку из параллельных металлических стержней. Решетку расположим так, чтобы стержни были горизонтальными или вертикальными. При одном из этих положений, когда электрический вектор параллелен стержням, в них возбуждаются токи, в результате чего решетка начинает отражать волны, подобно сплошной металлической пластине. Когда же вектор перпендикулярен стержням, токи в них не возбуждаются и электромагнитная волна проходит через решетку. |
Шкала электромагнитных волн
Электромагнитные волны имеют большое разнообразие. Они классифицируются по длине волны λ или связанной с ней частоте ν. Шкала электромагнитных волн включает в себя:
- радиоволны;
- оптическое излучение;
- ионизирующее излучение.
Укажем частоты и длины указанных волн, а также их подробную классификацию в таблице.
| Наименование диапазона волн | Длины волн (м) | Частоты (Гц) |
| Радиоволны | ||
| Инфразвук, звук | >105 | <3∙103 |
| Сверхдлинные волны (СДВ) | 104–105 | 3∙103–3∙104 |
| Длинные волны (ДВ) | 103–104 | 3∙104–3∙105 |
| Средние волны (СВ) | 102–103 | 3∙105–3∙106 |
| Короткие волны (КВ) | 10–100 | 3∙106–3∙107 |
Ультракороткие (УКВ):
|
|
|
| Оптические волны | ||
| Инфракрасное излучение | 0,78∙10–6–10–4 | 3∙1011–4∙1014 |
| Видимый свет | 0,38∙10–6–0,78∙10–6 | 4∙1014–7,5∙1014 |
| Ультрафиолетовое излучение | 10–7–0,38∙10–6 | 7,5∙1011–3∙1015 |
| Ионизирующее излучение | ||
| Рентгеновское излучение | 5∙10–12–10–8 | 3∙1016–6∙1019 |
| Гамма-излучение | <5∙10–12 | >6∙1019 |
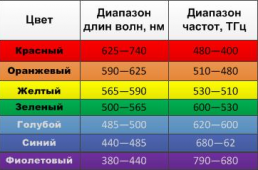
Частоты и длины волн электромагнитного излучения видимого спектра смотрите на рисунке ниже.
Задание EF17496
В электромагнитной волне, распространяющейся со скоростью →v, происходят колебания векторов напряжённости электрического поля →E и индукции магнитного поля →B. При этих колебаниях векторы →v, →E, →B. имеют взаимную ориентацию:
Ответ:
а) →B∥∥→E, →B∥∥→v, →E∥∥→v
б) →B⊥→E, →B∥∥→v, →E⊥→v
в) →B⊥→E, →B⊥→v, →E∥∥→v
г) →B⊥→E, →B⊥→v, →E⊥→v
Алгоритм решения
1.Вспомнить, какие величины периодически изменяются при распространении электромагнитной волны.
2.Вспомнить, какое взаимное расположение имеют векторы меняющихся величин электромагнитной волны.
3.Вспомнить, какой является электромагнитная волна — продольной или поперечной.
Решение
Электромагнитная волна представляет собой распространяющиеся с течением времени в пространстве электромагнитные колебания, характеризующиеся периодическим изменением в точках пространства вектора напряженности →E и вектора магнитной индукции →B. Эти векторы лежат и изменяются во взаимно перпендикулярных плоскостях. Поэтому вектора напряженности →E и вектор магнитной индукции →B перпендикулярны (→B⊥→E).
Электромагнитная волна — поперечная волна. Это значит, что векторы периодически меняющихся величин расположены перпендикулярно направлению распространения волны. Направление волны определяется направлением вектора ее скорости. Следовательно, вектор напряженности →E и вектор магнитной индукции →B перпендикулярны вектору скорости распространения волны (→B⊥→v, →E∥∥→v).
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17601
Какой объект, согласно классической электродинамике, не излучает электромагнитных волн?
Ответ:
а) ускоренно движущийся заряд
б) электромагнит, подключённый к генератору переменного тока
в) линия электропередачи
г) покоящийся электромагнит, подключённый к аккумулятору
Алгоритм решения
- Вспомнить основное условие возникновения электромагнитных волн.
- Проанализировать возможные источники электромагнитных волн и установить, в каком из них необходимое условие не выполняется.
Решение
Главное условие возникновения электромагнитных волн — наличие у движущегося заряда ускорения. Следовательно, ускоренно движущийся заряд излучает электромагнитные волны.
По линиям электропередачи протекает переменный ток, который периодически меняет свое направление. Следовательно, заряды внутри проводников движутся ускоренно, ведь для того, чтобы поменялась скорость (по модулю и направлению), необходимо наличие ускорения. Следовательно, линии электропередач тоже излучают электромагнитные волны. По этой же причине электромагнит, подключённый к генератору переменного тока, также излучает волны.
Покоящийся электромагнит, подключённый к аккумулятору, не может излучать электромагнитные волны. Аккумулятор — источник постоянного тока. Поэтому заряды движутся с постоянной скоростью (без ускорения), и сам электромагнит покоится (не имеет ускорения).
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17566
Выберите среди приведённых примеров электромагнитное излучение с минимальной длиной волны.
Ответ:
а) рентгеновское
б) ультрафиолетовое
в) видимое
г) инфракрасное
Алгоритм решения
- Вспомнить расположение видов волн на шкале.
- Определить тип волн, имеющих самую короткую длину волны из перечисленных вариантов.
Решение
Шкала электромагнитных волн классифицирует волны по длине или частоте волн. Чем меньше длина волны, тем выше ее частота. Наибольшей длиной волны обладают радиоволны, затем идем инфракрасное, видимое и ультрафиолетовое излучение. После — ионизирующее излучение (рентгеновское и гамма-излучение). Следовательно, наименьшей длиной волн из перечисленных вариантов обладает рентгеновское излучение.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 8.7k
«Без сомнения, все наши
знания начинаются с опыта».
Иммануил Кант
Задача 1. Интенсивность электромагнитной волны равна тридцать 30 мВт/м2.
Какова плотность энергии электромагнитной волны?
|
ДАНО: |
СИ |
РЕШЕНИЕ Интенсивность электромагнитной |
|
|
Ответ: 0,1 нДж/м3.
Задача 2. Электромагнитная волна с частотой 10 МГц переходит из вакуума в немагнитную
среду, диэлектрическая проницаемость которой равна 5. Найдите, насколько
уменьшится длина волны.
|
ДАНО: |
СИ |
РЕШЕНИЕ Скорость распространения волны При переходе электромагнитной Применим формулу для Показатель преломления определяется по формуле Тогда получаем Изменение длины волны равно |
|
|
Ответ: длина волны уменьшилась на
16,6 м.
Задача 3. Плотность потока излучения электромагнитной волны составляет
100 Вт/м2. Найдите плотность потока излучения после увеличения
линейной частоты волны вдвое.
|
ДАНО: |
РЕШЕНИЕ Интенсивность излучения Циклическая частота связана с линейной по соотношению Для упрощения решения, введём Тогда отношение плотностей потоков излучения Из данного отношения следует, что искомая плотность потока |
|
|
Ответ: 1600 Вт/м2.
Задача 4. В колебательном контуре максимальная сила тока составляет 2 А, а
максимальный заряд на конденсаторе равен 100 нКл. Найдите длину
электромагнитной волны в вакууме, на которую может быть настроен данный контур.
|
ДАНО: |
СИ |
РЕШЕНИЕ Циклическая частота в колебательном контуре рассчитывается Максимальная электрическая энергия определяется по формуле Максимальная магнитная энергия Исходя из закона сохранения Преобразуем данное равенство Циклическая частота рассчитывается по формуле Запишем соотношение, связывающее Тогда длина волны равна |
|
|
Ответ: 94,25 м.
Задача 5. Найдите наибольшую и наименьшую дальность обнаружения
цели радиолокатором, работающим в импульсном режиме. Частота повторения импульсов
равна 1900 Гц, а длительность импульса составляет 1 мкс.
|
ДАНО: |
СИ |
РЕШЕНИЕ Время, за которое луч радиолокатора возвращается на Время между последовательными излучениями импульсов не Время прохождения импульсом расстояния до цели не должно Составим уравнения для |
|
|
Ответ: lmax = 79 км; lmin = 150 м.


