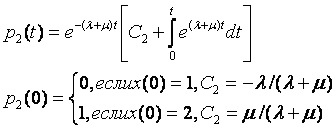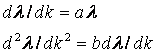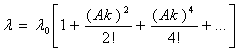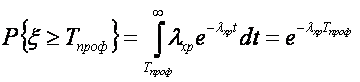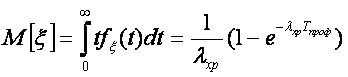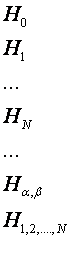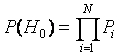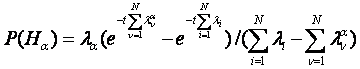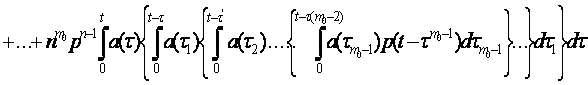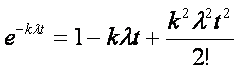Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 июня 2020 года; проверки требует 1 правка.
Типичная зависимость интенсивности отказов от времени: 


Интенси́вность отка́зов — отношение числа отказавших объектов (образцов аппаратуры, изделий, деталей, механизмов, устройств, узлов и т. п.) в единицу времени к среднему числу объектов, исправно работающих в данный отрезок времени при условии, что отказавшие объекты не восстанавливаются и не заменяются исправными. Другими словами, интенсивность отказов численно равна числу отказов в единицу времени, отнесенное к числу узлов, безотказно проработавших до этого времени. Следующие определения интенсивности отказов эквивалентны:
![lambda (t) = frac {n(t)} {N_{cp} Delta t} = frac{n(t)}{ left [N-n(t) right ] Delta t} = frac {f(t)} {P(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8b4223122e85e846b6b96e73e2ae6ed661ceb80)
где 











где 



Размерность интенсивности отказов обратна времени, обычно измеряется в 1/час.
Примеры[править | править код]
При испытании длительностью 3000 часов из 1000 изделий отказало 150. тогда интенсивность отказов этих изделий:

Например, средние значения интенсивностей отказов в период нормальной эксплуатации составляют:
Наиболее статистически надёжные данные по интенсивности отказов собраны для электронных компонентов.
См. также[править | править код]
- Наработка на отказ
- Показатели надежности
- Расчёт надёжности
- ГОСТ 27.002—89 (На викитеке)
Литература[править | править код]
- Половко А. М. Основы теории надежности — М.: Наука, 1964. — 446 с.
- Интенсивность отказов по ГОСТ 27.002-89 — восстановлен на территории РФ приказ № 1843-ст от 29.11.2012. (ИУС 3-2013).
-
Расчет интенсивности отказов.
Среднее значение
наработок изделий в партии до первого
отказа называется средней наработкой
до первого отказа. Этот термин применим
как для ремонтируемых, так и для
неремонтируемых изделий. Для неремонтируемых
изделий вместо названного можно применять
термин средняя наработка до отказа.
ГОСТом 13377 – 67 для
неремонтируемых изделий введен еще
один показатель надежности, называемый
интенсивностью отказов.
Интенсивность
отказов есть вероятность того, что
неремонтируемое изделие, проработавшее
безотказно до момента t,
откажет в последующую единицу времени,
если эта единица мала.
Интенсивность
отказов изделия есть функция времени
от его работы.
Задание :
– рассчитать
интенсивность отказов λ(t)
для заданных значений t
и Δt.
– в предположении,
что безотказность некоторого блока в
электронной системе управления автомобиля
характеризуется интенсивностью отказов,
численно равной рассчитанной, причем
эта интенсивность не меняется в течение
всего срока его службы, необходимо
определить наработку до отказа ТБ
такого блока.
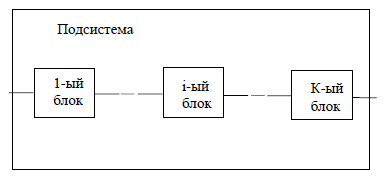
Подсистема
управления включает в себя k
последовательно соединенных электронных
блоков ( рис.2).
Рис.2 Подсистема
управления с последовательно включенными
блоками.
Эти блоки имеют
одинаковую интенсивность отказов,
численно равную рассчитанной. Требуется
определить интенсивность отказов
подсистемы λП
и среднюю наработку ее до отказа

построить зависимости вероятности
безотказной работы одного блока РБ(t)
и подсистемы РП(t)
от наработки и определить вероятности
безотказной работы блока РБ(t)
и подсистемы РП(t)
к наработке t=
TП.
Интенсивность
отказов λ(t)
рассчитывается по формуле:

Где
– статистическая вероятность отказа
устройства на интервале [t,t+Δt]
или иначе статистическая вероятность
попадания на указанный интервал случайной
величины Т.
Р(t)
– рассчитанная на шаге 1 – вероятность
безотказной работы устройства.
Δt=3*
103ч.
Заданное значение
103ч
– 6,5
Р(t)
= 0,4
Интервал [t,t+Δt]
= [6,5*103ч
;9,5*103ч]
= 20/50 = 0,4
λ(t)
= 0,4 / 0,4*3*103ч
= 0,00033
Предположим, что
интенсивность отказов не меняется в
течение всего срока службы объекта,
т.е. λ(t)
= λ = const,
то наработка до отказа распределена по
экспоненциальному (показательному)
закону.
В этом случае
вероятность безотказной работы блока:
(6)
РБ(t)
= exp
(-0.00033*6.5*103)
= exp(-2.1666)
= 0.1146
А средняя наработка
блока до отказа находится как:
(7)
= 1/0,00033 = 3030,30 ч.
При последовательном
соединении k
блоков интенсивность отказов образуемой
ими подсистемы:
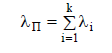
Т.к.интенсивности
отказов всех блоков одинаковы, то
интенсивность отказов подсистемы:
(9)
λП
= 4*0,00033 =
0,00132 ч.,
а вероятность
безотказной работы системы:
(10)
РП(t)
= exp
(-0.00132*6.5*103)
= exp
(-8,58) = 0.000188
С учетом (7) и (8)
средняя наработка подсистемы до отказа
находится как:

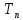
Вывод:
по мере приближения к предельному
состоянию – интенсивность отказов
объектов возрастает.
-
Расчет вероятности
безотказной работы.
Задание:
Для наработки t =

безотказной работы Рс(
системы (рис. 3), состоящей из двух
подсистем, одна из которых является
резервной.
Рис. 3 Схема системы
с резервированием.
Расчет ведется в
предположении, что отказы каждой из
двух подсистем независимы.
Вероятности
безотказной работы каждой системы
одинаковы и равны РП(
Тогда вероятность отказа одной подсистемы:
QП(
= 1 – 0,000188 = 0,99812
Вероятность отказа
всей системы
определяется из условия, что отказала
и первая, и вторая подсистемы, т.е.:
= 0,998122=
0,99962
Отсюда вероятность
безотказной работы системы:
,
Рс(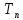
= 1 – 0,98 = 0,0037
Вывод:
в данном задании была рассчитана
вероятность безотказной работы системы
при отказе первой и второй подсистемы.
По сравнению с последова-тельной
структурой вероятность безотказной
работы системы меньше.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интенсивность отказов элементов | areliability.com блог инженера по надёжности
Интенсивность отказов
Интенсивность отказов, она же λ (в англоязычной литературе failure rate) является параметром, определяющим надёжность того или иного элемента (составной части) системы. λ, это как правило табличное значение, задаётся в размерности 10 в минус 6 степени отказов в час (отказов на миллион часов работы). Интересно, что в советской литературе использовалось более грамотное на мой взгляд понятие – опасность отказа.
К сожалению, λ для нужного оборудования найти порой бывает очень сложно. Чтобы как-то облегчить жизнь своим собратьям по цеху, инженерам по надёжности, ниже я выкладываю значения λ для некоторых видов оборудования. Источник: Н.М. Дубинский – «Надёжность систем газоснабжения», который в своей книге в свою очередь ссылается на данные национальных симпозиумов по контролю качества и надёжности, состоявшихся в США в 1961-1963 гг.
| Элементы | Интенсивность отказов, λ 10-6, ч-1 | Интенсивность отказов, λ 10-6, ч-1 | Интенсивность отказов, λ 10-6, ч-1 |
|---|---|---|---|
| Максимальная | Средняя | Минимальная | |
| Аккумуляторы (давления) | 19.3 | 7.2 | 0.35 |
| Арматура | 0.121 | 0.087 | 0.0035 |
| Арматура осветительная | 0.71 | 0.1 | 0.04 |
| Баки | 2.52 | 1.5 | 0.48 |
| Вентили соленоидные | 19.7 | 11 | 2.27 |
| Вентиляторы | 3.57 | 2.4 | 0.89 |
| >> вытяжные | 9 | 0.225 | 0.21 |
| Вентиляционные каналы | 1.3 | 0.51 | 0.21 |
| Вибрационные механизмы | 1.6 | 0.875 | 0.2 |
| Воздуходувки | 4.38 | 2.237 | 0.9 |
| >> с электродвигателем | 5.487 | 2.8 | 0.113 |
| Выводы электрические | 0.08 | 0.045 | 0.02 |
| Выключатели: | |||
| >> автоматические | 0.949 | 0.1375 | 0.045 |
| >> быстродействующие (на 1 контакт) | 2.1 | 0.4 | 0.09 |
| >> типа тумблер (на 1 контакт) | 0.123 | 0.06 | 0.015 |
| >> тепловые | 0.5 | 0.3 | 0.25 |
| Выпрямители | 0.75 | 0.6 | 0.28 |
| >> селеновые | 1.6 | 1.16 | 0.32 |
| Генераторы перменного тока | 18.82 | 15 | 11 |
| >> постоянного тока | 21 | 12.4 | 2.84 |
| Гнезда (на 1 штрек) | 0.02 | 0.01 | 0.001 |
| Датчики: | |||
| >> давления | 6.6 | 3.5 | 1.7 |
| >> оптические | 6.66 | 4.7 | 2.7 |
| >> температуры | 6.4 | 3.3 | 1.5 |
| >> уровня жидкости | 3.73 | 2.6 | 1.47 |
| Двигатели: | |||
| >> асинхронные | 11.2 | 8.6 | 4.49 |
| >> вентиляторные | 19 | 2.25 | 0.159 |
| >> гидравлические | 7.15 | 4.3 | 1.45 |
| >> синхронные | 6.25 | 3.59 | 0.159 |
| Держатели плавких предохранителей | 0.1 | 0.02 | 0.008 |
| Диафрагмы | 9 | 6 | 0.1 |
| Диоды | 1.47 | 0.2 | 0.16 |
| >> германиевые | 0.678 | 0.157 | 0.002 |
| >> кремнивые | 0.452 | 0.2 | 0.021 |
| Зажимы, клеммы | 0.0009 | 0.0005 | 0.0003 |
| Изоляторы | 1.54 | 0.05 | 0.03 |
| Изоляция | 0.72 | 0.5 | 0.011 |
| Кабели | 2.2 | 0.475 | 0.002 |
| Клапаны: | |||
| >> впускные | 5.33 | 3.4 | 1.33 |
| >> запорно-выпускные | 10.2 | 6.5 | 1.98 |
| >> контрольные | 8.1 | 5 | 2.02 |
| >> ножевые | 7.4 | 4.6 | 1.08 |
| >> обратные | 14.1 | 5.7 | 3.27 |
| >> переключающие | 1.62 | 0.5 | 0.26 |
| >> перепусные | 8.13 | 5.88 | 1.41 |
| >> предохранительные | 8.94 | 5.7 | 2.24 |
| >> разгрузочные | 19 | 10.8 | 1.98 |
| >> регулирующие | 19.8 | 8.5 | 1 |
| >> резервуарные | 10.8 | 6.88 | 2.7 |
| >> спускные | 15.31 | 5.7 | 3.41 |
| >> трехходовые | 7.41 | 4.6 | 1.87 |
| >> четырехходовые | 7.22 | 4.6 | 1.81 |
| >> шаровые | 7.7 | 4.6 | 1.11 |
| Конденсаторы | 2.385 | 0.1 | 0.001 |
| Коробки передач | 4.3 | 0.63 | 0.051 |
| Лампы накаливания | 32 | 8 | 5.2 |
| Лампы электронные: | |||
| >> диод | 2.2 | 0.8 | 0.24 |
| >> двойной диод | 1.89 | 1 | 0.38 |
| >> триод | 2.26 | 1.3 | 0.67 |
| >> двойной триод | 3.88 | 2 | 1.17 |
| >> тетрод | 2.9 | 1.6 | 0.88 |
| >> миниатюрные | 2 | 1.2 | – |
| Индуктор | 7.11 | 5.65 | 2.02 |
| Манометр | 7.8 | 4 | 0.135 |
| Манометры гидро/пневматические | – | 1.123 | – |
| Муфты | 1.1 | 0.4 | 0.06 |
| >> электромагнитные | 0.93 | 0.6 | 0.45 |
| >> предохранительные фрикционные | 0.94 | 0.3 | 0.07 |
| Нагреватели | 7.67 | 0.7 | 0.081 |
| Насосы: | |||
| >> вакуумные | 16.1 | 9 | 1.12 |
| >> с гидравлическим приводом | 45 | 14 | 6.4 |
| >> с механическим приводом | 31.3 | 13.5 | 3.33 |
| >> с пневматическим приводом | 49 | 14.7 | 6.9 |
| >> с электроприводом | 27.4 | 13.5 | 2.9 |
| Передачи зубчатные, редукторы | 0.36 | 0.2 | 0.11 |
| Передачи винтовые | 0.098 | 0.05 | 0.002 |
| Переключатели | 1.14 | 0.05 | 0.009 |
| Подшипники: | |||
| >> игольчатые | 1 | 0.5 | 0.02 |
| >> роликовые | 1 | 0.5 | 0.02 |
| >> скольжения | 0.42 | 0.21 | 0.008 |
| >> шариковые высокоскоростые | 3.53 | 1.8 | 0.072 |
| >> шириковые низкоскоростные | 1.72 | 0.875 | 0.035 |
| Потенициометры | 12.5 | 3 | 0.7 |
| Предохранители плавкие | 0.82 | 0.5 | 0.38 |
| Привод: | |||
| >> пневматический | 6.2 | 2.8 | 0.3 |
| >> ременной | 15 | 3.875 | 0.142 |
| Шайбы | 0.015 | 0.01 | 0.0005 |
| Прокладки: | |||
| >> кольцевые | 0.035 | 0.02 | 0.01 |
| >> резиновые | 0.03 | 0.02 | 0.01 |
| Пружины | 0.03 | 0.0125 | 0.004 |
| Регуляторы | 5.54 | 2.14 | 0.7 |
| >> давления | 15.98 | 7.5 | 3.55 |
| >> >> гидравлические | – | 3.55 | – |
| >> >> пневматические | 15.98 | 7.5 | 3.55 |
| Регуляторы напряжения угольные автоматические | 13.16 | 9.65 | 6.09 |
| Регуляторы пневматические | 6.21 | 2.4 | 0.77 |
| >> потока и давления | 5.54 | 2.14 | 0.77 |
| >> расхода гелия | 5.26 | 2.03 | 0.65 |
| >> малые выского давления | 0.144 | 0.08 | 0.044 |
| >> малые нормального давления | 0.324 | 0.18 | 0.1 |
| Серводвигатели | 5.61 | 1.51 | 0.101 |
| Сервомеханизмы | 3.4 | 2 | 1.1 |
| Соленоиды | 0.55 | 0.05 | 0.036 |
| Соединения: | |||
| >> вращающиеся | 9.55 | 7.55 | 6.89 |
| >> гибкие | 1.348 | 0.039 | 0.027 |
| >> гидравлические | 2.01 | 0.03 | 0.012 |
| >> механические | 1.96 | 0.02 | 0.011 |
| >> паяные | 1.05 | 0.004 | 0.0001 |
| >> пневматические | 1.15 | 0.04 | 0.021 |
| Счетчики | 5.25 | 4.2 | 3.5 |
| Счетчики электрические | 5.37 | 0.036 | 0.005 |
| Теплообменники | 18.6 | 15 | 2.21 |
| Трансформаторы | 2.08 | 0.15 | 0.01 |
| Турбины | 16.67 | 10 | 3.33 |
| Фильтры: | |||
| >> механические | 0.8 | 0.3 | 0.045 |
| >> электрические | 3 | 0.345 | 0.14 |
| Цилиндры: | |||
| >> гидравлические | 0.12 | 0.008 | 0.005 |
| >> двигателей | 0.81 | 0.007 | 0.005 |
| >> пневматические | 0.013 | 0.004 | 0.002 |
| Шестерни | 0.95 | 0.12 | 0.002 |
| Шланги | 3.22 | 2 | 0.05 |
| >> высокого давления | 5.22 | 3.93 | 0.157 |
| >> пневматические | – | 3.66 | – |
| Щетки электрических вращающихся устройств | 1.11 | 0.1 | 0.04 |
| Щеткодержатели | 4.11 | 1.3 | 0.87 |
| Электродвигатели: | |||
| >> переменного тока | 9.36 | 5.24 | 1.12 |
| >> постоянного тока | – | 9.36 | – |
| Элементы нагревательные | 0.04 | 0.02 | 0.01 |
| Ящики соединительные | 0.58 | 0.4 | 0.28 |
| Испарители | 20 | 15 | 5 |
Для некоторых компонентов производители выкладывают данные по надежности оборудования прямо на своих сайтах, но чаще всего там вы найдете не интенсивность отказов, а наработку на отказ, известную за рубежом как MTBF – Mean time between failures. Еще можно встретить такой параметр как MTTF – Mean time to failure.
Разница между ними в том, что MTBF, наработка между отказами, применяется для восстанавливаемого прибора, а MTTF, наработка до отказа, применяется для неремонтопригодных изделий.
Вот к примеру Cisco не стесняется и выкладывает MTBF для некоторых своих устройств на своем сайте:
Интенсивность отказов и наработка на отказ связаны друг с другом известными соотношениями:
(1)
(2)
Я сделал специальный калькулятор, с помощью которого вы можете быстро перевести MTBF в часах в интенсивность отказов (напоминаю, что размерность интенсивности отказов – число отказов на миллион часов работы). Обратите внимание, калькулятор автоматически преобразует получившееся число в размерность 10 в минус 6 степени отказов в час (отказов на миллион часов работы). Например, если вы введете в поле MTBF 1000000 часов, то на выходе вы получите 1 – один отказ на миллион часов работы. Данные вводите без точек, без текста, только числа.
И обратный калькулятор, с помощью которого вы можете быстро перевести λ в наработку до отказа в годах или часах. Например, по приведенной таблице вы нашли, что интенсивность отказов манометра составляет 1.3 на 10 в минус 6 степени. Для расчёта берите значение именно 1.3, степень вводить не надо, калькулятор автоматически переведёт в нужную размерность.
Зная интенсивность отказов оборудования и требуемое время непрерывной работы мы можем легко посчитать ВБР изделия по классической формуле надежности (формула 26 из ГОСТ Р МЭК 61078-2021):
(3)
Точно так же, можете воспользоваться моим калькулятором. Значения интенсивности отказов для многих элементов конструкций можно найти здесь. Например, по приведенной по ссылке таблице вы нашли, что интенсивность отказов манометра составляет 1.3 на 10 в минус 6 степени. Для расчёта берите значение именно 1.3, степень вводить не надо, калькулятор автоматически переведёт в нужную размерность.
Интенсивность отказов удобна тем, что зная интенсивности отказов каждого элемента системы мы можем легко определить его ВБР и наработку на отказ. Для этого нужно просто сложить все интенсивности отказов оборудования и воспользоваться формулой (3) – если хотим найти ВБР или формулой (1) если хотим найти наработку. Важно! Это будет справедливо только для схемы без резервирования элементов. Как считать ВБР и наработку если в системы используются различные схемы резервирования – приходите к нам учиться. Расскажем и детально покажем.
Интенсивность отказов электрических соединений
В методичке по проектированию РЭС (1996 года издания) обнаружилась интересная таблица про электрические соединения.
| Вид соединения | Переходное сопротивление, 10-3, Ом |
Механическая прочность, Мпа | Интенсивность отказов, λ 10-9, 1/ч |
Тепловое сопротивление, К/Вт |
|---|---|---|---|---|
| Сварка | 0.01 | 100…500 | 0.1 … 2.0 | 0.001 |
| Накрутка | 1…2 | 60… 80 | 0.2 … 0.5 | 0.0005 |
| Пайка | 2…3 | 10…40 | 1 … 10 | 0.002 |
| Обжимка | 1…10 | 20…50 | 2 … 5 | 0.0008…0.001 |
| Соединение токопроводящими клеями | 1…10 | 5…10 | 10 … 50 | 5 |
Дополнительно выкладываю справочник 2004 года «Надёжность электрорадиоизделий», разработанный одним из оборонных институтов страны. Думаю, что поскольку на дворе 2022 год, его можно выложить. Справочник доступен по ссылке.
Так же можно воспользоваться американским стандартом MIL-HDBK-217F. Потребуется знание английского языка.
Скачать MIL-HDBK-217F можно здесь. 6 мегабайт.
Для неэлектронных компонентов
Если интересует параметры по надежности неэлектронных компонентов, лучшим решением будет посмотреть справочник NRPD-91 (non-electronic reliability part data). Потребуется знание английского языка. Есть и более свежие версии этого справочника, они платные.
Скачать NRPD-91 можно здесь. 39 мегабайт.
Если вы хотите заказать у меня расчет надежности – нажмите на эту ссылку или на кнопку ниже.
Внимание! Если вас интересует корпоративное групповое обучение специалистов вашей компании, пожалуйста перейдите по ссылке ниже. Возможна адаптация учебной программы под ваши требования/пожелания/возможности как по объёму учёбы срокам обучения, формату обучения, так и по балансу теория/практика.
До встречи на обучении! С уважением, Алексей Глазачев. Инженер и преподаватель по надежности.
1. Основные понятия и определения надежности.
Надежность – свойство объекта выполнять заданные функции, сохраняя во времени и в заданных пределах значения, установленных эксплуатационных показателей.
Элемент— один или несколько однотипных устройств, предметов, имеющих количественные характеристики надежности, учитываемые при расчете надежности всего соединения.
Ячейка – отдельная механическая конструкция, не имеющая самостоятельного функционального назначения.
Узел (блок)— несколько деталей, ячеек, объединенных для выполнения определенной функции, но не имеющих как целое самостоятельного эксплуатационного назначения. ( регистр команд, счетчик циклов, дешифратор операций).
Устройство—соединение деталей, узлов, имеющее самостоятельное эксплуатационное назначение блок питания, арифметическое устройство (АУ) и т. д.
Прибор — группа блоков, имеющая конструктивно самостоятельное назначение.
Установка — группа приборов.
Система—устройство, состоящее из нескольких установок. Надежность его имеет самостоятельное значение.
Различают системы восстанавливаемые (после отказов их можно ремонтировать) и невосстанавливаемые
Отказ—это частичная или полная утрата свойств элемента, которая существенным образом снижает или приводит к полной потере работоспособности. Отказ наступает всякий раз, когда устройство не сохраняет своих параметров в заданных пределах.
По характеру возникновения отказы могут быть разделены на внезапные и постепенные. Внезапные отказы определяются резким изменением параметров, определяющих качество изделия -предвидеть невозможно. Постепенные отказы возникают при постепенном изменении параметров, определяющих качество изделия в результате старения или износа, когда эти параметры выходят за установленные пределы.
По признакам проявления: явные, неявные. По взаимосвязи между собой: зависимые и независимые. По степени взаимодействия: полные и частичные. По хар-ру воздействия: самовостанавлив, временные, перемежающиеся. По хар-ру устранения: расстройки, повреждения, аварии.
Неисправность — изменение характеристик системы без изменения качества функционирования всей аппаратуры.
Система исправна, если она соответствует всем предъявляемым требованиям, т. е. все ее параметры, как основные, так и второстепенные, находятся в заданных пределах. Выход любого параметра из этих пределов означает неисправность. Система работоспособна, если она нормально выполняет заданные функции и ее основные параметры находятся в пределах нормы. Утрата работоспособности означает отказ.
Простые системы. Они при отказе элементов либо полностью теряют работоспособность, либо продолжают свои функции в полном объеме, если отказавший элемент зарезервирован. Такие системы могут находиться только в двух состояниях: рабочем и нерабочем.
Сложные системы. Они обладают способностью при отказе элементов продолжать выполнение своих функций, но с пониженной эффективностью, т. е. могут находиться в нескольких рабочих состояниях. К сложным системам обычно относят многоканальные комплексы с разветвленной структурой, состоящие из нескольких самостоятельных, но взаимосвязанных устройств, например автоматизированные системы управления ПВО, предприятиями и др.
2. Вероятность исправной работы. Среднее время безотказной работы. Среднее время между отказами.
Вероятность исправной (безотказной) работы. Пусть имеется совокупность элементов, каждый из которых характеризуется неотрицательной случайной величиной Т, называемой длительностью его безотказной работы. Длительность безотказной работы будет «возрастом» элемента к моменту, когда произойдет отказ. Случайная величина Т является неотрицательной и имеет дискретное или непрерывное распределение.
Практический интерес представляет второй случай, когда время безотказной работы имеет непрерывное распределение. По определению, функцией распределения (интегральным законом распределения) случайной величины Т называется функция F (t) =Р {Т<=t}, определяемая как вероятность того, что элемент отказал до момента t. Для целей расчета надежности удобнее пользоваться функцией, дополнительной к F (t) и называемой вероятностью безотказной работы P(t). Эта функция задает вероятность того, что элемент не откажет до момента времени t. Очевидно, что Р (t) = = Р {Т > t}, Р(0)=1, Р(оо)=0 и является невозрастающей функцией времени.
При испытании партии изделий вероятность исправной работы

где N0—число изделий в начале испытаний; пk—число изделий, которые вышли из строя в интервале времени ?tk; t—время, для которого определяется вероятность исправной работы; ?tk—принятая продолжительность интервала времени наблюдения; N (t) — число изделий, исправно работающих в интервале [0, t]. Вероятность отказа
(1.2)
Согласно (1.2),
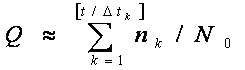
Среднее время безотказной работы. Под этим термином в теории надежности понимается математическое ожидание времени исправной работы:
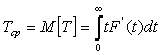
Практически среднее время исправной работы однотипных элементов
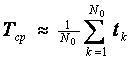
где N0—число элементов, над которыми проводятся испытания; tk—время исправной работы
k-го элемента. Так как трудно определить tk, удобнее пользоваться другим выражением:
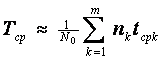
где 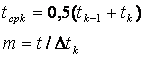
t—время, в течение которого вышли из строя все элементы; ?tk—величина интервала времени.
Величина Tср позволяет определить количество запасных элементов за время работы, но полностью не характеризует надежность элементов. При равенстве Тср у двух каких-либо групп элементов, имеющих разное распределение отказов, надежность может быть неодинаковая. Среднее время Тср до ремонта отличается от Т’ср после ремонта. Они равны, если элементы не изнашиваются, т. е. не зависят от времени.
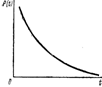
Q(t)=F(t). (1.8)
Вероятность того, что за время t не произойдет отказа,
P(t)=1-Q(t)=1-F(t), (1.9)
Q‘(t)=dF(t)/dt. (1.10)
Следовательно, среднее время работы есть математическое ожидание случайной величины:
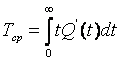
тогда из (1.9) получаем
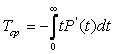
Интегрирование по частям
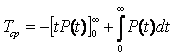
с учетом—[tP(t)]?0=0, дает выражение
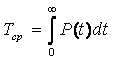
Число элементов, которые будут работать непрерывно к моменту t, определяется из (1.1):
N(t)=N0P(t). (1.15)
За интервал ?t число отказавших элементов
п (t) = N (t)-N(t + ?t) = N0 [Р (t)-Р (t +?t)]. (1.16)
Среднее время между отказами. Это математическое ожидание исправной работы между соседними отказами:
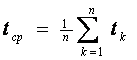
где п—число отказавших элементов; tk—время исправной работы между (k—1)-м и k-м отказом аппаратуры.
3. Интенсивность отказов. Частота отказов. Средняя и суммарная частота отказов. Среднее время восстановления.
Интенсивность отказов. Отношение числа отказавших изделий в единицу времени к среднему числу изделий, продолжающих исправно работать, есть интенсивность отказов (ч-1)
(1.19)
где п(t)—число отказавших элементов в отрезке времени от t—?t/2 до t+?t/2; ; Nk-i(t)— число исправных элементов в начале интервала времени ?t; Nk(t)—число исправно работающих элементов в конце интервала ?t.
Интенсивность отказов называют ?-характеристикой. Таким образом, интенсивность отказов показывает, какая часть элементов выходит из строя в единицу времени по отношению к среднему числу исправно работающих элементов.
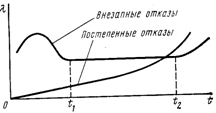
Как видно из рис. 1.1, работа элементов и систем характеризуется тремя этапами. Первый этап ([0, t1]—период доводки)—начальный, отличается небольшим количеством отказов. Здесь выходят из строя элементы с малым запасом прочности. Тренировка деталей повышает эксплуатационную надежность. Второй этап ([t1, t2] – период нормальной эксплуатации) характеризуется пониженным уровнем и примерным постоянством интенсивности отказов. Здесь отказы в основном носят внезапный характер. Продолжительность этого периода зависит от среднего срока службы элементов и от условий эксплуатации. Третий этап (от t2 и далее—период старения) обусловлен износом и старением элементов и характерен значительным ростом числа отказов. С наступлением этого периода дальнейшая эксплуатация системы нецелесообразна.
Частота отказов. Отношение числа отказавших изделий в единицу времени к первоначальному числу испытываемых изделий при условии, что число испытываемых изделий во время испытания уменьшается, есть частота отказов (ч-1)
(1.20)
где п (t)—число отказавших изделий в интервале времени от t—?t/2 до t+?t/2; N0—первоначальное число испытываемых изделий.
По величине частоты отказов рассчитывают число запасных изделий:
(1.21)
Рис. 1.2. Частота отказов а (t)

Подставляя в (1.20) значение п(t) из (1.16), получаем а(t)={N0[P(t)—P(t+?t)]}/(N0?t). Если ?t?0, то
a(t)=-P‘(t)=Q‘(t), (1.22)
т. е. частота отказов есть плотность распределения времени выхода элементов из строя.
Тогда
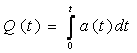

Подставляя в (1.19) значение п(t) из (1.16), получаем выражение интенсивности отказов в следующем виде:
?(t)=-dP/[P(t)dt]. (1.25)
Интегрируя обе части (1.25) в интервале от 0 до t, получаем, т.е.
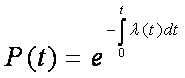
Рис. 1.3. Экспоненциальный закон надежности
Если ?(t)= const. то (1.26) представляет собой экспоненциальный закон надежности. По этому закону вероятность исправной работы элементов, обладающих интенсивностью отказов ?, убывает со временем по экспоненциальной кривой (рис. 1.3). Это справедливо на нормальном участке работы системы, когда эффект старения неощутим. Такую кривую называют функцией надежности. Она имеет большое значение для практического использования, когда необходимо знать, с какой вероятностью АСУ способна выполнить задание, требующее определенной продолжительности безотказной работы. Подставив значение Р (t) в (1.14), получим
Если ?(t) равна постоянной величине ,то
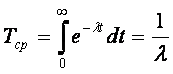
где ? = 1/Тcр—среднее число отказов в единицу времени.
Тогда (1.26) принимает вид
(1.28)
Важное характеристическое свойство показательного закона надежности, которое состоит в том, что вероятность безотказной работы P[t, t+?] в некотором интервале [t, t+?] не зависит от времени предшествующей работы t, а определяется только интенсивностью отказов и длиной интервала ?? Другими словами, будущее поведение элемента в смысле безотказного функционирования не зависит от прошлого, если нам известно, что до момента t элемент не отказал. Действительно, по формуле для полной вероятности имеем
4. Критерии надежности для восстанавливаемых систем.
Во введении было дано качественное определение надежности АСУ. Это определение должно быть дополнено количественными характеристиками. На их основании сравниваются между собой различные системы с точки зрения их надежности, кроме того, и технические условия включаются вполне определенные требования, что важно при разработке новых систем.
Количественные критерии применяют в зависимости от назначения систем или ее фактического использования. В связи с этим различают три класса систем.
К I классу относятся системы, которые по условиям не могут ремонтироваться во время работы. От этих систем требуется безотказная работа в течение заданного времени:
(1.35)
Системы II класса должны в произвольный момент времени быть готовыми к работе и не иметь неисправностей в течение заданного времени. Обычно этот класс систем длительно находится в состоянии готовности, а используется кратковременно, в случае необходимости. Аппаратура II класса ремонтируется во время эксплуатации. Характеристикой таких восстанавливаемых систем является вероятность успешного использования
(1.36)

К III классу относится аппаратура, использующаяся непрерывно, т. е. наибольшую часть времени работает безотказно. Так, при использовании машин для решения математических задач в вычислительных центрах желательно получить наибольший процент полезного рабочего времени в пределах каждого рабочего
цикла. В этом случае важной характеристикой, учитывающей возможность восстановления аппаратуры после появления отказов, является коэффициент готовности
(1.37)
Эта вероятность зависит от того, насколько быстро достигается восстановление рабочего состояния системы после отказа, поэтому данная характеристика для систем многоразового действия является важным параметром наряду с вероятностью безотказной работы. Современным требованиям отвечают те устройства, которые имеют высокую степень ремонтопригодности.
Дадим вывод коэффициента готовности при следующих предположениях: 1) поток отказов системы носит пуассоновский характер и интенсивность отказов равна ?; 2) время восстановления системы является случайной величиной, распределенной по экспоненциальному закону F(х)= 1-е?x, где ?— интенсивность восстановления; 3) система может находиться в двух состояниях: состоянии х(t)=1 (работоспособности) и состоянии x(t) = 2 (ремонта). Диаграмма состояний системы изображена на рис. 1.6.
Здесь tpi— интервал времени, в течение которого система работоспособна; tbi — интервал времени, в течение которого система ремонтируется. Это случайные величины, распределенные по показательному закону с параметрами ?и ? соответственно.
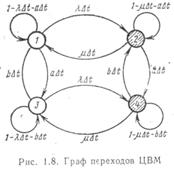
Поведение системы с точки зрения работоспособности опишем графом переходов (рис. 1.7). На этом рисунке кружки с номером обозначают состояние системы, а стрелки (дуги) – направление переходов системы и вероятности этих переходов за бесконечно малый интервал времени.
Вероятности переходов в силу сделанных предположений и свойства показательного закона надежности не зависят от времени t. Введем вероятности нахождения системы в состояниях 1 и 2 как p1(t) и p2(t). Очевидно, что pl(t) +p2(t) = 1 для любого момента времени.
Рассмотрим поведение системы в интервале времени [0, t+?t]. Тогда система в момент t+?t будет находиться в состоянии 1, если она в момент tнаходилась в этом состоянии и за время ?t не наблюдалось отказов, а также, если система в момент времени tнаходилась в состоянии 2 и завремя ?t был закончен ее ремонт.
Следовательно, р1(t+?t) = (1-??t)pl(t) + ?p2(t)?t +0(?t). Аналогичные рассуждения приводят к уравнению для р2(t+?t) = (1-??t)p2(t) + ?p1(t)?t +0(?t). Предельный переход ?t—>0 дает дифференциальные уравнения, описывающие поведение системы во времени:
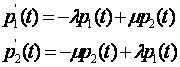
Решая (1.38), получаем дифференциальное уравнение для искомых вероятностей
(1.39)
Общий интеграл уравнения (1.39)
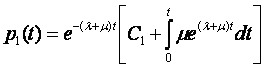
позволяет оценить вероятности состояния в зависимости от начального состояния:
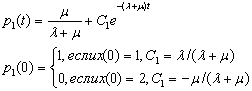
(1.42)
(1.43)
Таким же образом определяют вероятности нахождения системы в состоянии ремонта при условии, что в начальный момент система была или работоспособна [р21(t)] или неработоспособна [р22(t)]:
(1.44)
(1.45)
При t>? выражения (1.42) и (1.43) приобретают вид
(1.46)
При сравнении разных систем по коэффициенту готовности необходимо учитывать также и некоторые другие показатели рассматриваемой системы, в том числе стоимость, габариты, вес, эксплутационные расходы и др.
Проведем анализ работы АСУ на примере вычислительной системы, выполняющей случайные задания. Если заявка на решение задачи придет в момент, когда машина находится в ремонте, то задание не будет выполнено. Это может привести к нежелательным результатам. Аналогичная ситуация возникает, если во время решения задачи происходит отказ. Пусть нас интересует момент первого несвоевременного выполнения задания или невыполнение задания вообще. Назовем это событие отказом на выполнение. Оценим вероятность этого события в следующих предположениях:
1) закон отказов вычислительной машины (ВМ) носит пуассоновский характер, интенсивность отказов ?;
2) время восстановления подчинено показательному закону с интенсивностью ?;
- вероятность поступления задания стационарна и для бесконечно малого промежутка времени ?t определяется как ??t;
- время решения задачи имеет экспоненциальное распределение
с параметром ?;
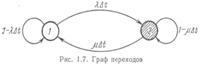
Возможны четыре состояния с точки зрения надежного функционирования системы: x=1 (BM исправна и простаивает из-за отсутствия задания); х = 2(ВМ в ремонте и задание на вычисления не поступало); х = 3 (ВМ исправна и решает задачу); х = 4 (ВМ в ремонте, заявка на решение поступила в систему).
Граф состояний с указанными вероятностями переходов для рассматриваемого случая изображен на рис. 1.8. Используя метод, примененный при выводе коэффициента готовности, получаем уравнения относительно вероятностей нахождения системы во всех состояниях:

Решая систему (1.47) и переходя к пределу, получаем стационарные вероятности нахождения системы во всех четырех состояниях:
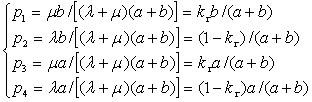
Тогда вероятность невыполнения задания определяется как
(1.49)
5. Количественные характеристики надежности при постепенных отказах.
Для аппаратуры, в которой имеют место постепенные отказы, обусловленные старением и износом, часто пользуются нормальным законом распределения. Поскольку значение времени безотказной работы — положительная величина, частота отказов
(1.50)
где С — постоянная усеченного нормального распределения, которую определяют из нормирующего условия 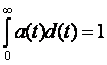
Если среднее квадратическое отклонение а невелико по сравнению с Т, то можно приближенно для расчетов пользоваться неусеченным нормальным распределением при С ?1/(?v2?). Тогда за время t исходное выражение количественного определения вероятности отказа элемента
a(t)= –P‘(t)=Q‘ (t)
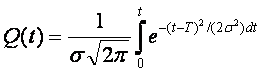
Здесь математическое ожидание времени исправной работы элемента, приближенно равное среднему времени исправной работы элемента, определяется экспериментально по результатам испытания партии однотипных элементов (испытания проводятся до выхода из строя всех элементов партии):
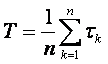
где tk —время работы k–гoэлемента до выхода его из строя; п — число испытываемых элементов партии (вместо Т может быть любой контролируемый параметр);
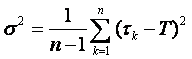
– дисперсия значений времени исправной работы различных элементов в испытуемой партии. Если п > 20, то можно заменить п-1 значением п. Если сделать замену вида
х = (1 — T)/?, то
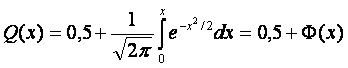
где первый член представляет половину площади, ограниченной кривой Гаусса, второй член Ф(х) — интеграл вероятности (значение этой функции см. в табл. П2).
Если (1.51) нормировано относительно х = (1 — T)/?, то
(1.55)
Вероятность исправной работы группы элементов, подверженных постепенным отказам,
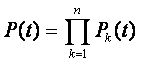
где n – число подгрупп с однотипными элементами.
6. Соотношение для определения надежности с учетом условий эксплуатации.
Формулы для вычисления надежности ЭВМ справедливы, если условия эксплуатации строго определены и соответствуют условиям, в которых получены характеристики ? и ?.
Условия эксплуатации в общем виде определяются комплексом интенсивностей внешних воздействий, климатических факторов (влажность, давление, температура), механических нагрузок (вибрации, ускорение, удары), эксплуатационных факторов (время работы, режим схемы, отклонения питающих напряжений). Если имеется п внешних факторов, то через ?1,?2,…,?n обозначим соответствующие интенсивности внешних воздействий. Обычно условия эксплуатации изменяются случайно в некоторых пределах, так что интенсивности внешних воздействий можно рассматривать как случайные величины со своими законами распределения вероятностей.
Пусть ?(?1,?2,…,?n,t) представляет собой многомерный закон распределения плотности вероятностей интенсивностей внешних воздействий в предполагаемых условиях эксплуатации.
Частота, и интенсивность отказов в функции интенсивностей внешних воздействий ?1,?2,…,?n будут
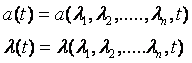
При этом надежность систем определяется как математическое ожидание функций интенсивностей:
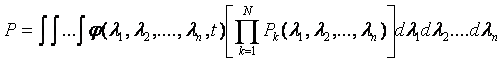
(1.58)
Таким образом, надежность основного устройства может быть определена при использовании соотношения .(1.58), если известны условные вероятности безотказной работы его узлов, функции интенсивностей внешних факторов Pk(?1,?2,…,?n) и плотность вероятностей ?(?1,?2,…,?n) интенсивностей внешних воздействий в предполагаемых условиях эксплуатации. Приближенная оценка надежности
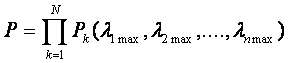
но величина надежности здесь существенно занижена.
Определить опытным путем переходные коэффициенты для самых разнообразных условий эксплуатации и для различных комбинаций воздействующих факторов и их величины практически почти невозможно. Поэтому возникает вопрос о получении математических зависимостей, позволяющих рассчитывать интенсивность отказов для различных условий эксплуатации и нагрузок. Для общности изложения в дальнейшем все внешние воздействия (в том числе и электрическая нагрузка) назовем термином «нагрузка».
Под коэффициентом нагрузки, который может изменяться от 0 до 1, понимается отношение ее рабочей величины к исходной номинальной нагрузке. Равенство коэффициента нагрузки нулю в некоторых случаях означает отсутствие нагрузки (электрической, вибрационной), в других условиях соответствует некоторому нормальному значению (тепловой). Итак, необходимо определить зависимость интенсивности отказов в виде ?=f(k), где k— обобщенное значение коэффициента нагрузки.
Из опыта эксплуатации ЭВМ известны следующие зависимости интенсивности отказов от коэффициента нагрузки:
а) при коэффициенте нагрузки, равном нулю, интенсивность отказов имеет некоторое значение ?0. Это объясняется тем, что даже при самых благоприятных условиях в радиодеталях протекают физико-химические процессы, приводящие к отказам;
б) функция ?1=f1(k) является монотонно возрастающей. С увеличением коэффициента нагрузки количество радиодеталей, выходящих из строя в единицу времени, возрастает;
в) функция ?‘=f2(k) является монотонно возрастающей. С увеличением коэффициента нагрузки на одну и ту же величину относительное изменение величины ? прямо пропорционально абсолютному значению коэффициента нагрузки;
г) при значениях коэффициента нагрузки, близких к нулю ?‘0=f2(k)=0. В этом случае незначительное изменение коэффициента не приводит к изменению величины ?.
Рассмотрим приращение функций ? и ?‘. В случае малых изменений коэффициента нагрузки ?k в первом приближении можно принять, что функции ?1 и ?2 линейно зависят от ?k и пропорциональны значению функции в начале интервала ?k. Таким образом, можно записать следующие выражения:
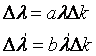
где а и b— некоторые коэффициенты.
При ?t>0 получим следующую систему уравнений:
произведя замену, получим d2?/dk2 — ab? = 0.
Решение этого дифференциального уравнения имеет вид
(1.61)
где А = vаb.
Так как f1(0) = ?0, f2(0) = 0, то, используя начальные условия, получаем
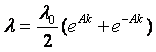
Данная функция удовлетворяет перечисленным выше условиям и свойствам.
Выражение (1.62) можно представить в следующем виде:
или
где ?0 — номинальная интенсивность отказов при воздействии нескольких видов нагрузок.
При малых значениях коэффициента нагрузки можно пренебречь слагаемыми начиная со второго члена. Тогда ? = ?0. Зная величину A для конкретного типа радиодеталей, можно установить диапазон вариации коэффициента нагрузки, при котором величина интенсивности отказов изменится незначительно. Это требование и следует соблюдать при проектировании ЭВМ. Используя (1.62), необходимо определить коэффициент нагрузки, в качестве которого можно принять: при электрической нагрузке – отношение рабочего значения некоторого электрического параметра (мощность, напряжение, ток) к его номинальному значению; при тепловой нагрузке – отношение абсолютной разности между рабочей температурой окружающей среды и номинальной температурой к номинальному значению температуры (20±5°С); при вибрационной нагрузке – отношение величины действующего ускорения к величине g0 = 9,81 м/с2, при влажности – отношение абсолютной разности между рабочим значением относительной влажности и его номинальным значением к номинальному значению влажности. За номинальное значение влажности принимают величину 65±15%. Аналогично определяют коэффициенты нагрузок для других случаев.
Если на некоторую радиодеталь действует несколько нагрузок k1,k2,…km, то при небольших их значениях можно считать воздействия независимыми. Тогда
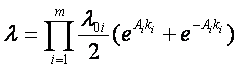
Подобный подход — приближенный и оказывается верным только при малых значениях коэффициентов нагрузок, так как между нагрузками существует корреляционная связь. Например, тепловой пробой совместно с электрическим вызывает выход триода из строя.
7. Параметры надежности при хранении систем.
Отказы аппаратуры и входящих в нее элементов наблюдаются не только .в процессе работы, но и в процессе хранения. Поэтому необходимо ввести параметры, характеризующие надежность системы при хранении.
Сохраняемость a(t) — вероятность того, что система (прибор, узел, деталь) сохраняет работоспособность в течение заданного срока хранения в определенных условиях и является аналогом вероятности безотказной работы при хранении. Понятие «работа» здесь используется условно лишь для удобства, так как речь идет на самом деле о неработающих элементах. Следовательно, сохраняемость характеризует те же параметры, что и вероятность безотказной работы, а именно ?хр и Tхр, связанные между собой зависимостью
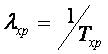
где Tхр—средняя «наработка» на отказ при хранении, равная математическому ожиданию времени между двумя последующими отказами; ?хр—интенсивность отказов элемента при хранении. Сохраняемость элемента
(1.65)
Так как сохраняемость принципиально ничем не отличается от работы (при условии справедливости экспоненциального закона), то определение параметров сохраняемости по данным эксперимента производится так же, как параметров безотказной работы.
Оценка
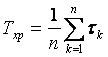
в случае испытания системы с заменой элементов и
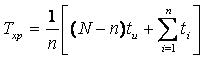
в случае испытания элементов без замены. Здесь п — число отказов; ?k — время между последовательными отказами; N—число элементов в партии, поставленной на испытание; tи — время испытания партии изделий; ti.— время работы 1-го изделия до отказа.
Готовность характеризуется коэффициентом готовности, который при работе и хранении различен. Это обусловлено тем, что отказ работающей системы устраняется сразу же после ее возникновения, а отказ хранящейся системы обнаруживается и устраняется лишь спустя некоторое время, при профилактике. От момента возникновения отказа до момента начала профилактики система неисправна. Коэффициент готовности kгпри хранении выводится следующим образом. Система не готова к работе в некоторый момент времени, если в ней имеется неустранимый отказ. В этом случае для некоторого интервала времени длительностью Тпроф (интервал времени между двумя последовательными профилактиками) kгесть отношение среднего времени, в течение которого в системе не было повреждений, к выражению (Тпроф + ?проф). Если повреждение устраняют через промежуток времени длины Тпроф, то в системе не будет повреждения от начала этого интервала до первого повреждения. Этот промежуток времени есть случайная величина ? с плотностью распределения вероятности
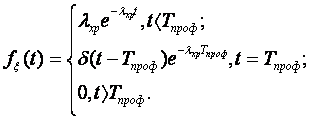
Случайная величина принимает значение в интервале [0, Tпроф], причем для значений, меньших Тпроф, функция плотности вероятности равна ?хре-?xpt. Вероятность того, что ? > Tпроф, будет
математическое ожидание случайной величины ?
тогда коэффициент готовности при хранении
(1.69)
где ?рем—среднее время ремонта.
Учитывая значения (1.68), получаем окончательное выражение для коэффициента готовности при хранении
8. Характеристики надежности сложных систем.
Отличительными чертами сложных систем, к которым относятся современные АСУ, являются: многоканальность, т. е. наличие нескольких каналов, каждый из которых выполняет определенную функцию, частную по отношению к общей задаче системы; многосвязность, т. е. большое количество функциональных связей между элементами системы; наличие вспомогательных и дублирующих устройств.
Благодаря перечисленным особенностям сложная система может находиться в нескольких рабочих состояниях, так как выход из строя некоторых ее элементов не вызывает полного отказа системы, т.е. прекращения выполнения ею заданных функций, но ухудшает в той или иной степени качество функционирования. Следовательно, отказ элемента переводит систему из состояния с полной работоспособностью в состояние с частичной работоспособностью.
ЛСУ можно характеризовать функциональной и эффективной надежностью.
Функциональная надежность РФ — вероятность того, что данная система будет удовлетворительно выполнять свои функции в течение заданного времени. Функциональная надежность отличается от определения надежности, данной в гл. 1, тем, что учитывает наличие схемы контроля в системе. В дальнейшем под функциональной надежностью понимается надежность, рассматриваемая в предыдущих главах.
Эффективная надежность РЭ — среднее значение (математическое ожидание) величины, характеризующей относительный объем и полезность выполняемых системой функций в течение заданного времени по сравнению с ее предельными возможностями. Введение критерия эффективной надежности объясняется тем, что одними показателями надежности, взятыми отдельно, не удается оценить функционирование сложной системы. Сложная система кроме надежности каждого блока и всей системы характеризуется еще относительной важностью потери системой тех или иных качеств поэтому под РЭ понимается некоторая количественная мера, оценивающая качество выполнения системой своих функций. В ряде случаев выполнение конкретной частной задачи с некоторой эффективностью требует работоспособности лишь части аппаратуры. С другой стороны, даже при полной работоспособности всех элементов системы нельзя говорить о выполнении некоторой задачи как о достоверном событии. Основная идея метода определения эффективной надежности заключается в том, что учитывают не только внутренние свойства самой системы, но и качество функционирования и выполнения задачи и выходной эффект.
Пусть система находится в каком-либо состоянии j. Эффективную надежность этой системы в данном состоянии называют частной (условной) эффективностью. Это может быть вероятность того, что система, находясь в состоянии j, способна решить задачу, выбранную случайным образом (независимо от состояния j) в соответствии с некоторым вероятностным законом из определенного множества задач. Тогда под эффективностью можно понимать количество задач, решенных системой в том пли ином состоянии.
Частная эффективность системы характеризуется вероятностью получения этой эффективности. В общем случае эффективная надежность системы со счетным множеством дискретных состояний определяется как математическое ожидание выходного эффекта
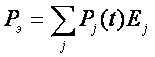
9. Матричный метод расчета надежности.
В ряде случаев отказ элемента системы приводит к изменению режимов работы других связанных с ним элементов, что может повлечь за собой изменение характеристик надежности этих элементов. Например, пробой конденсатора вызывает изменение тока в цепях схемы, в результате чего изменяются коэффициенты нагрузки элементов, а следовательно, и их надежность. В подобных случаях желательно при расчете надежности учитывать взаимозависимость отказов элементов и перераспределение интенсивностей отказов за счет изменения режимов работы, вызванных отказами. Для решения этой задачи может быть использован матричный метод анализа и расчета надежности (см. [4.5]), позволяющий учитывать последствие отказов.
Сущность метода состоит в том, что для определения вероятности безотказной работы ВМ от внезапных отказов с учетом последствия отказов составляется матрица всевозможных несовместимых событий x1, x2,…, xN, вычисляются вероятности всех этих событий, затем суммируются вероятности благоприятных гипотез, при которых система находится в работоспособном состоянии.
В общем случае матрица несовместимых событий для аппаратуры, состоящей из N элементов, за период t имеет следующий вид:
В этой матрице хi— состояние i-гo элемента; означает, что i элемент отказал; H0 — гипотеза, заключающаяся в том, что ни один из элементов не отказал; Нi — гипотеза, заключающаяся в том, что i-й элемент отказал; Н?,? — гипотеза отказа двух элементов ? и ?, причем вначале отказывает элемент ?, а потом ?.
Так как матрица образует полную группу несовместимых событий, то их можно принять за соответствующие гипотезы. Среди гипотез матрицы есть благоприятные с точки зрения работоспособности системы и неблагоприятные. Сумма вероятностей всех гипотез равна единице.
Сумма вероятностей благоприятных гипотез определяет надежность системы, т. е. вероятность безотказной работы за некоторое заданное время
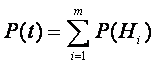
где m — число благоприятных гипотез.
Наиболее трудоемкой частью расчета является определение вероятностей гипотез (состояний), особенно для сложных устройств.
Вероятность отсутствия отказов элементов определяется произведением вероятностей безотказной работы всех элементов:
Вероятности остальных гипотез имеют более сложные выражения и определяются через условные вероятности частных событий. Приведем без вывода формулу для расчета вероятности отказа элемента :
где ???, ??? —изменение интенсивности отказов ?-ro элемента вследствие отказа ?-го элемента.
Таким образом, для выполнения расчета надежности с помощью данного метода необходимо знать интенсивности отказов элементов ? при нормальных режимах работы устройства и их изменения, вызванные сменой режимов за счет отказов различных элементов.
10. Повышение надежности автоматизированных систем управления путем резервировании. Методы резервирования. Общее постоянное резервирование с целой кратностью.
Резервированным соединением изделий называется такое соединение, при котором отказ наступает только после отказа основного изделия и всех резервных изделий.
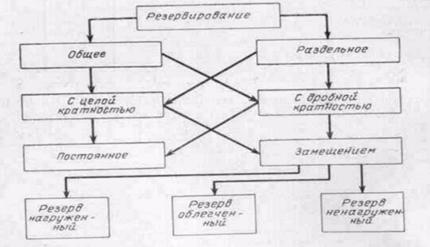
На практике применяются способы резервирования, приведенные на рис. 3.1. Схемные обозначения различных способов резервирования приведены на рис. 3.2. Общим резервированием называется метод повышения надежности, три котором резервируется изделие в целом (рис. 3.2,д). Раздельным резервированием называется
Рис. 3.1. Способы резервирования.
Рис. 3.2. Схемные обозначения различных способов резервирования: а — общее постоянное с целое кратностью: б — раздельное постоянное с целой кратностью, в — общее замещением с целой кратностью; г —раздельное замещением с целой кратностью; д — общее постоянное с дробной кратностью. е?раздельное замещением с дробной кратностью.
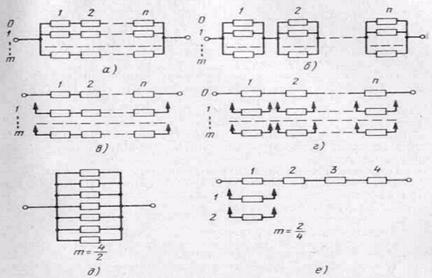
Различают резервирование с целой и дробной кратностью. Схемные обозначения обоих видов резервирования при постоянном включении резерва одинаковы. Для их различия на схеме указывается кратность резервирования m.
При резервировании с целой кратностью величина m есть целое число, при резервировании с дробной кратностью величина m есть дробное несокращаемое число. Например, m = 4/2 означает наличие резервирования с дробной кратностью, при котором число резервных элементов равно четырем, число основных — двум, а общее число элементов равно шести. Сокращать дробь нельзя, так как если m = 4/2=2, то это означает, что имеет место резервирование с целой кратностью, мри котором число резервных элементов равно двум, а общее число элементов равно трем.
По способу включения резервирование разделяется на постоянное и резервирование замещением. Постоянное резервирование — резервирование, при котором резервные изделия подключены к основным в течение всего времени работы и находятся в одинаковом с ними режиме. Резервирование замещением — резервирование, при котором резервные изделия замещают основные после их отказа.
При включении резерва по способу замещения резервные элементы до момента включения в работу могут находиться в трех состояниях:
— нагруженном резерве;
— облегченном резерве;
— ненагруженном резерве.
Приведем основные расчетные формулы для указанных выше видов резервирования.
1. Общее резервирование с постоянно включенным резервом с целой кратностью (рис. 3.2,а):

где pi(t) —вероятность безотказной работы i-го элемента в течение времени t; n — число элементов основной или любой резервной цепи; m — число резервных цепей (кратность резервирования).
При экспоненциальном законе надежности, когда pi(t)=e-?it

где 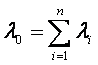
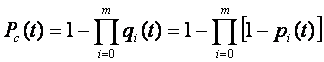
где qi(t), pi(t) — вероятность отказов и вероятность безотказной работы в течение времени t i-го изделия соответственно.
11. Раздельное постоянное резервирование с целой кратностью. Общее резервирование замещением с целой кратностью.
Раздельное резервирование с постоянно включенным резервом и с целой кратностью (рис. 3.2,6):
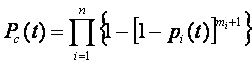
где pi(t) — вероятность безотказной работы i-гo элемента; mi—кратность резервирования i-гo элемента; n — число элементов основной системы.
При экспоненциальном законе надежности, когда pi(t)=e-?it
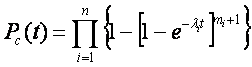
При равнонадежных элементах и одинаковой кратности их резервирования
(3.6)
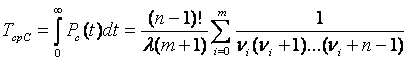
где ?i=(i+1)/(m+1)
.
12. Раздельное резервирование замещением с целой кратностью. Общее постоянное резервирование с дробной кратностью.
Раздельное резервирование замещением с целой кратностью (рис. 3.2,г):
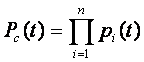
где pi(t) —вероятность безотказной работы системы из-за отказов элементов i-гo типа, резервированных по способу замещения. Вычисляется Pi(t) по формулам общего резервирования замещением (формулы (3.8), (3.9), (3.11).
Общее резервирование с дробной кратностью и постоянно включенным резервом (рис. 3.2,6):
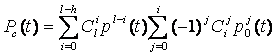
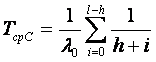
где ро(t) —вероятность безотказной работы основного или любого резервного элемента; l—общее число основных и резервных систем; h —число систем, необходимых для нормальной работы резервированной системы.
В данном случае кратность резервирования
m=(l—h)/h.
13. Скользящее резервирование. Вероятность безотказной работы резервированной системы в случае «обрыва» и «короткого замыкания».
. Скользяще резервирование.
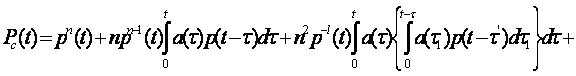
где ?’ = ?+?1; ?” = ? +?1+?2+…; ?m0-1=?+ ?1+…+?m0-1; n — число элементов основной системы; m0—число резервных элементов; p(t — ti) — вероятность безотказной работы одного элемента в течение времени t — ti; ti= t, t-?, t-?m0-1; а(?i) — частота отказов одного из основных элементов в момент времени ?i, ?i=?, ?1, ?2, …, ?m0-1.
При экспоненциальном законе надежности
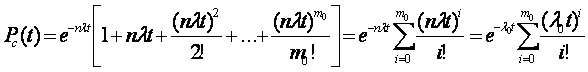
где ?0=n? — интенсивность отказов нерезервированной системы; ? — интенсивность отказов элемента; n — число элементов основной системы; Tcpo — среднее время безотказной работы нерезервированной системы; m0 — число резервных элементов.
В этом случае кратность резервирования
m=m0/n (3.19)
Приведенные выше формулы [кроме выражений (3.8), (3.11), (3.12)] могут быть использованы только в тех случаях, когда справедливо допущение об отсутствии последействия отказов.
Последействие отказов имеет место практически всегда при постоянном включении резерва, а также в случае резервирования замещением при недогруженном состоянии резерва.
Выражение (3.8) является основным при получении расчетных формул в случае учета влияния последействия отказов. При этом члены p(t—?) и am(?) должны быть записаны с учетом последействия отказав, вида резервирования и его кратности.
Элементы (резервированных устройств в ряде случаев могут иметь два вида отказов — «обрыв» и «короткое замыкание». В этом случае вычислять вероятность безотказной работы следует, суммируя вероятности всех благоприятных (не приводящих к отказу) гипотез, т. е.
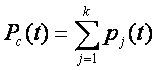
где pj(t) —.вероятность j-й благоприятной гипотезы, вычисленной с учетом двух видов отказов; k — число благоприятных гипотез.
При вычислениях рj(t) следует иметь виду, что для элементов сложной системы справедливы выражения
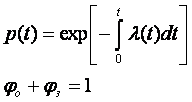
где ?(t) – интенсивность отказов элемента; ?0, ?З — вероятность возникновения «обрыва» и «короткого замыкания» соответственно.
При экспоненциальном законе надежности
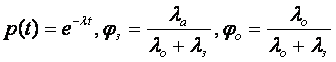
где ?0, ?З — интенсивность отказов элемента по «обрыву» и «короткому замыканию» соответственно.
14. Расчет надежности резервированных систем по схеме «гибели» («чистого размножения»). Выигрыш надежности.
Расчет надежности резервированных систем иногда полезно выполнять, используя схему «гибели» («чистого размножения»). В соответствии с этой схемой преобразование Лапласа вероятности возникновения n отказов вычисляется по формуле
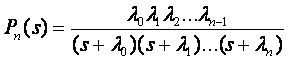
При неравных корнях знаменателя обратное преобразование Лапласа P»(s) будет
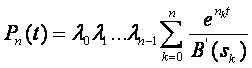
В формулах (3.23) и (3.24) приняты обозначения: ?0 — интенсивность отказов системы до выхода из строя первого элемента; ?1 — интенсивность отказов системы в промежутке времени от момента отказа первого элемента до второго; ?2 — интенсивность отказов системы в промежутке времени от момента отказа второго элемента до третьего и т.д.; n — число отказавших элементов; sk= -?k—k-й корень знаменателя выражения (3.23); B'(sk)—производная знаменателя в точке sk.
При одинаковых опасностях отказов ?i, т.е. ?0=?1=…=?n, расчетные формулы имеют вид
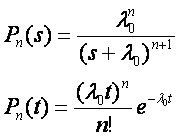
При расчетах надежности по формулам (3.23) — (3.25) следует помнить, что они не определяют вероятности безотказной работы (или вероятности отказа) резервированной системы, а определяют лишь вероятность n-го состояния системы, т.е. вероятность того, что в системе откажут n элементов. Для вычисления вероятности безотказной работы необходимо находить вероятности 0, 1, …, n отказов, когда система еще находится в работоспособном состоянии (исправна), и суммировать полученные вероятности.
Среднее время безотказной работы системы при использовании схемы «гибели» вычисляется по формуле
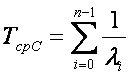
где ?i— интенсивность отказов системы до выхода из строя i-го элемента.
При схемной реализации резервирования в ряде случаев конкретные технические решения не приводятся к логическим схемам расчета надежности (рис. 3.2).
В этих случаях следует для получения аналитических выражений для количественных характеристик надежности использовать метод перебора благоприятных гипотез. Вероятность безотказной работы в этом случае вычисляется по выражению (3.20).
При анализе надежности резервированных устройств на этапе проектирования приходится сравнивать различные схемные решения. В этом случае за критерий качества резервирования принимается выигрыш надежности. Выигрышем надежности называется отношение количественной характеристики надежности резервированного устройства к той же количественной характеристике нерезервированного устройства или устройства с другим видом резервирования.
Наиболее часто используются следующие критерии качества резервированных устройств: Gq(t) — выигрыш надежности в течение времени t по вероятности отказов; Gp(t) — выигрыш надежности в течение времени t по вероятности безотказной работы; GT — выигрыш надежности ;по среднему времени безотказной работы.
При резервировании элементов электроники (резисторов, конденсаторов, контактов реле, диодов и т.п.) всегда произведение интенсивности отказов элемента на время его работы значительно меньше единицы, т.е. ?t<<1. Поэтому при вычислении Gg(t) и Gp(t) целесообразно функции вида е-k?t (экспоненциальный случай) разложить в ряд при небольшом k:
Если система исправна при отказе m элементов, то необходимо брать не менее чем m+2 членов разложения.