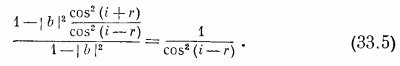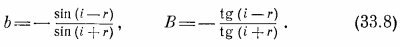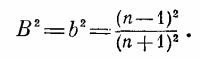Как найти интенсивность отраженного света

Главная >> Фейнмановские лекции по физике >> Том 3 >> Глава 33. Поляризация

Интенсивность отраженного света

Рассмотрим здесь количественную зависимость коэффициента отражения от угла падения. На фиг. 33.6, а показан пучок света, падающий на поверхность стеклянной пластинки, от которой он частично отражается, а остальная его часть преломляется и уходит в глубь стекла. Пусть падающий луч имеет единичную амплитуду и линейно поляризован перпендикулярно плоскости рисунка. Обозначим амплитуду отраженной волны буквой b, а амплитуду преломленной —буквой а. Отраженная и преломленная волны будут, разумеется, линейно поляризованы, а направления электрического поля в падающей, отраженной и преломленной волнах параллельны друг другу. На фиг. 33.6, б показана подобная же ситуация, но в предположении, что падающий луч поляризован в плоскости рисунка. Здесь через В и А обозначены соответственно амплитуды отраженной и преломленной волн.

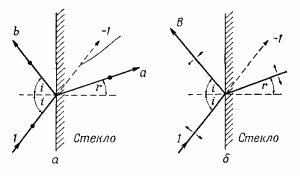
Мы хотим вычислить интенсивности отраженного луча в обоих случаях, приведенных на фиг. 33.6. Как мы уже знаем, в случае, показанном на фиг. 33.6,б, отраженной волны не возникает, если угол между отраженным и преломленным лучами прямой, но нам хотелось бы получить количественный результат — точную формулу для амплитуд В и b как функций угла падения i. Полезно усвоить следующий принцип. Индуцированные в стекле токи генерируют две волны. Прежде всего они создают волну отражения. Далее, если бы в стекле токов не было, падающая волна прошла бы его насквозь, не меняя направления. Вспомним, что все заряды во Вселенной создают некое результирующее поле. Источник, создавший падающий пучок, дает поле единичной амплитуды, которое само по себе должно было бы проходить внутрь стекла по пунктирной линии (см. фиг. 33.6). Но это поле внутри стекла не наблюдается, а, следовательно, токи, возбуждаемые в стекле, должны излучать поле с амплитудой —1 вдоль той же пунктирной линии. ЭТО позволяет вычислить амплитуды преломленных волн а и А.

Из фиг. 33.6, а видно, что поле с амплитудой b создается движением зарядов стекла, а внутри стекла это же движение дает поле с амплитудой а; следовательно, амплитуда b пропорциональна амплитуде а. Далее, если отвлечься от направления поляризации, можно было бы предположить, что отношение В/А равно отношению b/а, так как обе схемы на фиг. 33.6 можно считать одинаковыми. На самом деле это не совсем правильно, потому что на фиг. 33.6, б в отличие от ситуации, изображенной на фиг. 33.6, а, направления поляризаций не параллельны друг другу. В создании амплитуды В эффективно участвует только компонента А, параллельная В, т. е. Acos(i+r). Правильное соотношение пропорциональности выглядит поэтому так:

Теперь немного схитрим. Как мы знаем, на обоих рисунках фиг. 33.6 электрическое поле в стекле вызывает движение зарядов, которое генерирует поле с амплитудой, равной —1, поляризованное точно так же, как и в падающем луче, и распространяющееся вдоль пунктирной линии. Но из фиг. 33.6, б видно, что только перпендикулярная пунктирной линии компонента А дает полю необходимую поляризацию, тогда как на фиг. 33.6,а в создании поля на пунктирной линии эффективно участвует вся амплитуда а, поскольку ее поляризация параллельна поляризации поля с амплитудой —1. Следовательно, справедливо соотношение

Проверим правильность этого результата на уже известном нам факте. Положив (i+r) =90°, из (33.3) получим B=0, что и было найдено в свое время Брюстером; таким образом, наш результат по крайней мере не содержит очевидной ошибки.

По предположению падающая волна имеет единичную амплитуду; тогда |В|²/1² есть коэффициент отражения лучей, поляризованных в плоскости падения, а |b|²/1² — коэффициент отражения лучей, поляризованных перпендикулярно плоскости падения. Отношение этих двух коэффициентов определяется с помощью формулы (33.3).

А теперь сотворим чудо и вычислим не только отношение, но и каждый коэффициент |В|² и |b|² в отдельности! Из закона сохранения энергии вытекает, что энергия преломленной волны должна быть равна энергии падающей волны минус энергия отраженной волны, т. е. 1– |В|² в одном случае и 1–|b|² — в другом. Более того, энергия света, прошедшего внутрь стекла в случае, показанном на фиг. 33.6, а, и такая же энергия в случае фиг. 33.6, б относятся как квадраты амплитуд преломленных волн: |A|²/|а|². Возникает вопрос, возможно ли вычислить энергию волны в стекле, если кроме энергии электрического поля, вообще говоря, имеется и энергия движения атомов. Однако ясно, что любой вклад в полную энергию должен быть пропорционален квадрату амплитуды электрического поля. Следовательно,

Подставим сюда соотношение (33.2) и исключим A/a в написанном выражении, а величину В выразим через b с помощью формулы (33.3):

Здесь неизвестной величиной остается только b. Разрешая уравнение относительно |b|² , получаем

и, воспользовавшись (33.3), находим

Таким образом, мы нашли коэффициент отражения |b|² для падающей волны, поляризованной перпендикулярно плоскости падения, и коэффициент отражения |В|² для волны, поляризованной в плоскости падения!

Используя подобные приемы доказательства, можно пойти дальше и вывести, что b действительно. Для доказательства рассмотрим случай, когда свет приходит одновременно с обеих сторон поверхности стекла (ситуация, трудно осуществимая на опыте, но забавная в теоретическом отношении). Анализируя этот общий случай, можно убедиться в действительности величины b, откуда следует, что b = ±sin(i—r)/sin(i+r). Если взять очень тонкий слой, в котором отражение происходит от обеих поверхностей, и вычислить интенсивность отраженного света, то можно установить даже знак b. Доля света, отраженного тонким слоем, нам известна, поскольку мы знаем ток, генерируемый в таком слое, и даже получили формулу для поля, создаваемого током. Эти аргументы приводят к соотношениям

Формулы (33.8) для коэффициентов отражения как функций углов падения и преломления называются формулами Френеля.

В пределе, когда углы i и r стремятся к нулю, т. е. в случае падения по нормали, мы получаем В² ≈ b² ≈ (i—r)²/(i+ r)² для обеих поляризаций, поскольку и синусы, и тангенсы в этих условиях практически равны углам. Но, как мы уже знаем, sin i/sin r = n, а для малых углов i/r ≈ n. Отсюда совсем просто вывести, что коэффициент отражения в случае падения по нормали равен

Интересно вычислить, например, коэффициент отражения для воды. В этом случае n = ⁴/₃ и коэффициент отражения равен (¹/₇)² ≈ 2%. При падении лучей по нормали к поверхности от воды отражается только 2% всей энергии.

СМОТРИТЕ ТАКЖЕ:

Социальные комментарии Cackle

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 февраля 2023 года; проверки требуют 2 правки.

У этого термина существуют и другие значения, см. Отражение.

Отраже́ние — физический процесс взаимодействия волн или частиц с поверхностью, изменение направления волнового фронта на границе двух сред с разными свойствами, в котором волновой фронт возвращается в среду, из которой он пришёл. Одновременно с отражением волн на границе раздела сред, как правило, происходит преломление волн (за исключением случаев полного внутреннего отражения).

В акустике отражение является причиной эха и используется в гидролокации. В геологии оно играет важную роль в изучении сейсмических волн. Отражение наблюдается на поверхностных волнах в водоёмах. Отражение наблюдается со многими типами электромагнитных волн, не только для видимого света: отражение УКВ и радиоволн более высоких частот имеет важное значение для радиопередач и радиолокации. Даже жёсткое рентгеновское излучение и гамма-лучи могут быть отражены на малых углах к поверхности специально изготовленными зеркалами. В медицине отражение ультразвука на границах раздела тканей и органов используется при проведении УЗИ-диагностики.

История[править | править код]

Впервые закон отражения упоминается в «Катоптрике» Евклида, датируемой примерно 300 годом до н. э.

Законы отражения. Формулы Френеля[править | править код]

Закон отражения света — устанавливает изменение направления хода светового луча в результате встречи с отражающей (зеркальной) поверхностью: падающий и отражённый лучи лежат в одной плоскости с нормалью к отражающей поверхности в точке падения, и эта нормаль делит угол между лучами на две равные части^[1]. Широко распространённая, но менее точная формулировка «угол отражения равен углу падения» не указывает точное направление отражения луча. Тем не менее, выглядит это следующим образом:

Этот закон является следствием применения принципа Ферма к отражающей поверхности и, как и все законы геометрической оптики, выводится из волновой оптики. Закон справедлив не только для идеально отражающих поверхностей, но и для границы двух сред, частично отражающей свет. В этом случае, равно как и закон преломления света, он ничего не утверждает об интенсивности отражённого света.

Сдвиг Фёдорова[править | править код]

Сдвиг Фёдорова — явление малого (меньше длины волны) бокового смещения луча света с круговой или эллиптической поляризацией при полном внутреннем отражении. В результате смещения отражённый луч не лежит в одной плоскости с падающим лучом, как это декларирует закон отражения света геометрической оптики.

Явление теоретически предсказано Ф. И. Фёдоровым в 1954 году, позже обнаружено экспериментально.

Механизм отражения[править | править код]

В классической электродинамике, свет рассматривается как электромагнитная волна, которая описывается уравнениями Максвелла.

• При попадании электромагнитной волны (свет) на поверхность диэлектрика: возникают малые колебания диэлектрической поляризации в отдельных атомах, в результате чего каждая частица излучает вторичные волны во всех направлениях (как антенна-диполь). Все эти волны складываются и — в соответствии с принципом Гюйгенса — Френеля — дают зеркальное отражение и преломление^{[прояснить][источник не указан 2325 дней]}.
• При попадании электромагнитной волны (свет) на поверхность проводника: возникают колебания электронов (электрический ток), электромагнитное поле которого стремится компенсировать это воздействие, что приводит к практически полному отражению света.

В зависимости от резонансной частоты колебательных контуров в молекулярной структуре вещества при отражении излучается волна определённой частоты (определённого цвета). Так предметы приобретают цвет. Хотя цвет объекта определяется не только свойствами отражённого света (см. Цветовое зрение и Физиология восприятия цвета).

Виды отражения[править | править код]

Отражение света может быть зеркальным (то есть таким, как наблюдается при использовании зеркал) или диффузным (в этом случае при отражении не сохраняется путь лучей от объекта, а только энергетическая составляющая светового потока) в зависимости от природы поверхности.

Зеркальное отражение[править | править код]

Зеркальное отражение света отличает определённая связь положений падающего и отражённого лучей: 1) отражённый луч лежит в плоскости, проходящей через падающий луч и нормаль к отражающей поверхности, восстановленную в точке падения; 2) угол отражения равен углу падения. Интенсивность отражённого света (характеризуемая коэффициентом отражения) зависит от угла падения и поляризации падающего пучка лучей (см. Поляризация света), а также от соотношения показателей преломления n₂ и n₁ 2-й и 1-й сред. Количественно эту зависимость (для отражающей среды — диэлектрика) выражают формулы Френеля. Из них, в частности, следует, что при падении света по нормали к поверхности коэффициент отражения не зависит от поляризации падающего пучка и равен

В важном частном случае нормального падения из воздуха или стекла на границу их раздела (показатель преломления воздуха = 1,0; стекла = 1,5) он составляет 4 %.

Полное внутреннее отражение[править | править код]

Наблюдается для электромагнитных или звуковых волн на границе раздела двух сред, когда волна падает из среды с меньшей скоростью распространения (в случае световых лучей это соответствует бо́льшему показателю преломления).

С увеличением угла падения , угол преломления также возрастает, при этом интенсивность отражённого луча растет, а преломленного — падает (их сумма равна интенсивности падающего луча). При некотором критическом значении интенсивность преломленного луча становится равной нулю и происходит полное отражение света. Значение критического угла падения можно найти, положив в законе преломления угол преломления равным 90°:

Диффузное отражение света[править | править код]

При отражении света от неровной поверхности отраженные лучи расходятся в разные стороны (см. Закон Ламберта). По этой причине нельзя увидеть своё отражение, глядя на шероховатую (матовую) поверхность. Диффузным отражение становится при неровностях поверхности порядка длины волны и более. Таким образом, одна и та же поверхность может быть матовой, диффузно-отражающей для видимого или ультрафиолетового излучения, но гладкой и зеркально-отражающей для инфракрасного излучения.

Примечания

1. ↑ Ландсберг Г.С. Элементарный учебник физики: Учеб. пособие В 3 т. Т. 3. Колебания и волны. Оптика. Атомная и ядерная физика / под ред. Г. С. Ландсберга. — М.: ФИЗМАТЛИТ, 2009. — С. 220 – 221. — 656 с. — ISBN 978-5-9221-0351-0.

Ссылки[править | править код]

• Внутреннее отражение
• Уголковый отражатель
• Принцип Гюйгенса — Френеля

Интенсивность – отраженный свет

Cтраница 1

Интенсивность отраженного света зависит как от угла падения, так и от направления поляризации.
 [1]

Интенсивность отраженного света, измеренная в Аа, зависит от количества падающего света как в AI, так и в Аз. Другими словами, она является функцией распределения интенсивности источника света, используемого в спектрофотометре. Этот источник должен, следовательно, иметь то же спектральное распределение, что и источник, при котором обычно проводится визуальное сравнение образцов, включая ультрафиолетовую область спектра, которая часто возбуждает флюоресценцию в видимой области.
 [2]

Интенсивность отраженного света в случае полного внутреннего отражения получается в теории Френеля, как это ясно с самого начала, равной интенсивности падающей волны.
 [3]

Интенсивность отраженного света не зависит от длины волны.
 [4]

Интенсивность отраженного света пропорциональна длине волны.
 [5]

Интенсивность отраженного света обратно пропорциональна длине волны.
 [6]

Поскольку интенсивность отраженного света изменяется вместе с изменением толщины пленки, см. уравнение ( 16), для определения толщины пленки может быть применено точное измерение интенсивности.
 [7]

При измерении интенсивности отраженного света угол падения светового луча обычно отличен от нуля и составляет 5 – 10, поскольку коэффициент отражения при таких углах падения практически не отличается от его значения при нормальном падении. Условие feCnr выполняется для многих полупроводников в широком спектральном интервале в длинноволновой области за краем собственного поглощения даже при наличии значительной концен-центрации свободных носителей заряда. Это обстоятельство позволяет использовать формулу (6.13) для вычисления показателя преломления.
 [8]

Максимумы и минимумы интенсивности отраженного света при изменении длины волны наблюдаются на тех длинах волн, для которых разность фаз равна целому числу полуволн.
 [9]

Пространств, распределение интенсивности отраженного света зависит от соотношения между размерами неровностей h поверхности ( границы раздела) и длиной волны Я падающего излучения.
 [10]

Коэффициент отражения – отношение интенсивности отраженного света к интенсивности падающего света.
 [11]

С увеличением угла падения увеличивается интенсивность отраженного света.
 [12]

Как зависит в нефелометрическом методе интенсивность отраженного света от длины волны света.
 [13]

На рис. 284 показана зависимость интенсивности отраженного света от величины промежутка между призмами, выраженная в процентах от интенсивности падающего света.
 [15]

Страницы:  

   1

   2

   3

   4