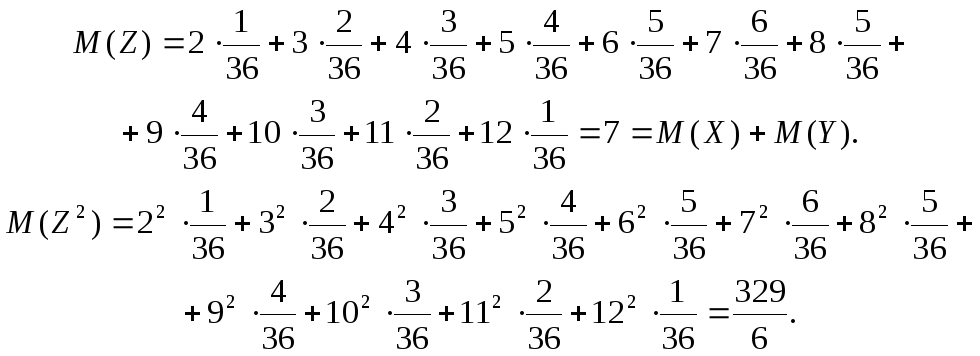Как найти интенсивность потока событий

Как найти интенсивность потока событий

Простейший поток событий

  • Краткая теория
  • Примеры решения задач

Краткая теория

Рассмотрим
события, которые наступают в случайные моменты времени.

Потоком
событий называют последовательность событий, которые наступают в случайные
моменты времени.

Примерами
потоков служат: поступление вызовов на АТС, на пункт неотложной медицинской
помощи, прибытие самолетов в аэропорт, клиентов на предприятие бытового
обслуживания, последовательность отказов элементов и многие другие.

Среди
свойств, которыми могут обладать потоки, выделим свойства стационарности,
отсутствия последействия и ординарности.

Свойство
стационарности характеризуется тем, что вероятность появления k событий на
любом промежутке времени зависит только от числа

 и от длительности

промежутка и не зависит от
начала его отсчета; при этом различные промежутки времени предполагаются
непересекающимися. Например, вероятности появления k событий на промежутках
времени

 одинаковой длительности

 времени равны между собой.

Итак,
если поток обладает свойством стационарности, то вероятность появления

 событий за промежуток времени длительности

 есть функция, зависящая только от

 и

.

Свойство отсутствия последcтвия характеризуется тем, что вероятность появления

 событий на любом промежутке времени не зависит
от того, появлялись или не появлялись события в моменты времени, предшествующие
началу рассматриваемого промежутка. Другими словами, условная вероятность
появления

 событий на любом промежутке времени,
вычисленная при любых предположениях о том, что происходило до начала
рассматриваемого промежутка (сколько событий появилось, в какой
последовательности), равна безусловной вероятности. Таким образом, предыстория
потока не сказывается на вероятности появления событий в ближайшем будущем.

Итак,
если поток обладает свойством отсутствия последействия, то имеет место взаимная
независимость появлений того или иного числа событий в непересекающиеся
промежутки времени.

Свойство ординарности характеризуется тем, что появление двух и более событий за малый
промежуток времени практически невозможно. Другими словами, вероятность
появления более одного события пренебрежимо мала по сравнению с вероятностью
появления только одного события.

Итак,
если поток обладает свойством ординарности, то за бесконечно малый промежуток
времени может появиться не более одного события.

Простейшим (пуассоновским) называют поток событий, который обладает свойствами
стационарности, отсутствия последействия и ординарности.

Интенсивностью
потока

 называют среднее число событий, которые
появляются в единицу времени.

Можно
доказать, что если постоянная интенсивность потока известна, то вероятность
появления

 событий простейшего потока за время
длительностью

 определяется формулой Пуассона:

Эта
формула отражает все свойства простейшего потока.

Смежные темы решебника:

  • Биномиальный закон распределения дискретной случайной величины
  • Геометрический закон распределения дискретной случайной величины
  • Гипергеометрический закон распределения дискретной случайной величины
  • Закон распределения Пуассона

Примеры решения задач

Пример 1

В течение
одной минуты диспетчеру такси поступает в среднем 4 вызова. Найти вероятность
того, что за 2 минуты поступит: а) 5 вызовов; б) хотя бы один вызов.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Поток
событий – простейший,

Воспользуемся
формулой Пуассона:

а) Пусть событие

 –  за 2 минуты поступит 5 вызовов

б) Пусть событие

 – за 2 минуты
поступит хотя бы один вызов. Противоположное событие

 – за две минуты
не поступит ни одного вызова:

Ответ: а)

 б)

.

Пример 2

В радиоаппаратуре за 10000 ч
непрерывной работы происходит замена 10 элементов. Найдите вероятность выхода
из строя радиоаппаратуры из-за выхода из строя элементов за 100 часов
непрерывной работы.

Решение

Поток событий – простейший,

Воспользуемся формулой Пуассона:

Пусть событие

 –  за 100 часов (

)  выйдет из
строя 1 элемент

Ответ:

.

Пример 3

Среднее число вызовов,
поступающих на АТС за одну минуту равно 2. Найти вероятность того, что за три
минуты поступит:

а) менее трех
вызовов;

б) 5 вызовов. Поток
вызовов – простейший. 

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Воспользуемся
формулой Пуассона:

а) Вероятность того,
что за 3 минуты поступит менее трех вызовов:

б) Вероятность того,
что за три минуты поступит 5 вызовов:

Пример 4

Среднее число заявок, поступивших в
билетную кассу в одну минуту равна 1,5. Найти вероятность того, что за 2 минуты
поступит 4 заявки (менее 4, не менее 4 заявок).

Решение

Из формулы Пуассона
вероятность появления 4 заявок за время длительностью

 мин:

Событие «поступило
менее четырех заявок» произойдет, если наступит одно из следующих несовместимых
событий:

1) поступило три
заявок;

2) поступило две
заявки;

3) поступил одна
заявка;

4) не поступило ни
одной заявки

Это события
несовместимы, поэтому применима теорема сложения вероятностей несовместимых
событий:

Событие «поступило
менее четырех заявок» и «поступило не менее четырех заявок» противоположны,
поэтому искомая вероятность того, что за 2 минуты поступит не менее четырех
заявок:

  • Краткая теория
  • Примеры решения задач
Источник

Простейший поток событий

Одним из основных понятий современной
теории массового обслуживания является
понятие простейшего (пуассоновского)
потока.

Потоком событий называют последовательность
событий, которые наступают в случайные
моменты времени.Примеры потоков:
поступление вызовов на АТС, поступление
вызовов на пункт неотложной медицинской
помощи, прибытие кораблей в порт,
последовательность отказов элементов
устройства.

Простейшим называют поток, обладающим
свойствами стационарности, ординарности
и отсутствия последствия.Свойство
стационарности характеризуется тем,
что вероятность наступленияkсобытий за промежуток времени длиныtне зависит от начала отсчета промежутка
времени, а зависит лишь от его длительности.
Например, вероятности наступления пяти
событий на промежутках времени (1,4),
(6,9), (8,11) одинаковой длительностиt
= 3 ед. времени равны между собой.

Свойство отсутствия последействия
характеризуется тем, что вероятность
наступления kсобытий
на любом промежутке времени не зависит
от того, сколько событий появилось до
начала рассматриваемого промежутка.

Свойство ординарности означает, что
вероятность наступления более одного
события за малые промежутки времени
пренебрежимо мала по сравнению с
вероятностью наступления одного события
и пренебрежимо мала по сравнению с
вероятностью не наступления событий.

Интенсивностью потока λ называют
среднее число событий, которые появляются
в единицу времени.Если интенсивность
потока известна, то вероятность того,
что за времяtнаступит
ровноkсобытий,
вычисляется по формуле:


Рt(k)
=
e-λt .

(17)

Пример
17.Среднее число вызовов поступающих
на АТС за одну минуту равно двум. Найти
вероятность того, что за 4 минуты поступит:
1) три вызова; 2) менее четырех вызовов;
3) не менее четырех вызовов.

Решение.По условиюλ= 2, t= 4.

1. Найдем
вероятность того, что поступит три
вызова:

Р4(3) =

2.
Вероятность поступления менее четырех
вызовов:

3. Найдем вероятность того, что за четыре
минуты поступит не менее четырех вызовов.
Так как события ”поступило менее трех
вызовов” и ”поступило не менее трех
вызовов” противоположные, то сумма
вероятностей этих событий равна единице:

отсюда

Так как
найденная вероятность близка к единице,
то полученный результат можно истолковать
так, что последнее событие – это почти
достоверное событие.

Случайные величины Математическое ожидание и дисперсия

Случайное событие, заключающееся в
появлении того или иного числа, называется
случайной величиной. Различают два
вида случайных величин (с.в.):дискретные
и непрерывные. Случайная величина,
принимающая отдельные изолированные
значения, называетсядискретной.

Законом распределения (или просто
распределением) называется соответствие
между возможными значениями с.в. и
вероятностями, с которыми она принимает
эти значения.Законы распределения
задают различными способами: при помощи
формул, в виде таблиц и т.д. случайные
величины обозначаются большими буквами
латинского алфавитаX,
Yи т.д.

Рассмотрим закон распределения
дискретной случайной величины:

Таблица 2

X

x1

x2

…

xk

…

xn

Y

p1

p2

…

pk

…

pn

Здесь
рk =
Вер=Р(читается: вероятность того, что случайная
величина примет значение равноеxk).
Так как в законе распределения перечислены
все возможные значения случайной
величины, то следует предполагать, чтоxkxiприkj,р1 + р2 +…+
рп = 1, и очевидно.

Пример18. В среднем по 10% договоров
страховая компания выплачивает страховые
суммы в связи с наступлением страхового
случая. Составить закон распределения
числа таких договоров среди наудачу
выбранных четырех.

Решение. Вероятностьpтого, что по договору будет выплачена
страховая сумма равнаследовательно,Пусть случайная величинаX–
число договоров, по которым выплачивается
страховая сумма среди наудачу выбранных
четырех. ТогдаX
принимает значения 0, 1, 2, 3, 4. Найдем
вероятности, соответствующие указанным
значениямX:

Таким
образом, получим закон распределения
случайной величины

X

0

1

2

3

4

p

0.6561

0.2916

0.0486

0.0036

0.0001

Проверка:
следовательно, закон распределения
составлен правильно.

Математическим
ожиданием случайной величины называется
сумма произведений возможных значений
случайной величины на вероятности, с
которыми она принимает свои возможные
значения.

(18)

Вероятностный смысл математического
ожидания заключается в том, что
математическое ожидание примерно равно
среднему арифметическому значений,
которые принимает случайная величина
в результате проведения достаточно
большого числа испытаний, т.е., если
проведено Nиспытаний
и с.в. значениеx1принялаN1
раз,x2
– N2 раз,
и т.д.xn
–Nnраз, то величинас очень большой вероятностью будет мало
отличаться отM(X).(Подробнее об этом смотрите в теме
«интервальные оценки параметров
распределения», а также [1,2].)

Пример19. В тесто для калорийных
булочек добавляют изюм. Определить
сколько изюминок попадает в каждую
булочку.

Решение. Пусть для изготовления
булочек замешиваютVкгтеста, а на одну булочку используютv кг(например, 0.1кг). Тогда из одного замеса можно
испечьN=V/vбулочек. Допустим, что в
каждую булочку необходимо положитьизюминок (например,=10).
Справедливо предположение, что в каждую
булочку изюминка может попасть независимо
от других. Введем случайную величинуX– число изюминок в булочке. Случайная
величинаXраспределена
по биноминальному закону (14):

Вер{X=m}=Pn(m)=,

где p = 1/N
= v/V,q =1-p,n =N,m=0,1,…,n,

где
=np.

Предположим, что N большое число,
тогда вероятностьpмала..

При больших значениях nпользоваться формулой (14) затруднительно.
Например, приN=200, вероятность того,
что в данную булочку попадет ровно 9
изюминок равна

P200(9)==.

Расчеты существенно упрощаются, если
рассмотреть предельный случай, когда
n,
а
=np остается постоянным числом (на
практике это соответствует тому, что
вероятность появления случайного
события мала, а число испытаний велико).
В этом предельном случае распределение
вероятностей подчиняетсяформуле
Пуассона (16).

Используя формулу (14), получим
P200(9)=0.12768; по формуле
(16) находимP200(9)
=0.12511.
Таким образом, ошибка при использовании
формулы Пуассона в данном случае равна
0.002.

Закон распределения Пуассона имеет
вид:

X

0

1

…

m

…

P

.

.

.

Дисперсией
называется математическое ожидание от
квадрата отклонения случайной величины
от ее математического ожидания:

(19)

Справедлива формула для вычисления
дисперсии:

(20)

где
Дисперсия случайной величины характеризует
рассеяние случайной величины относительно
ее среднего значения (математического
ожидания).

Свойства
математического ожидания и дисперсии:

  1. Математическое
    ожидание постоянной величины есть сама
    постоянная:

М(С) =
С.

  1. Константу
    можно выносить за знак математического
    ожидания:

М(СХ)
= С М(Х).

Здесь закон распределения с.в. СХполучается из закона распределения
с.в.Хумножением ее возможных
значений на постояннуюС, т.е. если
с.в. определена законом распределения,
представленном в таблице 1., тоСХопределяется следующей таблицей:

Таблица 3

X

Cx1

Cx2

…

Cxk

…

Cxn

P

p1

p2

…

pk

…

pn

  1. Математическое
    ожидание суммы двух случайных величин
    равно сумме их математических ожиданий:

М(Х + Y) = М(Х) +
М(Y).

Свойства дисперсиинепосредственно
следуют из соответствующих свойств
математического ожидания:

  1. Дисперсия
    постоянной величины равна нулю:

D(C) = 0.

  1. Постоянную
    можно выносить за знак дисперсии,
    возведя ее в квадрат:

D(C
X) = C2D(X).

  1. Дисперсия
    суммы независимых случайных величин
    равна сумме дисперсий:

D(X
+Y) = D(X)
+ D(Y),

где X иY
независимы(случайные величины
называютсянезависимыми, если закон
распределения каждой из них не зависит
от того, какие возможные значения приняла
другая с.в.).

Важным примером распределения дискретной
случайной величины является биноминальное
распределение. Пусть имеется некоторое
случайное событиеА, вероятность
появления которого в каждом из испытаний
постоянна и равнаp.
Производитсяnнезависимых испытаний. Случайная
величинаХ– число появлений событияАвnнезависимых
испытаниях. Возможными значениями с.в.Х, распределенной по биноминальному
закону, являются все целые числа от 0 доn. ВеличинаВер{Х
= k} – вероятность
того, что вnиспытаниях
событиеАпроизойдет ровноkраз – вычисляется поформуле Бернулли.

(21)

где q
= 1 – р.

Введем в рассмотрение случайные величины
Хi,i
= 1,2,… n-число
появлений событияАвi–испытании.
ТогдаХ = Х1 + Х2
+ …+ Хn –
общее число появлений событияАвnнезависимых
испытаниях – равно сумме числа появления
событияАв каждом изnиспытаний. Случайные величиныХi,
i = 1,2,…, nпринимают только два значения: 0 – с
вероятностьюqи 1 –
с вероятностьюp.

Следовательно,

Далее,


(22)

а так
как случайные величины Xi
независимы, то

(23)

Таким образом, математическое ожидание
числа появлений события Авnнезависимых испытаниях равно произведению
числа испытаний на вероятность появления
событияА, а дисперсия равна
произведению числа испытаний на
вероятность появления событияАи
на вероятность его не появления.

Найдем
математическое ожидание и дисперсию
случайной, имеющей распределение
Пуассона:

M(X)=m
=,D(X)=m2
–=.

Пример19.
Пусть некоторая случайная величина
распределена по закону Пуассона. По
результатам наблюдаемых значений 2; 1;
1; 3; 1; 4; 2; 5; 1; 7 найти неизвестный параметрслучайной величины.

Решение. Математическое ожиданиеM(X)случайной величины есть ее среднее
значение. Для случайной величины,
распределенной по закону Пуассона

Пример
20.Бросаются две игральные кости.
Случайная величинаХ– число очков,
выпавших на первой игральной кости;Y– на второй;Z–
суммарное число очков, выпавших на двух
игральных костях. Вычислить математическое
ожидание и дисперсию случайных величинХ,Y,Z.

Решение.Закон распределения с.в.Хзадается
таблицей:

Таблица 4

X

1

2

3

4

5

6

Р

Законы распределения с.в. XиYсовпадают, т.е.X
= Y, аZ
= X + Y.
Заметим, чтоZ = X
+ Y
2·X (!!) .

Вычислим математическое ожидание и
дисперсию с.в. Z,
пользуясь законом распределения,
заданным в таблице 1:

Пример
21.Из ящика, содержащего 3 черных и 5
белых шаров, наудачу извлекается 4 шара.
Случайная величинаХ– число
вытащенных белых шаров. Найти математическое
ожидание и дисперсию с.в.Х.

Решение.
Построим закон распределения с.в.Х.
Она может принимать любое значение от
1 до 4.

Таблица 5

X

1

2

3

4

P

p1

p2

р3

р4

Для того, чтобы понять, что представляет
собой сумма случайных величин, рассмотрим
следующий пример.

Пример 22. Производится стрельба из
трех орудий. Первое попадает при каждом
выстреле с вероятностью 0.8, второе –
0.5, третье – 0.6. Все орудия выстрелили по
одному разу. Случайная величина X – число
снарядов, попавших в цель. Требуется
построить закон распределения, найти
математическое ожидание и дисперсию
случайной величины X.

Решение.Введем обозначения:A-cобытие, заключающееся
в том, что первое орудие попало в цель,
B – второе орудие попало в цель, C – третье.
Далее находимP(X=0)=P

P(X=1)=P

=

P(X=2)=P

=

P(X=3)=P

Закон распределения нашей случайной
величины имеет вид:

X

0

1

2

3

P

0.04

0.26

0.46

0.24

Вычислим математическое ожидание и
дисперсию:

M(X)=

D(X)=M()-=

Введем в рассмотрение следующие случайные
величины: X1– число снарядов,
попавших в цель из первого орудия,X2
– число снарядов, попавших в цель
из первого орудия,

X3 – число снарядов, попавших
в цель из первого орудия. Законы
распределения этих случайных величин
имеют вид:

X1

0

1

X2

0

1

X3

0

1

P

0.2

0.8

P

0.5

0.5

P

0.4

0.6

M(X1)=

D(X1)=M()-M2(X1)=

Аналогично находим M(X2)
= 0.5; M(X3)
= 0.6; D(X2)
= 0.25; D(X3)
= 0.24.

Нетрудно видеть, что X=X1+X2+X3
,следовательно

М(X)= M(X1)+
M(X2)+
M(X3)=0.8+0.5+0.6=1.9.

Так как случайные величины X1,
X2, X3независимы,
то

D(X)= D(X1)+
D(X2)+
D(X3)=0.16+0.25+0.24=0.65.

Предположим, что из первого орудия
выстрелили 100 раз, из второго -200, из
третьего-250 раз, случайная величина X
число попаданий в цель. Построить закон
распределения такой случайной величины
сложно, так как она может принимать
очень много значений. возможные значения-
любое число от 0 до 550. Однако M(X)=D(X)=среднее квадратичное отклонение
Полученный результат можно интерпретировать
следующим образом (приближенно)- в цель
попадет 550 снарядов ‘плюс минус’ 11.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Измерение интенсивности входящего потока событий в модели распада

Время на прочтение
12 мин

Количество просмотров 6K

В классе поточных алгоритмов имеется подкласс, решающий задачу поиска тяжелых элементов (heavy hitters). В общем виде эта задача формулируется как «выявление во входящем потоке наиболее часто повторяющихся событий и измерение их интенсивности». В данной публикации сотрудника компании Qrator Labs Артема janatem Шворина предлагается эффективный алгоритм для решения этой задачи.

Введение

Алгоритмы нахождения тяжелых элементов помогают решать задачи, такие как борьба с перегрузкой сети, выявление сетевых аномалий и атак, управление динамической маршрутизацией. Например, известный веб-сервер NGINX позволяет ограничивать интенсивность запросов к определённому ресурсу, и для того, чтобы это делать, интенсивность должна быть измерена количественно.

В этой публикации мы хотим показать читателю ещё один подход к измерению интенсивности потока событий при наличии множества разных (не идентичных) потоков событий. Пусть задано множество типов событий. Требуется оценивать, насколько часто происходит событие данного типа, и обращать внимание на случаи, когда событие одного типа повторяется «слишком часто».

Важной характеристикой данного инструмента является его высокая эффективность, чтобы он не стал узким местом во всей системе анализа и фильтрации трафика. Речь в этом случае идет о том, чтобы обрабатывать одно событие за несколько десятков тактов центрального процессора современных компьютеров.

Помимо собственно измерения интенсивности требуется выделять типы событий, которые случаются наиболее часто. Их интенсивность нужно измерять более точно, в то время как редкие типы событий большой роли не играют, и оценивать их интенсивность не обязательно с высокой точностью.

В работе представлен разработанный нами алгоритм Decay-based count, основанный на модели распада радиоактивного вещества (см. раздел «Модель распада»), с высокой эффективностью решающий задачу поиска тяжелых элементов.

Задача поиска тяжелых элементов

Классификация задач

В описываемом классе задач можно выделить следующие подклассы:

Предлагаемый алгоритм относится к последнему из перечисленных подклассов.

Целевая архитектура

В зависимости от платформы, на которой предполагается запускать данный поточный алгоритм, имеется набор аппаратных ограничений. Иногда требуется встраивать нужную функциональность в сетевое оборудование (свитч, коммутатор и т. п.). Предлагаемый алгоритм предполагается использовать на универсальном процессоре, но при некоторых значениях параметров допускает встраивание в сетевое оборудование.

Параметры задачи

  • Абсолютное значение интенсивности потока, которое считается «опасным». Задачей алгоритма является выявление потоков, интенсивность которых превышает заданный порог.
  • Размер ключа — идентификатора, по которому определяется тип события. В данной реализации, как и во многих других алгоритмах, требуется хранить значения ключей в таблице, поэтому размер ключа влияет на затраты памяти.
  • Способ вычисления оценки интенсивности одного потока по временам прихода однотипных событий. По сути это алгоритмическое определение того, что такое интенсивность потока. В этом случае вычисляется экспоненциальное скользящее среднее, которое имеет единственный параметр — характерное время $tau$, в течение которого учитывается вес события после его прихода.

Точность решения

Накладные расходы

Как правило, основной характеристикой алгоритма является максимальная интенсивность входящего потока, которую он способен обработать. То есть важно лишь время обработки одного события. Однако на практике влияют и другие аппаратные ограничения, такие как размер памяти, используемой для хранения накопленной информации о потоке. Особенно жесткие аппаратные ограничения имеют место при встраивании функционала в сетевое оборудование. Но и на обычных компьютерах наличие большого количества оперативной памяти DRAM помогает далеко не всегда, поскольку доступ в DRAM может занимать неприемлемо много времени. Для того чтобы достичь требуемой производительности, приходится идти на компромисс с точностью измерения и ограничивать размер используемой памяти, чтобы она помещалась в кэш процессора. В данной реализации при осмысленных значениях параметров таблица помещается в L2 кэш процессора. В результате удалось добиться того, чтобы время обработки одного события составляло несколько десятков тактов процессора.

Методы оценки интенсивности потока

Для оценки интенсивности повторений событий заданного типа требуется посчитать количество событий в течение некоторого времени. Для этого нужно фиксировать время наступления события и каким-то образом сохранять его. Обычно для этой цели используют счетчик, который инкрементируется при наступлении соответствующего события. Тогда интенсивность оценивается как отношение значения счетчика к интервалу времени, в течение которого проводится измерение. Более аккуратные способы измерения актуального значения интенсивности используют различные варианты скользящего среднего. Например, экспоненциальное скользящее среднее (exponential moving average, EMA) — разновидность взвешенного скользящего среднего с экспоненциально убывающими весами.

В работе предлагается новый метод вычисления EMA. Здесь используется модель экспоненциального распада, которая описывает такое физическое явление как радиоактивный распад. Эта модель имеет ряд преимуществ по сравнению с традиционным подходом. Во-первых, представление данных оказывается более экономичным по памяти. Во-вторых, модель распада допускает эффективную по скорости реализацию операции обновления счетчика — она требует небольшое количество целочисленных арифметических операций и одно кэшируемое обращение к памяти.

Методы учета множества потоков

В задаче поиска тяжелых элементов проблемой является не только высокая интенсивность входного трафика, но и большое количество различных потоков (типов событий), за которыми приходится следить. Наивная реализация предполагает заведение отдельного счетчика на каждый поток, что приводит к значительному расходу памяти. При этом есть опасность не только в исчерпании всей доступной памяти, но в существенной замедлении скорости работы из-за промахов в кэш. Поэтому, как правило, отказываются от точного решения задачи поиска тяжелых элементов, выбрасывая часть накопленной информации о потоках. Известно множество методов ограничения объема используемой памяти и уменьшения времени обработки события, некоторые из которых приведены ниже:

  • Packet sampling
  • Space saving algorithm
  • HashParallel
  • HashPipe
  • Count-min sketch

Формализация задачи

Прежде чем переходить к описанию алгоритма, необходимо с достаточной математической строгостью сформулировать задачу измерения потока событий, что мы и сделаем в данном разделе.

Последовательность однотипных событий задается в виде множества элементарных событий

${event_k}_{kin I}$, где индекс

$k$ пробегает конечный или бесконечный дискретный интервал

$Isubsetmathbb{Z}$.

В простейшем случае событие определяется только временем его наступления:

$event_k = t_k$, причем события упорядочены во времени:

$t_{k_1} < t_{k_2}$ для

$k_1<k_2$. В большинстве реализаций систем учета событий время считается дискретной величиной:

$t_kinmathbb{Z}$, однако для теоретических рассуждений бывает удобно обобщить и считать время непрерывным:

$t_kinmathbb{R}$.

Основной вопрос, на который должны отвечать системы учета событий, — это оценка интенсивности потока. Интенсивность может быть строго формализована для равномерного потока событий. Равномерный поток

${t_k}$ определяется следующим образом:

$t_k = varphi+pk,quad kinmathbb{Z},$

где

$p>0$,

$varphiin[0,p)$ — параметры потока — период и фаза, соответственно. То есть события наступают через равные промежутки времени. Тогда интенсивность такого потока, по определению, выражается как

$r=1/p$.

Для неравномерных потоков формальное определение интенсивности

$r=r({t_k})$ может отличаться в зависимости от постановки задачи. Модель распада остается работоспособной и полезной и в этом случае, однако оценка качества вычисления истинной интенсивности дана ниже только для случая равномерных потоков.

В некоторых моделях требуется дополнительно учитывать некоторую характеристику события, например, его вес

$c_k$ — величина вклада данного события в измеряемую интенсивность. Тогда событие определяется не только временем его наступления, но и весом:

$event_k = (t_k, c_k)$.

В типичных реализациях систем учета событий заводится счетчик

$s$, который некоторым образом накапливает информацию о потоке событий, и в любой момент времени по его текущему значению можно получить оценку интенсивности потока

$hat{r}=hat{r}(s)$, такую что

$rapproxhat{r}$. Обновление счетчика происходит по приходу очередного события

$event_k$:

$s leftarrow update(s, event_k),$

где

$update()$ — некоторая функция, которая определяется реализацией. Ниже приведено несколько примеров с вариантами реализации функции

$update()$:

В некоторых задачах требуется различать потоки событий. Пусть имеется множество различных типов событий, занумерованных индексом

$i=1,dots N$, и требуется учитывать отдельно потоки сообщений каждого типа. Тогда событие описывается как

$event_k = (t_k, i_k)$ (или, с учетом веса события,

$event_k = (t_k, i_k, c_k)$), где

$i_k$ — тип события. Множество индексов

$k$, относящихся к данному типу события

$i$ обозначим

$I_i = {kmid i_k = i}$.

Модель распада

Модель распада описывается следующим образом:

$v(t) = v_0 e^{-lambda t},$

где

$v_0$ — «количество вещества» в нулевой момент времени,

$v(t)$ — количество в момент времени

$t$,

$lambda$ — параметр модели (так называемая постоянная распада). Название данной модели отражает тот факт, что она описывает физическое явление радиоактивного распада.

Дополнительно введем следующие обозначения:

$tau = 1/lambda,quadalpha = e^{lambda}.$

В нашем случае в качестве параметра модели вместо

$lambda$ удобнее использовать

$tau$, поскольку

$tau$ будет иметь размерность времени и неформально может определяться как характерный интервал времени, в течение которого собирается история событий.

Будем по определению считать, что каждому типу события соответствует величина

$v$, имеющая физический смысл «количества вещества» и зависящая от времени, которая при наступлении события скачком увеличивается на единицу, а в остальное время уменьшается по приведенному выше экспоненциальному закону.

На рис. 1 показано, как меняется со временем значение

$v$ для равномерных потоков с разной интенсивностью и для неравномерного потока.

Рисунок 1: Значение $v$ для разных потоков

Величина

$v$ не хранится явно в памяти, но может быть вычислена в любой момент. Хранится же значение

$s$, такое что в момент времени

$t_{now}$ величина

$v$ выражается следующим образом:

$v=alpha^{s-t_{now}}.$

Данное представление соответствует модели распада.

Вычисление счетчика в модели распада эквивалентно вычислению экспоненциального
скользящего среднего с точностью до нормирующего множителя (константы). Важной особенностью данного представления является то, что единственное значение, хранимое в счетчике, заменяет собой пару (время последнего события, накопленная величина), которую хранят при традиционном подходе.

Обновление счетчика

Нетривиальной операцией является обновление значения счетчика

$s$ при наступлении очередного события. В этом случае требуется заменить

$s$ на новое значение

$s'$, которое определяется из следующего равенства:

$alpha^{s'-t_{now}} = alpha^{s-t_{now}} + 1.$

Здесь слева стоит значение

$v$ сразу после наступления события, а справа — значение

$v$ непосредственно до события, увеличенное на вклад события (равный единице). Ниже будут предложены эффективные способы вычисления результата обновления.

В терминах функции

$update()$ из определения операция обновления выражается так:

$update_1(s, event_k) = t_k + log_alpha(1 + alpha^{s-t_k}).$

Здесь время исполнения операции

$t_{now}$ совпадает со временем

$t_k$ прихода сообщения.

Определение интенсивности

Пусть имеется равномерный поток событий интенсивности

$r$, то есть события наступают с периодом

$p=1/r$. Равномерный поток задается согласно определению.

Если измерение производится сразу после наступления очередного события, то есть

$t_{now}=t_n$ для некоторого

$n$, то накопленное в течение длительного времени значение счетчика

$s$ будет выражаться следующим рядом:

$alpha^{s-t_{now}} = sum_{k=-infty}^nalpha^{t_k-t_{now}}=sum_{k=0}^infty alpha^{-kp},$

откуда

$alpha^{-Delta s} + alpha^{-p} = 1,$

где

$Delta s = s-t_{now}$ — относительное значение счетчика.

В более общем случае момент измерения может оказаться между событиями:

$t_{now}=t_n+psi$,

$psiin[0,p)$. В этом случае значение счетчика будет отличаться в меньшую сторону на величину

$psi$:

$alpha^{-(Delta s+psi)} + alpha^{-p} = 1.$

Задача измерения интенсивности заключается в том, чтобы по значению счетчика оценить интенсивность. В предположении, что поток равномерный, можно получить оценки истинной интенсивности равномерного потока сверху и снизу, подставляя в предыдущее уравнение крайние значения

$psi=0$ и

$psi=p$:

$r^-le r < r^+,$

где

$begin{align}r^+&=r^+(Delta s)=frac1{log_alpha(1+alpha^{-Delta s})}\r^-&=r^-(Delta s)= left{begin{array}{ll}frac1{-log_alpha(1-alpha^{-Delta s})}&mbox{при }Delta s>0\ 0&mbox{иначе}end{array}right.end{align}$

Обе оценки

$r^+$ и

$r^-$ монотонно зависят от значения счетчика

$s$ (см. рис. 2), поэтому, например, сравнение текущего значения счетчика с пороговым значением не требует дополнительных вычислений.

Рисунок 2: График функций $r^-$ и $r^+$ для $tau=15$

В модели распада интенсивность произвольных (не обязательно равномерных) потоков по определению задается приведёнными выше оценками

$r^+$ и

$r^-$. Причем, если измерение происходит сразу после обработки события, то интенсивность считается в точности равной нижней оценке.

Границы применимости модели распада

Существуют ограничения на значение интенсивности, которая может быть корректно измерена в модели распада.

Во-первых, если время наступления событий измеряется как дискретная величина, то период потока не может быть меньшим единицы. То есть интенсивность потока не должна превышать

$r_{max}=1$. Отсюда следует ограничение на относительное значение счетчика

$Delta s = s-t_{now}$ — оно не должно превышать значения

$sigma_{max}$, которое определяется из формулы:

$r^-(sigma_{max}) = r_{max}.$

Величина

$sigma_{max}$ оценивается следующим образом:

$sigma_{max}=taulntau+omega(tau),$

где

$0leomega(tau)le1/2$.

Во-вторых, оценка интенсивности слабых (малоинтенсивных) потоков затруднена: при малых относительных значениях счетчика

$Delta s$ точность верхней и нижней оценки

$r^+$ и

$r^-$ ухудшается, а при отрицательных значениях

$Delta s$ нижняя оценка интенсивности вырождается в нуль.

Также есть ограничение на время работы реализаций модели распада, связанное с переполнением счетчиков. Поскольку значение счетчика не может убежать от

$t_{now}$ более, чем на

$sigma_{max}$, время работы системы фактически определяется разрядностью счетчика и длительностью одного такта. Если для хранения счетчика используется 64-разрядный регистр, то он не переполнится в течение 100 лет. Но в реализациях с малоразрядными регистрами должен быть предусмотрен механизм сброса счетчиков.

Алгоритмы учета множества потоков

Особенности модели распада

Особенностью использования EMA в качестве значения счетчика является то, что при прекращении потока событий накопленное значение быстро (экспоненциально по времени) деградирует и становится неотличимым от нуля. В модели распада этот факт используется для автоматического сброса счетчика: хотя значение счетчика

$s$ будет всё время возрастать с приходом событий, через некоторое время после прекращения потока событий величину

$v=alpha^{s-t_{now}}$ можно будет считать равной нулю, не меняя явно значения счетчика. Время

$T_{vanish}$, за которое любое накопленное ранее значение распадается до условного нуля, зависит от параметра

$tau$ и требуемой точности. Оно выражается как

$T_{vanish}=T_{min}+sigma_{max}$, где

$T_{min}$ — время распада значения, накопленного в результате единичного события. В разделе «Табличная реализация» дано точное выражение

$T_{min}$, но здесь достаточно иметь в виду следующий факт:

$T_{vanish} = O(taulntau)$ при фиксированной точности.

Отсюда следует оценка сверху на размер хранилища счетчиков при учете множества потоков для случая, когда информация вообще не будет теряться — достаточно иметь

$T_{vanish}cdot r_{max}$ ячеек. Есть множество применений задачи поиска тяжелых элементов, где не требуется больших значений

$tau$, и всё хранилище помещается оперативную память или даже в кэш процессора L3 или L2. В этом случае обеспечивается малое время доступа к хранилищу, так что задача становится выполнимой при высоких значениях интенсивности входного потока.

Для реализации хранилища годится хэш-таблица, где ключом является тип события. При этом пустыми считаются ячейки, у которых значение счетчика

$s$ удовлетворяет условию

$s-t_{now} le T_{min}$.

Численная реализация Decay-based count

Операция обновления значения

Введем следующее обозначение:

$rho_tau(x) = tauln(1+e^{x/tau}) = log_{alpha}(1+alpha^x).$

Тогда операция обновления выражается следующим образом:

$s' = t_{now} + rho_tau(s-t_{now}).$

Таким образом, задача сводится к эффективному вычислению приближения функции

$rho_tau$. Время удобно представлять целым числом, например, измерять его в тактах процессора, так что требуется построить целочисленное отображение

${R:mathbb{Z}tomathbb{Z}}$, такое, что:

$R_tau(T) approx rho_tau(T)quadmbox{для }Tinmathbb{Z}.$

Для данной задачи точность важна не относительная, а абсолютная, поскольку со значениями времени используются в основном аддитивные операции. Очевидно, что из-за целочисленности представления времени погрешность меньше 0.5 такта недостижима.
Кроме того, операция измерения текущего времени, как правило, дает некоторую погрешность. Например, если есть способ измерения времени с точностью в 10 тактов, то достаточно потребовать, чтобы

$R_tau$ давало приближение примерно такой же точности:

$left|R_tau(T) - rho_tau(T)right| le 10.$

Можно предложить несколько разных способов вычисления

$R_tau$ разной сложности и степени эффективности.

Вычисление $R_tau$: FPU

Проще всего использовать арифметику с плавающей точкой и непосредственно вычислять

$rho_tau$ по определению. Время выполнения этой операции составляет около 100 тактов процессора, что довольно много по сравнению предлагаемым ниже методом.

Вычисление $R_tau$: табличная реализация

Идея табличной реализации состоит в том, чтобы сохранить предвычисленные значения функции в таблице.

Во-первых, используя тождество

$rho_tau(-x) = -x + rho_tau(x),$

достаточно строить

$R_tau(T)$ только для

$Tle0$.

Во-вторых, поскольку

$rho_tau(x)to 0 mbox{ при } xto-infty,$

существует

$T_{min}>0$, такое что

$R_tau(T)=0$ при

$Tle-T_{min}$. Где

$T_{min}$ можно найти из следующих соображений:

$T_{min}=lceil t_{min}rceil,quad rho_tau(t_{min})=1/2,$

откуда

$T_{min}=lceil-log_alpha(alpha^{1/2}-1)rceil=lceil-tauln(e^{1/{2tau}}-1)rceil.$

Таким образом, достаточно определить

$R_tau(T)$ для

${T_{min}<Tle0}$.

График функции

$rho_tau(x)$ представлен на рис. 3. Особенность этой функции такова, что с изменением параметра

$tau$ будет происходить одинаковое масштабирование по обеим осям.

Рисунок 3: График функции $rho_tau(x)$

Очевидная реализация

$R_tau$ состоит в построении таблицы из

$T_{min}$ ячеек, где будут храниться предвычисленные значения. Поскольку все значения функции на данном интервале находятся в промежутке между 0 и

$rho_tau(0)=tauln2$, итоговый размер таблицы составляет

$T_{min}log_2(tauln2)$ бит.

Алгоритм обновления значения выглядит следующим образом:

$begin{align} t_{now}& leftarrow getTime()\ delta & leftarrow min{|s-t_{now}|, T_{min}}\ delta' &leftarrow R(-delta)\ s' &leftarrow delta' + max{s, t_{now}} end{align}$

Абсолютная точность этого метода составляет 1/2, поскольку он дает наилучшее целочисленное приближение вещественнозначной функции.

Результаты измерения эффективности

Сравнивались между собой следующие три реализации экспоненциального скользящего среднего:
1. наивная реализация EMA;
2. модель распада через FPU (то есть с вызовом функций exp() и log() математической библиотеки);
3. модель распада табличным методом.

Исходный код теста на си: pastebin.com/N1Xg9dud.

Время выполнения одного вызова функции update() при

$tau=100000$ (в этом случае таблица для вычисления

$R_tau$ помещается в кэш L1) в реализациях 1, 2 и 3 составляет 100, 125, 11 тактов процессора, соответственно.

Использование экспоненциального скользящего среднего — удобный способ подсчёта событий и оценки интенсивности. Однако данная операция вычислительно затратна, что сильно ограничивает возможности её применения. Наша реализация алгоритма на основе модели распада, во-первых, красива, а во-вторых, более эффективна, нежели наивная реализация вычисления ЕМА. Эффективность обеспечивается за счет двух факторов: табличное вычисление трансцендентной функции и более экономное по памяти представление счетчика.

Благодарности

Данная публикация подготовлена нами в пробном режиме в рамках проекта по освещению механизмов работы сети фильтрации Qrator. Спасибо Антону Орлову, Артему Гавриченкову, Евгению Наградову и Никите nikitadanilov Данилову за обсуждения и идеи.

Источник

Часть 1. Регулярные потоки. Особенности стационарного Пуассоновского (простейшего) потока событий.

Поток событий – последовательность однородных событий, следующих одна за другой в случайный момент времени.

Пример: поток вызовов на телефонной станции, поток событий в аэропорту.

Поток событий характеризуется интенсивностью потока λ.

Интенсивность потока – это среднее число событий, поступивший в СМО в единицу времени (частота появления события).

Поток события называется регулярным, если одно событие следует за другим через равные промежуток времени.

Регулярные потоки редко встречаются, но представляют собой предельный случай, который интересен.

Поток события называется простейшим (стационарным Пуассоновским), если он удовлетворяет 3 особенностям:

  • стационарный
  • ординарный
  • поток без последействия

Поток события называется стационарным, если его вероятностные характеристики не зависят от времени, то есть x(t)=x – постоянна.

Поток события называется ординарным, если события в нем появляются по одиночке, а не по группам.

Поток событий. Простейший Пуассоновский поток

То есть вероятность того, что за промежуток времени △t в СМО поступит более 1 события намного меньше вероятности того, что в систему △t придет 1 событие.

Поток без последействия – поток событий, удовлетворяющий следующему условию: если выбрать 2 непересекающихся промежутка времени τ₁ и τ₂, то число событий, появившихся на промежутке τ₁ не зависит от числа событий, появившихся на τ₂, то есть события в таком случае появляются независимо.

Из последнего определения следует, что регулярный поток не является потоком без последействия, так как в нем моменты появления события подчинены закономерности, а значит регулярный поток не является простейшим.

Источник

Определение. Потоком событий называется последовательность событий, происходящих один за другим в какие – то моменты времени.

Характер событий, образующих поток может быть различным, а если события отличаются друг от друга только моментом времени, в который они происходят, то такой поток событий называется Однородным.

Однородный поток можно изобразить последовательностью точек на оси, соответствующей времени:

T1 t2 tn

t

Определение. Поток событий называется Регулярным, если события следует одно за другим через строго определенные промежутки времени.

Определение. Поток событий называется Стационарным, если вероятность попадания того ли иного числа событий на участок времени t зависит только от длины участка и не зависит от того, где именно на оси расположен этот участок.

Стационарность потока событий означает, что плотность потока постоянна, отсутствуют промежутки времени, в течение которых событий больше чем обычно. Классический пример – “час пик” на транспорте.

Определение. Поток событий называется Потоком без последействий, если для любых неперекрещивающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, опадающих на другие.

Отсутствие последействий означает, что заявки в систему поступают независимо друг от друга. Поток выходных событий систем массового обслуживания обычно имеет последействие, даже если входной поток его не имеет. Пример – вход пассажиров на станцию метро – поток без последействия, т. к. причины прихода отдельного пассажира не связаны с причинами прихода всех остальных, а выход пассажиров со станции – поток с последействием, т. к. он обусловлен прибытием поезда.

Последействие, свойственное выходному потоку следует учитывать, если этот поток в свою очередь является входным для какой – либо другой системы.

Определение. Поток событий называется Ординарным, если вероятность попадания на элементарный участок DT двух или более событий достаточно мало по сравнению с вероятностью попадания одного события.

Условие ординарности означает, что заявки на систему приходят по одному, а не парами, тройками и т. д. Однако, если заявки поступают Только парами, Только тройками и т. д., то такой поток легко свести к ординарному.

Определение. Если поток событий стационарен, ординарен и без последействий, то такой поток называется Простейшим (пуассоновским) Потоком.

Это название связано с тем, что в этом случае число событий, попадающих на любой фиксированный интервал времени, распределено по распределению Пуассона.

В соответствии с этим законом распределения математическое ожидание числа точек, попавших попадающих на участок времени t, имеет вид:

L – плотность потока – среднее число событий в единицу времени.

Вероятность того, что за время t произойдет ровно Т событий, равна

Вероятность того, что в течение данного времени не произойдет ни одного события, равна:

Пусть Т – промежуток времени между двумя произвольными соседними событиями в простейшем потоке. Найдем функцию распределения

В соответствии с законом распределения Пуассона, получаем:

Математическое ожидание, дисперсия и среднее квадратическое отклонение этой величины соответственно равны:

Таким образом, для величины Т получили показательный закон распределения.

Пример. В бюро обслуживания в среднем поступает 12 заявок в час. Считая поток заказов простейшим, определить вероятность того, что: а) за 1 минуту не поступит ни одного заказа, б) за 10 минут поступит не более трех заказов.

Сначала найдем плотность (интенсивность) потока, выразив ее в количестве заявок в минуту. Очевидно, эта величина равна .

Далее находим вероятность того, что за время t = 1 мин не поступит ни одной заявки по формуле:

Вероятность того, что за 10 минут поступит не более трех заказов будет складываться из вероятностей того, что не поступит ни одного заказа, поступит один, два или ровно три заказа.

Пример. В ресторан прибывает в среднем 20 посетителей в час. Считая поток посетителей простейшим, и зная, что ресторан открывается в 11.00, определите:

а) вероятность того, что в 11.12 в ресторан придет 20 посетителей при условии, что в 11.07 их было 18

б) вероятность того, что между 11.28 и 11.30 в ресторане окажется новый посетитель, если известно, что предшествующий посетитель прибыл в 11.25.

Для ответ на первый вопрос фактически надо найти вероятность того, что в промежуток от 11.07 до 11.12 (t = 5 минут) придет ровно 2 посетителя. При этом мы знаем интенсивность потока посетителей – l = 20/60 = 1/3 посетителей в минуту. Конечно, данная величина носит условный характер, т. к. посетители не могут приходить по частям.

Искомая вероятность равна:

Теперь перейдем ко второму вопросу. Нам не сказано, сколько именно новых посетителей будет в промежутке от 11.28 до 11.30, главное чтобы был хоть один. Эта вероятность равна . Здесь Р0 (2) – вероятность того, что в этом промежутке не будет ни одного посетителя.

Если поток событий нестационарен, то его плотность l уже не является постоянной величиной, а зависит от времени.

Определение. Мгновенной плотностью Потока событий называется предел отношения среднего числа событий, приходящегося на элементарный отрезок времени (T, T + DT), к длине этого участка, которая стремиться к нулю.

Как видно из приведенного определения, с учетом того, что среднее число событий на участке времени равно математическому ожиданию, то можно сказать, что Мгновенная плотность потока равна производной по времени от математического ожидания числа событий на участке (0, T).

Определение. Нестационарным пуассоновским потоком Называется ординарный поток однородных событий без последействий с переменной плотностью l(t).

Для такого потока число событий, попадающих на участок длины t, начинающийся в точке T0, подчиняется закону Пуассона:

Здесь А – математическое ожидание числа событий на участке от T0 ДоT + T0 . Оно вычисляется по формуле:

Величина А на только от длины участка t, но и от его положения во времени. Закон распределения промежутка Т между двумя соседними событиями также будет зависеть от того, где на временной оси расположено первое из событий, а также от функции l(t) .

Вероятность того, что на участке времени от T0 До T + T0 не появится ни одного события, равна

Тогда, соответственно, вероятность появления хотя бы одного события на этом интервале времени будет равна:

Плотность распределения можно найти дифференцированием:

Эта плотность распределения уже не будет показательной. Она зависит от параметра T0 и вида функции l(T). Однако, условие отсутствия последействия в этом виде потока сохраняется.

< Предыдущая   Следующая >
Источник

Добавить комментарий