Интенсивность света I в выбранной точке – это модуль средней по времени величины плотности потока энергии, которую световая волна переносит.
Определение плотности потока электромагнитной энергии возможно при помощи вектора Умова-Пойнтинга P→. Отсюда следует, что математический вид определения интенсивности света записывается в виде формулы:
I=P→=E→×H→.
По выражению усреднение проводится за период времени t, причем больший по сравнению с периодом колебания волны T t≫T. Интенсивность света записывается как:
It=1T∫tt+TP→(t)dt.
В системе СИ единицей измерения является Втм2.
Модули амплитуд (Em и Hm) векторов напряженностей электрического E→ и магнитного H→ полей в электромагнитной волн записываются в виде отношения:
Имеем, что μ≈1. Необходимо выразить амплитуду Hm:
где n=εμ=ε при μ≈1 является показателем преломления вещества, в котором распространяется свет.
Модуль среднего значения вектора Умова-Пойнтинга пропорционален произведению амплитуд Em·Hm.
Интенсивность света не может быть измерена в связи с тем, что поле изменяется с высокой частотой ν=1015 Гц, соответственно период колебаний составляет T=10-15 с, а приемники колебаний обладают временем инерции существенно больше, чем 10-15 c.
Отсюда следует, что среднее значение интенсивности можно регистрировать. Также возможно измерение средней интенсивности, но не фазы поля.
Давление света
По закону сохранения при поглощении и отражении света телом ему сообщается импульс, равняющийся разности импульсов пучка света до и после этих процессов. Отсюда следует, что на тело действует сила, свет производит соответствующее давление на тело. Еще Кеплер выдвинул свое предположение о существовании давления света, которое было принято при рассмотрении отклонений хвостов комет от Солнца.
Последователи волновой теории отрицали давление света, отсутствие доказательств опытами о существовании светового давления служило аргументом против корпускулярной. То есть существование светового давления считалось следствием электромагнитной теории.
Если световая волна падает перпендикулярно плоскости поверхности тела и полностью поглощает свет, то определение давления p производится по формуле.
Где G считается плотностью импульса световой волны, P – модулем вектора Умова-Пойнтинга, с – скоростью света в вакууме.
Если происходит полное отражение света при помощи поверхности тела, то импульс, который при помощи него передается, имеет значение в 2 раза больше, также как и значение давления.
При падении световой волны на поверхность под углом относительно нормали, производя расчеты давления, применяют только перпендикулярную составляющую плотности потока энергии. Если имеются обычные условия, то давление крайне малое, то есть в 1010 раз меньше атмосферного.
П.Н. Лебедев в 1899 году смог измерить световое давление. Для этого он применил крутильные весы, находящиеся в вакууме. Позже его опыты определения существования давления света подтвердили электромагнитную теорию света Максвелла.
Давление электромагнитных волн считается результатом воздействия электрического поля волны частицы вещества, которые обладают электрическим зарядом, движутся упорядоченно, на них действуют силы Лоренца.
Примеры
Определить давление, оказываемое плоской световой волной, падающей перпендикулярно относительно поверхности тела и поглощаемой телом. Значение амплитуды напряженности электрического поля равняется 2 Вм.
Решение
Будем использовать формулу:
p=Pc (1.1).
Где P принимается за среднее значение модуля вектора Умова-Пойнтинга, c=3·108 мс – за скорость света в вакууме.
Для нахождения среднего значения модуля вектора Умова-Пойнтинга необходимо использовать:
P=E·H (1.2).
В условии имеем плоскую волну, тогда уравнение ее колебаний зафиксируем как:
E=Emcos ωt-kx, H=Hmcos ωt-kx (1.3).
Для нахождения значения амплитуды напряжения магнитного поля следует применить:
εε0Em=μμ0Hm (1.4).
Когда для вакуума ε=1, μ=1, можно выразить из (1.4) Hm. Получим:
Hm=ε0μ0Em (1.5),
где μ0=4π·10-7 Гнм, ε0=14π·9·109Фм. Это говорит о том, что средним значением модуля вектора Умова-Пойнтинга будет:
P=Emcos ωt-kx·ε0μ0Emcosωt-kx=ε0μ0Em2cosωt-kx==12ε0μ0Em2 (1.6).
Далее производим подстановку правой части выражения (1.6) в (1.1) вместо P, тогда искомое давление света:
p=12ε0μ0Em2c.
Заменим числовые значения и получим:
p=12·3·10814π·10-7·4π·9·109·4=4120π·6·108=1,77·1011 (Па)
Ответ: 17,7 пПа.
Определить интенсивность I плоской световой волны, распространяющейся вдоль Ох. Значение напряженности электрического поля волны равняется EmВм.
Решение
Из определения выявим интенсивность световой волны:
I=P (2.1).
Запись модуля вектора Умова-Пойтинга для плоской световой волны обозначится как:
P=EH=EmHmcos2ωt-kx (2.2).
Среднее значение P:
P=12EmHm 2.3, так как cos2ωt-kx=12.
Сравнивая с примером 1, можно произвести выражение амплитуды напряженности магнитного поля:
εε0Em=μμ0Hm→Hm=εε0μμ0Em (2.4).
Из (2.1), (2.3), (2.4) получим:
I=12εε0μμ0Em2.
Ответ: I=12εε0μμ0Em2.
ВОЛНОВАЯ ОПТИКА
ЛЕКЦИЯ № 8
Световые волны.
Законы геометрической (лучевой) оптики
Световые волны. Интенсивность света. Световой поток. Законы геометрической оптики. Полное внутреннее отражение
Оптика – это раздел физики, изучающий природу светового излучения, его распространение и взаимодействие с веществом. Раздел оптики, в котором изучается волновая природа света, называется волновой оптикой. Волновая природа света лежит в основе таких явлений, как интерференция, дифракция, поляризация. Раздел оптики, в котором не учитываются волновые свойства света и который основывается на понятии луча, называется геометрической оптикой.
§ 1. СВЕТОВЫЕ ВОЛНЫ
Согласно современным представлениям, свет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна, в других – как поток особых частиц (фотонов). Такое свойство называется корпускулярноволновым дуализмом (корпускула – частица, дуализм – двойственность). В этой части курса лекций будем рассматривать волновые явления света.
Световая волна – это электромагнитная волна с длиной волны в вакууме в диапазоне:
|
l 0 |
= (0,4 ¸ 0,76 ) ×10 − 6 м = 0,4 ¸ 0,76 мкм = 400 ¸ 760 нм = |
|||||||
|
= 4 000 ¸ |
||||||||
|
7 600 A . |
||||||||
|
A – |
ангстрем – единица измерения длины. 1A = 10−10 м. |
|||||||
|
Волны такого диапазона воспринимаются человеческим глазом. |
||||||||
|
Излучение с длиной волны меньше 400 нм называют ультрафиолетовым, а |
||||||||
|
с большей, чем 760 нм, – |
инфракрасным. |
|||||||
|
Частота n световой волны для видимого света: |
||||||||
|
n = |
с |
= (0,39¸0,75) × 1015 Гц, |
||||||
|
l0 |
||||||||
|
с = 3×108 м/с – скорость света в вакууме. |
||||||||
|
Скорость |
света |
совпадает |
со |
скоростью |
распространения |
|||
|
электромагнитной волны. |
Показатель преломления
Скорость распространения света в среде, как и любой электромагнитной волны, равна (см. (7.3)):

|
v = |
c |
. |
|||
|
εμ |
|||||
Для характеристики оптических свойств среды вводится показатель преломления. Отношение скорости света в вакууме к скорости света в данной среде называется абсолютным показателем преломления:
|
n = |
c |
. |
(8.1) |
|||
|
v |
||||||
|
С учетом (7.3) |
||||||
|
n = |
≈ |
, |
||||
|
εμ |
ε |
(8.2) |
так как для большинства прозрачных веществ μ=1.
Формула (8.2) связывает оптические свойства вещества с его электрическими свойствами. Для любой среды, кроме вакуума, n> 1. Для вакуума n = 1, для газов при нормальных условиях n≈ 1.
Показатель преломления характеризует оптическую плотность среды. Среда с большим показателем преломления называется оптически более плотной. Обозначим абсолютные показатели преломления для двух сред:
|
n1 = |
c |
и |
n 2 = |
c |
. |
||||
|
v1 |
|||||||||
|
v2 |
|||||||||
|
Тогда относительный показатель преломления равен: |
|||||||||
|
n21 = |
n2 |
= |
v1 |
, |
(8.3) |
||||
|
n1 |
v2 |
||||||||
|
где v1 и v2 – |
скорости света в первой и второй среде, соответственно. |
||||||||
|
Так как |
диэлектрическая |
проницаемость среды ε зависит от частоты |
электромагнитной волны, то n = n(ν) или n = n(λ) – показатель преломления будет зависеть от длины волны света (см. лекции № 16, 17).
Зависимость показателя преломления от длины волны (или частоты) называется дисперсией.
В световой волне, как и в любой электромагнитной волне, колеблются векторы E и H. Эти векторы перпендикулярны друг другу и направлению
вектора v . Как показывает опыт, физиологическое, фотохимическое, фотоэлектрическое и другие виды воздействий вызываются колебаниями электрического вектора. Поэтому световой вектор – это вектор напряженности электрического поля световой (электромагнитной) волны.
Для монохроматической световой волны изменение во времени и пространстве проекции светового вектора на направление, вдоль которого он
|
колеблется, будет описываться уравнением: |
|
|
E = Emсos(ωt − kr + α). |
(8.4) |
|
Сравните (7.4) и (8.4). |

Здесь k – волновое число; r – расстояние, отсчитываемое вдоль направления распространения волны; Em – амплитуда световой волны. Для плоской волны E m = const , для сферической убывает как 1/r.
§ 2. ИНТЕНСИВНОСТЬ СВЕТА. СВЕТОВОЙ ПОТОК
Частота световых волн очень велика, поэтому приемник света или глаз фиксирует усредненный по времени поток. Интенсивностью света называется модуль среднего по времени значения плотности энергии в данной точке пространства. Для световой волны, как и для любой электромагнитной волны, интенсивность (см (7.8)) равна:
I = <EH> .
Для световой волны μ≈ 1, поэтому из (7.5) следует:

 μ0H =
μ0H = 
 ε0 ε E ,
ε0 ε E ,
откуда с учетом (8.2):
|
H = |
ε0 |
E ~ nE . |
(8.5) |
||||||
|
ε |
|||||||||
|
μ |
0 |
||||||||
Подставим в (7.8) формулы (8.4) и (8.5). После усреднения получим:
|
I = |
1 |
nEm2 |
ε0 |
. |
||
|
2 |
μ0 |
Значит интенсивность световой волны:
Следовательно, интенсивность света пропорциональна квадрату амплитуды световой волны и показателю преломления. Заметим, что для
вакуума и воздуха n = 1, поэтому I ~ E2m (сравните с (7.9)).
Для характеристики интенсивности света с учетом его способности вызывать зрительное ощущение вводится величина Ф, называемая световым потоком. Действие света на глаз сильно зависит от длины волны. Наиболее
чувствителен глаз к излучению с длиной волны λз = 555 нм (зеленый цвет).
Для других волн чувствительность глаза ниже, а вне интервала (400– 760 нм) чувствительность глаза равна нулю.
Световым потоком называется поток световой энергии, оцениваемый по зрительному ощущению. Единицей светового потока является люмен (лм). Соответственно, интенсивность измеряется либо в энергетических единицах (Вт/м2), либо в световых единицах (лм/м2).
Интенсивность света характеризует численное значение средней энергии, переносимой световой волной в единицу времени через единицу площади площадки, поставленной перпендикулярно направлению распространения волны. Линии, вдоль которых распространяется световая энергия, называют лучами. Раздел оптики, в котором изучаются законы распространения светового
излучения на основе представлений о световых лучах, называется геометрической, или лучевой оптикой.
§ 3. ОСНОВНЫЕ ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
Геометрическая оптика – это приближенное рассмотрение распространения света в предположении, что свет распространяется вдоль некоторых линий – лучей (лучевая оптика). В этом приближении пренебрегают конечностью длин волн света, полагая, что λ→ 0.
Геометрическая оптика позволяет во многих случаях достаточно хорошо рассчитать оптическую систему. Но в ряде случаев реальный расчет оптических систем требует учета волновой природы света.
Первые три закона геометрической оптики известны с древних времен. 1. Закон прямолинейного распространения света.
Закон прямолинейного распространения света утверждает, что в
однороднойсреде свет распространяется прямолинейно.
Если среда неоднородна, т. е. ее показатель преломления изменяется от точки к точке, или n = n( r ) , то свет не будет распространяться по прямой. При
наличии резких неоднородностей, таких, как отверстия в непрозрачных экранах, границы этих экранов, наблюдается отклонение света от прямолинейного распространения.
2. Закон независимости световых лучей утверждает, что лучи при пересечениине возмущают друг друга. При больших интенсивностях этот закон не соблюдается, происходит рассеяние света на свете.
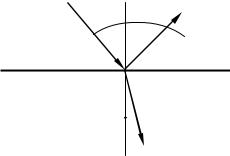
3 и 4. Законы отражения и преломления утверждают, что на границе раздела двух сред происходит отражение и преломление светового луча. Отраженный и преломленный лучи лежат в одной плоскости с падающим
лучом и перпендикуляром, восстановленным к границе раздела в точке падения
(рис. 8.1).
Угол падения равен углу отражения:
Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй среды к показателю преломления первой:
|
sini |
= |
n2 |
= n21 |
. |
(8.8) |
|
|
sinr n1 |
Закон преломления был открыт в XVIIв. В. Снеллиусом и Р. Декартом.
Законы отражения и преломления могут нарушаться в анизотропных средах, т. е. средах, преломления зависит от направления в пространстве.
Рис. 8.1
для которых показатель
From Wikipedia, the free encyclopedia
| luminous intensity | |
|---|---|
|
Common symbols |
Iv |
| SI unit | candela |
|
Other units |
|
| In SI base units | cd |
| Dimension | J |
In photometry, luminous intensity is a measure of the wavelength-weighted power emitted by a light source in a particular direction per unit solid angle, based on the luminosity function, a standardized model of the sensitivity of the human eye. The SI unit of luminous intensity is the candela (cd), an SI base unit.
Measurement[edit]
Photometry deals with the measurement of visible light as perceived by human eyes. The human eye can only see light in the visible spectrum and has different sensitivities to light of different wavelengths within the spectrum. When adapted for bright conditions (photopic vision), the eye is most sensitive to yellow-green light at 555 nm. Light with the same radiant intensity at other wavelengths has a lower luminous intensity. The curve which represents the response of the human eye to light is a defined standard function y(λ) or V(λ) established by the Commission Internationale de l’Éclairage (CIE) and standardized in collaboration with the ISO. [1]
Luminous intensity of artificial light sources is typically measured using and a goniophotometer outfitted with a photometer or a spectroradiometer. [2]
| Quantity | Unit | Dimension | Notes | ||
|---|---|---|---|---|---|
| Name | Symbol[nb 1] | Name | Symbol | Symbol[nb 2] | |
| Luminous energy | Qv[nb 3] | lumen second | lm⋅s | T J | The lumen second is sometimes called the talbot. |
| Luminous flux, luminous power | Φv[nb 3] | lumen (= candela steradian) | lm (= cd⋅sr) | J | Luminous energy per unit time |
| Luminous intensity | Iv | candela (= lumen per steradian) | cd (= lm/sr) | J | Luminous flux per unit solid angle |
| Luminance | Lv | candela per square metre | cd/m2 (= lm/(sr⋅m2)) | L−2J | Luminous flux per unit solid angle per unit projected source area. The candela per square metre is sometimes called the nit. |
| Illuminance | Ev | lux (= lumen per square metre) | lx (= lm/m2) | L−2J | Luminous flux incident on a surface |
| Luminous exitance, luminous emittance | Mv | lumen per square metre | lm/m2 | L−2J | Luminous flux emitted from a surface |
| Luminous exposure | Hv | lux second | lx⋅s | L−2T J | Time-integrated illuminance |
| Luminous energy density | ωv | lumen second per cubic metre | lm⋅s/m3 | L−3T J | |
| Luminous efficacy (of radiation) | K | lumen per watt | lm/W | M−1L−2T3J | Ratio of luminous flux to radiant flux |
| Luminous efficacy (of a source) | η[nb 3] | lumen per watt | lm/W | M−1L−2T3J | Ratio of luminous flux to power consumption |
| Luminous efficiency, luminous coefficient | V | 1 | Luminous efficacy normalized by the maximum possible efficacy | ||
| See also: SI · Photometry · Radiometry |
- ^ Standards organizations recommend that photometric quantities be denoted with a subscript “v” (for “visual”) to avoid confusion with radiometric or photon quantities. For example: USA Standard Letter Symbols for Illuminating Engineering USAS Z7.1-1967, Y10.18-1967
- ^ The symbols in this column denote dimensions; “L“, “T” and “J” are for length, time and luminous intensity respectively, not the symbols for the units litre, tesla and joule.
- ^ a b c Alternative symbols sometimes seen: W for luminous energy, P or F for luminous flux, and ρ for luminous efficacy of a source.
Relationship to other measures[edit]

Comparison of photometric and radiometric quantities
Luminous intensity should not be confused with another photometric unit, luminous flux, which is the total perceived power emitted in all directions. Luminous intensity is the perceived power per unit solid angle. If a lamp has a 1 lumen bulb and the optics of the lamp are set up to focus the light evenly into a 1 steradian beam, then the beam would have a luminous intensity of 1 candela. If the optics were changed to concentrate the beam into 1/2 steradian then the source would have a luminous intensity of 2 candela. The resulting beam is narrower and brighter, though its luminous flux remains unchanged.
Luminous intensity is also not the same as the radiant intensity, the corresponding objective physical quantity used in the measurement science of radiometry.
Units[edit]
Like other SI base units, the candela has an operational definition—it is defined by the description of a physical process that will produce one candela of luminous intensity. By definition, if one constructs a light source that emits monochromatic green light with a frequency of 540 THz, and that has a radiant intensity of 1/683 watts per steradian in a given direction, that light source will emit one candela in the specified direction.[3]
The frequency of light used in the definition corresponds to a wavelength in a vacuum of 555 nm, which is near the peak of the eye’s response to light. If the 1 candela source emitted uniformly in all directions, the total radiant flux would be about 18.40 mW, since there are 4π steradians in a sphere. Note that a typical modern candle produces very roughly one candela while releasing heat at roughly 80 W.
Prior to the definition of the candela, a variety of units for luminous intensity were used in various countries. These were typically based on the brightness of the flame from a “standard candle” of defined composition, or the brightness of an incandescent filament of specific design. One of the best-known of these standards was the English standard: candlepower. One candlepower was the light produced by a pure spermaceti candle weighing one sixth of a pound and burning at a rate of 120 grains per hour. Germany, Austria, and Scandinavia used the Hefnerkerze, a unit based on the output of a Hefner lamp.[4] In 1881, Jules Violle proposed the Violle as a unit of luminous intensity, and it was notable as the first unit of light intensity that did not depend on the properties of a particular lamp. All of these units were superseded by the definition of the candela.
Usage[edit]

Photopic (black) and scotopic (green) luminosity functions.[c 1] The photopic includes the CIE 1931 standard[c 2][c 3] (solid), the Judd–Vos 1978 modified data[c 4] (dashed), and the Sharpe, Stockman, Jagla & Jägle 2005 data[c 5] (dotted). The horizontal axis is wavelength in nm.
The luminous intensity for monochromatic light of a particular wavelength λ is given by
where
- Iv is the luminous intensity in candelas (cd),
- Ie is the radiant intensity in watts per steradian (W/sr),
is the standard luminosity function.
If more than one wavelength is present (as is usually the case), one must sum or integrate over the spectrum of wavelengths present to get the luminous intensity:
See also[edit]
- Brightness
- International System of Quantities
- Radiance
References[edit]
- ^ ISO/CIE 23539:2023 CIE TC 2-93 Photometry — The CIE system of physical photometry. ISO/CIE. 2023. doi:10.25039/IS0.CIE.23539.2023.
- ^ Schneider, T.; Young, R.; Bergen, T.; Dam-Hansen, C; Goodman, T.; Jordan, W.; Lee, D.-H; Okura, T.; Sperfeld, P.; Thorseth, A; Zong, Y. (2022). CIE 250:2022 Spectroradiometric Measurement of Optical Radiation Sources. Vienna: CIE – International Commission on Illumination. ISBN 978-3-902842-23-7.
- ^ “Base unit definitions: Candela”. The NIST Reference on Constants, Units, and Uncertainty. Retrieved 8 February 2008.
- ^ “Hefner unit, or Hefner candle”. Sizes.com. 30 May 2007. Retrieved 25 February 2009.
Curve data[edit]
- ^ “CIE Scotopic luminosity curve (1951)”. Archived from the original on 28 December 2008.
- ^ “CIE (1931) 2-deg color matching functions”. Archived from the original on 28 December 2008.
- ^ “CIE ‘physiologically-relevant’ luminous efficiency functions”. Archived from the original on 7 July 2019.
- ^ “Judd–Vos modified CIE 2-deg photopic luminosity curve (1978)”. Archived from the original on 28 December 2008.
- ^ “Sharpe, Stockman, Jagla & Jägle (2005) 2-deg V*(l) luminous efficiency function”. Archived from the original on 27 September 2007.
| Quantity | Unit | Dimension | Notes | ||
|---|---|---|---|---|---|
| Name | Symbol[nb 1] | Name | Symbol | Symbol[nb 2] | |
| Luminous energy | Qv[nb 3] | lumen second | lm⋅s | T J | The lumen second is sometimes called the talbot. |
| Luminous flux, luminous power | Φv[nb 3] | lumen (= candela steradian) | lm (= cd⋅sr) | J | Luminous energy per unit time |
| Luminous intensity | Iv | candela (= lumen per steradian) | cd (= lm/sr) | J | Luminous flux per unit solid angle |
| Luminance | Lv | candela per square metre | cd/m2 (= lm/(sr⋅m2)) | L−2J | Luminous flux per unit solid angle per unit projected source area. The candela per square metre is sometimes called the nit. |
| Illuminance | Ev | lux (= lumen per square metre) | lx (= lm/m2) | L−2J | Luminous flux incident on a surface |
| Luminous exitance, luminous emittance | Mv | lumen per square metre | lm/m2 | L−2J | Luminous flux emitted from a surface |
| Luminous exposure | Hv | lux second | lx⋅s | L−2T J | Time-integrated illuminance |
| Luminous energy density | ωv | lumen second per cubic metre | lm⋅s/m3 | L−3T J | |
| Luminous efficacy (of radiation) | K | lumen per watt | lm/W | M−1L−2T3J | Ratio of luminous flux to radiant flux |
| Luminous efficacy (of a source) | η[nb 3] | lumen per watt | lm/W | M−1L−2T3J | Ratio of luminous flux to power consumption |
| Luminous efficiency, luminous coefficient | V | 1 | Luminous efficacy normalized by the maximum possible efficacy | ||
| See also: SI · Photometry · Radiometry |
- ^ Standards organizations recommend that photometric quantities be denoted with a subscript “v” (for “visual”) to avoid confusion with radiometric or photon quantities. For example: USA Standard Letter Symbols for Illuminating Engineering USAS Z7.1-1967, Y10.18-1967
- ^ The symbols in this column denote dimensions; “L“, “T” and “J” are for length, time and luminous intensity respectively, not the symbols for the units litre, tesla and joule.
- ^ a b c Alternative symbols sometimes seen: W for luminous energy, P or F for luminous flux, and ρ for luminous efficacy of a source.
Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Интенсивность света
Определение 1
Интенсивностью света ($I$) в избранной точке называют модуль средней по времени величины плотности потока энергии, которую световая волна переносит. В свою очередь плотность потока электромагнитной энергии определяют с помощью вектора Умова — Пойнтинга ($overrightarrow{P}$). Значит, в математическом виде определение интенсивности света можно записать как:
[I=left|leftlangle overrightarrow{P}rightrangle right|=left|leftlangle overrightarrow{E}times overrightarrow{H}rightrangle right|left(1right),]
где усреднение производят за время ($t$) много большее, чем период ($T$) колебаний волны: ($tgg T$). Определение интенсивности света можно записать в виде:
[Ileft(tright)=frac{1}{T}intlimits^{t+T}_t{left|overrightarrow{P}left(tright)right|}dt(2)]
Единицами измерения интенсивности света в $СИ$, обычно служат $frac{Вт}{м^2}.$

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Модули амплитуд ($E_m и H_m$) векторов напряжённостей электрического ($overrightarrow{E}$) и магнитного ($overrightarrow{H}$) полей в электромагнитной волне связаны соотношением:
где считаем, что $mu approx 1.$ Выразим из (3) амплитуду $H_m$, получим:
где $n=sqrt{varepsilon mu }=sqrt{varepsilon}$ при $mu approx 1$- показатель преломления вещества, в котором распространяется свет. Из выражения (4) следует, что:
Модуль среднего значения вектора Умова — Пойнтинга пропорционален произведению амплитуд $E_m cdot H_m$, значит можно записать, что интенсивность света:
Примечание 1
Интенсивность света не может быть измеряна в связи с тем, что поле изменяется с высокой частотой ($nu ={10}^{15}Гц$), соответственно период колебаний составляет $T={10}^{-15}с$, тогда как приемники колебаний имеют время инерции существенно больше, чем ${10}^{-15}с$. Следовательно, регистрировать мы можем среднее значение интенсивности. Кроме того, можно измерять среднюю интенсивность, но не фазу поля.
«Интенсивность и давление света» 👇
Давление света
В соответствии с законом сохранения в случае, когда тело поглощает или отражает свет, ему сообщается импульс, который равен разности импульсов пучка света до и после поглощения или отражения. Значит, на тело действует сила, свет производит на тело соответствующее давление. Предположение о существовании давления света была выдвинута Кеплером, который рассматривал отклонение хвостов комет от Солнца.
Сторонниками волновой теории давление света отрицалось, отсутствие эмпирических доказательств существования светового давления считалось аргументом против корпускулярной теории света. Существование светового давления является следствием электромагнитной теории.
При перпендикулярном падении световой волны на плоскую поверхность тела, и полном поглощении света, его давление ($p$) определяют как:
где $G$ — плотность импульса световой волны, $P$ — модуль вектора Умова — Пойнтинга (надо отметить, что на практике часто используют его среднее значение), $c$ — скорость света в вакууме.
В случае полного отражения света поверхностью тела импульс, передаваемый светом в два раза больше, соответственно больше во столько же давление.
Если энергия световой волны поглощается телом частично, при этом плотность потока поглощаемой энергии ($P_{pog}$) вычисляется как:
при этом плотность потока отражаемой энергии ($P_{otr}$) выразим как:
Принимая во внимание выражения (8) и (9) давление определим:
Если световая волна падает на поверхность тела под углом к нормали, то при расчете давления используют только перпендикулярную составляющую плотности потока энергии. Давление света при обычных условиях кране мало, примерно в ${10}^{10} $меньше атмосферного.
Примечание 2
Первым световое давление измерил П.Н. Лебедев в 1899 г. Он использовал для этого крутильные весы, которые находились в вакууме. Значение опытов Лебедева в том, что существование давления света подтверждало электромагнитную теорию света Максвелла.
Определение 2
Итак, давление электромагнитных волн – результат того, что при воздействии электрического поля волны частицы вещества, обладающие электрическим зарядом, упорядочено движутся, на них действуют силы Лоренца.
Пример 1
Задание: Каким будет давление, которое оказывает плоская световая волна, которая падает перпендикулярно на поверхность тела и полностью телом поглощается? Амплитуда напряженности электрического поля при этом равна $2frac{В}{м}$.
Решение:
За основу решения задачи примем выражение:
[p=frac{leftlangle Prightrangle }{c}left(1.1right),]
где $leftlangle Prightrangle $ — среднее значение модуля вектора Умова — Пойнтинга, $c=3cdot {10}^8frac{м}{с}$ — скорость света в вакууме.
При этом среднее значение модуля вектора Умова — Пойнтинга найдем как:
[leftlangle Prightrangle =leftlangle Ecdot Hrightrangle left(1.2right).]
Так как по условию задачи мы имеем плоскую волну, то уравнение колебаний ее составляющих запишем как:
[E=E_m{cos left(omega t-kxright) }, H=H_m{cos left(omega t-kxright) }left(1.3right).]
Для того чтобы найти значение амплитуды напряжения магнитного поля воспользуемся соотношением:
[sqrt{varepsilon {varepsilon }_0}E_m=sqrt{mu {mu }_0}H_mleft(1.4right).]
Используем то, что для вакуума $varepsilon $=1, $mu =1$, выразим из (1.4) $H_m$, имеем:
[H_m=sqrt{frac{varepsilon_0}{mu_0}}E_mleft(1.5right),]
где $mu_0=4pi cdot {10}^{-7}frac{Гн}{м}, varepsilon_0=frac{1}{4pi cdot {9cdot 10}^9}frac{Ф}{м}$. В таком случае среднее значение модуля вектора Умова — Пойнтинга равно:
[leftlangle Prightrangle =leftlangle E_m{cos left(omega t-kxright) }cdot sqrt{frac{{varepsilon }_0}{{mu }_0}}E_m{cos left(omega t-kxright) }rightrangle =sqrt{frac{{varepsilon }_0}{{mu }_0}}{E_m}^2leftlangle {cos left(omega t-kxright) }rightrangle =frac{1}{2}sqrt{frac{{varepsilon }_0}{{mu }_0}}{E_m}^2left(1.6right).]
Подставим правую часть выражения (1.6) в формулу (1.1) вместо величины $leftlangle Prightrangle $, получим искомое давление света:
[p=frac{frac{1}{2}sqrt{frac{{varepsilon }_0}{{mu }_0}}{E_m}^2}{c}.]
Проведем вычисления:
[p=frac{1}{2cdot 3cdot {10}^8}sqrt{frac{1}{4pi cdot {10}^{-7}cdot 4pi cdot {9cdot 10}^9}}cdot 4=frac{4}{120pi cdot 6cdot {10}^8}=1,77cdot {10}^{11}(Па).]
Ответ: $p=17,7пПа.$
Пример 2
Задание: Какой будет интенсивность ($I$), плоской световой волны, которая распространяется вдоль $оси X$? Амплитуда напряженности электрического поля волны при этом равна $E_m(frac{В}{м})$.
Решение:
По определению интенсивность световой волны можно найти как:
[I=leftlangle Prightrangle left(2.1right).]
Для плоской световой волны модуль вектора Умова — Пойнтинга запишем как (см. Пример 1):
[P=EH=E_mH_mc{os}^2left(omega t-kxright)left(2.2right).]
Тогда среднее значение $leftlangle Prightrangle $ можно выразить как:
[leftlangle Prightrangle =frac{1}{2}E_mH_mleft(2.3right),]
так как $leftlangle c{os}^2left(omega t-kxright)rightrangle =frac{1}{2}.$
При этом так же, как в примере 1, выразим амплитуду напряженности магнитного поля:
[sqrt{varepsilon {varepsilon }_0}E_m=sqrt{mu {mu }_0}H_mto H_m=sqrt{frac{varepsilon {varepsilon }_0}{mu {mu }_0}}E_mleft(2.4right).]
Используя выражения (2.1), (2.3) и (2.4), запишем:
[I=frac{1}{2}sqrt{frac{varepsilon {varepsilon }_0}{mu {mu }_0}}{E_m}^2.]
Ответ: $I=frac{1}{2}sqrt{frac{varepsilon {varepsilon }_0}{mu {mu }_0}}{E_m}^2.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
На чтение 9 мин Просмотров 3к. Опубликовано 05.02.2021
Обновлено 05.02.2021
Содержание
- Что это такое интенсивность света
- Как и в чем измеряется интенсивность света
- Плотность и мощность светового потока
- Комфортная интенсивность освещения
Интенсивность света имеет значение как в рабочих, так и в жилых помещениях. Человек основную часть данных об окружающем мире воспринимает через зрение. Поэтому от качественного освещения зависит скорость усвоения информации, а также комфорт пребывания в помещении. Если свет слишком тусклый, глаза быстро устают, а если слишком яркий, создается дискомфорт для глаз. При выборе оптимальной интенсивности нужно учесть ряд параметров, также важно контролировать показатели с помощью специального оборудования.

Что это такое интенсивность света
Определение параметров усложняется тем, что формула интенсивности света сложна в расчетах и не может использоваться как единственные показатель. Поэтому надо учитывать сразу несколько важных аспектов, чтобы получить данные, которые помогут определить соответствие освещения установленным параметрам. Дома можно исходить и из собственных предпочтений, чтобы создать комфортную обстановку. В рабочих помещениях надо четко соблюдать регламент, чтобы создать комфортные условия труда.

Интенсивность света – термин, который объединяет в себе световой поток, яркость, силу света, цветовую температуру и т.д. При этом каждую величину можно вычислить отдельно.
Как и в чем измеряется интенсивность света
Так как интенсивность падающего света оценивается не по одному критерию, надо разобраться в самых важных показателях. В этом нет ничего сложного, главное – определить основные характеристики, которые имеют наибольшее значение. Используются такие параметры:
- Сила света – световая энергия, которая распространяется от любого источника в определенном направлении. Этот показатель используют в физике и других науках при проведении экспериментов со световыми волнами. Единицей измерения является кандела. В качестве эталона принимают пламя одной горящей свечи, у нее сила света примерно равна 1 канделе.
- Яркость освещения – еще один важный критерий, который отличается у разных источников света. От этого зависит создание комфортных условий. Измеряется в канделах, кроме того, есть и другие единицы измерения – ламберт, апостильб и стильб. Яркость важна при видео и фотосъемке, а чтобы получать качественные изображения, в условиях плохого освещения используют поляризаторы.
- Освещенность – отношение светового потока, исходящего от светильника, к площади его распространения под определенным углом. Чаще всего регламентируют горизонтальную освещенность, так как она имеет наибольшее значение для комфортных условий работы и отдыха. При этом большое значение имеет и плотность освещения, то есть оно должно распределяться по всей площади одинаково, без затемненных и слишком светлых мест. Основной единицей измерения является люкс.
Самым главным является последний критерий, так как он больше всего влияет на человеческое зрение. Для определения показателей используют такой прибор, как люксометр.

Он состоит из светоприемника и измерительного модуля, который может быть как аналоговым, так и электронным. В приемнике света используется фотоэлемент, воспринимающий волны заданной амплитуды, видимые человеческому глазу. Он преобразует их в электрический сигнал, который и выводится на экран.
По сути, это фотометр с четко заданным диапазоном спектральной чувствительности, который реагирует только на волны определенной длины. Анализатор может измерять как обычный свет, так и инфракрасное излучение, все зависит от настроек.
Плотность и мощность светового потока
Часто используют и эти термины для определения качества света. Так как трактовка бывает разной, иногда возникают сложности с тем, что подразумевается под этими показателями. Тут все достаточно просто:
- Плотность света – соотношение светового потока к площади его распространения. Этот параметр еще называют яркостью и измеряется он в канделах на квадратный метр. Показатель влияет на зрительное восприятие обстановки в помещении, так как важно, чтобы освещение было комфортным, для чего плотность должна попадать в определенный диапазон. При этом световой поток с яркостью, превышающей 500 Кд/м.кв. создает дискомфорт для зрения.
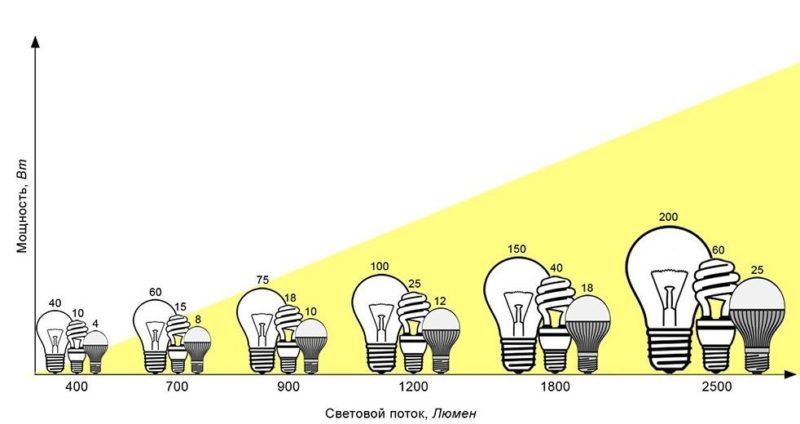
- Мощность светового потока определяет воздействие видимого излучения на зрительное восприятие. Единицей измерения является люмен, при этом в расчет берется общий показатель вне зависимости от направления освещения. То есть, лампа с одним и тем же световым потоком может освещать площадь и в 10, и в 100 кв.м. Поэтому гораздо проще и удобнее судить по показателям освещенности, так как при использовании конструкций с качественным отражателем можно создать комфортные условия при меньших затратах энергии.
Для обеспечения нужной мощности конструкции светильников часто оборудуют рассеивателями, а поверхности внутри делают отражающими. Это позволяет направить весь световой поток на ограниченное пространство, что повышает его интенсивность и позволяет экономить электричество. По схожему принципу действует линза Френеля, а также оптика, используемая в проекторах и другом оборудовании.
Комфортная интенсивность освещения
Комфорт освещения требует соблюдения целого ряда требований. При этом данный параметр невозможно унифицировать, так как у людей разные предпочтения, а выполнение различных видов работ требует разных условий. Наиболее комфортным для любого человека является свет солнца, именно на этот спектр и ориентируются при планировании искусственного освещения.
Ближе всего к естественному излучению свет обычных ламп накаливания, который образуется за счет раскаленной спирали. Но из-за высокого энергопотребления, сильного нагрева при работе, короткого срока службы из используют все меньше.
Важным показателем является световая температура, есть три разновидности:
- Теплый свет имеет желтый оттенок и подходит для создания обстановки, располагающей к расслаблению и отдыху. Чаще всего его используют в жилых помещениях.
- Нейтральный свет отличает большая яркость, еще его называют белым. Подходит для рабочих мест, а также для зон, где важно обеспечить хорошую видимость, например, рабочая зона на кухне.
- Холодное освещение отличает преобладание синих лучей в спектре. Оно подходит для мест, где выполняются точные работы. Дома использовать его не стоит, так как при длительном нахождении в помещении с холодным светом глаза начинают уставать.
Чтобы не измерять показатели освещенности, при выборе светильников и лампочек проще всего руководствоваться установленными нормами. В жилых помещениях стоит придерживаться таких показателей:
- Коридоры и прихожие – 50 Лк.
- Санузлы, душевые, ванные комнаты – 50 люксов.
- Кухни – 150 Лк.
- Детские комнаты и игровые зоны – 200 люксов.
- Жилые помещения (гостиные, спальни и т.д.) – 150 Лк.
При выборе светильников надо обращать внимание на особенности распространения светового потока. Самым комфортным является рассеянный или отраженный свет. Чтобы выделить функциональные зоны или обеспечить качественное освещение рабочего места, лучше использовать дополнительные светильники.

Изменить интенсивность света можно за счет замены ламп или установки новых светильников. Не стоит экономить на качестве освещения, так как это влияет не только на восприятие помещений, но и на комфорт пребывания в них.


