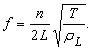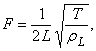Как найти интенсивность звуковой волны

Интенсивность звука
Размерность	MT−3
Единицы измерения
СИ	Вт/м²
СГС	эрг/с·см²
Примечания
скалярная величина

Интенсивность звука (сила звука) — скалярная физическая величина, характеризующая мощность, переносимую звуковой волной в направлении распространения. Количественно интенсивность звука равна среднему по времени потоку звуковой энергии через единичную площадку, расположенную перпендикулярно направлению распространения звука^[1][2]:

где t₀ — некоторый момент времени, T — время усреднения, dP — поток звуковой энергии (Дж/с), переносимый через площадку dS.

Используется также физическая величина мгновенная интенсивность звука, представляющая собой мгновенное значение потока звуковой энергии через единичную площадку, расположенную перпендикулярно направлению распространения звука^[2]:

Единица измерения в Международной системе единиц (СИ) — ватт на квадратный метр (Вт/м²).

Для плоской волны интенсивность звука может быть выражена через амплитуду звукового давления p₀ и колебательную скорость v:

где Z_S — удельное акустическое сопротивление среды.

Порог слышимости по интенсивности для человека зависит от частоты. Самый тихий звук частотой 1 кГц, который способно услышать ухо, имеет интенсивность порядка 10^-12 Вт/м². Болевой порог человека приблизительно равен 1 Вт/м². Физиологически доступный для восприятия частотный диапазон: от 16—20 Гц до 15—20 кГц.

См. также[править | править код]

• Громкость звука
• Плотность звуковой энергии

Примечания[править | править код]

Литература[править | править код]

• Интенсивность звука (сила звука) // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М.: Сов. энциклопедия, 1972. — Т. X. — С. 315–316. — 592 с.

ЗВУК И АКУСТИКА. Звук – это колебания, т.е. периодическое механическое возмущение в упругих средах – газообразных, жидких и твердых. Такое возмущение, представляющее собой некоторое физическое изменение в среде (например, изменение плотности или давления, смещение частиц), распространяется в ней в виде звуковой волны. Область физики, рассматривающая вопросы возникновения, распространения приема и обработки звуковых волн, называется акустикой. Звук может быть неслышимым, если его частота лежит за пределами чувствительности человеческого уха, или он распространяется в такой среде, как твердое тело, которая не может иметь прямого контакта с ухом, или же его энергия быстро рассеивается в среде. Таким образом, обычный для нас процесс восприятия звука – лишь одна сторона акустики.

ЗВУКОВЫЕ ВОЛНЫ

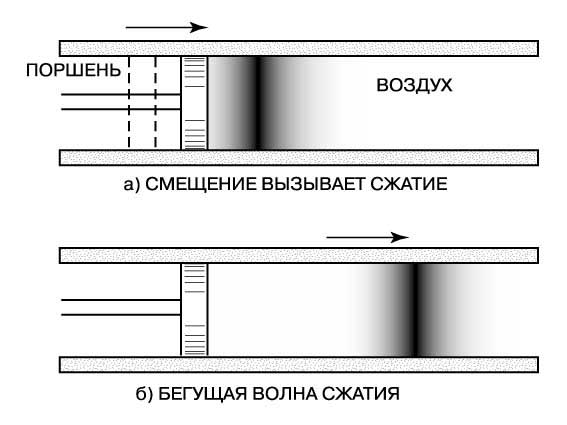
Рассмотрим длинную трубу, наполненную воздухом. С левого конца в нее вставлен плотно прилегающий к стенкам поршень (рис. 1). Если поршень резко двинуть вправо и остановить, то воздух, находящийся в непосредственной близости от него, на мгновение сожмется (рис. 1,а). Затем сжатый воздух расширится, толкнув воздух, прилегающий к нему справа, и область сжатия, первоначально возникшая вблизи поршня, будет перемещаться по трубе с постоянной скоростью (рис. 1,б). Эта волна сжатия и есть звуковая волна в газе.

Звуковая волна в газе характеризуется избыточным давлением, избыточной плотностью, смещением частиц и их скоростью. Для звуковых волн эти отклонения от равновесных значений всегда малы. Так, избыточное давление, связанное с волной, намного меньше статического давления газа. В противном случае мы имеем дело с другим явлением – ударной волной. В звуковой волне, соответствующей обычной речи, избыточное давление составляет лишь около одной миллионной атмосферного давления.

Важно то обстоятельство, что вещество не уносится звуковой волной. Волна представляет собой лишь проходящее по воздуху временное возмущение, по прохождении которого воздух возвращается в равновесное состояние.

Волновое движение, конечно, не является характерным только для звука: в форме волн распространяются свет и радиосигналы, и каждому знакомы волны на поверхности воды. Все типы волн математически описываются так называемым волновым уравнением.

Гармонические волны.

Волна в трубе на рис. 1 называется звуковым импульсом. Очень важный тип волны возбуждается, когда поршень колеблется туда-сюда подобно грузу, подвешенному на пружине. Такие колебания называются простыми гармоническими или синусоидальными, а возбуждаемая в этом случае волна – гармонической.

При простых гармонических колебаниях движение периодически повторяется. Промежуток времени между двумя одинаковыми состояниями движения называется периодом колебаний, а число полных периодов в секунду, – частотой колебаний. Обозначим период через Т, а частоту – через f; тогда можно написать, что f = 1/T. Если, например, частота равна 50 периодам в секунду (50 Гц), то период равен 1/50 секунды.

Математически простые гармонические колебания описываются простой функцией. Смещение поршня при простых гармонических колебаниях для любого момента времени t можно записать в виде

Здесь d – смещение поршня из положения равновесия, а D – постоянный множитель, который равен максимальному значению величины d и называется амплитудой смещения.

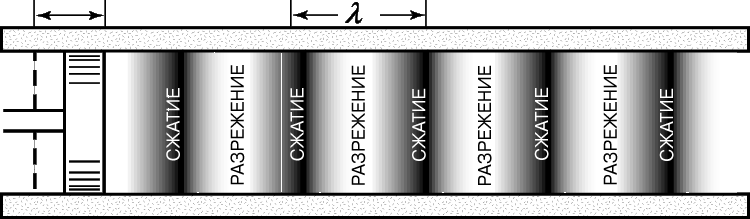
Предположим, что поршень колеблется в соответствии с формулой гармонических колебаний. Тогда при движении его вправо возникает, как и прежде, сжатие, а при движении влево давление и плотность будут уменьшаться относительно своих равновесных значений. Возникает не сжатие, а разрежение газа. В этом случае вправо будет распространяться, как показано на рис. 2, волна чередующихся сжатий и разрежений. В каждый момент времени кривая распределения давления по длине трубы будет иметь вид синусоиды, и эта синусоида будет двигаться вправо со скоростью звука v. Расстояние вдоль трубы между одинаковыми фазами волны (например, между соседними максимумами) называется длиной волны. Ее принято обозначать греческой буквой l (лямбда). Длина волны l есть расстояние, проходимое волной за время Т. Поэтому l = Tv, или v = lf.

Продольные и поперечные волны.

Если частицы колеблются параллельно направлению распространения волны, то волна называется продольной. Если же они колеблются перпендикулярно направлению распространения, то волна называется поперечной. Звуковые волны в газах и жидкостях – продольные. В твердых же телах существуют волны обоих типов. Поперечная волна в твердом теле возможна благодаря его жесткости (сопротивлению к изменению формы).

Самая существенная разница между этими двумя типами волн заключается в том, что поперечная волна обладает свойством поляризации (колебания происходят в определенной плоскости), а продольная – нет. В некоторых явлениях, таких, как отражение и прохождение звука через кристаллы, многое зависит от направления смещения частиц, так же как и в случае световых волн.

Скорость звуковых волн.

Скорость звука – это характеристика среды, в которой распространяется волна. Она определяется двумя факторами: упругостью и плотностью материала. Упругие свойства твердых тел зависят от типа деформации. Так, упругие свойства металлического стержня неодинаковы при кручении, сжатии и изгибе. И соответствующие волновые колебания распространяются с разной скоростью.

Упругой называется среда, в которой деформация, будь то кручение, сжатие или изгиб, пропорциональна силе, вызывающей деформацию. Такие материалы подчиняются закону Гука:

Напряжение = C ґ Относительная деформация,

где С – модуль упругости, зависящий от материала и типа деформации.

Скорость звука v для данного типа упругой деформации дается выражением

где r – плотность материала (масса единицы объема).

Скорость звука в твердом стержне.

Длинный стержень можно растянуть или сжать силой, приложенной к концу. Пусть длина стержня равна L, прикладываемая растягивающая сила – F, а увеличение длины – DL. Величину DL/L будем называть относительной деформацией, а силу, приходящуюся на единицу площади поперечного сечения стержня, – напряжением. Таким образом, напряжение равно F/A , где А – площадь сечения стержня. В применении к такому стержню закон Гука имеет вид

где Y – модуль Юнга, т.е. модуль упругости стержня для растяжения или сжатия, характеризующий материал стержня. Модуль Юнга мал для легко растяжимых материалов, таких, как резина, и велик для жестких материалов, например для стали.

Если теперь ударом молотка по торцу стержня возбудить в нем волну сжатия, то она будет распространяться со скоростью , где r, как и прежде, – плотность материала, из которого изготовлен стержень. Значения скоростей волн для некоторых типовых материалов приведены в табл. 1.

Таблица 1. СКОРОСТЬ ЗВУКА ДЛЯ РАЗНЫХ ТИПОВ ВОЛН В ТВЕРДЫХ МАТЕРИАЛАХ
Материал	Продольные волны в протяженных твердых образцах (м/с)	Волны сдвига и кручения (м/с)	Волны сжатия в стержнях (м/с)
Алюминий	6420	3040	5000
Латунь	4700	2110	3480
Свинец	5950	3240	5120
Железо	1960	690	1210
Серебро	3650	1610	2680
Нержавеющая сталь	5790	3100	5000
Флинтглас	3980	2380	3720
Кронглас	5100	2840	4540
Оргстекло	2680	1100	1840
Полиэтилен	1950	540	920
Полистирол	2350	1120	2240

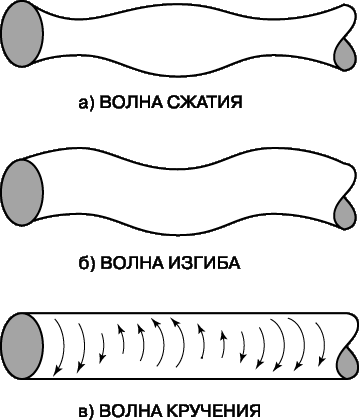
Рассмотренная волна в стержне является волной сжатия. Но ее нельзя считать строго продольной, так как со сжатием связано движение боковой поверхности стержня (рис. 3,а).

В стержне возможны и два других типа волн – волна изгиба (рис. 3,б) и волна кручения (рис. 3,в). Деформациям изгиба соответствует волна, не являющаяся ни чисто продольной, ни чисто поперечной. Деформации же кручения, т.е. вращения вокруг оси стержня, дают чисто поперечную волну.

Скорость волны изгиба в стержне зависит от длины волны. Такую волну называют «дисперсионной».

Волны кручения в стержне – чисто поперечные и недисперсионные. Их скорость дается формулой

где m – модуль сдвига, характеризующий упругие свойства материала по отношению к сдвигу. Некоторые типичные скорости волн сдвига приведены в табл. 1.

Скорость в протяженных твердых средах.

В твердых средах большого объема, где влиянием границ можно пренебречь, возможны упругие волны двух типов: продольные и поперечные.

Деформация в продольной волне – это плоская деформация, т.е. одномерное сжатие (или разрежение) в направлении распространения волны. Деформация, соответствующая поперечной волне, – это сдвиговое смещение, перпендикулярное направлению распространения волны.

Скорость продольных волн в твердых материалах дается выражением

где C_L – модуль упругости для простой плоской деформации. Он связан с модулем объемной деформации В (определение которого дается ниже) и модулем сдвига m материала соотношением C_L = B + 4/3m. В табл. 1 приводятся значения скоростей продольных волн для различных твердых материалов.

Скорость волн сдвига в протяженных твердых средах та же, что и скорость волн кручения в стержне из того же материала. Поэтому она дается выражением . Ее значения для обычных твердых материалов даны в табл. 1.

Скорость в газах.

В газах возможен только один тип деформации: сжатие – разрежение. Соответствующий модуль упругости В называется модулем объемной деформации. Он определяется соотношением

–DP = B(DV/V).

Здесь DP – изменение давления, DV/V – относительное изменение объема. Знак «минус» показывает, что при увеличении давления объем уменьшается.

Величина В зависит от того, изменяется или нет температура газа при сжатии. В случае звуковой волны можно показать, что давление изменяется очень быстро и теплота, выделяющаяся при сжатии, не успевает уходить из системы. Таким образом, изменение давления в звуковой волне происходит без теплообмена с окружающими частицами. Такое изменение называется адиабатическим. Установлено, что скорость звука в газе зависит только от температуры. При данной температуре скорость звука примерно одинакова для всех газов. При температуре 21,1° С скорость звука в сухом воздухе составляет 344,4 м/с и возрастает с повышением температуры.

Скорость в жидкостях.

Звуковые волны в жидкостях являются волнами сжатия – разрежения, как и в газах. Скорость дается той же формулой . Однако жидкость гораздо менее сжимаема, чем газ, и поэтому для нее во много раз больше величина В, больше и плотность r. Скорость звука в жидкостях ближе к скорости в твердых материалах, чем в газах. Она гораздо меньше, чем в газах, зависит от температуры. Например, скорость в пресной воде равна 1460 м/с при 15,6° С. В морской воде нормальной солености она при той же температуре составляет 1504 м/с. Скорость звука возрастает с повышением температуры воды и концентрации соли.

Стоячие волны.

Когда гармоническая волна возбуждается в ограниченном пространстве, так что она отражается от границ, возникают так называемые стоячие волны. Стоячая волна – это результат наложения двух волн, бегущих одна в прямом, а другая – в обратном направлении. Возникает не движущаяся в пространстве картина колебаний с чередованием пучностей и узлов. В пучностях отклонения колеблющихся частиц от их равновесных положений максимальны, а в узлах равны нулю.

Стоячие волны в струне.

В натянутой струне возникают поперечные волны, причем происходит смещение струны относительно ее первоначального, прямолинейного положения. При фотографировании волн в струне отчетливо видны узлы и пучности основного тона и обертонов.

Картина стоячих волн существенно облегчает анализ колебательных движений струны данной длины. Пусть имеется струна длиной L , закрепленная на концах. Любой вид колебаний такой струны может быть представлен как комбинация стоячих волн. Поскольку концы струны неподвижно закреплены, возможны только такие стоячие волны, которые имеют узлы в граничных точках. Самая низкая частота колебаний струны соответствует максимально возможной длине волны. Поскольку расстояние между узлами равно l/2, частота минимальна, когда длина струны равна половине длины волны, т.е. при l = 2L . Это так называемая основная мода колебаний струны. Соответствующая ей частота, называемая основной частотой или основным тоном, дается выражением f = v/2L, где v – скорость распространения волны вдоль струны.

Существует целая последовательность колебаний более высоких частот, которые соответствуют стоячим волнам с бóльшим числом узлов. Следующая более высокая частота, которая называется второй гармоникой или первым обертоном, дается выражением

f = v/L.

Последовательность гармоник выражается формулой f = nv/2L, где n = 1, 2, 3, и т.д. Это т.н. собственные частоты колебаний струны. Они возрастают пропорционально числам натурального ряда: высшие гармоники в 2, 3, 4… и т.д. раз больше частоты основного колебания. Такой ряд звуков называется натуральным или гармоническим звукорядом.

Все это имеет важное значение в музыкальной акустике, о чем подробнее будет сказано ниже. Пока же отметим, что в звуке, производимом струной, присутствуют все собственные частоты. Относительный вклад каждой из них зависит от того, в какой точке возбуждены колебания струны. Если, например, ущипнуть струну посередине, то сильнее всего возбудится основная частота, поскольку эта точка соответствует пучности. Вторая же гармоника будет отсутствовать, так как в центре находится ее узел. То же можно сказать и о других гармониках (см. ниже Музыкальная акустика).

Скорость волн в струне равна

где Т – сила натяжения струны, а r_L – масса единицы длины струны. Следовательно, спектр собственных частот струны дается выражением

Таким образом, увеличение натяжения струны приводит к повышению частот колебаний. Понизить же частоты колебаний при заданном T можно, взяв более тяжелую струну (большое r_L) или увеличив ее длину.

Стоячие волны в органных трубах.

Теория, изложенная применительно к струне, может быть применена и к колебаниям воздуха в трубе типа органной. Органную трубу можно упрощенно рассматривать как прямую трубу, в которой возбуждаются стоячие волны. Труба может иметь как закрытые, так и открытые концы. У открытого конца возникает пучность стоячей волны, а у закрытого – узел. Следовательно, труба с двумя открытыми концами имеет такую основную частоту, при которой на длине трубы укладывается половина длины волны. Труба же, у которой один конец открыт, а другой – закрыт, имеет основную частоту, при которой на длине трубы укладывается четверть длины волны. Таким образом, основная частота для трубы, открытой с обоих концов, равна f = v/2L, а для трубы, открытой с одного конца, f = v/4L (где L – длина трубы). В первом случае результат такой же, как и для струны: обертоны равны удвоенному, утроенному и т.д. значению основной частоты. Однако для трубы, открытой с одного конца, обертоны будут больше основной частоты в 3, 5, 7 и т.д. раз.

На рис. 4 и 5 схематически показана картина стоячих волн основной частоты и первого обертона для труб двух рассмотренных типов. Смещения из соображений удобства здесь показаны как поперечные, но на самом деле они продольные.

Резонансные колебания.

Стоячие волны тесно связаны с явлением резонанса. Собственные частоты, о которых говорилось выше, являются также резонансными частотами струны или органной трубы. Предположим, что вблизи открытого конца органной трубы помещен громкоговоритель, издающий сигнал одной определенной частоты, которую можно по желанию изменять. Тогда при совпадении частоты сигнала громкоговорителя с основной частотой трубы или с одним из ее обертонов труба будет звучать очень громко. Это происходит потому, что громкоговоритель возбуждает колебания воздушного столба со значительной амплитудой. Говорят, что труба в этих условиях резонирует.

Фурье-анализ и частотный спектр звука.

На практике звуковые волны одной-единственной частоты встречаются редко. Но сложные звуковые волны можно разлагать на гармоники. Такой метод называется фурье-анализом по имени французского математика Ж.Фурье (1768–1830), который первым применил его (в теории теплоты).

График зависимости относительной энергии звуковых колебаний от частоты называется частотным спектром звука. Существуют два основных типа таких спектров: дискретный и непрерывный. Дискретный спектр состоит из отдельных линий для частот, разделенных пустыми промежутками. В непрерывном спектре в пределах его полосы присутствуют все частоты.

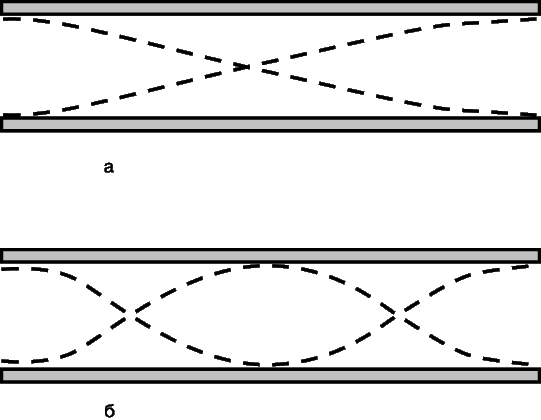
Периодические звуковые колебания.

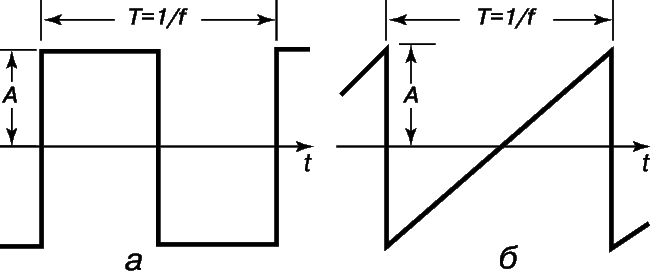
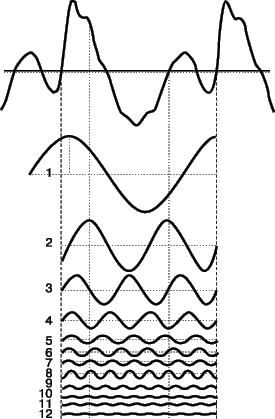
Звуковые колебания являются периодическими, если колебательный процесс, каким бы сложным он ни был, повторяется через определенный интервал времени. Его спектр всегда дискретный и состоит из гармоник определенной частоты. Отсюда и термин «гармонический анализ». Примером могут служить колебания прямоугольной формы (рис. 6,а) с изменением амплитуды от +А до –А и периодом T = 1/f. Другой простой пример – треугольные пилообразные колебания, показанные на рис. 6,б. Пример периодических колебаний более сложной формы с соответствующими гармоническими составляющими представлен на рис. 7.

Музыкальные звуки являются периодическими колебаниями и потому содержат гармоники (обертоны). Мы уже видели, что в струне наряду с колебаниями основной частоты в той или иной степени возбуждаются другие гармоники. Относительный вклад каждого обертона зависит от способа возбуждения струны. Набором обертонов в значительной степени определяется тембр музыкального звука. Эти вопросы подробнее рассматриваются ниже в разделе, посвященном музыкальной акустике.

Спектр звукового импульса.

Обычной разновидностью звука является звук малой длительности: хлопок в ладоши, стук в дверь, звук падающего на пол предмета, кукованье кукушки. Такие звуки не являются ни периодическими, ни музыкальными. Но их тоже можно разлагать в частотный спектр. В этом случае спектр будет непрерывным: для описания звука необходимы все частоты в пределах некоторой полосы, которая может быть весьма широкой. Знать такой частотный спектр необходимо для воспроизведения подобных звуков без искажений, поскольку соответствующая электронная система должна одинаково хорошо «пропускать» все эти частоты.

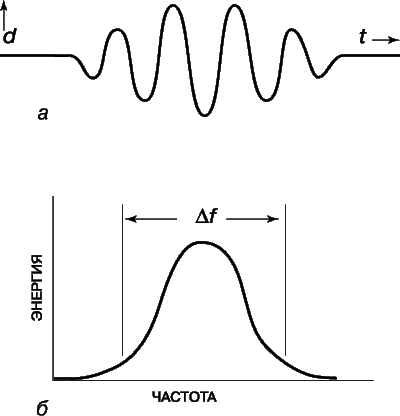
Основные особенности звукового импульса можно выяснить, рассмотрев импульс простой формы. Предположим, что звук представляет собой колебания длительностью Dt, при которых изменение давления таково, как показано на рис. 8,а. Примерный частотный спектр для этого случая представлен на рис. 8,б. Центральная частота соответствует колебаниям, которые мы имели бы при бесконечной протяженности того же сигнала.

Протяженность частотного спектра назовем шириной полосы Df (рис. 8,б). Ширина полосы – это приблизительный диапазон частот, необходимый для воспроизведения исходного импульса без чрезмерных искажений. Существует очень простое фундаментальное соотношение между Df и Dt, а именно

DfDt » 1.

Такое соотношение справедливо для всех звуковых импульсов. Его смысл в том, что чем короче импульс, тем больше частот он содержит. Предположим, что для обнаружения подводной лодки используется гидролокатор, излучающий ультразвук в виде импульса длительностью 0,0005 с с частотой сигнала 30 кГц. Ширина полосы составляет 1/0,0005 = 2 кГц, а частоты, реально содержащиеся в спектре импульса локатора, лежат в диапазоне от 29 до 31 кГц.

Шум.

Под шумом понимается любой звук, создаваемый многочисленными, не согласованными между собой источниками. Примером может служить шум листвы деревьев, колеблемой ветром. Шум реактивного двигателя обусловлен турбулентностью высокоскоростного выхлопного потока. Шум как раздражающий звук рассматривается в ст. АКУСТИЧЕСКОЕ ЗАГРЯЗНЕНИЕ ОКРУЖАЮЩЕЙ СРЕДЫ.

Интенсивность звука.

Громкость звука может быть различной. Нетрудно сообразить, что это связано с энергией, переносимой звуковой волной. Для количественных сравнений громкости нужно ввести понятие интенсивности звука. Интенсивность звуковой волны определяется как средний поток энергии через единицу площади волнового фронта в единицу времени. Иначе говоря, если взять единичную площадку (например, 1 см²), которая полностью поглощала бы звук, и расположить ее перпендикулярно направлению распространения волны, то интенсивность звука равна акустической энергии, поглощаемой за одну секунду. Интенсивность обычно выражается в Вт/см² (или в Вт/м²).

Приведем значение этой величины для некоторых привычных звуков. Амплитуда избыточного давления, возникающего при обычном разговоре, составляет примерно одну миллионную атмосферного давления, что соответствует акустической интенсивности звука порядка 10^–9 Вт/см². Полная же мощность звука, издаваемого при обычном разговоре, – порядка всего лишь 0,00001 Вт. Способность человеческого уха воспринимать столь малые энергии свидетельствует о его поразительной чувствительности.

Диапазон интенсивностей звука, воспринимаемых нашим ухом, очень широк. Интенсивность самого громкого звука, который может вынести ухо, примерно в 10¹⁴ раз больше минимальной, которую оно способно услышать. Полная мощность источников звука охватывает столь же широкий диапазон. Так, мощность, излучаемая при очень тихом шепоте, может быть порядка 10^–9 Вт, тогда как мощность, излучаемая реактивным двигателем, достигает 10⁵ Вт. Опять-таки интенсивности различаются в 10¹⁴ раз.

Децибел.

Поскольку звуки столь сильно различаются по интенсивности, удобнее рассматривать ее как логарифмическую величину и измерять в децибелах. Логарифмическая величина интенсивности представляет собой логарифм отношения рассматриваемого значения величины к ее значению, принимаемому за исходное. Уровень интенсивности J по отношению к некоторой условно выбранной интенсивности J₀ равен

Уровень интенсивности звука = 10 lg (J/J₀) дБ.

Такием образом, один звук, превышающий другой по уровню интенсивности на 20 дБ, превышает его в 100 раз по интенсивности.

В практике акустических измерений принято выражать интенсивность звука через соответствующую амплитуду избыточного давления Р_е. Когда давление измеряется в децибелах относительно некоторого условно выбранного давления Р₀, получают так называемый уровень звукового давления. Поскольку интенсивность звука пропорциональна величине P_e², а lg(P_e²) = 2lgP_e, уровень звукового давления определяется следующим образом:

Уровень звукового давления = 20 lg (P_e/P₀) дБ.

Условное давление Р₀ = 2Ч10^–5 Па соответствует стандартному порогу слышимости для звука с частотой 1 кГц. В табл. 2 приводятся уровни звукового давления для некоторых обычных источников звука. Это интегральные значения, полученные усреднением по всему слышимому диапазону частот.

Таблица 2. ТИПИЧНЫЕ УРОВНИ ЗВУКОВОГО ДАВЛЕНИЯ
Источник звука	Уровень звукового давления, дБ (отн. 2Ч10–5 Па)
Штамповочный цех	125
Машинное отделение на судне	115
Прядильно-ткацкий цех	105
В вагоне метро	95
В автомобиле при движении в потоке транспорта	85
Машинописное бюро	78
Бухгалтерия	63
Офис	50
Жилое помещение	43
Территория жилого района ночью	35
Студия радиовещания	25

Громкость.

Уровень звукового давления не связан простой зависимостью с психологическим восприятием громкости. Первый из этих факторов объективный, а второй – субъективный. Эксперименты показывают, что восприятие громкости зависит не только от интенсивности звука, но и от его частоты и условий эксперимента.

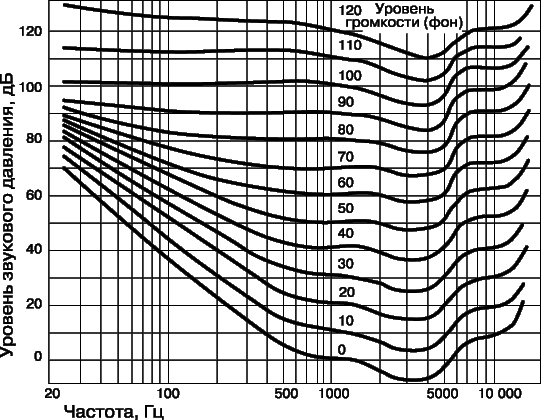
Громкости звуков, не привязанных к условиям сравнения, сравнивать невозможно. И все же сравнение чистых тонов представляет интерес. Для этого определяют уровень звукового давления, при котором данный тон воспринимается как равногромкий стандартному тону частотой 1000 Гц. На рис. 9 представлены кривые равной громкости, полученные в экспериментах Флетчера и Мэнсона. Для каждой кривой указан соответствующий уровень звукового давления стандартного тона 1000 Гц. Например, при частоте тона 200 Гц необходим уровень звука в 60 дБ, чтобы он воспринимался как равногромкий тону 1000 Гц с уровнем звукового давления 50 дБ.

Эти кривые используются для определения фона – единицы уровня громкости, которая тоже измеряется в децибелах. Фон – это уровень громкости звука, для которого уровень звукового давления равногромкого стандартного чистого тона (1000 Гц) равен 1 дБ. Так, звук частотой 200 Гц при уровне 60 дБ имеет уровень громкости в 50 фонов.

Нижняя кривая на рис. 9 – это кривая порога слышимости хорошего уха. Диапазон слышимых частот простирается примерно от 20 до 20 000 Гц (см. также СЛУХ).

Распространение звуковых волн.

Как и волны от камешка, брошенного в спокойную воду, звуковые волны распространяются во всех направлениях. Такой процесс распространения удобно характеризовать волновым фронтом. Волновой фронт – это поверхность в пространстве, во всех точках которой колебания происходят в одной фазе. Волновые фронты от камешка, упавшего в воду, представляют собой окружности.

Плоские волны.

Волновой фронт простейшего вида – плоский. Плоская волна распространяется только в одном направлении и представляет собой идеализацию, которая лишь приблизительно реализуется на практике. Звуковую волну в трубе можно считать приблизительно плоской, как и сферическую волну на большом расстоянии от источника.

Сферические волны.

К простым типам волн можно отнести и волну со сферическим фронтом, исходящую из точки и распространяющуюся во всех направлениях. Такую волну можно возбудить с помощью малой пульсирующей сферы. Источник, возбуждающий сферическую волну, называется точечным. Интенсивность такой волны убывает по мере ее распространения, поскольку энергия распределяется по сфере все большего радиуса.

Если точечный источник, создающий сферическую волну, излучает мощность 4pQ, то, поскольку площадь поверхности сферы радиусом r равна 4pr², интенсивность звука в сферической волне равна

J = Q/r²,

где r – расстояние от источника. Таким образом, интенсивность сферической волны убывает обратно пропорционально квадрату расстояния от источника.

Интенсивность любой звуковой волны в процессе ее распространения уменьшается вследствие поглощения звука. Это явление будет рассмотрено ниже.

Принцип Гюйгенса.

Для распространения волнового фронта справедлив принцип Гюйгенса. Для выяснения его рассмотрим известную нам форму волнового фронта в какой-либо момент времени. Ее можно найти и спустя время Dt, если каждую точку начального волнового фронта рассматривать как источник элементарной сферической волны, распространившейся за этот промежуток на расстояние vDt. Огибающая всех этих элементарных сферических волновых фронтов и будет новым волновым фронтом. Принцип Гюйгенса позволяет определять форму волнового фронта на протяжении всего процесса распространения. Из него следует также, что волны, как плоские, так и сферические, сохраняют свою геометрию в процессе распространения при условии, что среда однородна.

Дифракция звука.

Дифракцией называется огибание волнами препятствия. Дифракция анализируется с помощью принципа Гюйгенса. Степень такого огибания зависит от соотношения между длиной волны и размером препятствия или отверстия. Поскольку длина звуковой волны во много раз больше, чем световой, дифракция звуковых волн менее удивляет нас, нежели дифракция света. Так, можно разговаривать с кем-то стоящим за углом здания, хотя он и не виден. Звуковая волна с легкостью огибает угол, тогда как свет из-за малости своей длины волны дает резкие тени.

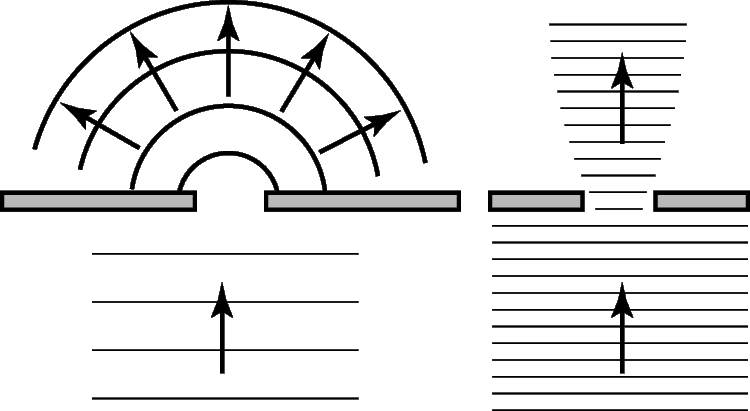
Рассмотрим дифракцию плоской звуковой волны, падающей на твердый плоский экран с отверстием. Для определения формы волнового фронта по другую сторону экрана нужно знать соотношение между длиной волны l и диаметром отверстия D. Если эти величины примерно одинаковы или l намного больше D, то получается полная дифракция: волновой фронт выходящей волны будет сферическим, а волна достигнет всех точек за экраном. Если же l несколько меньше D, то выходящая волна будет распространяться преимущественно в прямом направлении. И наконец, если l намного меньше D, то вся ее энергия будет распространяться по прямой. Эти случаи показаны на рис. 10.

Дифракция наблюдается и тогда, когда на пути звука оказывается какое-либо препятствие. Если размеры препятствия намного больше длины волны, то звук отражается, а позади препятствия формируется зона акустической тени. Когда размеры препятствия сравнимы с длиной волны или меньше ее, звук дифрагирует в какой-то мере во всех направлениях. Это учитывается в архитектурной акустике. Так, например, иногда стены здания покрывают выступами с размерами порядка длины волны звука. (На частоте 100 Гц длина волны в воздухе около 3,5 м.) При этом звук, падая на стены, рассеивается во всех направлениях. В архитектурной акустике это явление называется диффузией звука.

Отражение и прохождение звука.

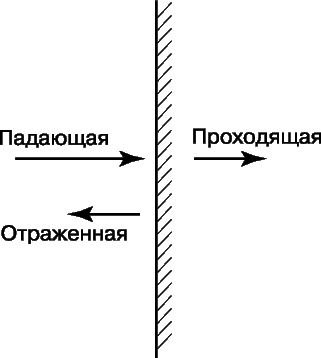
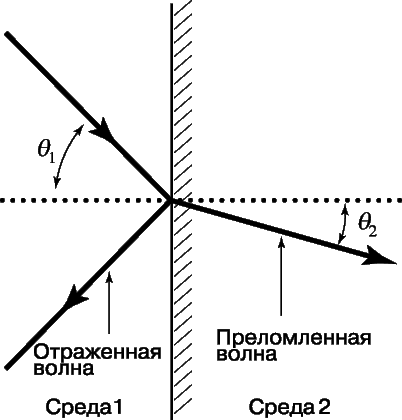
Когда звуковая волна, движущаяся в одной среде, падает на границу раздела с другой средой, одновременно могут происходить три процесса. Волна может отражаться от поверхности раздела, она может проходить в другую среду без изменения направления или изменять направление на границе, т.е. преломляться. На рис. 11 показан простейший случай, когда плоская волна падает под прямым углом к плоской поверхности, разделяющей два различных вещества. Если коэффициент отражения по интенсивности, который определяет долю отраженной энергии, равен R, то коэффициент прохождения будет равен T = 1 – R.

Для звуковой волны отношение избыточного давления к колебательной объемной скорости называется акустическим сопротивлением. Коэффициенты отражения и прохождения зависят от соотношения волновых сопротивлений двух сред, волновые сопротивления, в свою очередь, пропорциональны акустическим сопротивлениям. Волновое сопротивление газов гораздо меньше, чем жидкостей и твердых тел. Поэтому если волна в воздухе падает на толстый твердый объект или на поверхность глубокой воды, то звук почти полностью отражается. Например, для границы воздуха и воды отношение волновых сопротивлений составляет 0,0003. Соответственно этому энергия звука, проходящего из воздуха в воду, равна лишь 0,12% падающей энергии. Коэффициенты отражения и прохождения обратимы: коэффициент отражения есть коэффициент прохождения в обратном направлении. Таким образом, звук практически не проникает ни из воздуха в водный бассейн, ни из-под воды наружу, что хорошо знакомо всем, кто плавал под водой.

В рассмотренном выше случае отражения предполагалось, что толщина второй среды в направлении распространения волны велика. Но коэффициент прохождения будет значительно больше, если вторая среда представляет собой стенку, разделяющую две одинаковые среды, такую, как твердая перегородка между комнатами. Дело в том, что толщина стенки обычно меньше длины волны звука или сравнима с ней. Если толщина стенки кратна половине длины волны звука в стенке, то коэффициент прохождения волны при перпендикулярном падении очень велик. Перегородка была бы абсолютно прозрачной для звука этой частоты, если бы не поглощение, которым мы здесь пренебрегаем. Если толщина стенки намного меньше длины волны звука в ней, то отражение всегда мало, а прохождение велико, за исключением случая, когда приняты специальные меры по увеличению поглощения звука.

Рефракция звука.

Когда плоская звуковая волна падает под углом на границу раздела сред, угол ее отражения равен углу падения. Прошедшая же волна отклоняется от направления падающей волны, если угол падения отличен от 90°. Такое изменение направления движения волны называется рефракцией. Геометрия рефракции на плоской границе показана на рис. 12. Углы между направлением волн и нормалью к поверхности обозначены q₁ для падающей волны и q₂ – для преломленной прошедшей. В соотношение между этими двумя углами входит только отношение скоростей звука для двух сред. Как и в случае световых волн, эти углы связаны между собой законом Снеллиуса (Снелля):
 

Таким образом, если скорость звука во второй среде меньше, чем в первой, то угол преломления будет меньше угла падения, если же скорость во второй среде больше, то угол преломления будет больше угла падения.

Рефракция, обусловленная градиентом температуры.

Если скорость звука в неоднородной среде непрерывно меняется от точки к точке, то рефракция также меняется. Поскольку скорость звука и в воздухе, и в воде зависит от температуры, при наличии градиента температуры звуковые волны могут изменять направление своего движения. В атмосфере и океане из-за горизонтальной стратификации обычно наблюдаются вертикальные градиенты температуры. Поэтому вследствие изменений скорости звука по вертикали, обусловленных температурными градиентами, звуковая волна может отклоняться либо вверх, либо вниз.

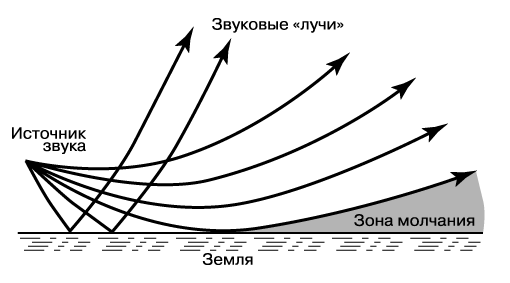
Рассмотрим случай, когда в каком-то месте вблизи поверхности Земли воздух теплее, чем в более высоких слоях. Тогда с увеличением высоты температура воздуха здесь понижается, а вместе с ней уменьшается и скорость звука. Звук, излучаемый источником вблизи поверхности Земли, вследствие рефракции будет уходить вверх. Это показано на рис. 13, где изображены звуковые «лучи».

Отклонение лучей звука, показанное на рис. 13, в общей форме описывается законом Снеллиуса. Если через q, как и раньше, обозначить угол между вертикалью и направлением излучения, то обобщенный закон Снеллиуса имеет вид равенства sinq/v = const, относящегося к любой точке луча. Таким образом, если луч переходит в область, где скорость v уменьшается, то угол q тоже должен уменьшаться. Поэтому звуковые лучи всегда отклоняются в направлении уменьшения скорости звука.

Из рис. 13 видно, что существует область, расположенная на некотором удалении от источника, куда звуковые лучи вообще не проникают. Это так называемая зона молчания.

Вполне возможно, что где-то на высоте, большей, чем показано на рис. 13, из-за градиента температуры скорость звука увеличивается с высотой. В таком случае первоначально отклонившаяся вверх звуковая волна здесь отклонится к поверхности Земли на большом удалении. Так бывает, когда в атмосфере образуется слой температурной инверсии, в результате чего оказывается возможным прием сверхдальних звуковых сигналов. При этом качество приема в удаленных точках бывает даже лучше, чем вблизи. В истории было много примеров сверхдальнего приема. Например, во время Первой мировой войны, когда атмосферные условия благоприятствовали соответствующей рефракции звука, канонаду на французском фронте можно было слышать в Англии.

Рефракция звука под водой.

Рефракция звука, обусловленная изменением температуры по вертикали, наблюдается и в океане. Если температура, а стало быть, и скорость звука, уменьшается с глубиной, звуковые лучи отклоняются вниз, в результате чего образуется зона молчания, подобная тому, как это показано на рис. 13 для атмосферы. Для океана соответствующая картина получится, если этот рисунок просто перевернуть (см. также ГИДРОЛОКАТОР).

Наличием зон молчания затрудняется обнаружение подводных лодок с гидролокатором, а рефракция, отклоняющая звуковые волны вниз, существенно ограничивает дальность их распространения вблизи поверхности. Тем не менее наблюдается также и рефракция с отклонением вверх. Она может создать более благоприятные условия для гидролокации.

Интерференция звуковых волн.

Наложение двух или большего числа волн называется интерференцией волн.

Стоячие волны как результат интерференции.

Рассмотренные выше стоячие волны – частный случай интерференции. Стоячие волны образуются в результате наложения двух волн одинаковой амплитуды, фазы и частоты, распространяющихся в противоположных направлениях.

Амплитуда в пучностях стоячей волны равна удвоенной амплитуде каждой из волн. Поскольку интенсивность волны пропорциональна квадрату ее амплитуды, это означает, что интенсивность в пучностях в 4 раза больше интенсивности каждой из волн или же в 2 раза больше суммарной интенсивности двух волн. Здесь нет нарушения закона сохранения энергии, поскольку в узлах интенсивность равна нулю.

Биения.

Возможна также интерференция гармонических волн разных частот. Когда две частоты мало различаются, возникают так называемые биения. Биения – это изменения амплитуды звука, происходящие с частотой, равной разности исходных частот. На рис. 14 представлена осциллограмма биений.

Следует иметь в виду, что частота биений – это частота амплитудной модуляции звука. Не следует также путать биения с разностной частотой, возникающей в результате искажений гармонического сигнала.

Биения часто используют при настройке двух тонов в унисон. Настройка частоты производится до тех пор, пока биения не перестанут прослушиваться. Даже если частота биений очень мала, человеческое ухо способно уловить периодическое нарастание и убывание громкости звука. Поэтому биения являются весьма чувствительным методом настройки в звуковом диапазоне. Если настройка не точна, то разность частот можно определить на слух, подсчитав число биений за одну секунду. В музыке на слух воспринимаются и биения высших гармонических составляющих, что применяется при настройке фортепиано (см. также ДОПЛЕРА ЭФФЕКТ).

Поглощение звуковых волн.

Интенсивность звуковых волн в процессе их распространения всегда уменьшается вследствие того, что определенная часть акустической энергии рассеивается. В силу процессов теплообмена, межмолекулярного взаимодействия и внутреннего трения звуковые волны поглощаются в любой среде. Интенсивность поглощения зависит от частоты звуковой волны и от других факторов, таких, как давление и температура среды.

Поглощение волны в среде количественно характеризуется коэффициентом поглощения a. Он показывает, насколько быстро уменьшается избыточное давление в зависимости от расстояния, проходимого распространяющейся волной. Убывание амплитуды избыточного давления –DР_е при прохождении расстояния Dх пропорционально амплитуде начального избыточного давления Р_е и расстоянию Dх. Таким образом,

–DP_e = aP_eDx.

Например, когда говорят, что потери на поглощение составляют 1 дБ/м, это означает, что на расстоянии 50 м уровень звукового давления уменьшается на 50 дБ.

Поглощение вследствие внутреннего трения и теплопроводности.

При движении частиц, связанном с распространением звуковой волны, неизбежно трение между разными частицами среды. В жидкостях и газах такое трение называется вязкостью. Вязкость, которой обусловлено необратимое превращение акустической энергии волны в теплоту, является главной причиной поглощения звука в газах и жидкостях.

Кроме того, поглощение в газах и жидкостях обусловлено потерями теплоты при сжатии в волне. Мы уже говорили, что при прохождении волны газ в фазе сжатия нагревается. В этом быстропротекающем процессе тепло обычно не успевает передаваться другим областям газа или стенкам сосуда. Но в действительности данный процесс неидеален, и часть выделяющейся тепловой энергии уходит из системы. С этим связано поглощение звука вследствие теплопроводности. Такое поглощение происходит в волнах сжатия в газах, жидкостях и твердых телах.

Поглощение звука, обусловленное как вязкостью, так и теплопроводностью, обычно увеличивается пропорционально квадрату частоты. Таким образом, звуки высоких частот поглощаются гораздо сильнее, чем низкочастотные. Например, при нормальных давлении и температуре коэффициент поглощения (обусловленного обоими механизмами) на частоте 5 кГц в воздухе составляет около 3 дБ/км. Поскольку поглощение пропорционально квадрату частоты, коэффициент поглощения на частоте 50 кГц составит 300 дБ/км.

Поглощение в твердых телах.

Механизм поглощения звука вследствие теплопроводности и вязкости, имеющий место в газах и жидкостях, сохраняется и в твердых телах. Однако здесь к нему добавляются новые механизмы поглощения. Они связаны с дефектами структуры твердых тел. Дело в том, что поликристаллические твердые материалы состоят из мелких кристаллитов; при прохождении звука в них возникают деформации, приводящие к поглощению звуковой энергии. Звук рассеивается и на границах кристаллитов. Кроме того, даже в монокристаллах имеются дефекты типа дислокаций, вносящие свой вклад в поглощение звука. Дислокации – это нарушения согласования атомных плоскостей. Когда звуковая волна вызывает колебания атомов, дислокации смещаются, а затем возвращаются в исходное положение, рассеивая энергию вследствие внутреннего трения.

Поглощением за счет дислокаций объясняется, в частности, почему не звенит колокольчик из свинца. Свинец – это мягкий металл, в котором очень много дислокаций, в связи с чем звуковые колебания в нем чрезвычайно быстро затухают. Но он хорошо зазвенит, если его охладить жидким воздухом. При низких температурах дислокации «замораживаются» в фиксированном положении, а потому не смещаются и не преобразуют звуковую энергию в теплоту.

МУЗЫКАЛЬНАЯ АКУСТИКА

Музыкальные звуки.

Музыкальная акустика изучает особенности музыкальных звуков, их характеристики, связанные с тем, как мы их воспринимаем, и механизмы звучания музыкальных инструментов.

Музыкальный звук, или тон, – это периодический звук, т.е. колебания, которые снова и снова повторяются через определенный период. Выше говорилось, что периодический звук можно представить в виде суммы колебаний с частотами, кратными основной частоте f: 2f, 3f, 4f и т.д. Отмечалось также, что колеблющиеся струны и воздушные столбы издают музыкальные звуки.

Музыкальные звуки различаются по трем признакам: громкости, высоте и тембру. Все эти показатели субъективные, но их можно связать с измеряемыми величинами. Громкость связана в основном с интенсивностью звука; высота звука, характеризующая его положение в музыкальном строе, определяется частотой тона; тембр, которым один инструмент или голос отличается от другого, характеризуется распределением энергии по гармоникам и изменением этого распределения во времени.

Высота звука.

Высота музыкального звука тесно связана с частотой, но не тождественна ей, поскольку оценка высоты звука носит субъективный характер.

Так, например, установлено, что оценка высоты одночастотного звука несколько зависит от уровня его громкости. При значительном повышении уровня громкости, скажем на 40 дБ, кажущаяся частота может уменьшиться на 10%. На практике эта зависимость от громкости не имеет значения, поскольку музыкальные звуки гораздо сложнее одночастотного звука.

В вопросе о взаимосвязи между высотой тона и частотой более существенно другое: если музыкальные звуки состоят из гармоник, то с какой частотой ассоциируется воспринимаемая высота звука? Оказывается, что это может быть и не та частота, которая соответствует максимальной энергии, и не самая низкая частота в спектре. Так, например, музыкальный звук, состоящий из набора частот 200, 300, 400 и 500 Гц, воспринимается как звук высотой 100 Гц. То есть высота звука ассоциируется с основной частотой гармонического ряда, даже если ее нет в спектре звука. Правда, чаще всего основная частота в той или иной мере в спектре присутствует.

Говоря о соотношении между высотой звука и его частотой, не следует забывать об особенностях человеческого органа слуха. Это особый акустический приемник, который вносит свои искажения (не говоря уже о том, что существуют психологические и субъективные аспекты слуха). Ухо способно выделять некоторые частоты, кроме того, звуковая волна претерпевает в нем нелинейные искажения. Частотная избирательность обусловлена различием между громкостью звука и его интенсивностью (рис. 9). Труднее объяснить нелинейные искажения, которые выражаются в появлении частот, отсутствующих в исходном сигнале. Нелинейность реакции уха обусловлена асимметрией движения различных его элементов.

Одной из характерных особенностей нелинейной приемной системы является то, что при возбуждении ее звуком с частотой f₁ в ней возбуждаются гармонические обертоны 2f₁, 3f₁,…, а в некоторых случаях и субгармоники типа ¹/₂ f₁. Кроме того, при возбуждении нелинейной системы двумя частотами f₁ и f₂ в ней возбуждаются суммарная и разностная частоты f₁ + f₂ и f₁ – f₂. Чем больше амплитуда исходных колебаний, тем больше вклад «лишних» частот.

Таким образом, в силу нелинейности акустических характеристик уха могут появиться частоты, отсутствующие в звуке. Такие частоты называются субъективными тонами. Предположим, что звук состоит из чистых тонов частот 200 и 250 Гц. Из-за нелинейности отклика дополнительно появятся частоты 250 – 200 = 50, 250 + 200 = 450, 2ґ200 = 400, 2ґ250 = 500 Гц и т.д. Слушающему будет казаться, что в звуке присутствует целый набор комбинационных частот, появление же их на самом деле обусловлено нелинейной реакцией уха. Когда музыкальный звук состоит из основной частоты и ее гармоник, очевидно, что основная частота эффективно усиливается разностными частотами.

Правда, как показали исследования, субъективные частоты возникают лишь при достаточно большой амплитуде исходного сигнала. Поэтому не исключено, что в прошлом роль субъективных частот в музыке сильно преувеличивалась.

Музыкальные стандарты и измерение высоты музыкального звука.

За основной тон, определяющий весь музыкальный строй, в истории музыки принимались звуки разной частоты. Сейчас общепринятая частота для ноты «ля» первой октавы составляет 440 Гц. Но в прошлом она менялась от 400 до 462 Гц.

Традиционный способ определения высоты звука – сравнение его с тоном стандартного камертона. Об отклонении частоты заданного звука от стандарта судят по наличию биений. Камертонами пользуются до сих пор, хотя теперь существуют и более удобные приборы для определения высоты звука, такие, как эталонный генератор стабильной частоты (с кварцевым резонатором), который можно плавно перестраивать в пределах всего звукового диапазона. Правда, точная калибровка такого прибора довольно сложна.

Широко распространен стробоскопический метод измерения высоты звука, при котором звук музыкального инструмента задает частоту вспышек стробоскопической лампы. Лампа освещает рисунок на диске, вращающемся с известной частотой, и по кажущейся частоте движения рисунка на диске при стробоскопическом освещении определяют основную частоту тона.

Ухо очень чувствительно к изменению высоты звука, но его чувствительность зависит от частоты. Она максимальна вблизи нижнего порога слышимости. Даже нетренированное ухо способно обнаружить разницу в частотах, равную всего лишь 0,3%, в диапазоне от 500 до 5000 Гц. Чувствительность можно повысить тренировкой. Музыканты обладают очень развитым чувством высоты звука, но оно не всегда помогает при определении частоты чистого тона, создаваемого эталонным генератором. Это говорит о том, что при определении на слух частоты звука важную роль играет его тембр.

Тембр.

Под тембром понимаются те особенности музыкальных звуков, которые придают музыкальным инструментам и голосам их неповторимую специфику, даже если сравнивать звуки одинаковой высоты и громкости. Это, так сказать, качество звука.

Тембр зависит от частотного спектра звука и его изменения во времени. Он определяется несколькими факторами: распределением энергии по обертонам, частотами, возникающими в момент появления или прекращения звука (так называемыми переходными тонами) и их затуханием, а также медленной амплитудной и частотной модуляцией звука («вибрато»).

Интенсивность обертонов.

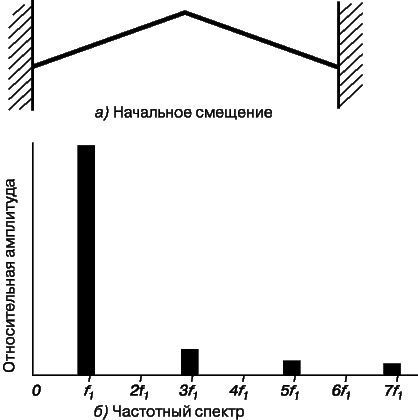
Рассмотрим натянутую струну, которая возбуждается щипком в ее средней части (рис. 15,а). Поскольку все четные гармоники имеют узлы посередине, они будут отсутствовать, и колебания будут состоять из нечетных гармоник основной частоты, равной f₁ = v/2l, где v – скорость волны в струне, а l – ее длина. Таким образом, будут присутствовать только частоты f₁, 3f₁, 5f₁ и т.д. Относительные амплитуды этих гармоник показаны на рис. 15,б.

Данный пример позволяет сделать следующий важный общий вывод. Набор гармоник резонансной системы определяется ее конфигурацией, а распределение энергии по гармоникам зависит от способа возбуждения. При возбуждении струны в ее середине доминирует основная частота и полностью подавляются четные гармоники. Если же струну закрепить в ее средней части и ущипнуть в каком-нибудь другом месте, то будут подавлены основная частота и нечетные гармоники.

Все это применимо и к другим известным музыкальным инструментам, хотя в деталях ситуация может сильно отличаться. В инструментах обычно имеется воздушная полость, дека или рупор для излучения звука. Все это и обусловливает структуру обертонов и возникновение формант.

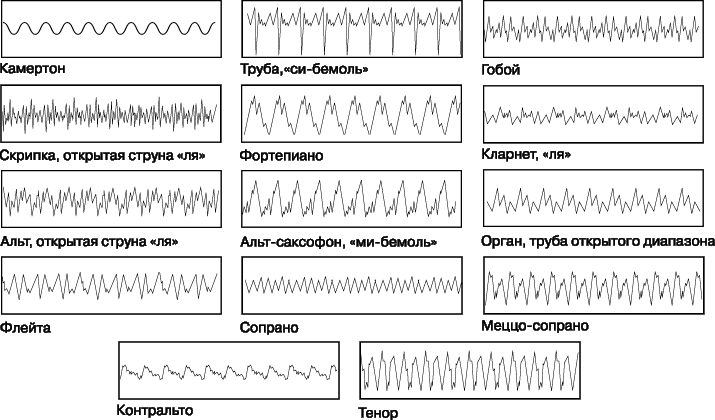
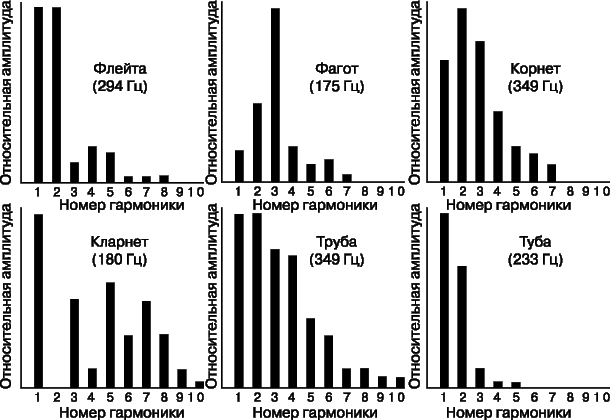
На рис. 16 показаны формы колебаний для различных инструментов и голосов, а на рис. 17 представлены некоторые частотные спектры для устойчивых тонов различных распространенных инструментов.

Форманты.

Как сказано выше, качество звука музыкальных инструментов зависит от распределения энергии по гармоникам. При изменении высоты звука многих инструментов и особенно человеческого голоса распределение по гармоникам изменяется так, что основные обертоны всегда располагаются примерно в одном и том же частотном диапазоне, который называется диапазоном формант. Одной из причин существования формант является применение резонансных элементов для усиления звука, таких, как дека и воздушный резонатор. Ширина естественных резонансов обычно велика, благодаря чему эффективность излучения на соответствующих частотах выше. У медных духовых инструментов форманты определяются раструбом, из которого выходит звук. Обертоны, приходящиеся на диапазон формант, всегда сильно подчеркиваются, так как излучаются с максимальной энергией. Формантами в значительной мере определяются характерные качественные особенности звуков музыкального инструмента или голоса.

Изменение тонов во времени.

Тон звучания любого инструмента редко остается постоянным во времени, и с этим существенно связан тембр. Даже когда инструмент выдерживает долгую ноту, наблюдается небольшая периодическая модуляция частоты и амплитуды, обогащающая звук, – «вибрато». Это особенно характерно для струнных инструментов типа скрипки и для человеческого голоса.

У многих инструментов, например у фортепиано, длительность звука такова, что постоянный тон не успевает сформироваться – возбуждаемый звук быстро нарастает, а затем следует его быстрое затухание. Поскольку затухание обертонов обычно обусловлено зависящими от частоты эффектами (такими, как акустическое излучение), очевидно, что распределение по обертонам меняется на протяжении звучания тона.

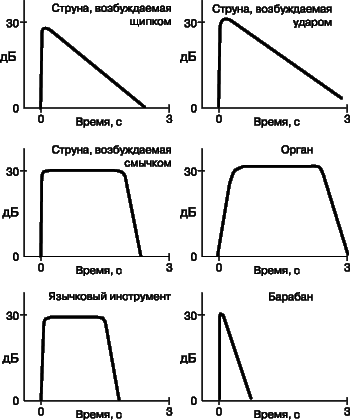
Характер изменения тона во времени (быстрота нарастания и спада звука) для некоторых инструментов схематически показан на рис. 18. Как нетрудно видеть, у струнных инструментов (щипковых и клавишных) постоянный тон практически отсутствует. В таких случаях говорить о спектре обертонов можно лишь условно, поскольку звук быстро меняется во времени. Характеристики нарастания и спада – тоже важная составляющая тембра таких инструментов.

Переходные тона.

Гармонический состав тона обычно быстро изменяется за короткое время после возбуждения звука. В тех инструментах, в которых звук возбуждается ударом по струнам или щипком, энергия, приходящаяся на высшие гармоники (а также на многочисленные негармонические составляющие), максимальна сразу же после начала звучания, а через доли секунды эти частоты замирают. Такие звуки, называемые переходными, придают специфическую окраску звуку инструмента. В фортепиано они обусловлены действием молоточка, ударяющего по струне. Иногда музыкальные инструменты с одинаковой структурой обертонов можно различить только по переходным тонам.

ЗВУЧАНИЕ МУЗЫКАЛЬНЫХ ИНСТРУМЕНТОВ

Музыкальные звуки можно возбуждать и изменять разными способами, в связи с чем музыкальные инструменты отличаются разнообразием форм. Инструменты большей частью создавались и совершенствовались самими музыкантами и искусными мастерами, не прибегавшими к научной теории. Поэтому акустическая наука не может объяснить, например, почему скрипка имеет такую форму. Однако вполне возможно описать свойства звука скрипки, исходя из общих принципов игры на ней и ее конструкции.

Под частотным диапазоном инструмента обычно понимают диапазон частот его основных тонов. Человеческий голос перекрывает примерно две октавы, а музыкальный инструмент – не менее трех (большой орган – десять). В большинстве случаев обертоны простираются до самой границы диапазона слышимого звука.

У музыкальных инструментов имеются три основные части: колеблющийся элемент, механизм для его возбуждения и вспомогательный резонатор (рупор или дека) для акустической связи между колеблющимися элементом и окружающим воздухом.

Музыкальный звук периодичен во времени, а периодические звуки состоят из ряда гармоник. Поскольку собственные частоты колебаний струн и воздушных столбов фиксированной длины гармонически связаны между собой, во многих инструментах основными колеблющимися элементами служат струны и воздушные столбы. За небольшим исключением (флейта – одно из них) на инструментах нельзя взять одночастотного звука. При возбуждении основного вибратора возникает звук, содержащий обертоны. У некоторых вибраторов резонансные частоты не являются гармоническими составляющими. Инструменты такого рода (например, барабаны и тарелки) используются в оркестровой музыке для особой выразительности и подчеркивания ритма, но не для мелодического развития.

Струнные инструменты.

Сама по себе колеблющаяся струна – плохой излучатель звука, а поэтому у струнного инструмента должен быть дополнительный резонатор для возбуждения звука заметной интенсивности. Это может быть замкнутый объем воздуха, дека или комбинация того и другого. Характер звучания инструмента определяется также способом возбуждения струн.

Ранее мы видели, что основная частота колебаний закрепленной струны длины L дается выражением

где Т – сила натяжения струны, а r_L–масса единицы длины струны. Следовательно, мы можем изменять частоту тремя способами: изменяя длину, натяжение или массу. Во многих инструментах используется небольшое число струн одинаковой длины, основные частоты которых определяются надлежащим выбором натяжения и массы. Прочие частоты получаются путем укорачивания длины струны пальцами.

В других инструментах, в частности в фортепиано, для каждой ноты предусматривается одна из многих предварительно настроенных струн. Настроить фортепиано, где диапазон частот велик, – задача непростая, особенно в области низких частот. Сила натяжения всех струн фортепиано практически одинакова (примерно 2 кН), а разнообразие частот достигается изменением длины и толщины струн.

Возбуждение струнного инструмента может осуществляться щипком (например, на арфе или банджо), ударом (на фортепиано), либо при помощи смычка (в случае музыкальных инструментов семейства скрипок). Во всех случаях, как было показано выше, число гармоник и их амплитуда зависят от способа возбуждения струны.

Фортепиано.

Типичным примером инструмента, где возбуждение струны производится ударом, является фортепиано. Большая дека инструмента обеспечивает широкий диапазон формант, поэтому тембр его очень однороден для любой возбуждаемой ноты. Максимумы главных формант приходятся на частоты порядка 400–500 Гц, а на низших частотах тоны особенно богаты гармониками, причем амплитуда основной частоты меньше, чем некоторых обертонов. В фортепиано удар молоточком на всех, кроме самых коротких, струнах приходится на точку, расположенную на расстоянии в 1/7 длины струны от одного из ее концов. Это обычно объясняется тем, что в данном случае значительно подавляется седьмая гармоника, диссонансная по отношению к основной частоте. Но вследствие конечной ширины молоточка подавляются и другие гармоники, расположенные вблизи седьмой.

Скрипичное семейство.

В скрипичном семействе инструментов долгие звуки извлекаются смычком, с помощью которого к струне прикладывается переменная вынуждающая сила, поддерживающая колебания струны. Под действием движущегося смычка струна за счет трения отводится в сторону, пока из-за увеличения силы натяжения не срывается. Вернувшись в исходное положение, она снова увлекается смычком. Этот процесс повторяется, так что на струну действует периодическая внешняя сила.

В порядке увеличения размеров и понижения частотного диапазона основные смычковые струнные инструменты располагаются следующим образом: скрипка, альт, виолончель, контрабас. Частотные спектры этих инструментов особенно богаты обертонами, что, несомненно, придает особую теплоту и выразительность их звучанию. В скрипичном семействе колеблющаяся струна акустически связана с воздушной полостью и корпусом инструмента, которыми в основном и определяется структура формант, занимающих весьма широкий частотный диапазон. Крупные представители скрипичного семейства имеют набор формант, смещенный в область низких частот. Поэтому одна и та же нота, взятая на двух инструментах скрипичного семейства, приобретает разную тембровую окраску из-за различия в структуре обертонов.

Скрипка имеет резко выраженный резонанс вблизи 500 Гц, обусловленный формой ее корпуса. Когда берется нота, частота которой близка к этому значению, может возникнуть нежелательный вибрирующий звук, называемый «волчьим тоном». Воздушная полость внутри скрипичного корпуса тоже имеет свои резонансные частоты, главная из которых расположена вблизи 400 Гц. Из-за своей особой формы скрипка обладаеь многочисленными тесно расположенными резонансами. Все они, кроме волчьего тона, не очень выделяются в общем спектре извлекаемого звука.

Духовые инструменты.

Деревянные духовые инструменты.

О собственных колебаниях воздуха в цилиндрической трубе конечной длины говорилось ранее. Собственные частоты образуют ряд гармоник, основная частота которого обратно пропорциональна длине трубы. Музыкальные звуки в духовых инструментах возникают благодаря резонансному возбуждению столба воздуха.

Колебания воздуха возбуждаются либо колебаниями в воздушной струе, падающей на острый край стенки резонатора, либо колебаниями гибкой поверхности язычка в воздушном потоке. В обоих случаях в локализованной области ствола инструмента возникают периодические изменения давления.

Первый из этих способов возбуждения основан на возникновении «краевых тонов». Когда из щели выходит поток воздуха, разбиваемый клинообразным препятствием с острым краем, периодически возникают вихри – то по одну, то по другую сторону клина. Частота их образования тем больше, чем больше скорость воздушного потока. Если такое устройство акустически связано с резонирующим воздушным столбом, то частота краевого тона «захватывается» резонансной частотой воздушного столба, т.е. частота образования вихрей определяется воздушным столбом. В таких условиях основная частота воздушного столба возбуждается только тогда, когда скорость воздушного потока превысит некоторое минимальное значение. В определенном интервале скоростей, превышающих это значение, частота краевого тона равна этой основной частоте. При еще большей скорости воздушного потока (вблизи той, при которой краевая частота в отсутствие связи с резонатором равнялась бы второй гармонике резонатора) краевая частота скачком удваивается и высота тона, испускаемого всей системой, оказывается на октаву выше. Это называется передувом.

Краевыми тонами возбуждаются воздушные столбы в таких инструментах, как орган, флейта и флейта-пикколо. При игре на флейте исполнитель возбуждает краевые тона, дуя сбоку в боковое отверстие вблизи одного из концов. Ноты одной октавы, начиная с «ре» и выше, получают за счет изменения эффективной длины ствола, открывая боковые отверстия, при нормальном краевом тоне. Более высокие же октавы получают передувом.

Другой способ возбуждения звучания духового инструмента основан на периодическом прерывании воздушного потока колеблющимся язычком, который называется тростью, так как изготавливается из тростника. Такой способ применяется в различных деревянных и медных духовых инструментах. Возможны варианты с одиночной тростью (как, например, в кларнете, саксофоне и инструментах типа гармони) и с симметричной двойной тростью (как, например, в гобое и фаготе). В обоих случаях колебательный процесс одинаков: воздух продувается через узкую щель, в которой давление в соответствии с законом Бернулли понижается. Трость при этом втягивается в щель и перекрывает ее. В отсутствие потока упругая трость выпрямляется и процесс повторяется.

В духовых инструментах перебор нот звукоряда, как и на флейте, осуществляется открыванием боковых отверстий и передувом.

В отличие от трубы, открытой с обоих концов, имеющей полный набор обертонов, труба, открытая только с одного конца, имеет только нечетные гармоники (см. выше). Такова конфигурация кларнета, а потому четные гармоники у него слабо выражены. Передув в кларнете происходит при частоте, в 3 раза превышающей основную.

В гобое вторая гармоника весьма интенсивна. Он отличается от кларнета тем, что канал его ствола имеет коническую форму, тогда как в кларнете сечение канала на большей части его длины постоянно. Частоты колебаний в стволе конической формы труднее рассчитать, чем в цилиндрической трубе, но все же там имеется полный набор обертонов. При этом частоты колебаний конической трубы с закрытым узким концом такие же, как и у цилиндрической трубы, открытой с обоих концов.

Медные духовые инструменты.

Медные, в том числе валторна, труба, корнет-а-пистон, тромбон, горн и туба, возбуждаются губами, действие которых в сочетании с мундштуком особой формы аналогично действию двойной трости. Давление воздуха при возбуждении звука здесь значительно выше, чем в деревянных духовых. Медные духовые, как правило, представляют собой металлический ствол с цилиндрической и конической секциями, заканчивающийся раструбом. Секции подобраны так, что обеспечивается полный спектр гармоник. Полная длина ствола лежит в пределах от 1,8 м для трубы до 5,5 м для тубы. Туба закручена в виде улитки для удобства в обращении, а не из акустических соображений.

При фиксированной длине ствола в распоряжении исполнителя имеются только ноты, определяемые собственными частотами ствола (причем основная частота обычно «неберущаяся»), а высшие гармоники возбуждаются повышением давления воздуха в мундштуке. Так, на горне фиксированной длины можно взять лишь несколько нот (вторую, третью, четвертую, пятую и шестую гармоники). На других медных инструментах частоты, лежащие между гармониками, берутся с изменением длины ствола. Уникален в этом смысле тромбон, длина ствола которого регулируется плавным перемещением выдвижной U-образной кулисы. Перебор нот всего звукоряда обеспечивается семью разными позициями кулисы с изменением возбуждаемого обертона ствола. В других медных инструментах это достигается путем эффективного увеличения полной длины ствола при помощи трех боковых каналов разной длины и в разных комбинациях. Это дает семь разных длин ствола. Как и на тромбоне, ноты всего звукоряда берутся возбуждением разных серий обертонов, соответствующих этим семи длинам ствола.

Тоны всех медных инструментов богаты гармониками. Это объясняется в основном наличием раструба, повышающего эффективность излучения звука на высоких частотах. Труба и валторна предназначены для игры в гораздо более широком диапазоне гармоник, чем у горна. Партия солирующей трубы в произведениях И.Баха содержит много пассажей в четвертой октаве ряда, доходящих до 21-й гармоники этого инструмента.

Ударные инструменты.

Ударные инструменты заставляют звучать, ударяя по телу инструмента и тем самым возбуждая его свободные колебания. От фортепиано, в котором колебания возбуждаются тоже ударом, такие инструменты отличаются в двух отношениях: колеблющееся тело не дает гармонических обертонов и оно само может излучать звук без дополнительного резонатора. К ударным инструментам относятся барабаны, тарелки, ксилофон и треугольник.

Колебания твердых тел гораздо сложнее, чем воздушного резонатора той же формы, поскольку в твердых телах больше типов колебаний. Так, вдоль металлического стержня могут распространяться волны сжатия, изгиба и кручения. Поэтому у цилиндрического стержня гораздо больше мод колебаний и, следовательно, резонансных частот, чем у цилиндрического воздушного столба. Кроме того, эти резонансные частоты не образуют гармонический ряд. В ксилофоне используются изгибные колебания твердых брусков. Отношения обертонов колеблющегося бруска ксилофона к основной частоте таковы: 2,76, 5,4, 8,9 и 13,3.

Камертон представляет собой колеблющийся изогнутый стержень, причем основной его вид колебаний возникает, когда оба плеча одновременно сближаются друг с другом или удаляются друг от друга. У камертона нет гармонического ряда обертонов, и используется только его основная частота. Частота его первого обертона более чем в 6 раз превышает основную частоту.

Еще один пример колеблющегося твердого тела, издающего музыкальные звуки, – колокол. Размеры колоколов могут быть разными – от маленького колокольчика до многотонных церковных колоколов. Чем больше колокол, тем ниже звуки, которые он издает. Форма и другие особенности колоколов претерпели много изменений в ходе их многовековой эволюции. Их изготовлением, требующим большого мастерства, занимаются очень немногие предприятия.

Первоначальный обертонный ряд колокола не является гармоническим, причем отношения обертонов неодинаковы для разных колоколов. Так, например, для одного большого колокола измеренные отношения частот обертонов к основной частоте составили 1,65, 2,10, 3,00, 3,54, 4,97 и 5,33. Но распределение энергии по обертонам быстро изменяется сразу после удара по колоколу, и, по-видимому, форма колокола подбирается таким образом, чтобы доминирующие частоты были связаны между собой приблизительно гармонически. Высота тона колокола определяется не основной частотой, а нотой, доминирующей сразу же после удара. Она соответствует примерно пятому обертону колокола. Спустя некоторое время в звуке колокола начинают преобладать низшие обертоны.

В барабане колеблющимся элементом служит кожаная мембрана, обычно круглая, которую можно рассматривать как двумерный аналог натянутой струны. В музыке барабан не имеет столь важного значения, как струна, поскольку естественный набор его собственных частот не является гармоническим. Исключение составляет литавра, мембрана которой натянута над воздушным резонатором. Последовательность обертонов барабана можно сделать гармонической за счет изменения толщины мембраны в радиальном направлении. Примером такого барабана может служить табла, используемая в классической индийской музыке.
ЗВУКА ВОСПРОИЗВЕДЕНИЕ И ЗАПИСЬ; УЛЬТРАЗВУК; ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ.

Энергия
звуковой волны. Интенсивность звука

Распространение
звуковой волны сопровождается переносом энергии, которая зависит от звукового
давления p
и колебательной скорости v
в каждой точке среды.

Средний
поток звуковой энергии, проходящий в единицу времени через единицу поверхности,
нормальной к направлению распространения волны, называется интенсивностью звука или силой звука
(Вт/м²): 

. 

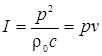
Векторная
величина, характеризующая также направление переноса энергии в волне, называется
вектором Умова: 

. 

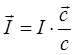
Наряду
с интенсивностью звука используют величину плотность звуковой
энергии 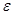(Дж/м³),
равную энергии колебаний в единице объема звукового поля.

Можно
показать, что в бегущей волне

. 

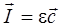
Таким
образом:          .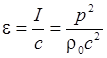

Передача
энергии звуковой волны в область, ранее не затронутую волнами, требует
непрерывного расходования энергии со стороны источника, возбуждающего звук. В
тех зонах, где волна уже возникла, энергия непрерывно передается дальше со
скоростью звука. Возникающие в среде переменные давления непрерывно совершают
работу, ввиду чего и возникает волновое сопротивление (импеданс) 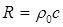 при колебательных движениях частиц
среды.

Формулы
для силы звука: 

 

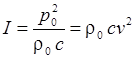
 подобны формулам закона Джоуля–Ленца для
мощности электрического тока, только мощность, затрачиваемая при действии сил
давления, расходуется не на выделение тепла, а на передачу энергии новым частям
среды. Поэтому величину 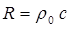 часто называют также сопротивлением
излучения среды.

Логарифмическая
шкала силы звука. Децибелы

Отношение
максимальной и минимальной интенсивности слышимого человеческим ухом звука очень
велико и составляет 10¹⁴ раз (для звукового давления 10⁷
раз). Поэтому для характеристики силы звука удобнее пользоваться
логарифмическими величинами:

уровнем
интенсивности звука,
выраженным в децибелах (дБ):

 

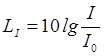
и
уровнем звукового давления
(дБ): 

,

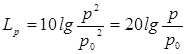
где
I₀
и p₀
– значения, соответствующие порогу слышимости на частоте 1000 Гц (,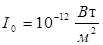
p₀
= 2∙10^-5 Па).

Значение
p₀ выбрано таким образом, чтобы при нормальных атмосферных
условиях L_I
= L_p.
Поэтому в дальнейшем будем использовать величину   L
=
L_I
 = L_p,
которую называют уровнем звука в
децибелах.

Уровень
звука, соответствующий порогу слышимости на частоте 1000 Гц, равен 0 дБ.
Болевой порог восприятия звука соответствует I_б
=
10² Вт/м² и р_б = 2∙10² Па, что
дает значение L_б
= 140 дБ.

Введению
логарифмических единиц измерения способствовало также то обстоятельство, что ухо
человека реагирует не на абсолютное изменение интенсивности звука, а на
относительное. Разница уровней в 1 дБ соответствует минимальной величине,
различимой слухом, при этом интенсивность звука изменяется в 1,26 раза или на
26%. Если же разница уровней составляет 3 дБ, то сила звука изменяется уже в 2
раза.

Рассмотрим,
как рассчитать суммарный уровень звука для звукового поля, создаваемого
несколькими источниками. Возьмем для простоты два
источника.

В
любой точке пространства звуковое давление равно:

 

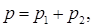
где
р₁ и р₂ – мгновенные значения звуковых
давлений, создаваемых в этой точке соответственно первым и вторым
источником.

Результирующая
интенсивность звука равна: 

 

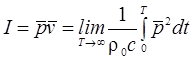
Если
источники звука некогерентные, то есть создаваемые ими давления не связаны по
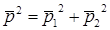
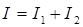
фазе, то средний квадрат звукового давления    и, следовательно,   – интенсивность суммарного звукового поля
равна сумме интенсивностей источников.

Таким
образом, если поле создается N
некогерентными источниками, то

I
=
I₁+I₂+…+I_N
,     а 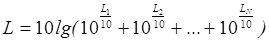      дБ, 

где
,  … – уровни звука, создаваемые
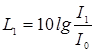
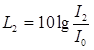
каждым

источником
в расчетной точке.

При
N
одинаковых источниках шума, равноудаленных от расчетной точки, с уровнями
звукового давления L₀,
суммарный уровень равен:

L
= L₀+10lgN.

Презентация к разделу 2

< Предыдущая                     Оглавление                      Следующая >

From Wikipedia, the free encyclopedia

Sound measurements
Characteristic	Symbols
Sound pressure	p, SPL,LPA
Particle velocity	v, SVL
Particle displacement	δ
Sound intensity	I, SIL
Sound power	P, SWL, LWA
Sound energy	W
Sound energy density	w
Sound exposure	E, SEL
Acoustic impedance	Z
Audio frequency	AF
Transmission loss	TL
v t e

Sound intensity, also known as acoustic intensity, is defined as the power carried by sound waves per unit area in a direction perpendicular to that area. The SI unit of intensity, which includes sound intensity, is the watt per square meter (W/m²). One application is the noise measurement of sound intensity in the air at a listener’s location as a sound energy quantity.^[1]

Sound intensity is not the same physical quantity as sound pressure. Human hearing is sensitive to sound pressure which is related to sound intensity. In consumer audio electronics, the level differences are called “intensity” differences, but sound intensity is a specifically defined quantity and cannot be sensed by a simple microphone.

Sound intensity level is a logarithmic expression of sound intensity relative to a reference intensity.

Mathematical definition[edit]

Sound intensity, denoted I, is defined by

where

• p is the sound pressure;
• v is the particle velocity.

Both I and v are vectors, which means that both have a direction as well as a magnitude. The direction of sound intensity is the average direction in which energy is flowing.

The average sound intensity during time T is given by

For a plane wave^{[citation needed]},

Where,

Inverse-square law[edit]

For a spherical sound wave, the intensity in the radial direction as a function of distance r from the centre of the sphere is given by

where

• P is the sound power;
• A(r) is the surface area of a sphere of radius r.

Thus sound intensity decreases as 1/r² from the centre of the sphere:

This relationship is an inverse-square law.

Sound intensity level[edit]

Sound intensity level (SIL) or acoustic intensity level is the level (a logarithmic quantity) of the intensity of a sound relative to a reference value.

It is denoted L_I, expressed in nepers, bels, or decibels, and defined by^[2]

where

• I is the sound intensity;
• I₀ is the reference sound intensity;
  • 1 Np = 1 is the neper;
  • 1 B = 1/2 ln(10) is the bel;
  • 1 dB = 1/20 ln(10) is the decibel.

The commonly used reference sound intensity in air is^[3]

being approximately the lowest sound intensity hearable by an undamaged human ear under room conditions.
The proper notations for sound intensity level using this reference are L_{I /(1 pW/m²)} or L_I (re 1 pW/m²), but the notations dB SIL, dB(SIL), dBSIL, or dB_SIL are very common, even if they are not accepted by the SI.^[4]

The reference sound intensity I₀ is defined such that a progressive plane wave has the same value of sound intensity level (SIL) and sound pressure level (SPL), since

The equality of SIL and SPL requires that

where p₀ = 20 μPa is the reference sound pressure.

For a progressive spherical wave,

where z₀ is the characteristic specific acoustic impedance. Thus,

In air at ambient temperature, z₀ = 410 Pa·s/m, hence the reference value I₀ = 1 pW/m².^[5]

In an anechoic chamber which approximates a free field (no reflection) with a single source, measurements in the far field in SPL can be considered to be equal to measurements in SIL. This fact is exploited to measure sound power in anechoic conditions.

Measurement[edit]

Sound intensity is defined as the time averaged product of sound pressure and acoustic particle velocity.^[6] Both quantities can be directly measured by using a sound intensity p-u probe comprising a microphone and a particle velocity sensor, or estimated indirectly by using a p-p probe that approximates the particle velocity by integrating the pressure gradient between two closely spaced microphones.^[7]

Pressure-based measurement methods are widely used in anechoic conditions for noise quantification purposes. The bias error introduced by a p-p probe can be approximated by^[8]

where is the “true” intensity (unaffected by calibration errors), is the biased estimate obtained using a p-p probe, is the root-mean-squared value of the sound pressure, is the wave number, is the density of air, is the speed of sound and is the spacing between the two microphones. This expression shows that phase calibration errors are inversely proportional to frequency and microphone spacing and directly proportional to the ratio of the mean square sound pressure to the sound intensity. If the pressure-to-intensity ratio is large then even a small phase mismatch will lead to significant bias errors. In practice, sound intensity measurements cannot be performed accurately when the pressure-intensity index is high, which limits the use of p-p intensity probes in environments with high levels of background noise or reflections.

On the other hand, the bias error introduced by a p-u probe can be approximated by^[8]

where is the biased estimate obtained using a p-u probe, and are the Fourier transform of sound pressure and particle velocity, is the reactive intensity and is the p-u phase mismatch introduced by calibration errors. Therefore, the phase calibration is critical when measurements are carried out under near field conditions, but not so relevant if the measurements are performed out in the far field.^[8] The “reactivity” (the ratio of the reactive to the active intensity) indicates whether this source of error is of concern or not. Compared to pressure-based probes, p-u intensity probes are unaffected by the pressure-to-intensity index, enabling the estimation of propagating acoustic energy in unfavorable testing environments provided that the distance to the sound source is sufficient.

References[edit]

External links[edit]

• How Many Decibels Is Twice as Loud? Sound Level Change and the Respective Factor of Sound Pressure or Sound Intensity
• Acoustic Intensity
• Conversion: Sound Intensity Level to Sound Intensity and Vice Versa
• Ohm’s Law as Acoustic Equivalent. Calculations
• Relationships of Acoustic Quantities Associated with a Plane Progressive Acoustic Sound Wave
• Table of Sound Levels. Corresponding Sound Intensity and Sound Pressure
• What Is Sound Intensity Measurement and Analysis?