Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 ноября 2021 года; проверки требуют 8 правок.
Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий заданные значения в заданном наборе точек, то есть решающий задачу интерполяции.
Определение[править | править код]
Интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и (7,9), а также полиномы 
Пусть задана 





Общий случай[править | править код]
Ж. Л. Лагранж предложил следующий способ вычисления таких многочленов:
где базисные полиномы 
Для любого 


Отсюда следует, что 



Случай равноотстоящих узлов интерполяции[править | править код]
Пусть узлы интерполяции 


Отсюда следует, что
Подставляя эти выражения в формулу для базисного полинома и вынося 
Теперь можно ввести замену переменной
и получить выражение для базисных полиномов через 
Данные величины называются коэффициентами Лагранжа. Они не зависят ни от 

Остаточный член[править | править код]
Если считать числа 




где 

![{displaystyle M_{n+1}=sup _{xin [x_{0},x_{n}]}|f^{(n+1)}(x)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db76edf92f62d841039c2daa8a306eb5e1de67e6)
Единственность[править | править код]
Существует единственный многочлен степени не превосходящей 

Это утверждение является обобщением того факта, что через любые две точки проходит единственная прямая.
С точки зрения линейной алгебры[править | править код]
На единственность интерполяционного многочлена можно также взглянуть с точки зрения СЛАУ. Рассмотрим систему уравнений 
Её можно переписать в виде системы уравнений 

Матрица 


С точки зрения китайской теоремы об остатках[править | править код]
По теореме Безу остаток от деления 


По китайской теореме об остатках у такой системы есть единственное решение по модулю 




Пример[править | править код]
Приближение функции 

Найдем формулу интерполяции для 
Получим
Реализация общего случая на языке программирования Python (не оптимальный вариант)[править | править код]
import numpy as np # данные для примера xi = np.array([-1.5, -0.75, 0, 0.75, 1.5]) yi = np.array([-14.1014, -0.931596, 0, 0.931596, 14.1014]) def get_coefficients(_pl: np.ndarray, _xi: np.ndarray): ''' Определение коэффициентов для множителей базисных полиномов l_i :param _pl: массив базисных полиномов :param _xi: массив значений x :return: ''' n = int(_xi.shape[0]) coefficients = np.empty((n, 2), dtype=float) for i in range(n): if i == _pl: coefficients[i][0] = float('inf') coefficients[i][1] = float('inf') else: coefficients[i][0] = 1 / (_xi[_pl] - _xi[i]) coefficients[i][1] = -_xi[i] / (_xi[_pl] - _xi[i]) filtered_coefficients = np.empty((n - 1, 2), dtype=float) j = 0 for i in range(n): if coefficients[i][0] != float('inf'): # изменение последовательности, степень увеличивается filtered_coefficients[j][0] = coefficients[i][1] filtered_coefficients[j][1] = coefficients[i][0] j += 1 return filtered_coefficients def get_polynomial_l(_xi: np.ndarray): ''' Определение базисных полиномов :param _xi: массив значений x :return: ''' n = int(_xi.shape[0]) pli = np.zeros((n, n), dtype=float) for pl in range(n): coefficients = get_coefficients(pl, _xi) for i in range(n - 1): # проходим по массиву coefficients if i == 0: continue elif i == 1: # на второй итерации занимаются 0-2 степени pli[pl][0] = coefficients[i - 1][0] * coefficients[i][0] pli[pl][1] = coefficients[i - 1][1] * coefficients[i][0] + coefficients[i][1] * coefficients[i - 1][0] pli[pl][2] = coefficients[i - 1][1] * coefficients[i][1] else: clone_pli = np.zeros(n, dtype=float) for val in range(n): clone_pli[val] = pli[pl][val] zeros_pli = np.zeros(n, dtype=float) for j in range(n-1): # проходим по строке pl массива pli product_1 = clone_pli[j] * coefficients[i][0] product_2 = clone_pli[j] * coefficients[i][1] zeros_pli[j] += product_1 zeros_pli[j+1] += product_2 for val in range(n): pli[pl][val] = zeros_pli[val] return pli def get_polynomial(_xi: np.ndarray, _yi: np.ndarray): ''' Определение интерполяционного многочлена Лагранжа :param _xi: массив значений x :param _yi: массив значений y :return: ''' n = int(_xi.shape[0]) polynomial_l = get_polynomial_l(_xi) for i in range(n): for j in range(n): polynomial_l[i][j] *= yi[i] L = np.zeros(n, dtype=float) for i in range(n): for j in range(n): L[i] += polynomial_l[j][i] return L # результат в виде массива коэффициентов многочлена при x в порядке увеличения степени # [ 0. -1.47747378 0. 4.8348476 0. ] # т.е. результирующий многочлен имеет вид: y(x) = -1.47747378*x + 4.8348476*x^3
Применения[править | править код]
Многочлены Лагранжа степеней от нулевой до пятой для функции
Численное интегрирование[править | править код]
Пусть для функции 

Полученное выражение можно использовать для приближённого вычисления определённого интеграла от функции 
Значения интегралов от 


Литература[править | править код]
- Березин, И. С., Жидков Н. П. Методы вычислений. Том I. — 2-е изд., стереотипное – М.: Физматлит. 1962.
Ссылки[править | править код]
- М. А. Тынкевич. Глава 7.6.1. Интерполяционный многочлен Лагранжа // Численные методы анализа. — Кемерово, 2002. — ISBN 5-89070-042-1. (недоступная ссылка)
- А. Г. Хованский. Полиномы Лагранжа и их применения. Видео-лекция. VI Летняя школа «Современная математика», Дубна, 2006.
См. также[править | править код]
- Схема Эйткена
- Интерполяционные формулы Ньютона
- Интерполяция с кратными узлами
- Схема разделения секрета Шамира
- Комбинаторная теорема о нулях
- Интерполяция алгебраическими многочленами
-
Интерполяция, полином Лагранжа
-
Общие положения
-
В
вычислительной практике часто приходится
иметь дело с функциями
,
заданными таблицами их значений для
некоторого конечного множества значенийх:
.
В
процессе же решения задачи необходимо
использовать значения
для промежуточных значений аргумента.
В этом случае строят функцию Ф(x),
достаточно простую для вычислений,
которая в заданных точкахx0,
x1,…,xn,называемых узлами интерполяции, принимает
значения
,
а в остальных точках отрезка (x0,xn),
принадлежащего области определения
,
приближенно представляет функцию
с той или иной степенью точности.
При
решении задачи в этом случае вместо
функции
оперируют с функцией Ф(x). Задача построения
такой функции Ф(x) называется задачей
интерполирования. Чаще всего интерполирующую
функцию Ф(x) отыскивают в виде алгебраического
полинома.
-
Интерполяционный полином
Для каждой функции
,
определенной на [a,b],
и любого набора узлов x0,
x1,….,xn(
xi
[a,b],
xi
xj
при ij
) среди алгебраических многочленов
степени не выше n существует единственный
интерполяционный многочлен Ф(x), который
может быть записан в форме:
,
(3.1)
где
– многочлен n-ой степени, обладающий
следующим свойством:
(3.2)
Для
интерполяционного полинома многочлен
имеет вид:
(3.3)
Этот
многочлен (3.1) и решает задачу
интерполирования и называется
интерполяционным полиномом Лагранжа.
Пример
В
качестве примера рассмотрим функцию
вида
на интервале
заданную табличным способом.
-
X
1
2
3
4
F(x)
1
4
9
16
Необходимо
определить значение функции в точке
x-2.5. Воспользуемся для этого полином
Лагранжа. Исходя из формул (3.1 и 3.3) запишем
этот полином в явном виде:
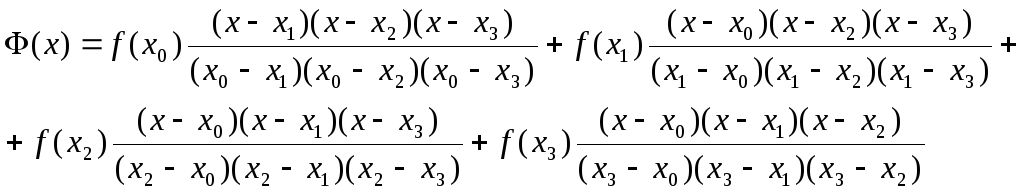
Тогда
подставляя в формулу (3.4) исходные
значения из нашей таблицы получим
Полученный
результат соответствует теории т.е.
.
-
Интерполяционная формула Лагранжа
Интерполяционный
полином Лагранжа может быть записан в
другой форме:
(3.5)
Запись
полинома в виде (3.5) более удобна для
программирования.
При
решении задачи интерполяции величина
n
называется порядком интерполирующего
полинома. При этом, как видно из формул
(3.1) и (3.5), число узлов интерполирования
всегда будет равно n+1
и значение x,
для которого
определяется величина
,
должно
лежать внутри области определения узлов
интерполяции
т.е.
. (3.6)
В
некоторых практических случаях общее
известное число узлов интерполяции m
может быть больше, чем порядок
интерполирующего полинома n.
В
этом случае, прежде чем реализовывать
процедуру интерполяции согласно формуле
(3.5), необходимо определить те узлы
интерполяции, для которых справедливо
условие (3.6). При этом следует помнить,
что наименьшая погрешность достигается
при нахождении значения x
в центре области интерполяции. Для
обеспечения этого предлагается следующая
процедура:
-
После ввода в
программу значения величины х
необходимо
проверить условие x0
x
xm,
где x0
и xm
– начальное и конечное значение узловых
точек интерполяции. -
При выполнения
предыдущего условия начинается поиск
области интерполяции, для чего находим
первое
xi
такое, для которого выполняется условие
xi
> x,
при этом номер i
будет соответствовать середине интервала
интерполяции. Для определения области
интерполяции ее левая граница будет
начинаться с номера
,
а заканчиваться узлом с номером.
-
После выполнения
пунктов 1 и 2 программируется формула
(3.5).
Основное назначение
интерполяции – это вычисление значений
табулированной функции для не узловых
(промежуточных) значений аргумента,
поэтому интерполяцию часто называют
«искусством чтения таблиц между
строками».
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для 





В простейшем случае 
Определение
Файл:Lagrangepolys.png Этот пример показывает интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и (7,9), а также полиномы yj lj(x), каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных xi
Лагранж предложил способ вычисления таких многочленов:
где базисные полиномы определяются по формуле:
Легко видеть что 
Отсюда следует, что 



Применения
Полиномы Лагранжа используются для интерполяции, а также для
численного интегрирования.
Пусть для функции 

В частности,
Значения интегралов от 


Для случая равномерного распределения по отрезку узлов интерполяции
В указанном случае можно выразить 

,
и, следовательно,
.
Подставив эти выражения в формулу полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим
Теперь можно ввести замену переменной
и получить полином от XY, который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования алгоритмов с многобайтным представлением чисел.
cs:Lagrangeova interpolace
nl:Lagrange-polynoom
sr:Лагранжов полином
uk:Многочлен Лагранжа
From Wikipedia, the free encyclopedia
This image shows, for four points ((−9, 5), (−4, 2), (−1, −2), (7, 9)), the (cubic) interpolation polynomial L(x) (dashed, black), which is the sum of the scaled basis polynomials y0ℓ0(x), y1ℓ1(x), y2ℓ2(x) and y3ℓ3(x). The interpolation polynomial passes through all four control points, and each scaled basis polynomial passes through its respective control point and is 0 where x corresponds to the other three control points.
In numerical analysis, the Lagrange interpolating polynomial is the unique polynomial of lowest degree that interpolates a given set of data.
Given a data set of coordinate pairs 






Although named after Joseph-Louis Lagrange, who published it in 1795,[1] the method was first discovered in 1779 by Edward Waring.[2] It is also an easy consequence of a formula published in 1783 by Leonhard Euler.[3]
Uses of Lagrange polynomials include the Newton–Cotes method of numerical integration, Shamir’s secret sharing scheme in cryptography, and Reed–Solomon error correction in coding theory.
For equispaced nodes, Lagrange interpolation is susceptible to Runge’s phenomenon of large oscillation.
Definition[edit]
Given a set of 










Notice that the numerator 




The Lagrange interpolating polynomial for those nodes through the corresponding values 
Each basis polynomial has degree 



The interpolating polynomial is unique. Proof: assume the polynomial 








Barycentric form[edit]
Each Lagrange basis polynomial 




By factoring 
If the weights 



The barycentric interpolation formula can also easily be updated to incorporate a new node 




For any 





This is called the second form or true form of the barycentric interpolation formula.
This second form has advantages in computation cost and accuracy: it avoids evaluation of 






Using this formula to evaluate 



Each Lagrange basis polynomial can also be written in barycentric form:
A perspective from linear algebra[edit]
Solving an interpolation problem leads to a problem in linear algebra amounting to inversion of a matrix. Using a standard monomial basis for our interpolation polynomial 






This construction is analogous to the Chinese remainder theorem. Instead of checking for remainders of integers modulo prime numbers, we are checking for remainders of polynomials when divided by linears.
Furthermore, when the order is large, Fast Fourier transformation can be used to solve for the coefficients of the interpolated polynomial.
Example[edit]
We wish to interpolate 


The node polynomial 
The barycentric weights are
The Lagrange basis polynomials are
The Lagrange interpolating polynomial is:
In (second) barycentric form,
Notes[edit]
Example of interpolation divergence for a set of Lagrange polynomials.
The Lagrange form of the interpolation polynomial shows the linear character of polynomial interpolation and the uniqueness of the interpolation polynomial. Therefore, it is preferred in proofs and theoretical arguments. Uniqueness can also be seen from the invertibility of the Vandermonde matrix, due to the non-vanishing of the Vandermonde determinant.
But, as can be seen from the construction, each time a node xk changes, all Lagrange basis polynomials have to be recalculated. A better form of the interpolation polynomial for practical (or computational) purposes is the barycentric form of the Lagrange interpolation (see below) or Newton polynomials.
Lagrange and other interpolation at equally spaced points, as in the example above, yield a polynomial oscillating above and below the true function. This behaviour tends to grow with the number of points, leading to a divergence known as Runge’s phenomenon; the problem may be eliminated by choosing interpolation points at Chebyshev nodes.[5]
The Lagrange basis polynomials can be used in numerical integration to derive the Newton–Cotes formulas.
Remainder in Lagrange interpolation formula[edit]
When interpolating a given function f by a polynomial of degree k at the nodes 

where ![{displaystyle f[x_{0},ldots ,x_{k},x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64e34bb84b1de65fda77f1fa9dddac063d1f5720)
The remainder can be bound as
Derivation[7][edit]
Clearly, 

























(Because the highest power of
in
is
)
The equation can be rearranged as
Since 

Derivatives[edit]
The dth derivative of a Lagrange interpolating polynomial can be written in terms of the derivatives of the basis polynomials,
Recall (see § Definition above) that each Lagrange basis polynomial is
The first derivative can be found using the product rule:
The second derivative is
The third derivative is
and likewise for higher derivatives.
Finite fields[edit]
The Lagrange polynomial can also be computed in finite fields. This has applications in cryptography, such as in Shamir’s Secret Sharing scheme.
See also[edit]
- Neville’s algorithm
- Newton form of the interpolation polynomial
- Bernstein polynomial
- Carlson’s theorem
- Lebesgue constant (interpolation)
- The Chebfun system
- Table of Newtonian series
- Frobenius covariant
- Sylvester’s formula
- Finite difference coefficient
- Hermite interpolation
References[edit]
- ^
Lagrange, Joseph-Louis (1795). “Leçon Cinquième. Sur l’usage des courbes dans la solution des problèmes”. Leçons Elémentaires sur les Mathématiques (in French). Paris. Republished in Serret, Joseph-Alfred, ed. (1877). Oeuvres de Lagrange. Vol. 7. Gauthier-Villars. pp. 271–287. Translated as “Lecture V. On the Employment of Curves in the Solution of Problems”. Lectures on Elementary Mathematics. Translated by McCormack, Thomas J. (2nd ed.). Open Court. 1901. pp. 127–149. - ^ Waring, Edward (1779). “Problems concerning interpolations”. Philosophical Transactions of the Royal Society. 69: 59–67. doi:10.1098/rstl.1779.0008.
- ^ Meijering, Erik (2002). “A chronology of interpolation: from ancient astronomy to modern signal and image processing” (PDF). Proceedings of the IEEE. 90 (3): 319–342. doi:10.1109/5.993400.
- ^ Berrut, Jean-Paul; Trefethen, Lloyd N. (2004). “Barycentric Lagrange Interpolation” (PDF). SIAM Review. 46 (3): 501–517. Bibcode:2004SIAMR..46..501B. doi:10.1137/S0036144502417715.
- ^ Quarteroni, Alfio; Saleri, Fausto (2003). Scientific Computing with MATLAB. Texts in computational science and engineering. Vol. 2. Springer. p. 66. ISBN 978-3-540-44363-6..
- ^ Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. “Chapter 25, eqn 25.2.3”. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 878. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- ^ “Interpolation” (PDF).
External links[edit]
- “Lagrange interpolation formula”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- ALGLIB has an implementations in C++ / C# / VBA / Pascal.
- GSL has a polynomial interpolation code in C
- SO has a MATLAB example that demonstrates the algorithm and recreates the first image in this article
- Lagrange Method of Interpolation — Notes, PPT, Mathcad, Mathematica, MATLAB, Maple at Holistic Numerical Methods Institute
- Lagrange interpolation polynomial on www.math-linux.com
- Weisstein, Eric W. “Lagrange Interpolating Polynomial”. MathWorld.
- Lagrange polynomial at ProofWiki
- Dynamic Lagrange interpolation with JSXGraph
- Numerical computing with functions: The Chebfun Project
- Excel Worksheet Function for Bicubic Lagrange Interpolation
- Lagrange polynomials in Python
Этот калькулятор может пригодиться при решении задач на интерполяцию полиномом Лагранжа. В таких задачах обычно требуется интерполировать значение неизвестной функции, соответствующее некоторому значению x, использую формулу интерполяционного многочлена Лагранжа, полученную из известного набора точек со значениями неизвестной функции (x, f(x)).
Калькулятор ниже обладает следующими функциями:
- Он находит формулу полинома Лагранжа для заданного набора точек.
- Он отображает пошаговый вывод формулы.
- Он вычисляет значения интерполяционного многочлена Лагранжа для заданных точек (интерполирует функцию полиномом Лагранжа в заданных точках интерполяции)
- Он отображает набор точек, значения в точках интерполяции, полином Лагранжа и все базисные полиномы на графике.
Как пользоваться
Сначала вводите набор точек – одна точка на строку в форме x f(x), значения разделены пробелом. Если вы хотите получить интерполяцию, вводите значения точек интерполяции в следующее поле в виде значений x, разделенных пробелом.
По умолчанию, калькулятор отображает формулу многочлена и его значения в точках интерполяции. Если нужно пошаговое решение, включите опцию “Показать пошаговое решение”. Также можно отключить отображение базисных полиномов.
Теория и формулы, как обычно, описаны под калькулятором.
Интерполяционный многочлен Лагранжа (полином Лагранжа)
Набор точек, одна точка на строку, значения разделяются пробелом
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Показать решение по шагам
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Показать базисные полиномы
Полином Лагранжа
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Интерполяционный многочлен Лагранжа
Предположим, что у нас есть набор значений, соответствующих неизвестной функции, при этом все x различны:
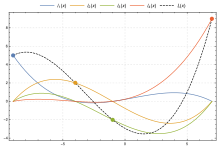
Сконструируем следующий многочлен (называемые многочленом Лагранжа):
где – базисный полином Лагранда
Если посмотреть на формулу базисного полинома для любого j, то видно что для всех точек i не равных j, значение этого полинома обращается в ноль, а в самой точке j значение этого полинома j равно единице. Таким образом,
и
что означает, что полином Лагранжа точно интерполирует значение функции в заданных точках.
Стоит заметить, что формула интерполяционного многочлена Лагранжа подвержена воздействию так называемого феномена Рунге. Феномен Рунге связан к увеличением колебаний полинома на краях интервала при использовании полиномов высоких степеней на равноудаленных друг от друга точках. Таким образом, наличие большого количества точек далеко не всегда приводит к улучшению точности интерполяции.
Однако также стоит заметить, что в отличие от некоторых других формул интерполяции, формула Лагранжа не требует того, чтобы точки в наборе были равноудалены друг от друга. Это используется в некоторых способах борьбы с феноменом Рунге, например, при использовании в качестве точек интерполяции узлов Чебышева.

























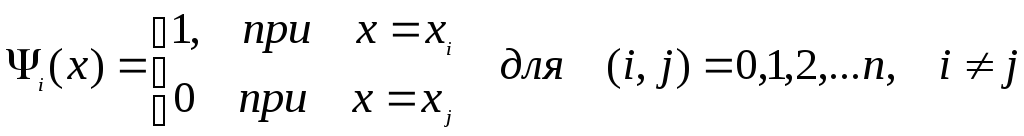
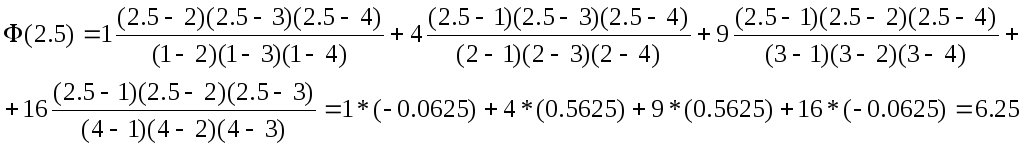









![{displaystyle {begin{aligned}ell _{j}(x)&={frac {(x-x_{0})}{(x_{j}-x_{0})}}cdots {frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}cdots {frac {(x-x_{k})}{(x_{j}-x_{k})}}\[10mu]&=prod _{begin{smallmatrix}0leq mleq k\mneq jend{smallmatrix}}{frac {x-x_{m}}{x_{j}-x_{m}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b82ad438455a15cfb4b9bb6d59d679e50b0b9d18)



![{displaystyle {begin{aligned}L(x)&=ell (x)sum _{j=0}^{k}{frac {w_{j}}{x-x_{j}}}y_{j}{Bigg /}ell (x)sum _{j=0}^{k}{frac {w_{j}}{x-x_{j}}}\[10mu]&=sum _{j=0}^{k}{frac {w_{j}}{x-x_{j}}}y_{j}{Bigg /}sum _{j=0}^{k}{frac {w_{j}}{x-x_{j}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58f9eb6e3f92fb5b031bbe3a0f2fcc2834cb042e)

![{displaystyle {begin{aligned}x_{0}&=1,&&&y_{0}=f(x_{0})&=1,\[3mu]x_{1}&=2,&&&y_{1}=f(x_{1})&=4,\[3mu]x_{2}&=3,&&&y_{2}=f(x_{2})&=9.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea731ecebd607939d03f1af637c7dc70d167a6bc)

![{displaystyle {begin{aligned}w_{0}&=(1-2)^{-1}(1-3)^{-1}={tfrac {1}{2}},\[3mu]w_{1}&=(2-1)^{-1}(2-3)^{-1}=-1,\[3mu]w_{2}&=(3-1)^{-1}(3-2)^{-1}={tfrac {1}{2}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56d4a7884aee5c67d2ab29351bfd9ae86cfbfceb)
![{displaystyle {begin{aligned}ell _{0}(x)&={frac {x-2}{1-2}}cdot {frac {x-3}{1-3}}={tfrac {1}{2}}x^{2}-{tfrac {5}{2}}x+3,\[5mu]ell _{1}(x)&={frac {x-1}{2-1}}cdot {frac {x-3}{2-3}}=-x^{2}+4x-3,\[5mu]ell _{2}(x)&={frac {x-1}{3-1}}cdot {frac {x-2}{3-2}}={tfrac {1}{2}}x^{2}-{tfrac {3}{2}}x+1.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13c47023b84eec7fc182f39ac958e7271498cd53)
![{displaystyle {begin{aligned}L(x)&=1cdot {frac {x-2}{1-2}}cdot {frac {x-3}{1-3}}+4cdot {frac {x-1}{2-1}}cdot {frac {x-3}{2-3}}+9cdot {frac {x-1}{3-1}}cdot {frac {x-2}{3-2}}\[6mu]&=x^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85823f6b26a12c40acee99588185334a6c14b864)


![{displaystyle R(x)=f[x_{0},ldots ,x_{k},x]ell (x)=ell (x){frac {f^{(k+1)}(xi )}{(k+1)!}},quad quad x_{0}<xi <x_{k},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02cf7851563959d1b06a7a07782bba6ae42c096b)









![{displaystyle {begin{aligned}ell _{j}'(x)&=sum _{begin{smallmatrix}i=0\inot =jend{smallmatrix}}^{k}{Biggl [}{frac {1}{x_{j}-x_{i}}}prod _{begin{smallmatrix}m=0\mnot =(i,j)end{smallmatrix}}^{k}{frac {x-x_{m}}{x_{j}-x_{m}}}{Biggr ]}\[5mu]&=ell _{j}(x)sum _{begin{smallmatrix}i=0\inot =jend{smallmatrix}}^{k}{frac {1}{x-x_{i}}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f7f5339a0a09570403bcdcf4176fbdc6871d07b)
![{displaystyle {begin{aligned}ell _{j}''(x)&=sum _{begin{smallmatrix}i=0\ineq jend{smallmatrix}}^{k}{frac {1}{x_{j}-x_{i}}}{Biggl [}sum _{begin{smallmatrix}m=0\mneq (i,j)end{smallmatrix}}^{k}{Biggl (}{frac {1}{x_{j}-x_{m}}}prod _{begin{smallmatrix}n=0\nneq (i,j,m)end{smallmatrix}}^{k}{frac {x-x_{n}}{x_{j}-x_{n}}}{Biggr )}{Biggr ]}\[10mu]&=ell _{j}(x)sum _{0leq i<mleq k}{frac {2}{(x-x_{i})(x-x_{m})}}\[10mu]&=ell _{j}(x){Biggl [}{Biggl (}sum _{begin{smallmatrix}i=0\inot =jend{smallmatrix}}^{k}{frac {1}{x-x_{i}}}{Biggr )}^{2}-sum _{begin{smallmatrix}i=0\inot =jend{smallmatrix}}^{k}{frac {1}{(x-x_{i})^{2}}}{Biggr ]}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d9f334e0ce26b8fd713e808986bf11888a7899e)

