Если множество
рациональных чисел объединить с
множеством иррациональных чисел, то
получится множество действительных
чисел. Множество действительных чисел
обычно означают буквой
![]() ;
;
используют также символическую запись![]() .
.
Действительные
числа изображают точками координатной
прямой (числовой оси).
Определение
1.8. Координатная прямая –
это всякая прямая, на которой выбраны
направление, принимаемое за положительное,
точка – начало отсчета и единица
измерения – масштабный отрезок, длина
которого принимается равной единице.
Пусть
![]() и
и![]() – действительные числа и
– действительные числа и![]() .
.
В таблице 1.1 даны названия, определения
и обозначения числовых множеств,
называемыхчисловыми
промежутками,
и их изображение на координатной прямой.
Каждый из числовых промежутков
определяется как множество действительных
чисел
![]() ,
,
удовлетворяющих определенным неравенствам.
Таблица 1.1
|
Название |
Неравенство, |
Обозначение |
Изображение |
|
отрезок от |
|
|
|
|
интервал от |
|
|
|
|
открытый слева промежуток от (полуинтервал) |
|
|
|
|
открытый справа промежуток от (полуинтервал) |
|
|
|
|
числовой |
|
|
|
|
открытый числовой луч от |
|
|
|
|
числовой луч от |
|
|
|
|
открытый числовой луч от |
|
|
|
1.5. Модуль действительного числа
Определение
1.9. Модулем неотрицательного действительного
числа
![]() называют
называют
само это число:
![]() ;
;
модулем
отрицательного действительного числа
![]() называют
называют
противоположное число:
![]() .
.
Или записывают
так:
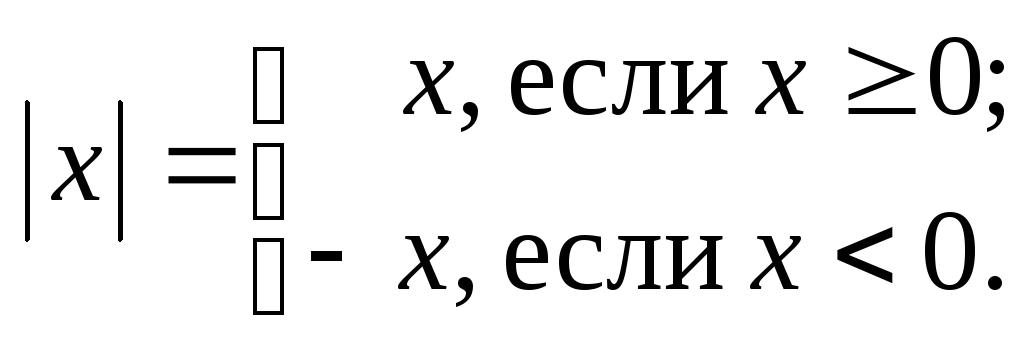
Например,
![]() ;
;![]() ;
;![]() (так как
(так как![]() ).
).
Свойства модулей
|
1. |
4. |
7. |
|
2. |
5. |
8. |
|
3. |
6. |
9. |
1.6. Метод математической индукции
Утверждение,
зависящее
от
натурального
числа
![]() ,
,
справедливо для любого![]() ,
,
если выполнены два условия:
1) утверждение
верно для
![]() ;
;
-
из справедливости
утверждения для
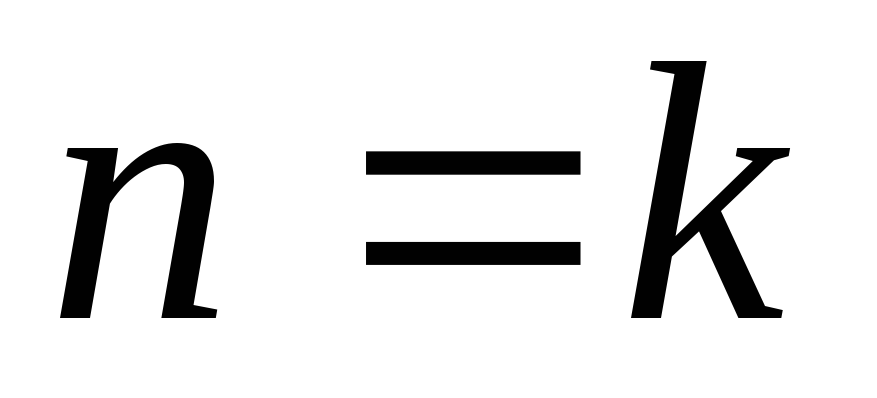 ,
,
где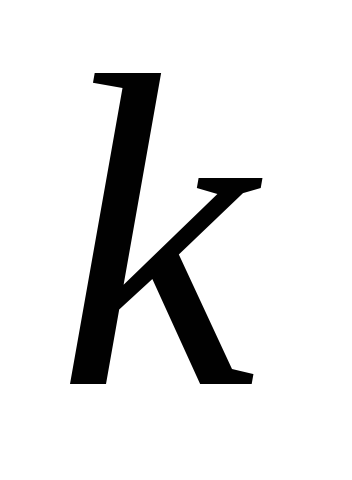 – любое натуральное
– любое натуральное
число, вытекает
справедливость утверждения и для
следующего натурального числа
![]() .
.
Замечание 1.1.
В некоторых
случаях утверждение является истинным
для
![]() ,
,
тогда в этом случае пункт1)
проверяют для
![]() ,
,
а пункт2)
доказывают
при
![]() .
.
Аналогично, если утверждение выполняется
лишь для![]() ,
,
тогда пункт1)
проверяют для
![]() ,
,
а пункт2)
доказывают при
![]() .
.
Пример 1.11.
Доказать,
что
|
|
(1.3) |
Решение. 1)
Проверим
справедливость этого утверждения для
![]() ,
,
то есть справедливость равенства![]() .
.
Очевидно,![]() .
.
2) Предположим,
что равенство (1.3) выполняется при
![]() ,
,
то есть справедливо равенство:
|
|
(1.4) |
Докажем, что тогда
проверяемое равенство (1.3) верно и при
![]() ,
,
то есть докажем равенство
|
|
(1.5) |
Подчеркнем, что
равенство (1.5) интересует нас не само по
себе, а интересует вопрос, вытекает ли
оно из равенства (1.4).
Рассмотрим левую
часть равенства (1.5) и воспользуемся в
процессе преобразований равенством
(1.4):
![]()
![]()
![]() .
.
Таким образом, из
равенства (1.4) вытекает равенство (1.5).
Оба условия принципа математической
индукции выполнены, следовательно,
равенство (1.3) справедливо для любого
натурального числа
![]() .
.
Пример 1.12.
Доказать,
что
![]() при
при![]()
Решение. 1)
При
![]() имеем:
имеем:![]() – делится на 17.
– делится на 17.
2) Предположим, что
утверждение выполняется при
![]() ,
,
то есть![]() ,
,
(![]() ,
,
где![]()
![]() ),
),
и докажем, что оно верно и при![]() ,
,
а именно
![]() .
.
Действительно,
![]()
![]() .
.
Оба условия принципа
математической индукции выполняются,
следовательно, выдвинутое утверждение
доказано.
Пример 1.13.
Доказать,
что для
![]() и
и![]() справедливо неравенство
справедливо неравенство
![]()
(его называют
неравенством
Бернулли
в честь швейцарского математика Якоба
Бернулли (1654-1705)).
Решение. 1)
При
![]() получим верное неравенство:
получим верное неравенство:
![]() (так как
(так как
![]() )
)
2) Предположим, что
неравенство Бернулли верно для
![]() (
(![]() ):
):
|
|
(1.6) |
Докажем, что
неравенство Бернулли верно и для
![]() ,
,
то есть докажем, что
![]() .
.
Умножим обе части
неравенства (1.6) на одно и тоже положительное
число
![]() ,
,
тогда получим:
![]() ,
,
что и требовалось
доказать. Следовательно, по принципу
математической индукции неравенство
Бернулли справедливо для любого
![]() .
.
Соседние файлы в папке Gmail
- #
- #
- #
- #
Напомним определения некоторых основных подмножеств действительных чисел. Если 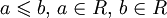 , то множество
, то множество 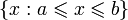 называется отрезком расширенной числовой прямой R и обозначается через
называется отрезком расширенной числовой прямой R и обозначается через ![[a,;b]](https://dic.academic.ru/pictures/wiki/files/49/186c5c676bac5b18c4105688c2eb69d2.png) , то есть
, то есть
![[a, b]stackrel{mathrm{def}}{=}{x: aleqslant xleqslant b}, ain overline{R}, bin overline{R} .](https://dic.academic.ru/pictures/wiki/files/49/1662dc0d24e95c9e84df5096ca46bc47.png)
В случае 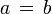 отрезок
отрезок ![[a,,, b]](https://dic.academic.ru/pictures/wiki/files/57/9e070be9629f1dc33d14853dc3686dc4.png) состоит из одной точки.
состоит из одной точки.
Если 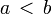 , то множество
, то множество 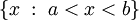 называется интервалом и обозначается через
называется интервалом и обозначается через  , т.е.
, т.е.
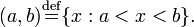
Интервал  называется внутренностью отрезка
называется внутренностью отрезка ![[a,, b].](https://dic.academic.ru/pictures/wiki/files/53/5ac2bbff3671a6b77208619abc7a33b4.png)
Множестваи
называются полуинтервалами.
Отрезки ![[a,, b]](https://dic.academic.ru/pictures/wiki/files/100/d2524b9940ce1c636bfb26ae09a941d2.png) , интервалы
, интервалы  и полуинтервалы
и полуинтервалы ![[a,, b), ,(a,, b]](https://dic.academic.ru/pictures/wiki/files/102/f23906a47b274318ffe7e8ee9d01084a.png) называются промежутками, а точки a и b – их концами: a – левым концом, а b – правым, а точки x такие, что
называются промежутками, а точки a и b – их концами: a – левым концом, а b – правым, а точки x такие, что  – их внутренними точками.
– их внутренними точками.
Если a и b конечны, т.е. 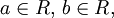 то промежуток с концами a и b называется также конечным промежутком, а число b ? a – его длиной. Если хотя бы одно из a и b является бесконечным, то промежуток с концами a и b называется бесконечным.
то промежуток с концами a и b называется также конечным промежутком, а число b ? a – его длиной. Если хотя бы одно из a и b является бесконечным, то промежуток с концами a и b называется бесконечным.
Замечание 1. Промежутки всех типов расширенной числовой прямой обладают следующим свойством: если точкипринадлежат некоторому промежутку с концами
и
то и весь отрезок
принадлежит этому промежутку.
Для промежутка каждого типа это непосредственно следует из его определения.
Важным понятием для дальнейшего является понятие  – окрестности точки расширенной числовой прямой. В случае
– окрестности точки расширенной числовой прямой. В случае  т.е. когда a является действительным числом,
т.е. когда a является действительным числом,  – окрестностью
– окрестностью 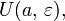 [1]
[1] 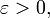 а числа a называется интервал
а числа a называется интервал 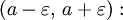
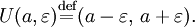
Если же 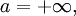 то
то
а если 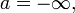 то
то
Таким образом, во всех случаях, т.е. когда a – действительно число и когда a – одна из бесконечностей 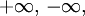 при уменьшении числа
при уменьшении числа  соответствующие
соответствующие  – окрестности
– окрестности  уменьшаются: если
уменьшаются: если 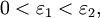 то
то 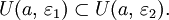
Иногда бывает удобно пополнить множество действительных чисел не двумя, а одной бесконечностью (без знака)  Ее
Ее  – окрестность
– окрестность 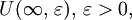 определяется равенством
определяется равенством
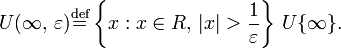
Иначе говоря,  – окрестность
– окрестность 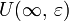 состоит из двух бесконечных интервалов
состоит из двух бесконечных интервалов 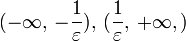 и самого элемента
и самого элемента  Этот элемент также называется иногда бесконечно удаленной точкой числовой прямой. В отличие от бесконечностей со знаком
Этот элемент также называется иногда бесконечно удаленной точкой числовой прямой. В отличие от бесконечностей со знаком  и
и  бесконечность
бесконечность 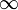 без знака не связана с действительными числами отношением порядка.
без знака не связана с действительными числами отношением порядка.
Всякая  – окрестность конечной или бесконечно удаленной точки числовой прямой называется ее окрестностью и часто обозначается просто через U(a). Иногда мы будем обозначать окрестность и другими буквами, например V, W.
– окрестность конечной или бесконечно удаленной точки числовой прямой называется ее окрестностью и часто обозначается просто через U(a). Иногда мы будем обозначать окрестность и другими буквами, например V, W.
Нередко с определенными выше окрестностями бесконечностей в пополнениях ими множества действительных чисел иногда рассматривают и окрестности бесконечностей  и
и 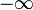 в самом множестве действительных чисел:
в самом множестве действительных чисел:  и
и 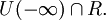 Сами бесконечности, конечно, уже не попадают в эти окрестности.
Сами бесконечности, конечно, уже не попадают в эти окрестности.
Лемма У любых двух различных точек расширенной числовой прямой (расширенной с помощью двух бесконечностей со знаком или при помощи только одной бесконечности без знака) существуют непересекающиеся окрестности.
Доказательство. Рассмотрим сначала случай расширенной числовой прямой R, полученной добавлением к множеству действительных чисел R двух бесконечностей со знаком. Покажем, что для любых 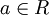 и
и 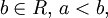 существуют такие
существуют такие 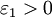 и
и 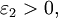 что
что 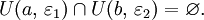 В самом деле, если a и b – действительные числа, то можно взять
В самом деле, если a и b – действительные числа, то можно взять 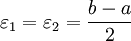 (рис. 1, а)[2] Если a – действительное число, а
(рис. 1, а)[2] Если a – действительное число, а 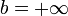 , то в качестве указанных
, то в качестве указанных 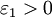 и
и 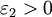 подходят, например,
подходят, например, 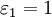 и
и 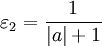 (рис. 1, б). Если
(рис. 1, б). Если 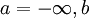 – действительное число, то можно взять
– действительное число, то можно взять  (рис. 1, в). Наконец, если
(рис. 1, в). Наконец, если 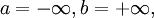 то при произвольном
то при произвольном 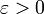 окрестности
окрестности 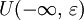 и
и  не пересекаются (рис. 1, г). Если же числовая прямая R дополнена лишь одной бесконечностью
не пересекаются (рис. 1, г). Если же числовая прямая R дополнена лишь одной бесконечностью 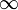 , то достаточно рассмотреть лишь случай
, то достаточно рассмотреть лишь случай 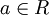 и
и 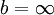 (так как случай
(так как случай 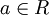 и
и 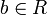 рассмотрен выше), в котором можно снова (как при
рассмотрен выше), в котором можно снова (как при 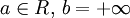 ) взять
) взять 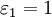 , а
, а 
Замечание 2. В случаеи их непересекающихся окрестностей
для любых
и
очевидно, справедливо неравенство
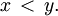
Его справедливость устанавливается непосредственной проверкой во всех возможных здесь случаях, т.е. при 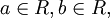 при
при 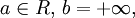 при
при 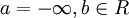 и при
и при 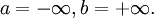 Легко убедиться, что пересечение двух окрестностей точки (конечной или бесконечно удаленной) является также окрестностью этой точки.
Легко убедиться, что пересечение двух окрестностей точки (конечной или бесконечно удаленной) является также окрестностью этой точки.
Примечания
- ^ Обозначение окрестности точки символом U происходит от нем. Umgebung – окрестность.
- ^ Рисунок 1
Источник
Л.Д. Кудрявцев Курс математического анализа, “Дрофа”
Wikimedia Foundation.
2010.
Рациональными числами называют числа, которые можно представить в виде обыкновенной дроби  , где
, где  и
и 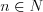 . Множество рациональных чисел обозначают
. Множество рациональных чисел обозначают  .
.
Рациональными являются натуральные и целые числа, а также конечные и периодические десятичные дроби, так как все они могут быть обращены в обыкновенную дробь.
Множество иррациональных чисел состоит из бесконечных непериодических десятичных дробей. Например, иррациональными являются числа:  ;
;  ;
;  .
.
Все рациональные и все иррациональные числа образуют множество действительных чисел. Запись  обозначает множество всех действительных чисел
обозначает множество всех действительных чисел  или множество всех точек числовой прямой.
или множество всех точек числовой прямой.
Координаты точек
Рассмотрим прямую, на которой указаны начало отсчета, положительное направление и единичный отрезок. Каждой точке этой прямой соответствует число, которое называют координатой точки на прямой.
Например, на рисунке 1.4 точка  имеет координату
имеет координату  , точка
, точка 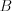 – координату
– координату  , а точка
, а точка 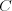 – координату
– координату  Записывают:
Записывают:  ,
,  ,
,  .
.

Расположим две координатные прямые 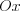 и
и 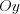 так, чтобы они пересекались под прямым углом (рис. 1.5). Говорят, что на плоскости задана прямоугольная декартова система координат. При этом прямую
так, чтобы они пересекались под прямым углом (рис. 1.5). Говорят, что на плоскости задана прямоугольная декартова система координат. При этом прямую 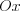 называют осью абсцисс, а прямую
называют осью абсцисс, а прямую 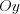 – осью ординат. Эти прямые (координатные оси) делят плоскость на четыре части, которые называют
– осью ординат. Эти прямые (координатные оси) делят плоскость на четыре части, которые называют  ,
,  ,
,  и
и  координатными четвертями.
координатными четвертями.
Каждой точке координатной плоскости соответствует пара чисел  , которые называют координатами точки на плоскости.
, которые называют координатами точки на плоскости.

На координатной плоскости (рис. 1.6) построим точку  с координатами
с координатами  и
и 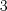 . Для этого отложим на оси
. Для этого отложим на оси 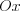
 единичных отрезка вправо и через эту точку проведем прямую, параллельную оси
единичных отрезка вправо и через эту точку проведем прямую, параллельную оси 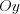 . Отложим на оси
. Отложим на оси 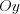
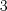 единичных отрезка вверх и через эту точку проведем прямую, параллельную оси
единичных отрезка вверх и через эту точку проведем прямую, параллельную оси 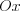 . В результате пересечения этих прямых получим точку
. В результате пересечения этих прямых получим точку  , которой соответствуют два числа: число
, которой соответствуют два числа: число  – абсцисса точки
– абсцисса точки  , число
, число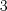 –ордината точки
–ордината точки  . Запишем:
. Запишем:  .
.
Изображения числовых множеств
Отрезок ![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) – это множество всех действительных чисел, удовлетворяющих неравенству
– это множество всех действительных чисел, удовлетворяющих неравенству  . С другой стороны это множество точек числовой прямой, состоящее из точек
. С другой стороны это множество точек числовой прямой, состоящее из точек  и
и  , а также всех точек, находящихся между ними (рис. 1.7).
, а также всех точек, находящихся между ними (рис. 1.7).
Например, на рисунке 1.8 отрезок ![[-2;3] LaTeX formula: [-2;3]](https://helpy.quali.me/uploads/formulas/dfcbf46c84a86a603bdc915d3b104328ef1d5d27.1.1.png) есть множество всех действительных чисел, удовлетворяющих неравенству
есть множество всех действительных чисел, удовлетворяющих неравенству  .
.

Интервал  – это множество всех действительных чисел, удовлетворяющих неравенству
– это множество всех действительных чисел, удовлетворяющих неравенству  . Если из отрезка
. Если из отрезка ![[a;b] LaTeX formula: [a;b]](http://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) исключить точки
исключить точки  и
и  , то получим интервал
, то получим интервал  (рис. 1.9).
(рис. 1.9).

Например, на рисунке 1.10 интервал  есть множество всех действительных чисел, удовлетворяющих неравенству
есть множество всех действительных чисел, удовлетворяющих неравенству  .
.
Полуинтервалы  и
и ![(a;b] LaTeX formula: (a;b]](https://helpy.quali.me/uploads/formulas/052ddd32d10a911045eafff92571f5a412c5585f.1.1.png) – множества всех действительных чисел, удовлетворяющих неравенствам
– множества всех действительных чисел, удовлетворяющих неравенствам  и
и  .
.
Например, полуинтервал  – это множество всех действительных чисел, удовлетворяющих неравенству
– это множество всех действительных чисел, удовлетворяющих неравенству  (рис. 1.11), а полуинтервал
(рис. 1.11), а полуинтервал ![(-3;0] LaTeX formula: (-3;0]](https://helpy.quali.me/uploads/formulas/b5ccda90157f5b5807010c857a693b368b1613d4.1.1.png) – множество всех действительных чисел, удовлетворяющих неравенству
– множество всех действительных чисел, удовлетворяющих неравенству  (рис. 1.12).
(рис. 1.12).

Отрезки, интервалы и полуинтервалы называют промежутками.
Длина отрезка. Чтобы найти длину отрезка, необходимо из координаты конца отрезка вычесть координату его начала, то есть длина отрезка ![[a;b] LaTeX formula: [a;b]](http://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) равна
равна  .
.
Середина отрезка. Чтобы найти середину отрезка, необходимо найти полусумму координат концов отрезка, то есть серединой отрезка ![[a;b] LaTeX formula: [a;b]](http://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png) является число
является число  .
.
Операции над числовыми множествами
Запись  означает, что имеем
означает, что имеем  -элементное множество
-элементное множество  , состоящее из элементов
, состоящее из элементов  . Так как каждый из этих элементов принадлежит множеству
. Так как каждый из этих элементов принадлежит множеству  , то записывают:
, то записывают:  ,
,  и т. д. Если некоторый элемент
и т. д. Если некоторый элемент  не принадлежит заданному множеству
не принадлежит заданному множеству  , то записывают:
, то записывают:  .
.
Например, запишем, что число  принадлежит множеству целых чисел, но не принадлежит множеству натуральных чисел:
принадлежит множеству целых чисел, но не принадлежит множеству натуральных чисел:  ,
,  .
.
Множество  является подмножеством множества
является подмножеством множества 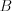 , если все элементы множества
, если все элементы множества  являются элементами множества
являются элементами множества 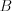 . Говорят, что множество
. Говорят, что множество 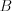 содержит в себе множество
содержит в себе множество  или, что множество
или, что множество  включается в множество
включается в множество 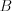 и записывают:
и записывают:  .
.
Например, множество натуральных чисел является подмножеством множества рациональных чисел, а множество рациональных чисел – подмножеством множества действительных чисел:  и
и  .
.
Объединением двух множеств  и
и 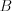 называют множество
называют множество 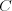 , состоящее из элементов, принадлежащих хотя бы одному из множеств
, состоящее из элементов, принадлежащих хотя бы одному из множеств  или
или 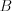 . Объединение множеств
. Объединение множеств  и
и 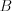 записывают так:
записывают так:  .
.
Примером объединения множеств является решение совокупности неравенств: решением совокупности неравенств  является объединение промежутков
является объединение промежутков  и
и  .
.
Пересечением двух множеств  и
и 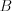 называют множество
называют множество 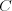 , состоящее из элементов, принадлежащих и множеству
, состоящее из элементов, принадлежащих и множеству  и множеству
и множеству 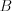 . Пересечение множеств
. Пересечение множеств  и
и 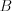 записывают так:
записывают так:  . Если множества
. Если множества  и
и 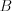 не содержат общих элементов, то их пересечение пусто:
не содержат общих элементов, то их пересечение пусто:  .
.
Примером пересечения множеств является решение системы неравенств: решением системы неравенств  является пересечение промежутков
является пересечение промежутков  и
и  .
.
Пример 1. Найдите длину и середину отрезка ![[-4;8] LaTeX formula: [-4;8]](https://helpy.quali.me/uploads/formulas/96b99006963c900b1ca5f0ad7d79b7bd3952a7cd.1.1.png) .
.
Решение. Длина отрезка равна:  .
.
Середина отрезка равна:  .
.
Ответ:  ;
;  .
.
Пример 2. Решите  и
и  .
.
Решение. Решением совокупности неравенств  является объединение промежутков
является объединение промежутков  и
и  (рис. 1.13). Запишем:
(рис. 1.13). Запишем:  .
.

Решение системы неравенств  показано на рисунке 1.14 – это промежуток
показано на рисунке 1.14 – это промежуток  .
.
Пример 3. Вычислите  .
.
Решение. Найдем значение выражения, записанного в числителе дроби:
1)  ;
;
2)  ;
;
3)  .
.
Найдем значение выражения, записанного в знаменателе дроби:
4)  ;
;
5)  ;
;
6)  ;
;
7) 
 ;
;
8)  .
.
Разделим числитель дроби на ее знаменатель:
 .
.
Ответ:  .
.
Пример 4. Найдите сумму всех чисел  , каждое из которых делится без остатка на
, каждое из которых делится без остатка на  и принадлежит промежутку
и принадлежит промежутку  .
.
Решение. Рассмотрим отрезок ![[-252;252] LaTeX formula: [-252;252]](https://helpy.quali.me/uploads/formulas/2406bab69a4fe4af7d119b19c5b46b3e00bab2e1.1.1.png) и интервал
и интервал  (рис. 1.15).
(рис. 1.15).

1. Рассмотрим отрезок ![[-252;252] LaTeX formula: [-252;252]](http://helpy.quali.me/uploads/formulas/2406bab69a4fe4af7d119b19c5b46b3e00bab2e1.1.1.png) . Сумма всех чисел, каждое из которых делится без остатка на
. Сумма всех чисел, каждое из которых делится без остатка на  и принадлежит этому отрезку, будет равна нулю (
и принадлежит этому отрезку, будет равна нулю (  ,
,  и т. д.).
и т. д.).
2. Рассмотрим интервал . Зная, что число
. Зная, что число делится на
делится на , но не принадлежит рассматриваемому интервалу, найдем все числа, кратные
, но не принадлежит рассматриваемому интервалу, найдем все числа, кратные  и не превосходящие число
и не превосходящие число  .
.
Получим:  ,
,  .
.
Тогда  .
.
Ответ:  .
.
Пример 5. Укажите все номера рациональных чисел данного множества: ![sqrt[3]{32sqrt[4]{2}}cdot 2^{1/4} LaTeX formula: sqrt[3]{32sqrt[4]{2}}cdot 2^{1/4}](https://helpy.quali.me/uploads/formulas/a4b55642f3767b50a31584a23ecbdc6fc5bd6270.1.1.png) (1);
(1);  (2);
(2);  (3);
(3);  (4);
(4);  (5).
(5).
Варианты ответов: а)  ,
, ,
,  ; б)
; б)  ,
,  ,
,  ; в)
; в)  ,
, 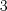 ,
,  ; г)
; г)  ,
, 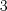 ,
,  ; д)
; д)  ,
, 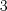 ,
,  .
.
Решение. Применим метод исключений, выполняя следующие преобразования.
1. Преобразуем любое число данного множества, например число (5): 
 .
.
Число (5) рациональное, значит, исключим варианты ответов, не содержащие этого числа, то есть варианты г) и д).
2. Преобразуем число (3):  . Число (3) иррациональное, значит, исключим вариант ответа в).
. Число (3) иррациональное, значит, исключим вариант ответа в).
3. Преобразуем любое из чисел (2) или (4), так как число (1) входит в оба оставшихся варианта ответа:  . Число (4) – рациональное.
. Число (4) – рациональное.
Ответ: б.
1. Обозначения числовых множеств:
1)  – множество натуральных чисел;
– множество натуральных чисел;
2)  – множество целых чисел;
– множество целых чисел;
3)  – множество рациональных чисел;
– множество рациональных чисел;
4)  – множество иррациональных чисел;
– множество иррациональных чисел;
5)  – множество действительных чисел;
– множество действительных чисел;
6)  – пустое множество.
– пустое множество.
2. Справедливо, что:  ;
;  ;
;  .
.

Числовые промежутки. Окрестность точки
Пусть 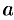 и
и 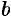 — действительные числа, причем
— действительные числа, причем 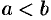 .
.
Числовыми промежутками (интервалами) называют подмножества всех действительных чисел, имеющих следующий вид:
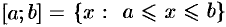 — отрезок (сегмент, замкнутый промежуток);
— отрезок (сегмент, замкнутый промежуток);
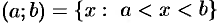 — интервал (открытый промежуток);
— интервал (открытый промежуток);
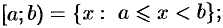
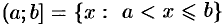 — полуоткрытые интервалы (или полуоткрытые отрезки);
— полуоткрытые интервалы (или полуоткрытые отрезки);

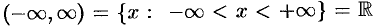 — бесконечные интервалы (промежутки).
— бесконечные интервалы (промежутки).
Числа 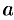 и
и 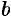 называются соответственно левым и правым концами этих промежутков. Символы
называются соответственно левым и правым концами этих промежутков. Символы 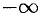 и
и 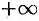 не числа, это символическое обозначение процесса неограниченного удаления точек числовой оси означала 0 влево и вправо.
не числа, это символическое обозначение процесса неограниченного удаления точек числовой оси означала 0 влево и вправо.
Пусть 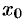 — любое действительное число (точка на числовой прямой). Окрестностью точки хо называется любой интервал
— любое действительное число (точка на числовой прямой). Окрестностью точки хо называется любой интервал 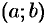 , содержащий точку
, содержащий точку 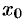 . В частности, интервал
. В частности, интервал 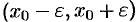 , где
, где 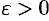 , называется
, называется 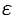 -окрестностью точки
-окрестностью точки 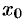 . Число
. Число 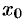 называется центром, а число
называется центром, а число 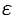 — радиусом.
— радиусом.
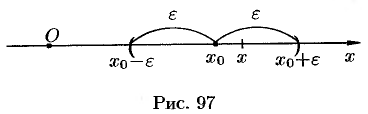
Если 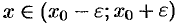 , то выполняется неравенство
, то выполняется неравенство 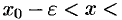
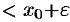 , или, что то же,
, или, что то же, 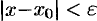 . Выполнение последнего неравенства означает попадание точки
. Выполнение последнего неравенства означает попадание точки 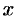 в
в 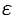 -окрестность точки
-окрестность точки 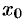 (см. рис. 97).
(см. рис. 97).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:


The addition x + a on the number line. All numbers greater than x and less than x + a fall within that open interval.
In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers x satisfying 0 ≤ x ≤ 1 is an interval which contains 0, 1, and all numbers in between. Other examples of intervals are the set of numbers such that 0 < x < 1, the set of all real numbers 
Real intervals play an important role in the theory of integration, because they are the simplest sets whose “length” (or “measure” or “size”) is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure.
Intervals are central to interval arithmetic, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematical approximations, and arithmetic roundoff.
Intervals are likewise defined on an arbitrary totally ordered set, such as integers or rational numbers. The notation of integer intervals is considered in the special section below.
Terminology[edit]
An open interval does not include its endpoints, and is indicated with parentheses.[1] For example, (0, 1) means greater than 0 and less than 1. This means (0, 1) = {x | 0 < x < 1}.
This interval can also be denoted by ]0, 1[, see below.
A closed interval is an interval which includes all its limit points, and is denoted with square brackets.[1] For example, [0, 1] means greater than or equal to 0 and less than or equal to 1.
A half-open interval includes only one of its endpoints, and is denoted by mixing the notations for open and closed intervals.[2] For example, (0, 1] means greater than 0 and less than or equal to 1, while [0, 1) means greater than or equal to 0 and less than 1.
A degenerate interval is any set consisting of a single real number (i.e., an interval of the form [a, a]).[2] Some authors include the empty set in this definition. A real interval that is neither empty nor degenerate is said to be proper, and has infinitely many elements.
An interval is said to be left-bounded or right-bounded, if there is some real number that is, respectively, smaller than or larger than all its elements. An interval is said to be bounded, if it is both left- and right-bounded; and is said to be unbounded otherwise. Intervals that are bounded at only one end are said to be half-bounded. The empty set is bounded, and the set of all reals is the only interval that is unbounded at both ends. Bounded intervals are also commonly known as finite intervals.
Bounded intervals are bounded sets, in the sense that their diameter (which is equal to the absolute difference between the endpoints) is finite. The diameter may be called the length, width, measure, range, or size of the interval. The size of unbounded intervals is usually defined as +∞, and the size of the empty interval may be defined as 0 (or left undefined).
The centre (midpoint) of a bounded interval with endpoints a and b is (a + b)/2, and its radius is the half-length |a − b|/2. These concepts are undefined for empty or unbounded intervals.
An interval is said to be left-open if and only if it contains no minimum (an element that is smaller than all other elements); right-open if it contains no maximum; and open if it contains neither. The interval [0, 1) = {x | 0 ≤ x < 1}, for example, is left-closed and right-open. The empty set and the set of all reals are both open and closed intervals, while the set of non-negative reals, is a closed interval that is right-open but not left-open. The open intervals are open sets of the real line in its standard topology, and form a base of the open sets.
An interval is said to be left-closed if it has a minimum element or is left-unbounded, right-closed if it has a maximum or is right unbounded; it is simply closed if it is both left-closed and right closed. So, the closed intervals coincide with the closed sets in that topology.
The interior of an interval I is the largest open interval that is contained in I; it is also the set of points in I which are not endpoints of I. The closure of I is the smallest closed interval that contains I; which is also the set I augmented with its finite endpoints.
For any set X of real numbers, the interval enclosure or interval span of X is the unique interval that contains X, and does not properly contain any other interval that also contains X.
An interval I is subinterval of interval J if I is a subset of J. An interval I is a proper subinterval of J if I is a proper subset of J.
Note on conflicting terminology[edit]
The terms segment and interval have been employed in the literature in two essentially opposite ways, resulting in ambiguity when these terms are used. The Encyclopedia of Mathematics[3] defines interval (without a qualifier) to exclude both endpoints (i.e., open interval) and segment to include both endpoints (i.e., closed interval), while Rudin’s Principles of Mathematical Analysis[4] calls sets of the form [a, b] intervals and sets of the form (a, b) segments throughout. These terms tend to appear in older works; modern texts increasingly favor the term interval (qualified by open, closed, or half-open), regardless of whether endpoints are included.
Notations for intervals[edit]
The interval of numbers between a and b, including a and b, is often denoted [a, b]. The two numbers are called the endpoints of the interval. In countries where numbers are written with a decimal comma, a semicolon may be used as a separator to avoid ambiguity.
Including or excluding endpoints[edit]
To indicate that one of the endpoints is to be excluded from the set, the corresponding square bracket can be either replaced with a parenthesis, or reversed. Both notations are described in International standard ISO 31-11. Thus, in set builder notation,
Each interval (a, a), [a, a), and (a, a] represents the empty set, whereas [a, a] denotes the singleton set {a}. When a > b, all four notations are usually taken to represent the empty set.
Both notations may overlap with other uses of parentheses and brackets in mathematics. For instance, the notation (a, b) is often used to denote an ordered pair in set theory, the coordinates of a point or vector in analytic geometry and linear algebra, or (sometimes) a complex number in algebra. That is why Bourbaki introduced the notation ]a, b[ to denote the open interval.[5] The notation [a, b] too is occasionally used for ordered pairs, especially in computer science.
Some authors such as Yves Tillé use ]a, b[ to denote the complement of the interval (a, b); namely, the set of all real numbers that are either less than or equal to a, or greater than or equal to b.
Infinite endpoints[edit]
In some contexts, an interval may be defined as a subset of the extended real numbers, the set of all real numbers augmented with −∞ and +∞.
In this interpretation, the notations [−∞, b] , (−∞, b] , [a, +∞] , and [a, +∞) are all meaningful and distinct. In particular, (−∞, +∞) denotes the set of all ordinary real numbers, while [−∞, +∞] denotes the extended reals.
Even in the context of the ordinary reals, one may use an infinite endpoint to indicate that there is no bound in that direction. For example, (0, +∞) is the set of positive real numbers, also written as 

Integer intervals[edit]
When a and b are integers, the notation ⟦a, b⟧, or [a .. b] or {a .. b} or just a .. b, is sometimes used to indicate the interval of all integers between a and b included. The notation [a .. b] is used in some programming languages; in Pascal, for example, it is used to formally define a subrange type, most frequently used to specify lower and upper bounds of valid indices of an array.
An integer interval that has a finite lower or upper endpoint always includes that endpoint. Therefore, the exclusion of endpoints can be explicitly denoted by writing a .. b − 1 , a + 1 .. b , or a + 1 .. b − 1. Alternate-bracket notations like [a .. b) or [a .. b[ are rarely used for integer intervals.[citation needed]
Classification of intervals[edit]
The intervals of real numbers can be classified into the eleven different types listed below[citation needed], where a and b are real numbers, and 
Properties of intervals[edit]
The intervals are precisely the connected subsets of 
The intervals are also the convex subsets of 


The intersection of any collection of intervals is always an interval. The union of two intervals is an interval if and only if they have a non-empty intersection or an open end-point of one interval is a closed end-point of the other – e.g., ![(a,b)cup [b,c]=(a,c]](https://wikimedia.org/api/rest_v1/media/math/render/svg/20dd7d6ce8ba23bfb9de0d90487008656b91eb94)
If 
Any element x of an interval I defines a partition of I into three disjoint intervals I1, I2, I3: respectively, the elements of I that are less than x, the singleton ![[x,x]={x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08cd03413513401836efbed8ca64419d73d3f481)
Dyadic intervals[edit]
A dyadic interval is a bounded real interval whose endpoints are 



Dyadic intervals have the following properties:
- The length of a dyadic interval is always an integer power of two.
- Each dyadic interval is contained in exactly one dyadic interval of twice the length.
- Each dyadic interval is spanned by two dyadic intervals of half the length.
- If two open dyadic intervals overlap, then one of them is a subset of the other.
The dyadic intervals consequently have a structure that reflects that of an infinite binary tree.
Dyadic intervals are relevant to several areas of numerical analysis, including adaptive mesh refinement, multigrid methods and wavelet analysis. Another way to represent such a structure is p-adic analysis (for p = 2).[6]
Generalizations[edit]
Multi-dimensional intervals[edit]
In many contexts, an 



For 

In higher dimensions, the Cartesian product of 
A facet of such an interval 






Complex intervals[edit]
Intervals of complex numbers can be defined as regions of the complex plane, either rectangular or circular.[7]
Topological algebra[edit]
Intervals can be associated with points of the plane, and hence regions of intervals can be associated with regions of the plane. Generally, an interval in mathematics corresponds to an ordered pair (x,y) taken from the direct product R × R of real numbers with itself, where it is often assumed that y > x. For purposes of mathematical structure, this restriction is discarded,[8] and “reversed intervals” where y − x < 0 are allowed. Then, the collection of all intervals [x,y] can be identified with the topological ring formed by the direct sum of R with itself, where addition and multiplication are defined component-wise.
The direct sum algebra 
Every interval can be considered a symmetric interval around its midpoint. In a reconfiguration published in 1956 by M Warmus, the axis of “balanced intervals” [x, −x] is used along with the axis of intervals [x,x] that reduce to a point. Instead of the direct sum 
- z = (x + y)/2 + j (x − y)/2.
This linear mapping of the plane, which amounts of a ring isomorphism, provides the plane with a multiplicative structure having some analogies to ordinary complex arithmetic, such as polar decomposition.
See also[edit]
- Arc (geometry)
- Inequality
- Interval graph
- Interval finite element
- Interval (statistics)
- Line segment
- Partition of an interval
- Unit interval
References[edit]
- ^ a b “Intervals”. www.mathsisfun.com. Retrieved 2020-08-23.
- ^ a b Weisstein, Eric W. “Interval”. mathworld.wolfram.com. Retrieved 2020-08-23.
- ^ “Interval and segment – Encyclopedia of Mathematics”. encyclopediaofmath.org. Archived from the original on 2014-12-26. Retrieved 2016-11-12.
- ^ Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. pp. 31. ISBN 0-07-054235-X.
- ^ “Why is American and French notation different for open intervals (x, y) vs. ]x, y[?”. hsm.stackexchange.com. Retrieved 28 April 2018.
- ^ Kozyrev, Sergey (2002). “Wavelet theory as p-adic spectral analysis”. Izvestiya RAN. Ser. Mat. 66 (2): 149–158. arXiv:math-ph/0012019. Bibcode:2002IzMat..66..367K. doi:10.1070/IM2002v066n02ABEH000381. S2CID 16796699. Retrieved 2012-04-05.
- ^ Complex interval arithmetic and its applications, Miodrag Petković, Ljiljana Petković, Wiley-VCH, 1998, ISBN 978-3-527-40134-5
- ^ Kaj Madsen (1979) Review of “Interval analysis in the extended interval space” by Edgar Kaucher[permanent dead link] from Mathematical Reviews
- ^ D. H. Lehmer (1956) Review of “Calculus of Approximations”[permanent dead link] from Mathematical Reviews
Bibliography[edit]
- T. Sunaga, “Theory of interval algebra and its application to numerical analysis” Archived 2012-03-09 at the Wayback Machine, In: Research Association of Applied Geometry (RAAG) Memoirs, Ggujutsu Bunken Fukuy-kai. Tokyo, Japan, 1958, Vol. 2, pp. 29–46 (547-564); reprinted in Japan Journal on Industrial and Applied Mathematics, 2009, Vol. 26, No. 2-3, pp. 126–143.
External links[edit]
- A Lucid Interval by Brian Hayes: An American Scientist article provides an introduction.
- Interval computations website Archived 2006-03-02 at the Wayback Machine
- Interval computations research centers Archived 2007-02-03 at the Wayback Machine
- Interval Notation by George Beck, Wolfram Demonstrations Project.
- Weisstein, Eric W. “Interval”. MathWorld.
![U(+infty,, varepsilon)stackrel{mathrm{def}}{=}({1over varepsilon} ,, +infty],](https://dic.academic.ru/pictures/wiki/files/99/c074324d06f100920bcc0382655bbe8b.png)
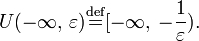
![{displaystyle {begin{aligned}{color {Maroon}(}a,b{color {Maroon})}={mathopen {color {Maroon}]}}a,b{mathclose {color {Maroon}[}}&={xin mathbb {R} mid a{color {Maroon}{}<{}}x{color {Maroon}{}<{}}b},\{}{color {DarkGreen}[}a,b{color {Maroon})}={mathopen {color {DarkGreen}[}}a,b{mathclose {color {Maroon}[}}&={xin mathbb {R} mid a{color {DarkGreen}{}leq {}}x{color {Maroon}{}<{}}b},\{}{color {Maroon}(}a,b{color {DarkGreen}]}={mathopen {color {Maroon}]}}a,b{mathclose {color {DarkGreen}]}}&={xin mathbb {R} mid a{color {Maroon}{}<{}}x{color {DarkGreen}{}leq {}}b},\{}{color {DarkGreen}[}a,b{color {DarkGreen}]}={mathopen {color {DarkGreen}[}}a,b{mathclose {color {DarkGreen}]}}&={xin mathbb {R} mid a{color {DarkGreen}{}leq {}}x{color {DarkGreen}{}leq {}}b}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0410c727e5c09b33b3074d6f7cfa99a624883079)
