Метод интервалов, решение неравенств

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:

где x — переменная,
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax 2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
- D 2 + bx + c.
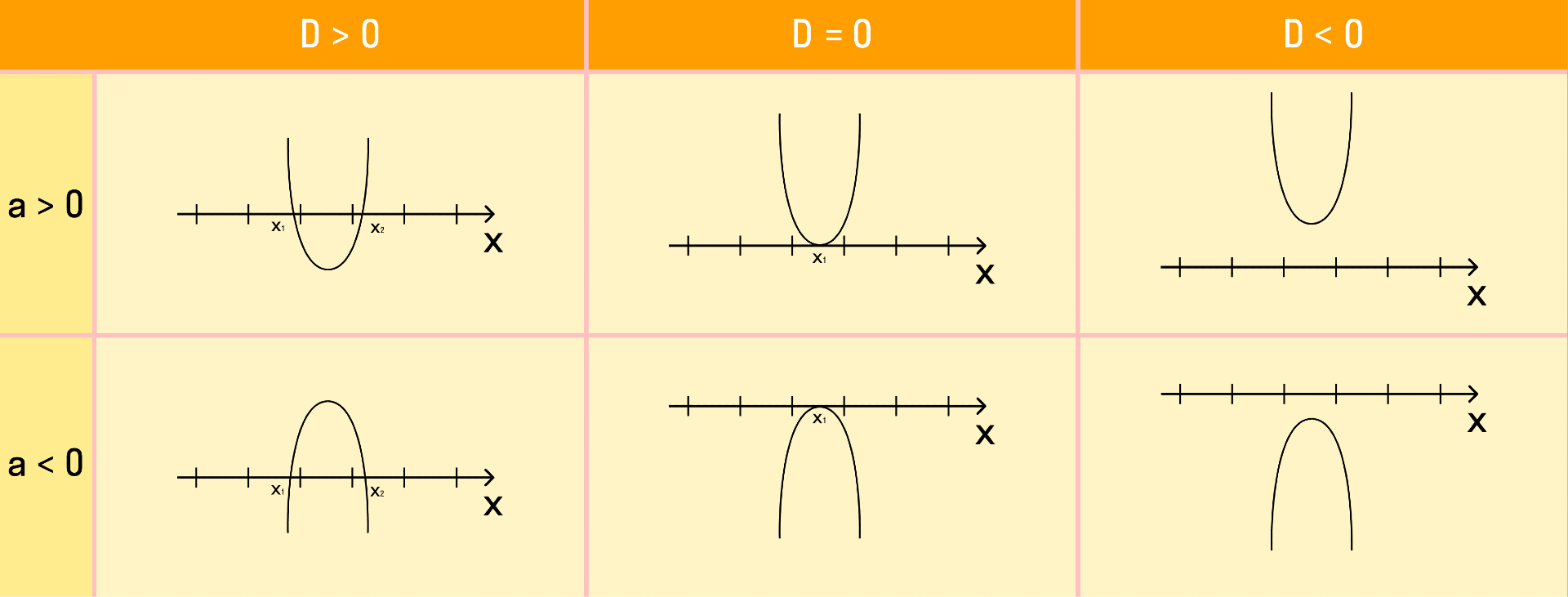
Если требуется найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, 2 + bx + c из левой части квадратного неравенства.
Изобразить координатную прямую и при наличии корней отметить их на ней. 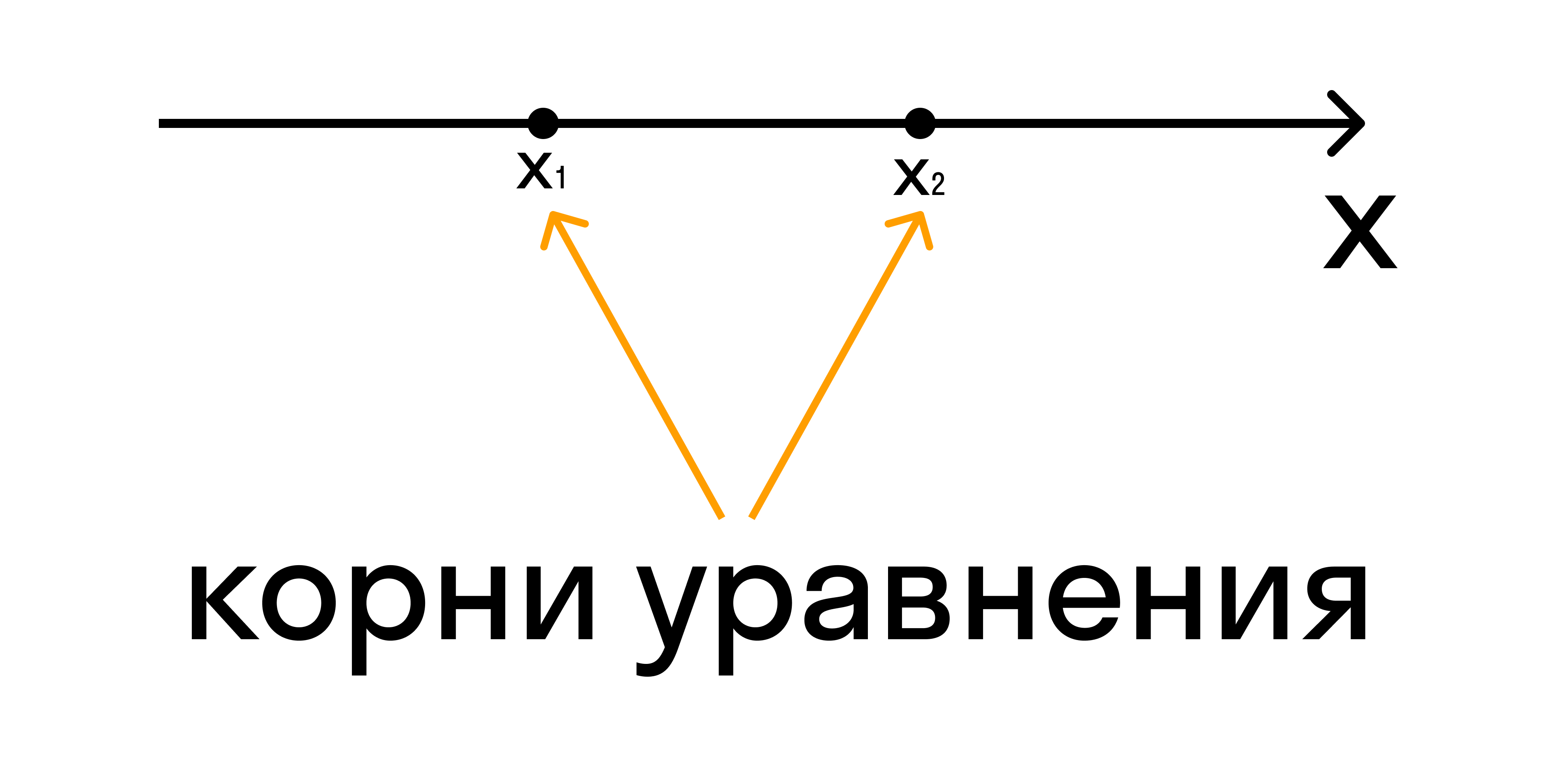
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.

Если неравенство со знаком 2 + 4x — 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).
Определим знак трехчлена x 2 + 4x — 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:
- 2 2 + 4 * 2 — 5 = 4 + 8 — 5 = 7.
7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.
Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:
- 0 2 + 4 * 0 — 5 = 0 + 0 — 5 = -5.
Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.
Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:
- (-6) 2 + 4 * (-6) — 5 = 36 — 24 — 5 = 7.
Следовательно, искомый знак — плюс.
Можно расставить знаки быстрее, если запомнить эти факты:
Плюс или минус: как определить знаки
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a 0, последовательность знаков: +, +,
если a 2 — 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x 2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
- Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
- Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
- Когда квадратный трехчлен корней не имеет (D
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.
Разложим квадратный трехчлен на множители. 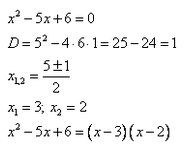
Неравенство примет вид:
Проанализируем два сомножителя:
Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.
Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.
Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.
В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.
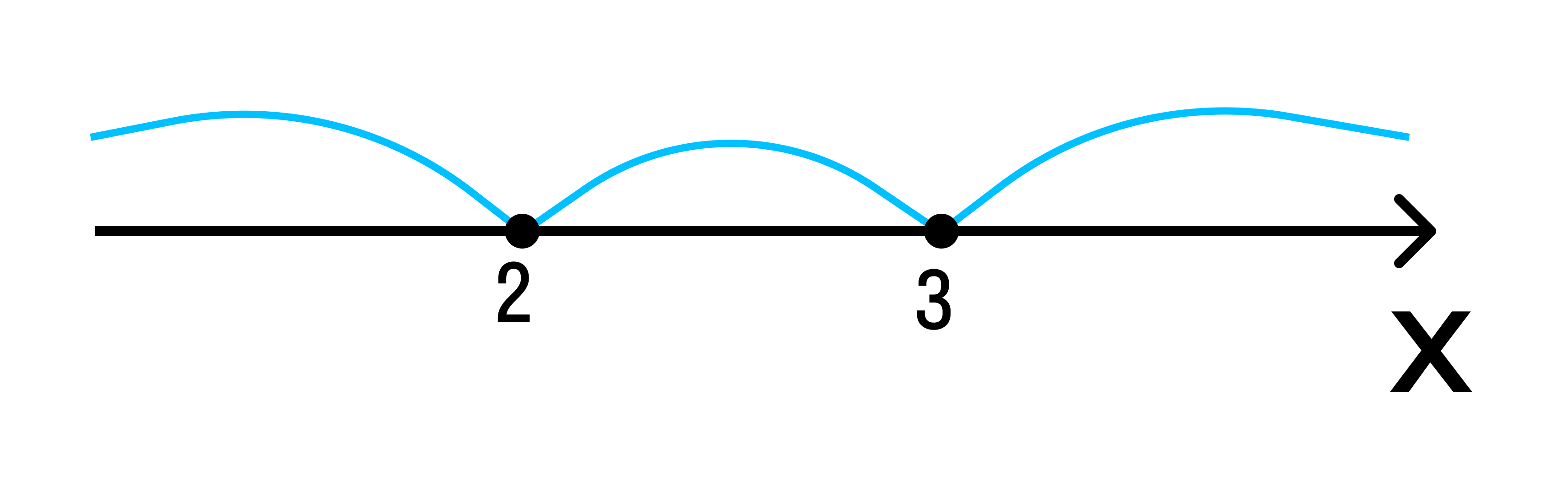
Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
- (25 — 3) (25 — 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.
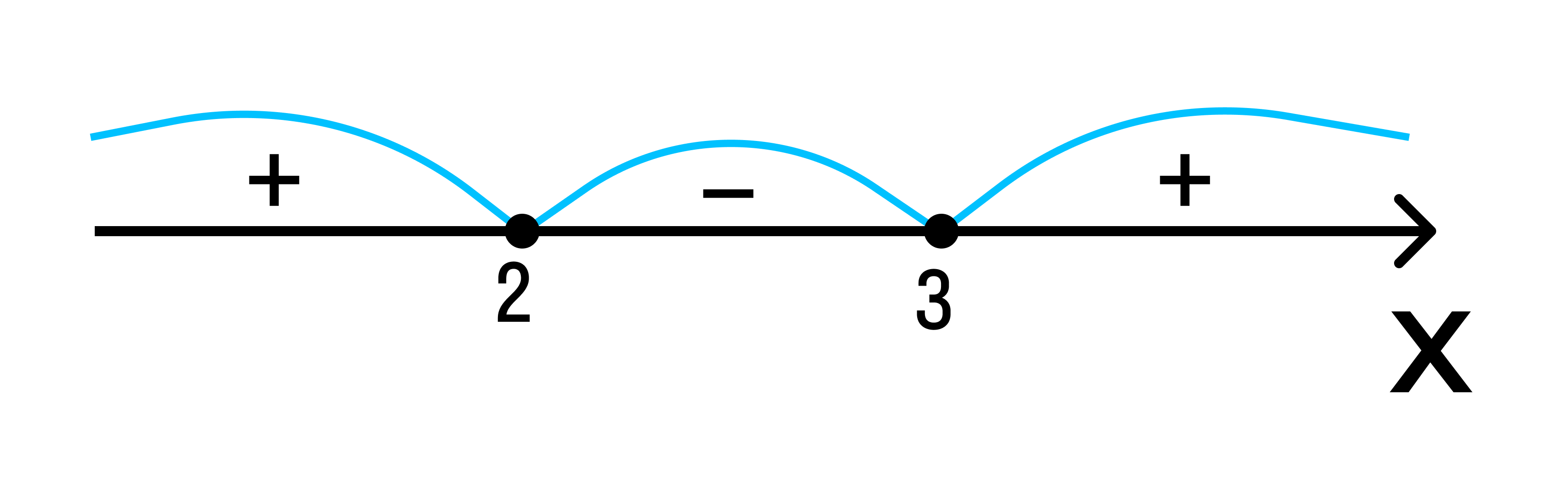
Исходное неравенство: (х — 3) * (х — 2) ≥ 0.
Если (х — 3) * (х — 2) > 0:
Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Отбор корней в тригонометрическом уравнение
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x — cosx = 0
cosx(sqrt(2)cosx — 1) = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx — 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
источники:
http://reshimvse.com/article.php?id=100
Отбор корней в тригонометрическом уравнение
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x – cosx = 0
cosx(sqrt(2)cosx – 1) = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx – 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 – 1/2 меньше или равно n меньше или равно -2 – 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 – 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 – 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 – 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
Способы отбора корней в тригонометрических уравнениях
Класс: 10
Автор проекта:
Шелкова Полина,
Класс: 10
Руководитель:
Злобова Людмила Викторовна,
учитель математики
ВВЕДЕНИЕ
Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον – «тригон» – треугольник и μετρειν – «метрео» – измеряю).
Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.
Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.
Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.
I РАЗДЕЛ (теоретический)
Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?
- Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
- Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
- Тригонометрические уравнения включены в КИМы ЕГЭ по математике.
Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку – это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.
Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.
Задачи:
- познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
- изучить соответствующую литературу;
- научиться решать тригонометрические уравнения;
- найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
- научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
- подготовиться к ЕГЭ по математике.
Приёмы отбора корней тригонометрического уравнения на заданном промежутке.
При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.
Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.
Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.
Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.
Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.
II РАЗДЕЛ (практический)
Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:
sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos 2 x−sin 2 x]
sinx−(cos 2 x−sin 2 x)=0;
sinx−(1−sin 2 x−sin 2 x)=0;
Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим
Вернемся к замене:

б) Рассмотрим три способа отбора корней, попадающих в отрезок  .
.
1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:


2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни: 

3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.

Нам останется только выбрать корни, которые попали в нужный нам отрезок.

ЗАКЛЮЧЕНИЕ
При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем – небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.
СПИСОК ЛИТЕРАТУРЫ
- Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
- Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова – М. Просвещение, 2017.
- С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных – М: Издательство: «Экзамен», 2005.
- Корянов А.Г., Прокофьев А.А. – Тригонометрические уравнения: методы решения и отбор корней. – М.: Математика ЕГЭ, 2012.
Уравнение – определение и вычисление с примерами решения
Содержание:
Уравнения
Уравнения-следствия и равносильные преобразования уравнений
1. Понятие уравнения и его корней
Определение:
Равенство с переменной называется уравнением. В общем виде уравнение с одной переменной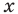
Под этой краткой записью понимают математическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны
Пример:
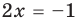 — линейное уравнение;
— линейное уравнение;
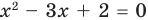 — квадратное уравнение;
— квадратное уравнение;
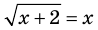 — иррациональное уравнение (содержит переменную под знаком корня)
— иррациональное уравнение (содержит переменную под знаком корня)
Корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство.
Решить уравнение — значит найти все его корни или доказать, что их нет
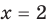 — корень уравнения
— корень уравнения 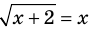 , так как при
, так как при 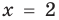 получаем верное равенство:
получаем верное равенство: 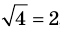 , то есть
, то есть 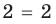
2. Область допустимых значений (ОДЗ)
Областью допустимых значений (или областью определения) уравнения называется общая область определения для функций 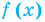 и
и 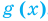 , стоящих в левой и правой частях уравнения
, стоящих в левой и правой частях уравнения
Для уравнения 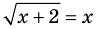 ОДЗ:
ОДЗ: 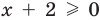 , то есть
, то есть 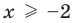 , так как область определения функции
, так как область определения функции 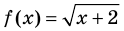 определяется условием:
определяется условием:  , а область определения функции
, а область определения функции 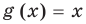 — множество всех действительных чисел
— множество всех действительных чисел
3. Уравнения-следствия
Если каждый корень первого уравнения является корнем второго, то второе уравнение называется следствием первого уравнения.
Если из правильности первого равенства следует правильность каждого последующего, то получаем уравнения-следствия.
При использовании уравнений-следствий не происходит потери корней исходного уравнения, но возможно появление посторонних корней. Поэтому при использовании уравнений-следствий проверка полученных корней подстановкой их в исходное уравнение является составной частью решения.
Пример:
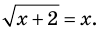
Решение:
► Возведем обе части уравнения в квадрат:
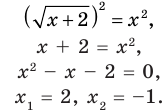
Проверка, 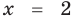 — корень (см. выше);
— корень (см. выше); 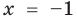 — посторонний корень (при
— посторонний корень (при 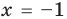 получаем неверное равенство
получаем неверное равенство 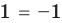 ).
).
4. Равносильные уравнения
Определение:
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни.
То есть каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого. (Схема решения уравнений с помощью равносильных преобразований приведена в пункте 5 этой таблицы)
Простейшие теоремы
- Если из одной части уравнения перенести в другую слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве)
- Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получим уравнение, равносильное заданному (на ОДЗ заданного уравнения)
5. Схема поиска плана решения уравнений
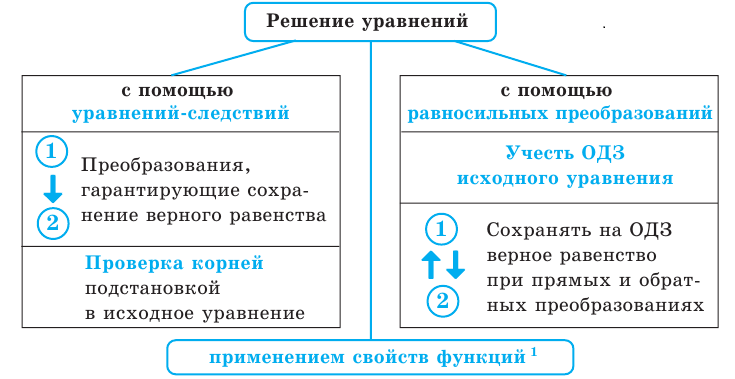
 – исходное уравнение;
– исходное уравнение;
 – уравнение, полученное в результате преобразования исходного;
– уравнение, полученное в результате преобразования исходного;
 – символические изображения направления выполненных преобразований
– символические изображения направления выполненных преобразований
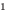 Применение свойств функций к решению уравнений рассмотрено в пункте 3.2.
Применение свойств функций к решению уравнений рассмотрено в пункте 3.2.
Объяснение и обоснование:
Понятие уравнения и его корней
Уравнение в математике чаще всего понимают как аналитическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны. Поэтому в общем виде уравнения с одной переменной 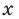 записывают так:
записывают так:
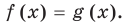
Часто уравнения определяют короче — как равенство с переменной.
Напомним, что корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.
Например, уравнение 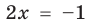 имеет единственный корень
имеет единственный корень 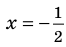 ,
,
а уравнение 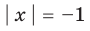 не имеет корней, поскольку значение
не имеет корней, поскольку значение 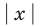 не может быть отрицательным числом.
не может быть отрицательным числом.
Область допустимых значений (ОДЗ) уравнения
Если задано уравнение 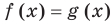 , то общая область определения для функций
, то общая область определения для функций 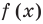 и
и 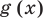 называется областью допустимых значений этого уравнения. (Иногда используются также термины «область определения уравнения» или «множество допустимых значений уравнения».) Например, для уравнения
называется областью допустимых значений этого уравнения. (Иногда используются также термины «область определения уравнения» или «множество допустимых значений уравнения».) Например, для уравнения 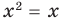 областью допустимых значений являются все действительные числа. Это можно записать, например, так:
областью допустимых значений являются все действительные числа. Это можно записать, например, так: 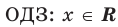 , поскольку функции
, поскольку функции 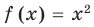 и
и 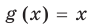 имеют области определения
имеют области определения 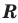 .
.
Понятно, что каждый корень данного уравнения принадлежит как области определения функции 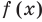 , так и области определения функции
, так и области определения функции 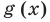 (иначе мы не сможем получить верное числовое равенство). Поэтому каждый корень уравнения обязательно принадлежит ОДЗ этого уравнения. Это позволяет в некоторых случаях применить анализ ОДЗ уравнения при его решении.
(иначе мы не сможем получить верное числовое равенство). Поэтому каждый корень уравнения обязательно принадлежит ОДЗ этого уравнения. Это позволяет в некоторых случаях применить анализ ОДЗ уравнения при его решении.
Например, в уравнении 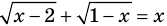 функция
функция 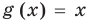 определена при всех действительных значениях
определена при всех действительных значениях 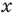 , а функция
, а функция 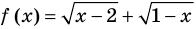 только при условии, что под знаком квадратного корня будут стоять неотрицательные выражения. Следовательно, ОДЗ этого уравнения задается системой
только при условии, что под знаком квадратного корня будут стоять неотрицательные выражения. Следовательно, ОДЗ этого уравнения задается системой 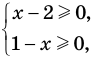 из которой получаем систему
из которой получаем систему 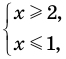 не имеющую решений. Таким образом, ОДЗ данного уравнения не содержит ни одного числа, и поэтому это уравнение не имеет корней.
не имеющую решений. Таким образом, ОДЗ данного уравнения не содержит ни одного числа, и поэтому это уравнение не имеет корней.
Заметим, что нахождение ОДЗ данного уравнения может быть полезным для его решения, но не всегда является обязательным элементом решения уравнения.
Методы решения уравнений
Для решения уравнений используют методы точного и приближенного решений. А именно, для точного решения уравнений в курсе математики 5-6 классов использовались зависимости между компонентами и результатами действий и свойства числовых равенств; в курсе алгебры 7-9 классов — равносильные преобразования уравнений, а для приближенного решения уравнений — графический метод.
Графический метод решения уравнений не дает высокой точности нахождения корней уравнения, и с его помощью чаще всего можно получить только грубые приближения корней. Иногда удобно графически определить количество корней уравнения или найти границы, в которых находятся эти корни. В некоторых случаях можно графически доказать, что уравнение не имеет корней. По указанным причинам в школьном курсе алгебры и начал анализа под требованием «решить уравнение» понимается требование «используя методы точного решения, найти корни данного уравнения». Приближенными методами решения уравнений можно пользоваться только тогда, когда об этом говорится в условии задачи (например, если ставится задача решить уравнение графически).
В основном при решении уравнений разных видов нам придется применять один из двух методов решения. Первый из них состоит в том, что данное уравнение заменяется более простым уравнением, имеющим те же корни,— равносильным уравнением. В свою очередь, полученное уравнение заменяется еще более простым, равносильным ему, и т. д. В результате получаем простейшее уравнение, которое равносильно заданному и корни которого легко находятся. Эти корни и только они являются корнями данного уравнения.
Второй метод решения уравнений состоит в том, что данное уравнение заменяется более простым уравнением, среди корней которого находятся все корни данного, то есть так называемым уравнением-следствием. В свою очередь, полученное уравнение заменяется еще более простым уравнением-следствием, и так далее до тех пор, пока не получим простейшее уравнение, корни которого легко находятся. Тогда все корни данного уравнения находятся среди корней последнего уравнения. Поэтому, чтобы найти корни данного уравнения, достаточно корни последнего уравнения подставить в данное и с помощью такой проверки получить корни данного уравнения (и исключить так называемые посторонние корни — те корни последнего уравнения, которые не удовлетворяют заданному).
В следующем пункте будет также показано применение свойств функций к решению уравнений определенного вида.
Уравнения-следствия
Рассмотрим более детально, как можно решать уравнения с помощью уравнений-следствий. При решении уравнений главное — не потерять корни данного уравнения, и поэтому в первую очередь мы должны следить за тем, чтобы каждый корень исходного уравнения оставался корнем следующего. Фактически это и является определением уравнения-следствия:
в том случае, когда каждый корень первого уравнения является корнем второго, второе уравнение называется следствием первого.
Это определение позволяет обосновать такой ориентир: для получения уравнения-следствия достаточно рассмотреть данное уравнение как верное числовое равенство и гарантировать (то есть иметь возможность обосновать), что каждое следующее уравнение мы можем получить как верное числовое равенство.
Действительно, если придерживаться этого ориентира, то каждый корень первого уравнения обращает это уравнение в верное числовое равенство, но тогда и второе уравнение будет верным числовым равенством, то есть рассматриваемое значение переменной является корнем и второго уравнения, а это и означает, что второе уравнение является следствием первого.
Применим приведенный ориентир к уравнению 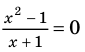 (пока что не используя известное условие равенства дроби нулю).
(пока что не используя известное условие равенства дроби нулю).
Если правильно то, что дробь равна нулю, то обязательно ее числитель равен нулю. Таким образом, из заданного уравнения получаем уравнение-следствие 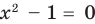 . Но тогда верно, что
. Но тогда верно, что 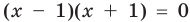 . Последнее уравнение имеет два корня:
. Последнее уравнение имеет два корня: 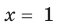 и
и 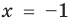 . Подставляя их в заданное уравнение, видим, что только корень
. Подставляя их в заданное уравнение, видим, что только корень 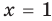 удовлетворяет исходному уравнению. Почему это случилось?
удовлетворяет исходному уравнению. Почему это случилось?
Это происходит поэтому, что, используя уравнения-следствия, мы гарантируем только то, что корни заданного уравнения не теряются (каждый корень первого уравнения является корнем второго). Но второе уравнение, кроме корней первого уравнения, имеет еще и другой корень, который не является корнем первого уравнения. Для первого уравнения этот корень является посторонним, и, чтобы его отсеять, выполняется проверка подстановкой корней в исходное уравнение. (Более полно причины появления посторонних корней рассмотрены в таблице 9.) Таким образом, чтобы правильно применять уравнения-следствия для решения уравнений, необходимо помнить еще один ориентир: при использовании уравнений-следствий возможно появление посторонних корней, и поэтому проверка подстановкой корней в исходное уравнение является составной частью решения.
Схема применения этих ориентиров дана в таблице 8. В пункте 3 этой таблицы приведено решение уравнения
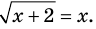 (1)
(1)
Для решения этого уравнения с помощью уравнений-следствий достаточно данное уравнение рассмотреть как верное числовое равенство и учесть, что в случае когда два числа равны, то и их квадраты также будут равны:
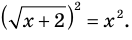 (2)
(2)
То есть мы гарантируем, что если равенство (1) верно, то и равенство (2) также будет верным, а это и означает (как было показано выше), что уравнение (2) является следствием уравнения (1). Если мы хотя бы один раз использовали уравнения-следствия (а не равносильные преобразования), то можем получить посторонние корни, и тогда в решение обязательно входит проверка полученных корней подстановкой их в заданное уравнение.
Замечание. Переход от данного уравнения к уравнению-следствию можно обозначить специальным значком 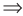 , но его использование для записи решения не является обязательным. Вместе с тем, если этот значок записан, то это свидетельствует о том, что мы воспользовались уравнениями-следствиями, и поэтому обязательно в запись решения необходимо включить проверку полученных корней.
, но его использование для записи решения не является обязательным. Вместе с тем, если этот значок записан, то это свидетельствует о том, что мы воспользовались уравнениями-следствиями, и поэтому обязательно в запись решения необходимо включить проверку полученных корней.
Равносильные уравнения
С понятием равносильности вы знакомы еще из курса алгебры 7 класса, где равносильными назывались те уравнения, которые имели одни и те же корни. Заметим, что равносильными считались и такие два уравнения, которые не имели корней. Формально будем считать, что и в этом случае уравнения имеют одни и те же корни, поскольку ответы к таким уравнениям одинаковы: «уравнения не имеют корней» (точнее: одинаковыми являются множества корней таких уравнений — они оба пустые, что обозначается символом 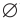 ).
).
В курсе алгебры и начал анализа мы будем рассматривать более общее понятие равносильности, а именно: равносильность на определенном множестве.
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни, то есть каждый корень первого уравнения является корнем второго и, наоборот, каждый корень второго уравнения является корнем первого.
Для уравнений, заданных на множестве всех действительных чисел (например, для линейных), мы можем однозначно дать ответ на вопрос: «Равносильны ли данные уравнения?» Например, уравнения 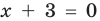 и
и 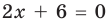 — равносильные, поскольку оба имеют одинаковый корень
— равносильные, поскольку оба имеют одинаковый корень 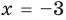 и других корней не имеют. Таким образом, каждое из них имеет те же решения, что и второе. При рассмотрении равносильности уравнений на множестве, которое отличается от множества всех действительных чисел, ответ на вопрос «Равносильны ли данные уравнения?» может существенно зависеть от того, на каком множестве мы рассматриваем эти уравнения. Например, если рассмотреть уравнения:
и других корней не имеют. Таким образом, каждое из них имеет те же решения, что и второе. При рассмотрении равносильности уравнений на множестве, которое отличается от множества всех действительных чисел, ответ на вопрос «Равносильны ли данные уравнения?» может существенно зависеть от того, на каком множестве мы рассматриваем эти уравнения. Например, если рассмотреть уравнения:
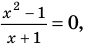 (3)
(3)
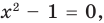 (4)
(4)
то, как было показано выше, уравнение (3) имеет единственный корень 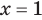 , а уравнение (4) — два корня:
, а уравнение (4) — два корня: 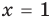 и
и 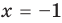 . Таким образом, на множестве
. Таким образом, на множестве
всех действительных чисел эти уравнения не являются равносильными, поскольку у уравнения (4) есть корень 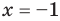 , которого нет у уравнения (3). Но на множестве положительных действительных чисел эти уравнения равносильны, поскольку на этом множестве уравнение (3) имеет единственный положительный корень
, которого нет у уравнения (3). Но на множестве положительных действительных чисел эти уравнения равносильны, поскольку на этом множестве уравнение (3) имеет единственный положительный корень 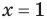 и уравнение (4) также имеет единственный положительный корень
и уравнение (4) также имеет единственный положительный корень 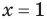 . Следовательно, на множестве положительных чисел каждое из этих уравнений имеет те же решения, что и второе.
. Следовательно, на множестве положительных чисел каждое из этих уравнений имеет те же решения, что и второе.
Укажем, что множество, на котором рассматривается равносильность уравнений, как правило, не задается искусственно (как в последнем случае), а чаще всего таким множеством является ОДЗ исходного уравнения. Договоримся, что далее
все равносильные преобразования уравнений (а также неравенств и систем уравнений и неравенств) мы будем выполнять на ОДЗ исходного уравнения (неравенства или системы).
Отметим, что в том случае, когда ОДЗ заданного уравнения является множество всех действительных чисел, мы не всегда будем ее записывать (как не записывали ОДЗ при решении линейных или квадратных уравнений). И в других случаях главное — не записать ОДЗ в решение уравнения, а реально учесть ее при выполнении равносильных преобразований данного уравнения.
Например, для уравнения 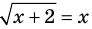 задается неравенством
задается неравенством 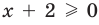 . Когда мы переходим к уравнению
. Когда мы переходим к уравнению  , то для всех его корней это уравнение является верным равенством. Тогда выражение
, то для всех его корней это уравнение является верным равенством. Тогда выражение 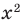 , стоящее в правой части этого равенства, всегда неотрицательно (
, стоящее в правой части этого равенства, всегда неотрицательно (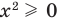 ), таким образом, и равное ему выражение
), таким образом, и равное ему выражение 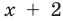 также будет неотрицательным:
также будет неотрицательным:  . Но это и означает, что ОДЗ данного уравнения (
. Но это и означает, что ОДЗ данного уравнения ( ) учтено автоматически для всех корней второго уравнения и поэтому при переходе от уравнения
) учтено автоматически для всех корней второго уравнения и поэтому при переходе от уравнения 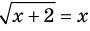 к уравнению
к уравнению 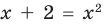 ОДЗ заданного уравнения можно не записывать в решение.
ОДЗ заданного уравнения можно не записывать в решение.
Для выполнения равносильных преобразований попробуем выделить общие ориентиры, аналогичные соответствующим ориентирам получения уравнений-следствий. Как указывалось выше, выполняя равносильные преобразования уравнений, необходимо учесть ОДЗ данного уравнения — это и есть первый ориентир для выполнения равносильных преобразований уравнений. По определению равносильности уравнений необходимо гарантировать, чтобы каждый корень первого уравнения был корнем второго и, наоборот, каждый корень второго уравнения был корнем первого. Для первой части этого требования мы уже выделили общий ориентир: достаточно гарантировать сохранение правильности равенства при переходе от первого уравнения ко второму.
Но тогда, чтобы выполнить вторую часть этого требования, достаточно второе уравнение рассмотреть как верное равенство (то есть взять такое значение переменной, которое является корнем второго уравнения) и гарантировать, что при переходе к первому верное равенство сохраняется (этот корень остается и корнем первого уравнения). Фактически из определения равносильности уравнений получаем, что каждое из равносильных уравнений является следствием другого уравнения). Таким образом, при выполнении равносильных преобразований мы должны гарантировать сохранение правильности равенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях — это и является вторым ориентиром для решения уравнений с помощью равносильных преобразований. (Соответствующие ориентиры схематически представлены в пункте 5 табл. 8.)
Например, чтобы решить с помощью равносильных преобразований уравнение 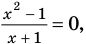 достаточно учесть его ОДЗ:
достаточно учесть его ОДЗ: 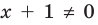 и условие равенства дроби нулю (дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю). Также следует обратить внимание на то, что на ОДЗ все необходимые преобразования можно выполнить как в прямом, так и в обратном направлениях с сохранением правильности равенства.
и условие равенства дроби нулю (дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю). Также следует обратить внимание на то, что на ОДЗ все необходимые преобразования можно выполнить как в прямом, так и в обратном направлениях с сохранением правильности равенства.
Запись решения в этом случае может быть такой:
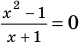 . ОДЗ:
. ОДЗ: 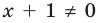 . Тогда
. Тогда 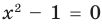 . Отсюда
. Отсюда 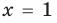 (удовлетворяет условию ОДЗ) или
(удовлетворяет условию ОДЗ) или 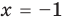 (не удовлетворяет условию ОДЗ).
(не удовлетворяет условию ОДЗ).
Для выполнения равносильных преобразований уравнений можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности уравнений обобщим также формулировки простейших теорем о равносильности, известных из курса алгебры 7 класса.
Теорема 1. Если из одной части уравнения перенести в другую часть слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве).
Теорема 2. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем уравнение, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований данного уравнения.
Замечание. Для обозначения перехода от данного уравнения к равносильному ему уравнению можно применять специальный значок  , но его использование при записи решений не является обязательным. Например, запись решения последнего из рассмотренных уравнений может быть такой.
, но его использование при записи решений не является обязательным. Например, запись решения последнего из рассмотренных уравнений может быть такой.
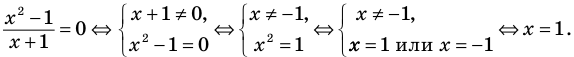
Пример №423
Решите уравнение 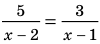 .
.
Решение:
► ОДЗ:  и
и 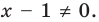
На этой ОДЗ данное уравнение равносильно уравнениям:
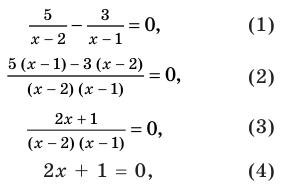
то есть 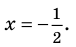
Учтем ОДЗ. При 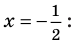
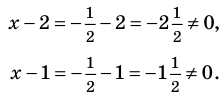
Таким образом, 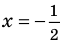 – корень.
– корень.
Ответ: 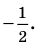
Используем равносильные преобразования для решения данного уравнения. Для этого необходимо учесть ОДЗ, поэтому зафиксируем ее ограничения в начале решения.
Укажем, что в уравнениях ограничения ОДЗ можно только зафиксировать, но не решать, а в конце проверить, выполняются ли эти ограничения для найденных корней.
При переносе члена данного уравнения из одной части уравнения в другую с противоположным знаком получаем уравнение (1), равносильное заданному.
Приводя к общему знаменателю, раскрывая скобки и приводя подобные члены, снова получаем верное равенство и можем обосновать, что при выполнении обратных действий равенство также не нарушается, таким образом, полученные уравнения (1)-(3) равносильны заданному (на его ОДЗ).
Дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю. Но второе условие уже учтено в ограничениях ОДЗ, таким образом, получаем уравнение (4), равносильное заданному уравнению на его ОДЗ. Поскольку все преобразования были равносильными только с учетом ОДЗ, то мы должны проверить, удовлетворяет ли полученное число ограничениям ОДЗ.
Причины появления посторонних корней и потери корней при решении уравнений
Наиболее типичные случаи появления посторонних корней и потери корней приведены в таблице 9. Там же указано, как в каждом из этих случаев получить правильное (или полное) решение.




Применение свойств функций к решению уравнений
1. Конечная ОДЗ
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения
Пример:
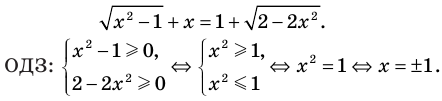
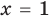 — корень (
— корень (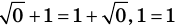 ),
),
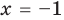 — не корень (
— не корень (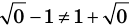 ).
).
2. Оценка левой и правой частей уравнения

Если надо решить уравнение вида 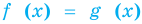 и выяснилось, что
и выяснилось, что  то равенство между левой и правой частями возможно тогда и только тогда, когда
то равенство между левой и правой частями возможно тогда и только тогда, когда  и
и 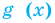 одновременно равны
одновременно равны 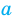
Пример:
►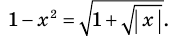
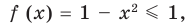
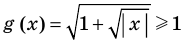 (так как
(так как 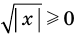 ).
).
Итак, заданное уравнение равносильно системе
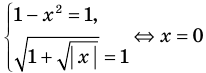
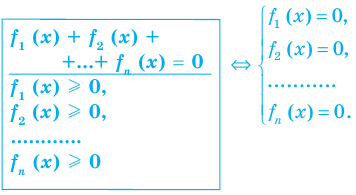
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю
Пример:
►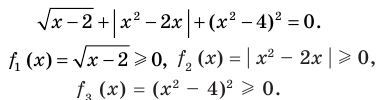
Итак, заданное уравнение равносильно системе
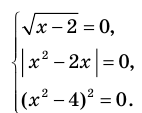
Из первого уравнения получаем 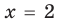 , что удовлетворяет всей системе
, что удовлетворяет всей системе
3. Использование возрастания и убывания функций
Схема решения уравнения
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку левой и правой частей уравнения)
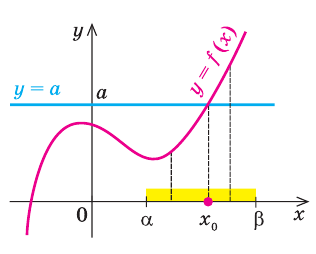
Теоремы о корнях уравнения
Если в уравнении 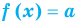 функция
функция 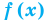 возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
Пример:
Уравнение 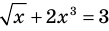 имеет единственный корень
имеет единственный корень 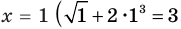 , то есть
, то есть 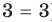 ), поскольку функция
), поскольку функция 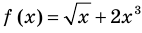 возрастает на всей области определения
возрастает на всей области определения 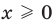
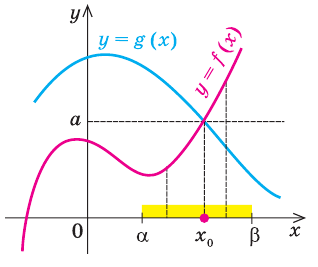
Если в уравнении 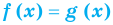 функция
функция 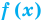 возрастает на некотором промежутке, а функция
возрастает на некотором промежутке, а функция 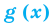 убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более чем один корень на этом промежутке.
убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более чем один корень на этом промежутке.
Пример:
Уравнение 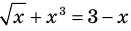 имеет единственный корень
имеет единственный корень 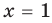 (
( 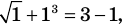 то есть
то есть 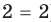 ), поскольку
), поскольку 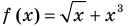 возрастает на всей области определения
возрастает на всей области определения  , a
, a 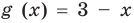 убывает (на множестве
убывает (на множестве 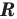 , а следовательно, и при
, а следовательно, и при 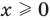 )
)
Объяснение и обоснование:
Конечная ОДЗ
Напомним, что в случае, когда дано уравнение 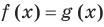 , общая область определения для функций
, общая область определения для функций 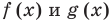 называется областью допустимых значений этого уравнения. Понятно, что каждый корень заданного уравнения принадлежит как области определения функции
называется областью допустимых значений этого уравнения. Понятно, что каждый корень заданного уравнения принадлежит как области определения функции 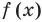 , так и области определения функции
, так и области определения функции 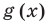 . Таким образом, каждый корень уравнения обязательно принадлежит ОДЗ этого уравнения. Это позволяет в некоторых случаях за счет анализа ОДЗ получить решение уравнения. Например, если дано уравнение
. Таким образом, каждый корень уравнения обязательно принадлежит ОДЗ этого уравнения. Это позволяет в некоторых случаях за счет анализа ОДЗ получить решение уравнения. Например, если дано уравнение 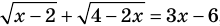 , то его ОДЗ можно записать с помощью системы
, то его ОДЗ можно записать с помощью системы 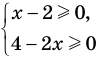 . Решая эту систему, получаем
. Решая эту систему, получаем 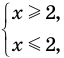 то есть
то есть  . Таким образом, ОДЗ данного уравнения состоит только из одного значения
. Таким образом, ОДЗ данного уравнения состоит только из одного значения  . Но если только для одного числа необходимо выяснить, является ли оно корнем данного уравнения, то для этого достаточно подставить это значение в уравнение. В результате получаем верное числовое равенство (
. Но если только для одного числа необходимо выяснить, является ли оно корнем данного уравнения, то для этого достаточно подставить это значение в уравнение. В результате получаем верное числовое равенство (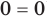 ). Следовательно,
). Следовательно,  — корень данного уравнения. Других корней у этого уравнения быть не может, поскольку все корни уравнения находятся в его ОДЗ, а там нет других значений, кроме
— корень данного уравнения. Других корней у этого уравнения быть не может, поскольку все корни уравнения находятся в его ОДЗ, а там нет других значений, кроме  .
.
Рассмотренный пример позволяет выделить ориентир для решения аналогичных уравнений:
если ОДЗ уравнения (а также неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Замечание. В том случае, когда ОДЗ — пустое множество (не содержит ни одного числа), мы можем сразу дать ответ, что данное уравнение не имеет корней.
Например, если необходимо решить уравнение 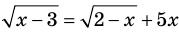 , то его ОДЗ задается системой
, то его ОДЗ задается системой 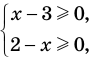 то есть системой
то есть системой 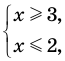 которая не имеет решений. Таким образом, ОДЗ данного уравнения не содержит ни одного числа, и поэтому это уравнение не имеет корней.
которая не имеет решений. Таким образом, ОДЗ данного уравнения не содержит ни одного числа, и поэтому это уравнение не имеет корней.
Оценка левой и правой частей уравнения
Некоторые уравнения можно решить с помощью оценки левой и правой частей уравнения.
Пусть дано уравнение 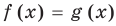 , и нам удалось выяснить, что для всех допустимых значений
, и нам удалось выяснить, что для всех допустимых значений 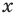 значение
значение 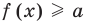 , а значение
, а значение 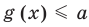 .
.
Рассмотрим два случая: 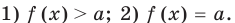
Если 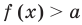 , то равенство
, то равенство 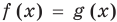 не может выполняться, потому что
не может выполняться, потому что 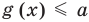 , то есть при
, то есть при 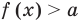 данное уравнение корней не имеет. Остается только случай
данное уравнение корней не имеет. Остается только случай 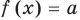 , но, учитывая необходимость выполнения равенства
, но, учитывая необходимость выполнения равенства 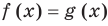 , имеем, что тогда и
, имеем, что тогда и 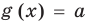 . Таким образом, мы обосновали, что выполнение равенства
. Таким образом, мы обосновали, что выполнение равенства 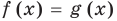 (при условии
(при условии 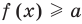 и
и 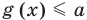 ) гарантирует одновременное выполнение равенств
) гарантирует одновременное выполнение равенств 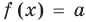 и
и 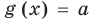 (и наоборот, если одновременно выполняются равенства
(и наоборот, если одновременно выполняются равенства 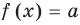 и
и 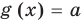 , то выполняется и равенство
, то выполняется и равенство 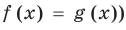 . Как было показано в п. 3.1, это и означает, что уравнение
. Как было показано в п. 3.1, это и означает, что уравнение 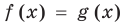 равносильно системе
равносильно системе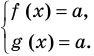
Коротко это можно записать так:
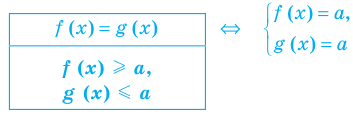
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 10.
Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения 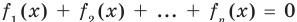 , в котором все функции-слагаемые неотрицательны
, в котором все функции-слагаемые неотрицательны 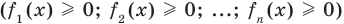 .
.
Если предположить, что 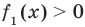 , то сумма всех функций, стоящих в левой части этого уравнения, может равняться нулю только тогда, когда сумма
, то сумма всех функций, стоящих в левой части этого уравнения, может равняться нулю только тогда, когда сумма  будет отрицательной. Но это невозможно, поскольку по условию все функции неотрицательные. Таким образом, при
будет отрицательной. Но это невозможно, поскольку по условию все функции неотрицательные. Таким образом, при 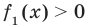 данное уравнение не имеет корней. Эти же рассуждения можно повторить для любой другой функции-слагаемого. Остается единственная возможность — все функции-слагаемые равны нулю (очевидно, что в этом случае равенство
данное уравнение не имеет корней. Эти же рассуждения можно повторить для любой другой функции-слагаемого. Остается единственная возможность — все функции-слагаемые равны нулю (очевидно, что в этом случае равенство 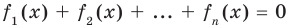 обязательно будет выполняться). Таким образом, сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю.
обязательно будет выполняться). Таким образом, сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю.
Например, чтобы решить уравнение 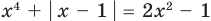 , достаточно перенести все члены в одну сторону, записать уравнение в виде
, достаточно перенести все члены в одну сторону, записать уравнение в виде 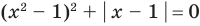 и учесть, что функции
и учесть, что функции 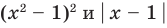 неотрицательные. Таким образом, данное уравнение равносильно системе
неотрицательные. Таким образом, данное уравнение равносильно системе 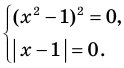
Из второго уравнения получаем 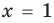 , что удовлетворяет и всей системе. Следовательно, данное уравнение имеет единственный корень
, что удовлетворяет и всей системе. Следовательно, данное уравнение имеет единственный корень 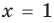 .
.
Использование возрастания и убывания функций к решению уравнений
Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения.
Полезно помнить специальные теоремы о корнях уравнения.
Теорема 1. Если в уравнении 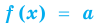 функция
функция 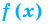 возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
возрастает (убывает) на некотором промежутке, то это уравнение может иметь не более чем один корень на этом промежутке.
Графически утверждение теоремы проиллюстрировано на рисунке 52. Прямая 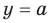 пересекает график возрастающей на промежутке
пересекает график возрастающей на промежутке 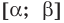 функции
функции 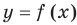 только в одной точке. Это и означает, что уравнение
только в одной точке. Это и означает, что уравнение 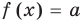 не может иметь больше одного корня на промежутке
не может иметь больше одного корня на промежутке 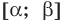 . Докажем это утверждение аналитически.
. Докажем это утверждение аналитически.
• Если на промежутке 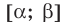 уравнение имеет корень
уравнение имеет корень 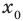 , то
, то 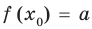 . Других корней быть не может, поскольку для возрастающей функции
. Других корней быть не может, поскольку для возрастающей функции 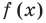 при
при 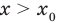 получаем неравенство
получаем неравенство 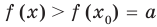 , а при
, а при 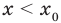 — неравенство
— неравенство 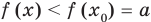 . Таким образом, при
. Таким образом, при 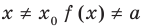 . Аналогично и для убывающей функции при
. Аналогично и для убывающей функции при 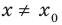 получаем
получаем 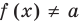 .
.
Теорема 2. Если в уравнении 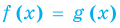 функция
функция 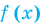 возрастает на некотором промежутке, а функция
возрастает на некотором промежутке, а функция 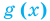 убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более чем один корень на этом промежутке.
убывает на этом же промежутке (или наоборот), то это уравнение может иметь не более чем один корень на этом промежутке.
Графически утверждение теоремы проиллюстрировано на рисунке 53.
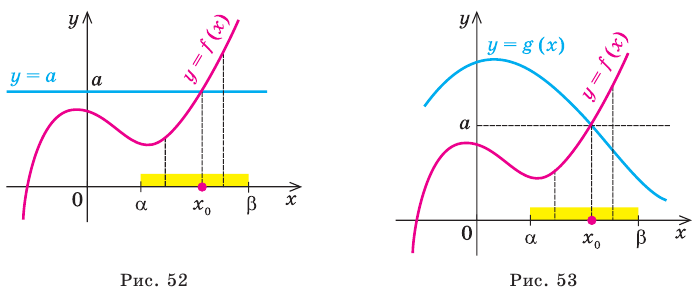
• Если на промежутке 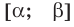 уравнение имеет корень
уравнение имеет корень 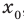 , то
, то 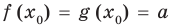 . Других корней быть не может, поскольку, например, для возрастающей функции
. Других корней быть не может, поскольку, например, для возрастающей функции 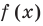 и убывающей функции
и убывающей функции 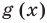 при
при 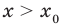 имеем
имеем 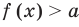 , a
, a 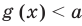 , таким образом,
, таким образом, 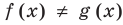 . Аналогично и при
. Аналогично и при 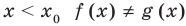 .
.
Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет.
Например, чтобы решить уравнение 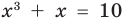 , достаточно заметить, что функция
, достаточно заметить, что функция 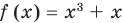 является возрастающей на всей числовой прямой (как сумма двух возрастающих функций) и что
является возрастающей на всей числовой прямой (как сумма двух возрастающих функций) и что  — корень
— корень 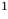 этого уравнения (
этого уравнения (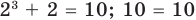 ). Таким образом, данное уравнение
). Таким образом, данное уравнение 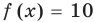 имеет единственный корень
имеет единственный корень 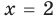 .
.
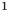 Корень
Корень  получен подбором. Как правило, подбор начинают с целых значений:
получен подбором. Как правило, подбор начинают с целых значений: 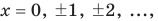 которые подставляются в данное уравнение.
которые подставляются в данное уравнение.
Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно.
Пример:
Решим с помощью теоремы 2 уравнение 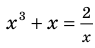 .
.
► Сначала следует учесть его ОДЗ: 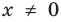 и вспомнить, что функция
и вспомнить, что функция 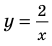 на всей области определения не является ни убывающей, ни возрастающей (п. 2.2), но она убывает на каждом из промежутков
на всей области определения не является ни убывающей, ни возрастающей (п. 2.2), но она убывает на каждом из промежутков 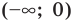 и
и 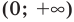 . Поэтому рассмотрим каждый из этих промежутков отдельно.
. Поэтому рассмотрим каждый из этих промежутков отдельно.
1) При 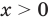 данное уравнение имеет корень
данное уравнение имеет корень 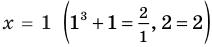 . Функция
. Функция 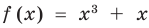 возрастает при
возрастает при  (как было показано выше, она возрастает на множестве
(как было показано выше, она возрастает на множестве 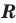 ), а функция
), а функция 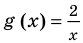 убывает на промежутке
убывает на промежутке  . Таким образом, данное уравнение
. Таким образом, данное уравнение 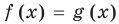 при
при 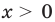 имеет единственный корень
имеет единственный корень 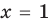 .
.
2) При 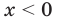 данное уравнение имеет корень
данное уравнение имеет корень 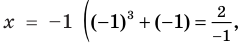
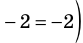 . Функция
. Функция 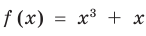 возрастает при
возрастает при 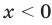 , а функция
, а функция 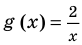 убывает на этом промежутке. Поэтому данное уравнение
убывает на этом промежутке. Поэтому данное уравнение 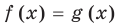 при
при 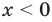 имеет единственный корень
имеет единственный корень 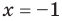 . В ответ следует записать все найденные корни (хотя на каждом из промежутков корень единственный, но всего корней — два). Итак, данное уравнение имеет только два корня: 1 и -1.
. В ответ следует записать все найденные корни (хотя на каждом из промежутков корень единственный, но всего корней — два). Итак, данное уравнение имеет только два корня: 1 и -1.
Примеры решения задач:
Пример №424
Решите уравнение 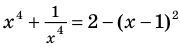 .
.
Решение:
► ОДЗ: 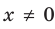 . На ОДЗ
. На ОДЗ 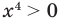 . Тогда функция
. Тогда функция 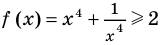 (как сумма двух взаимно обратных положительных чисел), а функция
(как сумма двух взаимно обратных положительных чисел), а функция 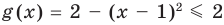 .
.
Таким образом, данное уравнение равносильно системе 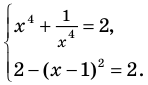 . Из второго уравнения системы получаем
. Из второго уравнения системы получаем  , что удовлетворяет и первому уравнению. Таким образом, система (а значит, и данное уравнение) имеет единственное решение
, что удовлетворяет и первому уравнению. Таким образом, система (а значит, и данное уравнение) имеет единственное решение  .
.
Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти.
Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ 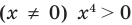 , то в левой части уравнения стоит сумма двух взаимно обратных положительных чисел, которая всегда больше или равна 2. В правой части из 2 вычитается неотрицательное число
, то в левой части уравнения стоит сумма двух взаимно обратных положительных чисел, которая всегда больше или равна 2. В правой части из 2 вычитается неотрицательное число 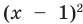 . Таким образом, при всех значениях
. Таким образом, при всех значениях 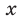 получаем значение, меньшее или равное 2. Равенство между левой и правой частями возможно тогда и только тогда, когда обе части равны 2.
получаем значение, меньшее или равное 2. Равенство между левой и правой частями возможно тогда и только тогда, когда обе части равны 2.
Пример №425
Решите систему уравнений 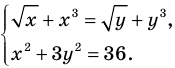
Решение:
► ОДЗ: 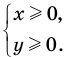 Рассмотрим функцию
Рассмотрим функцию 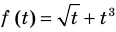 . На своей области определения
. На своей области определения 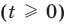 эта функция является возрастающей (как сумма двух возрастающих функций). Тогда первое уравнение заданной системы, которое имеет вид
эта функция является возрастающей (как сумма двух возрастающих функций). Тогда первое уравнение заданной системы, которое имеет вид 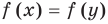 , равносильно уравнению
, равносильно уравнению 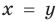 . Таким образом, на ОДЗ заданная система равносильна системе
. Таким образом, на ОДЗ заданная система равносильна системе 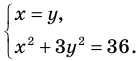
Подставляя 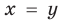 во второе уравнение системы, имеем
во второе уравнение системы, имеем 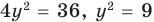 ,
, 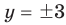 . Учитывая, что на ОДЗ
. Учитывая, что на ОДЗ  , получаем
, получаем 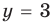 . Тогда
. Тогда 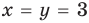 .
.
Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство 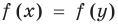 для возрастающей функции возможно тогда и только тогда, когда
для возрастающей функции возможно тогда и только тогда, когда 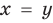 , поскольку возрастающая функция может принимать одинаковые значения только при одном значении аргумента. (Заметим, что такое же свойство будет иметь место и для убывающей функции.)
, поскольку возрастающая функция может принимать одинаковые значения только при одном значении аргумента. (Заметим, что такое же свойство будет иметь место и для убывающей функции.)
Замечание. Утверждение, обоснованное в комментарии к задаче 2, может быть использовано при решении аналогичных задач. Коротко его можно сформулировать так: если функция 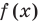 является возрастающей (или убывающей) на определенном множестве, то на этом множестве
является возрастающей (или убывающей) на определенном множестве, то на этом множестве 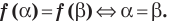
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/687140
http://www.evkova.org/uravnenie-opredelenie-i-vyichislenie-s-primerami-resheniya
[/spoiler]
Тригонометрические уравнения
-
Замена переменной и сведение к квадратному уравнению
-
Разложение на множители
-
Однородные уравнения
-
Введение дополнительного угла
-
Универсальная подстановка
-
Учет ОДЗ уравнения
-
Метод оценки
-
Тригонометрические уравнения повышенной сложности.
Приемы решения
В данной статье мы расскажем об основных типах тригонометрических уравнений и методах их решения. Тригонометрические уравнения чаще всего встречаются в задаче 12 ЕГЭ.
В вариантах ЕГЭ задача, где нужно решить уравнение, состоит из двух пунктов. Первый пункт – решение самого уравнения. Второй – нахождение его корней на некотором отрезке.
Некоторые из методов (например, замена переменной или разложение на множители) являются универсальными, то есть применяются и в других разделах математики. Другие являются специфическими именно для тригонометрии.
Необходимых формул по тригонометрии не так уж и много. Учите наизусть!
Тригонометрические формулы.
Любой метод решения тригонометрических уравнений состоит в том, чтобы привести их к простейшим, то есть к уравнениям вида sin x = a, cos x = a, tg x = a, ctg x = a.
Если вы не помните, как решать простейшие тригонометрические уравнения, — читайте материал на нашем сайте: Простейшие тригонометрические уравнения, часть 1.
О том, что такое арксинус, арккосинус, арктангенс и арккотангенс, — еще одна статья на нашем сайте: Простейшие тригонометрические уравнения,часть 2.
Теперь — сами методы. Теория и примеры решения задач.
к оглавлению ▴
Замена переменной и сведение к квадратному уравнению
Это универсальный способ. Применяется в любых уравнениях — степенных, показательных, тригонометрических, логарифмических, каких угодно. Замена не всегда видна сразу, и уравнение нужно сначала преобразовать.
1. а) Решите уравнение:
б) Найдите корни уравнения, принадлежащие отрезку
Решение:
а) Рассмотрим уравнение
Преобразуем его, применив основное тригонометрическое тождество:
Заменяя sin x на t, приходим к квадратному уравнению:
Решая его, получим:
Теперь вспоминаем, что мы обозначили за t. Первый корень приводит нас к уравнению
Оно не имеет решений, поскольку
Второй корень даёт простейшее уравнение
Решаем его:
б) Найдем корни уравнения на отрезке с помощью двойного неравенства.
Разделим обе части неравенства на
Вычтем из обеих частей неравенства:
Разделим на 2 обе части неравенства:
Единственное целое решение – это n=0. Тогда — это единственный корень, который принадлежит отрезку
Ответ:
2. а) Решите уравнение:
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение:
а)
Выразим косинус двойного угла по формуле
Получим:
Заменяя cosx на t, приходим к квадратному уравнению:
1)

2) нет решений, т. к.
Получим:
б) Отметим отрезок и найденные серии решений на единичной окружности.

Видим, что данному отрезку принадлежит только точка
Ответ: а)
б)
3. а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение:
а) Чтобы упростить уравнение применяем формулу приведения.
Так как получим:
Сделаем замену: Получим квадратное уравнение:
Сделаем обратную замену.
1) — нет решений, т. к.
2)
б) Найдем корни уравнения, принадлежащие отрезку , с помощью двойного неравенства.
Для серии решений получим:
Так как то
Для серии решений получим:
отсюда
У этого неравенства нет целых решенией, и значит, из второй серии ни одна точка в указанный отрезок не входит.
Ответ: а)
б)
к оглавлению ▴
Разложение на множители
Во многих случаях уравнение удаётся представить в таком виде, что в левой части стоит произведение двух или нескольких множителей, а в правой части — ноль. Произведение двух или нескольких множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю. Сложное уравнение, таким образом, распадается в совокупность более простых.
4. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке
Решение:
а) Применяем формулу синуса двойного угла:
Ни в коем случае не сокращайте на косинус! Ведь может случиться, что cos x обратится в нуль, и мы потеряем целую серию решений. Переносим всё в одну часть, и общий множитель выносим за скобки:
Полученное уравнение равносильно совокупности двух уравнений: cosx = 0 и 2sinx – 1 = 0.
Получим:
Все эти три серии решений являются ответом в части (а).
б) Отметим отрезок и найденные серии решений на единичной окружности.

Видим, что данному отрезку принадлежат точки
Ответ: а)
б)
5. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке
Решение:
Применим формулу суммы синусов:
Дальше действуем так же, как и в предыдущей задаче:
Решаем уравнение :
| (1) |
Решаем уравнение :
| (2) |
Ну что, перечисляем обе серии (1) и (2) в ответе через запятую? Нет! Серия (2) является в данном случае частью серии (1). Действительно, если в формуле (1) число n кратно 5, то мы получаем все решения серии (2).
Поэтому ответ в пункте (а):
б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:
Этот промежуток содержит 8 целых чисел: -2; -1; 0; 1; 2; 3; 4; 5.
Для каждого из этих n найдем x. Получим 8 решений на данном промежутке:
Ответ: а)
б)
6. В следующей задаче также применяется метод разложения на множители. Но это заметно не сразу.
а) Решите уравнение:
б) Найдите все корни уравнения на отрезке
Решение:
Используем формулу понижения степени:
Получаем:
Применяем формулу суммы косинусов:
Получаем:
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Уравнение равносильно совокупности:
б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:
1)
Решив неравенство, получим:
Так как n ∈ Z, получим для n целые значения: 0, 1, 2.
Им соответствуют решения:
2) Из серии решений на указанном отрезке лежит только корень
Но он уже входит в первую серию решений.
Можно также заметить, что вся вторая серия решений является подмножеством первой.
Ответ: а)
б)
к оглавлению ▴
Однородные уравнения
7. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке
Решение:
Такое уравнение называется однородным.
Степень каждого слагаемого в левой части равна двум. Точно так же, как в обычном многочлене степень каждого слагаемого равна двум. Мы помним, что степень одночлена — это сумма степеней входящих в него сомножителей.
Для однородных уравнений существует стандартный приём решения — деление обеих его частей на .
Возможность этого деления, однако, должна быть обоснована: а что, если косинус равен нулю?
Следующий абзац предлагаем выучить наизусть и всегда прописывать его при решении однородных уравнений.
Предположим, что cosx = 0. Тогда в силу уравнения и sinx = 0, что противоречит основному тригонометрическому тождеству. Следовательно, любое решение данного уравнения удовлетворяет условию cosx 0, и мы можем поделить обе его части на
.
В результате деления приходим к равносильному квадратному уравнению относительно тангенса:
Сделаем замену: получим:
б) Отметим отрезок и найденные серии решений на единичной окружности.
О том, как отметить на единичной окружности точки из первой серии решений, то есть арктангенс минус трех, читайте здесь: Простейшие тригонометрические уравнения, часть 2.

Видим, что данному отрезку принадлежат точки:
Ответ: а)
б)
8. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке
Если бы в правой части стоял нуль, уравнение было бы однородным. Мы поправим ситуацию изящным приёмом: заменим число 3 на выражение
Получили однородное уравнение второй степени.
Так как не существует такой точки на единичной окружности, в которой одновременно синус и косинус равнялись бы нулю, мы разделим обе части уравнения на .
Получим:
Выполним замену: tgx = y, получим:
Обратная замена:
Ответом в пункте (а) являются две серии решений.
б) Найдем корни уравнения, принадлежащие отрезку с помощью единичной окружности. Для этого отметим на ней данный отрезок и найденные серии решений.

Видим, что данному отрезку принадлежит только точка
Ответ: а)
б)
к оглавлению ▴
Введение дополнительного угла
Этот метод применяется для уравнений вида acosx + bsinx=c. Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа a и b являются значениями синуса и косинуса углов в 30°, 45° или 60°.
9. а) Решим уравнение:
б) Найдите все корни уравнения на отрезке
Решение:
Делим обе части на 2:
Замечаем, что
В левой части получили синус суммы:
отсюда
б) Отметим на единичной окружности отрезок и найденные серии решений.
Обратите внимание, что в этой задаче отрезок больше, чем полный круг. Как нам поступить? Один из способов – нарисовать рядом две окружности.

Видим, что данному отрезку принадлежат точки:
Ответ: а)
б)
Другой пример.
10. а) Решите уравнение:
б) Найдите все корни уравнения на отрезке
Решение:
Делим обе части на
Сделаем теперь для разнообразия в левой части косинус разности:
б) Найдем корни уравнения, принадлежащие отрезку с помощью единичной окружности. Отметим на ней данный отрезок и найденные серии решений.

Видим, что данному отрезку принадлежат точки 0 и
Ответ: а)
б)
Покажем, как применяется метод введения дополнительного угла в общем случае.
Рассмотрим уравнение
Делим обе части на
| (4) |
Для чего мы выполнили это деление? Всё дело в получившихся коэффициентах при косинусе и синусе. Легко видеть, что сумма их квадратов равна единице:
Это означает, что данные коэффициенты сами являются косинусом и синусом некоторого угла :
Соотношение (4) тогда приобретает вид:
или
Исходное уравнение сведено к простейшему. Теперь понятно, почему рассматриваемый метод называется введением дополнительного угла. Этим дополнительным углом как раз и является угол
к оглавлению ▴
Универсальная подстановка
Запомним две важные формулы:

Их ценность в том, что они позволяют выразить синус и косинус через одну и ту же функцию — тангенс половинного угла. Именно поэтому они получили название универсальной тригонометрической подстановки.
Единственная неприятность, о которой не надо забывать: правые части этих формул не определены при  . Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.
. Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.
11. а) Решите уравнение: 
б) Найдите все корни уравнения на отрезке
Решение:
Выражаем  , используя универсальную тригонометрическую подстановку:
, используя универсальную тригонометрическую подстановку:

Делаем замену  :
:

Получаем кубическое уравнение:


Оно имеет единственный корень  .
.
Стало быть,  , откуда
, откуда  .
.
Сужения ОДЗ в данном случае не было, так как уравнение с самого начала содержало  .
.
б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:
Получим, что
Ответ: а)
б)
Универсальная тригонометрическая подстановка может также пригодиться при решении задач по планиметрии из второй части ЕГЭ. Поэтому формулы лучше выучить.
к оглавлению ▴
Учет ОДЗ уравнения
12. а) Рассмотрим уравнение: 
б) Найдите все корни уравнения на отрезке
Решение:
Перепишем уравнение в виде, пригодном для возведения в квадрат:

Тогда наше уравнение равносильно системе:

Решаем уравнение системы:
 ,
,
 ,
,

Второе уравнение данной совокупности не имеет решений, а первое даёт две серии:

Теперь нужно произвести отбор решений в соответствии с неравенством  . Серия
. Серия  не удовлетворяет этому неравенству, а серия
не удовлетворяет этому неравенству, а серия  удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия
удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия  .
.
Ответ в пункте (а):  .
.
б) Найдем корни уравнения, принадлежащие отрезку с помощью двойного неравенства:
Неравенство имеет единственное целое решение
Тогда
Ответ: а)
б)
Мы рассмотрели основные методы решения тригонометрических уравнений, которые применяются в задаче 12 ЕГЭ.
Где же еще нам могут встретиться тригонометрические уравнения? Конечно, в задачах с параметрами. Или на олимпиадах по математике. Сейчас мы увидим еще несколько полезных приемов решения.
к оглавлению ▴
Метод оценки
В некоторых уравнениях на помощь приходят оценки  .
.
13. Рассмотрим уравнение: 
Так как оба синуса не превосходят единицы, данное равенство может быть выполнено лишь в том случае, когда они равны единице одновременно:

Таким образом, должны одновременно выполняться следующие равенства:

Обратите внимание, что сейчас речь идёт о пересечении множества решений (а не об их объединении, как это было в случае разложения на множители). Нам ещё предстоит понять, какие значения x удовлетворяют обоим равенствам. Имеем:

Умножаем обе части на 90 и сокращаем на π:
 ;
;
 ;
;

Правая часть, как видим, должна делиться на 5. Число n при делении на 5 может давать остатки от 0 до 4; иначе говоря, число n может иметь один из следующих пяти видов: 5n, 5m + 1, 5m + 2, 5m + 3 и 5m + 4, где . Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.
. Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.
Искать k, в принципе, уже не нужно. Сразу находим x:

Ответ: 
14. Рассмотрим уравнение: 
Ясно, что данное равенство может выполняться лишь в двух случаях: когда оба синуса одновременно равны 1 или −1. Действуя так, мы должны были бы поочерёдно рассмотреть две системы уравнений.
Лучше поступить по-другому: умножим обе части на 2 и преобразуем левую часть в разность косинусов:
 ;
;

Тем самым мы сокращаем работу вдвое, получая лишь одну систему:

Имеем:

Ищем пересечение:

Умножаем на 21 и сокращаем на π:

Данное равенство невозможно, так как в левой части стоит чётное число, а в правой — нечётное.
Ответ: решений нет.
Это был тренировочный пример. А в задачах ЕГЭ решения есть всегда.
Посмотрите, как применяется метод оценки в задачах с параметрами.
15. Страшное с виду уравнение  также решается методом оценок.
также решается методом оценок.
В самом деле, из неравенства  следует, что
следует, что  .
.
Следовательно,  , причём равенство возможно в том и только в том случае, когда
, причём равенство возможно в том и только в том случае, когда
Остаётся решить полученную систему. Это не сложно.
Перенесем в левую часть и вынесем общий множитель за скобки , получим:
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл.
Каждое уравнение равносильно совокупности:
Это значит, что синус угла х равен нулю, а его косинус равен 0, 1 или -1.
Или синус угла х равен 1, а косинус этого угла равен 0, 1 или -1.
Такие углы легко найти на тригонометрическом круге. Найденные серии решений запишем в ответ.
Ответ:
к оглавлению ▴
Тригонометрические уравнения повышенной сложности.
Приемы решения
16. Рассмотрим такое уравнение: 
Сделаем замену  .
.
Как выразить  через t? Имеем:
через t? Имеем:
 ,
,
откуда  . Получаем:
. Получаем:
Начнем со второго уравнения.
Так как и
то их сумма может быть равна 2, только оба слагаемых равны 1. Но на единичной окружности не существует точки, в которой одновременно синус и косинус равен единице. Значит, второе уравнение корней не имеет.
Решим первое уравнение методом введения дополнительного угла.
Для этого разделим обе части уравнения на и получим:
Ответ:
17. Помним формулы косинуса и синуса тройного угла:
 ,
,

Вот, например, уравнение:

Оно сводится к уравнению относительно  :
:
 ,
,
 ,
,

Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом имеет смысл. Уравнение равносильно совокупности:
Решим второе уравнение с помощью замены sinx = t.
Получим: или
Обратная замена:
А решением первого уравнения sinx = 0 являются числа вида
Ответ:
Интересно, что формулы синуса и косинуса тройного угла также могут пригодиться вам в решении задач по планиметрии из второй части ЕГЭ.
18. Как бороться с суммой четвёртых степеней синуса и косинуса?
Рассмотрим уравнение: 
Выделяем полный квадрат!
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

19. А как быть с суммой шестых степеней?
Рассмотрим такое уравнение: 
Раскладываем левую часть на множители как сумму кубов:  .
.
Получим:
 ;
;

С суммой четвёртых степеней вы уже умеете обращаться.
Мы рассмотрели основные методы решения тригонометрических уравнений. Знать их нужно обязательно, это — необходимая база.
В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Это приходит только с опытом. Именно этому мы и учим на наших занятиях.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Тригонометрические уравнения» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Автор проекта:
Шелкова Полина,
Класс: 10Руководитель:
Злобова Людмила Викторовна,
учитель математики
ВВЕДЕНИЕ
Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον – «тригон» – треугольник и μετρειν – «метрео» – измеряю).
Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.
Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.
Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.
I РАЗДЕЛ (теоретический)
Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?
- Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
- Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
- Тригонометрические уравнения включены в КИМы ЕГЭ по математике.
Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку – это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.
Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.
Задачи:
- познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
- изучить соответствующую литературу;
- научиться решать тригонометрические уравнения;
- найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
- научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
- подготовиться к ЕГЭ по математике.
Приёмы отбора корней тригонометрического уравнения на заданном промежутке.
При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.
Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.
Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.
Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.
Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.
II РАЗДЕЛ (практический)
Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:
sinx=cos2x;
sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos2x−sin2x]
sinx−(cos2x−sin2x)=0;
sinx−(1−sin2x−sin2x)=0;
sinx−(1−2sin2x)=0;
2sin2x+sinx−1=0.
Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим
2t2+t-1=0
D=b2-4ac, т.е. D=9
t1 = -1, t2 = ½.
Вернемся к замене:
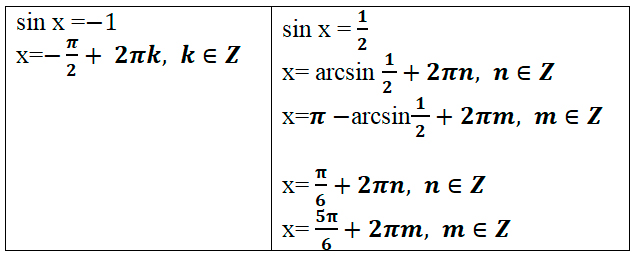
б) Рассмотрим три способа отбора корней, попадающих в отрезок 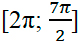 .
.
1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:
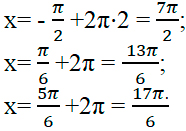
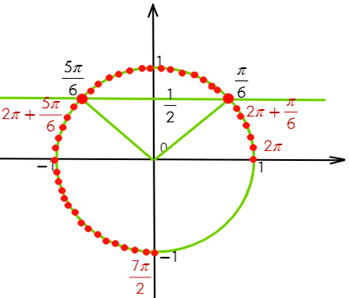
2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни: 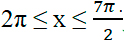

3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.
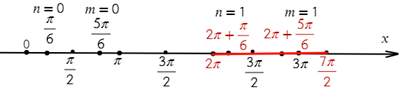
Нам останется только выбрать корни, которые попали в нужный нам отрезок.
Ответ:
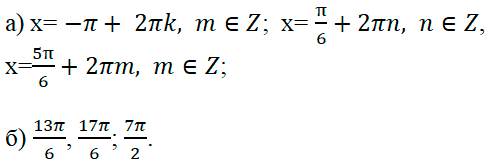
(Более подробный пример в приложении №1)
ЗАКЛЮЧЕНИЕ
При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем – небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.
СПИСОК ЛИТЕРАТУРЫ
- Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
- Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова – М. Просвещение, 2017.
- С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных – М: Издательство: «Экзамен», 2005.
- Корянов А.Г., Прокофьев А.А. – Тригонометрические уравнения: методы решения и отбор корней. – М.: Математика ЕГЭ, 2012.
Электронные ресурсы
- https://ru.wikipedia.org/wiki/Тригонометрия
- https://www.yaklass.ru/p/ege/matematika/podgotovka-k-ege-po-matematike-profilnyi-uroven-10744/trigonometricheskie-uravneniia-s-ogranicheniiami-zadacha-13-536475/re-a4b9cc95-fe96-40c2-b70c-f46548b726a0
- https://mat.1sept.ru/1999/no19.htm
- https://math-ege.sdamgia.ru/
- https://alexlarin.net/ege21.html
- https://www.academia.edu/10962821/МАТЕМАТИКА_ЕГЭ_2012_Тригонометрические_уравнения_методы_решений_и_отбор_корней_типовые_задания_С1
- http://teacher-andreeva.ru/wp-content/uploads/2016/03/тригоном-ур-я.pdf
- https://reshimvse.com/article.php?id=100
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Корень уравнения принадлежит промежутку
|
|||
|
Даны промежутки:
|
||
| Вернуться к началу |
|
||
|
sibiryk |
Заголовок сообщения: Re: Корень уравнения принадлежит промежутку
|
|
Мое решение: [math]begin{gathered}(3x + 1) times (x – 6) = (3x + 1) times (3x + 1) hfill \ x – 6 = 3x + 1 hfill \ – 2x = 7 hfill \ x = – 3,5 hfill \ end{gathered}[/math] Соответственно верный ответ: 1.
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Указать интервал которому принадлежит корень уравнения
в форуме Исследование операций и Задачи оптимизации |
faunasie |
1 |
358 |
27 ноя 2018, 14:34 |
|
Корень уравнения
в форуме MathCad |
Genya_111 |
1 |
195 |
19 дек 2021, 16:30 |
|
Странный корень уравнения
в форуме Линейная и Абстрактная алгебра |
AlexSam |
4 |
587 |
08 мар 2015, 10:54 |
|
Найдите корень уравнения
в форуме Начала анализа и Другие разделы школьной математики |
VICTORQQQQ |
2 |
337 |
28 фев 2017, 16:36 |
|
Найти корень уравнения
в форуме Тригонометрия |
vitgon |
5 |
427 |
13 ноя 2015, 12:14 |
|
Найти корень уравнения
в форуме Алгебра |
VICTORQQQQ |
2 |
363 |
28 фев 2017, 19:32 |
|
Лишний корень уравнения
в форуме Начала анализа и Другие разделы школьной математики |
Zhihar |
4 |
930 |
09 сен 2015, 15:56 |
|
Найти корень уравнения
в форуме Алгебра |
Blamere |
6 |
566 |
27 ноя 2013, 15:37 |
|
Найти корень уравнения
в форуме Алгебра |
demeopami |
5 |
210 |
20 май 2020, 16:37 |
|
Найти корень логарифмического уравнения
в форуме Алгебра |
SMOTRA |
2 |
417 |
30 май 2013, 13:05 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |




