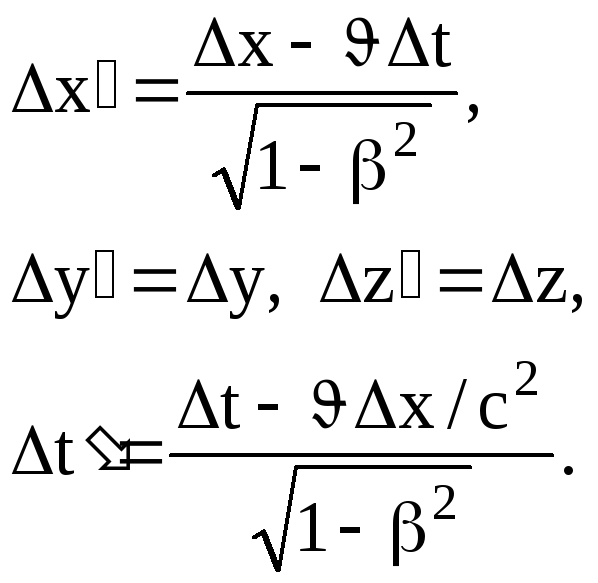Как найти интервал между событиями

Как найти интервал между событиями

У этого термина существуют и другие значения, см. Интервал.

Интервал в теории относительности — аналог расстояния между двумя событиями в пространстве-времени, являющийся обобщением евклидового расстояния между двумя точками. Интервал лоренц-инвариантен, то есть не меняется при переходе от одной инерциальной системы отсчёта к другой, и, даже более, является инвариантом (скаляром) в специальной и общей теории относительности.

Это свойство интервала делает его фундаментальным понятием, на основе которого может, в соответствии с принципом относительности, быть осуществлена ковариантная формулировка физических законов. В частности, преобразования Лоренца (преобразования координат, включая время, оставляющие неизменной запись всех фундаментальных уравнений физики при замене системы отсчёта) могут быть формально найдены как группа преобразований, сохраняющих интервал инвариантным.

Инвариантность интервала послужила основой для введения пространства Минковского, в котором смене инерциальных систем отсчёта соответствуют «вращения» этого пространства, что явилось первой явной формулировкой концепции пространства-времени.

Определение[править | править код]

Квадрат интервала — это симметричная билинейная форма на конфигурационном 4-мерном многообразии пространства-времени. При должным образом выбранных координатах (галилеевых — локально инерциальная система отсчёта с декартовыми пространственными координатами x,y,z и временем t) для бесконечно малого смещения в пространстве-времени он имеет вид

{displaystyle ds^{2}=c^{2},dt^{2}-dx^{2}-dy^{2}-dz^{2}}

(локально псевдоевклидово пространство-время, пространство Минковского в главном порядке, иначе говоря — многообразие с индефинитной псевдоримановой метрикой сигнатуры (+−−−)).

В случае плоского пространства-времени — то есть пространства времени без кривизны, к которому в современной физике относится случай отсутствия (или пренебрежимой малости) гравитации — такое же выражение имеет место и для конечных разностей координат:

{displaystyle s^{2}=c^{2}(Delta t)^{2}-(Delta x)^{2}-(Delta y)^{2}-(Delta z)^{2}}

(такое пространство уже точно и глобально является пространством Минковского, если, конечно, топологически оно эквивалентно {displaystyle mathbb {R} ^{4}} в своей естественной топологии).

Обычно интервал обозначается латинской буквой s.

В общей теории относительности используется обобщённое понятие интервала, дающее естественное обобщение расстояния между двумя точками. Вводится метрический тензор {displaystyle g_{ik}}, от которого требуется лишь симметричность и невырожденность. Выражение для квадрата интервала между двумя бесконечно близкими точками приобретает вид

{displaystyle ds^{2}=g_{ij},dx^{i},dx^{j},quad i,j=0dots 3,quad x^{0}=ct, x^{1}=x, x^{2}=y, x^{3}=z,}

где dx^{i} — дифференциалы координат, и по повторяющимся индексам подразумевается суммирование, то есть это выражение означает

{displaystyle sum _{i,j=0}^{3}g_{ij},dx^{i},dx^{j}.}

Обратим внимание, что таким образом определённая метрика не будет положительно определённой квадратичной формой, как обычно требуется в случае собственно римановых многообразий. Напротив, подразумевается, что всегда или почти всегда локально могут быть так выбраны пространственно-временные координаты {displaystyle t,x,y,z} (система отсчёта), что интервал для малой области пространства-времени в этих координатах запишется так же, как он записывается для лоренцевских координат (систем отсчёта) в плоском пространстве Минковского:

{displaystyle ds^{2}=c^{2},dt^{2}-dx^{2}-dy^{2}-dz^{2},}

так что через точку пространства-времени проходит бесконечно много линий, имеющих нулевую «длину» (при определении длины в пространстве-времени через его «физическую метрику» — то есть, как интеграл от {displaystyle {sqrt {dx^{2}+dy^{2}+dz^{2}-c^{2},dt^{2}}}}) — образующих световой конус; бесконечно много линий, длина которых вещественна — они все во внутренней области светового конуса; и бесконечно много тех, длина которых чисто мнима — вблизи данной точки они все во внешней области светового конуса с вершиной в ней, если они гладки.

  • Знак квадрата интервала — предмет соглашения. Он может быть выбран (и исторически был) противоположным. В наше время, пожалуй, чаще используется выбор знака как выше в этой статье. Однако иногда противоположный удобнее, если используется введённая Минковским и нередко удобная интерпретация временно́й координаты как чисто мнимой.
  • Нумерация координат x^i — также предмет соглашения, однако в современной литературе чаще всего они нумеруются как и здесь — от 0 до 3, причём временно́й координате приписывается индекс 0.
  • В теоретических построениях, использующих пространство-время большей размерности, определение интервала естественным образом обобщается добавлением в сумму ещё некоторого количества пространственных координат. При этом чаще всего (хотя не всегда) предполагается, что временна́я координата остаётся единственной, то есть обычно только одно слагаемое входит со знаком, противоположным всем остальным.
  • Многообразие с заданным на нём невырожденным интервалом (или, другими словами, невырожденной метрикой) называется псевдоримановым, точнее — собственно псевдоримановым, чтобы подчеркнуть отличие от риманова многообразия, в котором метрика — в отличие от интервала — положительно определённая, как и обычное евклидово расстояние.
  • Определения интервала несколько различаются в специальной и общей теории относительности. Это связано с тем, что интервал между двумя произвольными точками пространства-времени Минковского можно ввести, не сталкиваясь с трудностями, как длину соединяющей их прямой линии (геодезической), как это и сделано выше. Однако для общего вида искривлённого пространства-времени этого уже сделать так просто нельзя, так как точки могут соединяться несколькими различными геодезическими (или даже бесконечным их числом). Поэтому интервал в общей теории относительности определяют обычно в бесконечно малой окрестности заданной точки, где исходящие из неё различные геодезические ещё не пересекаются, а расстояние по геодезическим линиям от одной точки до другой называют мировой функцией.

Инвариантность интервала в специальной теории относительности[править | править код]

Используемые постулаты[править | править код]

Напрямую из принципа относительности, однородности и изотропности пространства, а также однородности времени следует, что при переходе от одной ИСО (инерциальной системы отсчёта) к другой ИСО интервал остаётся неизменным. Именно это его свойство позволяет формально вывести преобразования Лоренца и обосновывает оправданность введения пространства Минковского и неримановой метрики.

Инвариантность скорости света здесь имеет значение потому, что известно, что скорость света всегда одинакова хотя бы в одной системе отсчёта, а из этого и из принципа относительности следует, что она должна быть такой же в любой ИСО. Однако вместо скорости света можно было бы взять максимальную скорость движения тел или распространения взаимодействий, которая также, из принципа относительности, должна быть одинакова во всех инерциальных системах отсчёта. Если максимальная скорость распространения взаимодействий конечна, она, вследствие принципа относительности, должна совпадать со скоростью света, которую будем здесь обозначать, как обычно, c.

Для приводимого ниже доказательства существенно, что мы будем считать все изменения пространственных координат и времени малыми (бесконечно малыми), то есть всё будет формулировано для интервала между двумя бесконечно близкими в пространстве и времени событиями.

Доказательство[править | править код]

Вероятно, учитывая некоторые подводные камни, отмеченные в примечаниях, в доказательстве из учебника Ландау, приводимом ниже, проще всего сначала получить в явном виде преобразования Лоренца, из которых инвариантность интервала элементарно следует.

Сначала покажем, что если интервал между двумя событиями равен нулю в одной ИСО, то он равен нулю в любой ИСО. Действительно, пусть в ИСО K событие 1 произошло в точке {displaystyle x_{1},y_{1},z_{1}} в момент времени t_{1}, а событие 2 — в точке {displaystyle x_{2},y_{2},z_{2}} в момент t_{2}. По условию интервал между ними равен 0, то есть

{displaystyle c^{2}(t_{1}-t_{2})^{2}-(x_{1}-x_{2})^{2}-(y_{1}-y_{2})^{2}-(z_{1}-z_{2})^{2}=0.}

Это значит, что если из точки 1 испустить в точку 2 сигнал, движущийся со скоростью света, то он окажется в точке 2 через время {displaystyle t_{2}-t_{1}}. Но, из-за инвариантности скорости света, для событий 1 и 2, рассматриваемых в системе отсчёта K’, можно записать аналогично

{displaystyle c^{2}(t_{1}^{'}-t_{2}^{'})^{2}-(x_{1}^{'}-x_{2}^{'})^{2}-(y_{1}^{'}-y_{2}^{'})^{2}-(z_{1}^{'}-z_{2}^{'})^{2}=0.}

Это и доказывает, что равенство интервала нулю не зависит от ИСО.

Для дальнейшего вспомним, что мы рассматриваем интервал между бесконечно близкими событиями, следовательно, он должен быть бесконечно малой величиной. В силу однородности и изотропности пространства и однородности времени при смене ИСО новый интервал может быть лишь функцией старого интервала и скорости новой ИСО в старой ИСО, он не может зависеть от координат точки или момента времени. При смене ИСО к интервалу не может прибавляться слагаемое, не зависящее от интервала в старой ИСО, так как если в одной ИСО интервал равен 0, то и в другой ИСО он тоже 0. Значит, оба интервала будут бесконечно малы. Так как интервалы бесконечно малы, то они должны быть пропорциональны[1], как бесконечно малые одного порядка, учитывая, что один из них обращается в ноль тогда и только тогда, когда и второй, как мы уже выяснили вначале. Значит, при смене ИСО интервал преобразуется по правилу

{displaystyle ds_{2}^{2}=k({vec {V}}),ds_{1}^{2}.}

В силу изотропности пространства k не может зависеть от направления скорости, только от её модуля.

Это означает[2], что рассмотрев изменение интервала при переходе от системы 1 к системе 2, а потом обратно, учитывая, что V одинаково для прямого и обратного преобразования из изотропности пространства и принципа относительности (вторая система выглядит из первой ничем не отличимо от того, как первая система выглядит из второй), имеем

{displaystyle ds_{2}^{2}=K(V),ds_{1}^{2},}
{displaystyle ds_{1}^{2}=K(V),ds_{2}^{2},}

а следовательно (так как {displaystyle ds_{1}=ds_{1}})

{displaystyle K^{2}(V)=1}

для любого V.

Осталось отбросить случай K = −1. Это можно сделать рассмотрев три ИСО и изменение интервала между ними. Делая последовательный переход от первой СО к третьей, через вторую, имеем

{displaystyle ds_{3}^{2}=K^{2},ds_{1}^{2},}

а для прямого перехода сразу из первой в третью:

{displaystyle ds_{3}^{2}=K,ds_{1}^{2}.}

Отсюда видно, что {displaystyle K^{2}=K}, и следовательно остается лишь вариант

{displaystyle k(V)=1}

для любого V, то есть интервал не меняется при смене ИСО.

В заключение можно заметить, что из инвариантности бесконечно малых интервалов следует и инвариантность конечных, так как последние получаются простым интегрированием бесконечно малых.

Смысл знака квадрата интервала[править | править код]

  • Если {displaystyle ds^{2}geqslant 0}, то интервал называется времениподобным. Времениподобный интервал между событиями означает, что существует такая система отсчёта, в которой оба события произошли в одном и том же месте. Что ещё более важно, времениподобный интервал между событиями означает, что они могут быть причинно связаны. Легко убедиться, что для причинно связанных событий {displaystyle ds^{2}geqslant 0}, так как любое взаимодействие распространяется со скоростью не большей c, причём {displaystyle ds=0} соответствует событиям, связанным сигналом, распространяющимся со скоростью света. Этот сигнал не обязан быть именно световым, это может быть гравитационная волна, вообще любая безмассовая частица или даже ещё не открытое взаимодействие. Существенно лишь, что существует максимальная скорость распространения взаимодействия, одинаковая для всех систем отсчёта и равная, как следует из уравнений Максвелла, скорости света.
  • Если {displaystyle ds^{2}leqslant 0}, то интервал называется пространственноподобным, и значит можно выбрать такую инерциальную систему отсчёта, в которой оба события произошли в одно и то же время. События, интервал между которыми пространственноподобен, как указано выше, не могут быть причинно связанными, так как даже распространяющийся по прямой сигнал должен бы был для этого двигаться быстрее скорости света.
  • Если же {displaystyle ds^{2}=0}, то интервал называется светоподобным (иногда изотропным или нулевым). Направления в пространстве Минковского, вдоль которых интервал равен 0, называются изотропными. Также изотропными называются многообразия, для которых форма ds^2 тождественно равна 0. Свет распространяется всегда вдоль изотропных направлений.

Замечание. Поскольку инвариантен сам интервал, то, очевидно, знак его квадрата тоже оказывается инвариантным. Поэтому классификация интервалов по этому признаку, приводимая здесь, не зависит от системы отсчёта.

См. также[править | править код]

  • 4-импульс
  • Мировая линия
  • Собственная длина

Примечания[править | править код]

  1. ↑
    Это место в доказательстве, приводимом в учебнике Ландау и Лифшица, довольно нетривиально при кажущейся простоте. Возможно, Ландау с его любовью к шуткам решил здесь проверить, насколько читатели хорошо понимают изложение, с виду простое, но содержащее незаметные подводные камни. Хотя, конечно, в каком-то смысле рассматриваемое утверждение должно быть верным, исходя хотя бы из верного результата доказательства. Однако детальное рассмотрение того, почему коэффициент оказывается просто числом, не зависящим, например, от угла между вектором скорости и вектором, соединяющим точки событий, интервал между которыми рассматривается, в этом доказательстве опущено: его предлагается восстановить читателю.
  2. ↑
    С этого места доказательство несколько упрощено по сравнению с доказательством Ландау, однако если принять за доказанное то, что уже доказано до этого момента, согласно изложению Ландау, последующего достаточно.

Литература[править | править код]

  • Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
Источник

Преобразования
Лоренца и следствия из них приводят к
выводу об
относительности
длин и промежутков времени, значение
которых в
раз­личных
системах отсчета разное.

В
то же время относительный характер длин
и промежутков времени в теории Эйнштейна
означает относительность отдельных
компонентов какой-то реальной физической
величины, не зависящей от системы
от­счета, т.е. являющейся инвариантной
по отношению к преобразовани­ям
координат. В четырехмерном пространстве
Эйнштейна, в котором каждое событие
характеризуется четырьмя координатами
(х, у,
z
, t),
такой физической величиной является
интервал
между двумя событиями:

,
(7.15)

где,
– расстояние между точками обычного
трехмерного пространства, в котором
эти события
произошли. Введя обозначение t12
=t2
–t1
, получим

.

Покажем,
что интервал между двумя событиями
одинаков во
всех
инерциальных системах отсчета. Обозначив

t=t2
–t1,

,

,

,

выражение (7.15)
можно записать в виде

.

Интервал между
теми же событиями в системе К’ равен

.

(7.16)

Согласно
преобразованиям Лоренца (7.8),

Подставив
эти значения в (7.16), после элементарных
преобразований получим, что
,
т.е. (S’12)=S12

Обобщая полученные
результаты, можно сделать вывод, что
интервал, определяя пространственно-временные
соотношения между событи­ями, является
инвариантом при переходе от одной
инерциальной сис­темы отсчета к
другой. Инвариантность интервала
означает, что, несмот­ря на относительность
длин и промежутков времени, течение
событий носит объективный характер и
не зависит от системы отсчета.

Теория относительности,
таким образом, сформулировала новое
представление о пространстве и времени,
обобщенное далее в диалекти­ческом
материализме. Пространственно-временные
отношения являются не абсолютными
величинами, как утверждала механика
Галилея-Ньютона, а относительными.
Следовательно, представления об
абсолютном пространстве и времени
являются несостоятельными. Кроме того,
инва­риантность интервала между двумя
событиями свидетельствует о том, что
пространство и время органически связаны
между собой и образуют единую форму
существования материи – пространство
– время.

Пространство и
время не существуют вне материи и
независимо от нее. Дальнейшее развитие
относительности (общая теория
относительности) показало, что свойства
пространства-времени в данной области
определяются действующими в ней полями
тяготения.

7.6. Основной закон релятивистской динамики материальной точки

Согласно
представлениям классической механики,
масса тела есть величина постоянная.
Однако в конце XIX столетия на опытах с
быстро движущимися электронами было
установлено, что масса тела зависит от
скорости его движения, а именно: возрастает
с увеличением скорости по закону

,
(7.17)

где
m
– масса точки в системе отсчета,
относительно которой она дви­жется
со скоростью
,m0
– масса покоя материальной точки, т.е.
масса, измеренная в той инерциальной
системе отсчета, относительно которой
материальная точка находится в покое;
с – скорость света в вакууме.

Из
принципа относительности Эйнштейна,
утверждающего инва­риантность всех
законов природы при переходе от одной
инерциальной системы отсчета к другой,
следует условие инвариантности уравнений
физических законов относительно
преобразований Лоренца. Основной закон
динамики Ньютона

оказывается
также инвариантным по отношению к
преобразованиям Лоренца, если в нем
справа стоит производная по времени от
релятивистского импульса.

Основной
закон релятивистской динамики
и материальной
точки имеет
вид

(7.18)

или

,

где

(7.20)

релятивистский
импуль с
материальной точки.

Отметим, что
уравнение (7.19) внешне совпадает с основным
урав­нением ньютоновской механики
(2.7). Однако физический смысл его другой:
справа стоит производная по времени от
релятивистского им­пульса, определяемого
формулой (7.20). Таким образом, уравнение
(7.18) инвариантно по отношению к
преобразованиям Лоренца и, следова­тельно,
удовлетворяет принципу относительности
Эйнштейна. Следует учитывать, что ни
импульс, ни сила не являются инвариантными
вели­чинами. Более того, в общем случае
ускорение не совпадает по направ­лению
с силой.

В
силу однородности пространства в
релятивистской
механике
вы­полняется закон
сохранения релятивистского импульса:
релятивистский импульс замкнутой
системы сохраняется, т.е. не изменяется
с течением времени. Часто вообще не
оговаривают, что рассматривают
релятивистский импульс, т. к. если тела
движутся со скоростями, близкими к с,
то можно использовать только релятиви­стское
выражение для импульса.

Анализ
формул (7.17), (7.18) и (7.20) показывает, что
при скоростях, значительно меньших
скорости света, уравнение (7.18) переходит
в ос­новной закон классической
механики. Следовательно, условием
приме­нимости законов классической
(ньютоновской) механики является усло­вие
с.
Законы классической механики получаются
как следствие теории относительности
для предельного случая
с.
Таким образом, классическая механика
– это механика макротел, движущихся с
малыми скоростями.

Экспериментальное
доказательство зависимости массы от
скорости (7.17) является подтверждением
справедливости специальной теории
относительности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #

    27.02.2016327.68 Кб401в.doc

  • #

    27.02.2016759.81 Кб271г.doc

  • #
  • #
  • #
  • #
Источник

Итак, в теории относительности пространство и время потеряли свою абсолютность. Но это не значит, что в новой теории нет ничего абсолютного (кроме скорости света), т.е. не меняющегося при переходе от одной ИСО к другой. Одной из таких инвариантных величин стал так называемый интервал (s). Это величина, связывающая определенным образом промежуток времени Δt между двумя событиями и расстояние l между точками пространства, в которых они произошли.

По определению, квадрат интервала между событиями 1 и 2 равен: S2 = (cΔt)2 – l2

Интервал одинаков во всех ИСО. Его значение связывает в некий «узел» расстояния и промежутки времени между событиями. Пространство само по себе и время само по себе перестают быть самостоятельными и независимыми друг от друга. Можно говорить о едином пространстве-времени.

Времениподобные, пространственноподобные и светоподобные интервалы

По тому, положительна или отрицательна величина s2 для двух событий, можно сказать кое-что однозначно определенное про них.

Так, если s2 > о, т.е. cΔt > l, то можно найти такую систему отсчета, в которой эти события происходят в одной точке пространства (l = 0), но обязательно в разные моменты времени (Δt не равно о). Такие интервалы называют времениподобными. Так как квадрат такого интервала положительный, сам времениподобный интервал s является вещественным. При времениподобном интервале порядок событий 1 и 2 один и тот же во всех ИСО. Времениподобный интервал между событиями означает, что они могут быть причинно связаны. Если события 1 и 2 происходят с одним и тем же телом, то интервал между ними всегда времениподобный: ведь путь l, который проходит тело за время Δt, всегда меньше пути cΔt, проходимого за то же время светом.

Если s2 < о, т.е. cΔt < l, интервал называют пространственноподобным. В этом случае можно найти такую систему отсчета, в которой эти события происходят одновременно (Δt = о), но обязательно в разных точках пространства (l не равна о). Так как s2 < о, сам пространственноподобный интервал s является мнимым. При таком интервале порядок событий 1 и 2 может отличаться в разных ИСО. Но в любой ИСО эти события происходят в разных точках пространства (в частности, они не могут произойти с одним и тем же телом). Пространственноподобный интервал между событиями означает, что они не могут быть причинно связаны.

Наконец, если s2 = о, интервал называют светоподобным. Он связывает события, происходящие с одним и тем же световым сигналом.

Разделение интервалов на времениподобные, пространственноподобные и светоподобные является абсолютным, т.е. не зависящим от выбора ИСО.

Абсолютное будущее, абсолютное прошлое и абсолютно удаленные события

Возьмем произвольное событие О.

Для всех событий, разделенных с ним времениподобным интервалом, порядок событий будет одинаков во всех ИСО. Если в одной из систем отсчета некое событие Б произошло после события О, то это же будет наблюдаться во всех других ИСО. Такого рода события принадлежат абсолютному будущему по отношению к событию O. Если в одной из систем отсчета некое событие П произошло раньше события О, то это же будет наблюдаться во всех других ИСО. Такого рода события принадлежат абсолютному прошлому.

Все события, разделенные с событием О пространственноподобным интервалом — это абсолютно удалённые события от события О. Раньше или позже произошло такого рода событие, сказать определенно нельзя, но оно точно произошло в другой точке пространства, нежели событие О.

Вся теория относительности Эйнштейна базируется на этих представлениях о пространстве-времени. На их основе построены релятивистская механика и релятивистская электродинамика.

Источник

Интервал в теории относительности — расстояние между двумя событиями в пространстве-времени. Интервал не меняется при переходе от одной инерциальной системы отсчета к другой, что позволяет чисто формально получить преобразования Лоренца как группу преобразований, сохраняющих интервал. Также инвариантность интервала служит основой для введения пространста Минковского, в котором смене инерциальных систем отсчета соответсвуют “вращения” этого пространства.

Интервал является одним из фундаментальных физических понятий. Он лежит в основе специальной и общей теорий относительности. Свойство теории сохранять интервал при смене инерциальной системы отсчета называется Лоренц-инвариантностью.

Определение

Квадрат интервала – это симметричная билинейная форма на конфигурационном 4-хмерном многообразии пространства-времени. В случае псевдоевклидова пространства-времени Минковского он имеет вид:

{displaystyle ds^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}}

Обычно интервал обозначается латинской буквой S.

В общей теории относительности используется обобщенное понятие интервала, дающее естественное обобщение расстояния между двумя точками. Вводится метрический тензор {displaystyle g_{ik}}, от которого требуется лишь симметричность и невырожденность. Выражение для квадрата интервала приобретает вид:

{displaystyle !ds^{2}=g_{ij}dx^{i}dx^{j},~~i,j=1dots 4},

где {displaystyle dx^{i}} – дифференциалы координат, по повторяющимся индексам подразумевается суммирование. Обратим внимание, что таким образом опреденная метрика не будет положительно определенной формой, как обычно требуется. Напротив, существует бесконечно много линий, имеющих нулевую длину, т.к. вдоль них интервал оказывается вырожденным. Многообразие с определенным интервалом называется псевдоримановым.

Инвариантность интервала

Используемые постулаты

Напрямую из принципа относительности, однородности и изотропности пространства, а также однородности времени следует, что при переходе от одной ИСО (инерциальной системы отсчета) к другой ИСО интервал остается неизменным. Именно это его свойство позволяет формально вывести преобразования Лоренца и обосновывает оправданность введения пространства Минковского и неримановой метрики.

Особо подчеркнем, что для приведенного доказательства инвариантность скорости света значения не имеет! Важно лишь, что максимальная скорость распространения взаимодействий сущесвтует и одинакова во всех системах отсчета. Одинаковость этой скорости следует из принципа отосительности. Для краткости, в дальнейшем доказательстве под интервалом будем подразумевать интервал между двумя бесконечно близкими в пространстве и времени событиями, а под скоростью света – максимально возможную скорость распространения взаимодействий. Оказывается, что свет распространяется именно с такой скоростью, обозначаемой C.

Смысл знака квадрата интервала

  • Если {displaystyle ds^{2}geq 0}, то интервал называется времениподобным. Времениподобный интервал между событиями означает, что существует такая система отсчёта, в которой оба события произошли в одном и том же месте. Что еще более важно, времениподобный интервал между событиями означает, что они могут быть причинно связаны. Легко убедиться, что для причинно связанных событий {displaystyle ds^{2}geq 0}, т.к. любое взаимодействие распространяется со скоростью не большей C, причем {displaystyle ds=0} соответсвует событиям, связанным сиигналом, распространяющимся со скоростью света. Этот сигнал не обязан быть именно световым, это может быть гравитационная волна, вообще любая безмассовая частица или даже еще не открытое взаимодействие. Существенно лишь, что существует максимальная скорость распространения взаимодействия, одинаковая для всех систем отсчета и равная, как следует из уравнений Максвелла, скорости света.
  • Если {displaystyle ds^{2}leq 0}, то интервал называется пространственноподобным, и значит можно выбрать такую инерциальную систему отсчёта, в которой оба события произошли в одно и то же время. Пространственноподобные события, как указано выше, не могут быть причинно связанными, так как даже распространяющийся по прямой сигнал должен бы был для этого двигаться быстрее скорости света.

Литература

  • Ландау Л.Д., Лившиц Е.М.: Теория поля. – 1988

См. также

  • Мировая линия
  • Собственное время
  1. Википедия Интервал (в теории относительности) адрес
  2. Викисловарь — адрес
  3. Викицитатник — адрес
  4. Викиучебник — адрес
  5. Викитека — адрес
  6. Викиновости — адрес
  7. Викиверситет — адрес
  8. Викигид — адрес

Выделить Интервал (в теории относительности) и найти в:

  1. Вокруг света (в теории относительности) адрес
  2. Академик (в теории относительности)/ru/ru/ адрес
  3. Астронет адрес
  4. Элементы (в теории относительности)+&search адрес
  5. Научная Россия (в теории относительности)&mode=2&sort=2 адрес
  6. Кругосвет (в теории относительности)&results_per_page=10 адрес
  7. Научная Сеть
  8. Традиция — адрес
  9. Циклопедия — адрес
  10. Викизнание — (в теории относительности) адрес
  1. Google
  2. Bing
  3. Yahoo
  4. Яндекс
  5. Mail.ru
  6. Рамблер
  7. Нигма.РФ
  8. Спутник
  9. Google Scholar
  10. Апорт
  11. Онлайн-переводчик
  12. Архив Интернета
  13. Научно-популярные фильмы на Яндексе
  14. Документальные фильмы
  1. Список ru-вики
  2. Вики-сайты на русском языке
  3. Список крупных русскоязычных википроектов
  4. Каталог wiki-сайтов
  5. Русскоязычные wiki-проекты
  6. Викизнание:Каталог wiki-сайтов
  7. Научно-популярные сайты в Интернете
  8. Лучшие научные сайты на нашем портале
  9. Лучшие научно-популярные сайты
  10. Каталог научно-познавательных сайтов
  11. НАУКА В РУНЕТЕ: каталог научных и научно-популярных сайтов
  • Страница 0 – краткая статья
  • Страница 1 – энциклопедическая статья
  • Разное – на страницах: 2 , 3 , 4 , 5
  • Прошу вносить вашу информацию в «Интервал (в теории относительности) 1», чтобы сохранить ее

Комментарии читателей:

Источник

Макеты страниц

В дальнейшем мы будем часто пользоваться понятием события. Событие определяется местом, где оно произошло, и временем, когда оно произошло.

Таким образом, событие, происходящее с некоторой материальной частицей, определяется тремя координатами этой частицы и моментом времени, когда происходит событие.

Часто полезно из соображений наглядности пользоваться воображаемым четырехмерным пространством, на осях которого откладываются три пространственные координаты и время. В этом пространстве событие изображается точкой. Эти точки называются мировыми точками. Всякой частице соответствует некоторая линия (мировая линия) в этом четырехмерном пространстве. Точки этой линии определяют координаты частицы во все моменты времени. Равномерно и прямолинейно движущейся материальной частице соответствует прямая мировая линия.

Выразим теперь принцип инвариантности скорости света математически. Для этого рассмотрим две системы отсчета К и К, движущиеся друг относительно друга с постоянной скоростью. Координатные оси выберем при этом таким образом, чтобы оси х и к совпадали, а оси у и z были параллельны осям у и время в системах К и К обозначим через t и .

Пусть первое событие состоит в том, что отравляется сигнал, распространяющийся со скоростью света, из точки, имеющей координаты в системе К в момент времени в этой же системе. Будем наблюдать из системы К распространение этого сигнала. Пусть второе событие состоит в том, что сигнал приходит в точку в момент времени Сигнал распространяется со скоростью с; пройденное им расстояние равно поэтому . С другой стороны, это же расстояние равно Таким образом, мы можем написать следующую зависимость между координатами обоих событий в системе

Те же два события, т. е. распространение сигнала, можно наблюдать из системы К. Пусть координаты первого события в системе а второго: Поскольку скорость света в системах К и К одинакова, то, аналогично (2,1), имеем:

Если — координаты каких-либо двух событий, то величина

называется интервалом между этими двумя событиями.

Таким обрязом, из инвариантности скорости света следует, что если интервал между двумя событиями равен нулю в одной системе отсчета, то он равен нулю и во всякой другой системе.

Если два события бесконечно близки друг к другу, то для интервала между ними имеем:

Форма выражения (2,3) или (2,4) позволяет рассматривать интервал, с формальной математической точки зрения, как расстояние между двумя точками в воображаемом четырехмерном пространстве (на осях которого откладываем х, у, z и произведение ). Имеется, однако, существенное отличие в правиле составления этой величины по сравнению с правилом обычной геометрии: при образовании квадрата интервала квадраты разностей координат по различным осям суммируются не с одинаковыми, а с различными знаками.

Как было показано выше, если в некоторой инерциальной системе отсчета, то и в другой системе. С другой стороны, — бесконечно малые одинакового порядка. Из этих двух обстоятельств следует, что должны быть пропорциональны друг другу:

причем коэффициент а может зависеть только от абсолютной величины относительной скорости обеих инерциальных систем. Он не может зависеть от координат и времени, так как тогда различные точки пространства и моменты времени были бы не равноценны, что противоречит однородности пространства и времени. Он не может зависеть также и от направления относительной скорости, так как это противоречило бы изотропности пространства.

Рассмотрим три системы отсчета и пусть — скорости движения систем относительно К. Тогда имеем:

С тем же основанием можно написать:

где – абсолютная величина скорости движения относительно . Сравнивая друг с другом эти соотношения, найдем, что должно быть:

Но зависит не только от абсолютных величин вектороэ и , но и от угла между ними. Между тем последний вообще не входит в левую часть соотношения (2,5). Ясно поэтому, что это, соотношение может быть справедливым лишь, если функция сводится к постоянной величине, равной, как это следует из того же соотношения, единице.

Таким образом,

а из равенства бесконечно малых интервалов следует равенство также и конечных интервалов: .

Мы приходим, следовательно, к важнейшему результату: интервал между событиями одинаков во всех инерциальных системах отсчета, т. е. является инвариантом по отношению к преобразованию от одной инерциальной системы отсчета к любой другой. Эта инвариантность и является математическим выражением постоянства скорости света.

Пусть опять — координаты двух событий в некоторой системе отсчета К. Спрашивается, существует ли такая система отсчета К, в которой оба эти события происходили бы в одном и том же месте пространства.

Введем обозначения

Тогда квадрат интервала между событиями в системе К:

и в системе К:

причем в силу инвариантности интервала

Мы хотим, чтобы в системе К оба события произошли в одной точке, т. е. чтобы . Тогда

Следовательно, система отсчета с требуемым свойством существует, если , т. е. если интервал между обоими событиями вещественный. Вещественные интервалы называют времениподобными.

Таким образом, если интервал между двумя событиями времениподобный, то существует такая система отсчета, в которой оба события произошли в одном и том же месте. Время, которое пройдет между этими событиями в этой системе, равно

Если какие-нибудь два события происходят с одним и тем телом, то интервал между ними всегда времениподобный. Действительно, путь, который тело проходит между обоими событиями, не может быть больше так как скорость тела не может быть больше с. Поэтому всегда

Зададимся теперь вопросом, нельзя ли выбрать такую систему отсчета, в которой два события произошли бы в одно и то же время. По-прежнему мы имеем в системах К и Мы хотим, чтобы ; отсюда

Следовательно, искомую систему отсчета можно найти только в том случае, когда интервал между двумя событиями мнимый. Мнимые интервалы называют пространственноподобными.

Рис. 2

Таким образом, если интервал между двумя событиями пространственноподобный, то существует такая система отсчета, в которой оба события происходят одновременно. Расстояние между точками, где произошли эти события в этой системе отсчета, равно

Подразделение интервалов на времениподобные и пространственноподобные есть, в силу их инвариантности, понятие абсолютное. Это значит, что свойство интервала быть времениподобным или пространственноподобным не зависит от системы отсчета.

Возьмем какое-нибудь событие — назовем его событием О — в качестве начала отсчета времени и пространственных координат. Другими словами, в четырехмерной системе координат, на осях которой откладываются х, у z и i, мировая точка события О будет началом координат. Посмотрим теперь, в каком отношении к данному событию О находятся все остальные события. Для наглядности мы будем рассматривать только одну пространственную координату и время, откладывая их на двух осях (рис. 2). Прямолинейное равномерное движение частицы, проходящей точку при , изобразится прямой линией, проходящей через О и наклоненной к оси t под углом, тангенс которого равен скорости частицы. Поскольку наибольшая возможная скорость равна с, то существует наибольший угол, который может образовывать эта прямая с осью t.

На рис. 2 изображены Две прямые, изображающие распространение двух сигналов (со скоростью света) в противоположных направлениях, проходящих через событие О (т. е. проходящих при Все линии, изображающие движения частиц, могут лежать только внутри областей На прямых очевидно, Рассмотрим сначала события, мировые точки которых лежат внутри области Легко сообразить, что во всех точках этой области . Другими словами, интервалы между любым событием этой области и событием О — времениподобные. В этой области т. е. все события этой области происходят «после» события О. Но два события, разделенных времениподобным интервалом, ни в какой системе отсчета не могут происходить одновременно. Следовательно, нельзя выбрать и никакой системы отсчета, где бы какое-нибудь из событий области происходило «до» события О, т. е. когда было бы Таким образом, все события области являются будущими по отношению к О, и притом во всех системах отсчета. Эту область можно поэтому назвать «абсолютно будущей» по отношению к событию О.

Совершенно аналогично все события области являются «абсолютно прошедшими» по отношению к О, т. е. события этой области во всех системах отсчета происходят до события О.

Наконец, рассмотрим еще области . Интервал между любым событием этой области и событием О — пространственноподобный. В любой системе отсчета эти события происходят в разных местах пространства. Поэтому эти области можно назвать «абсолютно удаленными» по отношению к О. Понятия «одновременно», «раньше» и «позже» для этих событий, однако, относительны. Для всякого события этой области есть такие системы отсчета, где оно происходит позже события О, системы, где оно происходит раньше О, и, наконец, одна система отсчета, где оно происходит одновременно с О.

Заметим, что если рассматривать все три пространственные координаты вместо одной, то вместо двух пересекающихся прямых на рис. 2 мы имели бы «конус» в четырехмерной системе координат х, у, z, t, ось которого совпадает с осью t (этот конус называют световым конусом). Области «абсолютно будущего» и «абсолютно прошедшего» изображаются тогда соответственно двумя внутренними полостями этого конуса.

Два события могут быть причинно связаны друг с другом только в том случае, если интервал между ними времениподобный, что непосредственно следует из того, что никакое взаимодействие не может распространяться со скоростью, большей скорости света.

Как мы только что видели, как раз для таких событий имеют абсолютный смысл понятия «раньше» и «позже», что является необходимым условием для того, чтобы имели смысл понятия причины и следствия.

1

Оглавление

  • ПРЕДИСЛОВИЕ РЕДАКТОРА К СЕДЬМОМУ ИЗДАНИЮ
  • ПРЕДИСЛОВИЕ К ШЕСТОМУ ИЗДАНИЮ
  • ИЗ ПРЕДИСЛОВИЙ к ПЕРВОМУ И ВТОРОМУ ИЗДАНИЯМ
  • НЕКОТОРЫЕ ОБОЗНАЧЕНИЯ
  • ГЛАВА I. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ
  • § 1. Скорость распространения взаимодействий
  • § 2. Интервал
  • § 3. Собственное время
  • § 4. Преобразование Лоренца
  • § 5. Преобразование скорости
  • § 6. Четырехмерные векторы
  • § 7. Четырехмерная скорость
  • ГЛАВА II. РЕЛЯТИВИСТСКАЯ МЕХАНИКА
  • § 8. Принцип наименьшего действия
  • § 9. Энергия и импульс
  • § 10. Преобразование функции распределения
  • § 11. Распад частиц
  • § 12. Инвариантное сечение
  • § 13. Упругие столкновения частиц
  • § 14. Момент импульса
  • ГЛАВА III. ЗАРЯД В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ
  • § 15. Элементарные частицы в теории относительности
  • § 16. Четырехмерный потенциал поля
  • § 17. Уравнения движения заряда в поле
  • § 18. Калибровочная инвариантность
  • § 19. Постоянное электромагнитное поле
  • § 20. Движение в постоянном однородном электрическом поле
  • § 21. Движение в постоянном однородном магнитном поле
  • § 22. Движение заряда в постоянных однородных электрическом и магнитном полях
  • § 23. Тензор электромагнитного поля
  • § 24. Преобразование Лоренца для поля
  • § 25. Инварианты поля
  • ГЛАВА IV. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
  • § 26. Первая пара уравнений Максвелла
  • § 27. Действие для электромагнитного поля
  • § 28. Четырехмерный вектор тока
  • § 29. Уравнение непрерывности
  • § 31. Плотность и поток анергии
  • § 32. Тензор энергии-импульса
  • § 33. Тензор энергии-импульса электромагнитного поля
  • § 34. Теорема вириала
  • § 35. Тензор энергии-импульса макроскопических тел
  • ГЛАВА V. ПОСТОЯННОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
  • § 36. Закон Кулона
  • § 37. Электростатическая энергия зарядов
  • § 38. Поле равномерно движущегося заряда
  • § 39. Движение в кулоновом поле
  • § 40. Дипольный момент
  • § 41. Мультипольные моменты
  • § 42. Система зарядов во внешнем поле
  • § 43. Постоянное магнитное поле
  • § 44. Магнитный момент
  • § 45. Теорема Лармора
  • ГЛАВА VI. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
  • § 46. Волновое уравнение
  • § 47. Плоские волны
  • § 48. Монохроматическая плоская волна
  • § 49. Спектральное разложение
  • § 50. Частично поляризованный свет
  • § 51. Разложение электростатического поля
  • § 52. Собственные колебания поля
  • ГЛАВА VII. РАСПРОСТРАНЕНИЕ СВЕТА
  • § 53. Геометрическая оптика
  • § 54. Интенсивность
  • § 55. Угловой эйконал
  • § 56. Тонкие пучки лучей
  • § 57. Отображение широкими пучками лучей
  • § 58. Пределы геометрической оптики
  • § 59. Дифракция
  • § 60. Дифракция Френеля
  • § 61. Дифракция Фраунгофера
  • ГЛАВА VIII. ПОЛЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
  • § 62. Запаздывающие потенциалы
  • § 63. Потенциалы Лиенара — Вихерта
  • § 64. Спектральное разложение запаздывающих потенциалов
  • § 65. Функция Лагранжа с точностью до членов второго порядка
  • ГЛАВА IX. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
  • § 66. Поле системы зарядов на далеких расстояниях
  • § 67. Дипольное излучение
  • § 68. Дипольное излучение при столкновениях
  • § 69. Тормозное излучение малых частот
  • § 70. Излучение при кулоновом взаимодействии
  • § 71. Квадрупольное и магнитно-дипольное излучения Рассмотрим
  • § 72. Поле излучения на близких расстояниях
  • § 73. Излучение быстро движущегося заряда
  • § 74. Магнито-тормозное излучение
  • § 75. Торможение излучением
  • § 76. Торможение излучением в релятивистском случае
  • § 77. Спектральное разложение излучения в ультрарелятивистском случае
  • § 78. Рассеяние свободными зарядами
  • § 79. Рассеяние волн с малыми частотами
  • § 80. Рассеяние волн с большими частотами
  • ГЛАВА X. ЧАСТИЦА В ГРАВИТАЦИОННОМ ПОЛЕ
  • § 81. Гравитационное поле в нерелятивистской механике
  • § 82. Гравитационное поле в релятивистской механике
  • § 83. Криволинейные координаты
  • § 84. Расстояния и промежутки времени
  • § 85. Ковариантное дифференцирование
  • § 86. Связь символов Кристоффеля с метрическим тензором
  • § 87. Движение частицы в гравитационном поле
  • § 88. Постоянное гравитационное поле
  • § 89. Вращение
  • § 90. Уравнения электродинамики при наличии гравитационного поля
  • ГЛАВА XI. УРАВНЕНИЯ ГРАВИТАЦИОННОГО ПОЛЯ
  • § 91. Тензор кривизны
  • § 92. Свойства тензора кривизны
  • § 93. Действие для гравитационного поля
  • § 94. Тензор энергии-импульса
  • § 95. Уравнения Эйнштейна
  • § 96. Псевдотензор энергии-импульса гравитационного поля
  • § 97. Синхронная система отсчета
  • § 98. Тетрадное представление уравнений Эйнштейна
  • ГЛАВА XII. ПОЛЕ ТЯГОТЕЮЩИХ ТЕЛ
  • § 99. Закон Ньютона
  • § 100. Центрально-симметричное гравитационное поле
  • § 101. Движение в центрально-симметричном гравитационном поле
  • § 102. Гравитационный коллапс сферического тела
  • § 103. Гравитационный коллапс пылевидной сферы
  • § 104. Гравитационный коллапс несферических и вращающихся тел
  • § 105. Гравитационное поле вдали от тел
  • § 106. Уравнения движения системы тел во втором приближении
  • ГЛАВА XIII. ГРАВИТАЦИОННЫЕ ВОЛНЫ
  • § 107. Слабые гравитационные волны
  • § 108. Гравитационные волны в искривленном пространстве-времени
  • § 109. Сильная гравитационная волна
  • § 110. Излучение гравитационных волн
  • ГЛАВА XIV. РЕЛЯТИВИСТСКАЯ КОСМОЛОГИЯ
  • § 111. Изотропное пространство
  • § 112. Закрытая изотропная модель
  • § 113. Открытая изотропная модель
  • § 114. Красное смещение
  • § 115. Гравитационная устойчивость изотропного мира
  • § 116. Однородные пространства
  • § 117. Плоская анизотропная модель
  • § 118. Колебательный режим приближения к особой точке
  • § 119. Особенность по времени в общем космологическом решении уравнений Эйнштейна
Источник

Добавить комментарий