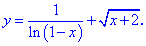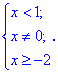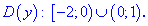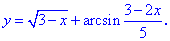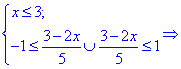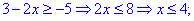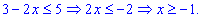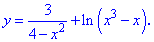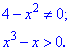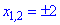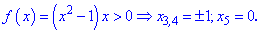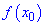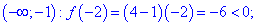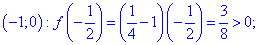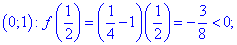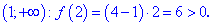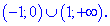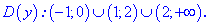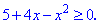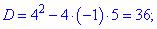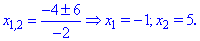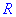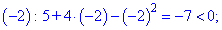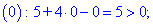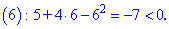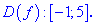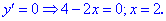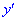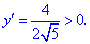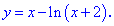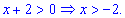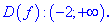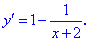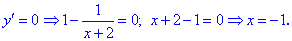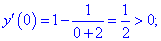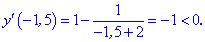Исследование функций должно начинаться с установления области определения и интервалов монотонности. Для этого студент должен обладать хорошими знаниями поведения элементарных функций и последующим теоретическим материалом.
Функция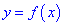 
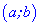
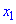
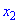
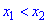
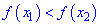
называется возрастающей на интервале 
если для любых двух точек 
и 
с этого промежутка и таких, что 
выполняется неравенство
.
Для того чтобы функция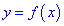 
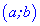
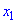
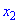
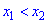
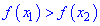
была убывающей на интервале 
необходимо, чтобы для любых 
и 
, принадлежащих к этому интервалу и удовлетворяющих условию 
исполнялось неравенство
.
Как возрастающие, так и убывающие функции называются монотонными, а интервалы в которых
функция возрастает или убывает – интервалами монотонности.
Область возрастания и убывания функции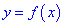 
характеризуется знаком ее производной: если в
некотором интервале производная больше нуля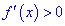 
, то функция возрастает в этом интервале;
если же наоборот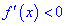 
– то функция убывает в этом интервале.
Интервалы монотонности могут прилегать друг к другу или точками, где производная равна нулю
или точками, где производная не существует. Эти точки называются критическими точками.
Для того, чтобы найти интервалы монотонности функции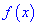 
нужно:
1) найти область определения функции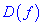 
;
2) вычислить производную данной функции;
3) найти критические точки из условия равенства нулю производной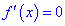 
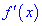
или при условии, что производная 
не существует;
4) разделить критическими точками область определения на интервалы, в каждом из которых определить знак производной.
На интервалах где производная положительная функция возрастает, а где отрицательная – убывает.
———————————–
Примеры.
Рассмотрим задачу из сборника В.Ю. Клепко, В.Л. Голец “Высшая математика в примерах и задачах” на нахождение интервалов монотонности функции.
1. (3.36.10)
Функция существует во всех точках где определен логарифм и он не обращается в нуль, а также где функция под корнем принимает неотрицательные значения. На основе этого находим
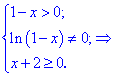
Итак, областью определения будут два интервала
2. (3.36.11)
С подкоренной функцией ведем себя как и в предыдущем примере, а функция 
определена на промежутке
. Находим область определения
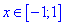
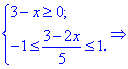
Единственным промежутком, который удовлетворяет эти условия являются следующий
.
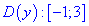
3. (3.36.13)
Область определения функции находим из двух условий
Первое условие дает две точки
в которых функция не существует.
С второго условия получим
Исследуем поведение функции в интервалах монотонности на которые разбивают заданные точки. Для этого
выбираем произвольные точки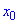 
из интервалов и проверяем знак 
Функция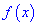 
принимает положительные значения в интервалах
Вместе с первым условием получим следующую область определения
——————————
Рассмотрим примеры исследования монотонности функции из сборника задач Дубовика В.П., Юрика И.И. “Высшая математика” .
І. (5.705) Показать, что функция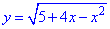 
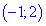
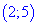
возрастает на интервале
и убывает в интервале 
.
1) Областью определения функции будет множество значений для которых подкоренная функция принимает неотрицательные значения.
Решим квадратное уравнение
Определим знак функции на всем интервале 
Таким образом получим следующую область определения
2) Найдем производную
.
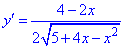
3) Приравняем ее к нулю и найдем критические точки:
Не стоит забывать и о точках, в которых производная не существует. Это корни уравнения в
знаменателе. Итак производная существует на интервале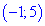 
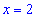
в точке 
меняет знак.
4) Знаки производной: подставляем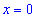 
в производную 
Так что на интервале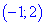 
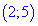
функция возрастает, а на 
– убывает.
ІІ. (5.715) Найти интервалы монотонности функции
1. Областью определения будет множество точек 
для которых существует логарифм функция. На
основе этого получим
Итак 
2) Найдем производную функции
3) Находим критические точки
Другая точка, где производная не существует это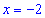 
, не принадлежит области определения функции.
Таким образом получили два интервала монотонности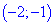 
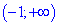
и 
.
4) Выясним где функция возрастает, а где убывает. Подставим точки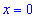 
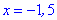
и 
в выражение для
производной
Исследуемая функция на интервале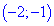 
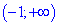
убывает и на 
растет.
При исследовании функций на монотонность определите все критические точки в которых производная равна нулю или не существует. Также не забывайте при этом учитывать область определения функции. Остальное зависит от Ваших знаний свойств элементарных функции, поскольку именно на их основе построены все задачи, которые Вам задают преподаватели.
———————————————-
Посмотреть материалы:
- Исследования функции и построения графика
- Наибольшее и наименьшее значение функции на отрезке
- Локальный экстремум функции. Примеры
- Выпуклость и вогнутисть графика функции
- Асимптоты функции
- Область определения функции
Исследование функции. Экстремумы и интервалы монотонности функции.
Функция
называетсявозрастающей
на интервале
,
если для любых точек
из этого интервала при выполнении
условия
выполняется неравенство
(большему значению аргумента соответствует
большее значение функции).
Аналогично, функция
называетсяубывающей
на интервале
,
если для любых точек
из этого интервала при выполнении
условия
выполняется неравенство
(большему значению аргумента соответствует
меньшее значение функции).
Возрастающие на
интервале
и убывающие на интервале
функции называютсямонотонными
на интервале
.
Знание производной
дифференцируемой функции позволяет
находить интервалы ее монотонности.
Теорема (достаточное
условие возрастания функции).
Если производная дифференцируемой на
интервале
функции
положительна на интервале
,
то функция
монотонно возрастает на этом интервале.
Теорема (достаточное
условие убывания функции).
Если производная дифференцируемой на
интервале
функции
отрицательна на интервале
,
то функция
монотонно убывает на этом интервале.
Геометрический
смысл
этих теорем состоит в том, что на
интервалах убывания функции касательные
к графику функции образуют с осью
тупые углы, а на интервалах возрастания
– острые (см.рис.
1).
Рис. 1.
Теорема (необходимое
условие монотонности функции). Если
функция
дифференцируема и
(
)
на интервале
,
то она не убывает (не возрастает) на этом
интервале.
Алгоритм нахождения
интервалов монотонности функции
:
-
Найти
. -
Найти нули
производной. -
На числовой оси
отметить область определения
,
нули производной и те точки, где
производная не существует. -
На каждом из
полученных интервалов определить знак
производной
. -
Сделать вывод о
возрастании или убывании функции
на каждом интервале.
.
,
.
на каждом интервале.Пример.
Найти интервалы монотонности функции
.
Точка
называетсяточкой
максимума функции
,
если существует некоторое число
такое, что для всех
,
удовлетворяющих условию
,
выполнено неравенство
.
Максимум функции
– это значение функции в точке максимума.
На рис
2 показан
пример графика функции, имеющей максимумы
в точках
.
Рис. 2.
Точка
называетсяточкой
минимума функции
,
если существует некоторое число
такое, что для всех
,
удовлетворяющих условию
,
выполнено неравенство
.
Нарис.
2 функция
имеет минимум в точке
.
Для максимумов и
минимумов есть общее название –
экстремумы.
Соответственно точки максимума и точки
минимума называются точками
экстремума.
Функция, определенная
на отрезке, может иметь максимум и
минимум только в точках, находящихся
внутри этого отрезка. Нельзя также
путать максимум и минимум функции с ее
наибольшим и наименьшим значением на
отрезке – это понятия принципиально
различные.
В точках экстремума
у производной есть особые свойства.
Теорема (необходимое
условие экстремума).
Пусть в точке
функция
имеет экстремум. Тогда либо
не существует, либо
.
Те точки из области
определения функции, в которых
не существует или в которых
,
называютсякритическими
точками функции.
Таким образом,
точки экстремума лежат среди критических
точек. В общем случае критическая точка
не обязана быть точкой экстремума. Если
производная функции в некоторой точке
равна нулю, то это еще не значит, что в
этой точке функция имеет экстремум.
Пример.
Рассмотрим
.
Имеем
,
но точка
не является точкой экстремума (см.рис
3).
Рис. 3.
Теорема (первое
достаточное условие экстремума).
Пусть в точке
функция
непрерывна, а производная
при переходе через точку
меняет знак. Тогда
– точка экстремума: максимума, если
знак меняется с «+» на «–», и минимума,
если с «–» на «+».
Если при переходе
через точку
производная не меняет знак, то в точке
экстремума нет.
Теорема (второе
достаточное условие экстремума).
Пусть в точке
производная дважды дифференцируемой
функции
равна
нулю (
),
а ее вторая производная в этой точке
отлична от нуля (
)
и непрерывна в некоторой окрестности
точки
.
Тогда
– точка экстремума
;
при
это точка минимума, а при
это точка максимума.
Алгоритм нахождения
экстремумов функции с помощью первого
достаточного условия экстремума:
-
Найти производную.
-
Найти критические
точки функции. -
Исследовать знак
производной слева и справа от каждой
критической точки и сделать вывод о
наличии экстремумов. -
Найти экстремальные
значения функции.
Алгоритм нахождения
экстремумов функции с помощью второго
достаточного условия экстремума:
-
Найти производную
. -
Найти вторую
производную
. -
Найти те точки,
в которых
. -
В этих точках
определить знак
. -
Сделать вывод о
существовании и характере экстремумов. -
Найти экстремальные
значения функции.
.
.
.
.
Пример.
Найти экстремумы функции
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интервалы возрастания и убывания функции
С помощью данного сервиса можно найти интервалы возрастания и убывания функции в онлайн режиме с оформлением решения в Word.
- Решение онлайн
- Видеоинструкция
Исследование функции с помощью производной
Определение: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)>f(x).
Определение: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)<f(x).
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная f′(x) обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции y=f(x) с помощью первой производной
- Найти производную функции f′(x).
- Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
- Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x). Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
- Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
- Вычислить значения функции в точках минимума и максимума.
С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.
Пример №1: Найти промежутки монотонности и экстремумы функции: f(x)=x3–3x2.
Решение: Найдем первую производную функции f′(x)=3x2–6x.
Найдем критические точки по первой производной, решив уравнение 3x2–6x=0; 3x(x-2)=0 ;x = 0, x = 2
Исследуем поведение первой производной в критических точках и на промежутках между ними.
| x | (-∞, 0) | 0 | (0, 2) | 2 | (2, +∞) |
| f′(x) | + | 0 | – | 0 | + |
| f(x) | возрастает | max | убывает | min | возрастает |
f(0) = 03 – 3*02 = 0
f(2) = 23 – 3*22 = -4
Ответ: Функция возрастает при x∈(-∞ ; 0)∪(2; +∞); функция убывает при x∈(0;2);
точка минимума функции (2;-4); точка максимума функции (0;0).
Правило нахождения экстремумов функции y=f(x) с помощью второй производной
- Найти производную f′(x).
- Найти стационарные точки данной функции, т.е. точки, в которых f′(x)=0.
- Найти вторую производную f″(x).
- Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
- Вычислить значения функции в точках экстремума.
Отсюда следует, что дважды дифференцируемая функция f(x) выпукла на отрезке [a, b], если вторая производная f”(x) ≥ 0 при всех х [a, b].
Все вычисления можно проделать в онлайн режиме.
Пример №2. Исследовать на экстремум с помощью второй производной функцию: f(x) = x2 – 2x – 3.
Решение: Находим производную: f′(x) = 2x – 2.
Решая уравнение f′(x) = 0, получим стационарную точку х=1. Найдем теперь вторую производную: f″(x) = 2.
Так как вторая производная в стационарной точке положительна, f″(1) = 2 > 0, то при x = 1 функция имеет минимум: fmin = f(1) = -4.
Ответ: Точка минимума имеет координаты (1; -4).
Найти интервалы монотонности функции
Онлайн калькулятор поможет найти промежутки монотонности функции. Функция называется монотонной на промежутке, если она на этом промежутке или возрастает, или убывает.
Например для исследования функции f(x) на монотонность необходимо:
Найти f(x).
Найти нули производной.
На числовой оси отметить область определения f(x), нули производной и те точки, где производная не существует.
На каждом из полученных интервалов определить знак производной f(x) .
Сделать вывод о возрастании или убывании функции на каждом интервале.
Интервалы возрастания функции при: >0
Интервалы убывания функции при: <0
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»
