Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция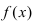 
- – она определена в этой точке и ее некоторой
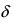-окрестности; - – существуют конечные лево- и правосторонние пределы от функции в этой точке и они равны между собой, т.е.
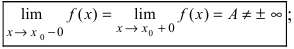
– предел функции в точке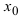 
равен значению функции в исследуемой точке, т.е.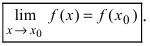 
Пример:
Найти область непрерывности функции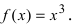 
Решение:
Данная функция непрерывна 
так как в каждой точке указанного интервала функция определена, в каждой точке существуют конечные и равные лево- и правосторонние пределы, а предел функции в каждой точке равен значению функции в этой точке.
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
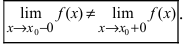
Пример:
Доказать, что функция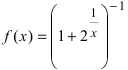 
в точке 
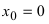имеет разрыв первого рода.
Решение:
Нарисуем график функции в окрестности нуля (Рис. 64):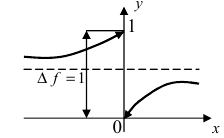 
Рис. 64. График функции 
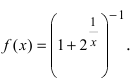Область определения функции: 
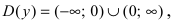т.е. точка 
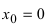является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке: 
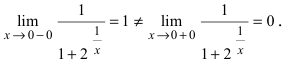Следовательно, в изучаемой точке данная функция терпит разрыв первого рода.
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция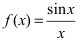
имеет в точке 
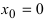устранимый разрыв.
Решение:
В точке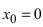 
функция имеет неопределенность 
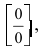поэтому эта точка является точкой, подозрительной на разрыв. Вычислив в этой точке лево- и правосторонний пределы 
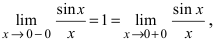убеждаемся, что данная точка является точкой устранимого разрыва.
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен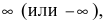 
т.е. в такой точке функция терпит бесконечный разрыв.
Пример:
Исследовать на непрерывность функцию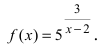 
Решение:
Найдем область определения этой функции: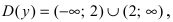 
т.е. точка
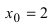является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке: 
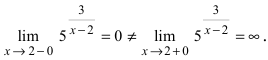Так как левосторонний предел конечен, а правосторонний предел бесконечен, то в изучаемой точке данная функция терпит разрыв II рода.
Пример:
Исследовать на непрерывность функцию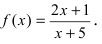 
Решение:
Найдем область определения этой функции: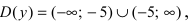 
т.е. точка 
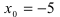является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке: 
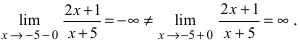Так как левосторонний и правосторонний пределы бесконечены, то в изучаемой точке данная функция терпит разрыв II рода.
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций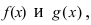 
которые определены в некоторой 
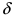-окрестности точки 
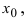в которой лево- и правосторонние пределы равны между собой. Так как функции 
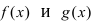непрерывны в некоторой 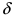-окрестности точки 
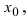то выполняются равенства: 
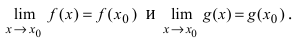В силу того, что существуют конечные пределы обеих функций, то по теореме о пределе суммы двух функций имеем, что 
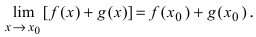Аналогично теорема доказывается для суммы (разности) любого конечного числа непрерывных функций. Нижеприведенные теоремы доказываются так же, как и теорема.
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций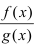 
при условии, что во всех точках общей области определения функция 
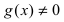, есть непрерывная функция.
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
- Заказать решение задач по высшей математике
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию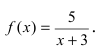 
Решение:
Согласно схеме исследования функции на непрерывность имеем:
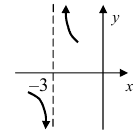
Рис. 65. Поведение графика функции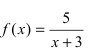 
в малой окрестности точки разрыва второго рода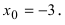 
Из рисунка видно, что график функции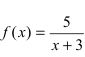 
—неограниченно приближается к вертикальной прямой 
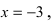нигде не пересекая эту прямую.
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке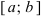 
.
Определение: Замкнутый интервал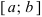 
будем называть сегментом.
Приведем без доказательства свойства непрерывных функций на сегменте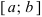 
.
Теорема: Если функция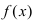 
непрерывна на сегменте 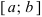, то она достигает своего наименьшего (
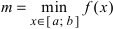) и наибольшего (
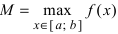) значения либо во внутренних точках сегмента, либо на его концах.
Пример:
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
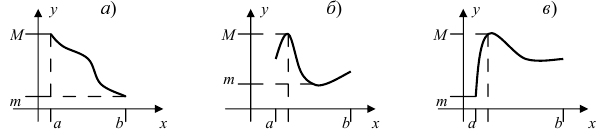
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 
и наибольшего 
значений на концах сегмента 
На графике б) функция достигает своего наименьшего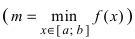 
и наибольшего значения 
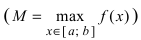во внутренних точках сегмента 
На графике в) функция достигает своего наименьшего значения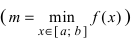 
на левом конце сегмента 
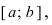а наибольшего значения 
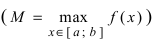во внутренней точке сегмента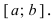 
Тб. Если функция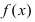 
непрерывна на сегменте 
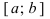и достигает своего наименьшего (
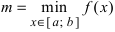) и наибольшего (
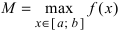) значений, то для любого вещественного числа С, удовлетворяющего неравенству 
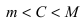, найдется хотя бы одна точка 
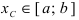такая, что 
.
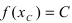Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).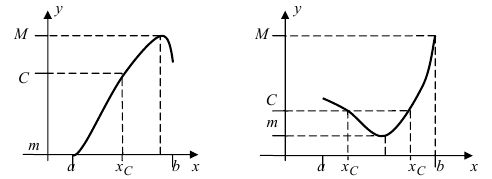 
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция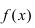 
непрерывна на сегменте 
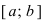и на его концах принимает значения разных знаков, то найдется хотя бы одна точка 
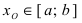такая, что
.
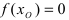Пример:
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
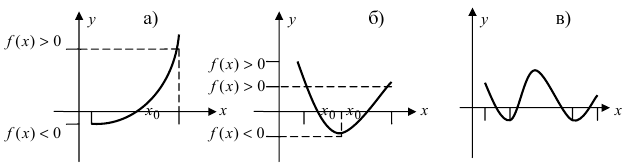
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
Непрерывность функции и точки разрыва
- Приращение аргумента и приращение функции
- Непрерывность функции в точке
- Непрерывность функции на промежутке
- Односторонние пределы
- Классификация точек разрыва
- Точки разрыва первого рода
- Точки разрыва второго рода
- Алгоритм исследования функции на непрерывность
- Примеры
п.1. Приращение аргумента и приращение функции
Приращением аргумента называют разность $$ triangle x= x-x_0 $$ где x – произвольное число, которое мало отличается от начальной точки (x_0). Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ triangle y=f(x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
 |
Пусть (y=3x-1) (x_0=1, x=1,1 ) Тогда begin{gather*} triangle x=x-x_0=0,1\ triangle y=(3x-1)-(3x_0-1)=\ =3(x-x_0 )=3triangle x=0,3 end{gather*} В данном случае приращение функции всегда в 3 три раза больше приращения аргумента. |
п.2. Непрерывность функции в точке и на промежутке
Функция (y=f(x)) непрерывна в точке (x_0), если в этой точке малому приращению аргумента (triangle x=x-x_0) соответствует малое приращение функции (triangle y=f(x)-f(x_0)): $$ lim_{triangle xrightarrow 0}triangle y=lim_{xrightarrow x_0}triangle y=0 $$
На «языке ε-δ» определение непрерывности будет следующим:
Функция (y=f(x)) непрерывна в точке (x_0), если для любого (varepsilongt 0) существует такое (delta(varepsilon)gt 0), что для любого (x, |x-x_0|ltdelta) выполняется (|f(x)-f(x_0)|ltvarepsilon:) $$ forall varepsilongt 0 existsdelta=delta(varepsilon)gt 0: forall x, |x-x_0|ltdeltaRightarrow |f(x)-a|ltvarepsilon $$
ε-δ определение непрерывности похоже на ε-δ определение предела функции, с той разницей, что модуль (|x-x_0|) может быть равен 0 для непрерывной функции, т.е. сама точка (x_0) входит в δ-окрестность.
Проанализируем предел приращения функции: begin{gather*} lim_{triangle xrightarrow 0}triangle y= lim_{triangle xrightarrow 0}left(f(x)-f(x_0)right)= lim_{triangle xrightarrow 0}f(x)-lim_{triangle xrightarrow 0}f(x_0)=\ =lim_{triangle xrightarrow 0}f(x)-f(x_0) end{gather*} т.к. (f(x_0)) – величина постоянная и от (triangle x) не зависит.
Для непрерывной функции: $$ lim_{triangle xrightarrow 0}triangle y =0 Leftrightarrow lim_{triangle xrightarrow 0}f(x)-f(x_0)=0Leftrightarrow lim_{triangle xrightarrow 0}f(x)=f(x_0) $$ Учитывая, что (triangle xrightarrow 0Leftrightarrow x-x_0rightarrow 0Leftrightarrow xrightarrow x_0)
получаем (lim{xrightarrow x_0}f(x)=f(x_0).)
Функция (y=f(x)) непрерывна в точке (x_0), если существует предел функции в этой точке и он равен значению функции в точке: $$ lim{xrightarrow x_0}f(x)=f(x_0) $$
Все три представленных определения непрерывности функции в точке эквивалентны.
Существуют и другие эквивалентные определения. Мы дадим ещё одно из них дальше, в этом же параграфе.
п.3. Непрерывность функции на промежутке
Промежуток – это интервал, отрезок, луч и т.п. (см. §16 справочника для 8 класса).
Функция (y=f(x)) непрерывна на промежутке, если она непрерывна в каждой точке этого промежутка.
График непрерывной функции – это непрерывная линия.
Кроме непрерывности, эта линия еще и «плавная», без «заломов».
При наличии заломов функция называется кусочно-непрерывной.
п.4. Односторонние пределы
Односторонний предел – это предел числовой функции при приближении к предельной точке с определенной стороны (слева или справа).
Обозначение односторонних пределов: begin{gather*} lim_{xrightarrow x_0 -0}f(x)=a – text{левый предел}\ lim_{xrightarrow x_0 +0}f(x)=b – text{правый предел} end{gather*}
Рассмотрим гиперболу (y=frac{1}{x-2}).
 |
У этой гиперболы две асимптоты (y=0) и (x=2). Точка (x_0=2) не входит в область определения. Если мы будем приближаться к (x_0=2) слева, начав, например с 1,5, мы будем постепенно опускаться по ветке гиперболы на минус бесконечность. Т.е., левый предел: $$ lim_{xrightarrow 2-0}frac{1}{x-2}=-infty $$ |
Если же мы будем приближаться к (x_0=2) справа, начав, например с 2,5, мы будем постепенно подниматься по ветке гиперболы на плюс бесконечность. Т.е., правый предел: $$ lim_{xrightarrow 2+0}frac{1}{x-2}=+infty $$ Левый и правый пределы в точке (x_0=2) для данной гиперболы не равны: $$ lim_{xrightarrow 2-0}frac{1}{x-2} ne lim_{xrightarrow 2+0}frac{1}{x-2} $$
Теперь рассмотрим параболу (y=x^2-2)
Областью определения параболы является вся числовая прямая (xinmathbb{R})
 |
В этом случае, если приближаться к (x_0=2) слева, мы получаем: $$ lim_{xrightarrow 2-0}(x^2-2)=2 $$ И если приближаться (x_0=2) справа, мы тоже получаем: $$ lim_{xrightarrow 2+0}(x^2-2)=2 $$ Левый и правый пределы равны: $$ lim_{xrightarrow 2-0}(x^2-2) =lim_{xrightarrow 2+0}(x^2-2) $$ |
Функция (y=f(x)) непрерывна в точке (x_0), если одновременно выполняются следующие три условия:
1) точка (x_0) принадлежит области определения функции (xin D);
2) левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ 3) предел функции в точке (x_0) равен значению функции в этой точке: $$ lim_{xrightarrow x_0}f(x)=f(x_0) $$
Это еще одно определение непрерывности, которым удобно пользоваться на практике.
п.5. Классификация точек разрыва
Точка (x_0) будет точкой разрыва для функции (y=f(x)), если выполняется хотя бы одно из условий:
1) точка (x_0) не принадлежит области определения функции (xnotin D);
2) левый и правый пределы в точке (x_0) не равны или бесконечны: $$ lim_{xrightarrow x_0 -0}f(x) nelim_{xrightarrow x_0 +0}f(x) text{или} lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=pminfty $$ 3) предел функции в точке (x_0) не совпадает со значением функции в этой точке: $$ lim_{xrightarrow x_0}f(x)ne f(x_0) $$
| Точки разрыва | 1-го рода Односторонние пределы существуют и конечны |
Устранимые Односторонние пределы равны между собой, но не равны (f(x_0)) |
| Неустранимые (скачок) Односторонние пределы не равны между собой |
||
| 2-го рода Хотя бы один из односторонних пределов бесконечен или не существует |
п.6. Точки разрыва первого рода
Устранимые точки разрыва 1-го рода
Левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x)=lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ НО:
либо точка (x_0) НЕ принадлежит области определения функции (xnotin D);
либо предел НЕ равен значению функции в точке (x_0): (lim_{xrightarrow x_0}f(x)ne f(x_0))
Например:
 |
(y=frac{x^2-4}{x-2}, x_0=2) Эта функция эквивалентна системе $$ y=frac{x^2-4}{x-2} Leftrightarrow begin{cases} y=x+2\ xne 2 end{cases} $$ При этом (lim_{xrightarrow 2-0}(x+2)=lim_{xrightarrow 2+0}(x+2)=4) В точке (x_0=2notin D) функция имеет устранимый разрыв. |
Разрыв можно устранить (функцию можно «склеить»), отдельно задав «гладкое» значение в особой точке: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} $$ В таком случае система станет эквивалентна всей прямой, т.е. станет непрерывной функцией: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} Leftrightarrow y=x+2 $$
Неустранимые точки разрыва 2-го рода (скачок)
Левый и правый пределы в точке (x_0) конечны, но не равны: $$ begin{cases} lim_{xrightarrow x_0 -0}f(x)=aneinfty\ lim_{xrightarrow x_0 +0}f(x)=bneinfty\ ane b end{cases} $$ Такой разрыв также называют скачком.
Величина скачка рассчитывается по формуле: $$ triangle y=lim_{xrightarrow x_0 +0}f(x)- lim_{xrightarrow x_0 -0}f(x)=b-a $$
Например:
 |
(y= begin{cases} x+1, xlt 2\ 3-x^2, xgeq 2 end{cases} , x_0=2) Односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}f(x)= lim_{xrightarrow 2-0}(x+1)=3\ lim_{xrightarrow 2+0}f(x)= lim_{xrightarrow 2+0}(3-x^2)=-1 end{gather*} Пределы не равны, но конечны. Функция в точке (x_0=2) делает скачок вниз. Величина скачка: $$ triangle y=-1-3=-4 $$ |
п.7. Точки разрыва второго рода
В точках разрыва 2-го рода хотя бы один из односторонних пределов бесконечен или не существует.
Например:
 |
(y=e^frac1x, x_0=0)
(x_0=0ne D) – точка не входит в ОДЗ Точка (x_0=0) – точка разрыва второго рода. |
На практике, при моделировании реальных процессов, разрывы 2-го рода в функциональных зависимостях встречаются довольно часто. Их положено заботливо анализировать и тщательно обходить, выбирая рабочие участки характеристических кривых, – чтобы «система не пошла в разнос».
п.8. Алгоритм исследования функции на непрерывность
На входе: функция (y=f(x))
Шаг 1. Найти ОДЗ функции, определить точки и промежутки, не принадлежащие ОДЗ.
Шаг 2. Составить множество точек, в которое входят точки и границы промежутков, не принадлежащие ОДЗ, а также – для кусочно-непрерывных функций – точки сшивания. Полученное множество состоит из точек, подозрительных на разрыв.
Шаг 3. Исследовать каждую из точек, подозрительных на разрыв, с помощью односторонних пределов. Если разрыв обнаружен, определить тип разрыва.
На выходе: список точек разрыва и тип разрыва для каждой точки.
п.9. Примеры
Пример 1. Исследуйте функцию на непрерывность:
a) ( y=frac{x+3}{x-1} )
ОДЗ: (x-1ne 0Rightarrow xne 1)
(x_0=1notin D) – точка не входит в ОДЗ, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 1-0}frac{x+3}{x-1}=frac{1-0+3}{1-0-1}=frac{4}{-0}=-infty\ lim_{xrightarrow 1+0}frac{x+3}{x-1}=frac{1+0+3}{1+0-1}=frac{4}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_0=1) – точка разрыва 2-го рода.
б) ( y=frac{x}{sqrt{x+2}-2} )
ОДЗ: ( begin{cases} x+2geq 0\ sqrt{x+2}-2ne 0 end{cases} Rightarrow begin{cases} xgeq -2\ sqrt{x+2}ne 2 end{cases} Rightarrow begin{cases} xgeq -2\ xne 2 end{cases} )
(x_0=-2) – левая граница ОДЗ
(x_1=2notin D)- точка не входит в ОДЗ
Точки (x_0) и (x_1) – подозрительные на разрыв
Исследуем (x_0=-2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} – text{предел не существует}\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{-2+0}{sqrt{-2+0+2}-2}=frac{-2}{-2}=1 end{gather*} Один из односторонних пределов не существует.
Точка (x_0=-2) – точка разрыва 2-го рода.
Исследуем (x_1=2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} =frac{2-0}{sqrt{2-0+2}-2}=frac{2}{-0}=-infty\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{2+0}{sqrt{2+0+2}-2}=frac{2}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_1=2) – точка разрыва 2-го рода.
в) ( y=frac{tgx}{3x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{tgx}{3x}=frac13lim_{xrightarrow -0}frac{tgx}{x}=frac13cdot 1=frac13\ lim_{xrightarrow +0}frac{tgx}{3x}=frac13lim_{xrightarrow +0}frac{tgx}{x}=frac13cdot 1=frac13 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) – точка разрыва 1-го рода, устранимый разрыв.
г) ( y= begin{cases} x+1, xlt 3\ x^2+3, xgeq 3 end{cases} )
ОДЗ: (xinmathbb{R})
(x_0=3)- точка сшивания, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 3-0}y=lim_{xrightarrow 3-0}(x+1)=3+1=4\ lim_{xrightarrow 3+0}y=lim_{xrightarrow 3+0}(x^2+3)=3^2+3=12 end{gather*} Односторонние пределы конечны, но неравны.
Точка (x_0=3) – точка разрыва 1-го рода, неустранимый разрыв (скачок).
Величина скачка: (lim_{xrightarrow 3+0}y-lim_{xrightarrow 3-0}y=12-4=8)
Пример 2. Доопределите функцию в точке разрыва так, чтобы она стала непрерывной в этой точке:
a) ( y=frac{2x^3-x^2}{7x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{2x^3-x^2}{7x}=frac{x^2(2x-1)}{7x}=frac{x(2x-1)}{7}) $$ y=frac{2x^3-x^2}{7x}Leftrightarrow y= begin{cases} frac{x(2x-1)}{7}\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{x(2x-1)}{7}=0, lim_{xrightarrow +0}frac{x(2x-1)}{7}=0 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) – точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=0).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{2x^3-x^2}{7x}, xne 0\ 0, x=0 end{cases} $$ б) ( y=frac{1-cos4x}{x^2} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{1-cos4x}{x^2}=frac{2sin^2 2x}{x^2}=frac{2sin^2 2x}{frac{(2x)^2}{4}}=8left(frac{sin2x}{2x}right)^2) $$ y=frac{1-cos4x}{x^2}Leftrightarrow y= begin{cases} 8left(frac{sin2x}{2x}right)^2\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8, lim_{xrightarrow +0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) – точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=8).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{1-cos4x}{x^2}, xne 0\ 8, x=0 end{cases} $$
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Непрерывность функции в точке
Функция f(x) является непрерывной в точке x0, если предел слева равен пределу справа и совпадает со значением функции в точке x0, т.е.: limx→x0-0f(x)=limx→x0+0f(x)=f(x0)
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
Дана функция f(x)=16(x-8)2-8. Необходимо доказать ее непрерывность в точке х0= 2.
Решение
В первую очередь, определим существование предела слева. Чтобы это сделать, используем последовательность аргументов хn, сводящуюся к х0 =2·(хn<2). Например, такой последовательностью может быть:
-2, 0, 1, 112, 134, 178, 11516,…, 110231024,…→2
Соответствующая последовательность значений функций выглядит так:
f(-2); f(0); f(1); f112; f134; f178; f11516;…; f110231024;…==8.667; 2.667; 0.167; -0.958; -1.489; -1.747; -1.874;…;-1.998;…→-2
на чертеже они обозначены зеленым цветом.
Достаточно очевидно, что такая последовательность сводится к -2, значит limx→2-016(x-8)2-8=-2.
Определим существование предела справа: используем последовательность аргументов хn, сводящуюся к х0= 2 (хn>2). Например, такой последовательностью может быть:
6, 4, 3, 212, 214, 218, 2116,…, 211024,…→2
Соответствующая последовательность функций:
f(6); f(4); f(3); f212; f214; f218; f2116;…; f211024;…==-7.333; -5.333; -3.833; -2.958; -2.489; -2.247; -2.247; -2.124;…; -2.001;…→-2
на рисунке обозначена синим цветом.
И эта последовательность сводится к -2, тогда limx→2+016(x-8)2-8=-2.
Действиями выше было показано, что пределы справа и слева являются равными, а значит существует предел функции f(x)=16x-82-8 в точке х0= 2, при этом limx→216(x-8)2-8=-2.
После вычисления значения функции в заданной точке очевидно выполнение равенства:
limx→2-0f(x)=limx→2+0f(x)=f(2)=16(2-8)2-8=-2 что свидетельствует о непрерывности заданной функции в заданной точке.
Покажем графически:
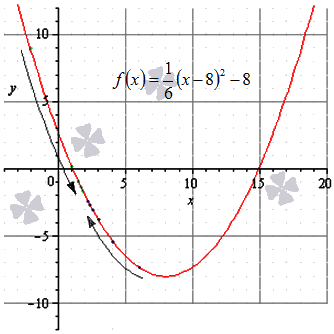
Ответ: Непрерывность функции f(x)=16(x-8)2-8 в заданной части доказано.
Устранимый разрыв первого рода
Функция имеет устранимый разрыв первого рода в точке х0, когда пределы справа и слева равны, но не равны значению функции в точке, т.е.:
limx→x0-0f(x)=limx→x0+0f(x)≠f(x0)
Задана функция f(x)=x2-25x-5. Необходимо определить точки ее разрыва и определить их тип.
Решение
Сначала обозначим область определения функции: D(f(x))⇔Dx2-25x-5⇔x-5≠0⇔x∈(-∞; 5)∪(5; +∞)
В заданной функции точкой разрыва может служить только граничная точка области определения, т.е. х0= 5. Исследуем функцию на непрерывность в этой точке.
Выражение x2-25x-5 упростим: x2-25x-5=(x-5)(x+5)x-5=x+5.
Определим пределы справа и слева. Поскольку функция g(x)=x+5 является непрерывной при любом действительном x, тогда:
limx→5-0(x+5)=5+5=10limx→5+0(x+5)=5+5=10
Ответ: пределы справа и слева являются равными, а заданная функция в точке х0= 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Функция имеет неустранимый разрыв первого рода в точке х0, когда пределы справа и слева не являются равными, т.е.: limx→x0-0f(x)≠limx→x0+0f(x). Точка х0 здесь – точка скачка функции.
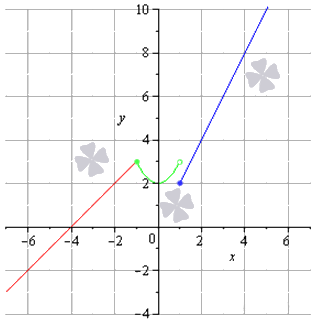
Задана кусочно-непрерывная функция f(x)=x+4, x<-1,x2+2, -1≤x<12x, x≥1. Необходимо изучить заданную функцию на предмет непрерывности, обозначить вид точек разрыва, составить чертеж.
Решение
Разрывы данной функции могут быть лишь в точке х0=-1 или в точке х0=1.
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
- слева от точки х0=-1 заданная функция есть f(x)=x+4, тогда в силу непрерывности линейной функции: limx→-1-0f(x)=limx→-1-0(x+4)=-1+4=3;
- непосредственно в точке х0=-1 функция принимает вид: f(x)=x2+2, тогда: f(-1)=(-1)2+2=3;
- на промежутке (-1; 1) заданная функция есть: f(x)=x2+2. Опираясь на свойство непрерывности квадратичной функции, имеем: limx→-1+0f(x)=limx→-1+0(x2+2)=(-1)2+2=3limx→1-0f(x)=limx→1-0(x2+2)=(1)2+2=3
- в точке х0=-1 функция имеет вид: f(x)=2x и f(1)=2·1=2.
- справа от точки х0 заданная функция есть f(x)=2x. В силу непрерывности линейной функции: limx→1+0f(x)=limx→1+0(2x)=2·1=2
Ответ: в конечном счете мы получили:
- limx→-1-0f(x)=limx→-1+0f(x)=f(-1)=3 – это означает, что в точке х0=-1 заданная кусочная функция непрерывна;
- limx→-1-0f(x)=3, limx→1+0f(x)=2 – таким образом, в точке х0=1 определён неустранимый разрыв первого рода (скачок).
Нам остается только подготовить чертеж данного задания.
Разрыв второго рода (бесконечный разрыв)
Функция имеет разрыв второго рода в точке х0, когда какой-либо из пределов слева limx→x0-0f(x) или справа limx→x0+0f(x) не существует или бесконечен.
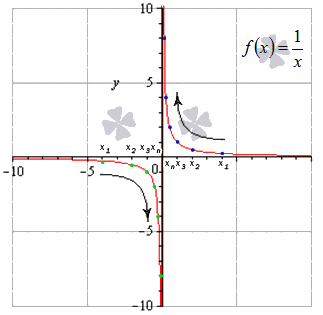
Задана функция f(x)=1x. Необходимо исследовать заданную функцию на непрерывность, определить вид точек разрыва, подготовить чертеж.
Решение
Запишем область определения функции: x∈(-∞; 0)∪(0; +∞).
Найдем пределы справа и слева от точки х0= 0.
Зададим произвольную последовательность значений аргумента, сходящуюся к х0 слева. К примеру:
-8; -4; -2; -1; -12; -14;…; -11024;…
Ей соответствует последовательность значений функции:
f(-8); f(-4); f(-2); f(-1); f-12; f-14;…; f-11024;…==-18;-14; -12; -1; -2; -4;…; -1024;…
Очевидно, что эта последовательность является бесконечно большой отрицательной, тогда limx→0-0f(x)=limx→0-01x=-∞.
Тепереь зададим произвольную последовательность значений аргумента, сходящуюся к х0 справа. К примеру: 8; 4; 2; 1; 12; 14;…; 11024;…, и ей соответствует последовательность значений функции:
f(8); f(4); f(2); f(1); f12; f14;…; f11024;…==18; 14; 12; 1; 2; 4;…; 1024;…
Эта последовательность – бесконечно большая положительная, а значит limx→0+0f(x)=limx→0+01x=+∞.
Ответ: точка х0= 0 – точка разрыва функции второго рода.
Проиллюстрируем:
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Рассмотрим
некоторую функцию f(x),
непрерывную в окрестности точки х0,
за исключением может быть самой этой
точки. Из определения точки разрыва
функции следует, что х = х0является
точкой разрыва, если функция не определена
в этой точке, или не является в ней
непрерывной.
Следует отметить также, что непрерывность
функции может быть односторонней.
Поясним это следующим образом.
Если
односторонний предел (см. выше)
,
то функция называется непрерывной
справа.
х0
Если
односторонний предел (см. выше)
,
то функция называется непрерывной
слева.
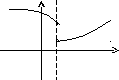
х0
Определение.Точка х0называетсяточкой разрыва функцииf(x), если
f(x) не определена в точке х0или не
является непрерывной в этой точке.
Определение.Точка х0называетсяточкой
разрыва 1- го рода, если в этой точке
функцияf(x)
имеет конечные, но не равные друг другу
левый и правый пределы.
Для выполнения условий этого определения
не требуется, чтобы функция была
определена в точке х = х0, достаточно
того, что она определена слева и справа
от нее.
Из определения можно сделать вывод, что
в точке разрыва 1 – го рода функция может
иметь только конечный скачок. В некоторых
частных случаях точку разрыва 1 – го
рода еще иногда называют устранимой
точкой разрыва, но подробнее об этом
поговорим ниже.
Определение.Точка х0называетсяточкой разрыва 2 – го рода,
если в этой точке функцияf(x)
не имеет хотя бы одного из односторонних
пределов или хотя бы один из них
бесконечен.
Пример.Функция Дирихле (Дирихле
Петер Густав(1805-1859) – немецкий математик,
член- корреспондент Петербургской АН
1837г)
не является
непрерывной в любой точке х0.
Пример.Функцияf(x)
=
имеет в точке х0= 0 точку разрыва
2 – го рода, т.к.
.
Пример.f(x) =
Функция не
определена в точке х = 0, но имеет в ней
конечный предел
,
т.е. в точке х = 0 функция имеет точку
разрыва 1 – го рода. Это – устранимая
точка разрыва, т.к. если доопределить
функцию:
График этой
функции:
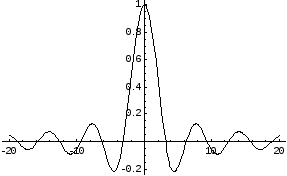
Пример.f(x) =
=
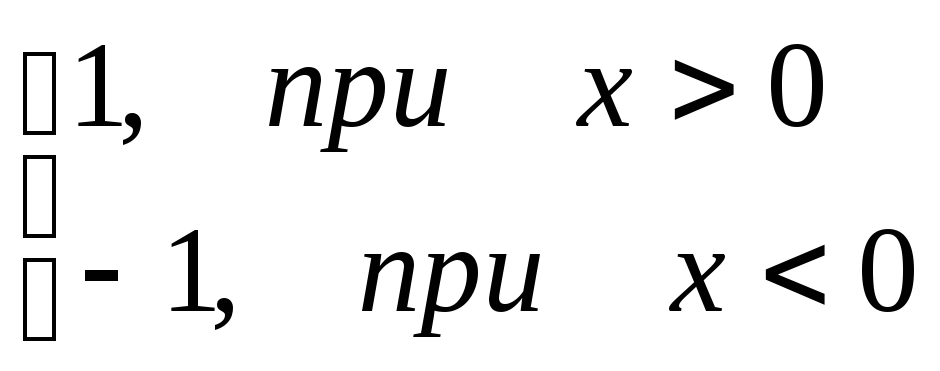
y
1
0 x
-1
Эта функция
также обозначается sign(x)
– знак х. В точке х = 0 функция не определена.
Т.к. левый и правый пределы функции
различны, то точка разрыва – 1 – го рода.
Если доопределить функцию в точке х =
0, положивf(0) = 1, то функция
будет непрерывна справа, если положитьf(0) = -1, то функция будет
непрерывной слева, если положитьf(x)
равное какому- либо числу, отличному от
1 или –1, то функция не будет непрерывна
ни слева, ни справа, но во всех случаях
тем не менее будет иметь в точке х = 0
разрыв 1 – го рода. В этом примере точка
разрыва 1 – го рода не является устранимой.
Таким образом,
для того, чтобы точка разрыва 1 – го рода
была устранимой, необходимо, чтобы
односторонние пределы справа и слева
были конечны и равны, а функция была бы
в этой точке не определена.
§9. Непрерывность функции на интервале и на отрезке.
Определение.Функцияf(x)
называетсянепрерывной на интервале
(отрезке), если она непрерывна в любой
точке интервала (отрезка).
При этом не
требуется непрерывность функции на
концах отрезка или интервала, необходима
только односторонняя непрерывность на
концах отрезка или интервала.
Свойства
функций, непрерывных на отрезке.
Свойство
1:(Первая теорема Вейерштрасса
(Вейерштрасс Карл (1815-1897)- немецкий
математик)). Функция, непрерывная на
отрезке, ограничена на этом отрезке,
т.е. на отрезке [a,b]
выполняется условие –M£f(x)£M.
Доказательство этого свойства основано
на том, что функция, непрерывная в точке
х0, ограничена в некоторой ее
окрестности, а если разбивать отрезок
[a,b] на
бесконечное количество отрезков, которые
“стягиваются” к точке х0, то
образуется некоторая окрестность точки
х0.
Свойство 2:Функция, непрерывная
на отрезке [a,b],
принимает на нем наибольшее и наименьшее
значения.
Т.е. существуют такие значения х1и х2, чтоf(x1)
=m,f(x2)
=M, причем
m£f(x)£M
Отметим эти наибольшие и наименьшие
значения функция может принимать на
отрезке и несколько раз (например –
f(x) =sinx).
Разность между наибольшим и наименьшим
значением функции на отрезке называется
колебанием функции на отрезке.
Свойство 3:(Вторая теорема
Больцано – Коши). Функция, непрерывная
на отрезке [a,b],
принимает на этом отрезке все значения
между двумя произвольными величинами.
Свойство 4:Если функцияf(x)
непрерывна в точке х = х0, то
существует некоторая окрестность точки
х0, в которой функция сохраняет
знак.
Свойство 5:(Первая теорема
Больцано (1781-1848) – Коши). Если функцияf(x)- непрерывная
на отрезке [a,b]
и имеет на концах отрезка значения
противоположных знаков, то существует
такая точка внутри этого отрезка, гдеf(x) = 0.
Т.е. если
sign(f(a)) ¹
sign(f(b)), то $
х0:
f(x0)
= 0.
Определение.Функцияf(x)
называетсяравномерно непрерывнойна отрезке [a,b],
если для любогоe>0
существуетD>0 такое,
что для любых точек х1Î[a,b]
иx2Î[a,b]
таких, что
ïх2– х1ï<D
верно
неравенство ïf(x2)
–f(x1)ï<e
Отличие
равномерной непрерывности от “обычной”
в том, что для любого eсуществует своеD, не
зависящее от х, а при “обычной”
непрерывностиDзависит отeи х.
Свойство
6:Теорема Кантора (Кантор Георг
(1845-1918)- немецкий математик). Функция,
непрерывная на отрезке, равномерно
непрерывна на нем.
(Это свойство
справедливо только для отрезков, а не
для интервалов и полуинтервалов.)
Пример.
Функция
непрерывна на интервале (0, а), но не
является на нем равномерно непрерывной,
т.к. существует такое числоD>0
такое, что существуют значения х1и х2такие, чтоïf(x1)
–f(x2)ï>e,e- любое
число при условии, что х1и х2близки к нулю.
Свойство
7:Если функцияf(x)
определена, монотонна и непрерывна на
некотором промежутке, то и обратная ей
функция х =g(y)
тоже однозначна, монотонна и непрерывна.
Пример.Исследовать на непрерывность функцию
и определить тип точек разрыва, если
они есть.
в точке х = -1
функция непрерывна в точке х = 1
точка разрыва 1 – го рода
у
3
2
-4
-1 0 1 х
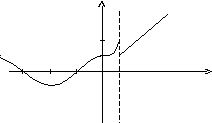
Пример.Исследовать на непрерывность
функцию и определить тип точек разрыва,
если они есть.
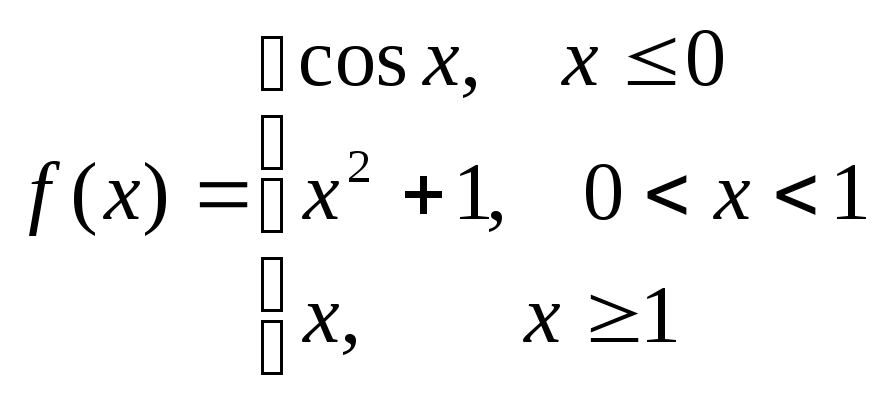
в точке х = 0
функция непрерывна в точке х = 1
точка разрыва 1 – го рода
у
2
1
-p-p/2 0 1x
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Непрерывность функции
4 раздела
от теории до практики
1 пример
Примеры решения задач
видео
Примеры решения задач
-
Понятие непрерывности функции.
Начать изучение
-
Точки разрыва.
Начать изучение
-
Свойства функций, непрерывных в точке.
Начать изучение
-
Локальные свойства непрерывной функции.
Начать изучение
-
Непрерывность суммы, произведения и частного.
Начать изучение
-
Непрерывность сложной функции.
Начать изучение
-
Свойства функций, непрерывных на отрезке.
Начать изучение
-
Ограниченность непрерывной на отрезке функции.
Начать изучение
-
Достижимость точных граней.
Начать изучение
-
Промежуточные значения.
Начать изучение
-
Существование и непрерывность функции, обратной для непрерывной и строго монотонной функции.
Начать изучение
Понятие непрерывности функции.
Определение 1
Функция (f(x)), определенная в некоторой окрестности точки (a), называется непрерывной в точке (a), если
$$
displaystyle lim_{xrightarrow a}f(x)=f(a)label{ref1}
$$
Таким образом, функция (f) непрерывна в точке (a), если выполнены следующие условия:
- функция (f) определена в некоторой окрестности точки (a), то есть существует число (delta_0>0) такое, что (U_{delta_{0}}(a)subset D(f));
- существует (displaystyle lim_{xrightarrow a}f(x)=A);
- (A=f(a)).
Определение непрерывности функции (f(x)) в точке (a), выраженное условием eqref{ref1}, можно сформулировать с помощью неравенств (на языке (varepsilon-delta)), с помощью окрестностей и в терминах последовательностей соответственно в виде
- (forall varepsilon>0 existsdelta>0:quadforall x:|x-a| < deltarightarrow|f(x)-f(a)| < varepsilon,)
- (forall varepsilon>0 existsdelta>0:quadforall xin U_{delta}(a)rightarrow f(x)in U_{varepsilon}(f(a)),)
- (displaystyleforall{x_{n}}: lim_{nrightarrowinfty}x_{n}=arightarrowlim_{nrightarrowinfty}f(x_{n})=f(a).)
Следует обратить внимание на то, что в определении непрерывности функции, в отличие от определения предела, рассматривается полная, а не проколотая окрестность точки (a), и пределом функции является значение этой функции в точке (a).
Назовем разность (x-a) приращением аргумента и обозначим (Delta x), а разность (f(x)-f(a)) — приращением функции, соответствующим данному приращению аргумента (Delta x), и обозначим (Delta y). Таким образом,
$$
Delta x=x-a,;Delta y=f(x)-f(a)=f(a+Delta x)-f(a).nonumber
$$
При этих обозначениях равенство eqref{ref1} примет вид
$$
lim_{Delta xrightarrow 0}Delta y=0.nonumber
$$
Таким образом, непрерывность функции в точке означает, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Пример 1
Показать, что функция (f(x)) непрерывна в точке (a), если:
- (f(x)=x^3, a=1);
- (f(x)=displaystyle frac{1}{x^{2}}, aneq 0);
- (f(x)=sqrt{x}, a>0);
- (f(x)=displaystyle left{begin{array}{lc}xsinfrac1x,&xneq0,\0,&x=0,end{array}right.a=0)
Решение
- (triangle)Если (xrightarrow 1), то по свойствам пределов (S 10, (11)) получаем (x^3rightarrow 1), то есть для функции (f(x)=x^3) в точке (x=1) выполняется условие eqref{ref1}. Поэтому функция (x^3) непрерывна в точке (x=1).
- Если (xrightarrow a), где (aneq 0), то, используя свойства пределов (S 10), получаем (displaystyle frac{1}{x}rightarrowfrac{1}{a},;displaystyle frac{1}{x^{2}}rightarrowfrac{1}{a^{2}}), то есть Функция (displaystyle frac{1}{x^{2}}) непрерывна в точке (x=a,;(aneq 0)).
- Так как (displaystyle |sqrt{x}-sqrt{a}|=frac{|x-a|}{sqrt{x}+sqrt{a}}), то отсюда получаем (0leq|sqrt{x}-sqrt{a}|;<;displaystylefrac{|x-a|}{sqrt{a}}). Следовательно, (sqrt{x}-sqrt{a}rightarrow 0) при (xrightarrow a). Это означает, что функция (sqrt{x}) непрерывна в точке (a), где (a>0).
- Функция (f) определена на (mathbb{R}), и при любом (xinmathbb{R}) выполняется неравенство (0leq|f(x)-f(0)|=|f(x)|leq|x|), так как (left|sin{frac{1}{x}}right|leq1) при (xneq 0). Следовательно, (displaystyle lim_{xrightarrow 0}f(x)=f(0)=0), то есть функция (f) непрерывна в точке (x=0.quadblacktriangle)
По аналогии с понятием предела слева (справа) вводится понятие непрерывности слева (справа). Если функция (f) определена на полуинтервале ((a-delta,a]) и (displaystyle lim_{xrightarrow a-0}f(x)=f(a)), то есть(f(a-0)=f(a)), то эту функцию называют непрерывной слева в точке (a).
Аналогично, если функция (f) определена на полуинтервале ([a,a+delta)) и (f(a+0)=f(a)), то эту функцию называют непрерывной справа в точке (a).
Например, функция (f(x)=[x]) непрерывна справа в точке (x=1) и не является непрерывной слева в этой точке, так как (f(1-0)=0,;f(1+0)=f(1)=1).
Очевидно, функция непрерывна в данной точке тогда и только тогда, когда она непрерывна как справа, так и слева в этой точке.
Точки разрыва.
Будем предполагать, что функция (f) определена в некоторой проколотой окрестности точки (a).
Точку (a) назовем точкой разрыва функции (f), если эта функция либо не определена в точке (a), либо определена, но не является непрерывной в точке (a).
Следовательно, (a) — точка разрыва функции (f), если не выполняется по крайней мере одно из следующих условий:
- (ain D(f));
- существует конечный (displaystyle lim_{xrightarrow a}f(x)=A);
- (A=f(a)).
Определение 2
Если (a) — точка разрыва функции (f), причем в этой точке существуют конечные пределы слева и справа, то есть (displaystyle lim_{xrightarrow a-0}f(x)=f(a-0)) и (displaystyle lim_{xrightarrow a+0}f(x)=f(a+0)), то точку (a) называют точкой разрыва первого рода.
Замечание 1
Если (x=a) — точка разрыва первого рода функции (f(x)), то разность (f(a+0)-f(a-0)) называют скачком функции в точке (a). В случае когда (f(a+0)=f(a-0)), точку (a) называют точкой устранимого разрыва. Полагая (f(a)=f(a+0)=f(a-0)=A), получим функцию
$$
f(x)=left{begin{array}{l}f(x),;если;xneq a,\A,;если;x=a,end{array}right.nonumber
$$
непрерывную в точке (a) и совпадающую с (f(x)) при (xneq a). В этом случае говорят, что функция доопределена до непрерывности в точке (a).
Пусть (x=a) — точка разрыва функции (f), не являющаяся точкой разрыва первого рода. Тогда ее называют точкой разрыва второго рода функции (f). В такой точке хотя бы один из односторонних пределов либо не существует, либо бесконечен.
Например, для функции (f(x)=displaystyle xsin{frac{1}{x}}) точка (x=0) — точка разрыва первого рода. Доопределив эту функцию по непрерывности, получим функцию
$$
overline{f}(x)=left{begin{array}{ll}
xsin{frac{1}{x}},;если;xneq 0,\
0,;если;x=0,
end{array}right.nonumber
$$
непрерывную в точке (x=0), так как
$$
lim_{xrightarrow 0}xsinfrac{1}{x}=0.nonumber
$$
Для функций (displaystyle sin{frac{1}{x}}) и (displaystyle frac{1}{x^2}) точка (x=0) — точка разрыва второго рода.
Теорема 1
Если функция (f) определена на отрезке ([a,b]) и монотонна, то она может иметь внутри этого отрезка точки разрыва только первого рода.
Доказательство
(circ) Пусть (x_0) — произвольная точка интервала ((a,b)). Функция (f) имеет в точке (x_{0}) конечные пределы слева и справа. Если, например, (f) — возрастающая функция, то
$$
f(x_{0}-0)leq f(x_{0})leq f(x_{0}+0),nonumber
$$
где (f(x_{0}-0)) и (f(x_{0}+0)) — соответственно пределы функции (f) слева и справа в точке (x_{0}).
В том случае, когда (f(x_{0}-0)neq f(x_{0}+0)) , точка (x_{0}) является точкой разрыва первого рода функции (f); если же (f(x_{0}-0)=f(x_{0}+0)), то точка (x_{0}) есть точка непрерывности функции (f). Аналогичное утверждение справедливо и для убывающей функции.(bullet)
Свойства функций, непрерывных в точке.
Локальные свойства непрерывной функции.
Свойство 1
Если функция (f) непрерывна в точке (a), то она ограничена в некоторой окрестности этой точки, то есть
$$
existsdelta>0quadexists C>0:;forall xin U_{delta}(a)rightarrow|f(x)|leq Cnonumber
$$
Свойство 2
Если функция (f) непрерывна в точке (a), причем (f(a)neq 0), то в некоторой окрестности точки (a) знак функции совпадает со знаком числа (f(a)), то есть
$$
existsdelta>0:quadforall xin U_{delta}(a)rightarrow operatorname{sign} f(x)=operatorname{sign} f(a).nonumber
$$
(circ) Эти утверждения следуют из свойств пределов. (bullet)
Непрерывность суммы, произведения и частного.
Свойство 3
Если функции (f) и (g) непрерывны в точке (a), то функции (f+g), (fg) и (f/g) (при условии (g(a)neq 0)) непрерывны в точке (a).
(circ) Это утверждение следует из определения непрерывности и свойств пределов. (bullet)
Непрерывность сложной функции.
Напомним, что такое сложная функция.
Пусть функции (y=varphi(x)) и (z=f(y)) определены на множествах (X) и (Y) соответственно, причем множество значений функции (varphi) содержится в области определения функции (f). Тогда функция, которая принимает при каждом (xin X) значение (F(x)=f(varphi(x))), называется сложной функцией или суперпозицией (композицией) функций (varphi) и (f).
Теорема 2
Если функция (z=f(y)) непрерывна в точке (y_0), а функция (y=varphi(x)) непрерывна в точке (x_0), причем (y_0=varphi(x_0)), то в некоторой окрестности точки (x_0) определена сложная функция (f(varphi(x_0))), и эта функция непрерывна в точке (x_0).
Доказательство
(circ) Пусть задано произвольное число (varepsilon>0). В силу непрерывности функции (f) в точке (y_0) существует число (rho=rho(varepsilon)>0) такое, что (U_rho(y_0)subset D(f)) и
$$
forall yin U_rho(y_0)rightarrow f(y)in U_{varepsilon}(z_{0}),label{ref2}
$$
где (z_{0}=f(y_{0})).
В силу непрерывности функции (varphi) в точке (x_{0}) для найденного в eqref{ref2} числа (rho>0) можно указать число (delta=delta_{rho}=delta(varepsilon)>0) такое, что
$$
forall xin U_delta(x_0)rightarrow phi (x)in U_rho (y_0).label{ref2′}
$$
Из условий eqref{ref2} и eqref{ref2′} следует, что на множестве (U_delta(x_0)) определена сложная функция (f(varphi(x))), причем
$$
forall xin U_delta(x_0)rightarrow f(y)=f(varphi(x))in U_{varepsilon}(z_{0}),nonumber
$$
где (z_0=f(varphi(x_0))=f(y_{0})), то есть
$$
forall varepsilon>0;exists delta>0:quad forall хin U_delta(x_0)rightarrow f(varphi(х))in U_varepsilon(varphi(x_0)).nonumber
$$
Это означает, в силу определения непрерывности, что функция (f(varphi(x))) непрерывна в точке (x_0). (bullet)
Замечание 2
Соответствие между окрестностями точек (x_0, y_0, z_0) представлено на рис. 11.1. По заданному числу (varepsilon>0) сначала находим (rho>0), а затем для чисел (rho>0) находим (delta>0).
Свойства функций, непрерывных на отрезке.
Функцию (f(x)) называют непрерывной на отрезке ([a,b]), если она непрерывна в каждой точке интервала ((a,b)) и, кроме того, непрерывна справа в точке (a) и непрерывна слева в точке (b).
Ограниченность непрерывной на отрезке функции.
Теорема 3
(Теорема Вейерштрасса)
Если функция (f) непрерывна на отрезке ([a,b]), то она ограничена, то есть
$$
exists C>0:forall xin[a, b]rightarrow|f(x)|leq C.label{ref3}
$$
Доказательство
(circ) Предположим противное, тогда
$$
forall C>0;exists x_{C}in [a,b]:;|f(x_{C})|>C.label{ref4}
$$
Полагая в этом выражении (C=1,2ldots,n,ldots,) получим, что
$$
forall ninmathbb{N}quadexists x_{n}in[a,b]:;|f(x_{n})|>n.label{ref5}
$$
Последовательность (x_n) ограничена, так как (aleq x_{n}leq b) для всех (ninmathbb{N}). По теореме Больцано-Вейерштрасса из нее можно выделить сходящуюся подпоследовательность, то есть существуют подпоследовательность (x_{n_k}) и точка (xi) такие, что
$$
lim_{krightarrowinfty}x_{n_{k}}=xi,label{ref6}
$$
где в силу условия eqref{ref5} для любого (kinmathbb{N}) выполняется неравенство
$$
aleq x_{n_{k}}leq b.label{ref7}
$$
Из условий eqref{ref6} и eqref{ref7} следует, что (xiin [а,b]) а из условия eqref{ref6} в силу непрерывности функции (f) в точке (xi) получаем
$$
displaystyle lim_{krightarrowinfty}f(x_{n_{k}})=f(xi).label{ref8}
$$
С другой стороны. утверждение eqref{ref5} выполняется при всех (ninmathbb{N}) и, в частности, при (n=n_k;(k=1,2,ldots)), то есть
$$
|f(x_{n_{k}})|>n_{k},nonumber
$$
откуда следует, что (displaystyle lim_{krightarrowinfty}f(x_{n_{k}})=infty), так как (n_{k}rightarrow +infty) при (krightarrowinfty). Это противоречит равенству eqref{ref8}, согласно которому последовательность ({f(x_{n_{k}})}) имеет конечный предел. По этому условие eqref{ref4} не может выполняться, то есть справедливо утверждение eqref{ref3}. (bullet)
Замечание 3
Теорема Вейерштрасса неверна для промежутков, не являющихся отрезками. Например, функция (f(x)=displaystyle frac{1}{x}) непрерывна на интервале ((0,1)), но не ограничена на этом интервале. Функция (f(x)=x^{2}) непрерывна на (mathbb{R}), но не ограничена на (mathbb{R}).
Достижимость точных граней.
Теорема 4
(Теорема Вейерштрасса)
Если функция (f) непрерывна на отрезке ([a,b]), то она достигает своей точной верхней и нижней грани, то есть
$$
existsxiin[a,b]:quad f(xi)=sup_{xin [a,b]} f(x),label{ref9}
$$
$$
existswidetilde{xi}in[a,b]:quad f(widetilde{xi})= displaystyle inf_{xin [a,b]} f(x).label{ref10}
$$
Доказательство
(circ) Так как непрерывная на отрезке функция (f(x)) ограничена (теорема 3), то есть множество значений, принимаемых функцией (f) на отрезке ([a,b]), ограничено, то существуют (displaystyle sup_{xin[a,b]}f(x)) и (displaystyle inf_{xin[a,b]}f(x)).
Докажем утверждение eqref{ref9}. Обозначим (M=displaystyle sup_{xin[a,b]}f(x)). В силу определения точной верхней грани выполняются условия
$$
forall хin [a,b]rightarrow f(x)leq M,label{ref11}
$$
$$
forallvarepsilon>0;exists x(varepsilon)in[a,b]:quad f(x(varepsilon))>M-varepsilon.label{ref12}
$$
Полагая (varepsilon=displaystyle frac{1}{2}, displaystyle frac{1}{3},ldots,frac{1}{n},ldots), получим в силу условия eqref{ref12} последовательность({x_n}), где (x_n=displaystyle xleft(frac1nright)), такую, что для всех (ninmathbb{N}) выполняются условия
$$
x_nin [a,b],label{ref13}
$$
$$
f(x_{n})>M-displaystyle frac{1}{n}.label{ref14}
$$
Из соотношений eqref{ref11}, eqref{ref13} и eqref{ref14} следует, что
$$
forall ninmathbb{N}rightarrow M-frac{1}{n};<;f(x_{n})leq M,nonumber
$$
откуда получаем
$$
lim_{xrightarrowinfty}f(x_{n})=M.label{ref15}
$$
Как и в теореме 3, из условия eqref{ref13} следует, что существуют подпоследовательность ({x_{n_k}}) последовательности ({x_n}) и точка (xi) такие, что
$$
lim_{krightarrowinfty}x_{n_k}=xi,quad где xiin[a,b].nonumber
$$
В силу непрерывности функции (f) в точке (xi)
$$
lim_{krightarrowinfty} f(x_{n_{k}})=f(xi).label{ref16}
$$
С другой стороны, ({f(x_{n_{k}})}) — подпоследовательность последовательности ({f(x_{n})}), сходящейся, согласно условию eqref{ref15}, к числу (М). Поэтому
$$
lim_{krightarrowinfty}f(x_{n_{k}})=M.label{ref17}
$$
В силу единственности предела последовательности из eqref{ref16} и eqref{ref17} заключаем, что (f(xi)=M=displaystyle sup_{xin [a,b]}f(x)). Утверждение eqref{ref9} доказано. Аналогично доказывается утверждение eqref{ref10}. (bullet)
Замечание 4
Теорема 4 неверна для интервалов: функция, непрерывная на интервале, может не достигать своих точных граней. Например, функция (f(x)=x^{2}) не достигает на интервале (0,1) своей точной нижней грани, равной нулю, и точной верхней грани, равной единице.
Промежуточные значения.
Теорема 5
(теорема Коши о нулях непрерывной функции)
Если функция (f) непрерывна на отрезке [a,b] и принимает в его концах значения разных знаков, то есть (f(a)f(b);<;0), то на отрезке [a,b] имеется хотя бы один нуль функции (f), то есть
$$
exists cin[a,b]:; f(c)=0.label{ref18}
$$
Доказательство
(circ) Разделим отрезок ([a,b]) пополам. Пусть (d) — середина этого отрезка. Если (f(d)=0), то теорема доказана, а если (f(d)neq 0), то в концах одного из отрезков ([a,d], [d,b]) функция (f) принимает значения разных знаков. Обозначим этот отрезок (Delta_{1}=[a_{1},b_{1}]). Пусть (d_{1}) — середина отрезка (Delta_1). Возможны два случая:
- (f(d_{1})=0), тогда теорема доказана;
- (f(d_{1})neq 0), тогда в концах одного из отрезков ([a_{1},d_{1}],;[d_{1},b_{1}]) функция (f) принимает значения разных знаков; такой отрезок обозначим (Delta_{2}=[a_{2},b_{2}]).
Продолжая эти рассуждения, получим:
-
- либо через конечное число шагов найдется точка (cin [a,b]) такая, что (f(c)=0); тогда теорема доказана;
- либо существует последовательность отрезков ({Delta_n}) такая, что (f(a_{n})f(b_{n});<;0) для всех (ninmathbb{N}), где (Delta_n=[a_{n},b_{n}]).
Во втором случае последовательность отрезков является стягивающейся (S 6,п.4), так как (Delta_nsubsetDelta_{n-1}) для любого (ninmathbb{N}) и
$$
b_{n}-a_{n}=displaystyle frac{b-a}{2^{n}}.label{ref19}
$$
По теореме Кантора существует точка (c), принадлежащая всем отрезкам последовательности ({Delta_n}), то есть
$$
exists c:;forall ninmathbb{N}rightarrow сin [a_{n},b_{n}]subset[a,b].label{ref20}
$$
Докажем, что
$$
f(с)=0.label{ref21}
$$
Предположим, что равенство eqref{ref21} не выполняется. Тогда либо (f(с)>0), либо (f(с);<;0). Пусть, например, (f(с)>0). По свойству сохранения непрерывной функцией знака (п.3 а))
$$
existsdelta>0:quad хin U_delta(c)rightarrow f(x)>0.label{ref22}
$$
С другой стороны, из неравенства eqref{ref19} следует, что (b_{n}-a_{n}rightarrow 0) при (nrightarrowinfty), и поэтому
$$
exists n_0inmathbb{N}:quad b_{n_{0}}-a_{n_{0}};<;delta.label{ref23}
$$
Так как (cinDelta_{n_0}) в силу условия eqref{ref20}, то из eqref{ref23}следует, что (Delta_{n_0}subset U_{delta}(c)) и согласно условию eqref{ref22} во всех точках отрезка (Delta_{n_0}) функция (f) принимает положительные значения. Это противоречит тому, что в концах каждого из отрезков (Delta_n) функция (f) принимает значения разных знаков.
Полученное противоречие доказывает, что должно выполняться условие eqref{ref21}. (bullet)
Замечание 5
Теорема 5 утверждает, что график функции (y=f(x)), непрерывной на отрезке ([a,b]) и принимающей в его концах значения разных знаков, пересекает ось (Ox) (рис. 11.2) хотя бы в одной точке отрезка ([a,b]).
Теорема 6
(теорема Коши о промежуточных значениях)
Если функция (f) непрерывна на отрезке ([a,b]) и (f(a)neq (b)), то для каждого значения (C), заключенного между (f(a)) и (f(b)), найдется точка (xiin [a,b]) такая, что (f(xi)=C).
Доказательство
(circ) Обозначим (f(a)=A, f(b)=B). По условию (Аneq В). Пусть, например, (A < B). Нужно доказать, что
$$
forall Cin[A,B] existsxiin[a,b]: f(xi)=C.label{ref24}
$$
Если (C=A), то утверждение eqref{ref24} выполняется при (xi=a), а если (C=B), то eqref{ref24} имеет место при (xi=b). Поэтому достаточно рассмотреть случай (A < C < B).
Пусть (varphi(х)=f(x)-C), тогда (varphi(a)=A-C < 0, varphi(b)=B-С>0) и по теореме 5 найдется точка (xiin [a,b]) такая, что (varpi(xi)=0), то есть (f(xi)=C). Утверждение eqref{ref24} доказано. (bullet)
Следствие
Если функция (f) непрерывна на отрезке ([a,b], m=displaystyle inf_{xin[a,b]} f(x), M=displaystyle sup_{xin[a,b]} f(x)), то множество значений, принимаемых функцией (f) на отрезке ([a,b]), есть отрезок ([m,M]).
(circ) Для всех (xin[a,b]) выполняется неравенство (mleq f(x)leq M), причем согласно теореме 4 функция (f) принимает на отрезке ([a,b]) значения, равные (m) и (М). Все значения из отрезка ([m,M]) функция принимает по теореме 6. Отрезок ([m,M]) вырождается в точку, если (f(x)=const) на отрезке ([a,b]). (bullet)
Существование и непрерывность функции, обратной для непрерывной и строго монотонной функции.
Ранее мы уже рассматривали понятие обратной функции. Докажем теорему о существовании и непрерывности обратной функции.
Теорема 7
Если функция (y=f(x)) непрерывна и строго возрастает на отрезке ([a,b]), то на отрезке ([f(a),(b)]) определена функция (x=g(y)), обратная к f, непрерывная и строго возрастающая.
Доказательство
(circ) Существование обратной функции. Обозначим (A=f(a),;B=f(b)). Так как f — возрастающая функция, то для всех (хin [a,b]) выполняется неравенство (Aleq f(x)leq B), где (A= displaystyle inf_{xin[a,b]} f(x),;B=sup_{xin[a,b]}f(x)), и в силу непрерывности f (следствие из теоремы 6) множество значений функции (E(f)=[A,B]).
Согласно определению обратной функции (S 9,п. 9) нужно доказать, что для каждого (у_0in [A,В]) уравнение
$$
f(x)=y_{0}label{ref25}
$$
имеет единственный корень (x=x_{0}), причем (x_0in [a,b]).
Существование хотя бы одного корня уравнения eqref{ref25} следует из теоремы 6. Докажем, что уравнение eqref{ref25} имеет на отрезке ([a,b]) единственный корень.
Предположим, что наряду с корнем (x=x_{0}) уравнение eqref{ref25} имеет еще один корень (x=widetilde{x}_{0}), где (widetilde{x}_{0}neq x_0); тогда (f(widetilde{x_0})=y_{0},;widetilde x_0in[a,b]).
Пусть, например, (widetilde{x}_0>x_0). Тогда в силу строгого возрастания функции (f) на отрезке ([a,b]) выполняется неравенство (f(widetilde{x}_0)>f(x_{0})). С другой стороны, (f(widetilde{x}_0)=f(x_0)=y_{0}). Отсюда следует, что неравенство (widetilde{x}_0>x_{0}) не может выполняться. Следовательно, (widetilde{x}_0=x_0). Существование обратной функции доказано, то есть на отрезке ([A,В]) определена функция (x=f^{-1}(y)=g(y)), обратная к (f), причем ((g)=[a,b]) и
$$
g(f(x))=x,quad xin[a,b],quad f(g(y))=y,quad uin [A,B].label{ref26}
$$
Монотонность обратной функции. Докажем, что (g(y)) — строго возрастающая на отрезке [A,В] функция, то есть
$$
forall;y_{1},;y_{2}in [A,B]:quad y_{1};<;y_{2}rightarrow g(y_{1});<;g(у_2).label{ref27}
$$
Предположим противное; тогда условие eqref{ref27} не выполняется, то есть
$$
exists;widetilde{y}_{1},widetilde{y}_{2}in [A,B]:;widetilde{y}_{1};<;y_2rightarrow g(widetilde{y}_1geq g(widetilde{y}_2).label{ref28}
$$
Обозначим (widetilde{x}_1=g(widetilde{y}_1),;widetilde{x}_2=g(widetilde{y}_2)), тогда (widetilde{x}_1,widetilde{x}_2in [a,b],;widetilde{x}_1geqwidetilde{x}_{2}) в силу eqref{ref28} и (f(widetilde{x}_{1})=widetilde{y}_{1},;f(widetilde{x}_{2})=widetilde{y}_{2}) согласно равенству eqref{ref26}.
Так как (f) — строго возрастающая функция, то из неравенства (widetilde{X}_1geqwidetilde{x}_2) следует неравенство (f(widetilde{x}_{1})geq f(widetilde{x}_{2})), то есть (widetilde{y}_{1}geqwidetilde{y}_{2}), что невозможно, так как (widetilde{y}_1;<;widetilde{y}_{2}) в силу eqref{ref28}. Таким образом, утверждение eqref{ref28} не может выполняться, и поэтому (g(y)) — строго возрастающая функция.
Непрерывность обратной функции. Пусть (y_0) — произвольная точка интервала ((A,B)). Докажем, что функция (g) непрерывна в точке (y_{0}). Для этого достаточно показать, что справедливы равенства
$$
g(y_{0}-0)=g(y_{0}),quad g(y_{0}+0)=g(y_{0}),label{ref29}
$$
где (g(y_{0}-0)) и (g(y_{0}+0)) — пределы функции (g) соответственно слева и справа в точке (y_0).
По теореме о пределах монотонной функции (S 10) пределы функции (g) слева и справа в точке (y_{0}) существуют и выполняются неравенства
$$
g(y_{0}-0)leq g(y_{0})leq g(y_{0}+0).label{ref30}
$$
Пусть хотя бы одно из равенств eqref{ref29} не выполняется, например, (g(y_0-0)neq g(y_0)), тогда
$$
g(y_0-0) < g(y_0).label{ref31}
$$
Так как для всех (yin[A,y_{0})) выполняется неравенство (aleq g(у)leq g(y_0-0)), где (g(у_0-0)=displaystyle sup_{Aleq y;<;y_0}g(y)), а при всех (yin [y_0,B]) справедливо неравенство (g(y_0)leq g(y)leq b), то из условия eqref{ref31} следует, что интервал (Delta=(g(y_0-0),g(y_{0}))) не принадлежит множеству значений функции (g). Это противоречит тому, что все точки отрезка ([a,b]), в том числе и точки интервала (Delta), принадлежат множеству E(g). Итак, первое из равенств eqref{ref29} доказано. Аналогично доказывается справедливость второго из равенств eqref{ref29}.
Тем же способом устанавливается, что функция (g) непрерывна справа в точке (A) и непрерывна слева в точке (B). (bullet)
Замечание 6
Если функция (f) непрерывна и строго убывает на отрезке ([a,b]), то обратная к ней функция (g) непрерывна и строго убывает на отрезке ([f(b),f(a)]).
Замечание 7
Аналогично формулируется и доказывается теорема о функции (g), обратной к функции (f), для случаев, когда функция (f) задана на интервале (конечном либо бесконечном) и полуинтервале.
Если функция (f) определена, строго возрастает и непрерывна на интервале ((a,b)), то обратная функция (g) определена, строго возрастает и непрерывна на интервале ((A,B)), где
$$
A=lim_{xrightarrow a+0}f(x),quad B=lim_{xrightarrow b-0}f(x).nonumber
$$
