Как найти интервал сходимости степенного ряда калькулятор

Как найти интервал сходимости степенного ряда калькулятор

bold{mathrm{Basic}} bold{alphabetagamma} bold{mathrm{ABGamma}} bold{sincos} bold{gedivrightarrow} bold{overline{x}spacemathbb{C}forall} bold{sumspaceintspaceproduct} bold{begin{pmatrix}square&square\square&squareend{pmatrix}} bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx}
ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square}
left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec
alpha beta gamma delta zeta eta theta iota kappa lambda mu
nu xi pi rho sigma tau upsilon phi chi psi omega
A B Gamma Delta E Z H Theta K Lambda M
N Xi Pi P Sigma T Upsilon Phi X Psi Omega
sin cos tan cot sec csc sinh cosh tanh coth sech
arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech
begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge
(square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil
overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset
vee wedge neg oplus cap cup square^{c} subset subsete superset supersete
int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod
lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x}
(2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5)
(1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1)
mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить}
arcsin sin sqrt{square} 7 8 9 div
arccos cos ln 4 5 6 times
arctan tan log 1 2 3 –
pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

  • sum_{n=0}^{infty}frac{x^{n}}{n!}

  • sum_{n=1}^{infty}nx^{n}

  • sum_{n=1}^{infty}frac{(x-3)^n}{n}

  • sum_{n=0}^{infty}x^{n}

  • Показать больше

Описание

Шаг за шагом найти интервал сходимости степенного ряда

power-series-calculator

ru

Блог-сообщения, имеющие отношение к Symbolab

  • The Art of Convergence Tests

    Infinite series can be very useful for computation and problem solving but it is often one of the most difficult…

    Read More

    • Введите Задачу

    Сохранить в блокнот!

    Войти

    Источник

    Назначение сервиса. Онлайн калькулятор предназначен нахождения области сходимости степенного ряда. Результаты вычисления оформляются в формате Word (см. пример).

    Например, исходный ряд 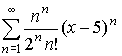подразделяется на три части: n^n, 2^n*n!, (x-5)^n.

    Правила ввода функций:

    1. Все математические операции выражаются через общепринятые символы (+,-,*,/,^). Например, (x-4)n, записываем как (x-4)^n.
    2. Число π ≡ pi, корень квадратный √¯ ≡ sqrt. Например, sqrt(n^2+n), en = exp(n)

    Пример. .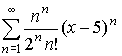

    Решение.

    Общий вид степенного ряда 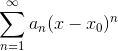. В нашем случае x0=5, .

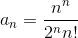    Известно, что область сходимости степенного ряда определяется величиной радиуса сходимости R:

    |x-x0|<R или x0-R<x<x0+R

    Сходимость ряда на границах (при x=x0±R) необходимо исследовать дополнительно.

    Найдем радиус сходимости ряда, используя формулу Даламбера:

    ;

    ;

    .

    .

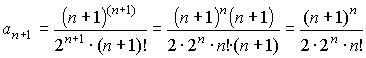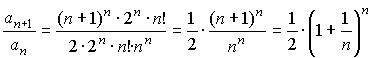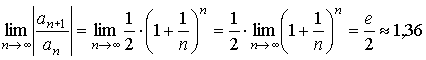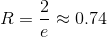
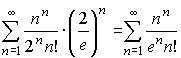    Для исследования сходимости этого ряда используем формулу Стирлинга 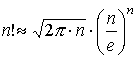формула Стирлинга, верную для факториалов больших чисел.

    Получим ряд сравнения. Этот ряд расходится.

    Проверим сходимость ряда при 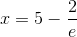. Подставляя это значение в исходный ряд, получим числовой ряд

    .

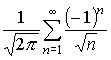    Этот ряд сходится (по признаку Лейбница).

    Итак, мы получили область сходимости исходного ряда:

    .

    Источник

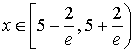    Калькулятор для нахождения интервала сходимости степенного ряда.

    Найдите интервал сходимости степенного ряда `sum_(n=1)^oo ((x-1)^(2n))/(n*9^n)`
    В ответе укажите границы интервала (a;b).

    Найдите интервал сходимости степенного ряда `sum_(n=1)^oo ((x-1)^(2n))/(n*9^n)` В ответе укажите границы интервала (a;b)

    Для решения задач необходимо зарегистрироваться.

    Источник

    Результаты 1-10 из 32 по запросу Сходимость рядов

    Предлагаем вашему вниманию калькулятор нового поколения
    для пошагового решения дифференциальных уравнений (бесплатно)

    С помощью данного калькулятора вы можете получить полное решение следующих дифференциальных уравнений:

    -однородное уравнение первого порядка;
    -уравнение, приводящееся к однородным;
    -линейное уравнение первого порядка;
    -уравнение Бернулли;
    -уравнение в полных дифференциалах;
    -уравнение Клеро;
    -уравнение …

    Тогда из сходимости ряда (3) следует сходимость ряда (2), а из расходимости ряда (2) следует расходимость ряда (3). 2.

    Блог » – 2013-08-20 10:45:55

    Необходимое условие сходимости ряда Достаточные признаки сходимости знакоположительного ряда: Первый, второй и третий признаки сравнения Их суть заключается в сравнении исследуемого числового ряда с рядом, сходимость или расходимость которого известна. Признак Даламбера Радикальный признак Коши Интегральный признак Коши Признак Раабе….Абеля Дирихле Алгоритм исследования числовых рядов на сходимость, следующий: 1) Проверяем необход…

    Блог » – 2013-07-28 17:07:07

    Источник

    Проверить сходимость ряда можно несколькими способами. Во-первых можно просто найти
    сумму ряда.
    Если в результате мы получим конечное число, то такой
    ряд сходится. Например, поскольку

    то данный ряд сходится. Если нам не удалось найти сумму ряда, то следует использовать другие методы для проверки сходимости ряда.

    Одним из таких методов является
    признак Даламбера, который записывается следующим образом:

    здесь

    и

    соответственно

    и

    члены ряда, а сходимость определяется значением
    . Если

    – ряд сходится, если

    – расходится. При

    – данный признак не даёт ответа и нужно проводить дополнительные исследования.

    В качестве примера, исследуем сходимость ряда

    с помощью признака Даламбера. Сначала запишем выражения для

    и
    .
    Теперь найдем соответствующий
    предел:

    Поскольку
    ,
    в соответствии с признаком Даламбера, ряд сходится.

    Еще одним методом, позволяющим проверить сходимость ряда является
    радикальный признак Коши, который записывается следующим образом:

    здесь

    – n-ый член ряда, а сходимость, как и в случае признака Даламбера, определяется значением
    . Если

    – ряд сходится, если

    – расходится. При

    – данный признак не даёт ответа и нужно проводить дополнительные исследования.

    В качестве примера, исследуем сходимость ряда

    с помощью радикального признака Коши. Сначала запишем выражение для

    Теперь найдем соответствующий предел:

    Поскольку
    ,
    в соответствии с радикальным признаком Коши, ряд расходится.

    Стоит отметить, что наряду с перечисленными, существуют и другие признаки сходимости рядов, такие как интегральный признак Коши, признак Раабе и др.

    Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha позволяет протестировать сходимость ряда. При этом, если калькулятор в качестве суммы ряда выдает конкретное число, то ряд сходится. В противном случае, необходимо обращать внимание на пункт «Тест сходимости ряда». Если там присутствует словосочетание «series converges», то ряд сходится. Если присутствует словосочетание «series diverges», то ряд расходится.

    Ниже представлен перевод всех возможных значений пункта «Тест сходимости ряда»:

    Текст на английском языке Текст на русском языке
    By the harmonic series test, the series diverges. При сравнении исследуемого ряда с гармоническим рядом
    ,
    исходный ряд расходится.
    The ratio test is inconclusive. Признак Даламбера не может дать ответа о сходимости ряда.
    The root test is inconclusive. Радикальный признак Коши не может дать ответа о сходимости ряда.
    By the comparison test, the series converges. По признаку сравнения, ряд сходится
    By the ratio test, the series converges. По признаку Даламбера, ряд сходится
    By the limit test, the series diverges. На основнии того, что
    ,
    или указанный предел не существует, сделан вывод о том, что ряд расходится.
    Источник

    Добавить комментарий