| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки

Примеры
-
sum_{n=0}^{infty}frac{x^{n}}{n!}
-
sum_{n=1}^{infty}nx^{n}
-
sum_{n=1}^{infty}frac{(x-3)^n}{n}
-
sum_{n=0}^{infty}x^{n}
- Показать больше
Описание
Шаг за шагом найти интервал сходимости степенного ряда
power-series-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
The Art of Convergence Tests
Infinite series can be very useful for computation and problem solving but it is often one of the most difficult…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Назначение сервиса. Онлайн калькулятор предназначен нахождения области сходимости степенного ряда. Результаты вычисления оформляются в формате Word (см. пример).
Например, исходный ряд 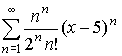 подразделяется на три части: n^n, 2^n*n!, (x-5)^n.
подразделяется на три части: n^n, 2^n*n!, (x-5)^n.
Правила ввода функций:
- Все математические операции выражаются через общепринятые символы (
+,-,*,/,^). Например, (x-4)n, записываем как(x-4)^n. - Число π ≡ pi, корень квадратный √¯ ≡ sqrt. Например, sqrt(n^2+n), en = exp(n)
Пример. 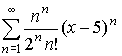 .
.
Решение.
Общий вид степенного ряда 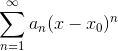 . В нашем случае x0=5,
. В нашем случае x0=5, 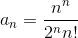 .
.
Известно, что область сходимости степенного ряда определяется величиной радиуса сходимости R:
|x-x0|<R или x0-R<x<x0+R
Сходимость ряда на границах (при x=x0±R) необходимо исследовать дополнительно.
Найдем радиус сходимости ряда, используя формулу Даламбера:
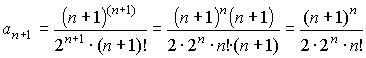 ;
;
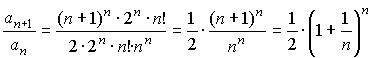 ;
;
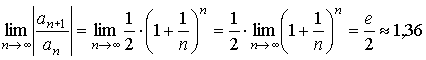 .
.
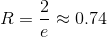
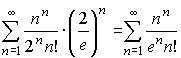 .
.
Для исследования сходимости этого ряда используем формулу Стирлинга 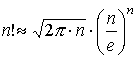 , верную для факториалов больших чисел.
, верную для факториалов больших чисел.
Получим ряд сравнения. Этот ряд расходится.
Проверим сходимость ряда при 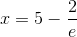 . Подставляя это значение в исходный ряд, получим числовой ряд
. Подставляя это значение в исходный ряд, получим числовой ряд
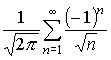 .
.
Этот ряд сходится (по признаку Лейбница).
Итак, мы получили область сходимости исходного ряда:
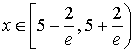 .
.
Пример 1:
Найти область сходимости ряда:

Решение от преподавателя:

Пример 2:
Найти область сходимости ряда:

Решение от преподавателя:

Пример 3:
Найти область сходимости ряда:

Решение от преподавателя:
Областью сходимости степенного ряда является интервал (-R;R), где: 
R – радиус сходимости. Вычислим его: 
x1 = 2 – 1 = 1
x2 = 2 + 1 = 3
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (1;3)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x = 1
Получаем ряд: 
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется 
б) По второму признаку Лейбница предел ряда должен стремится к 0. 
Второе условие Лейбница выполняется.
Ряд сходится, значит, x = 1 – точка сходимости.
При x = 3
получаем ряд: 
числовой знакоположительный ряд.
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл: 
Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 3 – точка расходимости.
Таким образом, данный степенной ряд является сходящимся при x [1;3)
Пример 4:
Исследовать область сходимости функционального ряда:![]()
Решение от преподавателя:

Пример 5:
Найти область сходимости степенного ряда:

Решение от преподавателя:


Пример 6:
Найти область сходимости ряда:

Решение от преподавателя:
 : общий член ряда имеет вид
: общий член ряда имеет вид  , при этом члены ряда не определены при х=-3/11, а если х≠-3/11, то
, при этом члены ряда не определены при х=-3/11, а если х≠-3/11, то

при любом х – ряд расходится всюду.
Пример 7:
Найти область сходимости ряда:
![]()
Решение от преподавателя:
Областью сходимости степенного ряда является интервал (-R;R), где: ![]()
R – радиус сходимости. Вычислим его: 
x1 = -1 – 2 = -3
x2 = -1 + 2 = 1
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-3;1)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x = -3
Получаем ряд: ![]()
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие не выполняется
1<2<3
б) По второму признаку Лейбница предел ряда должен стремится к 0. ![]()
Второе условие Лейбница не выполняется.
Ряд расходится, значит, x = -3 – точка расходимости.
При x = 1
получаем ряд: ![]()
числовой знакоположительный ряд.
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
![]()
Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 1 – точка расходимости.
Таким образом, данный степенной ряд является сходящимся при x (-3;1)
Пример 8:
Найти область сходимости ряда:

Решение от преподавателя:
 : общий член ряда имеет вид
: общий член ряда имеет вид  , при этом
, при этом

Следовательно, ряд сходится, если

и расходится, если

Если x=4/9, то ряд принимает вид  – знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).
– знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).
Если x=2/3, то ряд принимает вид  – такой ряд расходится (по признаку сравнения, т.к.
– такой ряд расходится (по признаку сравнения, т.к.  и ряд
и ряд  расходится (гармонический ряд)).
расходится (гармонический ряд)).
Окончательно получаем область сходимости исходного ряда: [4/9;2/3).
Пример 9:
Найдите множество абсолютной (условной) сходимости ряда:

Решение от преподавателя:

Пример 10:
Найти область сходимости ряда:

Решение от преподавателя:
 : общий член ряда имеет вид
: общий член ряда имеет вид  , при этом
, при этом

Следовательно, ряд сходится, если

и расходится, если

Если x=-3/7, то ряд принимает вид  – знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).
– знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).
Если x=-1/7, то ряд принимает вид  – такой ряд также сходится (обобщенный гармонический ряд с параметром p=11>1).
– такой ряд также сходится (обобщенный гармонический ряд с параметром p=11>1).
Окончательно получаем область сходимости исходного ряда: [-3/7;-1/7].
Пример 11:
Найдите множества абсолютной (условной) сходимости ряда

Решение от преподавателя:
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.
Проверяем выполнение признака Лейбница:
Если члены знакочередующегося ряда монотонно убывают по абсолютной величине и стремятся к нулю, то ряд сходится.
Ряд знакочередующийся. Составим ряд из абсолютных величин членов данного ряда

По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется

Второе условие Лейбница выполняется.
Данный ряд сходится, так как удовлетворяет условиям признака Лейбница для знакочередующихся рядов.
Следовательно, ряд условно сходящийся.
Следовательно, сходится условно и исходный ряд.
Область сходимости ряда:(-∞; +∞)
Пример 12:
Найти область сходимости ряда:

Решение от преподавателя:
 : общий член ряда имеет вид
: общий член ряда имеет вид  – обобщенный гармонический ряд с параметром
– обобщенный гармонический ряд с параметром  .
.
Такой ряд сходится, если

Однако  и поэтому
и поэтому  при любом х – ряд всюду расходится.
при любом х – ряд всюду расходится.
Пример 13:
Найти область сходимости ряда:

Решение от преподавателя:

По признаку Лейбница ряд расходится
Т. о., область сходимости имеет вид (-1; 1)
Пример 14:
Найти область сходимости ряда:

Решение от преподавателя:
 : общий член ряда имеет вид
: общий член ряда имеет вид  , при этом
, при этом

Следовательно, ряд сходится, если

и расходится, если

Если x=1/6, то ряд принимает вид  – такой ряд расходится (не выполнено необходимое условие сходимости).
– такой ряд расходится (не выполнено необходимое условие сходимости).
Если x=3/2, то ряд принимает вид  – такой ряд также расходится (также не выполнено необходимое условие сходимости).
– такой ряд также расходится (также не выполнено необходимое условие сходимости).
Окончательно получаем область сходимости исходного ряда:  .
.
Пример 15:
Найти область сходимости ряда:

Решение от преподавателя:

Выпишем общий член и следущий:
$$ u_n = frac{x^n}{n^2} $$
$$ u_{n+1} frac{x^{n+1}}{(n+1)^2} $$
Найдем отношения следующего и предыдущего члена ряда: $$ frac{u_{n+1}}{u_n} = frac{x^{n+1} n^2}{(n+1)^2 x^n} = frac{x n^2}{(n+1)^2} $$
Находим предел модуля полученного выражения:
$$ limlimits_{n to infty} bigg |frac{u_{n+1}}{u_n} bigg | = limlimits_{n to infty} bigg |frac{x n^2}{(n+1)^2} bigg | = $$
Так как $ n $ положительное, то палочки можно убрать. А $ x $ может принимать как положительные, так и отрицательные значения, поэтому его выносить за знак модуля не станем.
$$ = |x| limlimits_{n to infty} frac{n^2}{(n+1)^2} = frac{infty}{infty} = $$
Вынесем $ n^2 $ за скобки и выполним сокращение числителя и знаменателя:
$$ = |x| limlimits_{n to infty} frac{n^2}{n^2 (1+frac{1}{n})^2} = |x| limlimits_{n to infty} frac{1}{(1+frac{1}{n})^2} = $$
Вычисляем предел окончательно:
$$ =|x| cdot 1 = |x| $$
Итак, предел равен:
$$ limlimits_{n to infty} bigg |frac{x n^2}{(n+1)^2} bigg | = |x| $$
Составим строгое неравенство всегда меньшее единицы:
$$ |x|<1 $$
Раскроем модуль и получим, что интервал сходимости:
$$ -1 < x < 1 $$
Итак, интервал найден. Теперь необходимо найти область сходимости степенного ряда. А для этого исследуем поведение ряда на концах полученного интервала:
1) Возьмём левую границу $ x = -1 $
Подставляя $ x = -1 $ в исходный ряд, получаем ряд: $ sum_{n=1}^infty frac{(-1)^n}{n^2} $
Так как ряд знакочередующийся из-за $ (-1)^n $, то исследуем сходимость по признаку Лейбница:
1) Ряд знакочередующийся
2) $ limlimits_{n to infty} bigg | frac{(-1)^n}{n^2} bigg | = limlimits_{n to infty} frac{1}{n^2} = 0 $
Выполнены оба условия, значит ряд сходится и точку $ x=-1 $ можно включить в область сходимости.
2) Возьмём правую границу $ x = 1 $
Подставим $ x = 1 $ в исходный ряд и получим: $ sum_{n=1}^infty frac{1}{n^2} $
Текущий ряд попадает под общий гармонический ряд, в котором $ p = 2 $. А так как $ p>1 $, то ряд сходится. Значит, можно точку $ x = 1 $ записать в область сходимости.
Итого, подведем итог: область сходимости степенного ряда $ sum_{n = 1}^infty frac{x^n}{n^2} $ записывается в виде: $ -1 leqslant x leqslant 1 $
Найдем радиус сходимости $ R = frac{b-a}{2} = frac{1+1}{2} = 1 $
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Консультации по учебе, на самой крупной бирже
студенческих работ !
Калькулятор для нахождения интервала сходимости степенного ряда.
Найдите интервал сходимости степенного ряда `sum_(n=1)^oo ((x-1)^(2n))/(n*9^n)`
В ответе укажите границы интервала (a;b).


