В данной статье мы рассмотрим особенности алгоритма генератора случайных чисел в Excel, и на примерах рассмотрим, как использовать функции СЛЧИС и СЛУЧМЕЖДУ в Excel для генерации случайных чисел, случайных чисел с заданным количеством знаков после запятой, дат и времени.
- Генератор случайных чисел с использованием функции СЛЧИС
- Генератор случайных чисел от нуля до заданной верхней границы диапазона
- Генератор случайных чисел в диапазоне
- Генератор случайных целых чисел в Excel
- Генератор случайных целых чисел в диапазоне с помощью функции СЛУЧМЕЖДУ
- Создание случайных чисел с заданным количеством знаков после запятой
- Генератор случайных дат в Excel
- Генератор случайного времени в Excel
- Генератор случайных букв в Excel
- Как предотвратить повторное вычисление СЛЧИС и СЛУЧМЕЖДУ
- Генератор случайных чисел с помощью Анализа данных
- Пример генерации случайных чисел с нормальным распределением
Генератор случайных чисел с использованием функции СЛЧИС
Функция СЛЧИС является одной из двух функций, специально предназначенных для генерации случайных чисел в Excel. Данная функция возвращает случайное десятичное число (действительное число) между 0 и 1.
СЛЧИС() является энергозависимой функцией, что означает, что при каждом вычислении рабочего листа создается новое случайное число. И это происходит каждый раз, когда вы выполняете какое-либо действие на листе, например, обновляете формулу (не обязательно формулу СЛЧИС, любую другую формулу на листе), редактируете ячейку или вводите новые данные.
Функция СЛЧИС доступна во всех версиях: Excel 2016, Excel 2013, Excel 2010, Excel 2007, Excel 2003.
Поскольку функция Excel СЛЧИС не имеет аргументов, вы просто вводите =СЛЧИС() в ячейке и затем копируете формулу на столько ячеек, сколько хотите:

Генератор случайных чисел в Excel – Генерация случайных чисел
А теперь давайте сделаем еще один шаг и напишем несколько формул СЛЧИС для генерации случайных чисел в соответствии с определенными условиями.
Генератор случайных чисел от нуля до заданной верхней границы диапазона
Чтобы сделать генератор случайных чисел от нуля до любого значения N, вы несколько раз выполняете функцию СЛЧИС с помощью N:
=СЛЧИС()*N
Например, для создания последовательности случайных чисел, больших или равных 0, но менее 50, используйте следующую формулу:
=СЛЧИС()*50
Примечание. Значение верхней границы никогда не включается в возвращаемую случайную последовательность. Например, если вы хотите получить случайные числа от 0 до 10, включая 10, правильная формула =СЛЧИС()*11.
Генератор случайных чисел в диапазоне
Чтобы создать случайное число в диапазоне, т.е. случайное число между любыми двумя указанными вами числами, используйте следующую формулу СЛЧИС:
= СЛЧИС() * (B – A) + A
Где A – это нижнее значение границы (наименьшее число), а B – верхнее значение границы (наибольшее число).
Например, чтобы сделать генератор случайных чисел от 10 до 50, вы можете использовать следующую формулу:
= СЛЧИС()*(50-10)+10
Примечание. Эта формула генерации случайных чисел никогда не вернет число, равное наибольшему числу указанного диапазона (значение B).
Генератор случайных целых чисел в Excel
Чтобы функция Excel СЛЧИС создавала случайные целые числа, возьмите одну из вышеупомянутых формул и заверните ее в функцию ЦЕЛОЕ.
Чтобы сделать генератор случайных целых чисел от 0 до 50:
= ЦЕЛОЕ(СЛЧИС()*50)
Чтобы генерировать случайные целые числа от 10 до 50:
= ЦЕЛОЕ (СЛЧИС()*(50-10)+10)

Генератор случайных чисел в Excel – Генерация случайных целых чисел
Генератор случайных чисел в Excel в диапазоне с помощью функции СЛУЧМЕЖДУ
СЛУЧМЕЖДУ – это еще одна функция в Excel для создания генератора случайных чисел.. Она возвращает случайные целые числа в указанном диапазоне:
СЛУЧМЕЖДУ (нижняя граница; верхняя граница)
Очевидно, что нижняя граница – это наименьшее число, а верхняя граница – наибольшее число в диапазоне случайных чисел, которые вы хотите получить.
Подобно СЛЧИС, СЛУЧМЕЖДУ в Excel является изменчивой функцией, и она также возвращает новое случайное целое число каждый раз, когда ваша таблица пересчитывается или изменяется.
Например, того чтобы сделать генератор случайных целых чисел от 10 до 50 (включая 10 и 50) используйте следующую формулу СЛУЧМЕЖДУ:
= СЛУЧМЕЖДУ(10; 50)

Генератор случайных чисел в Excel – Генерация случайных чисел в заданном диапазоне
Функция СЛУЧМЕЖДУ в Excel может создавать как положительные, так и отрицательные числа случайные числа. Например, чтобы получить список случайных чисел от -10 до 10, введите следующую формулу на листе:
=СЛУЧМЕЖДУ(-10;10)
Функция СЛУЧМЕЖДУ доступна в следующих версиях: Excel 2016, Excel 2013, Excel 2010 и Excel 2007.
В более ранней версии Excel 2003, вы можете использовать формулу СЛЧИС, рассмотренную выше.
Далее в этой статье вы найдете еще несколько примеров формул, демонстрирующих, как использовать функцию СЛУЧМЕЖДУ для создания генератора случайных чисел, отличных от целых.
Создание случайных чисел с заданным количеством знаков после запятой
Хотя функция СЛУЧМЕЖДУ в Excel была предназначена для генерации случайных целых чисел, вы можете использовать ее для генерации случайных десятичных чисел с таким количеством десятичных знаков, сколько хотите.
Например, чтобы получить список чисел с одним десятичным знаком, вы умножаете нижнее и верхнее значения на 10, а затем делите возвращаемое значение на 10:
= СЛУЧМЕЖДУ(нижняя граница*10; верхняя граница*10)/10
Например, чтобы получить список чисел с одним десятичным знаком, вы умножаете нижнее и верхнее значения на 10, а затем делите возвращаемое значение на 10:
Следующая формула СЛУЧМЕЖДУ возвращает случайные десятичные числа от 1 до 50:
= СЛУЧМЕЖДУ(1*10;50*10)/10

Генератор случайных чисел в Excel – Генерация случайных чисел с одним знаком после запятой
Аналогичным образом, чтобы сделать генератор случайных чисел от 1 до 50 с двумя знаками после запятой, вы умножаете аргументы функции СЛУЧМЕЖДУ на 100, а затем делите результат на 100:
=СЛУЧМЕЖДУ(1*100; 50*100)/100

Генератор случайных чисел в Excel – Генерация случайных чисел с двумя знаками после запятой
Генератор случайных дат в Excel
Чтобы вернуть список случайных дат между данными двумя датами, используйте функцию СЛУЧМЕЖДУ в сочетании с ДАТА:
=СЛУЧМЕЖДУ (ДАТА (дата начала); ДАТА (дата окончания))
Например, чтобы получить список дат между 1 сентября 2017 и 20 ноября 2017 включительно, введите следующую формулу на листе:
=СЛУЧМЕЖДУ(ДАТА(2017;9;1);ДАТА(2017;11;21))
Не забудьте применить формат даты к ячейке (ячейкам), и вы получите список случайных дат, подобных этому:

Генератор случайных чисел в Excel – Генерация случайных дат
Генератор случайного времени в Excel
Во внутренней системе Excel времена хранятся как десятичные числа, и вы можете использовать стандартную функцию Excel СЛЧИС для вставки случайных действительных чисел, а затем просто применить формат времени к ячейкам:

Генератор случайных чисел в Excel – Генерация случайного времени функцией СЛЧИС и применение к ней формата Время
Чтобы сделать генератор случайного времени в указанном диапазоне, требуется более конкретная формула. Рассмотрим подробнее.
Генератор случайного времени в указанном диапазоне
Чтобы вставить произвольное время между любыми двумя указанными вами временными интервалами, используйте функцию ВРЕМЯ в сочетании с Excel СЛЧИС:
= ВРЕМЯ (время начала) + СЛЧИС () * (ВРЕМЯ (время начала) – ВРЕМЯ (время окончания))
Например, чтобы вставить случайное время между 5:30 и 18:00, вы можете использовать одну из следующих формул:
=ВРЕМЯ(5;30;0)+СЛЧИС()*(ВРЕМЯ(18;0;0)-ВРЕМЯ(5;0;0))

Генератор случайных чисел в Excel – Генерация случайного времени в заданном интервале
Генератор случайных букв в Excel
Чтобы вставить случайную букву, необходимо использовать комбинацию трех различных функций:
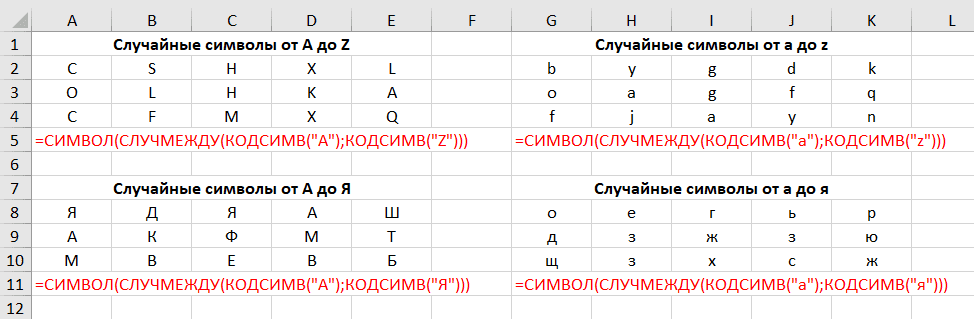
=СИМВОЛ(СЛУЧМЕЖДУ(КОДСИМВ(“A”);КОДСИМВ(“Z”)))
Где A – первый символ, а Z – последний символ в диапазоне букв, которые вы хотите включить (в алфавитном порядке).
Разберем функции, в приведенной выше формуле:
- КОДСИМВ возвращает числовые коды ANSI для указанных букв.
- СЛУЧМЕЖДУ принимает числа, возвращаемые функциями КОДСИМВ , как нижнее и верхнее значения диапазона.
- СИМВОЛ преобразует случайные коды ANSI, возвращаемые СЛУЧМЕЖДУ, в соответствующие буквы.

Генератор случайных чисел в Excel – Генерация случайных букв
Так как коды ANSI отличаются для прописных и строчных букв, эта формула учитывает регистр.
Если кто-то наизусть знает Коды символов ANSI, ничто не мешает вам передавать коды непосредственно в функцию СЛУЧМЕЖДУ.
Например, чтобы получить произвольные прописные буквы между A (код ANSI 65) и Z (код ANSI 90), вы пишете:
=СИМВОЛ(СЛУЧМЕЖДУ (65;90))
Чтобы генерировать строчные буквы между а (код ANSI 97) в z (код ANSI 122), вы используете следующую формулу:
=СИМВОЛ(СЛУЧМЕЖДУ(97;122))
Чтобы вставить случайный специальный символ, например! «# $% & ‘() * +, -. /, используйте функцию СЛУЧМЕЖДУ с нижним параметром, установленным на 33 (код ANSI для«! »), а верхний параметр – 47 (код ANSI для« / »).
=СИМВОЛ(СЛУЧМЕЖДУ(33;47))

Генератор случайных чисел в Excel – Генерация случайных символов
Как предотвратить повторное вычисление СЛЧИС и СЛУЧМЕЖДУ
Если вы хотите получить постоянный набор случайных чисел, дат или текстовых строк, которые не будут меняться каждый раз, то есть зафиксировать случайные числа, когда лист пересчитывается, используйте один из следующих способов:
- Чтобы остановить функции СЛЧИС или СЛУЧМЕЖДУ от пересчета в одной ячейке, выберите эту ячейку, переключитесь на панель формул и нажмите F9, чтобы заменить формулу на ее значение.
- Чтобы предотвратить функцию случайных чисел в Excel от автоматического обновления значений в нескольких ячейках, используйте функцию Вставить. Выберите все ячейки с формулой генерации случайных значений, нажмите Ctrl+C, чтобы скопировать их, затем щелкните правой кнопкой мыши выбранный диапазон и нажмите «Вставить специальные»–> «Значения».

Генератор случайных чисел в Excel – Вставка значений
Генератор случайных чисел с помощью Анализа данных
С помощью пакета анализа данных вы, например, можете сгенерировать случайные числа нормального распределения или другого распределения. По умолчанию данный пакет не подключен, поэтому необходимо его загрузить. Как это сделать, описано в этой статье.
Пример генерации случайных чисел нормального распределения
Для того чтобы сгенерировать случайные числа нормального распределения, переходим во вкладку «ДАННЫЕ», в группе «Анализ» выбираем «Анализ данных».

Генератор случайных чисел в Excel – Анализ данных
В открывшемся списке выбираем «Генерация случайных чисел» и нажимаем кнопку «ОК».

Генератор случайных чисел в Excel – Генерация случайных чисел
В открывшемся окне в списке «Распределение» выбираем «Нормальное», вводим число переменных, число случайных чисел, среднее и отклонение, а также место, где вы хотите разместить сгенерированные случайные числа.

Генератор случайных чисел в Excel – Генерация случайных чисел нормального распределения
После того, как все данные введены нажимаем кнопку «ОК», и в результате получаем сгенерированные случайные числа нормального распределения.
Ну вот на этом все. Теперь вы научились, как сделать генератор случайных чисел, чисел в диапазоне, чисел с заданным количеством знаков после запятой, случайных дат, случайного времени, а также случайных букв, а также, как сгенерировать случайные числа нормального распределения. Таким образом, владея данными знаниями, вы можете создать не только генератор случайных чисел в Excel, но и генератор паролей.
[ Генератор случайных чисел в Excel скачать ]
Skip to content
В статье объясняются особенности алгоритма получения случайных чисел Excel и показано, как использовать функции СЛЧИС и СЛУЧМЕЖДУ для чисел, дат, паролей и других текстовых выражений.
Прежде чем мы углубимся в различные методы производства случайных чисел в Excel, давайте определимся, что они собой представляют. Говоря простым языком, случайные данные – это последовательность цифр, букв или других символов, в которой отсутствуют какой-либо шаблон или закономерность.
Случайность имеет множество различных приложений в криптографии, статистике, лотерее, азартных играх и многих других областях. И поскольку она всегда была востребована, с древних времен существовали различные методы создания случайных чисел, такие как подбрасывание монет, бросание кубиков, тасование игральных карт и так далее. Конечно, мы не будем полагаться на такие «экзотические» техники в этом руководстве и сосредоточимся на том, что может предложить генератор случайных чисел Excel.
- Как работает алгоритм случайных чисел
- Функция СЛЧИС
- Случайные числа в указанном диапазоне при помощи функции СЛУЧМЕЖДУ
- Случайные числа с нужным количеством десятичных знаков
- Случайные даты в Excel
- Как вставить случайное время в Excel
- Случайные дата и время
- Как получить случайные буквы
- Создание текстовых строк и паролей
- Как предотвратить постоянный пересчет формул СЛЧИС и СЛУЧМЕЖДУ
- Как создать уникальные случайные числа в Excel
Создание случайных чисел в Excel – основы.
Случайные числа – это без всякой закономерности выбранная последовательность чисел. Но в жизни практически всегда применяются псевдослучайные числа. Их получают по заранее определенному сложному алгоритму. Для постороннего человека они выглядят случайными, но все же их можно предсказать, если узнать этот сложный алгоритм. Псевдослучайные числа применяются во всех компьютерных программах.
Хотя функции случайных чисел Excel удовлетворяют всем стандартным тестам на случайность, они все же не выдают истинные случайные числа. Но это не значит, что Excel для этих целей не годится. Псевдослучайные числа, создаваемые функциями Excel, прекрасно подходят для многих целей.
Давайте подробнее рассмотрим, как это происходит, чтобы вы знали, чего от стандартных функций Excel можно ожидать, а чего нельзя.
Как и большинство компьютерных программ, генератор случайных чисел Excel производит псевдослучайные числа с помощью некоторых математических формул. Для вас это означает, что теоретически эти числа, создаваемые Excel, предсказуемы. Но только при условии, что кто-то знает все детали алгоритма. Это причина того, что это никогда не было задокументировано и вряд ли когда-либо будет сделано.
Итак, как можно создавать случайные числа в Excel?
- Функции Excel СЛЧИС и СЛУЧМЕЖДУ (RAND и RANDBETWEEN в английской версии) возвращают псевдослучайные числа из равномерного распределения, также известного как прямоугольное распределение, где существует равная вероятность для всех значений, которые величина может принимать. Хороший пример равномерного распределения – бросок одной игральной кости. Итогом такой жеребьевки являются шесть возможных значений (1, 2, 3, 4, 5, 6), и каждое из них имеет одинаковую вероятность.
- Функции Excel СЛЧИС и СЛУЧМЕЖДУ, по слухам, инициализируются из системного времени компьютера. Технически начальное число является отправной точкой для создания последовательности чисел. И каждый раз, когда вызывается случайная функция Excel, используется новое начальное число, которое возвращает уникальную последовательность. Другими словами, при использовании генератора случайных чисел в Excel вы не можете получить повторяемую комбинацию ни с помощью функции СЛЧИС и СЛУЧМЕЖДУ, ни с помощью VBA, ни какими-либо другими способами.
- В ранних версиях Excel, до Excel 2003, алгоритм случайных чисел имел относительно небольшой диапазон (менее 1 миллиона неповторяющихся последовательностей чисел) и не прошел несколько стандартных тестов на случайность для длинных последовательностей. По этой причине, если кто-то все еще работает со старой версией Excel, вам лучше не использовать функцию СЛЧИС с большими имитационными моделями.
Это довольно длинное техническое введение закончено, и мы переходим к более практическим и более полезным вещам.
Функция случайного числа — СЛЧИС.
Функция СЛЧИС в Excel – одна из двух функций, специально разработанных для случайных чисел. Она возвращает произвольное десятичное число (действительное число) от 0 до 1.
СЛЧИС – это непостоянная функция, означающая, что новое случайное число возникает каждый раз при вычислении рабочего листа. А это происходит часто — когда вы выполняете какое-либо действие, например, редактируете формулу (не обязательно СЛЧИС, даже любую другую формулу на листе), редактируете ячейку или вводите новые данные.
Функция СЛЧИС доступна во всех версиях Excel, начиная с самых ранних.
Поскольку она не имеет аргументов, вы просто записываете её в ячейку, а затем копируете куда это необходимо:

А теперь давайте составим несколько формул СЛЧИС для создания случайных чисел в соответствии с вашими условиями.
Ограничение верхней границы диапазона случайных чисел.
Чтобы создать массив от нуля до любого значения N, вы умножаете функцию СЛЧИС на N:
СЛЧИС() * N
Например, чтобы создать последовательность чисел, больше или равных 0, но меньше 50, используйте следующую формулу:
=СЛЧИС()*50

Примечание. Значение верхней границы никогда не включается в возвращаемую последовательность. Например, если вы хотите получить случайные числа от 0 до 10, включая 10, правильная формула будет =СЛЧИС()*11.
Обратите также внимание, что количество отображаемых десятичных знаков определяется форматом ячеек. В данном случае установлено 2 знака после запятой, хотя на самом деле их гораздо больше. Об округлении их мы поговорим чуть ниже.
Случайные числа в интервале «от-до».
Чтобы создать случайное число между любыми двумя указанными вами величинами, используйте следующую формулу СЛЧИС:
СЛЧИС() * ( B – A ) + A
Где A – значение нижней границы (наименьшее число), а B – значение верхней границы (наибольшее).
Например, чтобы записать на ваш лист случайные числа от 10 до 50, вы можете использовать следующую формулу:
=СЛЧИС()*(50-10)+10

Примечание. Эта формула никогда не вернет число, равное максимальному значению указанного диапазона (то есть, B).
Случайные целые числа.
Чтобы функция Excel СЛЧИС выдавала целые числа, возьмите любую из вышеупомянутых формул и оберните ее в функцию ЦЕЛОЕ().
Чтобы создать случайные целые числа от 0 до 50:
=ЦЕЛОЕ(СЛЧИС()*50)
Чтобы получить их в интервале от 10 до 50:
=ЦЕЛОЕ(СЛЧИС()*(50-10)+10)

А теперь рассмотрим более новую функцию — СЛУЧМЕЖДУ().
Функция Excel СЛУЧМЕЖДУ — как получить случайные целые числа в указанном диапазоне
СЛУЧМЕЖДУ – еще одна функция, предоставляемая Excel для случайных чисел. Она возвращает их в указанном вами диапазоне:
СЛУЧМЕЖДУ(нижнее_значение; верхнее_значение)
Как и СЛЧИС, СЛУЧМЕЖДУ в Excel – это непостоянная функция, которая возвращает новый результат каждый раз, когда ваша электронная таблица пересчитывается. А происходит это при любом изменении на листе.
Например, чтобы решить ту же задачу, которую мы рассматривали чуть выше: получить случайные целые числа от 10 до 50 (включая 10 и 50), используйте следующую формулу:
=СЛУЧМЕЖДУ(10; 50)

Функция СЛУЧМЕЖДУ в Excel может создавать как положительные, так и отрицательные числа. Например, чтобы получить список целых чисел от -10 до 10, введите следующую формулу:
=СЛУЧМЕЖДУ(-10; 10)
Функция СЛУЧМЕЖДУ доступна в Excel 2019 – 2007. В более ранних версиях вы можете использовать формулу СЛЧИС, рассмотренную нами выше.
Далее в этом руководстве вы найдете еще несколько примеров формул, демонстрирующих, как использовать функцию СЛУЧМЕЖДУ для записи случайных значений, отличных от целых.
Как создавать случайные числа с нужным количеством десятичных знаков.
Хотя функция СЛУЧМЕЖДУ в Excel была разработана для возврата целых чисел, вы можете заставить ее возвращать случайные десятичные числа с любым количеством знаков после запятой.
Например, чтобы получить список чисел с одним десятичным знаком, вы умножаете нижнее и верхнее значения на 10, а затем делите возвращаемое значение на 10:
СЛУЧМЕЖДУ( нижнее значение * 10; верхнее значение * 10) / 10
Следующая формула СЛУЧМЕЖДУ() возвращает случайные десятичные числа от 1 до 50:
=СЛУЧМЕЖДУ(1*10; 50*10)/10

Однако, обратите внимание, что среди полученных результатов встречаются и значения без десятых, то есть десятичный знак может быть равен нулю.
Аналогичным образом, чтобы выдать случайные числа от 1 до 50 с двумя десятичными знаками, вы умножаете аргументы функции СЛУЧМЕЖДУ на 100, а затем также делите результат на 100:
=СЛУЧМЕЖДУ(1*100; 50*100) / 100
Как получить случайные даты в Excel
Как вы знаете, даты в Excel представляют собой числа. Поэтому рассматриваемые нами подходы вполне применимы и к ним.
Чтобы вернуть список произвольных дат в каком-то временном интервале, используйте функцию СЛУЧМЕЖДУ в сочетании с ДАТАЗНАЧ:
СЛУЧМЕЖДУ(ДАТАЗНАЧ( дата начала ), ДАТАЗНАЧ( дата окончания ))
Например, чтобы получить список дат с 1 июня 2015 года по 30 июня 2015 года включительно, введите следующую формулу в свой рабочий лист:
=СЛУЧМЕЖДУ(ДАТАЗНАЧ(“1-Июл-2021”); ДАТАЗНАЧ(“31-Авг-2021”))
В качестве альтернативы вы можете использовать функцию ДАТА:
=СЛУЧМЕЖДУ(ДАТА(2021,7,1),ДАТА(2021,8,31))
Не забудьте применить формат даты, и вы получите список случайных дат, подобный этому:

Для некоторых дополнительных опций, таких как получение списка будних или выходных дней, можно использовать расширенный генератор случайных чисел и дат .
Как вставить случайное время в Excel
Учитывая, что во внутренней системе Excel время хранится как десятичное число от 0 до 1, вы можете использовать стандартную функцию Excel СЛЧИС для вставки случайных действительных чисел, а затем просто применить формат времени к этим ячейкам:

Чтобы вернуть случайное время в соответствии с вашими критериями, требуются более сложные формулы, как показано ниже.
Случайное время в указанном интервале.
Чтобы вставить случайное время между любыми двумя указанными вами значениями времени, используйте функцию ВРЕМЯ() или ВРЕМЗНАЧ() вместе с СЛЧИС():
ВРЕМЯ( время начала ) + СЛЧИС() * (ВРЕМЯ( время начала ) – ВРЕМЯ( время окончания ))
или
ВРЕМЗНАЧ ( время начала ) + СЛЧИС () * (ВРЕМЗНАЧ ( время начала ) – ВРЕМЗНАЧ ( время окончания ))
Например, чтобы вставить время между 6:00 и 20:30, вы можете использовать любую из следующих формул:
=ВРЕМЯ(6;0;0) + СЛЧИС() * (ВРЕМЯ(20;30;0) – ВРЕМЯ(6;0;0))
=ВРЕМЗНАЧ(“6:00:00”) + СЛЧИС() * (ВРЕМЗНАЧ(“20:30:00”) – ВРЕМЗНАЧ(“6:00:00”))

Случайные дата и время.
Чтобы создать список случайных дат и времени, используйте комбинации функций СЛУЧМЕЖДУ и ДАТАЗНАЧ:
СЛУЧМЕЖДУ(ДАТАЗНАЧ( начальная дата) ; ДАТАЗНАЧ( конечная дата )) + СЛУЧМЕЖДУ(ВРЕМЗНАЧ( время начала ) * 10000; ВРЕМЗНАЧ( время окончания ) * 10000) / 10000
Предположим, вы хотите вставить произвольные даты между 1 июня 2021 года и 31 августа того же года со временем между 8:30 и 17:00. Следующая формула подойдет для вас:
=СЛУЧМЕЖДУ(ДАТАЗНАЧ(“1-июн-2021”); ДАТАЗНАЧ(“31-авг-2021”)) + СЛУЧМЕЖДУ(ВРЕМЗНАЧ(“8:30”) * 10000; ВРЕМЗНАЧ(“17:00”) * 10000) / 10000
Вы также можете указать дату и время, используя функции ДАТА и ВРЕМЯ соответственно:
=СЛУЧМЕЖДУ(ДАТА(2021;6;1); ДАТА(2021;8;31)) + СЛУЧМЕЖДУ(ВРЕМЯ(8;30;0) * 10000; ВРЕМЯ(17;0;0) * 10000) / 10000

Выбирайте тот вариант, который больше подходит для вашей задачи.
Как получить случайные буквы в Excel
Чтобы вернуть случайную букву, требуется комбинация трех разных функций:
=СИМВОЛ(СЛУЧМЕЖДУ(КОДСИМВ(“А”);КОДСИМВ(“Я”)))
Где A – первый символ, а Я – последний символ в диапазоне букв, который вы хотите использовать (в алфавитном порядке).
В приведенной выше формуле:
- КОДСИМВ() возвращает коды ANSI для указанных букв.
- СЛУЧМЕЖДУ() принимает код, возвращаемый функцией КОДСИМВ, как нижнее и верхнее значения диапазона.
- СИМВОЛ() преобразует коды ANSI, возвращаемые СЛУЧМЕЖДУ, в соответствующие буквы.
Примечание. Так как код ANSI различный для прописных и строчных букв, эта формула чувствительна к регистру.
Если кто-то помнит таблицу кодов символов ANSI, ничто не мешает вам передать коды букв непосредственно в функцию СЛУЧМЕЖДУ.
Например, чтобы получить заглавные буквы между A (код ANSI 192) и Я (код ANSI 223), вы пишете:
=СИМВОЛ(СЛУЧМЕЖДУ(192;223))
Чтобы получить строчные буквы от а (код ANSI 224) до я (код ANSI 255), используйте следующую формулу:
=СИМВОЛ(СЛУЧМЕЖДУ(224;255))

Коды символов:
- 192-223 — прописные буквы А-Я
- 224-255 — строчные буквы а-я
Чтобы вставить случайный специальный символ, например, ! “# $% & ‘() * +, -. /, используйте функцию СЛУЧМЕЖДУ с первым параметром, установленным на 33 (код ANSI для “!’), и вторым параметром 47 (код ANSI для “/”).
=СИМВОЛ(СЛУЧМЕЖДУ(33;47))
Создание текстовых строк и паролей в Excel
Чтобы создать произвольную текстовую строку в Excel, вам просто нужно объединить несколько функций СИМВОЛ и СЛУЧМЕЖДУ.
Например, чтобы получить список паролей, состоящих из 4 символов, вы можете использовать формулу, подобную этой:
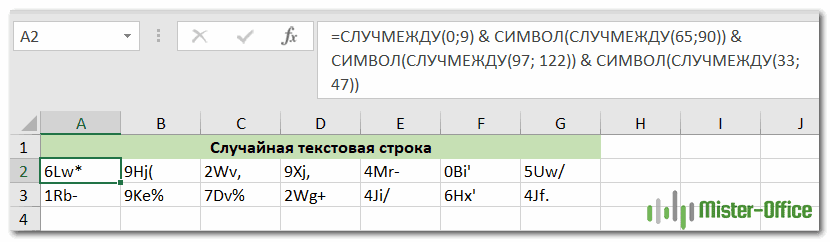
=СЛУЧМЕЖДУ(0;9) & СИМВОЛ(СЛУЧМЕЖДУ(65;90)) & СИМВОЛ(СЛУЧМЕЖДУ(97; 122)) & СИМВОЛ(СЛУЧМЕЖДУ(33;47))
Чтобы сделать запись более компактной, я ввел коды ANSI непосредственно в формулу. Четыре функции возвращают следующие случайные значения:
- СЛУЧМЕЖДУ(0;9) — возвращает числа от 0 до 9.
- СИМВОЛ(СЛУЧМЕЖДУ(65;90)) —прописные буквы от A до Z.
- СИМВОЛ(СЛУЧМЕЖДУ(97; 122)) — получаем строчные буквы от a до z.
- СИМВОЛ(СЛУЧМЕЖДУ(33;47)) — добавляем специальные символы.
Текстовые строки, полученные с помощью приведенной выше формулы, будут иметь вид « 4Np# » или « 2Yu& ».
Внимание! Если вы используете аналогичную формулу для создания случайных паролей, они не будут слишком надежными. Конечно, вы можете создавать более длинные текстовые строки, связывая больше функций. Однако невозможно изменить порядок следования, т.е. первая по счёту функция всегда возвращает цифру, вторая функция возвращает заглавную букву и так далее.
Если вы ищете расширенный генератор случайных паролей в Excel, способный создавать текстовые строки любой длины и шаблона, вы можете проверить возможности Advanced Random Generator для тестовых строк.
Кроме того, имейте в виду, что текстовые строки, созданные с помощью приведенной выше формулы, будут изменяться каждый раз, когда ваш рабочий лист пересчитывается. А это автоматически происходит после ввода либо корректировки любого значения либо формулы на листе.
Чтобы гарантировать, что ваши строки или пароли остаются неизменными после их создания, вам нужно будет заблокировать функцию СЛУЧМЕЖДУ от обновления значений, что подводит нас непосредственно к следующему разделу.
Как предотвратить постоянный пересчет формул СЛЧИС и СЛУЧМЕЖДУ.
Если вы хотите получить постоянный набор чисел, дат или текстовых строк, который не будет меняться каждый раз при пересчете таблицы, используйте один из следующих методов:
- Чтобы функции СЛЧИС или СЛУЧМЕЖДУ не пересчитывались в одной определённой ячейке, выберите её, переключитесь на строку формул и нажмите клавишу
F9, чтобы заменить формулу ее значением. - Чтобы предотвратить пересчет, используйте инструмент Специальная вставка. Выделите все ячейки с формулой, нажмите
Ctrl + C, чтобы скопировать их в буфер обмена. Затем щелкните правой кнопкой мыши выбранный диапазон и выберите Специальная вставка > Значения. Или же можете нажатьShift + F10 а потом V, что также позволит вставить ранее скопированные значения вместо формул. - Можно использовать специальный инструмент преобразования формул в значения, который является составной частью надстройки Ultimate Suite.
Как создать уникальные случайные числа в Excel
Ни одна из случайных функций Excel не умеет создавать уникальные случайные значения. Совпадения всегда возможны, особенно если вы получаете целые числа, используя округление. Если вы хотите создать список без дубликатов , выполните следующие действия:
- Используйте функцию СЛЧИС или СЛУЧМЕЖДУ для создания списка чисел. Создайте больше значений, чем вам действительно нужно, потому что некоторые из них будут дублироваться и будут удалены позже.
- Преобразуйте формулы в значения, как описано выше.
- Удалите повторяющиеся значения с помощью встроенного инструмента Excel (см. Как удалить дубликаты в Excel) или специального инструмента для удаления дубликатов в Excel.
Также вы можете воспользоваться специальным генератором случайных значений в Excel, в котором есть опция получения случайных цифровых и текстовых значений. Более подробно читайте о нем по этой ссылке.
 Расширенный генератор случайных чисел для Excel – Теперь, когда вы знаете, как использовать случайные функции в Excel, позвольте мне продемонстрировать вам более быстрый, простой и не требующий формул способ создания списка случайных чисел, дат или текстовых строк…
Расширенный генератор случайных чисел для Excel – Теперь, когда вы знаете, как использовать случайные функции в Excel, позвольте мне продемонстрировать вам более быстрый, простой и не требующий формул способ создания списка случайных чисел, дат или текстовых строк…
Ф
ункция
СЛУЧМЕЖДУ(
)
, английский вариант RANDBETWEEN(),
возвращает случайное ЦЕЛОЕ число в заданном интервале.
Синтаксис функции
СЛУЧМЕЖДУ(
нижняя_граница;верхняя_граница
)
Нижн_граница
— наименьшее целое число, которое возвращает функция.
Верхн_граница
— наибольшее целое число, которое возвращает функция.
Если значение
нижняя_граница
больше значения
верхняя_граница
, функция вернет ошибку #ЧИСЛО! Предполагается, что границы диапазона – целые числа. Если введено число с дробной частью, то дробная часть будет отброшена.
Если необходимо получить случайное число, например, в интервале от 0 до 0,1, то нужно написать следующую формулу:
=СЛУЧМЕЖДУ(0;10)/100
(с точностью 0,01, т.е. случайные значения будут 0,02; 0,05 и т.д.)
=СЛУЧМЕЖДУ(0;1000)/10000
(с точностью 0,0001, т.е. случайные значения будут 0,0689; 0,0254 и т.д.)
Если необходимо получить не целое, а вещественное число, например, в интервале от 3 до 10, то нужно использовать функцию
СЛЧИС()
:
=СЛЧИС()*(10-3)+3
(точностью 15 знаков, т.е. случайные значения будут 7,68866700270417; 8,68428856478223 и т.д.)
Если требуется сгенерировать случайное число от -2,699 до 30,02, причем оно должно быть округлено до тысячных (количество знаков после запятой случайного числа = максимальному количеству знаков после запятой границ интервала), то сначала нужно определить количество знаков после запятой у обоих границ (см.
файл примера
). Это можно сделать с помощью формулы =
ДЛСТР(A15)-1-ДЛСТР(ЦЕЛОЕ(A15))
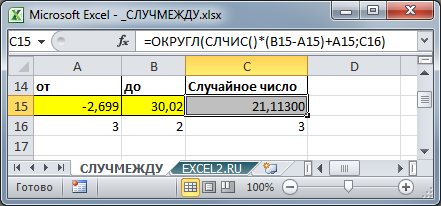
Затем воспользоваться функцией
СЛЧИС()
, округлив значение.
Примечание
. Границы интервала должны быть заданы константой. В случае расчетных значений интервалов результат непредсказуем (см.
Проблемы округления в MS EXCEL
). Совет: Если границы интервала рассчитываются формулами, что в них можно задать необходимую точность.
Функция пересчитывает свое значение после каждого ввода нового значения в любую ячейку листа (или изменения значения ячейки) или нажатии
клавиши
F9
.
У нас есть последовательность чисел, состоящая из практически независимых элементов, которые подчиняются заданному распределению. Как правило, равномерному распределению.
Сгенерировать случайные числа в Excel можно разными путями и способами. Рассмотрим только лучше из них.
Функция случайного числа в Excel
- Функция СЛЧИС возвращает случайное равномерно распределенное вещественное число. Оно будет меньше 1, больше или равно 0.
- Функция СЛУЧМЕЖДУ возвращает случайное целое число.
Рассмотрим их использование на примерах.
Выборка случайных чисел с помощью СЛЧИС
Данная функция аргументов не требует (СЛЧИС()).
Чтобы сгенерировать случайное вещественное число в диапазоне от 1 до 5, например, применяем следующую формулу: =СЛЧИС()*(5-1)+1.

Возвращаемое случайное число распределено равномерно на интервале [1,10].
При каждом вычислении листа или при изменении значения в любой ячейке листа возвращается новое случайное число. Если нужно сохранить сгенерированную совокупность, можно заменить формулу на ее значение.
- Щелкаем по ячейке со случайным числом.
- В строке формул выделяем формулу.
- Нажимаем F9. И ВВОД.
Проверим равномерность распределения случайных чисел из первой выборки с помощью гистограммы распределения.
- Сформируем «карманы». Диапазоны, в пределах которых будут находиться значения. Первый такой диапазон – 0-0,1. Для следующих – формула =C2+$C$2.
- Определим частоту для случайных чисел в каждом диапазоне. Используем формулу массива {=ЧАСТОТА(A2:A201;C2:C11)}.
- Сформируем диапазоны с помощью знака «сцепления» (=”[0,0-“&C2&”]”).
- Строим гистограмму распределения 200 значений, полученных с помощью функции СЛЧИС ().
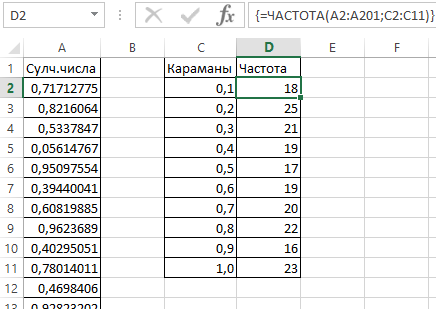
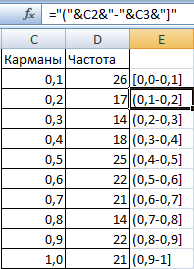
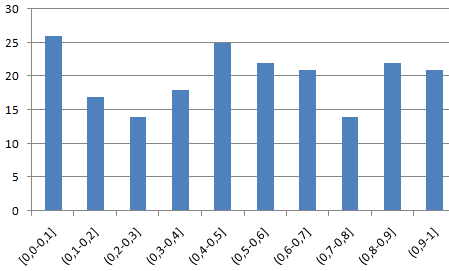
Диапазон вертикальных значений – частота. Горизонтальных – «карманы».
Функция СЛУЧМЕЖДУ
Синтаксис функции СЛУЧМЕЖДУ – (нижняя граница; верхняя граница). Первый аргумент должен быть меньше второго. В противном случае функция выдаст ошибку. Предполагается, что границы – целые числа. Дробную часть формула отбрасывает.
Пример использования функции:
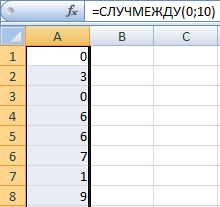
Случайные числа с точностью 0,1 и 0,01:
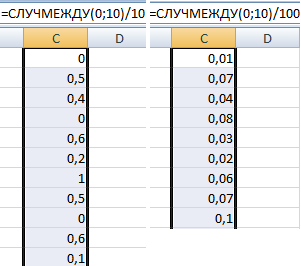
Как сделать генератор случайных чисел в Excel
Сделаем генератор случайных чисел с генерацией значения из определенного диапазона. Используем формулу вида: =ИНДЕКС(A1:A10;ЦЕЛОЕ(СЛЧИС()*10)+1).
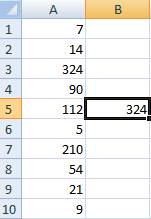
Сделаем генератор случайных чисел в диапазоне от 0 до 100 с шагом 10.
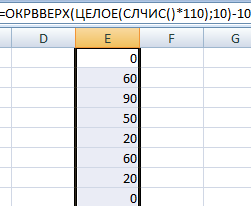
Из списка текстовых значений нужно выбрать 2 случайных. С помощью функции СЛЧИС сопоставим текстовые значения в диапазоне А1:А7 со случайными числами.
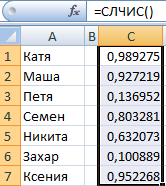
Воспользуемся функцией ИНДЕКС для выбора двух случайных текстовых значений из исходного списка.
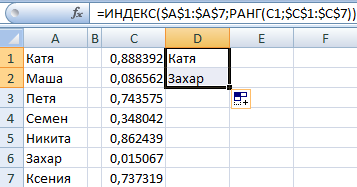
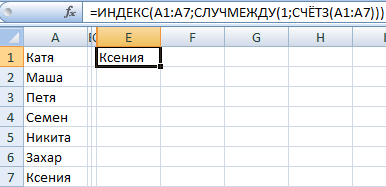
Чтобы выбрать одно случайное значение из списка, применим такую формулу: =ИНДЕКС(A1:A7;СЛУЧМЕЖДУ(1;СЧЁТЗ(A1:A7))).
Генератор случайных чисел нормального распределения
Функции СЛЧИС и СЛУЧМЕЖДУ выдают случайные числа с единым распределением. Любое значение с одинаковой долей вероятности может попасть в нижнюю границу запрашиваемого диапазона и в верхнюю. Получается огромный разброс от целевого значения.
Нормальное распределение подразумевает близкое положение большей части сгенерированных чисел к целевому. Подкорректируем формулу СЛУЧМЕЖДУ и создадим массив данных с нормальным распределением.
Себестоимость товара Х – 100 рублей. Вся произведенная партия подчиняется нормальному распределению. Случайная переменная тоже подчиняется нормальному распределению вероятностей.
При таких условиях среднее значение диапазона – 100 рублей. Сгенерируем массив и построим график с нормальным распределением при стандартном отклонении 1,5 рубля.
Используем функцию: =НОРМОБР(СЛЧИС();100;1,5).
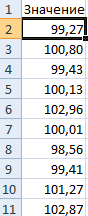
Программа Excel посчитала, какие значения находятся в диапазоне вероятностей. Так как вероятность производства товара с себестоимостью 100 рублей максимальная, формула показывает значения близкие к 100 чаще, чем остальные.
Перейдем к построению графика. Сначала нужно составить таблицу с категориями. Для этого разобьем массив на периоды:
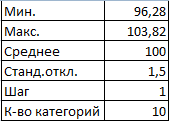
- Определим минимальное и максимальное значение в диапазоне с помощью функций МИН и МАКС.
- Укажем величину каждого периода либо шаг. В нашем примере – 1.
- Количество категорий – 10.
- Нижняя граница таблицы с категориями – округленное вниз ближайшее кратное число. В ячейку Н1 вводим формулу =ОКРВНИЗ(E1;E5).
- В ячейке Н2 и последующих формула будет выглядеть следующим образом: =ЕСЛИ(G2;H1+$E$5;””). То есть каждое последующее значение будет увеличено на величину шага.
- Посчитаем количество переменных в заданном промежутке. Используем функцию ЧАСТОТА. Формула будет выглядеть так:
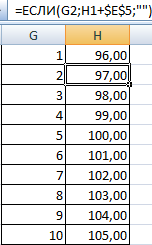
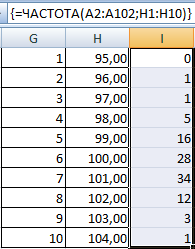
На основе полученных данных сможем сформировать диаграмму с нормальным распределением. Ось значений – число переменных в промежутке, ось категорий – периоды.
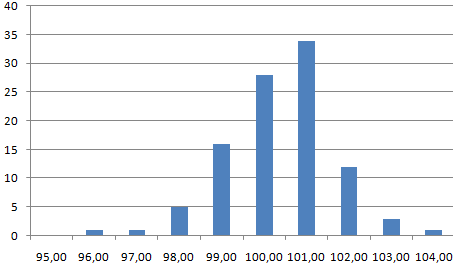
График с нормальным распределением готов. Как и должно быть, по форме он напоминает колокол.
Сделать то же самое можно гораздо проще. С помощью пакета «Анализ данных». Выбираем «Генерацию случайных чисел».
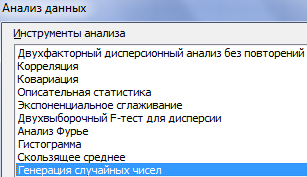
О том как подключить стандартную настройку «Анализ данных» читайте здесь.
Заполняем параметры для генерации. Распределение – «нормальное».
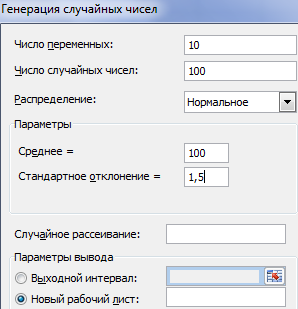
Жмем ОК. Получаем набор случайных чисел. Снова вызываем инструмент «Анализ данных». Выбираем «Гистограмма». Настраиваем параметры. Обязательно ставим галочку «Вывод графика».
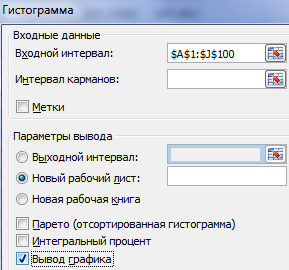
Получаем результат:
Скачать генератор случайных чисел в Excel
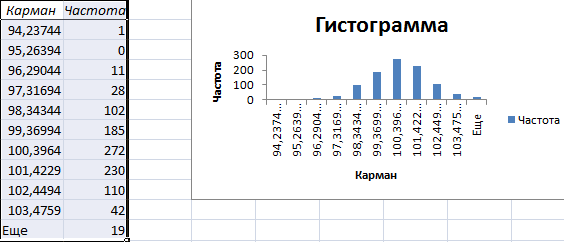
График с нормальным распределением в Excel построен.
В этой серии статей мы обсудим моделирование пучков ионов или электронов с помощью методов трассировки частиц. Начнем мы с короткой справки о функциях распределения вероятностей и о разных способах выборки случайных чисел на их основе в программном пакете COMSOL Multiphysics®. В последующих заметках мы покажем, как этот функционал используется для точного моделирования распространения ионных или электронных пучков в реальных системах.
Актуальность использования функций распределения вероятностей
Энергетические пучки ионов и электронов важны для фундаментальных исследований в области высоких энергий и ядерной физики. Используются они и в разных прикладных задачах: в катодно-лучевых трубках, при производстве медицинских изотопов и для нейтрализации ядерных отходов. Для построения точной вычислительной модели распространения пучка особенно важны исходные значения положений частиц и компонент скорости.
Для запуска пучка ионов или электронов при проведении трассировки частиц часто требуется сделать выборку этих частиц в виде дискретных точек в т.н. фазовом пространстве. Однако перед тем, как разбираться в концепции фазового пространства и ее связи с пучками ионов и электронов, давайте поговорим о функциях распределения вероятностей и методах работы с ними в COMSOL Multiphysics.
Справка о функциях распределения вероятностей
Начнем с некоторых определений. Непрерывная случайная переменная x — это рандомно определяемая переменная, которая может принимать бесконечное множество значений. Например, предположим, что точка x1 выбрана случайно на отрезке длины L. Затем точка x2 выбирается в другом месте на этом отрезке. Если эти две точки не совпадают, можно выбрать третью точку x_3 = (x_1+x_2)/2, которая находится на том же отрезке, потом четвертую — x_4 = (x_1+x_3)/2 и так далее, таким образом получив бесконечное число несовпадающих точек. См. скриншот ниже.
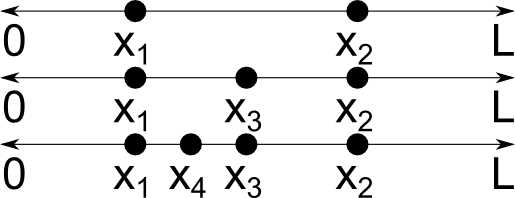
Кстати, другой тип рандомной переменной — дискретная случайная переменная, которая может принимать только конкретные значения. Представьте себе, что вы подбрасываете монетку или вытягиваете карту из колоды: количество результатов конечно.
Одномерная функция распределения вероятностей (probability distribution function — PDF) или плотность распределения вероятностей f(x) описывает вероятность того, что непрерывная случайная переменная примет определенное значение. Например, функция распределения вероятностей вида
(1)
f(x) = left{ begin{array}{cc} 0 & xleq 0\ 1 & 0
описывает переменную x, которая может с равномерной вероятностью принять любое из значений открытого интервала(0; 1), но не может принять какое-либо иное значение. Эта функция распределения вероятностей, в данном случае описывающая равномерное распределение, показана на графике ниже.
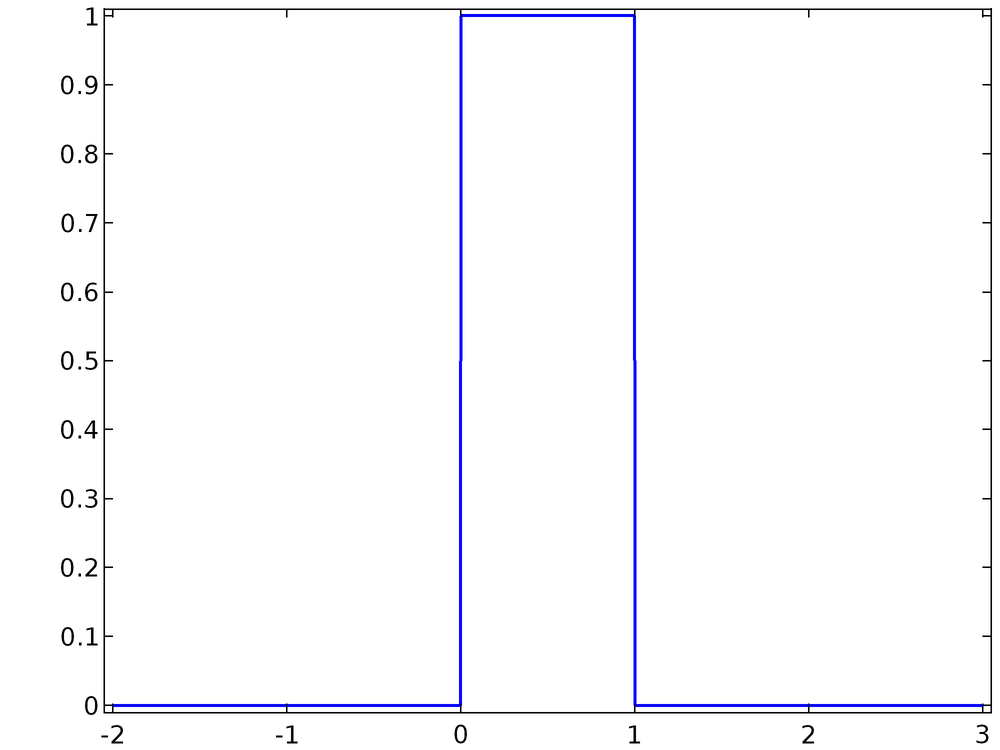
Функции распределения вероятностей могут также применяться в контексте дискретных случайных переменных и даже тех переменных, которые непрерывны в одних интервалах и дискретны в других. Как один из вариантов реализации последней из указанных ситуаций, такую случайную переменную можно рассматривать как непрерывную, уточнив, что функция распределения вероятностей включает в себя одну или несколько дельта-функций Дирака. В этой серии статей мы будем рассматривать только непрерывные случайные переменные.
Функция распределения вероятностей считается нормированной, если
int_{-infty}^{infty} f(x)dx = 1.
Другими словами, суммарная вероятность того, что x примет значение из интервала (-∞; ∞), равна единице.
Интегральная или кумулятивная функция распределения F(x) (cumulative distribution function — CDF) представляет собой вероятность того, что значение непрерывной случайной переменной окажется в интервале (-∞; x). Функция распределения вероятностей и интегральная функция распределения связаны соотношением
F(x) = int_{-infty}^{x} f(x^prime) dx^prime.
Из определения выше следует тот факт, что если функция распределения вероятностей является нормированной, то
textrm{lim}_{x rightarrow infty} F(x) = 1.
Функция распределения вероятностей из уравнения (1) и соответствующая интегральная функция распределения показаны на графике ниже. Функция распределения вероятностей, записанная таким образом, является нормированной.
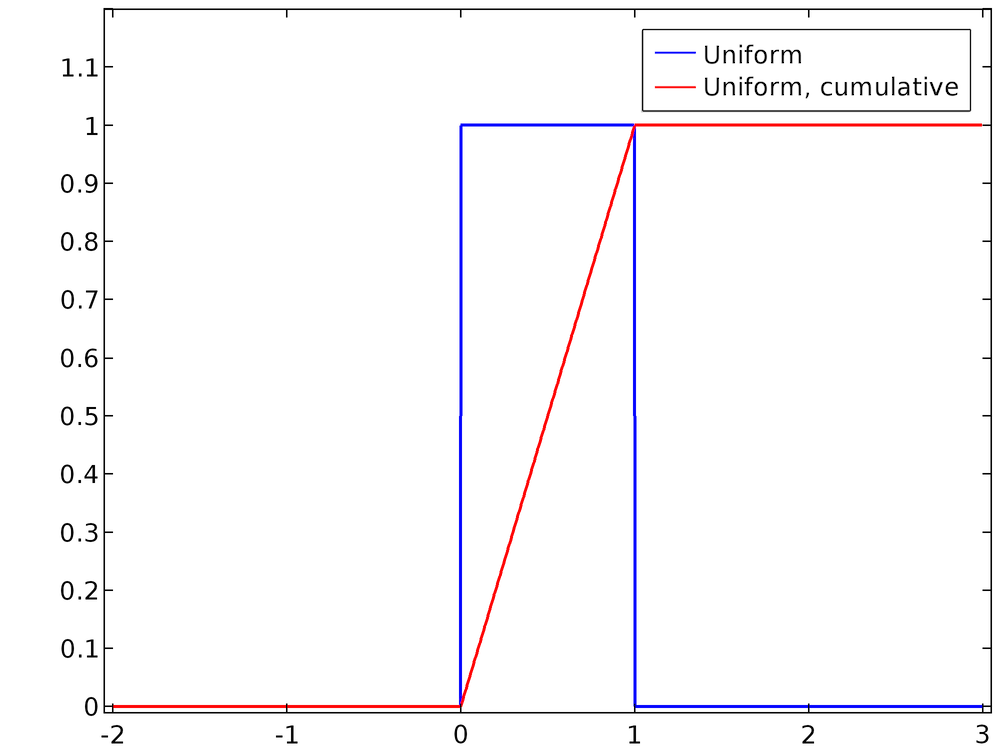
Выборка из одномерного распределения
Выбор случайного значения из равномерного распределения обычно довольно прост. В большинстве языков программирования уже имеются готовые процедуры для генерации равномерно распределенных случайных чисел. Однако предположим, что мы имеем гораздо более произвольное распределение, как, например, показанное ниже.
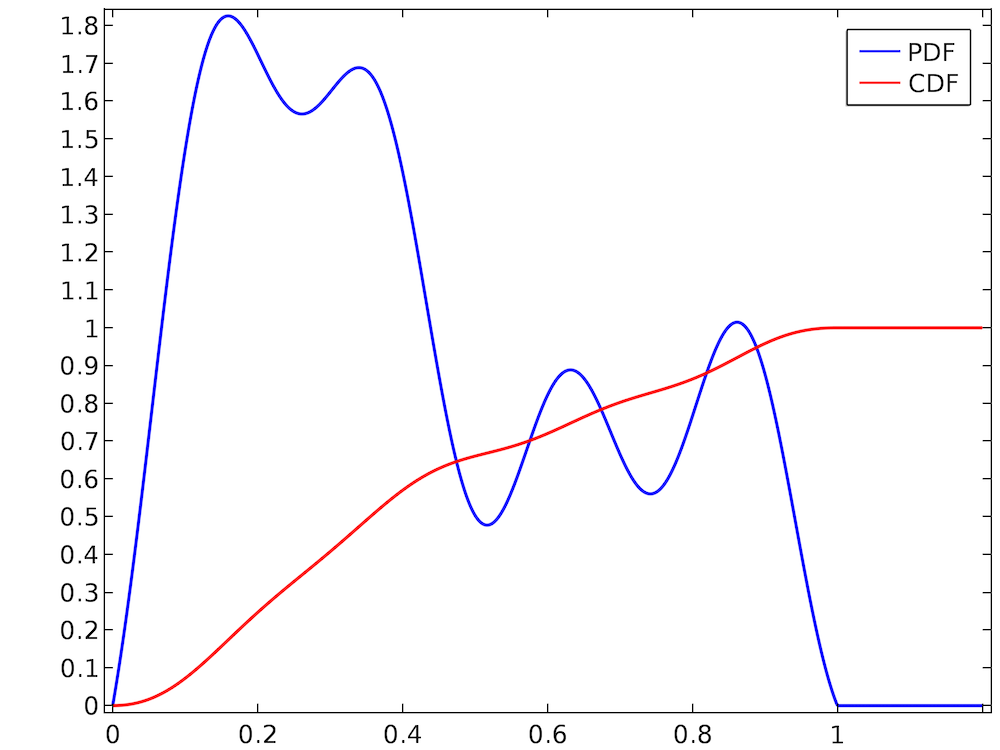
Случайная переменная принимает значения в интервале (0; 1), и функция распределения вероятностей является нормированной, потому что значение интегральной функции распределения на правом конце интервала равно 1. Однако распределение очевидно не является равномерным: к примеру, намного вероятнее, что случайное число попадет в интервал (0,2; 0,3), чем в интервал (0,7; 0,8). Использовать в такой ситуации встроенную процедуру для выборки равномерно распределенных случайных чисел из интервала (0; 1) было бы некорректно. Поэтому нам нужны альтернативные способы выборки случайных чисел из этой произвольно выглядящей функции распределения вероятностей.
Это приводит нас к одной из фундаментальных методик выборки (сэмплирования) значений из функции распределения вероятностей — выборки через обратное преобразование (inverse transform sampling). Пусть U — равномерно распределенное случайное число от нуля до единицы. (Другими словами, U соответствует функции распределения, заданной уравнением (1).) Тогда для выборки случайного числа с (возможно, неравномерной) функцией распределения вероятностей f(x) выполним следующее:
- Нормируем функцию f(x), если она еще не нормирована.
- Берем интеграл нормированной функции распределения вероятностей f(x), чтобы вычислить интегральную функцию распределения F(x).
- Рассчитываем обратную функцию для F(x). Итоговая функция представляет собой обратную интегральную функцию распределения, или квантильную функцию F-1(x). Поскольку мы уже нормировали f(x), для ясности мы назовем ее обратной нормальной интегральной функцией распределения.
- Подставляем значение равномерно распределенного случайного числа U в обратную нормальную интегральную функцию распределения.
Если подвести итог, F-1(U) является случайным числом с функцией распределения вероятностей f(x), если число U in left(0,1right). Рассмотрим пример, в котором данный метод используется для выборки из неравномерной функции распределения вероятностей.
Пример 1. Распределение Рэлея
Распределение Рэлея довольно часто фигурирует в уравнениях динамики разреженного газа и физики пучков. Оно описывается как
(2)
f(x) = left{ begin{array}{cc} 0 & x<0 \ frac{x}{sigma^2}expleft(-frac{x^2}{2sigma^2}right) & x geq 0end{array}right. ,
где σ — масштабный коэффициент, который предварительно задается (на входе задачи). Мы можем проверить, действительно ли распределение Рэлея, записанное в таком виде, является нормированным:
begin{aligned} int_{0}^{infty} frac{x}{sigma^2} expleft(-frac{x^2}{2sigma^2}right)dx &= lim_{x rightarrow infty} left.-expleft(-frac{x^prime^2}{2sigma^2}right)right|^x_0\ &= 1-lim_{x rightarrow infty}expleft(-frac{x^2}{2sigma^2}right)\ &= 1. end{aligned}
Интегральная функция распределения —
begin{aligned} F(x) &=int_{0}^{x} frac{x^prime}{sigma^2} expleft(-frac{x^prime^2}{2sigma^2}right)dx^prime\ &= left.-expleft(-frac{x^prime^2}{2sigma^2}right)right|^x_0\ &= 1-expleft(-frac{x^2}{2sigma^2}right). end{aligned}
Для σ = 1 нормированное распределение Рэлея и его интегральная функция распределения показаны на графике ниже. Очевидно, что для высоких значений x интегральная функция распределения приближается к единице.
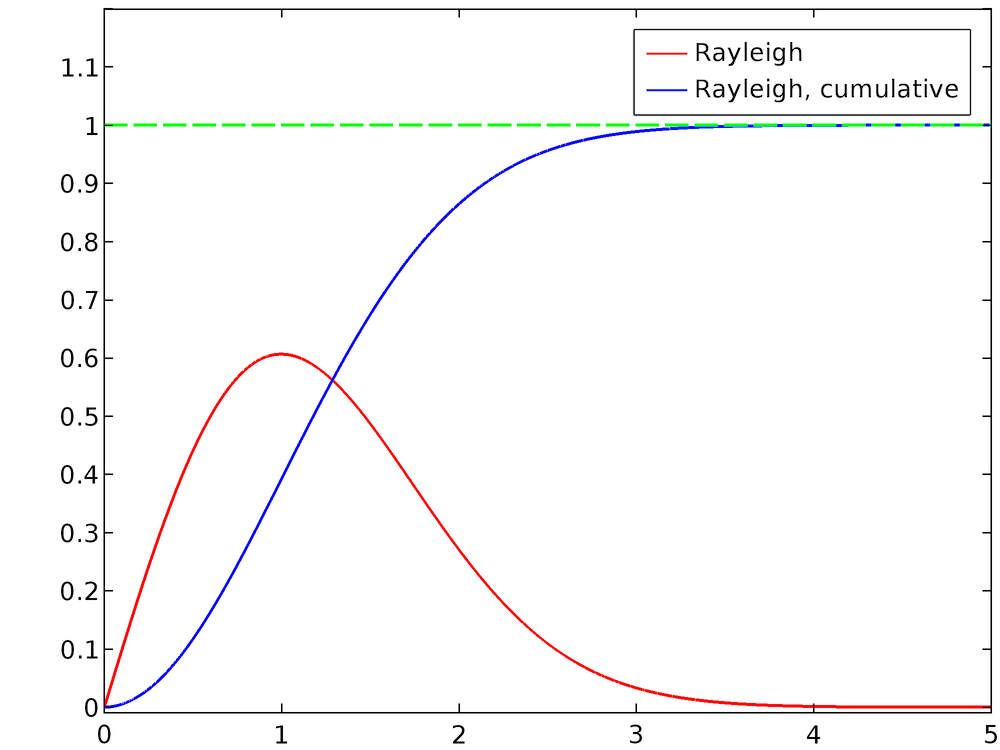
Чтобы вычислить обратную нормальную интегральную функцию распределения, зададим y = F(x) и найдем x:
begin{aligned} y &= F(x)\ y &= 1-expleft(-frac{x^2}{2sigma^2}right)\ expleft(-frac{x^2}{2sigma^2}right) &= 1-y\ -frac{x^2}{2sigma^2} &= logleft(1-yright)\ x &= sigma sqrt{-2 logleft(1-yright)}. end{aligned}
Теперь подставим равномерно распределенное случайное число U вместо переменной y,
x = sigma sqrt{-2 logleft(1-Uright)}.
Поскольку U равномерно распределено на интервале (0; 1) и его значение еще не определено, можно далее упростить это выражение, зная, что U и 1 – U следуют одной и тоже функции распределения вероятностей. Таким образом, мы приходим к финальному выражению для значения x из выборки,
(3)
x = sigma sqrt{-2 log U}.
В последующем мы обсудим, как уравнение (3) можно использовать в модели COMSOL для выборки значений из распределения Рэлея.
Учтите, что обратную нормальную интегральную функцию распределения не всегда возможно рассчитать аналитически. Аналитическое решение в замкнутой форме для интеграла любой функции не всегда существует, и не всегда возможно записать выражения для обратной интегральной функции распределения. Распределение Рэлея было использовано здесь не “случайно”, поскольку его обратную интегральную функцию распределения можно вывести, не прибегая к численным или приближенным техникам.
Выборка случайных чисел в COMSOL Multiphysics®
Результаты приведенного выше анализа можно использовать в COMSOL Multiphysics для выборки из произвольного одномерного распределения, например распределения Рэлея. Для начала давайте рассмотрим встроенные в пакет инструменты для выборки из распределений особых типов.
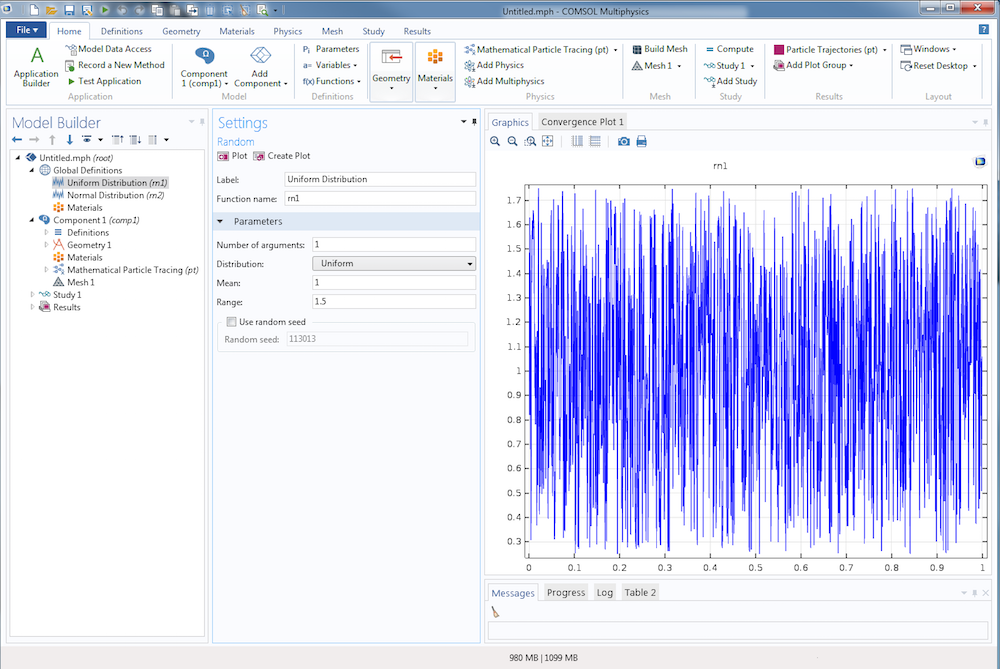
В COMSOL Multiphysics доступно несколько способов задать псевдослучайные числа (о значении термина «псевдослучайный» мы поговорим позже). Задать псевдослучайное число с равномерным или нормальным распределением можно с помощью функции Random (Случайная величина), доступной в узлах Global Definitions (Глобальные определения) и Definitions (Определения). Если используется распределение Uniform (Равномерное), укажите значения параметров Mean (Среднее значение) и Range (Диапазон). Для среднего значения μu и диапазона σu функция распределения вероятностей выглядит так:
f(x) = left{ begin{array}{cc} 0 & x leq mu_u-frac{sigma_u}{2}\ frac{1}{sigma_u} & mu_u-frac{sigma_u}{2} < x < mu_u + frac{sigma_u}{2} \ 0 & mu_u + frac{sigma_u}{2} leq x end{array}right. .
Пример равномерного распределения со средним значением 1 и диапазоном 1.5 показан ниже.
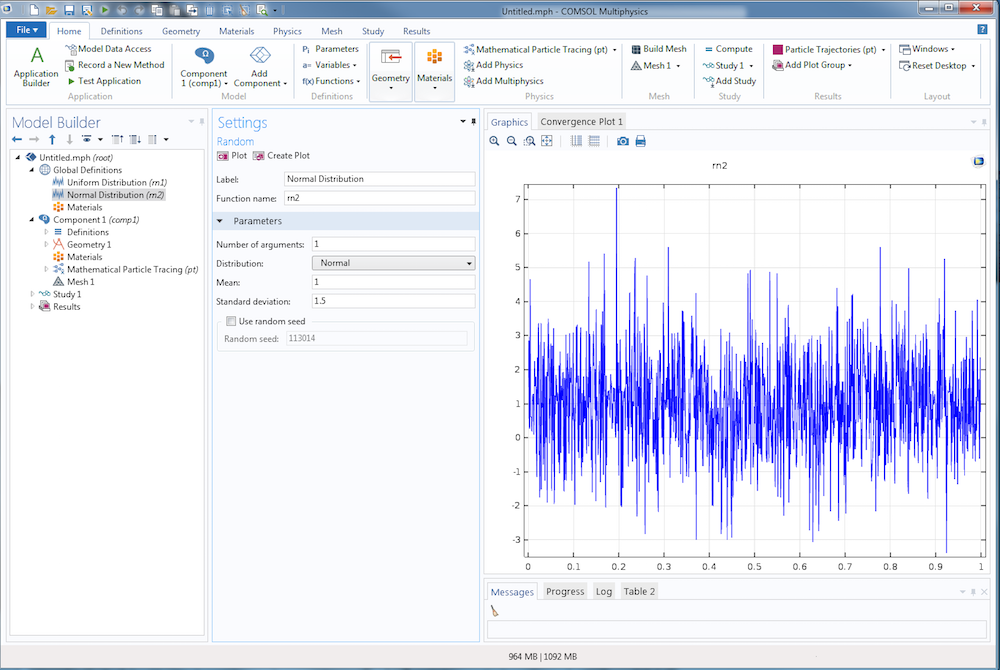
Если используется распределение Normal (Нормальное), или распределение Гаусса, укажите значения параметров Mean (Среднее значение) и Standard Deviation (Среднеквадратичное отклонение). Для среднего значения μn и среднеквадратичного отклонения σn функция распределения вероятностей выглядит так:
f(x) = frac{1}{sigma_n sqrt{2pi}} expleft(-frac{left(x-mu_n right)^2}{2sigma_n^2}right).
Пример равномерного распределения со средним значением 1 и среднеквадратичным отклонением 1,5 показан ниже. Как и в случае с равномерным распределением, кривая рваная и непредсказуемая. В отличие от равномерного распределения, точки на кривой расположены очень плотно вблизи прямой y = 1, от которой их плотность идет на спад.
Ниже приведено сравнение двух распределений при стандартных настройках, когда среднее значение равно 0, а диапазон или среднеквадратичное отклонение равны 1.
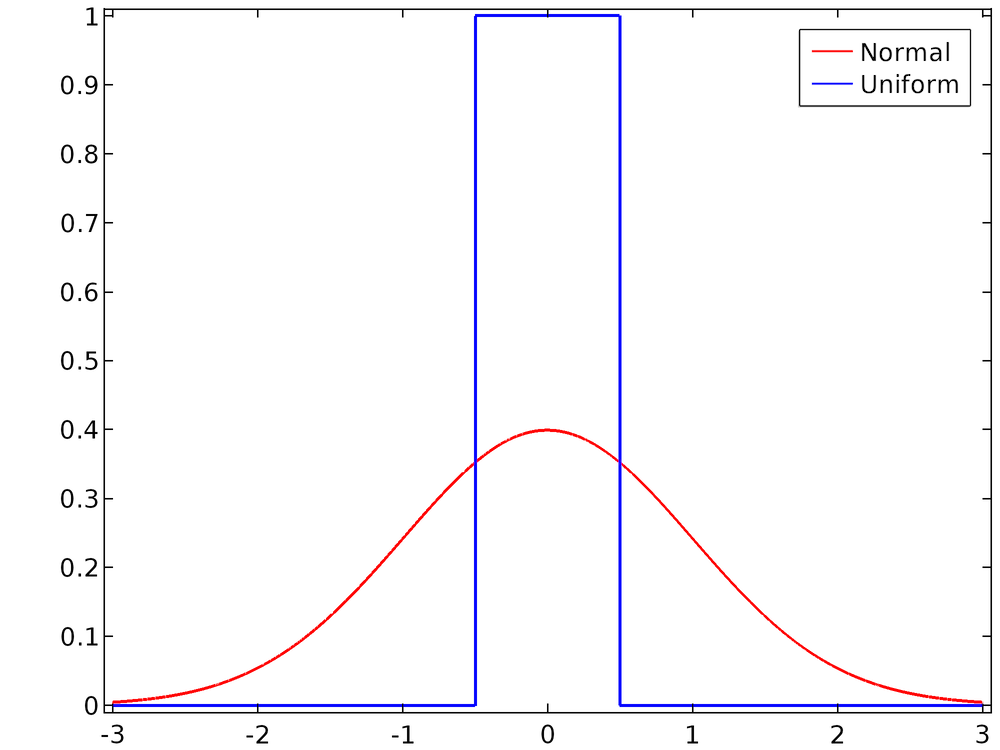
Сравнение равномерной функции распределения вероятностей с диапазоном 1 и распределения Гаусса со среднеквадратичным отклонением 1.
Как альтернативу использования функции Random можно использовать также встроенные операторы random и randomnormal в любом выражении. В операторе random реализовано равномерное распределение со средним значением 0 и диапазоном 1; в randomnormal — нормальное распределение со средним значением 0 и среднеквадратичным отклонением 1.
Учитывая, что для уравнения (3) нам требуется число U, равномерно выбранное из интервала (0; 1), нам доступны две опции:
- Использование функции Random со средним значением 0,5 и диапазоном 1.
- Использование встроенного оператора
randomс добавлением постоянной величины 0,5.
В следующем примере мы допустим, что используется второй подход.
Случайные, псевдослучайные и начальные числа
Как уже упоминалось, вышеупомянутые методики используются для генерации псевдослучайных чисел. «Псевдослучайное» число — это случайное число, однозначно сгенерированное из исходного значения, или начального числа (seed). Для встроенного оператора random в качестве начального числа используется значение его аргумента (или аргументов). Для сравнения, истинно случайные числа не могут быть сгенерированы одной только программой и требуют некоторого источника энтропии — естественного процесса, по существу непредсказуемого и неповторимого, например, радиоактивного распада или атмосферного шума.
Работать с псевдослучайными числами удобнее, чем с истинно случайными, по нескольким причинам. Их воспроизводимость может быть полезна при поиске проблем в моделях Монте-Карло, поскольку можно получить одинаковый результат, выполнив моделирование несколько раз с одним и тем же начальным числом, упростив при этом обнаружение изменений в других областях модели. Поскольку для псевдослучайных чисел не требуется источника естественной энтропии, которая может иметь лишь конечную величину в той или иной среде и длиться конечный период времени, псевдослучайные числа менее вероятно приведут к увеличению требуемого времени моделирования, в отличие от истинно случайных чисел.
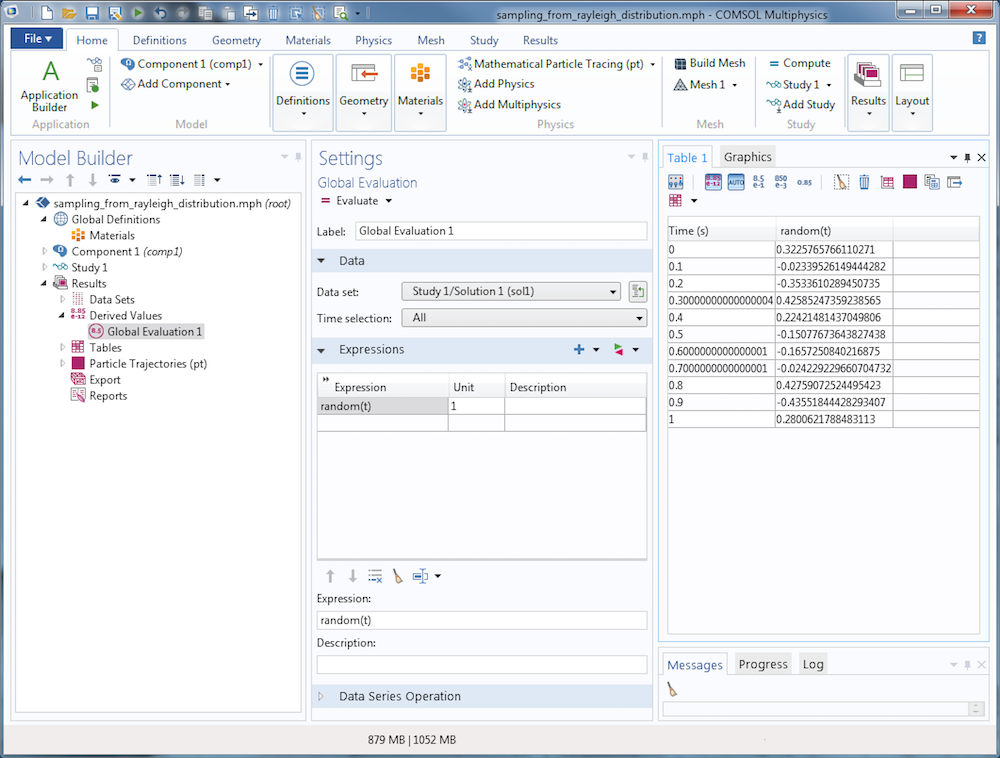
Несмотря на удобство использования псевдослучайных чисел, следует всегда держать в уме и учитывать некоторые особенности их использования. Результирующее псевдослучайное число будет отличаться для разных значений начального числа, хотя одно и то же начальное число даст при повторении одинаковое значение. Чтобы увидеть этой в любой модели COMSOL, создайте узел Global Evaluation (Расчет глобальных выражений) и несколько раз проведите расчет встроенной функции random с постоянным начальным числом, скажем random(1). Результат не покажет очевидной связи с числом 1 (в этой связи число будет выглядеть случайным), однако значение останется без изменений после нескольких повторных расчетов (и поэтому распределение значений уже не покажется случайным). См. скриншот ниже.
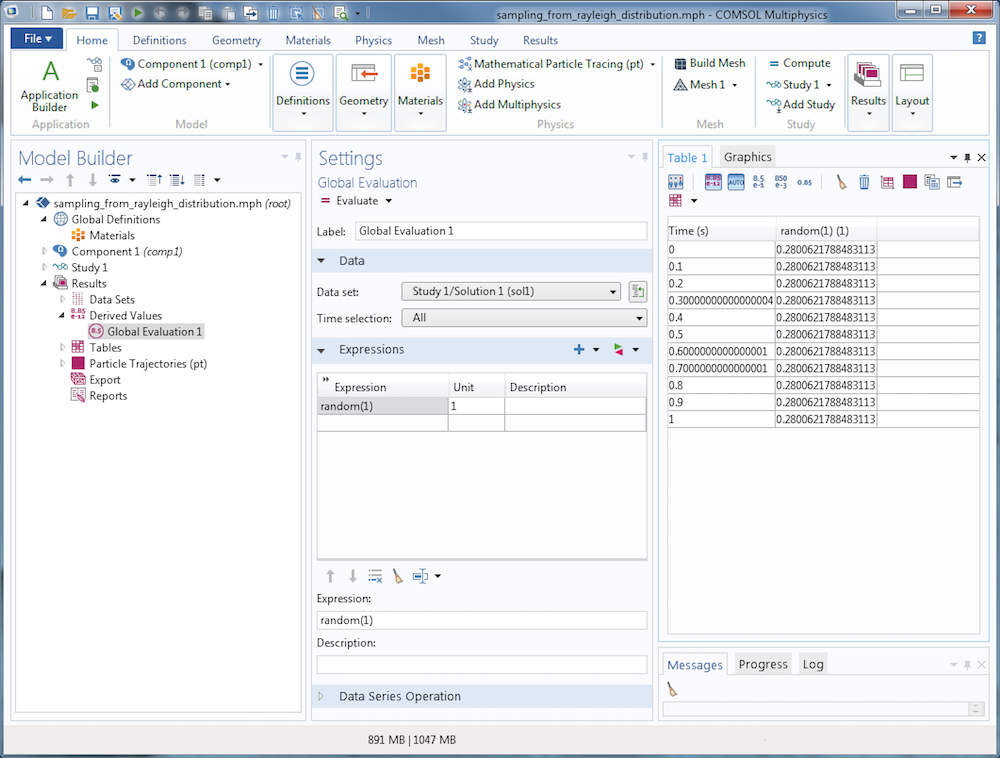
Если при каждом вычислении случайного числа будет использоваться иное начальное число, результаты каждый раз будут разными. Просмотрите и сопоставьте с предыдущей таблицу на следующем скриншоте, в которой используется в качестве входного аргумента для случайной функции переменная времени.
Расчеты с использованием техник Монте-Карло для систем частиц, как правило, включают в себя большие группы частиц, испускаемых со случайными исходными условиями и подвергающихся воздействию случайных сил. Вот несколько примеров случайных явлений, связанных с группами частиц:
- При излучении ионных и электронных пучков, для исходного положения каждой частицы в фазовом пространстве выполняется выборка на основе распределения, которая и является главной темой следующей статьи в этой серии
- Нейтрализация ионов в разреженном фоновом газе в следствие случайных столкновений, сопровождающихся обменом заряда
- Турбулентная дисперсия частиц в потоках текучей среды с высоким критерием Рейнольдса
- Моделирование диффузии частиц при броуновском движении
Очевидно, что если для каждой частицы будут использоваться одинаковые псевдослучайные числа, то такое моделирование будет некорректно отражать реальную физику процесса. Например в случае взаимодействия ионов с фоновым газом, каждая частица будет сталкиваться с молекулами или атомами газа в точности столько же раз, сколько и все другие. Чтобы исправить это, любым случайным числам, используемым в моделировании трассировки частиц, следует назначить начальные числа, уникальные для каждой их них.
Один из вариантов реализации такого подхода является использование при выборе начального числа индекса частицы, который уникален для каждой частицы. Переменная индекса частицы выглядит как <scope>.pidx, где <scope> представляет собой уникальный идентификатор для экземпляра физического интерфейса. Для интерфейса Mathematical Particle Tracing (Математическая трассировка частиц) индекс частицы обычно записывается как pt.pidx. Функция вида random(pt.pidx) присвоит всем частицам разные псевдослучайные числа.
Еще одна сложность связана с тем, что на частицы воздействуют случайные силы на протяжении всего их существования. Например, если для определения случайного столкновения с молекулой газа используется случайное число, это же случайное число не следует использовать для данной частицы в каждый момент времени — ведь тогда частица будет сталкиваться с молекулой на каждом временном шаге или не будет сталкиваться с ней вовсе! Для решения этой проблемы можно задать случайное начальное число, в котором используется несколько аргументов: хотя бы один аргумент, отличающийся для каждой частицы, и один, отличающийся на разных временных шагах моделирования. Если для моделирования необходима выборка нескольких псевдослучайных чисел, независимых друг от друга, могут потребоваться дополнительные аргументы. В этом случае типовая случайная функция может выглядеть так: random(pt.pidx,t,1), где заключительный аргумент 1 можно заменить другими численными значениями, если требуются дополнительные псевдослучайные числа.
Результаты: распределение Рэлея
Давайте вернемся к исходной задаче выборки/сэмплирования из распределения Рэлея. Предположим, что имеется совокупность частиц и требуется выбрать одно число для каждой частицы так, чтобы результирующие значения соответствовали распределению Рэлея. В этом примере мы будем использовать уравнение (2) с σ = 3. В модели COMSOL определим следующие переменные:
| Имя переменной | Выражение | Описание |
|---|---|---|
rn
|
0.5+random(pt.pidx)
|
Случайный аргумент
|
sigma
|
3
|
Масштабирующий параметр
|
val
|
sigma*sqrt(-2*log(rn))
|
Значение, сэмплированное из распределения Рэлея
|
Обратите внимание на то, что последняя строка — не что иное, как уравнение (3). Следующий график представляет собой гистограмму значения rn для совокупности 1000 частиц. Плавная кривая — это точное распределение Рэлея, определенное с помощью отдельного задания и построения аналитической функции (опция Analytic).
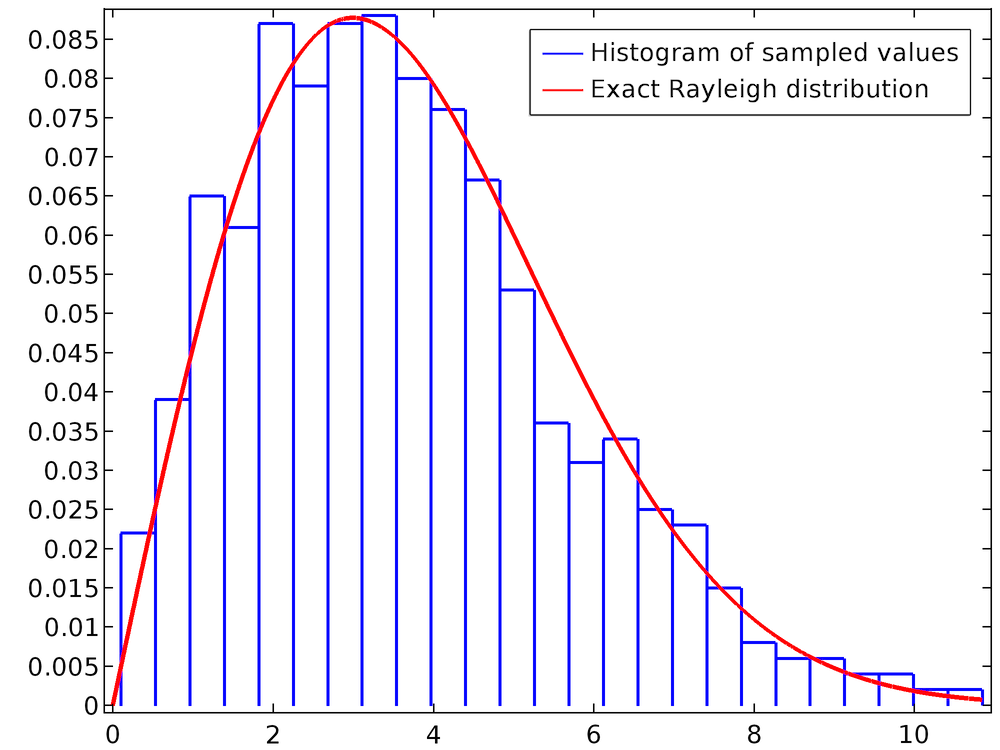
Для точного “воспроизведения” функции распределения вероятностей с большим количеством мелких деталей может потребоваться больше частиц.
Примечание по использованию интерполяционных функций
Если функция распределения вероятностей реализуется в COMSOL Multiphysics с помощью интерполяционной функции (Interpolation), а не аналитической (Analytic) или кусочной (Piecewise), то можно использовать встроенные опции для автоматического задания случайной функции на ее основе.
Предположим, что имеется интерполяционная функция с линейной интерполяцией между следующими точками данных:
| x | f(x) |
|---|---|
| 0 | 0 |
| 0.2 | 0.6 |
| 0.4 | 0.7 |
| 0.6 | 1.2 |
| 0.8 | 1.2 |
| 1 | 0 |
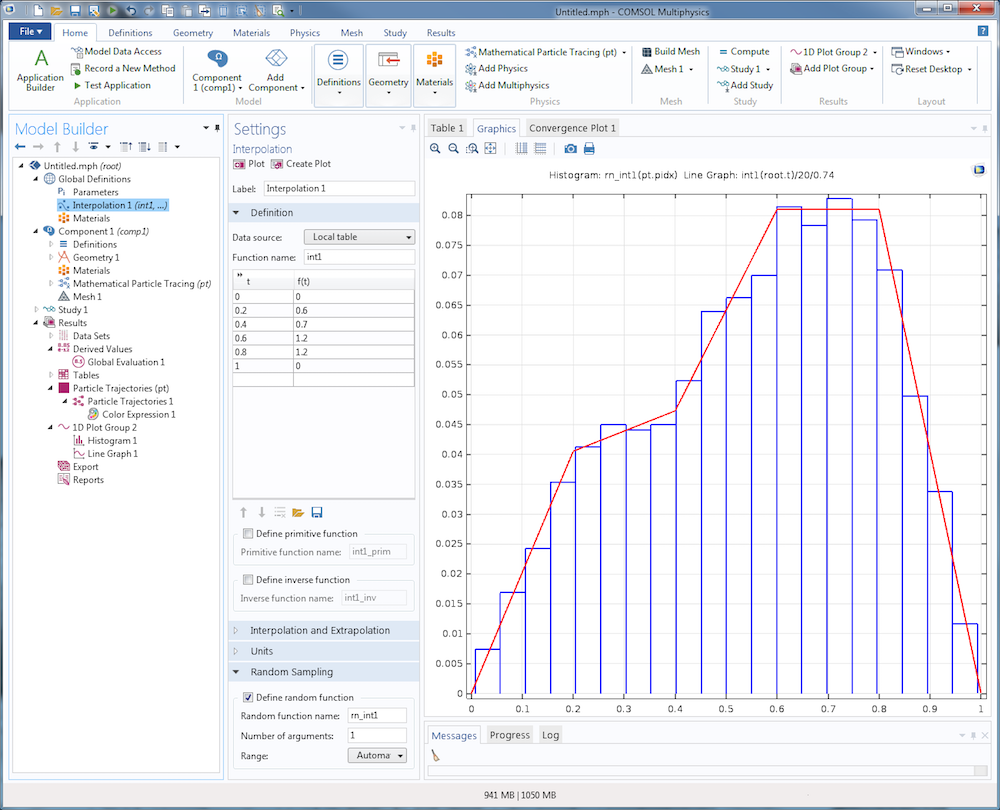
На следующем снимке экрана показано, как можно ввести эти данные в соотвествующие поля узла фукнции Interpolation. Установив флажок Define random function (Определить случайную функцию) в окне настроек для интерполяционной функции, можно автоматически задать функцию rn_int1 для расчета выборки из этого распределения. В графическом окне гистограмма показывает случайную выборку из 1000 точек данных и непрерывную кривую самой интерполяционной функции. Для корректировки количества столбцов и нормировки интерполяционной функции добавлены дополнительные коэффициенты 20 и 0.74, соответственно.
Использование функций распределения вероятностей в физике пучков
Итак, в данном материале мы разобрали, как связаны функции распределения вероятностей, интегральные функции распределения и их обратные функции. Мы также рассмотрели несколько приемов расчета выборки из равномерной и неравномерной функции распределения вероятностей в моделях COMSOL. В следующей статье из серии Распределения в фазовом пространстве для физики пучков» мы начнем обсуждение непосредственно физики ионных и электронных пучков и выясним, почему для точного моделирования систем пучков предельно важно использовать функции распределения вероятностей.
Ссылки на другие части данной серии
- Распределения в фазовом пространстве и эмиттанс для заряженных пучков частиц в 2D постановке (часть 2)
- Распределения в фазовом пространстве для заряженных пучков частиц в 3D постановке (часть 3)
Список литературных источников
- Humphries, Stanley. Charged particle beams. Courier Corporation, 2013.
- Davidson, Ronald C., and Hong Qin. Physics of intense charged particle beams in high energy accelerators. Imperial college press, 2001.
