Как найти интервал варьирования - Сайт, где вы сможете решить свои вопросы

Интервалом
варьирования факторов называется
некоторое число, причем свое для каждого
фактора, прибавление которого к основному
уровню дает верхний, а вычитание –
нижний уровень фактора.

Для
упрощения записи условий эксперимента
и обработки экспериментальных данных,
масштабы по осям выбираются так, чтобы
верхний уровень соответствовал плюс
единицы, нижний – минус единицы, а
основной – нулю. Для факторов с непрерывной
областью определения это можно сделать
с помощью преобразования.

(48)

где -кодированное
значение фактора;

-натуральное
значение фактора;

-натуральное
значение основного уровня;

J_j-интервал
варьирования;

j-номер
фактора.

На
выбор интервала варьирования накладываются
ограничения снизу (он не может быть
меньше ошибки, с которой экспериментатор
фиксирует уровень фактора, иначе верхний
и нижний уровень окажутся неразличимыми)
и сверху (верхний или нижний уровни не
должны выходить за пределы области
определения).

Для
данного случая:

Точность
фиксирования факторов лежит в пределах
2-5%. Такая точность определяется как
средняя.
Сведений
о кривизне поверхности отклика нет.
Диапазон
изменения параметра оптимизации –
разность между его наибольшим и
наименьшим значениями.

Y_max=
0,32, Y_min
= 0,1.

Y_max–
Y_min=
0,32-0,1=0,22.

Определяем
интервал варьирования как средний.

Интервалы
варьирования, выбранные с учетом
указанных условий, приведены в таблице
2. В этой же таблице приведены значения
верхнего (обозначен +1) и нижнего (обозначен
–1) уровней факторов.

Таблица
2 – Уровни факторов и интервалы
варьирования

№	Наименование фактора	Уровни факторов	Интервал варьирования
-1	0	+1
	Расстояние между электродами, мм	3	4	5	1
	Напряжение на третьей паре электродов, кВ	1	2	3	1

3.3.2 Число опытов полного факторного эксперимента. Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом.

В
рассмотренном случае число уровней
каждого фактора равно двум, тогда число
факторов эксперимента можно определить
по следующей формуле:

(49)

где N
–
число опытов;

к
– число факторов.

Для
четырех факторного эксперимента:
.

Используя
кодированные значения факторов, условия
эксперимента можно записать в виде
таблице, где отражены все возможные
сочетания уровней факторов. Такая
таблица называется матрицей планирования
эксперимента.

Таким
образом, условия эксперимента определены
однозначно и записаны в таблице 3.

3.3.3
Свойства
полного факторного эксперимента.
Составленная
матрица планирования проверяется на
соответствие свойствам полного факторного
эксперимента.

Таблица
3 – Матрица планирования эксперимента
2²

№ опыт	х₁	Х₂	J
1	-1	-1	J₁
2	-1	+1	J₂
3	+1	-1	J₃
4	+1	+1	J₄

Симметричность
относительно центра эксперимента:

(50)

где j
–
номер фактора, j=к;

N
– число опытов.

Условия
нормировки:

(51)

Ортогональность
матрицы:

(52)

где j
≠ U;
j, U =0,1,2… k.

Составленная
матрица полностью соответствует заданным
свойствам.

3.3.4
Проведение
эксперимента.

Реализация
плана эксперимента.

Согласно
условиям, указанным в матрицах планирования
проведем эксперимент, результаты
которого занесены в таблицу 4, причем
для каждого варианта осуществлено по
пять параллельных опытов.

Таблица
4 – Экспериментальные данные

№ опыт.	D, мм	U₃, кВ	I_ск, мкА
1	2	3	4	5
1	3	1	0,125	0,144	0,127	0,134	0,158
2	3	3	0,315	0,282	0,321	0,312	0,294
3	5	1	0,112	0,080	0,182	0,150	0,090
4	5	3	0,320	0,287	0,326	0,317	0,299

Крутизна
статической характеристики вычисляется
по формуле:

(53)

где

Соседние файлы в папке ПРОШЛЫЙ

#
#
#
03.02.201932.21 Кб1PERETEN
#
03.02.201932.69 Кб2PLAK1.CDW
#
03.02.201933.96 Кб2PLAK2.CDW
#
#
#
#
#
#
03.02.2019267.78 Кб1VP.DOC

Источник

Полный факторный эксперимент

Как выбрать локальную область
факторного пространства, где ее выбирать и какого размера она должна быть? Это
важный этап принятия неформализованных решений, предшествующих построению
плана первой серии эксперимента.

Весь процесс исследования
можно считать состоящим из последовательности этапов, часть из которых полностью
формализованы, а часть требуют «интуитивных» решений. Причем, по мере развития
теории, формальные этапы будут играть все большую роль, но до конца не вытеснят
неформализованные этапы.

Принятие решений
перед планированием эксперимента

При выборе области
эксперимента должны учитываться следующие соображения.

Прежде всего, надо оценить
границы областей определения факторов. При этом должны учитываться ограничения
нескольких типов. Первый тип: принципиальные ограничения для значений
факторов, которые не могут быть нарушены ни при каких обстоятельствах.
Например, если фактор – температура, то нижним пределом будет абсолютный нуль.
Второй тип – ограничения, связанные с технико-экономическими соображениями,
например, со стоимостью сырья, дефицитностью отдельных компонентов, временем
ведения процесса. Третий тип ограничений, с которым чаще всего приходится
иметь дело, определяется конкретными условиями проведения процесса, например,
существующей аппаратурой, технологией, организацией. В реакторе, изготовленном
из некоторого материала, температуру нельзя поднять выше температуры плавления
этого материала или выше рабочей температуры данного катализатора.

Оптимизация обычно начинается
в условиях, когда объект уже подвергался некоторым исследованиям. Информацию,
содержащуюся в результатах предыдущих исследований, будем называть априорной (т.е.
полученной до начала эксперимента). Мы можем использовать априорную информацию
для получения представления о параметре оптимизации, о факторах, о наилучших
условиях ведения процесса и характере поверхности отклика, т.е. о том, как
сильно меняется параметр оптимизации при небольших изменениях значений
факторов, а также о кривизне поверхности. Для этого можно использовать графики
(или таблицы) однофакторных экспериментов, осуществлявшихся в предыдущих
исследованиях или описанных в литературе. Если однофакторную зависимость нельзя
представить линейным уравнением (в рассматриваемой области), то в многомерном
случае, несомненно, будет существенная кривизна. Обратное утверждение, к
сожалению, не очевидно.

Итак, выбор экспериментальной
области факторного пространства связан с тщательным анализом априорной информации.

Выбор основного уровня

Наилучшим условиям,
определенным из анализа априорной информации, соответствует комбинация (или
несколько комбинаций) уровней факторов. Каждая комбинация является многомерной
точкой в факторном пространстве. Ее можно рассматривать как исходную точку для
построения плана эксперимента. Назовем ее основным (нулевым) уровнем. Построение
плана эксперимента сводится к выбору экспериментальных точек, симметричных
относительно нулевого уровня.

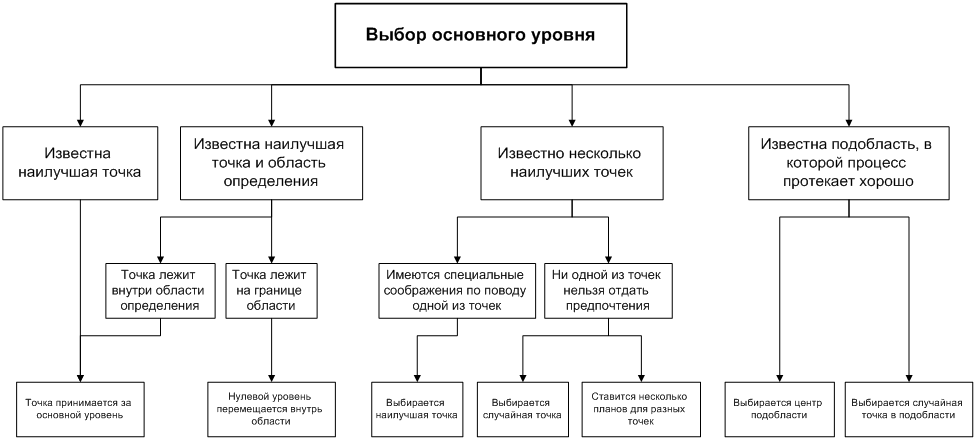
В разных случаях мы
располагаем различными сведениями об области наилучших условий. Если имеются
сведения о координатах одной наилучшей точки и нет информации о границах
определения факторов, то остается рассматривать эту точку в качестве основного
уровня. Аналогичное решение принимается, если границы известны и наилучшие
условия лежат внутри области.

Положение усложняется, если
эта точка лежит на границе (или весьма близко к границе) области. Тогда приходится
основной уровень выбирать с некоторым сдвигом от наилучших условий.

Может случиться, что
координаты наилучшей точки неизвестны, но есть сведения о некоторой подобласти,
в которой процесс идет достаточно хорошо. Тогда основной уровень
выбирается либо в центре, либо в случайной точке этой подобласти. Сведения о
подобласти можно получить, анализируя изученные ранее подобные процессы, из
теоретических соображений или из предыдущего эксперимента.

Наконец, возможен случай с
несколькими эквивалентными точками, координаты которых различны. Когда
отсутствуют дополнительные данные (технологического, экономического характера и
т.д.), выбор произволен. Конечно, если эксперимент недорог и требует немного
времени, можно приступить к построению планов экспериментов вокруг нескольких
точек.

Резюмируем наши рассуждения о
принятии решений при выборе основного уровня в виде блок-схемы

Рисунок 2

После того как нулевой
уровень выбран, переходим к следующему шагу – выбору интервалов варьирования.

Выбор интервалов варьирования.

Теперь наша цель
состоит в том, чтобы для каждого фактора выбрать два уровня, на которых он
будет варьироваться в эксперименте.

Интервалом варьирования
факторов называется некоторое число (свое для каждого фактора), прибавление которого
к основному уровню дает верхний, а вычитание – нижний уровни фактора. Другими
словами, интервал варьирования – это расстояние на координатной оси между основным
и верхним (или нижним) уровнем. Таким образом, задача выбора уровней сводится к
более простой задаче выбора интервала варьирования.

Заметим еще, что для
упрощения записи условий эксперимента и обработки экспериментальных данных
масштабы по осям выбираются так, чтобы верхний уровень соответствовал +1,
нижний –1, а основной – нулю. Для факторов с непрерывной областью определения
это всегда можно сделать с помощью преобразования

где

– кодированное
значение фактора;

– натуральное значение фактора;

– натуральное значение основного уровня;

– интервал варьирования;

– номер фактора.

Для качественных факторов,
имеющих два уровня, один уровень обозначается +1, а другой –1; порядок уровней
не имеет значения.

На выбор интервалов варьирования
накладываются естественные ограничения сверху и снизу. Интервал варьирования
не может быть меньше той ошибки, с которой экспериментатор фиксирует уровень фактора.
Иначе верхний и нижний уровни окажутся неразличимыми. С другой стороны,
интервал не может быть настолько большим, чтобы верхний или нижний уровни
оказались за пределами области определения. Внутри этих ограничений обычно еще остается
значительная неопределенность выбора, которая устраняется с помощью интуитивных
решений.

Обратите внимание, что при
решении задачи оптимизации мы стремимся выбрать для первой серии экспериментов такую
подобласть, которая давала бы возможность для шагового движения к оптимуму. В задачах
же интерполяции интервал варьирования охватывает всю описываемую область.

Выбор интервалов варьирования
– задача трудная, так как она связана с неформализованным этапом планирования
эксперимента. Возникает вопрос, какая априорная информация может быть полезна
на данном этапе? Это – сведения о точности, с которой экспериментатор фиксирует
значения факторов, о кривизне поверхности отклика и о диапазоне изменения
параметра оптимизации. Обычно эта информация является ориентировочной (в некоторых
случаях она может оказаться просто ошибочной), но это единственная разумная
основа, на которой можно начинать планировать эксперимент. В ходе эксперимента
ее часто приходится корректировать.

Точность фиксирования
факторов определяется точностью приборов и стабильностью уровня в ходе опыта.
Для упрощения схемы принятия решений мы введем приближенную классификацию,
полагая, что есть низкая, средняя и высокая точности. Можно, например, считать,
что поддержание температуры в реакторе с погрешностью не более 1% соответствует
высокой, не более 5% – средней, а более 10% – низкой точности.

Источником сведений о
кривизне поверхности отклика могут служить уже упоминавшиеся графики однофакторных
зависимостей, а также теоретические соображения. Из графиков сведения о кривизне
можно получить визуально. Некоторое представление о кривизне дает анализ
табличных данных, так как наличию кривизны соответствует непропорциональное изменение
параметра оптимизации при равномерном изменении фактора. Мы будем различать три
случая: функция отклика линейна, функция отклика существенно нелинейна и
информация о кривизне отсутствует.

Наконец, полезно знать, в
каких диапазонах меняются значения параметра оптимизации в разных точках факторного
пространства. Если имеются результаты некоторого множества опытов, то всегда
можно найти наибольшее или наименьшее значения параметра оптимизации. Разность
менаду этими значениями будем называть диапазоном изменения параметра
оптимизации для данного множества опытов. Условимся различать широкий и узкий
диапазоны. Диапазон будет узким, если он не существенно отличается от разброса
значений параметра оптимизации в повторных опытах (этот разброс определяет
ошибку опыта). В противном случае будем считать диапазон широким. Учтем также
случай, когда информация отсутствует. Итак, для принятия решений используется
априорная информация о точности фиксирования факторов, кривизне поверхности
отклика и диапазоне изменения параметра оптимизации. Каждое сочетание
градаций перечисленных признаков определяет ситуацию, в которой нужно
принимать решение. При принятых градациях возможно З³ = 27 различных ситуаций. Они
представлены на рис. 3, 4, 5 в виде кружочков, цифры в которых соответствуют
порядковым номерам ситуаций.

Теперь мы приблизились к
принятию решения о выборе интервалов варьирования. Для интервалов также введем
градацию. Будем рассматривать широкий, средний и узкий интервалы варьирования, а
также случай, когда трудно принять однозначное решение. Размер интервала варьирования
составляет некоторую долю от области определения фактора. Можно, например,
условиться о следующем: если интервал составляет не более 10% от области
определения, считать его узким, не более 30% – средним, и в остальных случаях –
широким. Это, конечно, весьма условно, и в каждой конкретной задаче приходится
специально определять эти понятия, которые зависят не только от размера области
определения, но и от характера поверхности отклика и от точности фиксирования
факторов.

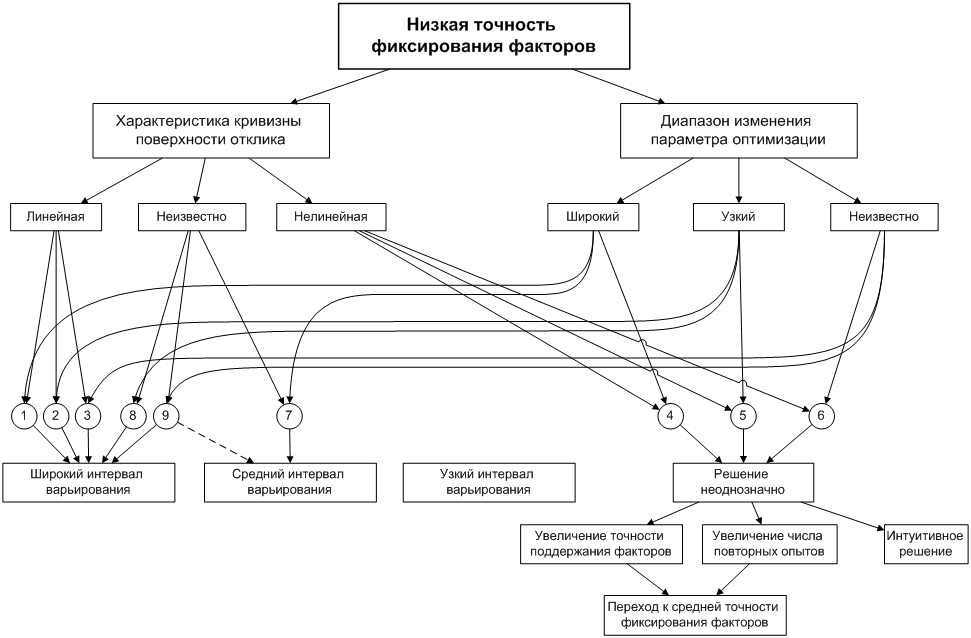
Перейдем к рассмотрению блок-схем
принятия решений. На первой схеме (рис. 3) представлены девять ситуаций,
имеющих место при низкой точности фиксирования факторов. При выборе решений учитываются
информация о кривизне поверхности отклика и о диапазоне изменения параметра
оптимизации. Типичное решение – широкий интервал варьирования, узкий интервал
варьирования совершенно не используется, что вполне понятно при низкой
точности.

Средний интервал
варьирования в этой схеме выбирается дважды, причем в девятой ситуации как
редко применяемая альтернатива. Здесь отсутствует информация об обоих
признаках и выбор широкого интервала представляется более естественным.

Наибольшие трудности
возникают, когда поверхность отклика нелинейна. Появляется противоречие между
низкой точностью фиксирования факторов и кривизной. Первая требует расширения
интервала, а вторая – сужения. Решение оказывается неоднозначным. Как
поступить? Приходится рассматривать дополнительные рекомендации (см.
блок-схему). Прежде всего, нужно выяснить, нельзя ли увеличить точность
эксперимента либо за счет инженерных решений, либо за счет увеличения числа
повторных опытов. Если это возможно, то решения принимаются на основе
блок-схемы (рис. 4) для средней точности фиксирования факторов. Если это
невозможно, то для принятия решения нет достаточных оснований и оно становится
интуитивным.

Эта блок-схема, как и
последующие, служит весьма грубым приближением к действительности. На практике
учитывается ещё масса обстоятельств. Например, решения, принимаемые по каждому
фактору в отдельности, корректируются при рассмотрении совокупности факторов.

Рисунок 3

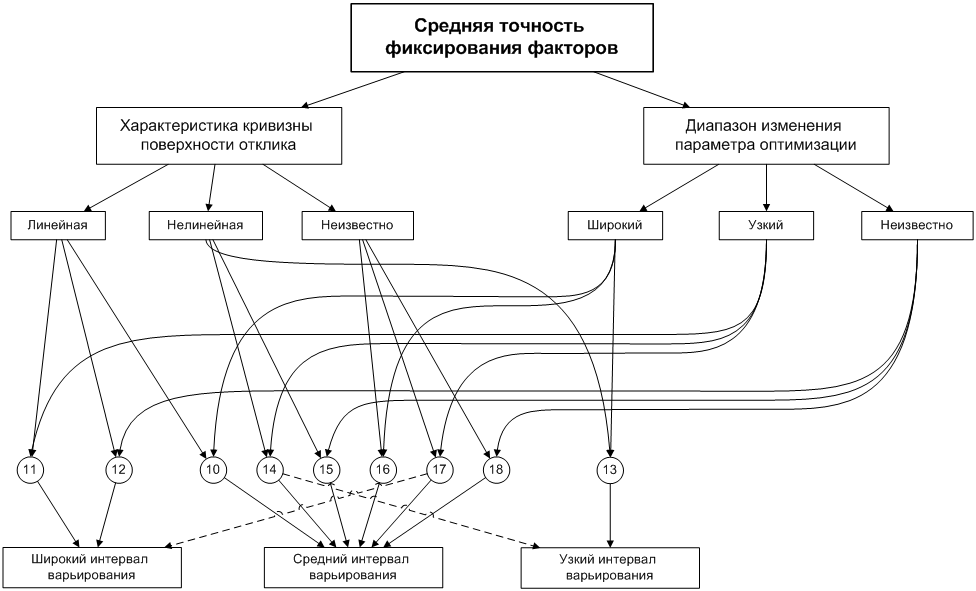
Рисунок 4

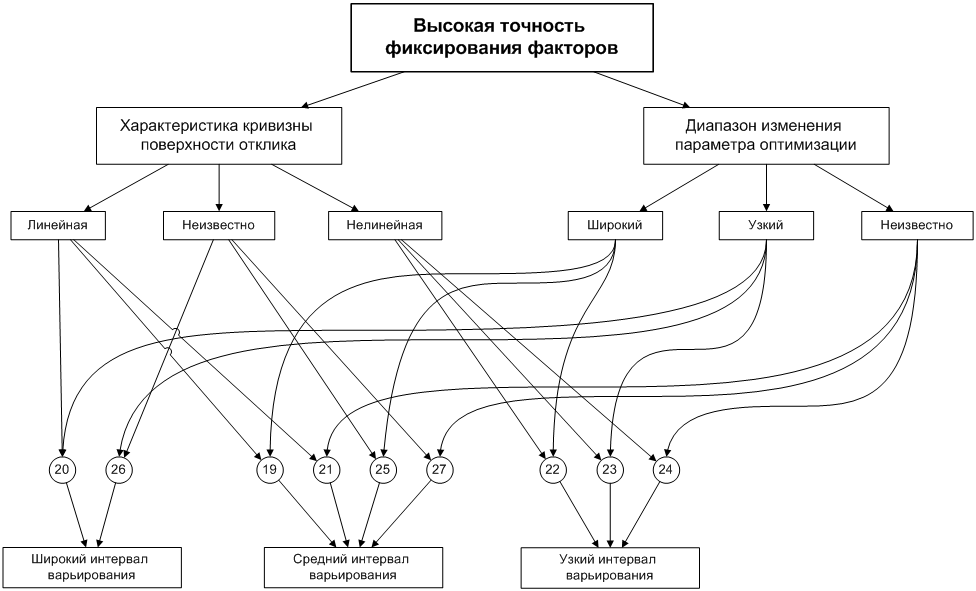
Рисунок 5

На рис. 4 изображена
блок-схема для случая средней точности фиксирования фактора. Характерен выбор
среднего интервала варьирования. Лишь в случае нелинейной поверхности и
широкого диапазона рекомендуется узкий интервал варьирования. При сочетаниях
линейной поверхности с узким диапазоном и отсутствием информации о диапазоне
выбирается широкий интервал варьирования. Пунктиром, как и выше, показаны редко
применяемые альтернативы.

Наконец, на рис. 5 построена
блок-схема для случая высокой точности фиксирования фактора. Сочетание высокой
точности с нелинейностью поверхности всегда приводит к выбору узкого
интервала. Довольно часто выбирается средний интервал и лишь в двух случаях
широкий. В обеих последних блок-схемах отсутствуют неоднозначные решения.

Источник

Варианты для выполнения работы

I. Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных — результатов наблюдений.

Почти все встречающиеся в жизни величины (урожайность сельскохозяйственных растений, продуктивности скота, производительность труда и заработная плата рабочих, объем производства продукции и т.д.) принимают неодинаковые значения у различных членов совокупности. Поэтому возникает необходимость в изучении их изменяемости. Это изучение начинается с проведения соответствующих наблюдений, обследований.

В результате наблюдений получают сведения о численной величине изучаемого признака у каждого члена данной совокупности.

Пример. Имеются данные о размере прибыли 100 коммерческих банков. Прибыль, млн. рублей.

30,2	51,9	43,1	58,9	34,1	55,2	47,9	43,7	53,2	34,9
47,8	65,7	37,8	68,6	48,4	67,5	27,3	66,1	52,0	55,6
54,1	26,9	53,6	42,5	59,3	44,8	52,8	42,3	55,9	48,1
44,5	69,8	47,3	35,6	70,1	39,5	70,3	33,7	51,8	56,1
28,4	48,7	41,9	58,1	20,4	56,3	46,5	41,8	59,5	38,1
41,4	70,4	31,4	52,5	45,2	52,3	40,2	60,4	27,6	57,4
29,3	53,8	46,3	40,1	50,3	48,9	35,8	61,7	49,2	45,8
45,3	71,5	35,1	57,8	28,1	57,6	49,6	45,5	36,2	63,2
61,9	25,1	65,1	49,7	62,1	46,1	39,9	62,4	50,1	33,1
33,3	49,8	39,8	45,9	37,3	78,0	64,9	28,8	62,5	58,7

Из данной таблицы видно, что интересующий нас признак (прибыль банков) меняется от одного члена совокупности к другому, варьирует. Варьирование есть изменяемость признака у отдельных членов совокупности.

Вариационным рядом называется последовательность вариант, записанных в возрастающем порядке и соответствующих им частот.

Число, показывающее, сколько раз повторяется в данной совокупности каждое значение признака, называется частотой.

Составим ранжированный вариационный ряд (выпишем варианты в порядке возрастания):

20,4	25,1	26,9	27,3	27,6	28,1	28,4	28,8	29,3	30,2
31,4	33,1	33,3	33,7	34,1	34,9	35,1	35,6	35,8	36,2
37,3	37,8	38,1	39,5	39,8	39,9	40,1	40,2	41,4	41,8
41,9	42,3	42,5	43,1	43,7	44,5	44,8	45,2	45,3	45,5
45,8	45,9	46,1	46,3	46,5	47,3	47,8	47,9	48,1	48,4
48,7	48,9	49,2	49,6	49,7	49,8	50,1	50,3	51,8	51,9
52,0	52,3	52,5	52,8	53,2	53,6	53,8	54,1	55,2	55,6
55,9	56,1	56,3	57,4	57,6	57,8	58,1	58,7	58,9	59,3
59,5	60,4	61,7	61,9	62,1	62,4	62,5	63,2	64,9	65,1
65,7	66,1	67,5	68,6	69,8	70,1	70,3	70,4	71,5	78,0

В нашем случае каждое значение признака (варианта вариационного ряда) повторилось только один раз, т.е. значение частоты для всех вариант равно единице. Перейдем к интервальному вариационному ряду, так как интересующий нас признак принимает дробные, практически не повторяющиеся значения.

Для этого необходимо определить число интервалов (классов) и длину интервала (классного промежутка), после чего произвести разноску, т.е. подсчитать для каждого интервала число вариант, попавших в него.

Количество классов устанавливают в зависимости от степени точности, с которой ведется обработка, и количества объектов в выборке. Считается удобным при объеме выборки (n) в пределах от 30 до 60 вариант распределять их на 6-7 классов, при n от 60 до 100 вариант — на 7-8 классов, при n от 100 и более вариант — на 9-17 классов.

Нужное количество групп также может быть ориентировочно вычислено по формуле Стерджесса:

где — число групп (классов, интервалов) ряда распределения; n — объем выборки.

Можно также использовать выражение:

При они дают примерно одинаковые результаты.

В рассматриваемом примере о размере прибыли коммерческих банков, n=100. Применяя формулу Стерджесса, получим:

Однако Таким образом, число интервалов может быть равно 8, 9, 10 и т.д.

Нахождение нужного количества групп и их размеров часто бывает взаимообусловлено. Для того, чтобы как-то определиться с числом интервалов, найдем размах вариации — разность между наибольшей и наименьшей вариантой:

$[R=x_{max}-x_{min}]$

где — размах вариации,

$x_{max}$ — наибольшее значение варьирующего признака,

$x_{min}$ — наименьшее значение варьирующего признака.

Найдем размах вариации для рассматриваемой задачи:

Для того, чтобы найти длину интервала (величину классового промежутка) необходимо разделить размах вариации на число классов и полученную величину округлить таким образом, чтобы было удобно производить сначала разноску, а затем и различные вычисления. Рекомендую округлять до единиц, до которых округлены варианты в исходной таблице, в нашем случае до десятых.

$[happrox frac{R}{k}]$

Согласно формуле получаем

$[happrox frac{57,6}{8}=7,2]$

Теперь необходимо определиться с началом первого интервала. Для этого можно использовать формулу:

$[x_1approx x_{min}-frac{h}{2}]$

$[x_1approx 20,4-frac{7,2}{2}=16,8.]$

Замечание. За начало первого интервала можно принять некоторое значение, несколько меньшее $x_{min}$ или само значение $x_{min}$ . Далее в табличном виде я покажу оба варианта.

Прибавив к началу первого интервала (нижней границе) шаг, получим верхнюю границу первого интервала и одновременно нижнюю границу второго интервала. Выполняя последовательно указанные действия, будем находить границы последующих интервалов до тех пор, пока не будет получено или перекрыто $x_{max}$ .

Таким образом, верхняя граница одного интервала одновременно является нижней границей другого интервала. Чтобы не возникало сомнений, в какой интервал отнести варианту, попавшую на границу, условимся относить ее к верхнему интервалу.

Составим теперь рабочую таблицу для построения интервального вариационного ряда и произведем подсчет частот вариант, попавших в тот или иной интервал.

Как и обещал покажу две таблицы построения ряда:

1. Отсчет ведем от $x_{min}$ , т.е. нижняя граница первого интервала совпадает с $x_{min}$ .

Группы банков по размеру прибыли (границы интервалов)	Количество банков, принадлежащих данной группе (частоты, )	Накопленные частоты,
20,4 — 27,6	4	4
27,6 — 34,8	11	15
34,8 — 42	16	31
42 — 49,2	21	52
49,2 — 56,4	21	73
56,4 — 63,6	15	88
63,6 — 70,8	10	98
70,8 — 78	2	100

2. Начало первого интервала определяем с помощью формулы: $x_1approx x_{min}-frac{h}{2}$ .

Группы банков по размеру прибыли (границы интервалов)	Количество банков, принадлежащих данной группе (частоты, )	Накопленные частоты,
16,8 — 24	1	1
24 — 31,2	9	10
31,2 — 38,4	13	23
38,4 — 45,6	17	40
45,6 — 52,8	23	63
52,8 — 60	18	81
60 — 67,2	11	92
67,2 — 74,4	7	99
74,4 — 81,6	1	100

Как мы видим в 1-м случае у нас получилось восемь интервалов, что полностью совпадает с результатом, который нам дала формула Стерджесса. Во втором случае у нас получилось девять интервалов, так как при поиске начала первого интервала пользовались специальной формулой.

Для дальнейшего исследования я буду пользоваться результатами второй таблицы, так как там ярко выражен модальный интервал (одна мода) и медиана практически точно попадает на середину вариационного ряда.

Мы получили интервальный вариационный ряд — упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами попаданий в каждый из них значений величины.

II. Графическая интерпретация вариационных рядов.

№ п/п	Границы интервалов, $[x_{i}; x_{i+1})$	Середины интервалов, $x_{i}^{*}=frac{x_i+x_{i+1}}{2}$	Частоты интервалов,	Относительные частоты $W_i=frac{n_i}{n}$	Плотность относит. частоты $frac{W_i}{h}$	Плотность частоты $frac{n_i}{h}$
1	16,8 — 24	20,4	1	0,01	0,001	0,139
2	24 — 31,2	27,6	9	0,09	0,013	1,250
3	31,2 — 38,4	34,8	13	0,13	0,018	1,806
4	38,4 — 45,6	42	17	0,17	0,024	2,361
5	45,6 — 52,8	49,2	23	0,23	0,032	3,194
6	52,8 — 60	56,4	18	0,18	0,025	2,500
7	60 — 67,2	63,6	11	0,11	0,015	1,528
8	67,2 — 74,4	70,8	7	0,07	0,010	0,972
9	74,4 — 81,6	78	1	0,01	0,001	0,139

Строим графики:

Далее найдем моду вариационного ряда:

$[M_o(X)=x_{M_o}+hfrac{(n_2-n_1)}{(n_2-n_1)+(n_2-n_3)}]$

где

$x_{M_o}$ — начало модального интервала;

— длина частичного интервала (шаг);

n_1 — частота предмодального интервала;

n_2 — частота модального интервала;

— частота послемодального интервала.

Определим модальный интервал — интервал, имеющий наибольшую частоту. Из таблицы видно, что модальным является интервал (45,6 — 52,8).

$[M_o(X)=45,6+7,2frac{(23-17)}{(23-17)+(23-18)}=]$

$[=45,6+7,2cdot frac{6}{6+5}=45,6+3,93=49,5]$

Медиана

Для интервального ряда медиана находится по формуле:

$[M_e(X)=x_{M_e}+hfrac{0,5n-S_{M_{e}-1}}{n_{M_e}}]$

где

$x_{M_e}$ — начало медианного интервала;

— длина частичного интервала (шаг);

— объем совокупности;

$S_{M_{e}-1}$ — накопленная частота интервала, предшествующая медианному;

$n_{M_e}$ — частота медианного интервала.

Определим медианный интервал — интервал, в котором впервые накопленная частота превышает половину объема выборки.Так как объем выборки n=100, то n/2=50. По таблице найдем интервал, где впервые накопленные частоты превысят это значение. Таким является интервал (45,6 — 52,8).

Получаем,

$[M_e(X)=45,6+7,2frac{0,5cdot 100-40}{23}approx 48,7.]$

III. Расчет сводных характеристик выборки.

Для определения $x_B, D_{B}, sigma_{B}$ составим расчетную таблицу. Для начала определимся с ложным нулем С. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).

Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю. В нашем случае С=49,2.

Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.

Условными называют варианты, определяемые равенством:

$[U_i=frac{(x_i-C)}{h}]$

Произведем расчет условных вариант согласно формуле:

$[U_1=frac{20,4-49,2}{7,2}=-4]$

$[U_2=frac{27,6-49,2}{7,2}=-3]$

$[U_3=frac{34,8-49,2}{7,2}=-2]$

$[U_4=frac{42-49,2}{7,2}=-1]$

$[U_5=frac{49,2-49,2}{7,2}=0]$

$[U_6=frac{56,4-49,2}{7,2}=1]$

$[U_7=frac{63,6-49,2}{7,2}=2]$

$[U_8=frac{70,8-49,2}{7,2}=3]$

$[U_9=frac{78-49,2}{7,2}=4]$

N п/п	Середины интервалов, $x_{i}^{*}$	Частоты интервалов,	Условные варианты,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,
1	20,4	1	-4	-4	16	-64	256	9	81
2	27,6	9	-3	-27	81	-243	729	36	144
3	34,8	13	-2	-26	52	-104	208	13	13
4	42	17	-1	-17	17	-17	17	0	0
5	49,2	23	0	0	0	0	0	23	23
6	56,4	18	1	18	18	18	18	72	288
7	63,6	11	2	22	44	88	176	99	891
8	70,8	7	3	21	63	189	567	112	1792
9	78	1	4	4	16	64	256	25	625

Контроль:

$[sum n_i U_i^2 + 2sum n_iU_i+n=sum n_i{(U_i+1)}^2]$

$[sum n_i{(U_i+1)}^2=389]$

Контроль:

$[sum n_i U_i^4 + 4sum n_iU_i^3+6sum n_iU_i^2+4sum n_iU_i+n=sum n_i{(U_i+1)}^4]$

$[sum n_i{(U_i+1)}^4=3857]$

Равенство выполнено, следовательно вычисления произведены верно.

Вычислим условные моменты 1-го, 2-го, 3-го и 4-го порядков:

$[M_1^{*}=frac{sum n_iU_i}{n}=frac{-9}{100}=-0,09;]$

$[M_2^{*}=frac{sum n_iU_i^2}{n}=frac{307}{100}=3,07;]$

$[M_3^{*}=frac{sum n_iU_i^3}{n}=frac{-69}{100}=-0,69;]$

$[M_4^{*}=frac{sum n_iU_i^4}{n}=frac{2227}{100}=22,27.]$

Найдем выборочные среднюю, дисперсию и среднее квадратическое отклонение :

$[x_{B}=M_1^{*}cdot h+C=-0,09cdot 7,2+49,2=48,552;]$

$[D_{B}=(M_2^{*}-{(M_1^{*})}^2)h^2=(3,07-{(-0,09)}^2){7,2}^2approx 158,73.]$

$[sigma_{B}=sqrt{D_B}=sqrt{158,73}=12,6.]$

Также для оценки отклонения эмпирического распределения от нормального используют такие характеристики, как асимметрия и эксцесс.

Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

$[a_s=frac{m_3}{sigma_B^3}]$

Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции): если «длинная часть» кривой расположена правее моды, то асимметрия положительна, если слева — отрицательна.

Эксцесс эмпирического распределения определяется равенством:

$[e_k=frac{m_4}{sigma_B^4}-3]$

где — центральный эмпирический момент четвертого порядка.

Для нормального распределения эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.

Вычисляем центральные эмпирические моменты третьего и четвертого порядков:

$[m_3=(M_3^*-3M_1^*M_2^*+2{(M_1^*)}^3)cdot h^3=51,3;]$

$[m_4=(M_4^*-4M_3^*M_1^*+6M_2^*{(M_1^*)}^2-3{(M_1^*)}^4)cdot h^4=59580,97;]$

Найдем асимметрию и эксцесс:

$[a_s=frac{51,3}{{12,6}^3}=0,026]$

$[e_k=frac{59580,97}{{12,6}^4}-3=-0,635]$

IV. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.

Проверим генеральную совокупность значений размера прибыли банков по критерию Пирсона

Правило. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу : генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:

$[chi^2_{nabl}=sum frac{ {(n_i-n_i^{'})}^2}{n_i^{'}}]$

и по таблице критических точек распределения , по заданному уровню значимости и числу степеней свободы найти критическую точку $chi^2_{kp}(alpha;k)$ , где s — количество интервалов.

Если $chi^2_{nabl}<chi^2_{kp}$ — нет оснований отвергнуть нулевую гипотезу.

Если $chi^2_{nabl}>chi^2_{kp}$ — нулевую гипотезу отвергают.

Найдем теоретические частоты , для этого составим следующую таблицу.

Середины интервалов, $x_{i}^{*}$	Частоты интервалов,	Произведем расчет, $x_{i}^{*}-x_B$	Произведем расчет, $V_i=frac{(x_{i}^{*}-x_B)}{sigma_B}$	Значения функции Гаусса,	Произведем расчет, $frac{nh}{sigma_B}$	Теоретические частоты, $n_i^{'}=57 cdotvarphi(V_i)$
20,4	1	-28,152	-2,23	0,0332	57	2
27,6	9	-20,952	-1,66	0,1006	57	6
34,8	13	-13,752	-1,09	0,2203	57	13
42	17	-6,552	-0,52	0,3485	57	20
49,2	23	0,648	0,05	0,3984	57	23
56,4	18	7,848	0,62	0,3292	57	19
63,6	11	15,048	1,19	0,1965	57	11
70,8	7	22,248	1,77	0,0833	57	5
78	1	29,448	2,34	0,0258	57	1
						$sum n_i^{'}=100$

Вычислим $chi^2_{nabl}$ , для чего составим расчетную таблицу.

		$n_i^{'}$	$n_i-n_i^{'}$	${(n_i-n_i^{'})}^2$	$frac{{(n_i-n_i^{'})}^2}{n_i^'}$		$frac{n_i^2}{n_i^{'}}$
1	1	2	-1	1	0,5	1	0,5
2	9	6	3	9	1,5	81	13,5
3	13	13	0	0	0	169	13
4	17	20	-3	9	0,45	289	14,45
5	23	23	0	0	0	529	23
6	18	19	-1	1	0,05	324	17,05
7	11	11	0	0	0	121	11
8	7	5	2	4	0,8	49	9,8
9	1	1	0	0	0	1	1
	100	100			Наблюдаемое значение критерия, $chi^2_{nabl}=3,30$		103,30

Контроль:

$[sumfrac{n_i^2}{n_i^{'}}-n=sum frac{{(n_i-n_i^{'})}^2}{n_i^'}]$

$[sumfrac{n_i^2}{n_i'}-n=103,3-100=3,3]$

$[sum frac{{(n_i-n_i')}^2}{n_i'}=3,3]$

Вычисления произведены правильно.

Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариант) s=9;

По таблице критических точек распределения по уровню значимости и числу степеней свободы k=6 находим $chi^2_{kp}(0,025;6)=14,4.$

Так как $chi^2_{nabl}<chi^2_{kp}$ — нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

На рисунке построены нормальная (теоретическая) кривая по теоретическим частотам (зеленый график) и полигон наблюдаемых частот (коричневый график). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.

V. Интервальные оценки.

Интервальной называют оценку, которая определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал, который с заданной надежностью покрывает заданный параметр.

Интервальной оценкой (с надежностью ) математического ожидания (а) нормально распределенного количественного признака Х по выборочной средней при известном среднем квадратическом отклонении sigma генеральной совокупности служит доверительный интервал

$[x_B-frac{tsigma}{sqrt{n}}<a<x_B+frac{tsigma}{sqrt{n}},]$

где $frac{tsigma}{sqrt{n}}=delta$ — точность оценки, n — объем выборки, t — значение аргумента функции Лапласа (см. приложение 2), при котором $phi(t)=frac{gamma}{2}$ ;

при неизвестном среднем квадратическом отклонении sigma (и объеме выборки n<30)

$[x_B-frac{t_{gamma}cdot S}{sqrt{n}}<a<x_B+frac{t_{gamma}cdot S}{sqrt{n}},]$

$[S=sqrt{frac{n}{n-1}D_B}]$

где S — исправленное выборочное среднее квадратическое отклонение, $t_{gamma}$ находят по таблице приложения по заданным n и .

В нашем примере среднее квадратическое отклонение известно, . А также , , . Поэтому для поиска доверительного интервала используем первую формулу:

$[x_B-frac{tsigma}{sqrt{n}}<a<x_B+frac{tsigma}{sqrt{n}}]$

Все величины, кроме t, известны. Найдем t из соотношения $phi(t)=frac{0,95}{2}=0,475.$ По таблице приложения находим t=1,96. Подставив t=1,96, , , в формулу, окончательно получим искомый доверительный интервал:

$[48,55-frac{1,96cdot 12,6}{10}<a<48,55+frac{1,96cdot 12,6}{10}]$

Интервальной оценкой (с надежностью ) среднего квадратического отклонения нормально распределенного количественного признака Х по «исправленному» выборочному среднему квадратическому отклонению S служит доверительный интервал

(при q<1), (*)

(при q>1),

где q — находят по таблице приложения по заданным n и .

По данным и n=100 по таблице приложения 4 найдем q=0,143. Так как q<1, то, подставив $S=sqrt{frac{n}{n-1}D_B}=sqrt{frac{100}{99}cdot 158,73}approx 12,66, quad quad q=0,143$ в соотношение (*), получим доверительный интервал: