Как найти интервальную оценку параметра

Содержание:

Интервальные оценки параметров распределения. Непрерывное и дискретное распределения признаков:

В материалах сегодняшней лекции мы рассмотрим интервальные оценки параметров распределения, а именно непрерывное и дискретное распределения признаков генеральной и выборочной совокупности.

Статистические ряды и их геометрическое изображение дают представление о распределении наблюдаемой случайной величины X по данным выборки. Во многих задачах вид распределения случайной величины X известен, необходимо получить приближённое значение неизвестных параметров этого распределения: m,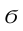

Пусть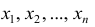

Точечной оценкой 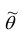неизвестного параметра 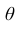называется приближённое значение этого параметра, полученное по выборке.

Очевидно, что 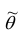зависит от элементов выборки 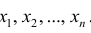. Будем считать, что 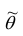– случайная величина и является функцией 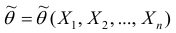системы случайных величин, одной из реализации которой является данная выборка.

Точечная оценка 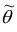должна удовлетворять свойствам:

1. Состоятельность. Оценка 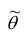 параметра 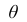называется
состоятельной, есл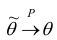и при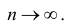

Состоятельность оценки можно установить с помощью теоремы: если 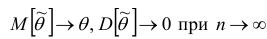, то 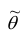– состоятельная оценка.

2.    Несмещённость. Оценка 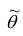параметра 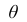называется несмещённой, если 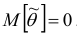. Для несмещённых оценок систематическая ошибка оценивания равна нулю.

Для оценки параметра 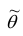может быть предложено несколько несмещённых оценок. Мерой точности 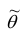считают её дисперсию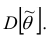
Отсюда вытекает третье свойство.

3.    Эффективность. Несмещённая оценка 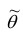параметра 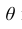называется эффективной, если она имеет наименьшую дисперсию по сравнению с другими несмещёнными оценками этого параметра.

Запишем точечные оценки числовых характеристик случайной величины X.

1. Точечная оценка 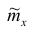математического ожидания (выборочного среднего) 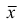находится по формуле

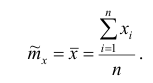
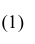
Проверим свойства оценки:

а) состоятельность следует из теоремы Чебышева: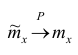 при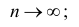
б) несмещённость:

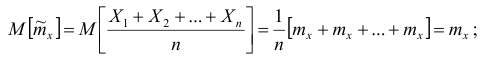
в)эффективность:

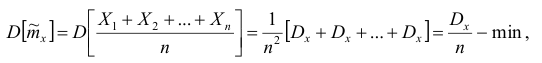
так как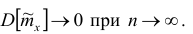

2.    Точечная оценка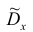 дисперсии 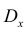находится по формуле

она обладает свойствами:    состоятельность, несмещённость,

эффективность.

3.    Точечная оценка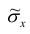 среднеквадратического отклонения равна

 

Интервальные оценки

При статистической обработке результатов наблюдений необходимо знать не только точечную оценку 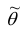параметра 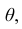но и уметь оценить точность этой оценки

Характеристики вариационного ряда

В материалах сегодняшней лекции мы рассмотрим характеристики вариационного ряда.

Вариационные ряды

Установление закономерностей, которым подчиняются массовые случайные явления, основано на изучении статистических данных — сведений о том, какие значения принял в результате наблюдений интересующий исследователя признак.

Пример:

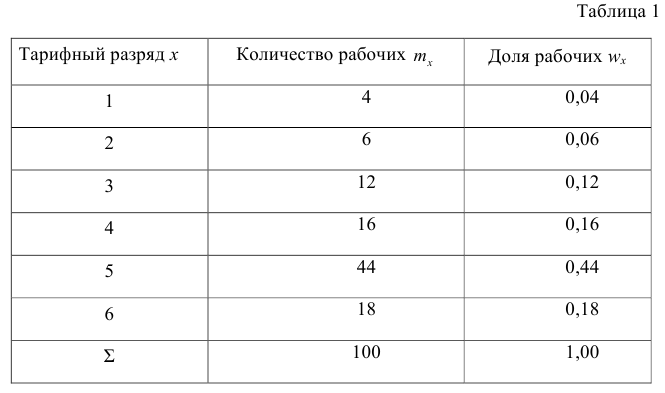
Исследователь, интересующийся тарифным разрядом рабочих механического цеха, в результате опроса 100 рабочих получил следующие сведения:

Здесь признаком является тарифный разряд, а полученные о нём сведения образуют статистические данные. Для изучения данных прежде всего необходимо их сгруппировать. Расположим наблюдавшиеся значения признака в порядке возрастания. Эта операция называется ранжированием статистических данных. В результате получим следующий ряд, который называется ранжированным:
(1, 1, 1, 1) – 4 раза; (2, 2, 2, 2, 2, 2) – 6 раз; (3, 3, …, 3) – 12 раз; (4, 4, …, 4) –

16 раз; (5, 5, …, 5) – 44 раза; (6, 6, …, 6) – 18 раз.
Из ранжированного ряда следует, что признак (тарифный разряд) принял шесть различных значений: первый, второй и т.д. до шестого разряда.

В дальнейшем различные значения признака условимся называть вариантами, а под варьированием — понимать изменение значений признака. Если признак по своей сущности таков, что различные его значения не могут отличаться друг от друга меньше чем на некоторую конечную величину, то говорят, что это дискретно варьирующий признак.

Тарифный разряд — дискретно варьирующий признак: его различные значения не могут отличаться друг от друга меньше, чем на единицу. В примере этот признак принял 6 различных значений — 6 вариантов: вариант 1 повторился 4 раза, вариант 2-6 раз и т.д. Число, показывающее. сколько раз встречается вариант л* в ряде наблюдений, называется частотой варианта 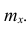Ранжированный ряд представим в виде табл. 1.

Вместо частоты варианта x можно рассматривать её отношение к общему числу наблюдений n, которое называется частостью варианта х и обозначается 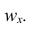Так как общее число наблюдений равно сумме частот всех вариантов 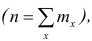то справедлива следующая цепочка равенств: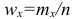

Таблица, позволяющая судить о распределении частот (или частостей) между вариантами, называется дискретным вариационным рядом.

В примере 1 была поставлена задача изучить результаты наблюдений. Если просмотр первичных данных не позволил составить представление о варьировании значений признака, то, рассматривая вариационный, ряд, можно сделать следующие выводы: тарифный разряд колеблется от 1-го до 6-го; наиболее часто встречается 5-й тарифный разряд; с ростом тарифного разряда (до 5-го разряда) растёт число рабочих, имеющих соответствующий разряд.

Наряду с понятием частоты используют понятие накопленной частоты, которую обозначают 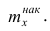Накопленная частота показывает, во скольких наблюдениях признак принял значения, меньшие заданного значения х. Отношение накопленной частоты к общему числу наблюдений называют накопленной частостью и обозначают 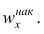Очевидно, что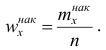

В дискретном вариационном ряду накопленные частоты (частости) вычисляются для каждого варианта и являются результатом последовательного суммирования частот (частостей). Накопленные частоты (частости) для вариационного ряда, заданного в табл. 1, вычислены в табл. 2.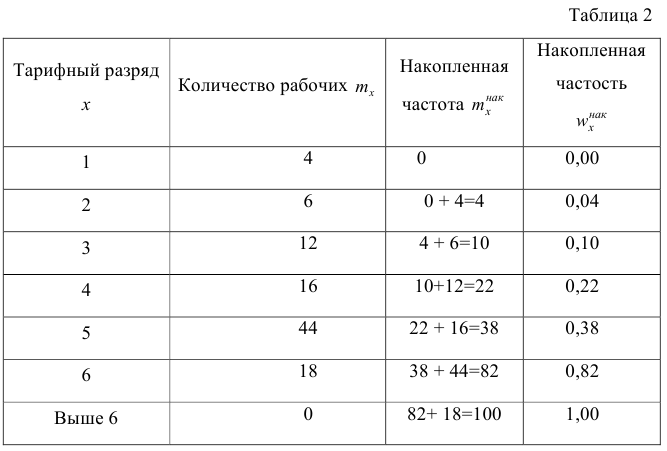

Например, варианту 1 соответствует накопленная частота, равная нулю, так как среди опрошенных рабочих не было таких, у которых тарифный разряд был бы меньше 1-го; варианту 5 соответствует накопленная частота 38, так как было 4+6+12+16 рабочих с тарифным разрядом, меньшим 5-го, накопленная частость для этого варианта равна 0,38 (38: 100); если тарифный разряд выше 6-го, то ему соответствует накопленная частота 100, так как тарифный разряд всех опрошенных рабочих не выше 6-го.

Пример:

Исследователь, изучающий выработку на одного рабочего-станочника механического цеха в отчётном году в процентах к предыдущему году, получил следующие данные (в целых процентах) по 117 рабочим:

В этом примере признаком является выработка в отчётном году в процентах к предыдущему. Очевидно, что значения, принимаемые этим признаком, могут отличаться одно от другого на сколь угодно малую величину, т. е. признак может принять любое значение в некотором числовом интервале (только для упрощения дальнейших расчетов полученные данные округлены до целых процентов). Такой признак называют непрерывно варьирующим. По приведенным данным трудно выявить характерные черты варьирования значений признака. Построение дискретного вариационного ряда также не даст желаемых результатов (слишком велико число различных наблюдавшихся значений признака). Для получения ясной картины объединим в группы рабочих, у которых величина выработки колеблется, например, в пределах 10%. Сгруппированные данные представим в табл. 3.

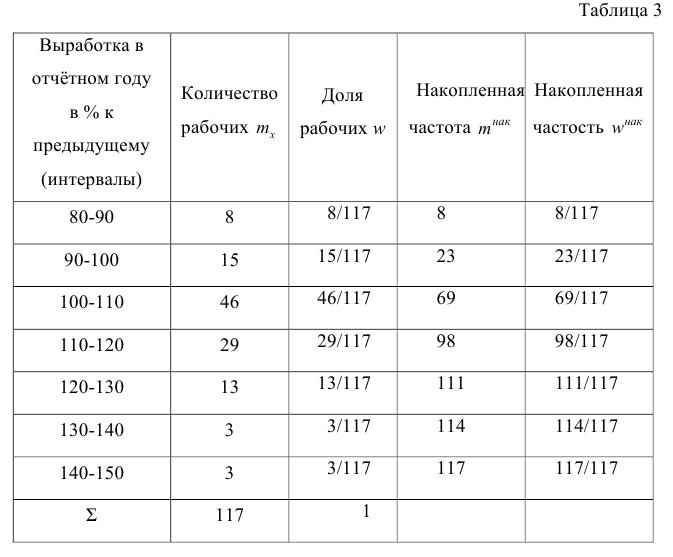
В табл. 3 частоты m показывают, во скольких наблюдениях признак принял значения, принадлежащие тому или иному интервалу. Такую частоту называют интервальной, а отношение её к общему числу наблюдений — интервальной частостью w. Таблицу, позволяющую судить о распределении частот (или частостей) между интервалами варьирования значений    признака, называют интервальным вариационным рядом.

Интервальный вариационный ряд, представленный в табл. 3, позволяет выявить закономерности распределения рабочих по интервалам выработки. В табл. 3 для верхних границ интервалов приведены накопленные    частоты (частости)    (они получены последовательным суммированием интервальных частот (частостей), начиная с частоты (частости) первого интервала). Например, для верхней границы третьего интервала, равной 110, накопленная частота равна 69; так как 8+15+46 рабочих имели выработку меньше 110%, накопленная частость равна 69/117.

Интервальный вариационный ряд строят по данным наблюдений за непрерывно    варьирующим признаком, а также за дискретно варьирующим, если велико число наблюдавшихся вариантов. Дискретный вариационный ряд строят только для дискретно варьирующего признака.

Иногда интервальный вариационный ряд условно заменяют дискретным. Тогда серединное значение интервала принимают за вариант х, а соответствующую интервальную частоту — за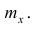

Построение интервального вариационного ряда

Для построения интервального вариационного ряда необходимо определить величину интервала, установить полную шкалу интервалов, в соответствии с ней сгруппировать результаты наблюдений. В примере 2 при выборе величины интервала учитывались требования наибольшего удобства отсчётов. Интервал был принят равным 10% и оказался удачным. Построенный интервальный ряд позволил выявить закономерности варьирования значений признака. Для определения оптимального интервала h, т.е. такого, при котором построенный интервальный ряд не был бы слишком громоздким и в то же время позволял выявить характерные черты рассматриваемого явления, можно использовать формулу Стэрджеса

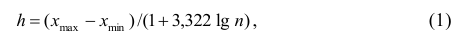
где 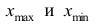— соответственно максимальный и минимальный варианты. Если h — дробное число, то за величину интервала следует взять либо ближайшее целое число, либо ближайшую несложную дробь.

За начало первого интервала рекомендуется принимать величину 

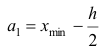начало второго интервала совпадает с концом первого и равно

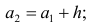начало третьего интервала совпадает с концом второго и равно 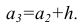Построение интервалов продолжают до тех пор, пока начало следующего по порядку интервала не будет больше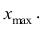

После установления шкалы интервалов следует сгруппировать результаты наблюдений. Границы последовательных интервалов записывают в столбец слева, а затем, просматривая статистические данные в том порядке, в каком они были получены, проставляют чёрточки справа от соответствующего интервала. В интервал включается данные, большие или равные нижней границе интервала и меньшие верхней границы. Целесообразно каждые пятое и шестое наблюдения отмечать диагональными черточками, пересекающими квадрат из четырёх предшествующих. Общее количество чёрточек, проставленных против какого-либо интервала, определяет его частоту.

Графическое изображение вариационных рядов

Графическое изображение вариационного ряда позволяет представить в наглядной форме закономерности варьирования значений признака. Наиболее    широко используются    следующие    виды графического изображения вариационных рядов: полигон, гистограмма, кумулятивная
кривая.

Полигон, как правило, служит для изображения дискретного вариационного ряда. Для его построения в прямоугольной системе координат наносят точки с координатами 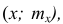где x — вариант, а 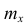— соответствующая ему частота. Иногда вместо точек 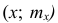строят точки (х; 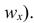. Затем эти точки соединяют последовательно отрезками. Крайние левую и правую точки соединяют соответственно с точками, изображающими ближайший снизу к наименьшему и ближайший сверху к наибольшему варианты. Полученная ломаная линия называется полигоном.

Гистограмма служит для изображения только интервального вариационного ряда. Для её построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, изображающие интервалы варьирования, и на этих отрезках, как на основании, строят прямоугольники с высотами, равными частотам (или частостям) соответствующего интервала. В результате получают ступенчатую фигуру, состоящую из прямоугольников, которую и называют гистограммой.

Если по оси абсцисс выбрать такой масштаб, чтобы ширина интервала была равна единице, и считать, что по оси ординат единица масштаба соответствует одному наблюдению, то площадь гистограммы равна общему числу наблюдений, если по оси ординат откладывались частоты, и эта площадь равна единице, если откладывались частости.

Иногда интервальный ряд изображают с помощью полигона. В этом случае интервалы заменяют их серединными значениями и к ним относят интервальные частоты. Для полученного дискретного ряда строят полигон.

Кумулятивная кривая (кривая накопленных частот или накопленных частостей) строится следующим образом. Если вариационный ряд дискретный, то в прямоугольной системе координат строят точки с координатами 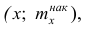где х — вариант, 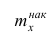— соответствующая накопленная частота. Иногда вместо точек 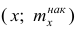строят точки 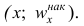Полученные точки соединяют отрезками.

Если вариационный ряд интервальный, то по оси абсцисс откладывают интервалы. Верхним границам интервалов соответствуют накопленные частоты (или накопленные частости); нижней границе первого интервала — накопленная частота, равная нулю. Построив кумулятивную кривую, можно приблизительно установить число наблюдений (или их долю в общем количестве наблюдений), в которых признак принял значения, меньшие заданного.

Построение вариационного ряда — первый шаг к осмысливанию ряда наблюдений. Однако на практике этого недостаточно, особенно когда необходимо сравнить два ряда или более. Сравнению подлежат только так называемые однотипные вариационные ряды, т. е. ряды, которые построены по результатам обработки сходных статистических данных. Например, можно сравнивать распределения рабочих по возрасту на двух заводах или распределения времени простоев станков одного вида. Однотипные вариационные ряды обычно имеют похожую форму при графическом изображении, однако могут отличаться друг от друга, а именно: иметь различные значения признака, вокруг которых концентрируются наблюдения (меры этой качественной особенности называется средними величинами); различаться рассеянием наблюдений вокруг средних величин (меры этой особенности получили название показателей вариации).

Средние величины и показатели вариации позволяют судить о характерных особенностях вариационного ряда и называются статистическими характеристиками. К статистическим характеристикам относятся также показатели, характеризующие различия в скошенности полигонов и различия в их островершинности.

Средние величины

Средние величины являются как бы «представителями» всего ряда наблюдений, поскольку вокруг них концентрируются наблюдавшиеся значения признака. Заметим, что только для качественно однородных наблюдений имеет смысл вычислять средние величины.

Различают несколько видов средних величин: средняя арифметическая, средняя геометрическая, средняя гармоническая, средняя квадратическая, средняя кубическая и т.д. При выборе вида средней величины необходимо прежде всего ответить на вопрос: какое свойство ряда мы хотим представить средней величиной или, иначе говоря, какая цель преследуется при вычислении средней? Это свойство, получившее название определяющего, и определяет вид средней. Понятие определяющего свойства впервые введено советским статистиком А. Я. Боярским.

Наиболее распространенной средней величиной является средняя арифметическая. Пусть 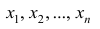— данные наблюдений; 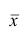— средняя арифметическая. Свойство, определяющее среднюю арифметическую, формулируется следующим образом:    сумма результатов наблюдений должна остаться неизменной, если каждое из них заменить средней арифметической, т.е.

Так как 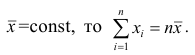Отсюда получаем следующую формулу для
вычисления средней арифметической по данным наблюдений:

Если по наблюдениям построен вариационный ряд, то средняя арифметическая

где x- — вариант, если ряд дискретный, и центр интервала, если ряд интервальный;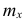 — соответствующая частота.

Частоты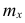 в формуле (4) называют весами, а операцию умножения x на 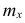— операцией взвешивания. Среднюю арифметическую, вычисленную по формуле (4), называют взвешенной в отличие от средней арифметической, вычисленной по формуле (3).

Очевидно, что если по данным наблюдений построен дискретный вариационный ряд, то формулы (3) и (4) дают одинаковые значения средней арифметической. Если же по наблюдениям построен интервальный ряд, то средние арифметические, вычисленные по формулам

(3) и (4), могут не совпадать, так как в формуле (4) значения признака внутри каждого интервала принимаются равными центрам интервалов. Ошибка, возникающая в результате такой замены, вообще говоря, очень мала, если наблюдения, распределены равномерно вдоль каждого интервала, а не скапливаются к одноименным границам интервалов (т.е. либо все к нижним границам, либо все к верхним границам).

Среднюю арифметическую для вариационного ряда можно вычислять по формуле

которая является следствием формулы (4). Действительно,

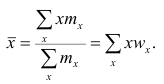
Свойство, определяющее среднюю арифметическую, сводилось к требованию неизменности суммы наблюдений при замене каждого из них средней арифметической. При решении практических задач может оказаться необходимым вычислить такую среднюю 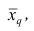при замене которой каждого наблюдения, осталась бы неизменной сумма q-x степеней наблюдений, т.е. чтобы

где q — положительное или отрицательное число. Среднюю 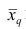называют степенной средней q-го порядка. Из определяющего свойства (6) получим следующую формулу для вычисления 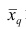по данным наблюдений:

Сравнивая формулы (7) и (3), можно сделать вывод, что степенная средняя первого порядка есть не что иное, как средняя арифметическая, т.е.

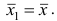
При q=-l из формулы (7) получаем выражение для средней гармонической, при q=2 — для среднеквадратической, при q=3 — для средней кубической и т.д.

Средней геометрической 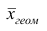называют корень n-й степени из произведения наблюдений  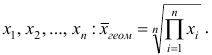  Можно доказать, что средняя геометрическая является предельным случаем степенной средней q-го порядка при q=0, т.е.

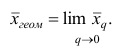
Рассмотрим основные свойства средней арифметической.

1°. Сумма отклонений результатов наблюдений от средней арифметической равна нулю.

Доказательство. Исходя из определяющего свойства (2) средней арифметической, получаем

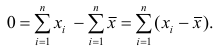
Если по результатам наблюдений построен вариационный ряд и средняя арифметическая взвешенная, то свойство 1° формулируется так: сумма произведений отклонений вариантов от средней арифметической на соответствующие частоты равна нулю. Действительно, на основании формулы (4) получаем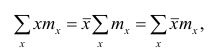

или

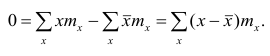
2°. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число, то средняя арифметическая уменьшится (увеличится) на то же число. (Доказательство свойств 2° и 3° проведём в предположении, что по результатам наблюдений построен вариационный ряд и средняя арифметическая — взвешенная).

Доказательство. Очевидно, что при уменьшении вариантов на одно и то же число с соответствующие им частоты останутся прежними. Поэтому взвешенная средняя арифметическая для изменённого вариационного ряда такова:

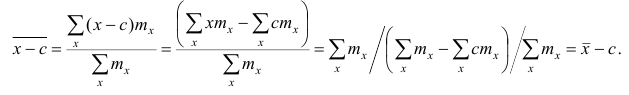
Аналогично можно показать, что 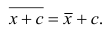Это свойство позволяет среднюю арифметическую вычислять не по данным вариантам, а по уменьшенным (увеличенным) на одно и то же число с. Если среднюю арифметическую, вычисленную для измененного ряда, увеличить (уменьшить) на число с, то получим среднюю арифметическую для первоначального вариационного ряда.

3°. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число раз, то средняя арифметическая уменьшится (увеличится) во столько же раз.

Доказательство. Очевидно, что при уменьшении вариантов в k раз их частоты останутся прежними. Поэтому средняя арифметическая для изменённого ряда

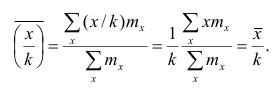
Аналогично можно доказать, что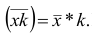Рассмотренное свойство позволяет среднюю арифметическую вычислять не по данным вариантам, а по уменьшенным (увеличенным) в одно и то же число k раз. Если среднюю арифметическую, вычисленную для изменённого ряда, увеличить

(уменьшить) в k раз, то получим среднюю арифметическую для первоначального вариационного ряда.

4°. Если ряд наблюдений состоит из двух групп наблюдений, то средняя арифметическая всего ряда равна взвешенной средней арифметической групповых средних, причём весами являются объёмы групп.

Пусть 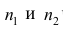число наблюдений соответственно в 1-й и 2-й группах; —

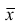средняя арифметическая для всего ряда 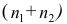наблюдений; 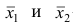— средние арифметические соответственно для 1-й и 2-й групп наблюдений. Требуется доказать, что

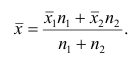
Доказательство.    Исходя    из определяющего свойству средней арифметической, имеем:    произведение 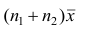равно сумме (/?! +/;2) наблюдавшихся значений признака; 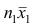равно сумме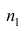наблюдавшихся значений, образующих первую группу: 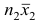равно сумме 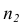наблюдавшихся значений, образующих вторую группу.

Следовательно,

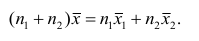
Следствие. Если ряд наблюдений состоит из k групп наблюдений, то средняя арифметическая всего ряда 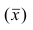равна взвешенной средней арифметической групповых средних 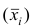причём весами являются объёмы групп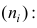

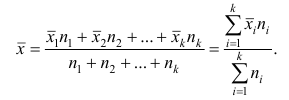
5°. Средняя арифметическая для сумм (разностей) взаимно соответствующих значений признака двух рядов наблюдений с одинаковым числом наблюдений равна сумме (разности) средних арифметических этих рядов.

Пусть 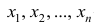— один ряд наблюдений, 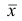— его средняя арифметическая; 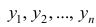— другой ряд наблюдений, 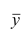— его средняя арифметическая 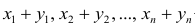—    ряд сумм соответствующих наблюдений, 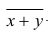— его средняя арифметическая. Требуется доказать, что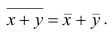

Доказательство. Имеем

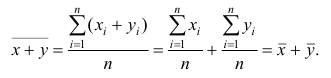
Аналогично можно показать, что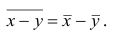

Следствие. Средняя арифметическая алгебраической суммы соответствующих значений признака нескольких рядов наблюдений с одинаковым числом наблюдений равна алгебраической сумме средних арифметических этих рядов.

Вычисление средней арифметической вариационного ряда непосредственно по формуле (4) приводит к громоздким расчётам, если числовые значения вариантов и соответствующие им частоты велики. Поэтому часто используют следующий способ, основанный на свойствах 3° и 2° средней арифметической: среднюю вычисляют не по первоначальным вариантам л-, а по уменьшенным на не которое число с, а затем разделённым на некоторое число k т.е. для вариантов 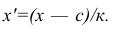Зная среднюю арифметическую 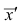для измененного ряда, легко вычислить среднюю арифметическую для первоначального ряда:

Действительно, принимая во внимание свойства 3° и 2° средней арифметической, получаем

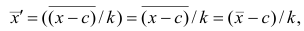откуда    следует,    что

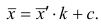Очевидно, что от выбора числовых значений с и к зависит, насколько простым будет вычисление средней арифметической для измененного ряда. Значения с и k обычно выбирают так, чтобы новые варианты 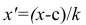были небольшими целыми числами. Если ряд дискретный, то в качестве с берётся вариант, занимающий серединное положение в вариационном ряду (если таких вариантов два, то за k принимается тот, которому соответствует большая частота); за k принимают наибольший общий делитель вариантов (х-с). Если ряд интервальный, то его заменяют дискретным; тогда с — центр серединного интервала (если таких интервала два, то берётся тот, которому соответствует большая частота); за к принимают длину интервала h

Медиана и мода

Наряду со средними величинами в качестве описательных характеристик вариационного ряда применяют медиану и моду.

Медианой 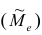называют значение признака, приходящееся на середину ранжированного ряда наблюдений.

Пусть проведено нечётное число наблюдений, т.е. n=2q—1, и результаты наблюдений проранжированы и выписаны в следующий ряд:

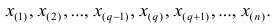Здесь 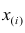значение признака, занявшее i-е порядковое место в ранжированном ряду. На середину ряда приходится значение 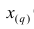Следовательно,

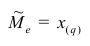
Если проведено чётное число наблюдений, т.е. n=2q, то на середину ранжированного ряда 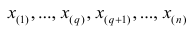приходятся значения 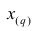и

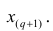В этом случае за медиану принимают среднюю арифметическую значений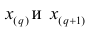

, т.е.

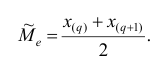
Покажем на примерах на практическом занятии, как определяется медиана дискретного и интервального вариационных рядов.

В общем случае медиана для интервального вариационного ряда определяется по формуле

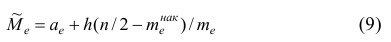
или по следующей формуле, полученной из формулы (9) в результате деления числителя и знаменателя входящей в неё дроби на n:

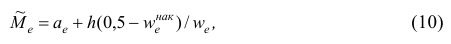
где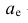 — начало медианного интервала, т.е. такого, которому соответствует первая из накопленных частот (накопленных частостей), равная или большая половине всех наблюдений (>0,5); 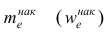—частота (частость), накопленная к началу медианного интервала; 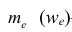—частота (частость) медианного интервала.

Модой 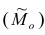называют такое значение признака, которое наблюдалось наибольшее число раз. Нахождение моды для дискретного вариационного ряда не требует каких-либо вычислений, так как ею является вариант, которому соответствует наибольшая частота.

В случае интервального вариационного ряда мода вычисляется по следующей формуле (вывод формулы можно найти в кн.: Венецкий И. Г Кильдишев Г. С. Теория вероятностей и математическая статистика. М., 1975.):

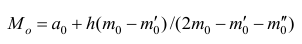
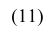
или по тождественной формуле:

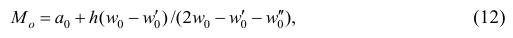
где 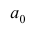— начало модального интервала, т.е. такого, которому соответствует наибольшая частота (частость); 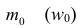— частота (частость) модального интервала; 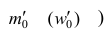— частота (частость) интервала, предшествующего модальному; 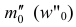— частота (частость) интервала, следующего за модальным.

Моду используют в случаях, когда нужно ответить на вопрос, какой товар имеет наибольший спрос, каковы преобладающие в данный момент уровни производительности труда, себестоимости и т. д. Модальная производительность, себестоимость и т.д. помогают вскрыть ресурсы, имеющиеся в экономике.

Показатели вариации

Средние величины, характеризуя вариационный ряд числом, не отражают изменчивости наблюдавшихся значений признака, т.е. вариацию. Простейшим показателем вариации является вариационный размах 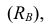равный разности между наибольшим и наименьшим вариантами, т.е.
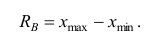(13)
Вариационный размах — приближённый показатель вариации, так как почти не зависит от изменения вариантов, а крайние варианты, которые используются для его вычисления, как правило, ненадёжны.

Более содержательными являются меры рассеяния наблюдений вокруг средних величин. Средняя арифметическая является основным видом средних, поэтому ограничимся рассмотрением мер рассеяния наблюдений вокруг средней арифметической.

Сумма отклонений результатов наблюдений 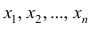от средней арифметической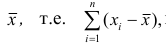не может характеризовать вариацию наблюдений около средней арифметической. В силу свойства 1° эта сумма равна нулю. Берут или абсолютные величины, или квадраты разностей 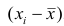. В результате получают различные показатели вариации.

Средним линейным отклонением (d) называют среднюю арифметическую абсолютных величин отклонений результатов наблюдений от их средней ар и ф метической:

Эмпирической дисперсией 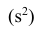называют среднюю арифметическую квадратов отклонений результатов наблюдений от их средней ар и ф м ети ч ес ко й:

Если по результатам наблюдений построен вариационный ряд, то эмпирическая дисперсия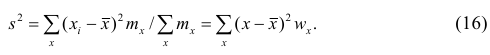

Вместо эмпирической дисперсии в качестве меры рассеяния наблюдений вокруг средней арифметической часто используют эмпирическое среднеквадратическое отклонение, равное арифметическому значению корня квадратного из дисперсии и имеющее ту же размерность, что и значения признака.

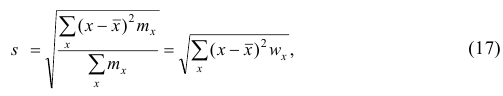
где x — вариант (если ряд дискретный) и центр интервала (если ряд интервальный); 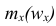— соответствующая частота (частость); 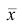— средняя арифметическая.

Для краткости величину 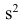часто будем называть просто дисперсией, не употребляя термина «эмпирическая». Однако при этом всегда следует помнить, что в этом случае дисперсия вычислена по результатам наблюдений на основании опытных данных, т.е. является эмпирической. Аналогичное замечание относится и к величине s.

Приведем свойство минимальности эмпирической дисперсии: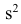 меньше взвешенной средней арифметической квадратов отклонений вариантов от любой постоянной величины, отличной от средней арифметической, т.е.

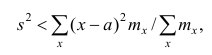
если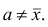

Доказательство. Найдём экстремум функции 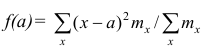. Для

этого решим уравнение 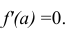Имеем:

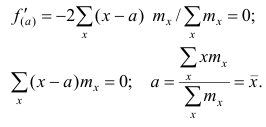
Так как 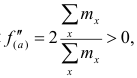то функция f(a) имеет в точке 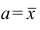минимум.
Можно показать, что среднее линейное отклонение не обладает свойством минимальности. Поэтому наиболее употребительными мерами рассеяния
 

Для вариационного ряда среднеквадратическое отклонение наблюдений вокруг средней арифметической являются эмпирическая дисперсия и эмпирическое среднеквадратическое отклонение.

Итальянский статистик Коррадо Джинни предложил в качестве показателя вариации использовать величину 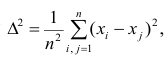 где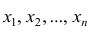– ряд наблюдений. Особенность этого показателя состоит в том, что он зависит только от разностей между наблюдениями и измеряет как бы «внутреннюю изменчивость» значений признака, а не их рассеяние вокруг какой-либо точки. Можно показать, что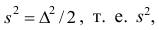являсь мерой рассеяния значений признака вокруг средней арифметической, характеризует также и внутреннюю их изменчивость.

Свойства эмпирической дисперсии

Рассмотрим основные свойства эмпирической дисперсии, знание которых позволит упростить её вычисление.

1 °. Дисперсия постоянной величины равна нулю.

Доказательство этого свойства очевидно вытекает из того, что дисперсия является показателем рассеяния наблюдений вокруг средней арифметической, а средняя арифметическая постоянной равна этой постоянной.

2°. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число с, то дисперсия не изменится.

Доказательство свойств 2° и 3° проведём в предположении, что по результатам наблюдений построен вариационный ряд.

Доказательство. Если все варианты уменьшить на число с, то в соответствии со свойством 2° средней арифметической средняя для измененного вариационного ряда равна 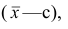следовательно, его дисперсия

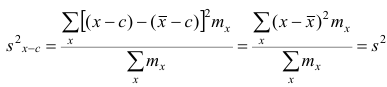
,т.е. совпадает с дисперсией первоначального вариационного ряда. Аналогично можно показать, что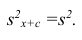

Доказанное свойство позволяет вычислять дисперсию не по данным вариантам, а по уменьшенным, (увеличенным) на одно и то же число с, так как дисперсия, вычисленная для измененного ряда, равна первоначальной.

3°. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число k раз, то дисперсия уменьшится (увеличится) в 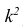раз.

Доказательство. Если все варианты уменьшить в k раз, то, согласно свойству 3 средней арифметической, средняя для измененного вариационного ряда равна 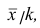следовательно, его дисперсия

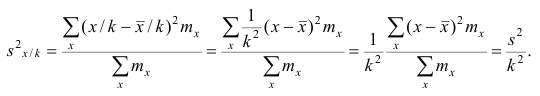
Аналогично можно показать, что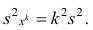

Это свойство позволяет эмпирическую дисперсию вычислять не по данным вариантам, а по уменьшенным (увеличенным) в одно и то же число k раз. Если дисперсию, вычисленную для измененного ряда, увеличить (уменьшить) в 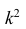раз, то получим дисперсию для первоначального вариационного ряда.

Следствие. Если все варианты уменьшить (увеличить) в k раз, то среднеквадратическое отклонение уменьшится (увеличится) в число раз, равное k.

Следствие очевидно вытекает из определения среднеквадратического
отклонения.

Прежде чем рассматривать следующее свойство дисперсии, докажем теорему.

Теорема. Эмпирическая дисперсия равна разности между средней
арифметической    квадратов наблюдений и    квадратом    средней
арифметической,    т.е.        

Доказательство    проведём для случая    взвешенных    средних    арифметических, т.е.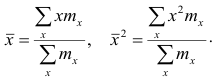

Доказательство. Тождественно преобразуя выражения для дисперсии, имеем

 

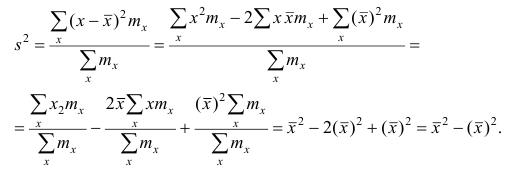
4°, Если ряд наблюдений состоит из двух групп наблюдений, то дисперсия всего ряда равна сумме средней арифметической групповых дисперсий и средней арифметической квадратов отклонений групповых средних от средней всего ряда, причем ‘ при вычислении средних арифметических весами являются объемы групп.

Пусть 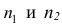— число наблюдений соответственно в 1-й и 2-й группах; 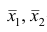— средние арифметические для 1-й и 2-й групп наблюдений; 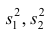— дисперсии для 1-й и 2-й групп наблюдений; 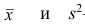— средняя арифметическая и дисперсия для всего ряда 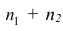наблюдений. Требуется доказать, что

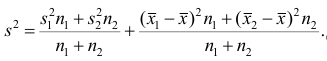Доказательство.

Пусть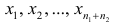— ряд наблюдавшихся значений признака, причем к первой группе относятся наблюдения 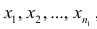, а ко второй — наблюдения 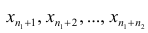Обозначим символом i порядковый номер наблюдения, попавшего в 1-ю группу, а через j — порядковый номер наблюдения, попавшего во 2-ю группу. На основании теоремы о дисперсии имеем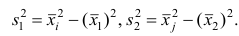Следовательно, первое слагаемое имеет вид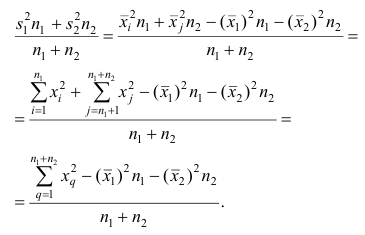

В соответствии со свойством 4° средней арифметической можно записать 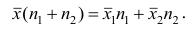Учитывая последнее равенство, преобразуем второе слагаемое:

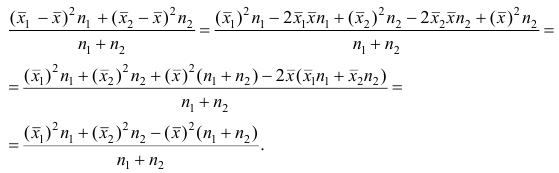
Используя найденные выражения для слагаемых, получаем

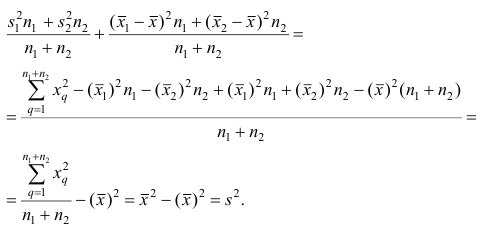
Свойство 4° можно обобщить на случай, когда ряд наблюдений состоит из любого количества групп наблюдений. Введём понятия межгрупповой и внутригрупповой дисперсий.

Если ряд наблюдений состоит из k групп наблюдений, то межгрупповой дисперсией называют среднюю арифметическую квадратов отклонений групповых средних 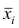от средней всего ряда наблюдений 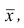причём весами являются объёмы групп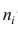т.е.

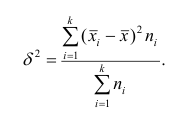
Средней групповых дисперсий или внутригрупповой дисперсией 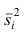называют среднюю арифметическую групповых дисперсий 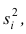причём весами являются объёмы групп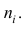

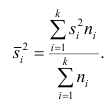
Следствие (свойства 4°). Если ряд наблюдений состоит из k групп наблюдений, то дисперсия всего ряда s2 равна сумме внутригрупповой и межгрупповой дисперсий, т.е.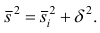

Вычисление дисперсии вариационного ряда непосредственно по формуле (16) приводит к громоздким расчётам, если числовые значения вариантов и соответствующие им частоты велики. Поэтому часто дисперсию вычисляют не по первоначальным вариантам х, а по вариантам 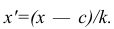Зная 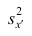 (дисперсию для измененного ряда), легко вычислить дисперсию 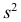для первоначального ряда:

Действительно, принимая во внимание свойства 3° и 2° дисперсии, получаем

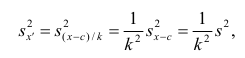
откуда следует, что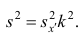

Требования к с  и k предъявляют те же, что и в упрощенном способе вычисления средней арифметической.
 

Эмпирические центральные и начальные моменты

Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия о моментах вариационного ряда.

Эмпирическим начальным моментом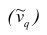 порядка q называют взвешенную среднюю арифметическую q-x степеней вариантов, т.е.

Эмпирический начальный момент нулевого порядка

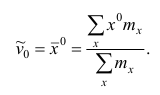
Эмпирический начальный момент первого порядка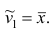
Эмпирический начальный момент второго порядка 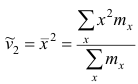 и т.д.
Эмпирическим центральным моментом 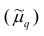порядка q называют взвешенную среднюю арифметическую q-x степеней отклонений вариантов от их средней арифметической, т.е.

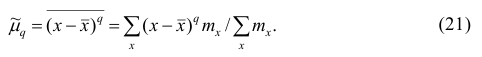
Эмпирический центральный момент нулевого порядка

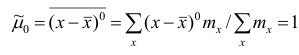Эмпирический центральный момент первого порядка  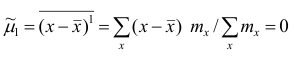(в силу свойства 1° средней арифметической).

Эмпирический центральный момент второго порядка

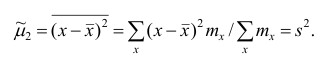
В дальнейшем для краткости величину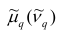 часто будем называть просто центральным моментом (начальным моментом), не употребляя термин «эмлирический».

Используя формулу бинома Ньютона, разложим в ряд выражение для центрального момента q-го порядка:

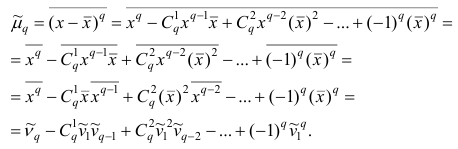
В проведенных тождественных преобразованиях использованы свойства 5° и 3° средней арифметической; 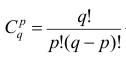 — число сочетаний из q элементов по р элементов

Итак, центральный момент q-го порядка выражается через начальные моменты следующим образом:

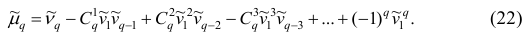
Полагая q = 0, 1, 2,…, можно получить выражения центральных моментов различных порядков через начальные моменты:

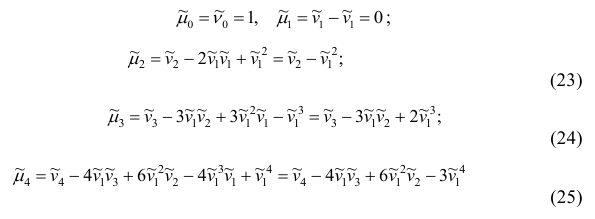
 и т.д.

Заметим, что формула (23) для центрального момента второго порядка, как и следовало ожидать, аналогична формуле (18) для дисперсии.

Рассмотрим свойства центральных моментов, которые позволят значительно упростить их вычисление.

1°. Если все варианты уменьшить (увеличить) на одно и то же число с, то центральный момент q-го порядка не изменится.

Доказательство. Если все варианты уменьшить на число с, то средняя арифметическая для измененного ряда равна 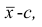поэтому центральный момент q-го порядка

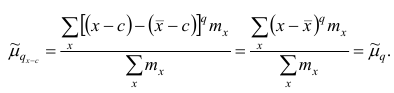
Аналогично можно показать, что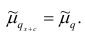

2°. Если все варианты уменьшить (увеличить) в одно и то же число k раз, то центральный момент q-го порядка уменьшится (увеличится) в 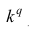раз. Доказательство. Если все варианты уменьшить в одно и то же число k раз,

то средняя арифметическая для измененного вариационного ряда равна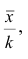

поэтому центральный момент q-го порядка

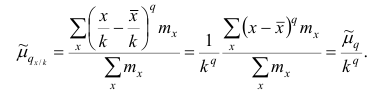
Аналогично можно показать, что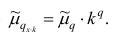

Для облегчения расчётов центральные моменты вычисляют не по первоначальным вариантам х, а по вариантам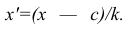 Зная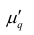 (центральный момент q-го порядка для измененного ряда), легко вычислить центральный момент q-го порядка для первоначального ряда:

внимание свойства центрального момента, получаем

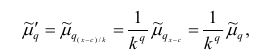
откуда следует, что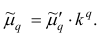

Эмпирические асимметрия и эксцесс

Эмпирическим коэффициентом асимметрии 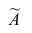называют отношение центрального момента третьего порядка к кубу среднеквадратического отклонения:

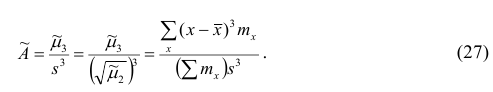
Если полигон вариационного ряда скошен, т.е. одна из его ветвей, начиная от вершины, зримо длиннее другой, то такой ряд называют асимметричным. Из формулы (27) следует, что если в вариационном ряду преобладают варианты, меньшие 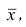то эмпирический коэффициент асимметрии отрицателен; говорят, что в этом случае имеет место левосторонняя асимметрия. Если же в вариационном ряду преобладают варианты, большие 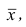то эмпирический коэффициент асимметрии положителен; в этом случае имеет место правосторонняя асимметрия. При левосторонней асимметрии левая ветвь полигона длиннее правой. При правосторонней, более длинной является правая ветвь.

Эмпирическим эксцессом или коэффициентом крутости 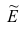называют уменьшенное на 3 единицы отношение центрального момента четвертого порядка к четвертой степени среднеквадратического отклонения:

За стандартное значение эксцесса принимают нуль-эксцесс так называемой нормальной кривой (см. рис. 1).

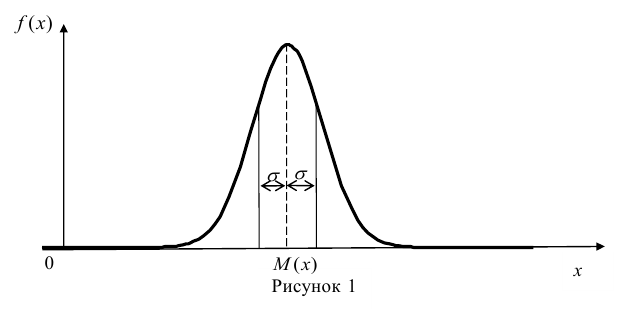
Кривые, у которых эксцесс отрицательный, по сравнению с нормальной менее крутые, имеют, более плоскую вершину и называются «плосковершинными» Кривые с положительным эксцессом более крутые по сравнению с нормальной кривой, имеют более острую вершину и называются «островершинными».

Интервальные оценки параметров распределений

Доверительный интервал, доверительная вероятность:

Точечная оценка неизвестного параметра 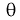, найденная по выборке объема  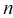из генеральной совокупности, не позволяет непосредственно узнать ошибку, которая получается, когда вместо точного значения неизвестного параметра  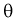принимается некоторое его приближение (оценка)  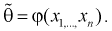Поэтому чаще пользуются интервальной оценкой, основанной на определении некоторого интервала, накрывающего неизвестное значение параметра  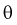с определенной вероятностью. На рис. 10.1 изображен интервал длиной 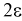, внутри которого в любом месте может находиться неизвестное значение параметра .

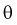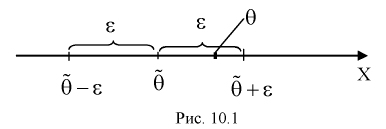
Чем меньше разность 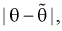 тем лучше качество оценки. И если записать  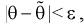то 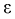 будет характеризовать точность оценки.
 

Доверительной вероятностью оценки называется вероятность 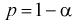выполнения неравенства  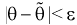. Доверительную вероятность р обычно задают заранее: 0,9; 0,95; 0,9973. И доверительная вероятность показы­вает, что с вероятностью р параметр  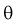будет накрываться данным интервалом

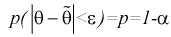   или

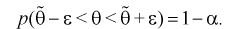                       (10.1)

Из  (10.1) видно, что неизвестный параметр 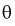 находится внутри интервала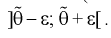 
 

Доверительным интервалом называется интервал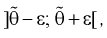 накрывающий неизвестный параметр 0 с заданной доверительной вероятностью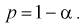  

Длина его (см. рис. 10.1) 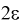. Параметр  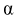-уровень значимости.

Доверительный интервал для математического ожидания случайной величины X при известной дисперсии

Доверительный интервал для математического ожидания случайной величины X при известной дисперсии (или )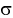

Пусть эксперимент Е описывается нормальной случайной величиной X.
Плотность распределения 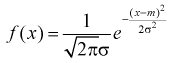. Предположим, что известна дисперсия  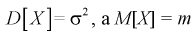– неизвестна. Тогда точечную оценку математического ожидания можно получить из выборки объемом  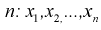– и она определится так: 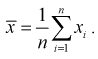Рассматривая выборку  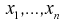как 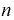 независимых случайных величин, имеющих одно и тоже нормальное распределение, определим числовые характеристики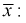

 

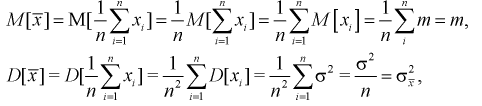
откуда получим

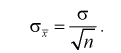       (10.2)

Для определения доверительного интервала рассмотрим разность между оценкой и параметром: 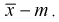 Нормируем ее (сделаем безразмерной), т. е. разделим на  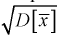и обозначим как случайную величину U:

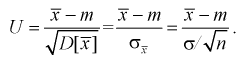    (10.3)

Покажем, что случайная величина U имеет нормированный нормальный закон распределения. Найдем ее числовые характеристики:

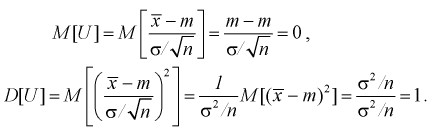
Таким образом 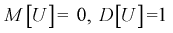– это значит, что U имеет нормированное нормальное распределение, график которого изображен на рис. 10.2.

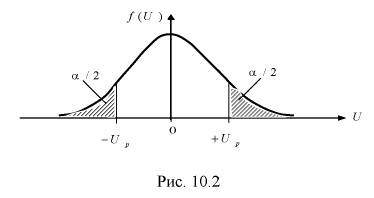
Зная плотность распределения случайной величины U, легко найти вероятность попадания случайной величины U в интервал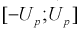 (см. рис. 10.2):

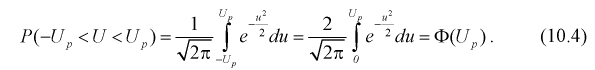
Левая часть этого уравнения представляет собой доверительную вероятность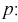

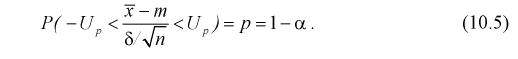
Тогда из (10.4) и (10.5) следует уравнение

Решая уравнение (10.6), по таблицам функции Лапласа для заданной доверительной вероятности 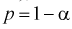 можно найти границы доверительного интервала для U, т. е. квантили  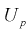. Считая, что квантили  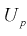известны, преобразуем правую часть уравнения (10.5), подставляя в нее (10.3):

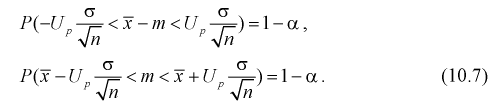
Считая, что 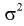– известна, из (10.7) следует, что доверительный интер­вал  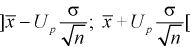накрывает неизвестное математическое ожидание  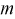с заданной доверительной вероятностью  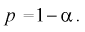Точность оценки ма­тематического ожидания или длина доверительного интервала

Замечания по формуле (10.8):

1. при увеличении объема выборки 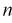 из (10.8) видим, что е уменьшается, значит, уменьшается длина доверительного интервала, а точность оценки увеличивается;
2. увеличение доверительной вероятности 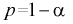 приводит к увеличению длины доверительного интервала (см. рис. 10.2, где квантили  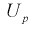увеличиваются), т. е. е увеличивается, а точность оценки падает;
3. если задать точность е и доверительную вероятность 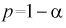 , то можно найти объем выборки, который обеспечит заданную точность:

Пример №1

Сколько конденсаторов одного номинала надо измерить, чтобы с вероят­ностью 0,95 можно было утверждать, что мы с точностью 1 % определили их среднее значение – математическое ожидание.
Обозначим 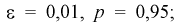 по таблицам функции Лапласа найдем квантиль для заданной доверительной вероятности 0,95:  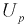= 1,96. Для проведения расчетов положим  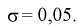Подставляя эти значения в (10.9), получим

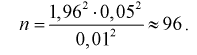
Доверительный интервал для математического ожидания нормальной случайной величины X при НЕизвестной дисперсии

Доверительный интервал для математического ожидания нормальной случайной величины X при неизвестной дисперсии или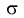

Пусть эксперимент описывается случайной величиной X с нормальным распределением с неизвестными параметрами 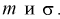 Для определения точечных оценок этих параметров из генеральной совокупности извлечена выборка  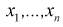объемом 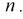. Тогда точечные оценки этих параметров определяются так:

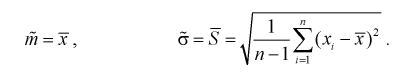
Здесь использовали для оценки дисперсии 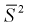 – модифицированную выборочную дисперсию, несмещенную оценку. Для построения доверительного интервала рассмотрим разность между оценкой и параметром:  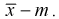. Нормиру­ем ее, т. е. разделим на  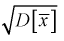и обозначим результат как случайную величину t. Ранее мы показали, что  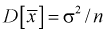но т. к. здесь  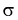неизвестна, возьмем ее оценку  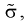и тогда  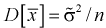. Тогда случайная величина t принимает вид

Умножим числитель и знаменатель в (10.10) на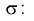

 

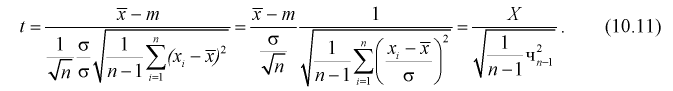
Здесь X – нормированная нормальная случайная величина, знаменатель – распределение 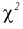с 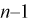 степенями свободы. Поэтому, согласно определению (см. раздел 9.3, формула (9.5)), можно утверждать, что случайные величины  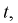определяемые по формулам (10.10) и (10.11), имеют закон распределения Стьюдента с  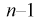степенями свободы.
Зная закон распределения случайной величины t и задавая доверительную вероятность 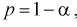, можно найти вероятность попадания ее в интервал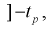 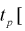(рис. 10.3).

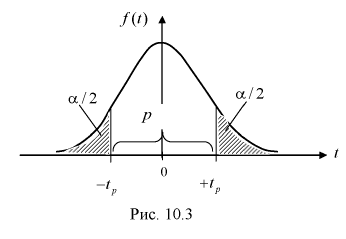
Из таблиц распределений Стьюдента по заданной доверительной вероятности  и числу степеней свободы находим квантили 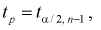 удовлетворяющие условию

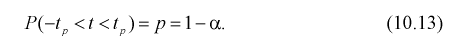
Подставляя в (10.13) вместо t равенство (10.10), получаем

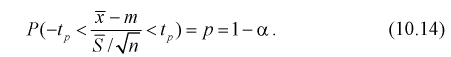
Разрешим неравенство в левой части формулы (10.14) относительно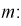

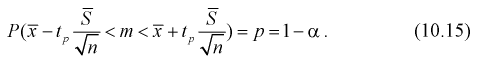
Отсюда непосредственно следует, что доверительный интервал 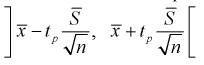  накрывает неизвестный параметр  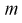– (математическое ожидание) с доверительной вероятностью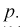

Интервал (10.15) несколько шире интервала (10.7), определенного для той же выборки и той же доверительной вероятности. Зато в (10.15) используется меньшая априорная информация – 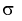 знать не надо.

Можно обозначить ширину доверительного интервала или точность через 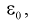 , и из (10.15) следует

Все замечания, сделанные по формуле (10.8), справедливы и для формулы (10.16).
 

Пример №2

Даны результаты четырех измерений напряжения сети (значения приве­дены в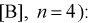

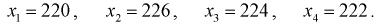
Считаем, что X – напряжение сети – является нормальной случайной величиной. Построить доверительный интервал с вероятностью 0,95 для истинного напряжения сети –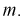

Найдем точечную оценку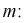

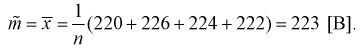
Из таблиц распределения Стьюдента для 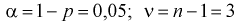– число степеней свободы; находим квантиль  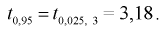Вычислим модифицированную выборочную дисперсию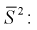

 
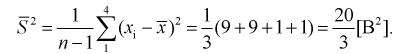
Тогда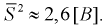
Полученные значения подставим в формулу (10.16):

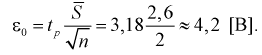
Найдем левую и правую границы доверительного интервала для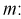

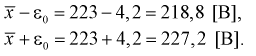
Таким образом, истинное напряжение сети с вероятностью 0,95 накрывается доверительным интервалом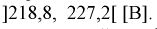

Найдем минимальное число измерений, чтобы с вероятностью 0,95 точ­ ность определения истинного напряжения сети не превышала 0,5 В, т. е. 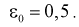 Из (10.16) имеем
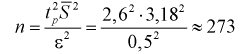 измерения.
 

Видим, что число измерений  велико. Следует отметить, что значение квантиля 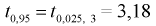 зависит от  и при увеличении  будет убывать. При больших  значение квантиля стремится к постоянной величине и равно 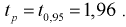. Тогда после коррекции значения квантиля вычисляем по формуле (10.16) скорректированное значение  :

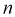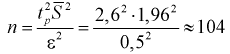 измерения.

Доверительный интервал для дисперсии или ст нормальной случайной величины X

Рассмотрим вероятностный эксперимент с нормальной моделью, где параметры  неизвестны. Предположим, что по выборке 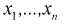 найдены точечные оценки этих параметров:

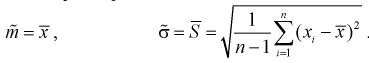
Составим вспомогательную случайную величину

Эта случайная величина имеет распределение 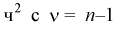 степенями свободы. Покажем это, подставив в (10.17) выражение для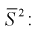

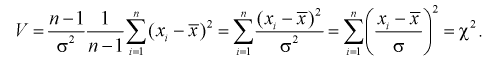
Это и есть распределение хи-квадрат с 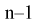 степенью свободы. На рис. 10.4 приведен график этого распределения.

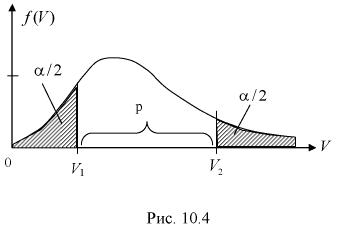
Зная закон распределения случайной величины У, определим вероятность того, что случайная величина 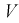 попадет в интервал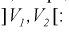

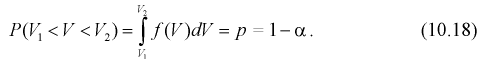
Здесь 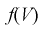 плотность распределения  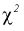с 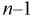 степенями свободы. Из рис. 10.4 видно, что кривая для плотности распределения  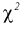несимметрична относительно центра распределения, поэтому границы доверительного интервала или квантили  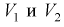для данной вероятности  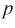не определяются однозначно. Чтобы избежать неопределенности будем их находить из условия

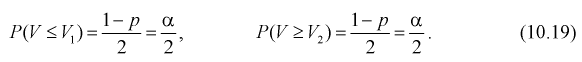
Это означает, что площади заштрихованных фигур равны. Задавая доверительную вероятность 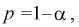 по таблицам распределения  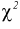для числа сте­пеней свободы  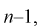используя условия (10.19), находим квантили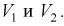

Считая 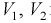 и р известными, перепишем (10.18) в следующем виде:

Подставим в (10.20) значение 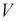, определяемое формулой (10.17):

Решаем неравенство в левой части (10.21) относительно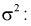

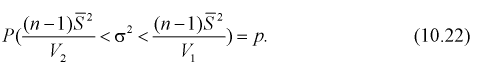
 Из (10.22) записываем доверительный интервал для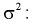

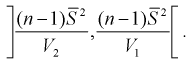
Для среднего квадратического отклонения 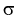 доверительный интервал имеет следующий вид:

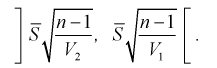
Можно ввести коэффициенты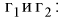

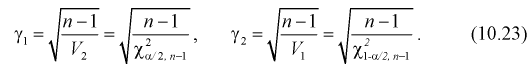
Тогда доверительный интервал для о определится следующим обра­зом:

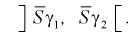
Коэффициенты 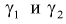 , соответствующие доверительной вероятности  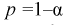и числу степеней свободы 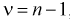, находятся по таблицам распределения .
 

Пример №3

В предыдущем разделе (10.3) приведен пример для измеренных значений напряжения сети. Продолжим и найдем доверительный интервал для среднего квадратического отклонения  .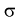

Найдена точечная оценка для 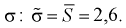 Задавая доверительную ве­роятность  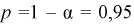, зная число степеней свободы 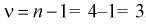, по таблицам распределения  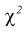, используя (10.23), находим коэффициенты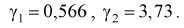
Тогда нижняя граница для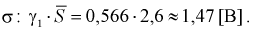
Верхняя граница для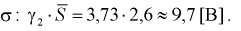
И окончательно: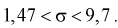

Пример №4

Случайная величина 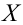 имеет нормальное распределение с известным средним квадратическим отклонением  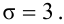Найти доверительный интервал для оценки неизвестного математического ожидания  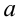с надежностью  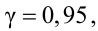если по данным выборки объемом 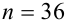вычислено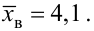 
Решение. Определим значение 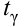  по табл. П2:

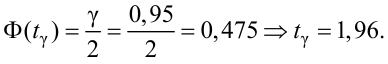
Точность оценки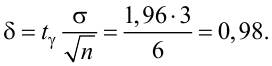 

Подставим в неравенство (4.1):  

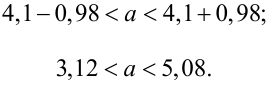
Смысл полученного результата: если произведено достаточно большое число выборок по 36 в  каждой,  то 95 % из  них  определяют  такие  доверительные 
интервалы, в которых 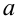 заключено, и лишь в 5 % случаев оно может выйти за границы доверительного интервала.

Пример №5

Для исследования нормального распределения 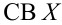 извлечена выборка (табл. 4.1).

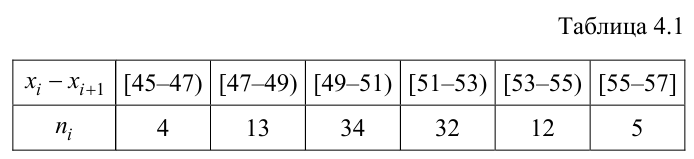
Найти с надежностью 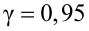 доверительные интервалы для математического ожидания и среднего квадратического отклонения исследуемой СВ.

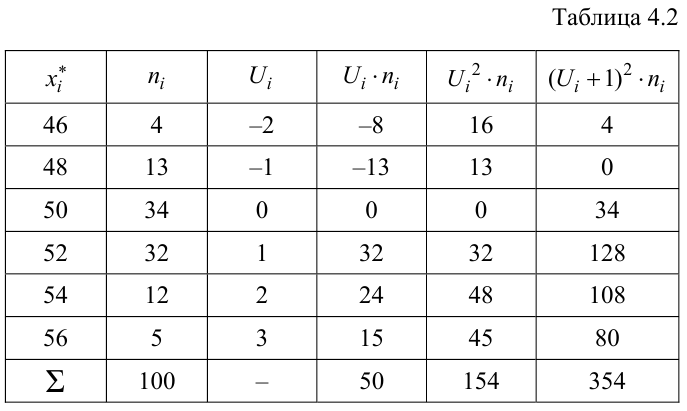
Решение. Найдем несмещенные оценки для математического ожидания и дисперсии, используя метод произведений (табл. 4.2).

Контроль: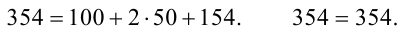 

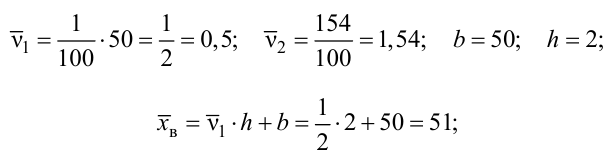
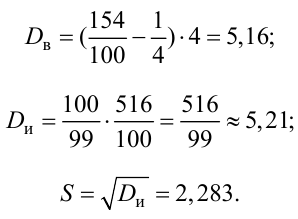
По табл. П3 по данным 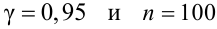 находим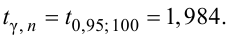 

Для определения доверительного интервала для математического ожидания используем неравенство (4.2):

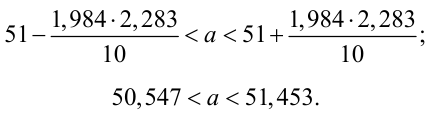
Таким образом, интервал (50, 547; 51, 453) накрывает точку 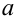 с вероятностью 0,95.

Для определения доверительного интервала для среднего квадратического отклонения используем неравенство (4.3). По табл. П4 по заданным 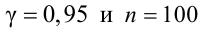 находим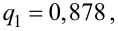 

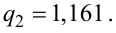
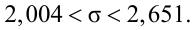
С вероятностью 0,95 неизвестное значение 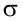 накрывается интервалом (2,004; 2,651).

Интервальные оценки параметров распределения

Точечной
называют оценку параметров распределения,
которая выражается одним числом,
например, среднее арифметическое
является точечной оценкой математического
ожидания, статистическая дисперсия
является точечной оценкой дисперсии.
Точечные оценки могут сильно отличаться
от оцениваемого параметра при небольших
объемах выборки. Поэтому при небольших
объемах выборки следует пользоваться
интервальными оценками.

Интервальной
называют
оценку, которая определяет интервал,
внутри которого находится оцениваемый
параметр распределения.

Интервальные оценки математического ожидания

Пусть
для выборки объема
признакаполучены среднее арифметическоеи статистическая дисперсия.
Зададим промежуток длиныс серединой в точкеи найдем вероятностьтого, что неизвестное математическое
ожиданиерасположено внутри интервала,
т.е. найдем

.
(9)

Промежуток
называетсядоверительным
интервалом.

Промежуток
называетсяточностью
среднего
арифметического.

Величина
называетсядоверительной
вероятностью или надежностью среднего
арифметического.

Здесь
возникают три задачи в математической
статистике

1)построение
доверительного интервала для по
заданной надёжности
:

2)
определение
–
надёжности оценки математического
ожиданияпри заданной точности,

3)
определение минимального количество
опытов
,
обеспечивающих необходимые надёжностьи точностьпри оценке.

Задача о надежности определения математического ожидания при заданной точности

1.
Пусть объем выборки велик, например
.
В этом случае, в соответствии с теоремой
Ляпунова среднее арифметическое как
сумма большого числа случайных величин
будет распределено приближенно нормально.
Действительно, среднее выборочноеможно рассматривать как случайную
величину, равную суммеслучайных величин. Выборочные значенияможно рассматривать как значения
одинаково распределенных случайных
величинс одним и тем же математическим ожиданиеми
одной и той же дисперсией(Значенияизменяются от выборки к выборке). Найдем
математическое ожидание и дисперсию
среднего арифметического

.
(10)

Найдем
дисперсию среднего арифметического

(11)

Следовательно,
дисперсия среднего арифметического в
раз меньше статистической дисперсии
самой случайной величины.
Отсюда среднеквадратичное отклонение
среднего выборочного равно.

Среднее
арифметическое при больших значениях
имеет нормальное распределение,
Следовательно,

.
(12)

где
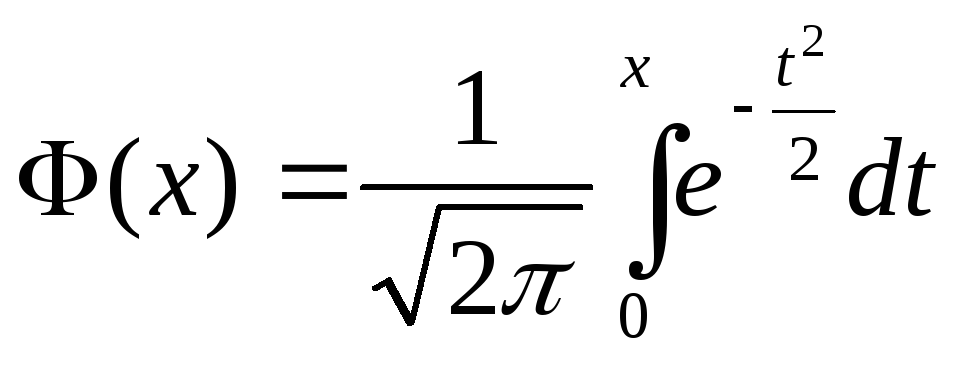– функция Лапласа, Следовательно,–
оценкас точностьюи с надежностью,
т.е. с вероятностьюнеизвестное математическое ожиданиенаходится в интервале.

Формулу
(12) используют тогда, когда известна
дисперсия случайной величины. При
больших объемах выборки можно заменить
в формуле (12) на
.

2).
Пусть объем выборки невелик ().
В этом случае уже нельзя предположить,
что среднее арифметическое распределено
нормально. Английский статистик Госсет,
писавший под псевдонимом Стьюдент,
нашел закон распределения случайной
величины–
центрированного и нормированного
среднего арифметического. Плотность
этого распределения имеет вид

,
(13)

где
,число степеней свободы.

Отметим,
что в некоторых изданиях плотность
распределения
обозначается.
Распределение Стьюдента зависит только
от числа степеней свободыи не зависит от неизвестных параметров.
Эта особенность является его большим
преимуществом.

Распределение
Стьюдента близко к нормальному при
больших значениях
(практически при).
Пусть задан интервал.
Вычислимс помощью распределения Стьюдента. Если,то
.
Следовательно,

,
Здесь было учтено, что
является четной функцией. Для функции,
где,
существуют подробные таблицы. По
заданной надежностии объему выборки по таблицам находится
значение,
отсюда определяется доверительный
интервал для математического ожидания

При
оценке математического ожидания с
помощью среднего арифметического при
большом значении
часто пользуются правилом,
которое позволяет грубо оценить интервал
возможных значений математического
ожидания.

.
Отсюда
и следовательно

.

Пример
1.
Из очень большой партии деталей отобрано
72 детали. Их средний вес
.
Дисперсия.
С какой вероятностью можно утверждать,
что средний вес деталей всей партии не
меньше 649 г и не больше 651 г.

Решение.
Здесь
,,.

Считаем,
что
распределено нормально. Тогда.

Пример
2.
Из очень большой партии цилиндрических
деталей отобрано 10 деталей. Измерены
диаметры деталей и найдено их среднее
арифметическое
.
Дисперсия.Найти
надежность того, что среднее значение
диаметров всей партии заключено между
5.96 и 6.08 мм.

Решение.
В данном случае объем выборки мал
Поэтому нужно использовать распределение
Стьюдента.

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

1. Точечные и интервальные оценки параметров распределения
2. Примеры решения задач

Точечные и интервальные оценки параметров распределения

Оценка параметра распределения совокупности в общем случае является случайной величиной, которая определяется по данным выборки и используется вместо неизвестного значения параметра, который нужно оценить.

Оценка называется обоснованной, если она совпадает по вероятности с соответствующим параметром при 

Оценка называется несмещенной, если ее математическое ожидание совпадает со значением параметра.

В случае выбора из всех известных несмещенных обоснованных оценок определенной оценки, необходимо указать критерий, по которому сделан выбор.

Чаще всего используется критерий, который состоит в выборе оценки, имеющей наименьшую возможную дисперсию. Такая оценка называется эффективной. Нижняя граница дисперсии несмещенной оценки параметра (которую будем обозначать ) определяется по формуле:

где – плотность распределения случайной величины (для дискретной случайной величины ).

Оценки параметров распределения находят методами максимальной правдоподобности и моментов. Метод максимальной правдоподобности состоит вот в чем. Пусть закон распределения случайной величины определяется через параметр  который в общем случае -мерный. Тогда для выборки общий закон распределения представляется функцией правдоподобности (запишем, например, для непрерывных величин):

За оценки максимальной правдоподобности параметров  берутся выборочные функции, которые является решением системы уравнений:

Использование метода моментов основывается на сходстве (по вероятности) статистических моментов распределения с соответствующими теоретическими моментами распределения, которые в этом случае должны существовать. Как известно, теоретические моменты распределения выражаются через параметры распределения. Составим систему уравнений, в которой попарно приравняем соответствующие теоретические и статистические моменты. Решением этой системы являются оценки для параметров распределения.

Пусть есть точечная оценка параметра  Найдем для параметра интервальную оценку, воспользовавшись условием  В этом случае  называется точностью оценки, а – ее надежностью. Тогда интервальная оценка (доверительный интервал) для параметра  принимает вид  Параметр  – не случайная величина, надежность  можно рассматривать как вероятность того, что случайный интервал покрывает действительное значение параметра. Величины  и  тесно связаны с объемом выборки  Если задать две из этих величин, то модно найти третью. Для этого нужно знать закон распределения для 

Примеры решения задач

Пример 1. Выборка объемом  сделана из совокупности, распределенной по закону Релея 

Найти оценку для параметра  и преобразовать ее в  несмещенность, обоснованность и эффективность.

Решение. Применим метод максимальной правдоподобности. Построим функцию правдоподобности, составим и решим уравнение для определения оценки:

Проверим оценку на несмещенность, найдя ее математическое ожидание:

Преобразование выполнено согласно свойствам математического ожидания и с учетом того, что результаты выборки являются независимыми одинаково распределенными случайными величинами. Найдем  случайной величины, распределенной по закону Релея:

Тогда  то есть оценка несмещенная.

Проверку обоснованности оценки выполним, второй формой неравенства Чебышева, то есть оценим вероятность  Чтобы найти дисперсию оценки, выполним вычисления:

(Последний интервал, который является математическим ожиданием квадрата случайной величины, равен и вычислялся ранее). Тогда  Следовательно, получим:

Подставляя дисперсию оценки в неравенство Чебышева, получим:

 если 

Следовательно, оценка обоснованная.

Находим дисперсию эффективной оценки:

Дисперсия эффективной оценки совпадает с дисперсией найденной оценки для  а это означает, что оценка эффективная.

Пример 2. Методом моментов найти оценку параметра  геометрического распределения поп данным выборки объемом 

Решение. Геометрический закон распределения определяется формулой Поскольку нужно найти оценку одного параметра, сравниваем теоретические и статистические начальные моменты первого порядка:

Пример 3. По данным выборки объемом  из нормально распределенной совокупности, дисперсия которой а надежность  найти интервальную оценку для математического ожидания этой совокупности.

Решение. Интервальная оценка для математического ожидания, если дисперсия совокупности известна, представляется в виде  где где  – функция Лапласа.

Для построения оценки рассматривалась выборочная функция  которая имеет нормальный закон распределения с нулевым математически ожиданием и единичной дисперсией. 

Пример 4. Решить предыдущую задачу для случая, когда дисперсия совокупности неизвестна.

Решение. В этом случае интервальную оценку построим с помощью выборочной функции  которая распределена по закону Стьюдента с  степенями свободы. Доверительный интервал где  где – функция распределения Стьюдента с  степенями свободы. Если количество степеней свободы превышает 20, то распределение Стьюдента практически не отличается от нормального закона распределения с нулевым математическим ожиданием и единичной дисперсией. 

Пример 5. По результатам выборки объемом из нормально распределенной совокупности с надежностью  найти доверительный интервал для дисперсии совокупности.

Решение. Для определения доверительного интервала берем выборочную функцию  которая имеет распределение с  степенями свободы. Доверительный интервал представляется в виде Значения и  определяются с помощью таблиц распределения  с соответствующим количеством степеней свободы: 

Пример 6. Найти с надежностью  интервальную оценку для вероятности наступления события в каждом из независимых повторных испытаний, если событие произошло  раз.

Решение. Для определения доверительного интервала берем выборочную функцию  которая имеет закон распределения близкий к нормальному, с нулевым математическим ожиданием и единичной дисперсией. Доверительный интервал:

где – значение найдено по таблицам функции Лапласа. Вычислим  и  – левую и правую границы доверительного интервала:

Получим интервал 

Пример 7. Определить минимальный объем выборки  для того, чтобы с надежностью  можно было получить оценку математического ожидания нормально распределенной совокупности  если среднее квадратическое отклонение в генеральной совокупности и оценка находится с помощью выборочной средней величины.

Решение. Воспользовавшись формулой получаем Найдем  из формулы  По таблицам функции Лапласа  следовательно, 

Пример 8. Из партии однотипных высокоомных сопротивлений взяли для контроля 10 штук. Измерения показали такие отклонения от номинала, кОм:

Найти выборочную среднюю и дисперсию отклонения фактического значения сопротивления от номинала в этой партии и определить точность оценки математического ожидания выборочной средней величиной с надежностью (использовать распределение Стьюдента).

Решение. Считаем, что отклонение  имеет нормальный закон распределения с неизвестными параметрами и  Находим числовые характеристики  и  выборочной совокупности: Точность оценки определяем по формуле  Значение  ищем по таблицам функции распределения Стьюдента с 9 степенями свободы: 

Следовательно, получим такой доверительный интервал для математического ожидания: 

Пример 9. В ВТК были измерены диаметры 200 валов, изготовленных на станке-автомате. Отклонения измеренных диаметров от номинала, мкм, приведены в таблице.

Считая, что выборка сделана из нормально распределенной совокупности, определить с надежностью  точность оценки дисперсии выборочной дисперсией 

Решение. С помощью условных моментов распределения, вычислим выборочную дисперсию  составив таблицу:

найдем условные моменты распределения и выборочную дисперсию на основании расчетов в таблице:

Точность оценки равна половине длины доверительного интервала Значения и вычислим с помощью таблиц распределения  с  степенями свободы. Но в этой задаче объем выборки тогда как таблицы составлены для значений  которые не превышают 30. Поэтому воспользуемся тем, что при распределение  приближается к нормальному закону распределения с соответствующими математическим ожиданием и дисперсией. Выборочная функция  имеет распределение  с  степенями свободы. Поэтому 

Выборочная функция распределена нормально с нулевым математическим ожиданием и единичной дисперсией. Доверительный интервал найдем из условия:

Выполним преобразование для определения границ доверительного интервала:

Следовательно, доверительный интервал для дисперсии такой: 

Найдем точность оценки как половину длины доверительного интервала:

Согласно значению по таблицам функции Лапласа 

Окончательно получим: 

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 мая 2022 года; проверки требует 1 правка.

В математической статистике интервальной оце́нкой называется результат использования выборки для вычисления интервала возможных значений неизвестного параметра, оценку которого нужно построить. Следует отличать от точечной оценки, которая даёт лишь одно значение. Самым распространенным видом интервальных оценок являются доверительные интервалы.

Определение[править | править код]

Пусть  — случайная выборка объёма , порождённая случайной величиной с функцией распределения вероятностей , известной с точностью до параметра . Располагая выборкой , необходимо найти оценку параметра . В общем случае имеется нулевая вероятность того, что  — что точечная оценка совпадёт с параметром . Поэтому для оценивания параметра используется интервальная оценка.

Проблема состоит в нахождении на основании выборки статистик , , которые с достоверностью удовлетворяют неравенству . Зададимся достаточно малым числом  — уровнем значимости. Тогда интервал называется интервальной оценкой параметра , если .

Интервал называется доверительным интервалом параметра на уровне значимости или с надежностью ^[1].

Свойства интервальных оценок[править | править код]

История[править | править код]

Ежи Нейман определил интервальное оценивание («оценивание интервалами») как отличное от точечного оценивания («оценивание единичной оценкой»). Он распознал что, поскольку результаты того времени публиковались в виде «оценка ± стандартное отклонение», учёные-статистики на самом деле имели в виду интервальное оценивание.

См. также[править | править код]

• Точечная оценка

Примечания[править | править код]

Литература[править | править код]

• Колемаев В. А. Теория вероятностей и математическая статистика. — М.: Высшая школа, 1991. — 400 с. — ISBN 5-06-001545-9.
• Маталыцкий М. А., Хацкевич Г.А. Теория вероятностей, математическая статистика и случайные процессы. — Минск: Вышэйшая школа, 2012. — 720 с.