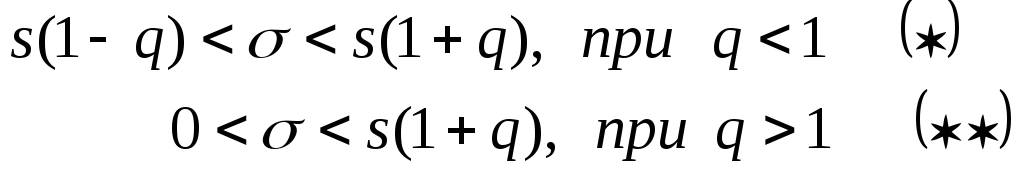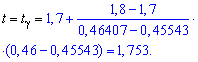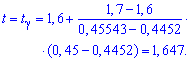-
Интервальные оценки
Любая точечная оценка
неизвестного
параметра а представляет собой
случайную величину. Принимая оценку
за
значение параметра а, мы, как правило,
совершаем ошибку, даже в том случае,
когда оценка является несмещенной и
состоятельной. Поэтому важно знать,
каковы точность и надежность используемой
оценки. Задача состоит в том, чтобы уметь
находить границы, в которых с определенной
вероятностью заключено неизвестное
значение параметра. Эту задачу решают
следующим образом.
Пусть по сделанной выборке удалось
найти два числа а1 и
а2 такие, что при любых
значениях параметра а выполняется
равенство
(14)
В этом случае числа а1
и а2 называют доверительными
границами, а интервал (а1;
а2) — доверительным
интервалом, соответствующими
доверительной вероятности
. Число
называют также надежностью оценки.
Нижняя и верхняя границы а1
и а2 доверительного
интервала находятся по сделанной выборке
и, следовательно, являются случайными
величинами. Поэтому доверительный
интервал (а1; а2)
также определяется случайным образом.
Если случайное событие
происходит,
то говорят, что доверительный интервал
(а1; а2)
накрывает неизвестный параметр а.
Равенство (14) означает, что интервал
(а1; а2)
накрывает неизвестный параметр а
с вероятностью
.
Выбор доверительной вероятности
(надежности) определяется конкретными
условиями. Обычно берут
равной 0,90; 0,95; 0,99. Если конкретные условия
задачи
позволяют считать все события, вероятность
которых меньше 0,10 (соответственно 0,05;
0,01), невозможными, то считают практически
достоверным, что доверительный интервал
накрывает неизвестный параметр, и за
значение параметра принимают середину
доверительного интервала. При этом
считают практически достоверным, что
ошибка не будет превосходить числа
.
В математической статистике используются
разнообразные методы отыскания
доверительных интервалов для неизвестных
параметров случайных величин. В качестве
примера покажем, как можно найти
доверительный интервал для неизвестного
параметра случайной величины,
распределенной по биномиальному закону.
Рассмотрим снова случайную величину
X— число наступлений события А в
серии из п независимых опытов, в
каждом из которых событие А происходит
с вероятностью р. Как мы уже знаем,
в случае, когда р неизвестно, в
качестве оценки вероятности р
берется частота, причем эта оценка
является несмещенной и состоятельной.
Можно доказать, что при большом числе
опытов границы а1 и а2
доверительного интервала, соответствующего
надежности
, приближенно выражаются формулами
,
(15)
где k — число наступлений
события A в п опытах,
а х — корень уравнения
Корень этого уравнения находится по
таблице значений функции Лапласа Ф0(х)
(см. таблицу 1). Формулами (15) можно
пользоваться при
138
п >50, k
>5, п – k >5
(16)
т. е. во многих практически важных
случаях. Если же условия (16) не выполняются,
то для построения доверительного
интервала пользуются другими формулами.
Пример 5. С автоматической линии
было отобрано и проверено 400 деталей,
10 деталей оказались бракованными. Найти
доверительный интервал, накрывающий с
надежностью 0,9 неизвестную вероятность
изготовления бракованной детали.
Решение: по условию имеем п = 400, k
= 10,
=
0,9. Так как надежность
= 0,9 задана, то получаем уравнение Ф0(х)=
. Из таблицы значений функции Лапласа
Ф0(Х) (см. приложение 1) следует, что
1,645. По формулам (15) находим границы
доверительного интервала:
.
Таким образом, если считать неизвестную
вероятность равной
,
то с вероятностью 0,9 ошибка не превзойдет
числа
.
1. Интервальной оценкой (с
надежностью
)
математического ожидания а нормально
распределенного признака Х по
выборочной средней
при известном среднем квадратическом
отклонении
генеральной
совокупности служит доверительный
интервал
,
(15)
где
– точность оценки, п– объем выборки
, t –значение аргумента
функции Лапласа Ф0(t),
при котором Ф0(t)=
, при неизвестном среднем квадратическом
отклонении
(и
объеме выборки п<30)
,
(16)
где s– «исправленное»
выборочное среднее квадратическое
отклонение ,
– находят по таблице (см. приложение 2)
по заданным
.
2. Интервальной оценкой (с
надежностью
)
среднего квадратического отклонении
нормально распределенного признака Х
по «испраленному» выборочному
среднему квадратическому отклонению
s служит доверительный
интервал
(17)
где q– находят по
таблице (см. приложение3) по заданным
.
Пример 6. Найти доверительный
интервал для оценки с надежностью 0,95
неизвестного математического ожидания
а нормально распределенного признака
Х генеральной совокупности, если
генеральное среднее квадратическое
отклонение
,
выборочная средняя
,
объем выборки
.
139
Решение: воспользуемся формулой (15):
.
Все величины, кроме t,
известны. Найдем t
из соотношения Ф0(t)=
.
По таблице 1 находим t=1,96.
Подставив t=1,96,
,
,
в (15), получим доверительный интервал:
.
Пример 7. По данным выборки объема
16
из генеральной совокупности найдено
«исправленное» среднеквадратическое
отклонение s=1 нормально
распределенного количественного
признака. Найти доверительный интервал,
покрывающий генеральное среднее
квадратическое отклонение
с надежностью 0,95.
Решение: задача сводится к отысканию
доверительного интервала по формулам
(17):
По данным задачи
0,95
и
16
по таблице 3 найдем q=0,44.
Т.к. q<1 , т о
подставив s=1 и
q=0,44 в (*), получим
доверительный интервал
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Чаще всего оценки делятся на два вида: точечная оценка и интервальная оценка.
Определение 1
Точечная оценка — оценка, которая определяется одним числом.
В математической статистике, при оценке различных совокупностей чаще сего используется интервальная оценка.
Определение 2
Интервальная оценка — оценка, которая определяется двумя числами, которые являются концами интервала.
Для понятия интервальной оценки используются параметры точности и надежности оценки.
Определение 3
Точность оценки — положительное число $delta >0$, характеризующие величину расхождения между оценками выборки и генеральной совокупности, а именно:
[left|Q-Q^*right|1.]
Определение 4
Надежность или доверительная вероятность оценки $Q по Q^*$ – вероятность $gamma $, удовлетворяющее равенству:
[Pleft(Q^*-delta
Чаще всего надежность имеет значения $0,95, 0,99 и 0,999$, то есть значения, близкие к единице.
Доверительный интервал
Определение 5
Доверительный интервал — интервал $(Q^*-delta ,Q^*+delta )$, который покрывает неизвестную величину $Q$ c надежностью $gamma $, то есть $Q^*-delta
Понятие доверительного интервала существует для оценки многих параметров выборки: математического ожидания, среднего квадратического отклонения, дисперсии
В данной статье мы не будем вдаваться в подробности вывода формул для нахождения доверительных интервалов.
- Доверительный интервал для оценки математического ожидания при заданном среднем квадратическом отклонении $sigma $.
[left(overline{x}-frac{sigma t}{sqrt{n}};overline{x}+frac{sigma t}{sqrt{n}}right)]
где $t$ находится из равенства $2Фleft(tright)=gamma $.
- Доверительный интервал для оценки математического ожидания при неизвестном среднем квадратическом отклонении $sigma $.
[left(overline{x}-frac{St}{sqrt{n}},overline{x}+frac{St}{sqrt{n}}right)]
- Доверительный интервал для оценки среднего квадратического отклонения.
[left(Sleft(1-qright),Sleft(1+qright)right), при q1.]
- Доверительный интервал для оценки дисперсии.
[left(S^2left(1-qright),S^2left(1+qright)right), при q1.]
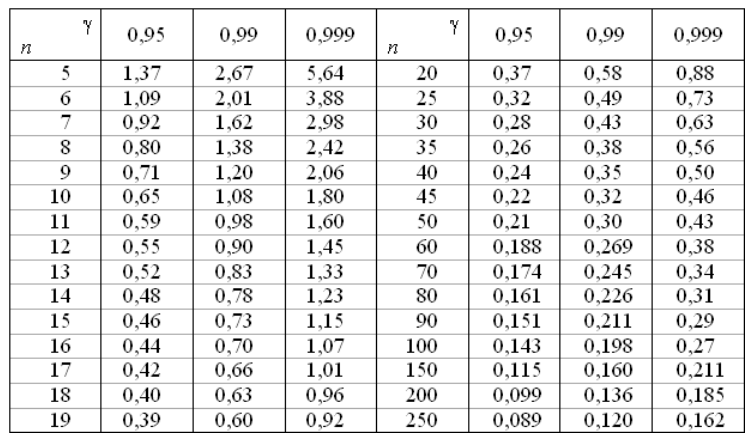
В последних двух пунктах $q$ имеет табличное значение (таблица 1).
Рисунок 1. Значения величины $q$.
Пример задачи на нахождения доверительных интервалов
Пример 1
Пусть величина $X$ имеет нормальное распределение с дисперсией $sigma =2$ и исправленным среднем квадратическим отклонением $S=1,8$. Пусть объем выборки $n=25$, а надежность равна $gamma =0,99$.
Найти:1) доверительный интервал для оценки математического ожидания.
2) доверительный интервал для оценки среднего квадратического отклонения.
3) доверительный интервал для оценки дисперсии.
Решение:
1) Для нахождения доверительного интервала для оценки математического ожидания необходимо найти интервал вида
[left(overline{x}-frac{sigma t}{sqrt{n}};overline{x}+frac{sigma t}{sqrt{n}}right)]
Параметр $t$ найдем из формулы
[2Фleft(tright)=gamma ]
Откуда
[Фleft(tright)=frac{gamma }{2}=frac{0,99}{2}=0,495]
Из таблицы значений функции Лапласа получим, что $t=2,6$.
Имеем интервал:
[left(overline{x}-frac{4,6}{sqrt{25}};overline{x}+frac{4,6}{sqrt{25}}right)=left(overline{x}-0,92;overline{x}+0,92right)]
2) Для начала найдем значение величины $q$. Так как $n=25$ и $gamma =0,99$, то из таблицы 1, получим, что $q=0,49$.
Видим, что $q
[left(Sleft(1-qright),Sleft(1+qright)right)] [left(1,8cdot 0,51;1,8cdot 1,49right)=(0,918;2,682)]
3) Так как, как было показано в пункте 2, $q
[left(S^2left(1-qright),S^2left(1+qright)right)]
end{enumerate}
Получим:
[left(1,6524;4,8276right)]
Содержание:
- Точечные и интервальные оценки параметров распределения
- Примеры решения задач
Точечные и интервальные оценки параметров распределения
Оценка параметра распределения совокупности 
в общем случае является случайной величиной, которая определяется по данным выборки и используется вместо неизвестного значения параметра, который нужно оценить.
Оценка называется обоснованной, если она совпадает по вероятности с соответствующим параметром при 
Оценка называется несмещенной, если ее математическое ожидание совпадает со значением параметра.
В случае выбора из всех известных несмещенных обоснованных оценок определенной оценки, необходимо указать критерий, по которому сделан выбор.
Чаще всего используется критерий, который состоит в выборе оценки, имеющей наименьшую возможную дисперсию. Такая оценка называется эффективной. Нижняя граница дисперсии несмещенной оценки параметра 
(которую будем обозначать 
) определяется по формуле:
где 
– плотность распределения случайной величины (для дискретной случайной величины 
).
Оценки параметров распределения находят методами максимальной правдоподобности и моментов. Метод максимальной правдоподобности состоит вот в чем. Пусть закон распределения случайной величины определяется через параметр 
который в общем случае 
-мерный. Тогда для выборки 
общий закон распределения представляется функцией правдоподобности (запишем, например, для непрерывных величин):
За оценки максимальной правдоподобности параметров 
берутся выборочные функции, которые является решением системы уравнений:
Использование метода моментов основывается на сходстве (по вероятности) статистических моментов распределения с соответствующими теоретическими моментами распределения, которые в этом случае должны существовать. Как известно, теоретические моменты распределения выражаются через параметры распределения. Составим систему 
уравнений, в которой попарно приравняем соответствующие теоретические и статистические моменты. Решением этой системы являются оценки для параметров распределения.
Пусть есть точечная оценка 
параметра 
Найдем для параметра интервальную оценку, воспользовавшись условием 
В этом случае 
называется точностью оценки, а 
– ее надежностью. Тогда интервальная оценка (доверительный интервал) для параметра 
принимает вид 
Параметр 
– не случайная величина, надежность 
можно рассматривать как вероятность того, что случайный интервал покрывает действительное значение параметра. Величины 
и 
тесно связаны с объемом выборки 
Если задать две из этих величин, то модно найти третью. Для этого нужно знать закон распределения для 
Примеры решения задач
Пример 1. Выборка объемом 
сделана из совокупности, распределенной по закону Релея
Найти оценку для параметра 
и преобразовать ее в несмещенность, обоснованность и эффективность.
Решение. Применим метод максимальной правдоподобности. Построим функцию правдоподобности, составим и решим уравнение для определения оценки:
Проверим оценку на несмещенность, найдя ее математическое ожидание:
Преобразование выполнено согласно свойствам математического ожидания и с учетом того, что результаты выборки являются независимыми одинаково распределенными случайными величинами. Найдем 
случайной величины, распределенной по закону Релея:
Тогда 
то есть оценка несмещенная.
Проверку обоснованности оценки выполним, второй формой неравенства Чебышева, то есть оценим вероятность 
Чтобы найти дисперсию оценки, выполним вычисления:
(Последний интервал, который является математическим ожиданием квадрата случайной величины, равен 
и вычислялся ранее). Тогда 
Следовательно, получим:
Подставляя дисперсию оценки в неравенство Чебышева, получим:
если 
Следовательно, оценка обоснованная.
Находим дисперсию эффективной оценки:
Дисперсия эффективной оценки совпадает с дисперсией найденной оценки для 
а это означает, что оценка эффективная.
Пример 2. Методом моментов найти оценку параметра 
геометрического распределения поп данным выборки объемом 
Решение. Геометрический закон распределения определяется формулой 
Поскольку нужно найти оценку одного параметра, сравниваем теоретические и статистические начальные моменты первого порядка:
Пример 3. По данным выборки объемом 
из нормально распределенной совокупности, дисперсия которой 
а надежность 
найти интервальную оценку для математического ожидания этой совокупности.
Решение. Интервальная оценка для математического ожидания, если дисперсия совокупности 
известна, представляется в виде 
где 
где 
– функция Лапласа.
Для построения оценки рассматривалась выборочная функция 
которая имеет нормальный закон распределения с нулевым математически ожиданием и единичной дисперсией.
Пример 4. Решить предыдущую задачу для случая, когда дисперсия совокупности неизвестна.
Решение. В этом случае интервальную оценку построим с помощью выборочной функции 
которая распределена по закону Стьюдента с 
степенями свободы. Доверительный интервал 
где 
где 
– функция распределения Стьюдента с 
степенями свободы. Если количество степеней свободы превышает 20, то распределение Стьюдента практически не отличается от нормального закона распределения с нулевым математическим ожиданием и единичной дисперсией.
Пример 5. По результатам выборки объемом 
из нормально распределенной совокупности с надежностью 
найти доверительный интервал для дисперсии совокупности.
Решение. Для определения доверительного интервала берем выборочную функцию 
которая имеет распределение 
с 
степенями свободы. Доверительный интервал представляется в виде 
Значения 
и 
определяются с помощью таблиц распределения 
с соответствующим количеством степеней свободы: 
Пример 6. Найти с надежностью 
интервальную оценку для вероятности наступления события 
в каждом из 
независимых повторных испытаний, если событие произошло 
раз.
Решение. Для определения доверительного интервала берем выборочную функцию 
которая имеет закон распределения близкий к нормальному, с нулевым математическим ожиданием и единичной дисперсией. Доверительный интервал:
где 
– значение найдено по таблицам функции Лапласа. Вычислим 
и 
– левую и правую границы доверительного интервала:
Получим интервал 
Пример 7. Определить минимальный объем выборки 
для того, чтобы с надежностью 
можно было получить оценку математического ожидания нормально распределенной совокупности 
если среднее квадратическое отклонение в генеральной совокупности 
и оценка находится с помощью выборочной средней величины.
Решение. Воспользовавшись формулой 
получаем 
Найдем 
из формулы 
По таблицам функции Лапласа 
следовательно, 
Пример 8. Из партии однотипных высокоомных сопротивлений взяли для контроля 10 штук. Измерения показали такие отклонения от номинала, кОм:
Найти выборочную среднюю и дисперсию отклонения фактического значения сопротивления от номинала в этой партии и определить точность оценки математического ожидания выборочной средней величиной с надежностью 
(использовать распределение Стьюдента).
Решение. Считаем, что отклонение 
имеет нормальный закон распределения с неизвестными параметрами 
и 
Находим числовые характеристики 
и 
выборочной совокупности: 
Точность оценки 
определяем по формуле 
Значение 
ищем по таблицам функции распределения Стьюдента с 9 степенями свободы: 
Следовательно, получим такой доверительный интервал для математического ожидания: 
Пример 9. В ВТК были измерены диаметры 200 валов, изготовленных на станке-автомате. Отклонения измеренных диаметров от номинала, мкм, приведены в таблице.
Считая, что выборка сделана из нормально распределенной совокупности, определить с надежностью 
точность оценки дисперсии 
выборочной дисперсией 
Решение. С помощью условных моментов распределения, вычислим выборочную дисперсию 
составив таблицу:
найдем условные моменты распределения и выборочную дисперсию на основании расчетов в таблице:
Точность оценки 
равна половине длины доверительного интервала 
Значения 
и 
вычислим с помощью таблиц распределения 
с 
степенями свободы. Но в этой задаче объем выборки 
тогда как таблицы составлены для значений 
которые не превышают 30. Поэтому воспользуемся тем, что при 
распределение 
приближается к нормальному закону распределения с соответствующими математическим ожиданием и дисперсией. Выборочная функция 
имеет распределение 
с 
степенями свободы. Поэтому 
Выборочная функция 
распределена нормально с нулевым математическим ожиданием и единичной дисперсией. Доверительный интервал найдем из условия:
Выполним преобразование для определения границ доверительного интервала:
Следовательно, доверительный интервал для дисперсии такой: 
Найдем точность оценки как половину длины доверительного интервала:
Согласно значению 
по таблицам функции Лапласа 
Окончательно получим: 
Лекции:
- Проверка статистических гипотез
- Дисперсионный анализ
- Элементы теории корреляции
- Выборка из генеральной совокупности. Вариационный ряд. Гистограмма относительных частот
- Выборочная функция распределения
- Закон больших чисел в форме Чебышева
- Теорема Бернулли
- Центральная предельная теорема
- Теория случайных процессов и теория массового обслуживания
- Первичная обработка и графическое представление выборочных данных
Продолжаем разбирать индивидуальное задание по теории вероятностей. Приведенная схема вычислений поможет найти доверительный интервал. Формулы для интервала доверия несложные, в этом Вы скоро убедитесь. Приведенные задачи задавали экономистам ЛНУ им. И.Франка. ВУЗы других городов Украины имеют подобную программу обучения, поэтому для себя часть полезного материала найдет каждый студент.
Индивидуальное задание 1
Вариант 11
Задача 2. Найти доверительный интервал для оценки с надежностью γ неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности:
а) если γ=0,92, генеральная среднее квадратичное отклонение σ=4,0, выборочное среднее 
=15,0, а объем выборки n=16;
б) если γ=0,99, подправленное среднее квадратичное отклонение s=4,0, выборочное среднее 
=20,0, а объем выборки n=16.
Решение: а) Из уравнения 
с помощью функции Лапласа методом интерполяции находим t
Границы интервала доверия ищем по формулам:
После вычислений получим интервал доверия 
с надежностью 
0,92.
- а) если
=0,9, генеральная среднее квадратичное отклонение s=3,0, выборочное среднее 
=7,0, а объем выборки n=9; - б) если =0,95, подправленное среднее квадратичное отклонение s=3,0, выборочное среднее =15,0, а объем выборки n=9.
Решение: а) Из уравнения на функцию Лапласа 
с помощью таблиц методом интерполяции находим t
Интерполяцию используем для уточнения t (когда в таблице значений функции Лапласа Ф(t) находится между двумя соседними).
Границы интервала доверия ищем по формулам:
Окончательно получаем такой интервал доверия 
с надежностью 
=0,9 2.
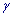
б) Поскольку n=9<30 и среднее квадратичное отклонение 
неизвестно, то для нахождения границ интервала доверия используем формулы
,
где значение t 
ищем с помощью таблиц распределения Стьюдента:
Формулы как видите не сложные и найти интервал доверия может как студент, так и школьник.
Мы нашли интервал доверия
с надежностью 
=0,95.
Задача 3. Найти интервал доверия для оценки с надежностью 
=0,95 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 17, а подправленное среднее квадратичное отклонение σ=11,2.
Решение: Формулы для интервала доверия 
достаточно просты.
По таблице находим значение функции q
Далее по формулам вычисляем интервал доверия
После вычислений он будет лежать в пределах
Вариант-12Задача 2. Найти доверительный интервал для оценки с надежностью 
неизвестного математического ожидания и нормально распределенного признака Х генеральной совокупности:
а) если =0,94, генеральная среднее квадратичное отклонение 
=5,0, выборочное среднее 
=18,0, а объем выборки n=25;
б) если =0,999, подправленное среднее квадратичное отклонениеs=5,0, выборочное среднее =26,0, а объем выборки n=25.
Решение: а) Из уравнения на функцию Лапласа 
с помощью таблиц распределения методом интерполяции находим t
Крайние точки доверительного интервала ищем по формуле:
Итак, интервал принимает множество значений 
с надежностью 0,94.
2, б) Поскольку n=25<30 и среднее квадратичное отклонение неизвестно, то для нахождения границ интервала доверия используем формулы
где значение t – 
ищем с помощью таблиц распределения Стьюдента:
Далее находим границы интервала доверия.
Таким образом нашли доверительный интервал 
с надежностью 
0,999.
Задача 3. Найти доверительный интервал для оценки с надежностью =0,999 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 45, а подправленное среднее квадратичное отклонение s=15,1.
Решение: Найдем интервал доверия по формуле
По таблице находим значение функции q
После этого выполняем вычисления границ интервала доверия
Как видите формулы для вычисления доверительного интервала не сложные, поэтому с легкостью применяйте их на контрольных и тестах по теории вероятностей.
Готовые решения по теории вероятностей
- Предыдущая статья – Построение уравнения прямой регрессии Y на X
- Следующая статья – Проверка гипотез о нормальном распределении генеральной совокупности
