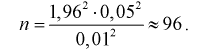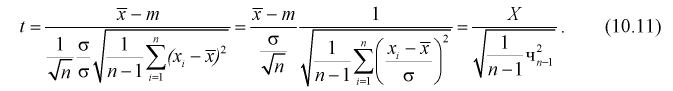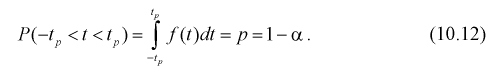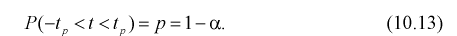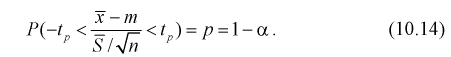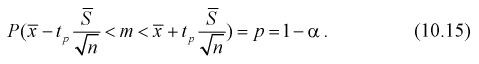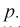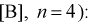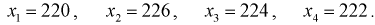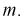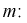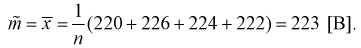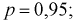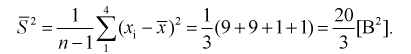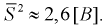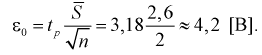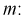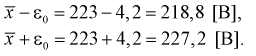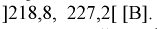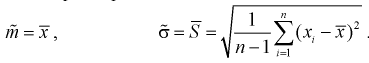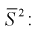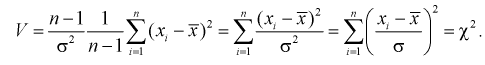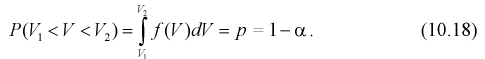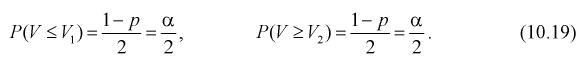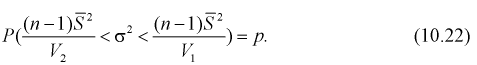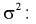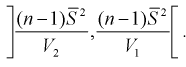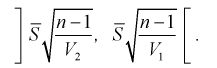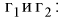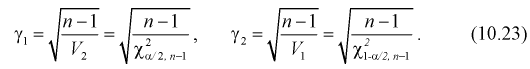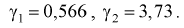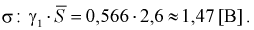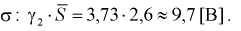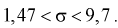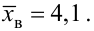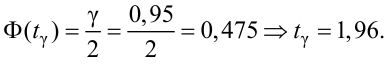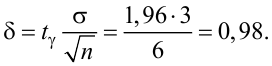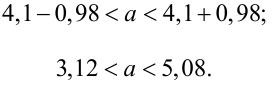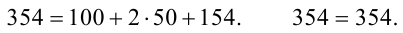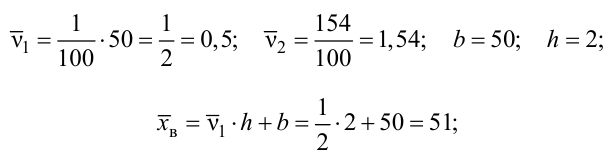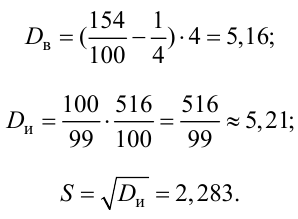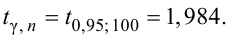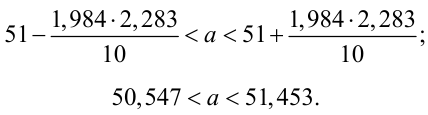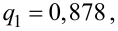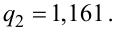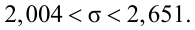Содержание:
Интервальные оценки параметров распределения. Непрерывное и дискретное распределения признаков:
В материалах сегодняшней лекции мы рассмотрим интервальные оценки параметров распределения, а именно непрерывное и дискретное распределения признаков генеральной и выборочной совокупности.
Статистические ряды и их геометрическое изображение дают представление о распределении наблюдаемой случайной величины X по данным выборки. Во многих задачах вид распределения случайной величины X известен, необходимо получить приближённое значение неизвестных параметров этого распределения: m,
Пусть
Точечной оценкой 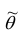
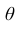
Очевидно, что 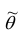
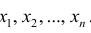
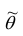
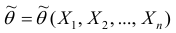
Точечная оценка 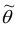
1. Состоятельность. Оценка 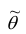
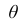
состоятельной, если 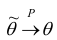
Состоятельность оценки можно установить с помощью теоремы: если 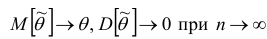
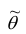
2. Несмещённость. Оценка 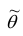
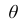
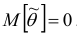
Для оценки параметра 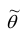
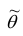
Отсюда вытекает третье свойство.
3. Эффективность. Несмещённая оценка 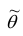
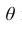
Запишем точечные оценки числовых характеристик случайной величины X.
1. Точечная оценка 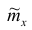
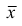
Проверим свойства оценки:
а) состоятельность следует из теоремы Чебышева: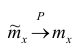
б) несмещённость:
в)эффективность:
так как
2. Точечная оценка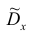
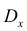
она обладает свойствами: состоятельность, несмещённость,
эффективность.
3. Точечная оценка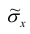
Интервальные оценки
При статистической обработке результатов наблюдений необходимо знать не только точечную оценку 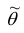
Характеристики вариационного ряда
В материалах сегодняшней лекции мы рассмотрим характеристики вариационного ряда.
Вариационные ряды
Установление закономерностей, которым подчиняются массовые случайные явления, основано на изучении статистических данных — сведений о том, какие значения принял в результате наблюдений интересующий исследователя признак.
Пример:
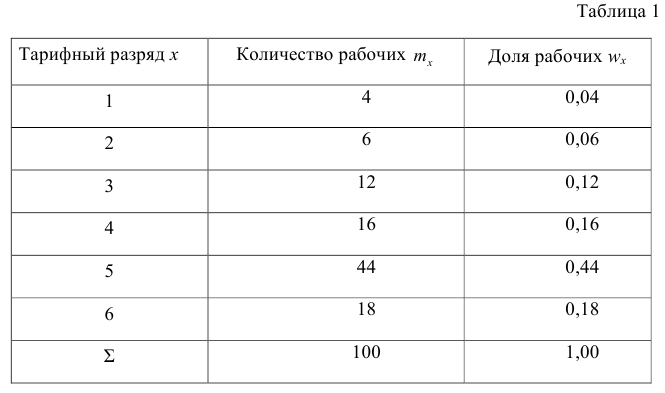
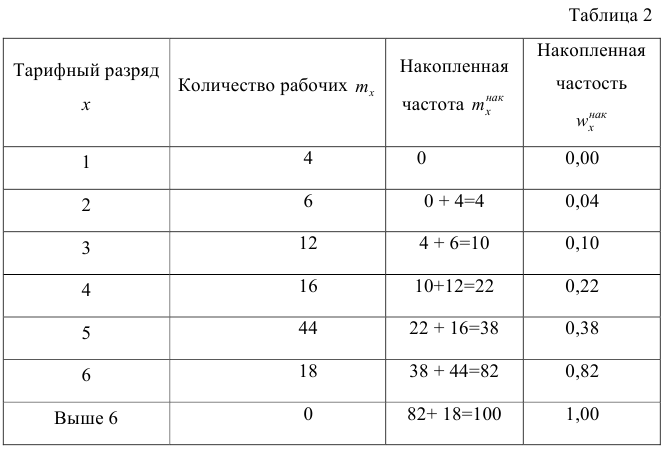
Исследователь, интересующийся тарифным разрядом рабочих механического цеха, в результате опроса 100 рабочих получил следующие сведения:
Здесь признаком является тарифный разряд, а полученные о нём сведения образуют статистические данные. Для изучения данных прежде всего необходимо их сгруппировать. Расположим наблюдавшиеся значения признака в порядке возрастания. Эта операция называется ранжированием статистических данных. В результате получим следующий ряд, который называется ранжированным:
(1, 1, 1, 1) – 4 раза; (2, 2, 2, 2, 2, 2) – 6 раз; (3, 3, …, 3) – 12 раз; (4, 4, …, 4) –
16 раз; (5, 5, …, 5) – 44 раза; (6, 6, …, 6) – 18 раз.
Из ранжированного ряда следует, что признак (тарифный разряд) принял шесть различных значений: первый, второй и т.д. до шестого разряда.
В дальнейшем различные значения признака условимся называть вариантами, а под варьированием — понимать изменение значений признака. Если признак по своей сущности таков, что различные его значения не могут отличаться друг от друга меньше чем на некоторую конечную величину, то говорят, что это дискретно варьирующий признак.
Тарифный разряд — дискретно варьирующий признак: его различные значения не могут отличаться друг от друга меньше, чем на единицу. В примере этот признак принял 6 различных значений — 6 вариантов: вариант 1 повторился 4 раза, вариант 2-6 раз и т.д. Число, показывающее. сколько раз встречается вариант л* в ряде наблюдений, называется частотой варианта 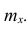
Вместо частоты варианта x можно рассматривать её отношение к общему числу наблюдений n, которое называется частостью варианта х и обозначается 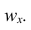
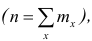
Таблица, позволяющая судить о распределении частот (или частостей) между вариантами, называется дискретным вариационным рядом.
В примере 1 была поставлена задача изучить результаты наблюдений. Если просмотр первичных данных не позволил составить представление о варьировании значений признака, то, рассматривая вариационный, ряд, можно сделать следующие выводы: тарифный разряд колеблется от 1-го до 6-го; наиболее часто встречается 5-й тарифный разряд; с ростом тарифного разряда (до 5-го разряда) растёт число рабочих, имеющих соответствующий разряд.
Наряду с понятием частоты используют понятие накопленной частоты, которую обозначают 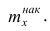
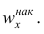
В дискретном вариационном ряду накопленные частоты (частости) вычисляются для каждого варианта и являются результатом последовательного суммирования частот (частостей). Накопленные частоты (частости) для вариационного ряда, заданного в табл. 1, вычислены в табл. 2.
Например, варианту 1 соответствует накопленная частота, равная нулю, так как среди опрошенных рабочих не было таких, у которых тарифный разряд был бы меньше 1-го; варианту 5 соответствует накопленная частота 38, так как было 4+6+12+16 рабочих с тарифным разрядом, меньшим 5-го, накопленная частость для этого варианта равна 0,38 (38: 100); если тарифный разряд выше 6-го, то ему соответствует накопленная частота 100, так как тарифный разряд всех опрошенных рабочих не выше 6-го.
Пример:
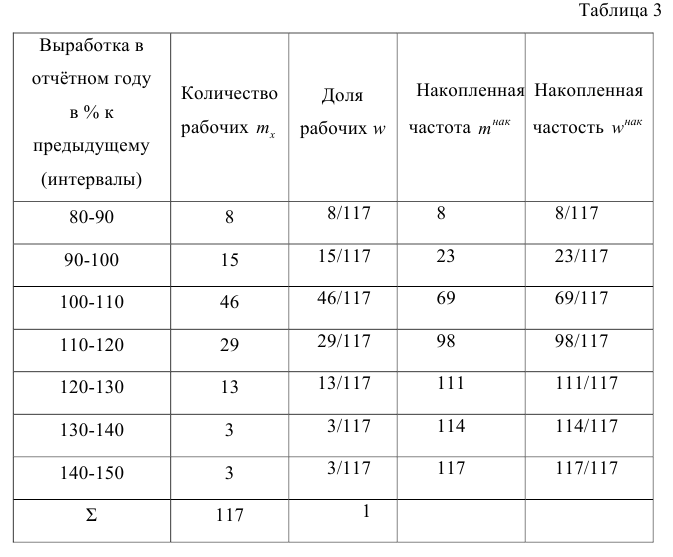
Исследователь, изучающий выработку на одного рабочего-станочника механического цеха в отчётном году в процентах к предыдущему году, получил следующие данные (в целых процентах) по 117 рабочим:
В этом примере признаком является выработка в отчётном году в процентах к предыдущему. Очевидно, что значения, принимаемые этим признаком, могут отличаться одно от другого на сколь угодно малую величину, т. е. признак может принять любое значение в некотором числовом интервале (только для упрощения дальнейших расчетов полученные данные округлены до целых процентов). Такой признак называют непрерывно варьирующим. По приведенным данным трудно выявить характерные черты варьирования значений признака. Построение дискретного вариационного ряда также не даст желаемых результатов (слишком велико число различных наблюдавшихся значений признака). Для получения ясной картины объединим в группы рабочих, у которых величина выработки колеблется, например, в пределах 10%. Сгруппированные данные представим в табл. 3.
В табл. 3 частоты m показывают, во скольких наблюдениях признак принял значения, принадлежащие тому или иному интервалу. Такую частоту называют интервальной, а отношение её к общему числу наблюдений — интервальной частостью w. Таблицу, позволяющую судить о распределении частот (или частостей) между интервалами варьирования значений признака, называют интервальным вариационным рядом.
Интервальный вариационный ряд, представленный в табл. 3, позволяет выявить закономерности распределения рабочих по интервалам выработки. В табл. 3 для верхних границ интервалов приведены накопленные частоты (частости) (они получены последовательным суммированием интервальных частот (частостей), начиная с частоты (частости) первого интервала). Например, для верхней границы третьего интервала, равной 110, накопленная частота равна 69; так как 8+15+46 рабочих имели выработку меньше 110%, накопленная частость равна 69/117.
Интервальный вариационный ряд строят по данным наблюдений за непрерывно варьирующим признаком, а также за дискретно варьирующим, если велико число наблюдавшихся вариантов. Дискретный вариационный ряд строят только для дискретно варьирующего признака.
Иногда интервальный вариационный ряд условно заменяют дискретным. Тогда серединное значение интервала принимают за вариант х, а соответствующую интервальную частоту — за
Построение интервального вариационного ряда
Для построения интервального вариационного ряда необходимо определить величину интервала, установить полную шкалу интервалов, в соответствии с ней сгруппировать результаты наблюдений. В примере 2 при выборе величины интервала учитывались требования наибольшего удобства отсчётов. Интервал был принят равным 10% и оказался удачным. Построенный интервальный ряд позволил выявить закономерности варьирования значений признака. Для определения оптимального интервала h, т.е. такого, при котором построенный интервальный ряд не был бы слишком громоздким и в то же время позволял выявить характерные черты рассматриваемого явления, можно использовать формулу Стэрджеса
где 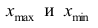
За начало первого интервала рекомендуется принимать величину
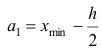
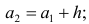
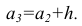
После установления шкалы интервалов следует сгруппировать результаты наблюдений. Границы последовательных интервалов записывают в столбец слева, а затем, просматривая статистические данные в том порядке, в каком они были получены, проставляют чёрточки справа от соответствующего интервала. В интервал включается данные, большие или равные нижней границе интервала и меньшие верхней границы. Целесообразно каждые пятое и шестое наблюдения отмечать диагональными черточками, пересекающими квадрат из четырёх предшествующих. Общее количество чёрточек, проставленных против какого-либо интервала, определяет его частоту.
Графическое изображение вариационных рядов
Графическое изображение вариационного ряда позволяет представить в наглядной форме закономерности варьирования значений признака. Наиболее широко используются следующие виды графического изображения вариационных рядов: полигон, гистограмма, кумулятивная
кривая.
Полигон, как правило, служит для изображения дискретного вариационного ряда. Для его построения в прямоугольной системе координат наносят точки с координатами 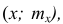
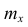
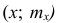
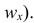
Гистограмма служит для изображения только интервального вариационного ряда. Для её построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, изображающие интервалы варьирования, и на этих отрезках, как на основании, строят прямоугольники с высотами, равными частотам (или частостям) соответствующего интервала. В результате получают ступенчатую фигуру, состоящую из прямоугольников, которую и называют гистограммой.
Если по оси абсцисс выбрать такой масштаб, чтобы ширина интервала была равна единице, и считать, что по оси ординат единица масштаба соответствует одному наблюдению, то площадь гистограммы равна общему числу наблюдений, если по оси ординат откладывались частоты, и эта площадь равна единице, если откладывались частости.
Иногда интервальный ряд изображают с помощью полигона. В этом случае интервалы заменяют их серединными значениями и к ним относят интервальные частоты. Для полученного дискретного ряда строят полигон.
Кумулятивная кривая (кривая накопленных частот или накопленных частостей) строится следующим образом. Если вариационный ряд дискретный, то в прямоугольной системе координат строят точки с координатами 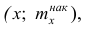
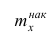
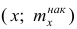
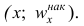
Если вариационный ряд интервальный, то по оси абсцисс откладывают интервалы. Верхним границам интервалов соответствуют накопленные частоты (или накопленные частости); нижней границе первого интервала — накопленная частота, равная нулю. Построив кумулятивную кривую, можно приблизительно установить число наблюдений (или их долю в общем количестве наблюдений), в которых признак принял значения, меньшие заданного.
Построение вариационного ряда — первый шаг к осмысливанию ряда наблюдений. Однако на практике этого недостаточно, особенно когда необходимо сравнить два ряда или более. Сравнению подлежат только так называемые однотипные вариационные ряды, т. е. ряды, которые построены по результатам обработки сходных статистических данных. Например, можно сравнивать распределения рабочих по возрасту на двух заводах или распределения времени простоев станков одного вида. Однотипные вариационные ряды обычно имеют похожую форму при графическом изображении, однако могут отличаться друг от друга, а именно: иметь различные значения признака, вокруг которых концентрируются наблюдения (меры этой качественной особенности называется средними величинами); различаться рассеянием наблюдений вокруг средних величин (меры этой особенности получили название показателей вариации).
Средние величины и показатели вариации позволяют судить о характерных особенностях вариационного ряда и называются статистическими характеристиками. К статистическим характеристикам относятся также показатели, характеризующие различия в скошенности полигонов и различия в их островершинности.
Средние величины
Средние величины являются как бы «представителями» всего ряда наблюдений, поскольку вокруг них концентрируются наблюдавшиеся значения признака. Заметим, что только для качественно однородных наблюдений имеет смысл вычислять средние величины.
Различают несколько видов средних величин: средняя арифметическая, средняя геометрическая, средняя гармоническая, средняя квадратическая, средняя кубическая и т.д. При выборе вида средней величины необходимо прежде всего ответить на вопрос: какое свойство ряда мы хотим представить средней величиной или, иначе говоря, какая цель преследуется при вычислении средней? Это свойство, получившее название определяющего, и определяет вид средней. Понятие определяющего свойства впервые введено советским статистиком А. Я. Боярским.
Наиболее распространенной средней величиной является средняя арифметическая. Пусть 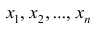
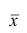
Так как 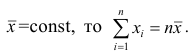
вычисления средней арифметической по данным наблюдений:
Если по наблюдениям построен вариационный ряд, то средняя арифметическая
где x- — вариант, если ряд дискретный, и центр интервала, если ряд интервальный;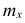
Частоты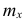
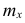
Очевидно, что если по данным наблюдений построен дискретный вариационный ряд, то формулы (3) и (4) дают одинаковые значения средней арифметической. Если же по наблюдениям построен интервальный ряд, то средние арифметические, вычисленные по формулам
(3) и (4), могут не совпадать, так как в формуле (4) значения признака внутри каждого интервала принимаются равными центрам интервалов. Ошибка, возникающая в результате такой замены, вообще говоря, очень мала, если наблюдения, распределены равномерно вдоль каждого интервала, а не скапливаются к одноименным границам интервалов (т.е. либо все к нижним границам, либо все к верхним границам).
Среднюю арифметическую для вариационного ряда можно вычислять по формуле
которая является следствием формулы (4). Действительно,
Свойство, определяющее среднюю арифметическую, сводилось к требованию неизменности суммы наблюдений при замене каждого из них средней арифметической. При решении практических задач может оказаться необходимым вычислить такую среднюю 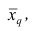
где q — положительное или отрицательное число. Среднюю 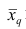
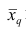
Сравнивая формулы (7) и (3), можно сделать вывод, что степенная средняя первого порядка есть не что иное, как средняя арифметическая, т.е.
При q=-l из формулы (7) получаем выражение для средней гармонической, при q=2 — для среднеквадратической, при q=3 — для средней кубической и т.д.
Средней геометрической 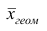
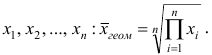
Рассмотрим основные свойства средней арифметической.
1°. Сумма отклонений результатов наблюдений от средней арифметической равна нулю.
Доказательство. Исходя из определяющего свойства (2) средней арифметической, получаем
Если по результатам наблюдений построен вариационный ряд и средняя арифметическая взвешенная, то свойство 1° формулируется так: сумма произведений отклонений вариантов от средней арифметической на соответствующие частоты равна нулю. Действительно, на основании формулы (4) получаем
или
2°. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число, то средняя арифметическая уменьшится (увеличится) на то же число. (Доказательство свойств 2° и 3° проведём в предположении, что по результатам наблюдений построен вариационный ряд и средняя арифметическая — взвешенная).
Доказательство. Очевидно, что при уменьшении вариантов на одно и то же число с соответствующие им частоты останутся прежними. Поэтому взвешенная средняя арифметическая для изменённого вариационного ряда такова:
Аналогично можно показать, что 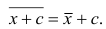
3°. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число раз, то средняя арифметическая уменьшится (увеличится) во столько же раз.
Доказательство. Очевидно, что при уменьшении вариантов в k раз их частоты останутся прежними. Поэтому средняя арифметическая для изменённого ряда
Аналогично можно доказать, что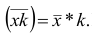
(уменьшить) в k раз, то получим среднюю арифметическую для первоначального вариационного ряда.
4°. Если ряд наблюдений состоит из двух групп наблюдений, то средняя арифметическая всего ряда равна взвешенной средней арифметической групповых средних, причём весами являются объёмы групп.
Пусть 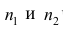
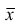
средняя арифметическая для всего ряда 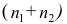
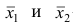
Доказательство. Исходя из определяющего свойству средней арифметической, имеем: произведение 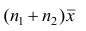
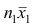
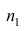
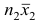
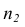
Следовательно,
Следствие. Если ряд наблюдений состоит из k групп наблюдений, то средняя арифметическая всего ряда 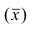
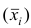
5°. Средняя арифметическая для сумм (разностей) взаимно соответствующих значений признака двух рядов наблюдений с одинаковым числом наблюдений равна сумме (разности) средних арифметических этих рядов.
Пусть 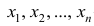
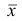
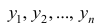
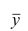
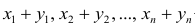
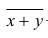
Доказательство. Имеем
Аналогично можно показать, что
Следствие. Средняя арифметическая алгебраической суммы соответствующих значений признака нескольких рядов наблюдений с одинаковым числом наблюдений равна алгебраической сумме средних арифметических этих рядов.
Вычисление средней арифметической вариационного ряда непосредственно по формуле (4) приводит к громоздким расчётам, если числовые значения вариантов и соответствующие им частоты велики. Поэтому часто используют следующий способ, основанный на свойствах 3° и 2° средней арифметической: среднюю вычисляют не по первоначальным вариантам л-, а по уменьшенным на не которое число с, а затем разделённым на некоторое число k т.е. для вариантов 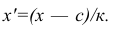
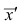
Действительно, принимая во внимание свойства 3° и 2° средней арифметической, получаем
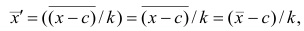
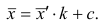
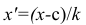
Медиана и мода
Наряду со средними величинами в качестве описательных характеристик вариационного ряда применяют медиану и моду.
Медианой 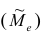
Пусть проведено нечётное число наблюдений, т.е. n=2q—1, и результаты наблюдений проранжированы и выписаны в следующий ряд:
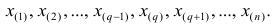
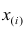
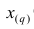
Если проведено чётное число наблюдений, т.е. n=2q, то на середину ранжированного ряда 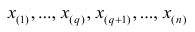
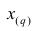
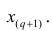
, т.е.
Покажем на примерах на практическом занятии, как определяется медиана дискретного и интервального вариационных рядов.
В общем случае медиана для интервального вариационного ряда определяется по формуле
или по следующей формуле, полученной из формулы (9) в результате деления числителя и знаменателя входящей в неё дроби на n:
где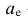
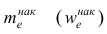
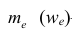
Модой 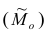
В случае интервального вариационного ряда мода вычисляется по следующей формуле (вывод формулы можно найти в кн.: Венецкий И. Г Кильдишев Г. С. Теория вероятностей и математическая статистика. М., 1975.):
или по тождественной формуле:
где 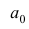
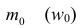
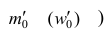
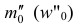
Моду используют в случаях, когда нужно ответить на вопрос, какой товар имеет наибольший спрос, каковы преобладающие в данный момент уровни производительности труда, себестоимости и т. д. Модальная производительность, себестоимость и т.д. помогают вскрыть ресурсы, имеющиеся в экономике.
Показатели вариации
Средние величины, характеризуя вариационный ряд числом, не отражают изменчивости наблюдавшихся значений признака, т.е. вариацию. Простейшим показателем вариации является вариационный размах 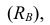
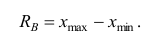
Вариационный размах — приближённый показатель вариации, так как почти не зависит от изменения вариантов, а крайние варианты, которые используются для его вычисления, как правило, ненадёжны.
Более содержательными являются меры рассеяния наблюдений вокруг средних величин. Средняя арифметическая является основным видом средних, поэтому ограничимся рассмотрением мер рассеяния наблюдений вокруг средней арифметической.
Сумма отклонений результатов наблюдений 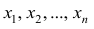
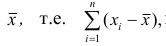
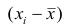
Средним линейным отклонением (d) называют среднюю арифметическую абсолютных величин отклонений результатов наблюдений от их средней ар и ф метической:
Эмпирической дисперсией 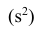
Если по результатам наблюдений построен вариационный ряд, то эмпирическая дисперсия
Вместо эмпирической дисперсии в качестве меры рассеяния наблюдений вокруг средней арифметической часто используют эмпирическое среднеквадратическое отклонение, равное арифметическому значению корня квадратного из дисперсии и имеющее ту же размерность, что и значения признака.
где x — вариант (если ряд дискретный) и центр интервала (если ряд интервальный); 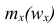
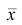
Для краткости величину 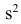
Приведем свойство минимальности эмпирической дисперсии: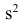
если
Доказательство. Найдём экстремум функции 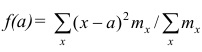
этого решим уравнение 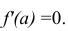
Так как 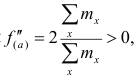
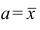
Можно показать, что среднее линейное отклонение не обладает свойством минимальности. Поэтому наиболее употребительными мерами рассеяния
Для вариационного ряда среднеквадратическое отклонение наблюдений вокруг средней арифметической являются эмпирическая дисперсия и эмпирическое среднеквадратическое отклонение.
Итальянский статистик Коррадо Джинни предложил в качестве показателя вариации использовать величину 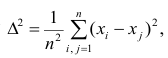
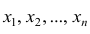
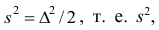
Свойства эмпирической дисперсии
Рассмотрим основные свойства эмпирической дисперсии, знание которых позволит упростить её вычисление.
1 °. Дисперсия постоянной величины равна нулю.
Доказательство этого свойства очевидно вытекает из того, что дисперсия является показателем рассеяния наблюдений вокруг средней арифметической, а средняя арифметическая постоянной равна этой постоянной.
2°. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число с, то дисперсия не изменится.
Доказательство свойств 2° и 3° проведём в предположении, что по результатам наблюдений построен вариационный ряд.
Доказательство. Если все варианты уменьшить на число с, то в соответствии со свойством 2° средней арифметической средняя для измененного вариационного ряда равна 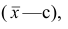
,т.е. совпадает с дисперсией первоначального вариационного ряда. Аналогично можно показать, что
Доказанное свойство позволяет вычислять дисперсию не по данным вариантам, а по уменьшенным, (увеличенным) на одно и то же число с, так как дисперсия, вычисленная для измененного ряда, равна первоначальной.
3°. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число k раз, то дисперсия уменьшится (увеличится) в 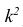
Доказательство. Если все варианты уменьшить в k раз, то, согласно свойству 3 средней арифметической, средняя для измененного вариационного ряда равна 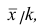
Аналогично можно показать, что
Это свойство позволяет эмпирическую дисперсию вычислять не по данным вариантам, а по уменьшенным (увеличенным) в одно и то же число k раз. Если дисперсию, вычисленную для измененного ряда, увеличить (уменьшить) в 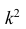
Следствие. Если все варианты уменьшить (увеличить) в k раз, то среднеквадратическое отклонение уменьшится (увеличится) в число раз, равное k.
Следствие очевидно вытекает из определения среднеквадратического
отклонения.
Прежде чем рассматривать следующее свойство дисперсии, докажем теорему.
Теорема. Эмпирическая дисперсия равна разности между средней
арифметической квадратов наблюдений и квадратом средней
арифметической, т.е.
Доказательство проведём для случая взвешенных средних арифметических, т.е.
Доказательство. Тождественно преобразуя выражения для дисперсии, имеем
4°, Если ряд наблюдений состоит из двух групп наблюдений, то дисперсия всего ряда равна сумме средней арифметической групповых дисперсий и средней арифметической квадратов отклонений групповых средних от средней всего ряда, причем ‘ при вычислении средних арифметических весами являются объемы групп.
Пусть 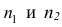
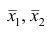
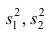
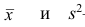
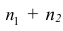
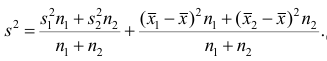
Пусть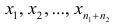
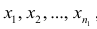
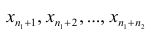
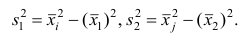
В соответствии со свойством 4° средней арифметической можно записать 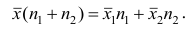
Используя найденные выражения для слагаемых, получаем
Свойство 4° можно обобщить на случай, когда ряд наблюдений состоит из любого количества 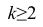
Если ряд наблюдений состоит из k групп наблюдений, то межгрупповой дисперсией 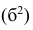
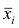
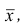
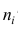
Средней групповых дисперсий или внутригрупповой дисперсией 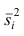
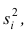
Следствие (свойства 4°). Если ряд наблюдений состоит из k групп наблюдений, то дисперсия всего ряда s2 равна сумме внутригрупповой и межгрупповой дисперсий, т.е.
Вычисление дисперсии вариационного ряда непосредственно по формуле (16) приводит к громоздким расчётам, если числовые значения вариантов и соответствующие им частоты велики. Поэтому часто дисперсию вычисляют не по первоначальным вариантам х, а по вариантам 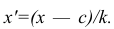
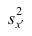
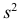
Действительно, принимая во внимание свойства 3° и 2° дисперсии, получаем
откуда следует, что
Требования к с и k предъявляют те же, что и в упрощенном способе вычисления средней арифметической.
Эмпирические центральные и начальные моменты
Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия о моментах вариационного ряда.
Эмпирическим начальным моментом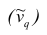
Эмпирический начальный момент нулевого порядка
Эмпирический начальный момент первого порядка
Эмпирический начальный момент второго порядка 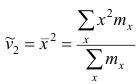
Эмпирическим центральным моментом 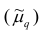
Эмпирический центральный момент нулевого порядка
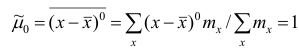
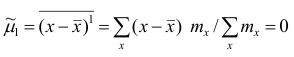
Эмпирический центральный момент второго порядка
В дальнейшем для краткости величину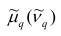
Используя формулу бинома Ньютона, разложим в ряд выражение для центрального момента q-го порядка:
В проведенных тождественных преобразованиях использованы свойства 5° и 3° средней арифметической; 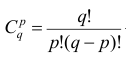
Итак, центральный момент q-го порядка выражается через начальные моменты следующим образом:
Полагая q = 0, 1, 2,…, можно получить выражения центральных моментов различных порядков через начальные моменты:
и т.д.
Заметим, что формула (23) для центрального момента второго порядка, как и следовало ожидать, аналогична формуле (18) для дисперсии.
Рассмотрим свойства центральных моментов, которые позволят значительно упростить их вычисление.
1°. Если все варианты уменьшить (увеличить) на одно и то же число с, то центральный момент q-го порядка не изменится.
Доказательство. Если все варианты уменьшить на число с, то средняя арифметическая для измененного ряда равна 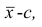
Аналогично можно показать, что
2°. Если все варианты уменьшить (увеличить) в одно и то же число k раз, то центральный момент q-го порядка уменьшится (увеличится) в 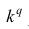
то средняя арифметическая для измененного вариационного ряда равна
поэтому центральный момент q-го порядка
Аналогично можно показать, что
Для облегчения расчётов центральные моменты вычисляют не по первоначальным вариантам х, а по вариантам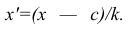
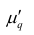
внимание свойства центрального момента, получаем
откуда следует, что
Эмпирические асимметрия и эксцесс
Эмпирическим коэффициентом асимметрии 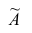
Если полигон вариационного ряда скошен, т.е. одна из его ветвей, начиная от вершины, зримо длиннее другой, то такой ряд называют асимметричным. Из формулы (27) следует, что если в вариационном ряду преобладают варианты, меньшие 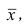
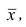
Эмпирическим эксцессом или коэффициентом крутости 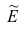
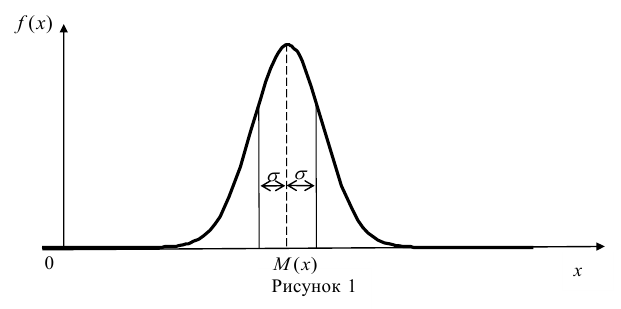
За стандартное значение эксцесса принимают нуль-эксцесс так называемой нормальной кривой (см. рис. 1).
Кривые, у которых эксцесс отрицательный, по сравнению с нормальной менее крутые, имеют, более плоскую вершину и называются «плосковершинными» Кривые с положительным эксцессом более крутые по сравнению с нормальной кривой, имеют более острую вершину и называются «островершинными».
Интервальные оценки параметров распределений
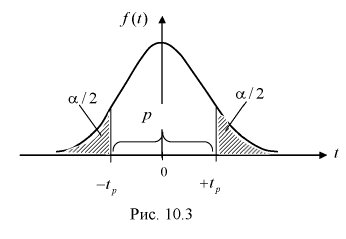
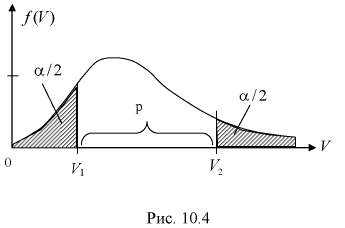
Доверительный интервал, доверительная вероятность:
Точечная оценка неизвестного параметра 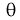
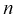
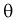
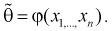
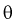
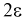
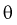
Чем меньше разность 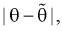
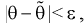
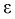
Доверительной вероятностью оценки называется вероятность 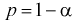
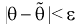
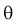
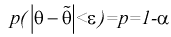
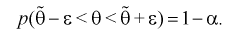
Из (10.1) видно, что неизвестный параметр 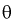
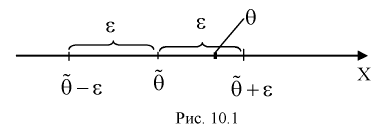
Доверительным интервалом называется интервал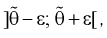
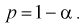
Длина его (см. рис. 10.1) 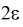
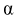
Доверительный интервал для математического ожидания случайной величины X при известной дисперсии
Доверительный интервал для математического ожидания случайной величины X при известной дисперсии (или 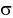
Пусть эксперимент Е описывается нормальной случайной величиной X.
Плотность распределения 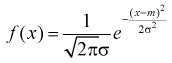
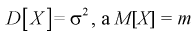
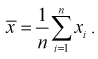
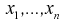
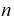
откуда получим
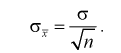
Для определения доверительного интервала рассмотрим разность между оценкой и параметром: 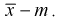
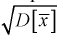
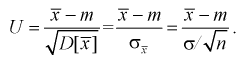
Покажем, что случайная величина U имеет нормированный нормальный закон распределения. Найдем ее числовые характеристики:
Таким образом 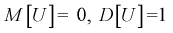
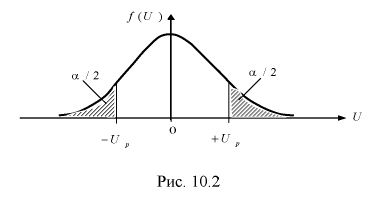
Зная плотность распределения случайной величины U, легко найти вероятность попадания случайной величины U в интервал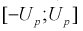
Левая часть этого уравнения представляет собой доверительную вероятность
Тогда из (10.4) и (10.5) следует уравнение
Решая уравнение (10.6), по таблицам функции Лапласа для заданной доверительной вероятности 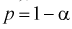
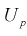
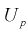
Считая, что 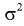
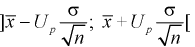
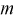
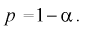
Замечания по формуле (10.8):
- при увеличении объема выборки
из (10.8) видим, что е уменьшается, значит, уменьшается длина доверительного интервала, а точность оценки увеличивается;
- увеличение доверительной вероятности
приводит к увеличению длины доверительного интервала (см. рис. 10.2, где квантили
увеличиваются), т. е. е увеличивается, а точность оценки падает;
- если задать точность е и доверительную вероятность
, то можно найти объем выборки, который обеспечит заданную точность:
Пример №1
Сколько конденсаторов одного номинала надо измерить, чтобы с вероятностью 0,95 можно было утверждать, что мы с точностью 1 % определили их среднее значение – математическое ожидание.
Обозначим 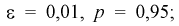
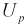
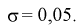
Доверительный интервал для математического ожидания нормальной случайной величины X при НЕизвестной дисперсии
Доверительный интервал для математического ожидания нормальной случайной величины X при неизвестной дисперсии или
Пусть эксперимент описывается случайной величиной X с нормальным распределением с неизвестными параметрами 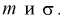
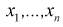
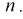
Здесь использовали для оценки дисперсии 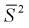
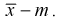
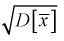
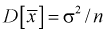
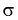
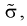
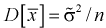
Умножим числитель и знаменатель в (10.10) на
Здесь X – нормированная нормальная случайная величина, знаменатель – распределение 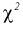
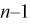
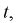
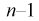
Зная закон распределения случайной величины t и задавая доверительную вероятность 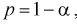
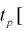
Из таблиц распределений Стьюдента по заданной доверительной вероятности 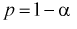
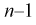
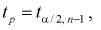
Подставляя в (10.13) вместо t равенство (10.10), получаем
Разрешим неравенство в левой части формулы (10.14) относительно
Отсюда непосредственно следует, что доверительный интервал 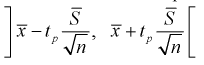
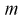
Интервал (10.15) несколько шире интервала (10.7), определенного для той же выборки и той же доверительной вероятности. Зато в (10.15) используется меньшая априорная информация – 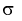
Можно обозначить ширину доверительного интервала или точность через 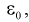
Все замечания, сделанные по формуле (10.8), справедливы и для формулы (10.16).
Пример №2
Даны результаты четырех измерений напряжения сети (значения приведены в
Считаем, что X – напряжение сети – является нормальной случайной величиной. Построить доверительный интервал с вероятностью 0,95 для истинного напряжения сети –
Найдем точечную оценку
Из таблиц распределения Стьюдента для 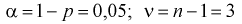
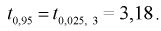
Тогда
Полученные значения подставим в формулу (10.16):
Найдем левую и правую границы доверительного интервала для
Таким образом, истинное напряжение сети с вероятностью 0,95 накрывается доверительным интервалом
Найдем минимальное число измерений, чтобы с вероятностью 0,95 точ ность определения истинного напряжения сети не превышала 0,5 В, т. е. 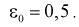
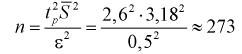
Видим, что число измерений 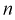
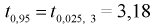
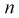
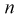
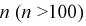
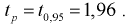
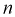
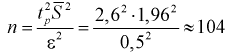
Доверительный интервал для дисперсии или ст нормальной случайной величины X
Рассмотрим вероятностный эксперимент с нормальной моделью, где параметры 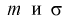
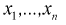
Составим вспомогательную случайную величину
Эта случайная величина имеет распределение 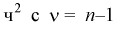
Это и есть распределение хи-квадрат с 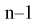
Зная закон распределения случайной величины У, определим вероятность того, что случайная величина 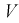
Здесь 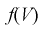
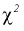
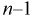
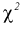
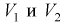
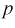
Это означает, что площади заштрихованных фигур равны. Задавая доверительную вероятность 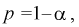
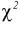
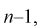
Считая 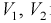
Подставим в (10.20) значение 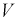
Решаем неравенство в левой части (10.21) относительно
Из (10.22) записываем доверительный интервал для
Для среднего квадратического отклонения 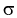
Можно ввести коэффициенты
Тогда доверительный интервал для о определится следующим образом:
Коэффициенты 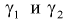
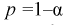
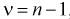
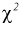
Пример №3
В предыдущем разделе (10.3) приведен пример для измеренных значений напряжения сети. Продолжим и найдем доверительный интервал для среднего квадратического отклонения 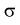
Найдена точечная оценка для 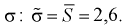
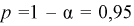
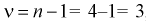
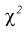
Тогда нижняя граница для
Верхняя граница для
И окончательно:
Пример №4
Случайная величина 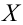
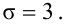
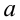
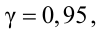
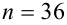
Решение. Определим значение 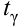
Точность оценки
Подставим в неравенство (4.1):
Смысл полученного результата: если произведено достаточно большое число выборок по 36 в каждой, то 95 % из них определяют такие доверительные
интервалы, в которых 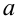
Пример №5
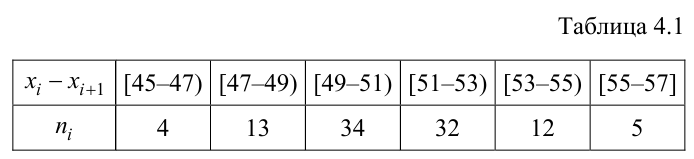
Для исследования нормального распределения 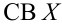
Найти с надежностью 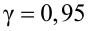
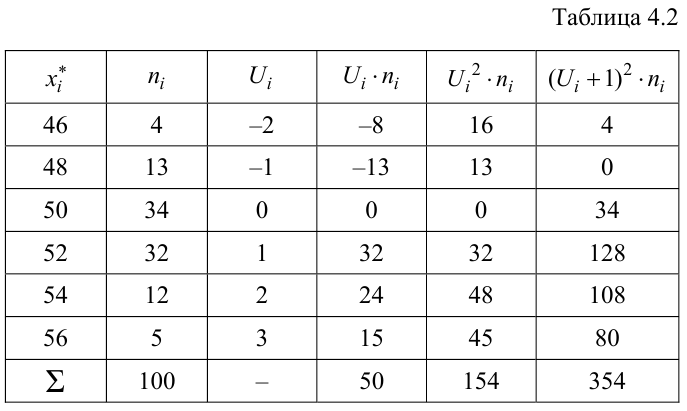
Решение. Найдем несмещенные оценки для математического ожидания и дисперсии, используя метод произведений (табл. 4.2).
Контроль:
По табл. П3 по данным 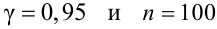
Для определения доверительного интервала для математического ожидания используем неравенство (4.2):
Таким образом, интервал (50, 547; 51, 453) накрывает точку 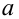
Для определения доверительного интервала для среднего квадратического отклонения используем неравенство (4.3). По табл. П4 по заданным 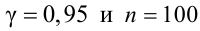
С вероятностью 0,95 неизвестное значение 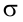
- Алгебра событий – определение и вычисление
- Свойства вероятности
- Многомерные случайные величины
- Случайные события – определение и вычисление
- Основные законы распределения дискретных случайных величин
- Непрерывные случайные величины
- Закон больших чисел
- Генеральная и выборочная совокупности
Построение вариационного ряда
На практике
вариационный ряд представляет собой
неубывающую последовательность вариантов
(x(1),…,x(n))
–
последовательность элементов выборки
измерений, расположенных в порядке
неубывания.
Первый элемент
выборки x(1)
называется
минимальным и обозначать его xmin,
последний элемент выборки x(n)
будем
называть максимальным и обозначать
xmax.
Разность между максимальным и минимальным
элементами выборки xmax
– xmin
называют
размахом выборки и обозначают r.
Построение статистических оценок математического ожидания и дисперсии.
Статистические
оценки основных числовых характеристик
случайных величин (математического
ожидания и дисперсии) подразделяются
на два вида: точечные и интервальные.
Напомним определения
математического ожидания и дисперсии
для дискретных случайных величин.
Математическим
ожиданиемдискретной случайной
величиныM[X]
называется сумма произведений всех
возможных значений случайной величинына вероятности
этих значений:
M[X]
=
Другое обозначение
математического ожидания случайной
величины – m.
Дисперсией
случайной величины называется
математическое ожидание квадрата
соответствующей центрированной случайной
величины:
D[X]
=M[(X-m)]
Согласно этому
определению, дисперсия дискретной
случайной величины может быть найдена
по формуле:
D[X] =
p
.
Рассмотрим
построение точечных оценок математического
ожидания и дисперсии.
Построение точечных оценок
Математическим
ожиданиемслучайной величиныM[X]
называется сумма произведений всех
возможных значений случайной величинына вероятности
этих значений:
M[X]
=
Дисперсией
случайной величины называется
математическое ожидание квадрата
соответствующей центрированной случайной
величины:
D[X] =
M[(X-m)]
=p
.
Дисперсия
характеризует рассеяние значений
случайной величины около ее математического
ожидания (среднего значения).
Реализация точечной
оценки математического ожидания
называется выборочным средним и
определяется по формуле:
.
Для дисперсии
реализацией точечной оценки служит
выборочная дисперсия
=
и исправленная
выборочная дисперсия
,
которая
является несмещенной и состоятельной
точечной оценкой дисперсии.
Построение интервальных оценок
Интервальной
называют оценку, которая определяется
как интервал с двумя концами (в общем
случае случайными), накрывающий
оцениваемый параметр.
Доверительным
называется интервал со случайными
концами, который с доверительной
вероятностью (надежностью) βсодержит
(или накрывает) неизвестный оцениваемый
параметр. Поскольку концы интервала
представляют собой случайные величины,
то их называютдоверительными границами.
Интервальная оценка математического ожидания случайной величины
Интервальной
оценкой математического ожидания СВ
называется случайный интервал вида:
.
Границы доверительного
интервала для
:
=
=
Реализация
доверительного интервала для
математического ожидания имеет вид:
Для нахождения
интервальной оценки математического
ожидания необходимо вычислить реализацию
точечной оценки среднего квадратического
отклонения (реализацию стандартного
отклонения):
.
Из таблиц
распределения Стьюдента по значениям
n
и
находим значение t,
как решение уравнения:
-вероятность
практически достоверного события
-граница практически
достоверных значений дроби Стьюдента
Tn-1
Интервальная
оценка дисперсии случайной величины
Интервальной
оценкой дисперсии служит интервал ID
= (1,
2),
где
1
= (nx)/t1
, 2
= (nx)/t2,
t1,
t2
находят из таблиц 2
–распределения
по входам
1,
2 и (n-1).
Вероятности
1 и
2 вычисляют
по формулам:
1=(1+)/2,
2=(1-)/2.
Здесь
– доверительная вероятность,
= 1–.
Таким
образом, интервальная оценка дисперсии
– это случайный интервал вида:
(
,
).
Реализация
интервальной оценки дисперсии – это
интервал
(
,
).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В статистике имеются два подхода к оцениванию неизвестных параметров распределений: точечный и интервальный. В соответствии с точечным оцениванием, которое рассмотрено в предыдущем разделе, указывается лишь точка, около которой находится оцениваемый параметр. Желательно, однако, знать, как далеко может отстоять в действительности этот параметр от возможных реализаций оценок в разных сериях наблюдений.
Ответ на этот вопрос – тоже приближенный – дает другой способ оценивания параметров – интервальный. В соответствии с этим способом оценивания находят интервал, который с вероятностью, близкой к единице, накрывает неизвестное числовое значение параметра.
Понятие интервальной оценки
Точечная оценка является случайной величиной и для возможных реализаций выборки принимает значения лишь приближенно равные истинному значению параметра
. Чем меньше разность
, тем точнее оценка. Таким образом, положительное число
, для которого
, характеризует точность оценки и называется Ошибкой оценки (или предельной ошибкой).
Доверительной вероятностью (или надежностью) называется вероятность β, с которой осуществляется неравенство , т. е.
. (3.20)
Заменив неравенство равносильным ему двойным неравенством
, или
, получим
. (3.21)
Интервал 
, неизвестный параметр
, называется Доверительным интервалом (или интервальной оценкой), соответствующим доверительной вероятности β.
Случайной величиной является не только оценка , но и ошибка
: ее значение зависит от вероятности β и, как правило, от выборки. Поэтому доверительный интервал случаен и выражение (3.21) следует читать так: “Интервал
накроет параметр
с вероятностью β ”, а не так: “Параметр
попадет в интервал
с вероятностью β ”.
Смысл доверительного интервала состоит в том, что при многократном повторении выборки объема в относительной доле случаев, равной β, доверительный интервал, соответствующий доверительной вероятности β, накрывает истинное значение оцениваемого параметра. Таким образом, доверительная вероятность β характеризует Надежность доверительного оценивания: чем больше β, тем вероятнее, что реализация доверительного интервала содержит неизвестный параметр.
Следует, однако, иметь в виду, что с ростом доверительной вероятности β в среднем растет длина доверительного интервала, то есть уменьшается точность доверительного оценивания. Выбор доверительной вероятности определяется конкретными условиями; обычно используются значения β, равные 0,90; 0,95; 0,99.
Вероятность (3.22)
называется Уровнем значимости и характеризует относительное число ошибочных заключений в общем числе заключений.
В формуле (3.21) границы доверительного интервала симметричны относительно точечной оценки. Однако не всегда удается построить интервал, обладающий таким свойством. Более общим является следующее определение.
Доверительным интервалом (или Интервальной оценкой) параметра с доверительной вероятностью β, 0< β <1, называется интервал со случайными границами
,
, накрывающий с вероятностью β неизвестный параметр
, т. е.
. (3.23)
Иногда вместо двусторонних доверительных интервалов рассматривают односторонние доверительные интервалы, полагая или
.
Построение интервальных оценок
Доверительный интервал задается своими концами и
. Однако найти функции
и
из условия (3.23) невозможно, поскольку закон распределения этих функций зависит от закона распределения ξ и, следовательно, зависит от неизвестного параметра
. Используют следующий прием, позволяющий в ряде случаев построить доверительный интервал. Подбирается такая функция
, чтобы:
– ее закон распределения был известен и не зависел от неизвестного параметра ;
– функция Была непрерывной и строго монотонной по
.
Тогда для любого β можно выбрать два числа и
так, чтобы выполнялось равенство

Отсюда находят и
как квантили функции распределения
. Границы искомого доверительного интервала выражают через найденные квантили и выборочные данные, используя для этого соотношения, связывающие новую и старую случайные величины.
Если плотность распределения случайной величины Симметрична, то доверительный интервал симметричен относительно точечной оценки
, и для нахождения границ доверительного интервала вместо условия (3.23) можно использовать соотношение (3.21).
Основные статистические распределения
Построение разного рода оценок и статистических критериев часто основывается на использовании ряда специальных распределений случайных величин.
Нормальное распределение. Случайная величина имеет нормальное распределение с параметрами
и
, что обозначается как


График плотности вероятности случайной величины, имеющей нормальное распределение, представлен на рисунке 3.5, на котором видно, что максимум функции находится в точке .
Поскольку нормальное распределение подробно изучается в курсе теории вероятностей, напомним свойства нормальной случайной величины, которые будут использоваться в дальнейшем.
Рис. 3.5
1) ,
.
2) Случайная величина называется Центрированной, если ее математическое ожидание равно нулю. Для того чтобы центрировать случайную величину, надо вычесть из нее математическое ожидание:
.
3) Случайная величина называется Нормированной, если ее дисперсия равна единице, а математическое ожидание равно нулю.
Для того чтобы нормировать случайную величину, надо ее поделить на среднее квадратическое отклонение:

Центрированная и нормированная нормальная случайная величина называется стандартной. Таким образом, стандартной будет случайная величина

. (3.26)
Вероятность попадания случайной величины в интервал (α,β) вычисляется по формуле

Где 
Для стандартной нормальной случайной величины и симметричного промежутка формула (3.27) принимает следующий вид:
. (3.28)
Распределение (хи-квадрат). Если
,
независимые стандартные нормальные случайные величины, то говорят, что случайная величина

Имеет распределение хи-квадрат с степенями свободы, что обозначается как
. Графики плотности вероятности для двух значений степени свободы приведены на рис.3.6.
Рис. 3.6
С увеличением числа степеней свободы плотность вероятности стремится к нормальной. При
плотность вероятности постоянно убывает, а при
имеет единственный максимум
,
,
.
Распределение Стьюдента. Пусть ,
,
,
– независимые стандартные нормальные случайные величины. Тогда случайная величина

Имеет распределение Стьюдента с степенями свободы, что обозначается как
, при этом
,

На рис.3.7 приведены кривые стандартного нормального распределения (кривая 1) и плотности распределения Стьюдента (кривая 2).
Рис. 3.7
При плотность распределения Стьюдента стремится к плотности стандартной нормальной случайной величины.
На практике, как правило, используется не плотность вероятности, а Квантиль Распределения. Напомним, что квантилью порядка (или уровня) непрерывной случайной величины
называется такое ее значение
, которое удовлетворяет равенству
,
Где – функция распределения, а
– заданное значение вероятности. Рис.3.8 поясняет понятие квантили порядка
.
Рис. 3.8
Следующая теорема устанавливает свойства основных выборочных характеристик, вычисленных по выборке, соответствующих нормальному распределению.
Теорема Фишера. Пусть – случайная выборка из генеральной совокупности



1) случайная величина имеет распределение
;
2) случайная величина имеет распределение
;
3) случайная величина имеет распределение
.
Доказательство теоремы приведено в [2].
Интервальные оценки математического ожидания нормального распределения
Интервальная оценка математического ожидания при известной дисперсии. Построим доверительный интервал для математического ожидания наблюдаемой случайной величины при известной дисперсии
по выборке
.
Образуем вспомогательную случайную величину 

. Согласно утверждению 1 теоремы Фишера, случайная величина
имеет нормальное распределение

не зависит от неизвестного параметра.
Доверительный интервал, соответствующий надежности β, определяется из условия (3.20), которое в нашем случае имеет вид
. (3.31)
Неравенства и

они выполняются или не выполняются одновременно, поэтому соотношение (3.31) можно записать в виде

Поскольку случайная величина имеет стандартное нормальное распределение, вероятность в левой части формулы (3.32) можно выразить через нормальную стандартную функцию распределения по формуле (3.7):

Приравняв правую часть формулы (3.33) заданной доверительной вероятности β, получим уравнение 
является квантилью порядка

вычисляется по формуле


Интервальная оценка математического ожидания при неизвестной дисперсии. По выборке из нормального распределения
требуется построить доверительный интервал для неизвестного математического ожидания
при неизвестной дисперсии D=σ2.
Введем новую случайную величину 
– несмещенная выборочная дисперсия.
Статистика согласно утверждению 3 теоремы Фишера имеет распределение Стьюдента с
степенями свободы. Рассуждая аналогично случаю, когда дисперсия известна, получим следующий доверительный интервал для математического ожидания:

Где – квантиль порядка

. Поскольку с увеличением числа степеней свободы распределение Стьюдента быстро приближается к нормальному, то для больших выборок
интервалы (3.34) и (3.35) практически совпадают.
Пример 3.2. По результатам 9 измерений напряжения батареи получено среднее арифметическое значение 30,6В. Точность вольтметра характеризуется средним квадратическим отклонением 0,2В. Требуется найти доверительный интервал для истинного значения напряжения батареи, соответствующий доверительной вероятности β=0,95, предполагая, что контролируемый признак имеет нормальный закон распределения.
Решение. Для нахождения доверительного интервала воспользуемся формулой (3.34). Квантиль порядка 

Поскольку предельная ошибка


Интервальная оценка дисперсии нормального распределения
Построим доверительный интервал для дисперсии D=σ2 наблюдаемой случайной величины ~
по случайной выборке
при неизвестном математическом ожидании.
Введем случайную величину (статистику) 
Которая согласно утверждению 2 теоремы Фишера имеет распределение с
степенями свободы. Поскольку плотность распределения этого закона асимметрична, доверительный интервал, соответствующий надежности β, найдем из формулы (3.31) в виде:
. (3.37)
Обычно доверительный интервал для случайной величины
выбирают так, чтобы вероятность ее попадания за пределы этого интервала влево и вправо была одинаковой ( рис. 3.9):

Тогда условия для определения значений и
будут иметь вид:


По таблице квантилей – распределения ( табл. С Приложения) найдем


Рис. 3.9.
Неравенства 


Следовательно, интервал

Является доверительным интервалом дисперсии, соответствующим доверительной вероятности β.
Пример 3.3. По данным выборочного контроля найти выборочное математическое ожидание и несмещенную оценку дисперсии нормальной случайной величины ξ. Найти доверительные интервалы для них, соответствующие доверительной вероятности β=0,98.
Таблица 3.4
|
|
42 |
43 |
45 |
46 |
48 |
51 |
52 |
54 |
|
|
1 |
2 |
3 |
6 |
4 |
3 |
1 |
1 |
Решение. Выборочное математическое ожидание найдем по формуле (3.14), используя табл.3.4
При

Несмещенную выборочную дисперсию вычислим по формуле (3.19):

.
Доверительный интервал для математического ожидания определим по формуле (3.35). При из таблицы А Приложения находим квантиль распределения Стьюдента

,
Получим искомый доверительный интервал для математического ожидания:
.
Границы доверительного интервала для дисперсии определим по формуле (3.20). По таблице квантилей распределения χ2 (см. табл. С Приложения) при определим квантили:


Подставив эти значения, а также и
в формулу (3.20), получим искомый доверительный интервал для дисперсии

Вопросы для самопроверки
2. Что называется выборкой?
3. Как произвести оценку выборочного математического ожидания и выборочной дисперсии?
4. Как найти функцию распределения для дискретной случайной величины?
5. Что такое несмещенная оценка параметра?
6. Дайте определение состоятельной оценки.
7. Что такое интервальная оценка?
| < Предыдущая | Следующая > |
|---|
Интервальный вариационный ряд и его характеристики
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Общий вид интервального вариационного ряда
| Интервалы, (left.left[a_{i-1},a_iright.right)) | (left.left[a_{0},a_1right.right)) | (left.left[a_{1},a_2right.right)) | … | (left.left[a_{k-1},a_kright.right)) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k – число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).
Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg 100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала (left.left[a_{i-1},a_iright.right)) – это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) – середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
| (f_i) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| (S_i) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:
Построим кумуляту и эмпирическую функцию распределения:
Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$
п.3. Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) – соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).
Например:
Для распределения учеников по росту получаем:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
Для распределения учеников по росту получаем:
| $x_i$ | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
| (x_i^2w_i) – результат | 852,64 | 1660,12 | 2886,84 | 9826 | 10455,72 | 2767,68 | 1129,08 | 29578,08 |
$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$
п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.
Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
п.6. Алгоритм исследования интервального вариационного ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
| (f_i) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| (x_i) | 20 | 24 | 28 | 32 | 36 | ∑ |
| (f_i) | 1 | 7 | 12 | 6 | 4 | 30 |
| (w_i) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| (S_i) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | – |
| (x_iw_i) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| (x_i^2w_i) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.
5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).
Содержание:
- Точечные и интервальные оценки параметров распределения
- Примеры решения задач
Точечные и интервальные оценки параметров распределения
Оценка параметра распределения совокупности 
Оценка называется обоснованной, если она совпадает по вероятности с соответствующим параметром при
Оценка называется несмещенной, если ее математическое ожидание совпадает со значением параметра.
В случае выбора из всех известных несмещенных обоснованных оценок определенной оценки, необходимо указать критерий, по которому сделан выбор.
Чаще всего используется критерий, который состоит в выборе оценки, имеющей наименьшую возможную дисперсию. Такая оценка называется эффективной. Нижняя граница дисперсии несмещенной оценки параметра 

где 

Оценки параметров распределения находят методами максимальной правдоподобности и моментов. Метод максимальной правдоподобности состоит вот в чем. Пусть закон распределения случайной величины определяется через параметр 


За оценки максимальной правдоподобности параметров 
Использование метода моментов основывается на сходстве (по вероятности) статистических моментов распределения с соответствующими теоретическими моментами распределения, которые в этом случае должны существовать. Как известно, теоретические моменты распределения выражаются через параметры распределения. Составим систему 
Пусть есть точечная оценка 











Примеры решения задач
Пример 1. Выборка объемом 
Найти оценку для параметра 
Решение. Применим метод максимальной правдоподобности. Построим функцию правдоподобности, составим и решим уравнение для определения оценки:
Проверим оценку на несмещенность, найдя ее математическое ожидание:
Преобразование выполнено согласно свойствам математического ожидания и с учетом того, что результаты выборки являются независимыми одинаково распределенными случайными величинами. Найдем 
Тогда 
Проверку обоснованности оценки выполним, второй формой неравенства Чебышева, то есть оценим вероятность 
(Последний интервал, который является математическим ожиданием квадрата случайной величины, равен 

Подставляя дисперсию оценки в неравенство Чебышева, получим:

Следовательно, оценка обоснованная.
Находим дисперсию эффективной оценки:
Дисперсия эффективной оценки совпадает с дисперсией найденной оценки для 
Пример 2. Методом моментов найти оценку параметра 
Решение. Геометрический закон распределения определяется формулой 
Пример 3. По данным выборки объемом 


Решение. Интервальная оценка для математического ожидания, если дисперсия совокупности 



Для построения оценки рассматривалась выборочная функция 
Пример 4. Решить предыдущую задачу для случая, когда дисперсия совокупности неизвестна.
Решение. В этом случае интервальную оценку построим с помощью выборочной функции 





Пример 5. По результатам выборки объемом 

Решение. Для определения доверительного интервала берем выборочную функцию 






Пример 6. Найти с надежностью 



Решение. Для определения доверительного интервала берем выборочную функцию 
где 


Получим интервал
Пример 7. Определить минимальный объем выборки 



Решение. Воспользовавшись формулой 




Пример 8. Из партии однотипных высокоомных сопротивлений взяли для контроля 10 штук. Измерения показали такие отклонения от номинала, кОм:
Найти выборочную среднюю и дисперсию отклонения фактического значения сопротивления от номинала в этой партии и определить точность оценки математического ожидания выборочной средней величиной с надежностью 
Решение. Считаем, что отклонение 








Следовательно, получим такой доверительный интервал для математического ожидания:
Пример 9. В ВТК были измерены диаметры 200 валов, изготовленных на станке-автомате. Отклонения измеренных диаметров от номинала, мкм, приведены в таблице.
Считая, что выборка сделана из нормально распределенной совокупности, определить с надежностью 

Решение. С помощью условных моментов распределения, вычислим выборочную дисперсию 
найдем условные моменты распределения и выборочную дисперсию на основании расчетов в таблице:
Точность оценки 












Выборочная функция 
Выполним преобразование для определения границ доверительного интервала:
Следовательно, доверительный интервал для дисперсии такой:
Найдем точность оценки как половину длины доверительного интервала:
Согласно значению 
Окончательно получим:
Лекции:
- Проверка статистических гипотез
- Дисперсионный анализ
- Элементы теории корреляции
- Выборка из генеральной совокупности. Вариационный ряд. Гистограмма относительных частот
- Выборочная функция распределения
- Закон больших чисел в форме Чебышева
- Теорема Бернулли
- Центральная предельная теорема
- Теория случайных процессов и теория массового обслуживания
- Первичная обработка и графическое представление выборочных данных
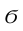
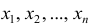
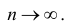
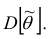
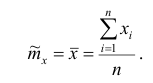
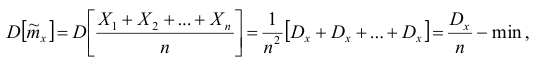
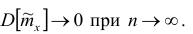



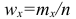
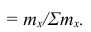
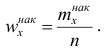

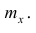
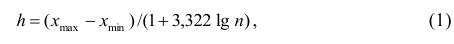
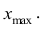




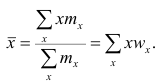


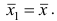
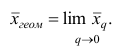
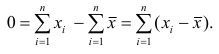
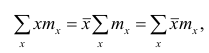
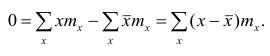
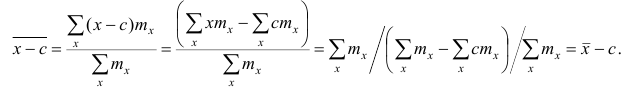
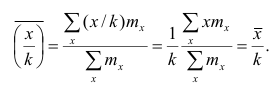
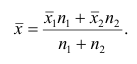
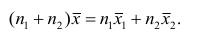
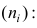
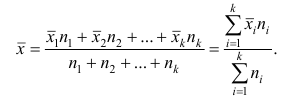
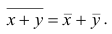
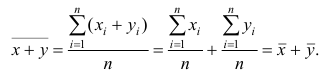
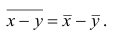

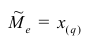
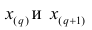
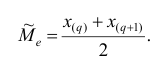
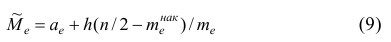
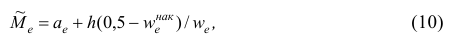
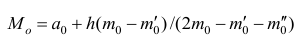
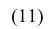
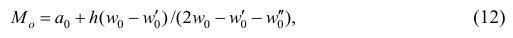


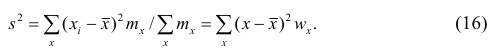
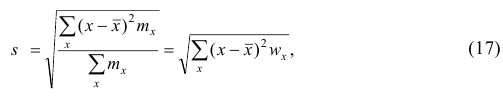
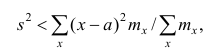
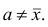
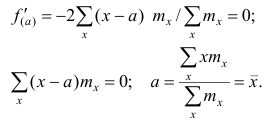
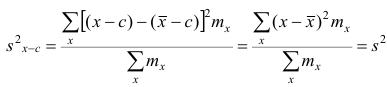
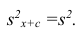
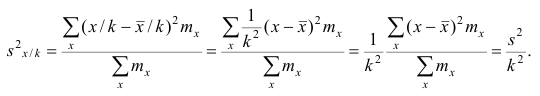
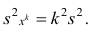

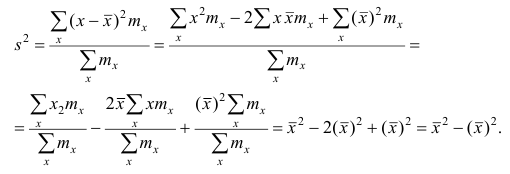
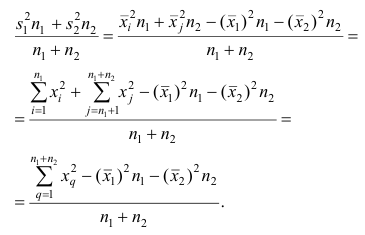
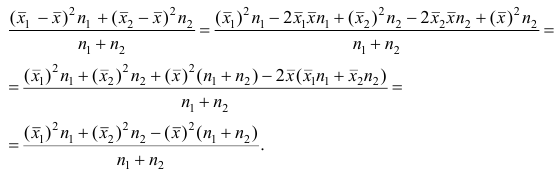
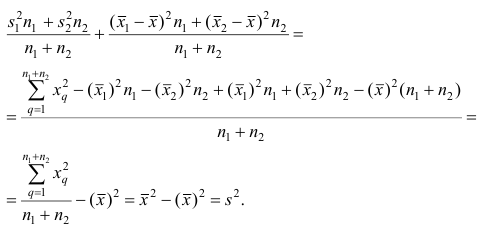
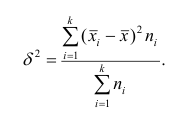
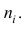
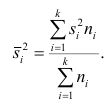
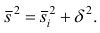

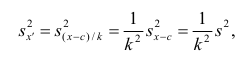
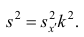

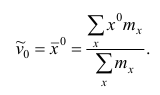
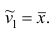
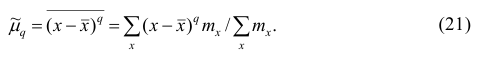
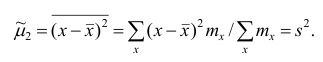
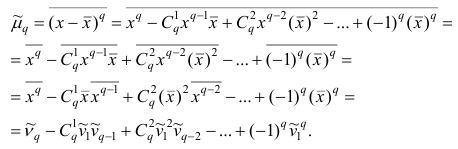
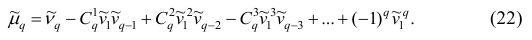
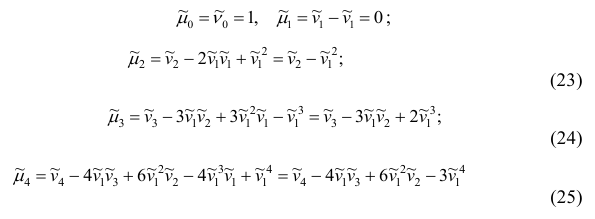
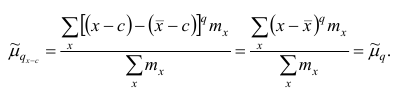
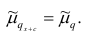
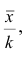
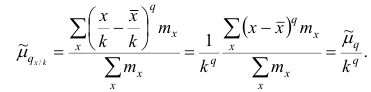
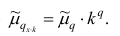

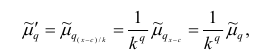
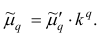
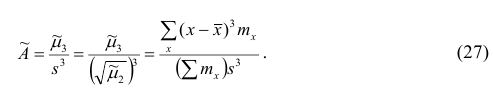

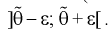
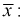
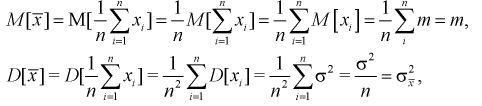
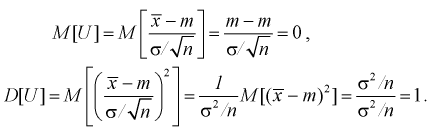

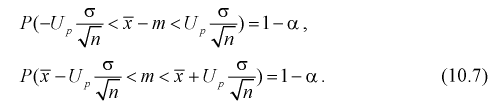

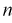 из (10.8) видим, что е уменьшается, значит, уменьшается длина доверительного интервала, а точность оценки увеличивается;
из (10.8) видим, что е уменьшается, значит, уменьшается длина доверительного интервала, а точность оценки увеличивается;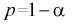 приводит к увеличению длины доверительного интервала (см. рис. 10.2, где квантили
приводит к увеличению длины доверительного интервала (см. рис. 10.2, где квантили 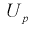 увеличиваются), т. е. е увеличивается, а точность оценки падает;
увеличиваются), т. е. е увеличивается, а точность оценки падает;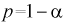 , то можно найти объем выборки, который обеспечит заданную точность:
, то можно найти объем выборки, который обеспечит заданную точность: