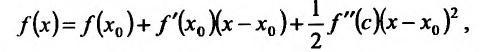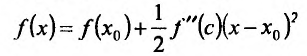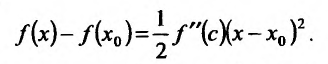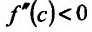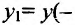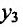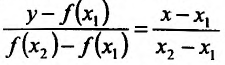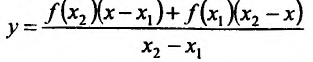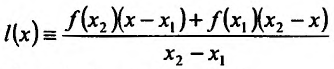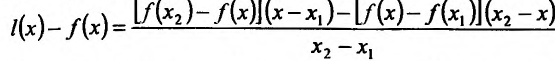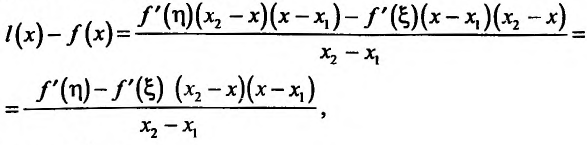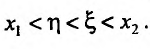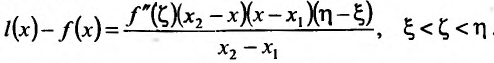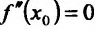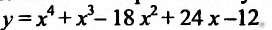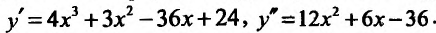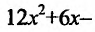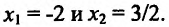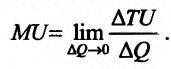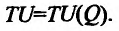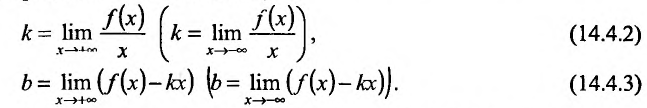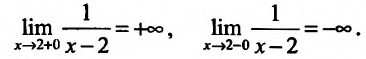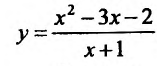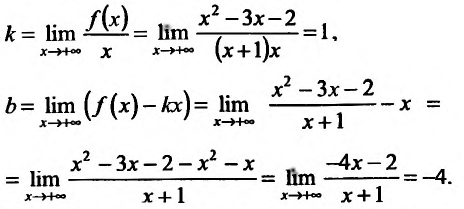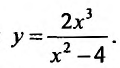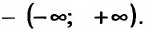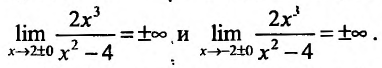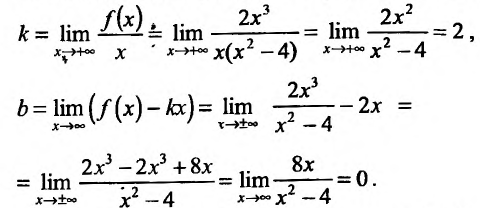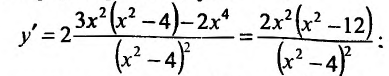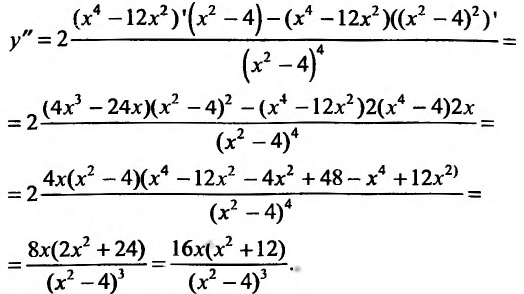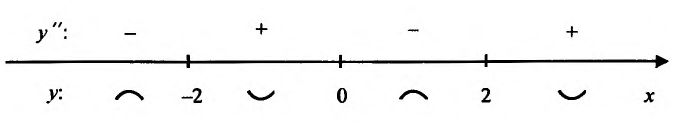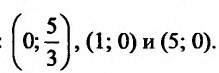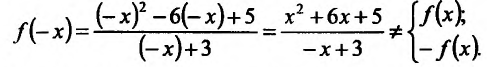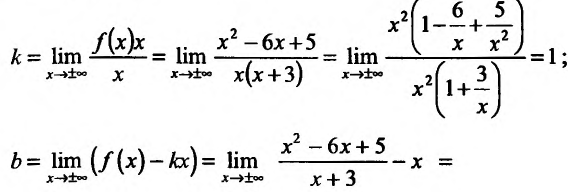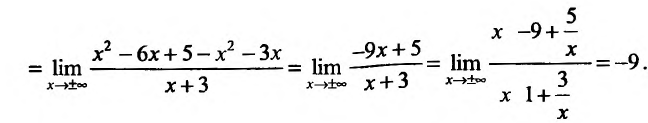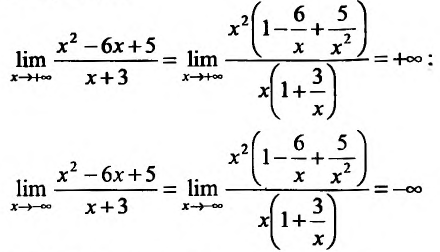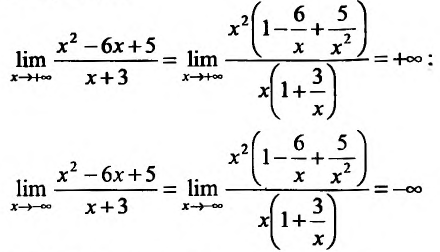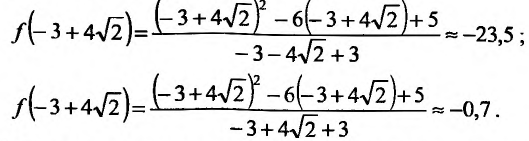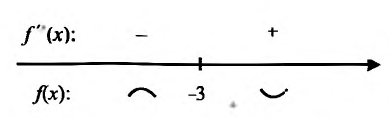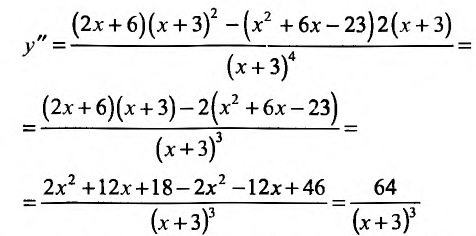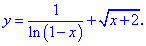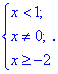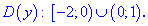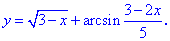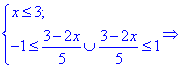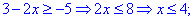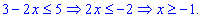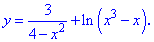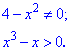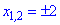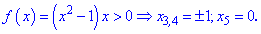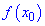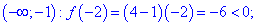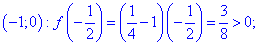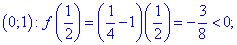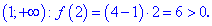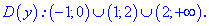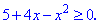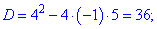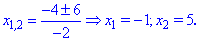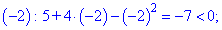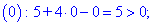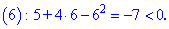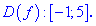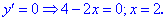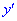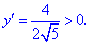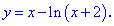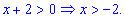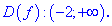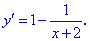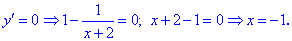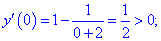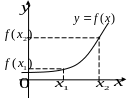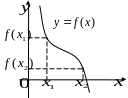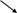Содержание:
Критерий монотонности функции:
Прежде всего, сформулируем определение монотонной функции:
- Функция f называется неубывающей (невозрастающей) на интервале (а,b), если для любых двух точек
- Функция f называется возрастающей (убывающей) на интервале (а,b), если для любых двух точек
из интервала (а, b), удовлетворяющих условию
справедливо неравенство
Неубывающие и невозрастающие функции называют монотонными функциями.
Монотонные функции
Возрастающие и убывающие функции называются строго монотонными функциями.
Например, функция у = х- возрастающая (строго монотонная) на всей числовой оси; функция 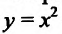
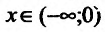
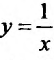
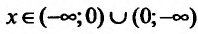
Теорема 14.1.1. (Критерий монотонности) Пусть функция 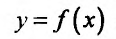
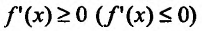
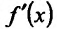
Доказательство: Пусть 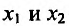
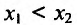
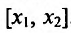
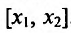
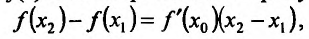
где 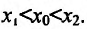
Необходимость. Пусть функция f дифференцируема на интервале (а, b) и не убывает (не возрастает) на этом интервале. Требуется доказать, что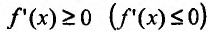
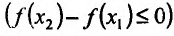
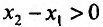
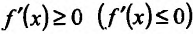
Достаточность. Пусть теперь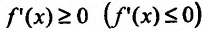
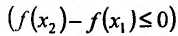
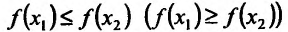
Поскольку 
Аналогично теорема доказывается и для возрастающей (убывающей) функции.
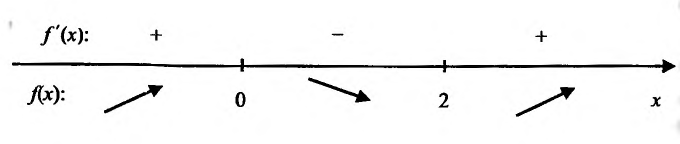
Из доказанной теоремы следует, что для определения интервалов монотонности функции нужно:
- Найти область определения функции.
- Вычислить ее производную.
- Приравнять производную к нулю; полученные нули производной разобьют область определения на интервалы, в которых производная сохраняет знак.
- Определить знак производной в каждом интервале при помощи “пробной” точки и сделать вывод.
Пример:
Найти интервалы монотонности функции
Решение:
Область определения заданной функции – вся числовая ось 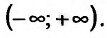
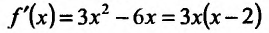
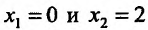
Составим схему изменения знаков производной:
Согласно теореме’ 14.1.1, данная функция возрастает при 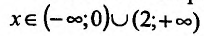
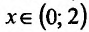
Функция 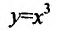
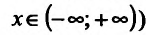
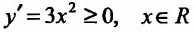
Функция 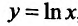
Экстремумы функций
Определение 14.2.1. Пусть функция f определена в некоторой окрестности точки 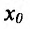
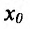
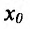
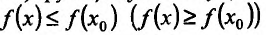
Если выполняются строгие неравенства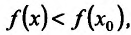
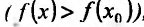
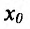
Точки максимума и минимума (строгого максимума и минимума) называются точками экстремума (строгого экстремума).
Теорема 14.2.1 .(необходимое условие экстремума) Если точка 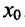
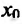
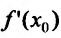
Справедливость этой теоремы следует из теоремы Ферма в силу определения точек экстремума. Действительно, если 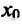
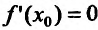
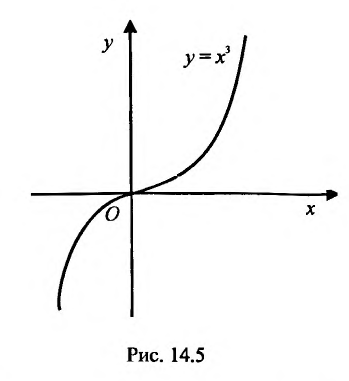
Функция может достигать экстремума также в точке, в которой производная не существует. Например, функция 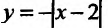
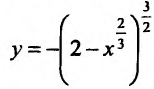
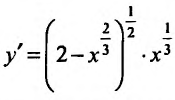
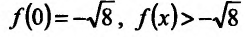
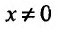
Из приведенных рассуждений следует, что точки экстремума функции нужно искать среди тех точек её области определения, где производная функции равна нулю или не существует.
Если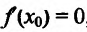
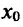
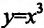
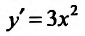
Точки области определения функции, в которых производная равна нулю, называются стационарными, а в которых производная не существует, называются критическими.
Каждая стационарная (критическая) точка – это точка возможного экстремума. Однако сделать заключение о том, что в данной стационарной (критической) точке на самом деле экстремум, можно лишь на основании дополнительного исследования, т.е. на основании достаточных условий экстремума.
Теорема 14.2.2. (первое достаточное условие экстремума) Пусть функция f определена, дифференцируема в некоторой окрестности точки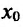
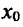
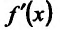
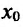
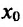
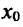
- если
на
и
на
, то точка
– точка максимума функции f(x);
- если
на
и
на
, то точка
– точка минимума функции f(x);
Если же в пределах указанной окрестности точки 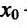
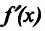
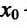
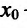
Доказательство. Докажем первое утверждение теоремы.
Предположим, что 
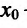
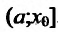
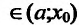
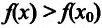
Пусть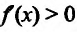
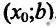
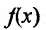
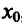
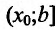
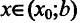
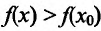
В результате получается, что при любом 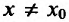
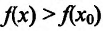
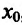
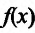
Второе утверждение теоремы доказывается аналогично.
Пример:
Найти точки экстремума функции’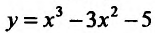
Решение:
Поскольку 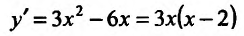
Производная функции 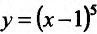
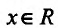
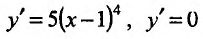
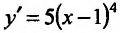
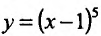
Теорема 14.2.3. (второе достаточное условие экстремума) Если функция f определена в некоторой окрестности точки 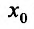
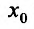

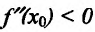
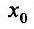
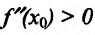
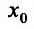
Доказательство: Поскольку функция f дважды дифференцируема в точке 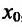
в виде:
где точка с расположена между 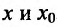
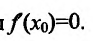
или
Поскольку 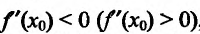
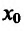
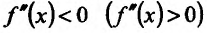
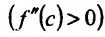
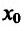
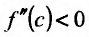
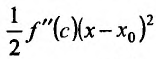
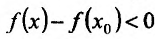
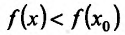
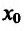
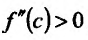
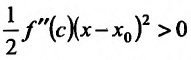
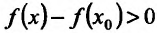
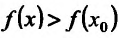
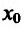
Пример:
Найти точки экстремума функции 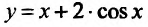
Решение:
Вычислим первую и вторую производные заданной функции: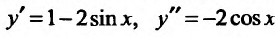
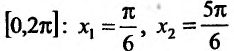
Теперь находим знак второй производной в каждой стационарной точке и определяем ее характер, используя теорему 14.2.3. Поскольку
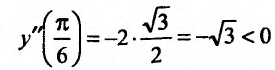
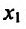
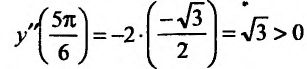
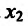
Теорема 14.2.4. (третье достаточное условие экстремума). Пусть функция f определена в некоторой окрестности точки 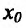
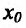
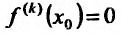
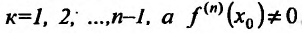
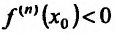
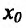
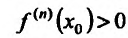
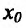
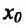
Пример:
Исследовать на экстремум функцию 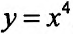
Решение:
Функция определена, непрерывна и дифференцируема на всей числовой оси. Найдем первую производную- 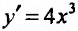
Сформулированные теоремы позволяют решать определенный круг задач. Например, требуется определить наибольшее (найме шее) значение функции f на отрезке [а, b]. Для этого следует на ней все точки, в которых производная функции либо равна нулю, ли’ не существует. Затем из этих точек выбираем те, которые принадлежат отрезку
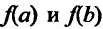
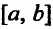
Пример:
Найти наибольшее и наименьшее значениях функции 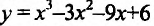
Решение:
Вычислив производную и приравняв ее к ну: 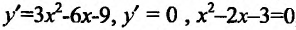
Отрезку [-2;2] принадлежит только одна точка 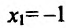
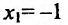
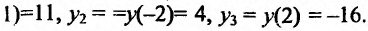
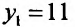
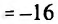
Выпуклость и точки перегиба
Пусть функция f определена на интервале (а; b) и пусть точки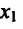
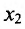
Разрешим это уравнение относительно у:
ИЛИ
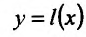
Ясно, что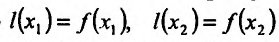
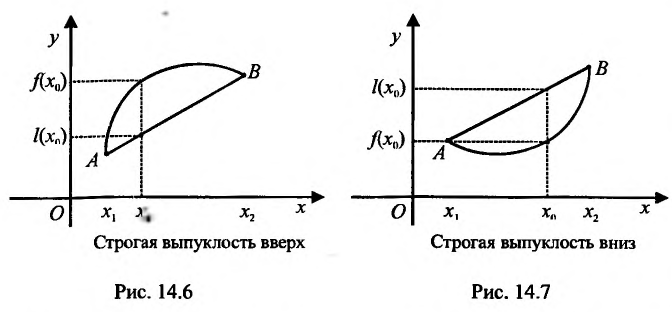
Определение 14.3.1. Функция f называется выпуклой вверх (выпуклой вниз) на интервале 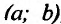
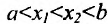
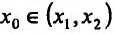
соответственно. А сам интервал называется интервалом выпуклости вверх (выпуклости вниз).
Геометрически это означает, что любая точка хорды АВ (т.е. отрезка прямой у=1(х) с концами в точках А и В) лежит не выше (не ниже) точки графика функции , соответствующей тому же значению аргумента.
Если неравенства (14.3.1) и (14.3.2) строгие, то функция f называется строго выпуклой вверх (рис. 14.6) (строго выпуклой вниз (рис. 14.7)). В этом случае любая точка хорды АВ, исключая ее концы, лежит ниже (выше) соответствующей точки графика функции
Теорема 14.3.1. (достаточное условие строгой выпуклости) Если функция f определена и дважды дифференцируема на интервале (а,b), то 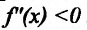
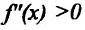
Доказательство. Пусть функция f определена и дважды непрерывно дифференцируема на интервале (а, b). Возьмем некоторые точки 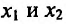
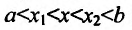
Применяя теорему Лагранжа к каждой разности, т.е. к 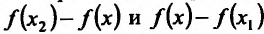
где
Снова применим теорему Лагранжа к разности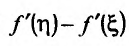
Отсюда видно, что если 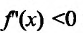
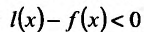
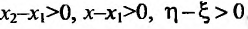
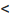

Заметим, что условие знакопостоянства второй производной не является необходимым условием. Так, функция 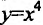
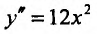
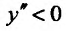
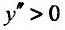
Определение 14.3.2. Пусть фунщия f определена в некоторой окрестности точки 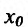
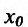
Теорема 14.3.2. (необходимое условие точки перегиба) Если функция f определена и дважды непрерывно дифференцируема на (а,b) и 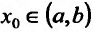
Доказательство. Пусть задана функция f, которая определена и дважды’ непрерывно дифференцируема на (а.b) и пусть точка 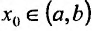
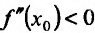
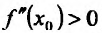
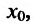
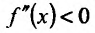
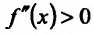
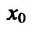
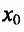
Из теоремы вытекает, что точками перегиба дважды дифференцируемой функции могут быть лишь точки, в которых вторая производная обращается в нуль либо не существует.
Сформулируем и докажем теперь достаточные условия точки перегиба.
Теорема 14.3.3. Если функция f определена и дважды дифференцируема на интервале (а,b), кроме, быть может точки 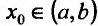
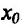
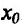
Действительно, в силу теоремы 14.3.1 точка 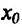
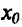
Теорема 14.3.4. Если f трижды непрерывно дифференцируема на (а,b) и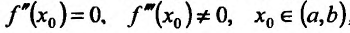
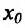
Доказательство (проведем для случая f”(x0) > 0). Так как по предположению 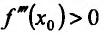
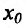
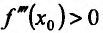
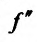
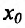
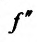
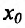
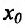
Теорема 14.3.5. Пусть функция f непрерывно дифференцируема n раз на (а,b), причем
Итак, из изложенного материала вытекает, что выпуклость вверх или вниз графика функции f зависит от знака ее второй производной. Оказывается, что и расположение графика функции относительно касательной также связано со знаком второй производной, т.е. если функция f имеет вторую производную, все значения которой имеют один и тот же знак, то все точки графика функции f лежат над (под) касательной.
Рассмотрим пример, иллюстрирующий исследование графика функции на выпуклость и точки перегиба.
Пример 14.3.1. Найти интервалы выпуклости и точки перегиба графика функции
Решение. Функция определена для всех 
Приравняв вторую производную к нулю 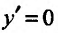
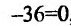
Составляет схему изменения знаков второй производной:
Следовательно, у”>0 на интервалах 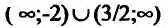
Рассмотрим пример из микроэкономики:
В количественной теории полезности предполагается, что потребитель может дать количественную оценку (в некоторых единицах измерения) полезности любого количества потребляемого им товара.
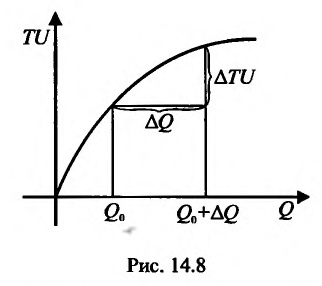
Это означает существование функции полезности TU аргумента Q -количества купленного товара. Введём понятие предельной полезности, как добавочной полезности, прибавляемой каждой последней порцией товара. Построим прямоугольную систему координат и отложим по горизонтальной оси Ох количество потребляемого товара Q, а по вертикальной оси Оу – общую полезность TU (см. рис. 14.3). Рассмотрим график функции TU = TU(Q). Точка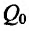
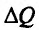
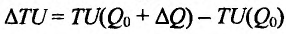
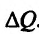
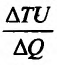
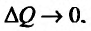
Но предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю, равен производной функции.
Следовательно, предельная полезность равна производной функции полезности TU=TU(Q). Закон убывающей предельной полезности сводится к уменьшению этой производной с ростом величины Q. Отсюда следует выпуклость графика функции
Асимптоты графика функции
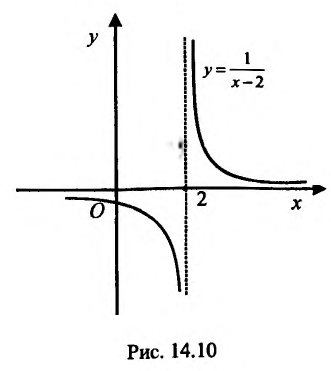
Рассмотрим функцию f определенную на интервале (а;b), . Если 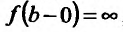
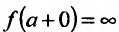
Заметим, что вертикальными асимптотами являются, как правило, нули знаменателей дробно-рациональных функций.
Если функция f определена на и для постоянных 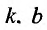
то прямая у = kх + b- называется наклонной асимптотой вправо графика функции f Если соотношение (14.4.1) выполняется и при , то прямая 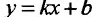
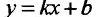
И наоборот, если пределы (14.4.2) и (14.4.3) существуют и конечны, то прямая у = kх + b- наклонная вправо (влево) асимптота графика функции f
Рассмотрим геометрический смысл асимптоты. Пусть 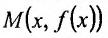
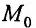
На рис. 14.9 видно, что отрезок 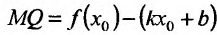
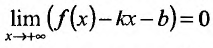
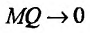
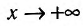
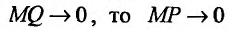
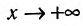
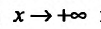
Пример:
График функции 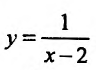
Пример:
Найти асимптоты графика функции
Решение:
Область определения функции D(f): 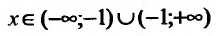
Так как значения пределов останутся такими же и при 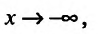
- Заказать решение задач по высшей математике
Общая схема исследования функций и построение их графиков
Под исследованием функций понимается изучение ее изменения в зависимости от изменения аргумента. Исследование функций и построение их графиков можно проводить по следующей схеме:
- Найти область определения и множество значений функции; исследовать на непрерывность, найти точки разрыва и выяснить характер точек разрыва; определить вертикальные асимптоты. Найти точки пересечения с осями координат.
- Исследовать функцию на периодичность; четность, нечетность.
- Исследовать поведение функции на границе области определения; найти асимптоты графика функции.
- Исследовать функцию на монотонность, выяснить характер экстремумов.
- Определить интервалы выпуклости графика функции, точки перегиба.
- Составить таблицу значений функции куда включаются все точки графика функции, найденные на предыдущих этапах исследования и необходимые дополнительные контрольные точки.
- Используя все полученные результаты построить график функции.
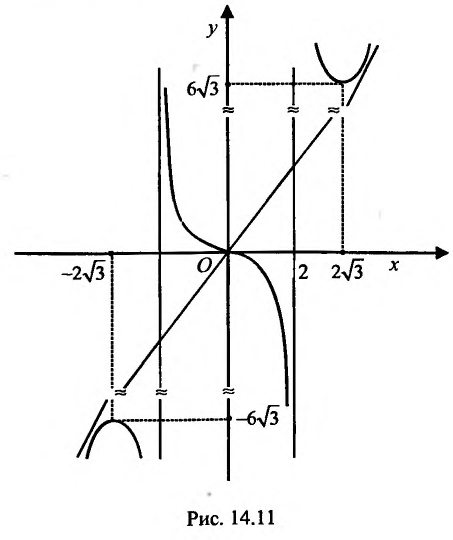
Пример:
Построить график функции
Решение:
Проведем полное исследование функции по указанной схеме.
1. Функция определена и непрерывна при всех 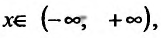
Прямые- х = ±2 являются вертикальными асимптотами, т.к.
График пересекает оси координат в точке O(0; 0).
2. Функция не периодическая. Функция не четная, т.к. выпол-
няется равенство: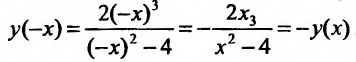
функции симметричный относительно начала координат. Поэтому достаточно провести исследование функции на полуинтервале
3. Найдем наклонную асимптоту. Для этого вычислим пределы:
Подставив значения k и b уравнение 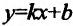
4. Для нахождения промежутков возрастания и убывания найдем первую производную:
приравняем ее к нулю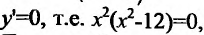
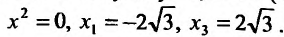

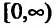
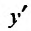
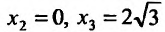
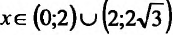
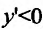
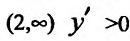
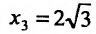
5. Для нахождения промежутков выпуклости и точек перегиба, найдем вторую производную
Вторая производная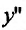
На интервале 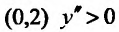
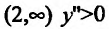
6. Используя результаты исследования и учитывая нечетность функции, строим график (рис. 14.11).
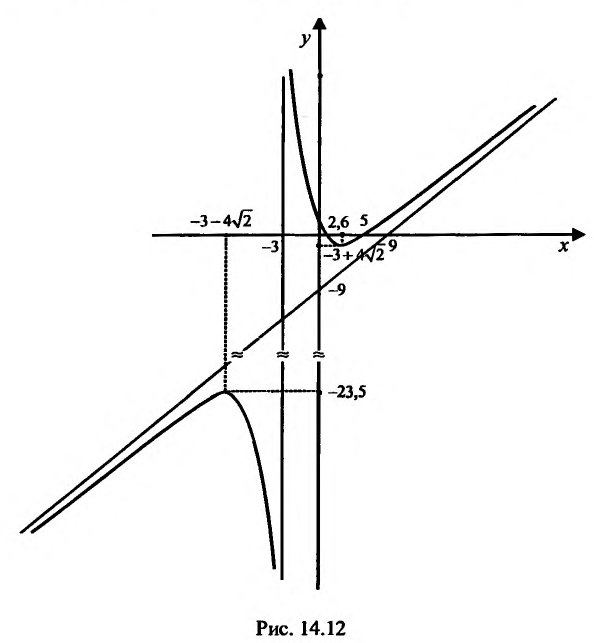
Пример:
Провести полное исследование целевой функции потребления 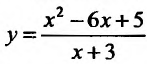
Решение:
Проведём полное и разностороннее изучение свойств функции, применив изложенную выше схему.
1) Функция определена и непрерывна для всех 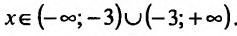
как 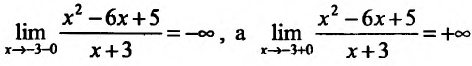
-3 является вертикальной асимптотой. Если х=0, то 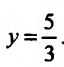
у=О, тс получим уравнение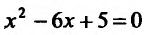
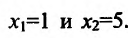
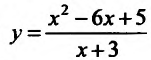
координат в точках:
2) Функция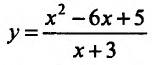
3) Исследуемая функция не является ни чётной, ни нечётной, гак как
4) Исследуем существование наклонных асимптот. Для этого вычислим пределы;
Итак, при 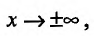
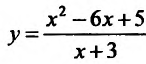
Исследуем повеление функции на границе области определения. Поведение функции в окрестности точки х = -3 исследовано. Поэтому изучим поведение функции при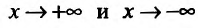
5) Первая производная
обращается в нуль в точках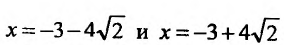
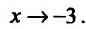
Поскольку 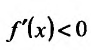
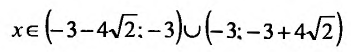
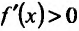
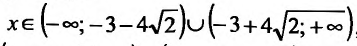
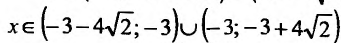
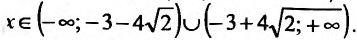
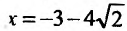
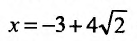
6) Вторая производная не обращается в нуль и стремится к бесконечности при 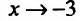
Поскольку 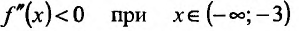
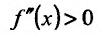
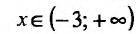
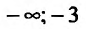
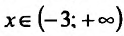
По результатам исследования строим график функции. Вначале строим систему координат; затем вертикальную и горизонтальную асимптоты; наносим точки пересечения с осями координат и точки экстремума функции. Затем строим график (рис. 14.12).
- Предел и непрерывность функции двух переменны
- Дифференцируемость функции нескольких переменных
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной
План урока:
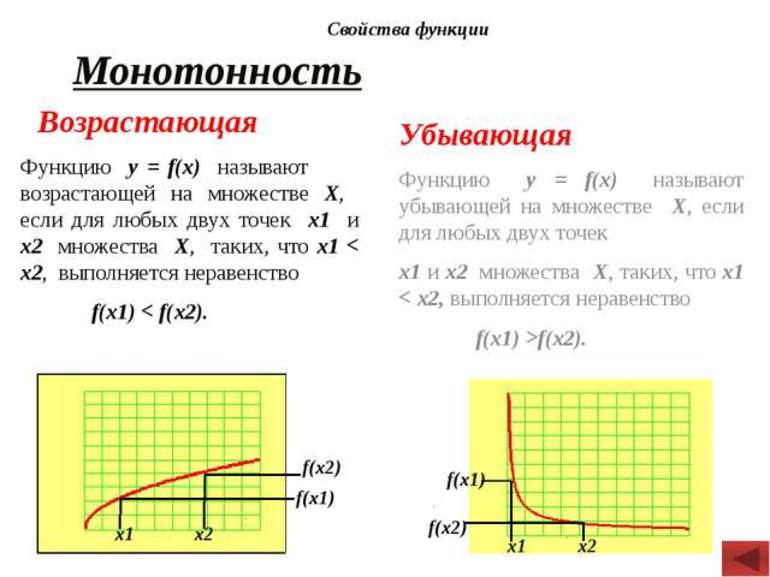
Возрастание и убывание функций
Промежутки монотонности основных функций
Свойства монотонных функций
Четные и нечетные функции
Свойства четных и нечетных функций
Ограниченные и неограниченные функции
Квадратичная функция
Возрастание и убывание функций
Посмотрим на график произвольной функции:
Видно, что область определения ф-ции – это промежуток [– 6; 4].
На графике сначала ф-ция как бы «поднимается». При увеличении х растет значение у. Так происходит до точки (1; 5). После этого ситуация меняется, при увеличении аргумента значение ф-ции начинает падать. В математике принято говорить, что ф-ция возрастает на промежутке [– 6; 1] и функция убывает на промежутке [1; 4]. Можно сказать и иначе – ф-ция у является возрастающей функцией на множестве [– 6; 1] и убывающей функцией на множестве [1; 4].
Рассмотрим это определение возрастающей функции подробнее. Построим произвольную возрастающую ф-цию и выберем на ней две точки со значениями аргумента х1 и х2. Также отметим значения ф-ции в этих точках, у(х1) и у(х2):
По определению, если х1 меньше х2, то и у(х1) <у(х2). Другими словами, из двух точек та, которая располагается левее (то есть имеет меньшее значение х), будет одновременно располагаться и ниже, (то есть иметь меньшее значение у).
Мы видим возрастание функции на промежутке [– 6; 5]. Однако она также будет возрастать и на любом другом промежутке, который является частью отрезка [– 6; 5]. Например, можно сказать, что она возрастает на промежутке [1; 3] или [– 2; 0].
Аналогично дается и определение убывающей ф-ции:
По сравнению с определением возрастающей ф-ции изменился лишь один символ, в последнем неравенстве для у(х1) и у(х2) стоит знак «больше» а не меньше. Покажем пример убывания функции.
Заметим, что в приведенных определениях используются строгие неравенства со знаками «>»и «<». Однако в математике используются и нестрогие неравенства, содержащие знаки «≤» и «≥». С их использованием можно записать ещё 2 определения:
Приведем пример неубывающей ф-ции:
Здесь х1<x2<x3<x4. Видно, что, например, у(х1) <у(х2). Однако у(х2) = у(х3). Получается, что на графике ф-ции есть плоская «площадка» на промежутке [1; 3]. Для всех значений х из этого промежутка у = 3,5. Из-за этой площадки ф-цию нельзя считать строго возрастающей.
Теперь покажем пример невозрастающей ф-ции:
Здесь также есть плоские «площадки», из-за которых ф-цию нельзя считать просто убывающей.
Ясно, что всякая возрастающая ф-ция является неубывающей, а каждая убывающая ф-ция одновременно считается и невозрастающей.
В математике часто вместо всех этих терминов используют понятие монотонности. Дадим определение монотонной функции:
Если же ф-ция убывает или возрастает на промежутке (то есть не имеет плоской площадки), то говорят, что она строго монотонна.
Рассмотрим ф-цию, изображенную на рисунке:
Ф-ция возрастает на промежутках [– 6; –2] и [3; 4,5], а также убывает на промежутках [– 2; 1,5] и [2,5; 3]. Значит, на каждом из этих промежутков ф-ция строго монотонна. На отрезке [-2; 3] ф-ция невозрастающая, поэтому здесь она просто монотонна. Любой промежуток, на котором ф-ция монотонна, называют промежутком монотонности.
Различают как промежутки убывания функции, так и промежутки возрастания функции.
Понятно, что если ф-ция строго монотонна, то она и просто монотонна. В большинстве школьных задач не важна строгость монотонности, поэтому слово «строго» часто опускают.
Во всех данных определениях рассматривалось поведение ф-ции на каком-то отдельном числовом промежутке. Одна и та же ф-ция может на одном числовом промежутке возрастать, а на другом убывать. Однако некоторые ф-ции сохраняют свой характер на всей своей области определения. Например, линейная ф-ция у = 2х – 3 возрастает на протяжении всей числовой прямой, то есть на промежутке (– ∞; + ∞):
В большинстве случаев промежутки монотонности ф-ции очевидны, исходя из графика ф-ции. Однако и без их построения можно аналитически доказывать монотонность ф-ции.
Пример. Докажите, что ф-ция у = 2х – 3 возрастает на промежутке (– ∞; + ∞).
Решение. Выберем произвольные числа х1 и х2, причем х1< х2. Разность (х2 – х1) будет, очевидно, положительным числом. Найдем теперь разность (у(х2) – у(х1)):
у(х2) – у(х1) = (2х2 – 3) – (2х1 – 3) = 2х2– 3 – 2х1+ 3 = 2х2 – 2х1 = 2(х2 – х1)
Так как (х2 – х1) – положительное число, то и 2(х2 – х1), а значит, и (у(х2) – у(х1)) – тоже положительное число. Если же разность двух числе положительна, то уменьшаемое больше вычитаемого. Значит, у(х2) > у(х1). По определению получаем, что у = 2х – 3 – возрастающая ф-ция.
Промежутки монотонности основных функций
Мы ранее уже изучили несколько видов ф-ций. Посмотрим, какие у них промежутки монотонности.
Поведение линейной ф-ции у = kх + b зависит исключительно от значение коэффициента k. Если он больше нуля, то функция возрастает на промежутке (– ∞; + ∞), то есть на всей числовой прямой. Если же k< 0, то ф-ция будет убывать. Если k = 0, то график будет выглядеть как горизонтальная линия. Её можно считать одновременно и неубывающей, и невозрастающей ф-цией. Приведем примеры на рисунке:
Поведение обратной пропорциональности у = k/х также зависит от значения k. Если он больше нуля, то ф-ция убывает на двух промежутках: (– ∞;0) и (0; + ∞).
Здесь стоит обратить внимание, что, хотя у ф-ции нет ни одного участка, на котором бы она возрастала, нельзя утверждать, что обратная пропорциональность убывает на всей своей области определения (– ∞; 0)∪(0; + ∞). Например, сравним значение ф-ции у = 5/х при х1 = – 1 и х2 = 1:
у(– 1) = 5/(– 1) = – 5
у(1) = 5/1 = 5
Получили, что для этих значений х1<x2, а у(– 1) <у(1), поэтому ф-цию нельзя считать убывающей на всей области определения.
Если в обратной пропорциональности коэффициент k отрицательный, то ф-ция возрастает на промежутках (– ∞;0) и (0; + ∞):
Ф-ция
возрастает на всей своей области определения, то есть на промежутке [0; + ∞):
Поведение степенной ф-ции у = хn зависит от показателя n. Если он нечетный, то получается ф-ция, возрастающая на всей числовой прямой:
Если же число n четное, то степенная ф-ция будет убывать на промежутке (– ∞:0] и возрастать на промежутке [0; + ∞):
Пример. Найдите значения параметра a, при котором ф-ция
у = (5а – 2)х +16
является возрастающей.
Решение. Данная ф-ция является линейной ф-цией вида у = kx + b, где в роли коэффициента k выступает выражение (5а – 2). Ф-ция будет возрастать, если этот коэффициент будет больше нуля, то есть
5а – 2> 0
5а> 2
а > 0,4
Получаем, что ф-ция будет возрастающей при значениях а, больших 0,4, или, другими словами, при а∊(4; + ∞).
Ответ: а∊(4; + ∞).
Свойства монотонных функций
Монотонные функции имеют ряд примечательных свойств, которые могут помогать при решении задач. Вспомним, что некоторые ф-ции могут при различных значениях аргументов принимать одинаковое значение. Например, таковой является степенная ф-ция у = х2:
у(2) = 4
у(– 2) = 4
С точки зрения графиков это означает, что горизонтальная линия может пересекать график ф-ции в нескольких точках:
С другой стороны, это значит, что уравнение х2 = 4 имеет два корня, 2 и ( – 2).
Если же ф-ция строго монотонна, то такая ситуация невозможна. Любое ее значение может быть получено только при одном значении аргумента.
Действительно, если ф-ция монотонна, то любая горизонтальная прямая сможет пересечь ее график не более чем в одной точке:
Это также означает, что, если у(х) – строго монотонная ф-ция, а b– произвольное число, то уравнение у(х) = b имеет не более одного корня. Так, у уравнения х3 = 8 есть только один корень (он равен 2), потому что х3 – монотонная ф-ция.
Рассмотрим следующее свойство монотонных функций.
Действительно, ранее мы уже изучали сжатие и растягивание графиков. умножение ф-ции на постоянное число как раз и ведет к подобным преобразованиям. Ясно, что при этом не происходит изменение монотонности ф-ций:
Например, парабола у = х2 возрастает на промежутке [0; + ∞), значит, и ф-ция у = 3х2 также возрастает на этом же промежутке:
Проще говоря, при умножении ф-ции на положительное число ее промежутки монотонности не изменяются.
А что же произойдет при умножении ф-ции на отрицательное число. Она не только сожмется или растянется, но ещё и отобразится симметрично относительно оси Ох. В результате промежутки возрастания ф-ции превратятся в промежутки убывания, и наоборот.
Проиллюстрируем это на примере ф-ций у = х2 и у = – х2:
Видно, что на промежутке (– ∞; 0] ф-ция у = – х2 возрастает, в то время как обычная парабола убывает. На промежутке [0; + ∞)ситуация противоположная.
Если две ф-ции одновременно возрастают на одном промежутке, то и их сумма также будет возрастать на этом промежутке.
Например, ф-ции у = х5 и у = 4х возрастают на всей числовой прямой. Следовательно, возрастающей является и ф-ция у = х5 + 4х.
Пример. Решите уравнение
х7 + 2х – 3 = 0
Решение. Можно заметить, что число 1 является корнем этого уравнения. Действительно, подставим единицу в уравнение и получим верное равенство:
17 + 2•1 – 3 = 0
1 + 2 – 3 = 0
0 = 0
Докажем, что других корней уравнение не имеет. В его левой части стоит сумма двух возрастающих ф-ций, у = х7 и у = 2х – 3. Следовательно, и ф-ция у = х7 + 2х – 3 также является возрастающей на всей числовой прямой. Это значит, что исследуемое уравнение имеет не более 1 корня, то есть корень х = 1 – единственный.
Ответ: 1.
Пример. Докажите, что у уравнения
не более одного корня.
Решение.
Выражение в левой части имеет смысл только при положительных х. Ведь если х < 0, то под корнем окажется отрицательное число, а если х = 0, то ноль окажется в знаменателе. Другими словами, уравнение имеет смысл на промежутке (0; + ∞). При этом левая часть представляет собой сумму трех слагаемых:
Первое и третье из них являются возрастающими ф-циями. Второе слагаемое – это взятая со знаком «минус» ф-ция у = 2/х. Так как у = 2/х убывает на промежутке (0; + ∞), то у = – 2/х на нем же возрастает. В итоге получаем, что в левой части сумма трех возрастающих ф-ций, значит, и всё это выражение – возрастающая ф-ция. Из этого следует, что у уравнения есть не более одного корня. Попробуйте сами подобрать его.
Четные и нечетные функции
При изучении степенных ф-ций мы заметили, что при четном показатели степени n их график симметричен относительно оси Оу:
Почему так происходит? Дело в том, что у этих ф-ций противоположным значениям аргументов соответствует одно и то же значение у. Убедимся в этом на примере у = х2:
- у(1) = 12 = 1 и у(– 1) = (– 1)2 = 1;
- у(2) = 22 = 4 и у(– 2) = (– 2)2 = 4;
- у(3) = 32 = 9 и у(– 3) = (– 3)2 = 9.
В общем случае эту особенность можно доказать так:
у(– х) = (– х)2 = х2 = у(х)
В математике есть специальный термин для обозначения ф-ций, обладающих таким свойством. Их называют четным функциями.
Определение четной функции можно записать и так, чтобы в нем фигурировали формулы:
Для проверки того, является ли функция четной, достаточно подставить в нее вместо аргумента х величину (– х).
Пример. Докажите, что ф-ция у = х4 + 3х2 является четной.
Решение. Подставим в ф-цию значение (– х):
у(– х) = (– х)4 + 3(– х)2 = х4 + 3х2
Получили исходную ф-цию у(х). Значит, исследуемая функция является четной.
Пример. Четна ли ф-ция
Решение снова подставим в ф-цию значение (– х):
Получили изначальную ф-цию. Следовательно, она – четная.
Почему же четные ф-ции симметричны относительно оси Оу? Из определения следует, что если графику четной ф-ции принадлежит точка (х0;у0), то ему же принадлежит точка (– х0;у0). Посмотрим, как они располагаются на координатной плоскости:
Они симметричны относительно оси Оу. Если же для каждой точки графика есть симметричная точка, также ему принадлежащая, то и в целом график симметричен относительно вертикальной оси.
Теперь посмотрим на степенные ф-ции, у которых нечетный показатель степени. В качестве примера можно привести у = х3 и у = х5. Видно, что они симметричны относительно центра координат:
Такая симметрия (относительно точки), называется центральной. Геометрически она означает, каждой точке графика в I четверти с двумя положительными координатами соответствует точка графика в III четверти с такими же координатами, но взятыми со знаком «минус»:
Существует множество ф-ций, обладающих подобной симметрией. В математике их все называют нечетными функциями. У них противоположным значениям аргументов соответствуют противоположные значения ф-ции, а график нечетной функции всегда симметричен относительно начала координат.
Чаще используется определение, содержащее формулу:
Покажем это свойство у ф-ции у = х3:
- у(1) = 13 = 1 и у(– 1) = (– 1)3 = – 1;
- у(2) = 23 = 8 и у(– 2) = (– 2)3 = – 8;
- у(3) = 33 = 27 и у(– 3) = (– 3)3 = – 27.
Для того, чтобы доказать нечетность ф-ции, надо поставить в нее (– х) вместо х. Если получилась исходная ф-ция с противоположным знаком, то это значит, что ф-ция нечетная.
Пример. Докажите, что ф-ция у = х5 + х – нечетная.
Решение: Подставим (– х):
у(– х) = (– х)5 + (– х) = –х5 – х = – (х5 + х) = – у(х)
Получили исходную ф-цию, но со знаком «минус», поэтому ф-ция является нечетной.
Пример. Докажите нечетность ф-ции у = 5/х + 4х.
Решение. Подставляем в ф-цию (– х):
у = 5/(– х) + 4(– х) = – 5/х – 4х = – (5/х + 4х) = – у(х)
Снова получили исходную ф-цию со знаком минус, следовательно, мы исследовали нечетную ф-цию.
Известно, что любое целое число либо четное, либо нечетное. Однако с ф-циями всё по-другому. Существует множество ф-ций, которые не относятся ни к тем, ни к другим. Чтобы доказать, что ф-ция не является ни четной, ни нечетной, достаточно продемонстрировать, что хотя бы для одного значения х не выполняются условия у(– х) = у(х) и у(– х) = – у(х).
Пример. Докажите, что у = х3 + х2 – ни четная, ни нечетная ф-ция.
Решение. Определим значение ф-ции при, например, х = 1 и х = –1
у(1) = 13 + 12 = 2
у(– 1) = (– 1)3 + (– 1)2 = 0
Получили, что при противоположных х значения у не являются ни одинаковыми, ни противоположными. Значит, рассматриваемая ф-ция не подходит под приведенные определения четности и нечетности.
Свойства четных и нечетных функций
Рассмотрим важные свойства, помогающие быстро определять четность и нечетность ф-ций.
Например, так как четной является ф-ция у = х6, то также четными будут и ф-ции:
- у = 2х6;
- у = 3х6;
- у = – х6;
- у = – 12х6;
- у = 0,135х6.
Так, ф-ции у = х3 и у = 1/х – нечетны. Значит, нечетна и их сумма у = х3 + 1/х.
Другими словами, ф-цию можно «перевернуть», и она всё равно сохранит свою четность. Так, ф-ция 5х4 + х2 четная, поэтому и ф-ция
останется такой же.
Вообще рассматриваемое свойство ф-ции часто называют ее четностью. Так, про две рассматриваемые ф-ции у = х3 и у = х9 можно сказать, что они обладают одинаковой четностью (обе нечетные), а у = х5 и у = х7 обладают различной четностью (одна из них четная, а другая нечетная).
Например, ф-ции у = 5х3 + 6х и у = 9х5 имеют одинаковую четность (обе нечетные), а потому их произведение у = 9х5(5х3 + 6х) является четным. С другой стороны, у = х5 и у = х8 + у6 имеют различную четность, следовательно, их произведение у = х5(х8 + у6) нечетное.
Докажем справедливость этого правила. Пусть есть две ф-ции, у = у(х) и g = g(х), которые обладают какой-нибудь четностью. Определим четность их произведения у(х)•g(х). Для этого рассмотрим 3 различных случая:
- И у = у(х), и g = g(х) – четные. Тогда у(– х) = у(х), g(– х) = g(х), и мы получаем следующее:
у(– х)•g(– х) = у(х)•g(х).
- Обе рассматриваемые ф-ции – нечетные. Тогда у(– х) = – у(х), g(– х) = – g(х), и получается следующее:
у(– х)•g(– х) = (– у(х))•(– g(х)). = (– 1)(– 1)у(х)•g(х) = у(х)•g(х).
- Если же одна из ф-ций, например, у(х), будет четной, а вторая – нечетной, то их произведение будет следующим:
у(– х)•g(– х) = у(х)•(– g(х)) = – у(х)•g(х).
Пример. Определите четность ф-ции у = (8х4 + 3х2)(7х5 + 2х)
Решение. Ф-ция из условия представляет собой произведение двух других ф-ций: у = 8х4 + 3х2 и у = 7х5 + 2х. Первая из них является суммой двух четных и поэтому сама четная. Вторая ф-ция, наоборот, нечетная. Следовательно, их произведение – это тоже нечетная ф-ция.
Ответ: Нечетная ф-ция.
Пример. Определите четность ф-ции у = (х6 + х2)(х10 + х8)
Решение. Так как ф-ции у = х6 + х2 и у = х10 + х8 имеют одинаковую четность (обе четные), то их произведение является четным.
Ответ: Четная ф-ция.
Для изучения следующего свойства ф-ций необходимо сначала рассмотреть понятие сложной ф-ции. Так называют ф-цию, которую получают подстановкой одной «простой» ф-ции в другую.Например, пусть есть ф-ции g = х2 и у = х3 + 2х. Подставив вторую в первую, получим
g = (х3 + 2х)2
Ещё пример сложной ф-ции:
у = 2(9х2 + 4х + 1)3 + 3(9х2 + 4х + 1)
Она получена путем подстановки выражения 9х2 + 4х + 1 в ф-цию у = х3 + 3х. В общем случае, если в ф-цию у = f (x) подставляют g(x), то используют запись у = f (g(x)). Иногда вместо термина «сложная функция» используют аналогичное понятие «композиция функций».
Итак, сформулируем ещё одно свойство четных функций:
Например, пусть есть четная ф-ция у = х2. Подставим ее в любую другую ф-цию, скажем, в у = 5х + 7 + 1/х. В итоге получим новую, сложную ф-цию
у = 5х2 + 7 + 1/(х2)
которая будет четной. При этом природа ф-ции у = 5х + 7 + 1/х не играет никакой роли. Мы могли бы взять любую другую ф-цию, например, у = 958,235х3 – 12,25х2 + 19х + 2/3, и подставив в нее х2 вместо х, получить ф-цию
у = 958,235(х2) 3 – 12,25(х2) 2 + 19х2+ 2/3
которая будет четной.
Ограниченные и неограниченные функции
Ещё раз рассмотрим ф-цию у = х2. Очевидно, что все точки ее графика лежат выше оси Ох (кроме точки (0;0), лежащей непосредственно на оси Ох). Ось Ох – это, по сути, горизонтальная прямая у = 0. Можно провести ряд других горизонтальных линий, каждая из которых лежит ниже параболы и не пересекает её:
В математике говорят, что ф-ция у = х2 ограничена снизу. То есть для любого допустимого х выполняется неравенство у(х) ⩾ а, где а – это какое-то произвольное число. И действительно, неравенство х2⩾ 0 выполняется при всех значениях х. Также выполняются неравенства
х2⩾ – 1,5
х2⩾ – 3
х2⩾ – 5
Дадим определение функции, ограниченной снизу
Очевидно, что если неравенство у(х) ⩾ а выполняется хотя бы для одного числа а, то оно выполняется и для всех а, которые ещё меньше. Так, из справедливости неравенства х2⩾ 0 автоматически следует справедливость неравенства х2⩾ – 1,5, так как
– 1,5 ⩽ 0.
Аналогично в математике существует понятие функции, ограниченной сверху.
В качестве примера ограниченной сверху ф-ции можно привести у = 4 – х2:
Ясно, что неравенство 4 – х2⩽ 4 выполняется при всех х, то есть ни одна точка графика не лежит выше прямой у = 4.
Иногда бывает так, что функция ограничена одновременно и снизу, и сверху. Их называют ограниченными функциями.
Ф-ция, не попадающее под это определение, называется неограниченной функцией. В качестве примера неограниченной функции можно привести линейную ф-цию у = х + 1.
График ограниченной ф-ции находится в своеобразной «полосе» из горизонтальных линий, которые ограничивают его сверху и снизу. Примером ограниченной ф-ции является
С одной стороны, у этой дроби и числитель, и знаменатель – положительное число, поэтому она ограничена снизу прямой у = 0. С другой стороны, дробь тем больше, чем меньше ее знаменатель (если они оба положительны). Минимальное значение выражения х2 + 1 – это единица (при х = 0), а поэтому максимальное значение дроби равно 4/1 = 4. Поэтому график ограничен сверху прямой у = 4.
Пример. Ограничена ли ф-ция
Решение. Выделим в ф-ции целую часть:
Так как величина 5х2 + 5 всегда положительна, то и дробь
а значит, и вообще вся ф-ция положительна, то есть ограничена снизу прямой у = 0
С другой стороны, дробь будет принимать максимальное значение при минимальном значении знаменателя, которое равно 5 (при х = 0) При х = 0 имеем
Получается, что ф-ция ограничена сверху прямой у = 1,4.
Ответ: ограничена.
Пример. Ограничена ли ф-ция
Решение. Величина х2 всегда положительна, то есть х2⩾ 0. Преобразуем это неравенство, умножив его на (– 1) и добавив к нему 16:
х2⩾ 0
– х2⩽ 0
16 – х2⩽ 16
Получили, что подкоренное выражение не превосходит 16, а значит, и корень из него не больше, чем
То есть график будет ограничен прямой у = 4 сверху. С другой стороны, арифметический квадратный корень не может быть отрицательным числом, а потому его график ограничен снизу прямой у = 0. Для наглядности покажем график исследуемой ф-ции:
Ответ: ограничена.
Квадратичная функция
В качестве ф-ции можно использовать квадратный трехчлен, например:
у = 2х2 + 6х – 10
у = – 1,5х2 + 19х + 0,5
у = 0,005х2 + 654,25х – 124
Все эти ф-ции заданы с помощью выражения, представляющего собой квадратный трехчлен, поэтому в математике их называют квадратичными функциями.
Если коэффициент перед х2 окажется равным нулю, то ф-ция превратится из квадратичной в линейную:
0х2 + bx + c = bx + c
Попытаемся понять, как выглядит график квадратичной функции. Для этого начнем рассматривать частные случаи и использовать правило растяжения и сжатия, а также параллельного переноса графиков ф-ций.
Если в выражение для квадратичной ф-ции подставить значения
а =1
b= 0
с = 0
то получится уже известная нам степенная ф-ция у = х2:
1х2 + 0x + 0 = х2
Её графиком является парабола.
График ф-ции у = ах2 – это тоже парабола (где а – некоторое число), которая однако, получена из «обычной» параболы у = х2 путем сжатия или растяжения графика. Если коэффициент а является отрицательным, то парабола «перевернется» то есть отобразится симметрично относительно оси Ох. Покажем примеры нескольких графиков у = ах2:
Напомним, что при добавлении к ф-ции какого-нибудь постоянного числа n ее график переносится на n единиц вверх. Зная это можно легко получить график ф-ции у = ах2 + с из графика у = ах2:
Таким образом, графиком ф-ции у = ах2 + с является парабола, чья вершина поднята на с единиц вверх.
Как изменится график квадратичной ф-ции у = ах2 + с, если в вместо х возводить в квадрат выражение (х +m), где m – произвольное число? В этом случае ф-ция примет вид у = а(х +m)2 + с. Вершина параболы должна будет сместиться на m единиц влево:
Теперь докажем, что любая квадратичная ф-ция может быть представлена как в виде у = а(х + m) + n, где m и n – некоторые числа (в том числе и отрицательные). Похожие преобразования мы производили, когда учились решать квадратные уравнения. Запишем саму квадратичную ф-цию:
у = ах2 + bх + с
Вынесем множитель а за скобки:
Далее попытаемся преобразовать трехчлен в скобках, используя формулу квадрата суммы. Для этого добавим к нему и сразу же вычтем величину (b/2a)2:
Теперь раскроем внешние скобки:
Теперь произведем две замены:
Используя их, можно записать:
Получили, что любую квадратичную ф-цию можно свести к виду у = а(х + m)2 + n. Что это значит и для чего мы это доказывали? Из этого факта следует, что график любой квадратичной ф-ции может быть получен из обычной параболы у = х2 за счет трех действий.
- Необходимо растянуть график у = х2 в а раз и получить график у = ах2. Если число а является отрицательным, то график не только растянется, но ещё «перевернется» ветвями вниз, то есть отобразится симметрично относительно оси Ох.
- Необходимо сдвинуть график у = ах2 на n единиц вверх и получить график у = ах2 + n. Если n< 0, то график переместится вниз, а не вверх.
- Полученный график у = ах2 + n следует сместить влево на m единиц и получить график у = а(х + m)2 + n. Если m отрицательно, то график сместится не влево, а вправо.
Итак, как будет выглядеть график квадратичной ф-ции? В общем случае он является параболой, центр которой располагается не в точке (0;0), а в некоторой другой точке (х0; у0):
Если мы вернемся к доказательству того, что любую квадратичную ф-цию можно представить в виде у = а(х + m)2 + n, то увидим, что число m рассчитывается по формуле
Так как график из-за этого числа m перемещается влево, а не вправо, то координата вершины х0 рассчитывается по формуле:
Нет смысла составлять такую же формулу для определения координаты вершины у0, ведь можно подставить х0 в сам ф-цию и так узнать вторую координату вершины.
Пример. Определите вершину параболы, задаваемой ф-цией
у = 2х2 + 8х + 5
Решение. Выпишем коэффициенты а, b и c квадратичной ф-ции:
а = 2
b = 8
c = 5
Зная их, легко рассчитаем координату х вершины параболы:
Теперь подставим это число в исходную ф-цию и определим координату у вершины параболы:
у0 = у(х0) = 2(– 2)2 + 8(– 2) + 5 = 8 – 16 + 5 = – 3
Ответ (– 2; – 3)
Напомним, что нули ф-ции – это те точки, в которых ее график пересекает ось Ох. Для их поиска необходимо приравнять ф-цию к нулю и решить уравнение. В случае с квадратичной ф-цией мы получим квадратной уравнение.
Пример. Постройте график ф-ции у = х2 – 4х + 3, отметьте на нем вершину параболы и нули ф-ции.
Решение. Приравняем ф-цию к нулю:
х2 – 4х + 3 = 0
Решим это уравнение
D = b2 – 4ас = (– 4)2 – 4•1•3 = 16 – 12 = 4
Итак, нашли нули ф-ции: 1 и 3. Теперь найдем вершину параболы:
у0 = у(х0) = 22 – 4•2 + 3 = 4 – 8 + 3 = – 1
Вершина находится в точке (2; – 1). Теперь отметим ее, а также нули ф-ции на графике, и соединим их линией, похожей на параболу:
При необходимости для точности построения всегда можно вычислить значение ф-ции в нескольких дополнительных точках и провести параболу через них. Здесь мы этого делать не будем
Ответ: вершина параболы – точка (2; – 1), нули ф-ции х1 = 1 и х2 = 3
Обратите внимание, что в рассмотренном примере вершина параболы оказалась ниже нулей, поэтому ее ветви смотрят вверх. Вообще, если коэффициент а > 0, то ветви смотрят вверх, а если а < 0, то они смотрят вниз. Также можно заметить ещё одно свойство квадратичной функции – вершина параболы находится точно посередине между нулями ф-ции. То есть если нули ф-ции равны 1 и 3, то координата х вершины параболы равна их среднему арифметическому:
х0 = (х1 + х2)/2 = (1 + 3)/2 = 2
Заметим, что не все квадратичные ф-ции имеют нули, ведь не каждое квадратное уравнение имеет решение.
Пример. Постройте графики ф-ций
у = – 2х2– 4х + 6
у = – 3х2 + 6х – 4
Решение. Начнем с первой ф-ции. Сначала найдем ее нули:
– 2х2 – 4х + 6 = 0
D = b2 – 4ас = (– 4)2 – 4•(– 2)•6 = 16+48 = 64
Найдем вершину. Сначала используем обычную формулу:
Далее просто проверим себя, найдя среднее арифметическое нулей ф-ции:
Как и ожидалось, получились одинаковые результаты! Вычислим теперь у0:
у0 = у(х0) = – 2(– 1)2 – 4(– 1) + 6 = – 2 + 4 + 6 = 8
Итак, вершина первой ф-ции – это точка (– 1; 8).
Перейдем ко второй ф-ции. Попробуем найти ее нули:
– 3х2 + 6х – 4 = 0
D = b2 – 4ас = 62 – 4•(– 3)•(– 4) = 36–48 = – 16
Дискриминант отрицательный, значит, корней у уравнения нет. Не будет и нулей и ф-ции. Найдем вершину параболы
Найдем координату у0 вершины:
у0 = у(х0) = – 3•12 + 6•1 – 4 = – 3 + 6 – 4 = – 1
Отметим, что у обоих графиков коэффициент а отрицательный, а потому их ветви будут смотреть вниз. Построим их графики:
Иногда приходится решать обратную задачу – по графику квадратичной ф-ции находить выражение, задающее эту ф-цию. Для ее решения необходимо подставлять в общий вид квадратичной ф-ции
у = ах2 + bx + c
значения квадратичной функции, взятые из графика (то есть координаты точек параболы) и получать уравнения, из которых можно найти величины a, b и c.
Пример. Запишите выражение для квадратичной ф-ции, имеющей следующий график:
Решение. Заметим, что графику параболы принадлежит точка с координатами (0; 3). Подставим эти числа, х = 0 и у = 3, в квадратичную ф-цию:
у = ах2 + bx + c
3 = а•02 + b•02 + c
3 = c
Итак, мы нашли, что коэффициент с = 3. Осталось найти а и b. Возьмем ещё одну точку, скажем, (1; 0), и подставим ее координаты (вообще в большинстве случаев удобно брать точки, одна из координат которой равна 0 или, на худой конец, единице):
у = ах2 + bx + 3
0 = а•12 + b•1 + 3
a + b = – 3
Возьмем точку с координатами (– 3; 0):
у = ах2 + bx + 3
0 = а•(– 3)2 + b•(– 3) + 3
9а – 3b = – 3
Получили два уравнения с двумя неизвестными: a + b = – 3 и 9а – 3b = – 3. Решим систему, составленную из них:
Подставим первое уравнение во второе и получим:
9а – 3(– 3 – а) = – 3
9а + 9 + 3а = – 3
12а = – 3 – 9
12а = – 12
а = – 1
Нашли а. Теперь подставим его в уравнение для b:
b = – 3 – а = – 3 – (– 1) = – 2
Получили b = – 2. Мы нашли все коэффициенты, а потому можем записать ф-цию в аналитическом виде:
у = – х2 – 2х + 3
Ответ:– х2 – 2х + 3
Общие сведения
Функцией вида р = f(r) называется зависимость ее значения от переменной величины “r” или аргумента. Функциональные тождества бывают простыми и сложными. К первым относится класс выражений, состоящих из одной переменной простого типа. Во втором случае содержится несколько аргументов или аргумент является также функцией, т. е. подчиняется определенному закону.
Монотонной называется функция, постоянно убывающая или возрастающая на заданном промежутке. Если она постоянно убывает или возрастает, то считается строго монотонной. Пусть дана функция р = f(r). Она дифференцируема на некотором интервале (а;b), является возрастающей или убывающей, когда справедливы равенства f(r1) <= f(r2) или f(r1) >= f(r2) соответственно. Кроме того, нужно учитывать, что r1 < r2 или r1 <= r2. Необходимо отметить, что точки r1 и r2 должны принадлежать (а;b).
Когда f(r) является строгой (только убывающей или возрастающей — постоянство), тогда знак «<=» или «>=» следует заменить на строгий «<» или «>»: f(r1) < f(r2) или f(r1) > f(r2) соответственно. Вышеописанные понятия можно записать математическим способом, который считается более компактным:
- Возрастающая: ∀ r1, r2 ∈ (a;b): r1 < r2 ⇒ f(r1) <= f(r2). Расшифровывается запись таким образом: для любых (∀) точек r1 и r2, принадлежащих (∈) интервалу (a;b), при условии, что r1 < r2, следует (⇒) выполнение неравенства f(r1) <= f(r2).
- Строго возрастающая: ∀ r1, r2 ∈ (a;b): r1 < r2 ⇒ f(r1) < f(r2).
- Убывающая: ∀ r1, r2 ∈ (a;b): r1 > r2 ⇒ f(r1) >= f(r2).
- Строго убывающая: ∀ r1, r2 ∈ (a;b): r1 > r2 ⇒ f(r1) > f(r2).
Следует отметить, что промежутками монотонности функции называются интервалы, на которых она возрастает или убывает. После определений необходимо рассмотреть основные теоремы, позволяющие использовать соотношения для решения различных задач.
Теорема о пределе
Теорема о пределе монотонной функции применяется для решения задач по высшей математике с использованием пределов. Ее формулировка следующая: если функция вида р = f(r) является дифференцируемой и монотонной на интервале (а;b), то в точке r0, принадлежащей заданному интервалу, она имеет конечные пределы с левой и правой стороны, а в точках r0 = a и r0 = b у нее существуют правосторонние и левосторонние границы.
Чтобы доказать утверждение, следует задать некоторую функцию, которая является монотонной. Кроме того, она должна возрастать на некотором интервале [а;b]. После этого нужно выбрать любую точку r0 ∈ (a;b]. В результате этого для ∀ r ∈ [a;r0) ⇒ f(r) <= f(r0) ⇒ f(r) ограничена сверху на [a;r0) ⇒ при существующих (∃ – знак существования) верхних границах (sup) функции f(r) = M <= f(r0). По определению для ∀ r ∈ [a;r0) ⇒ f(r) <= M.
Следует предположить, что существует некоторая переменная “e”, которая больше нуля. Она также определена на текущем интервале. Следовательно, выполняется неравенство М – е < f(e). Пусть q = r0 – e и t – значение r0 c левой границей 0 – q. Если выполняется условие ∀ r ∈ (е;r0) = (t;r0), то f(e) <= f(r). В итоге получается, что ∀ е > 0 ∃ q > 0 для r ∈ (t;r0): М – е < f(e) < f(r) <= M < M + e. Следовательно, |f(r) – M| < e. Левый предел, в котором х стремится к точке r0: lim [f(r)] |(r -> r0 – 0) = M. Отсюда следует такое соотношение: f(r0 – 0) = sup f(r), a <= r < r0.
Таким же образом доказывается правосторонний предел в точке r0 ∈ [a;b). Получается такое соотношение: f(r0 + 0) = inf f(r), r0 < r <= b. Теорема доказана. Кроме того, существуют следствия, полученные при доказательстве утверждения о пределе:
- Возрастание: f(r0 – 0) = lim [f(r)] |(r -> r0 – 0) <= lim [f(r)] |(r -> r0 + 0) = f(r0 + 0).
- Убывание: f(r0 – 0) = lim [f(r)] |(r -> r0 – 0) >= lim [f(r)] |(r -> r0 + 0) = f(r0 + 0).
Чтобы понять математические обозначения sup и inf, необходимо представить множество значений функции. Первый термин обозначает максимальное значение сверху, а второй — минимальное снизу.
Критерии возрастания и убывания
Существуют определенные признаки, по которым можно определить монотонность функции p = f(r) на некотором интервале (а;b). Для этого в математике есть еще три теоремы:
- Для убывающей и возрастающей.
- Если является строго убывающей или строго возрастающей.
- Определение по точке, производной и интервалу.
Первая теорема имеет такую формулировку: дифференцируемая функция p = f(r) на интервале (а;b) является убывающей, когда выполняется неравенство f'(r) <= 0, а также возрастающей при f'(r) >= 0 соответственно (при r ∈ данному интервалу).
Формулировка следующего утверждения только для строго возрастающей монотонной функции. В первом случае должно выполняться не одно, а два условия: f'(r) > 0 и f'(r) тождественно не эквивалентна нулю на промежутке в любой точке, принадлежащей интервалу. Для строго убывающей условия немного отличаются от предыдущих: f'(r) < 0 и производная f'(r) также не равна нулевому значению на указанном промежутке. Третья теорема позволяет определить характер монотонности p = f(r) в заданной точке r0 ∈ (а;b). Существует два варианта соотношений: для убывающей f'(r0) < 0 и возрастающей: f'(r0) > 0.
Основные свойства
Для функций на интервале (а;b) существуют некоторые утверждения, позволяющие исследовать составные выражения, а также решать различные задачи. К свойствам монотонных функций относятся следующие:
- Сумма двух убывающих (возрастающих) k = f(t) и l = f(v) является возрастающим (убывающим) выражением.
- Если k = f(t) возрастает, то -k = f(t) (противоположная) будет убывать. При убывании первой вторая будет возрастать соответственно.
- Когда у k = f(t) есть обратная вида k2 = 1 / f(t), тогда при убывании первой вторая будет возрастать. Если первая возрастает, то вторая убывает.
- Результатом произведения двух убывающих (возрастающих) является убывающая функция. Также должны выполняться такие условия: k = f(t) >= 0 и l = f(v) >= 0.
- Если k = f(t) возрастает или убывает на (а;b), а l = f(t) возрастает или убывает на (c;d), и (а;b) входит в (c;d), то композиция функций к∘ l (k(l(t))) также возрастает или убывает.
После изучения теорем и основных свойств нужно определить минимум базовых знаний, которые необходимы для исследования на монотонность любого выражения. Кроме того, следует знать графики некоторых функций. Для их построения можно использовать специальные онлайн-калькуляторы и программы, позволяющие выделять результаты разными цветами.
Базовые знания
Для исследования функции на монотонность специалисты рекомендуют руководствоваться некоторыми правилами, которые объединяются в универсальный алгоритм. Он является достаточным для выполнения такого задания и имеет следующий вид:
- Найти производную первого порядка – f'(r).
- Приравнять выражение, полученное в первом пункте, к 0.
- Найти критические точки, решив уравнение во втором пункте.
- Определить знак f'(r) на промежутках, полученных в результате разбиения критическими точками. Найти промежутки убывания и возрастания.
Последний пункт следует реализовывать при помощи таблицы. Необходимо строго придерживаться алгоритма, поскольку неверные действия способны существенно повлиять на результат.
Нахождение производной
Для поиска производной необходимо выполнить такие шаги: вынести константу, упростить выражение и воспользоваться таблицей дифференциалов элементарных функций (рис. 1). Первые два элемента считаются подготовительными, поскольку позволяют оптимизировать процесс вычисления. Для упрощения следует применять формулы сокращенного умножения, свойства дробей, разложение на множители и т. д. После приведения выражения к упрощенному виду нужно воспользоваться таблицей производных элементарных функций.
Рисунок 1. Дифференциалы простых выражений.
Однако при решении задач не всегда попадаются простые выражения. Для составных существуют определенные правила:
- Сумма: [k(t) + l(t)]’ = k'(t) + l'(t).
- Разность: [k(t) – l(t)]’ = k'(t) – l'(t).
- Произведение: [k(t) * l(t)]’ = k'(t) * l(t) + l'(t) * k(t).
- Частное: [k(t) / l(t)]’ = [k'(t) * l(t) – l'(t) * k(t)] / (l(t))^2.
- Сложная: [k(l(t))]’ = l'(t) * k'(t).
Специалисты рекомендуют для проверки использовать программы, но это не значит, что задачи должны решаться только с помощью онлайн-сервисов и математических пакетов.
Корни уравнений и критические точки
Следующим этапом является решение равенства с неизвестным. Необходимо отметить, что уравнения делятся на следующие виды: линейные, квадратные, кубические, биквадратные, тригонометрические, логарифмические, степенные, показательные и иррациональные.
Первый тип решается по очень простому алгоритму: следует перенести неизвестные в одну часть, а известные — в другую. Для решения квадратного уравнения (aw^2 + bw + c = 0) нужно его упростить, разложить на множители или вычислить дискриминант. Последний вычисляется по следующей формуле: D = b^2 – 4ac. Количество корней зависит от значения D и определяется по таким формулам:
- Два решения при D > 0: w1 = (-b – [D]^(1/2)) / 2a и w2 = (-b + [D]^(1/2)) / 2a.
- D = 0 (одно): w = (-b) / 2a.
- Нет корней, когда D < 0.
Используя метод разложения на множители, можно решить без D. Например, в выражении x(x-1)(x-4) = 0 рассматривается три уравнения: x1 = 0, х2 -1 = 0 и х3 – 4 = 0. Решение кубических и биквадратных равенств с неизвестной осуществляется методом разложения на множители. При этом понижается степень до 2, а дальше находятся его корни.
Для нахождения корней других уравнений следует воспользоваться заменой, а затем свести к линейному или квадратному. Следует отметить, что решая трансцендентные (логарифмы и показатели), следует знать правила логарифмирования и свойства степени. Корни также находятся при помощи замены.
Критическими называются точки, в которых функция меняет свое поведение (четность, периодичность, экстремумы и т. д.). При исследовании они записываются в специальную таблицу поведения в виде промежутков.
Пример решения
Задачи бывают нескольких типов. В одних следует найти промежутки монотонности, а во-вторых — доказать на основании теорем, что она возрастает или убывает на заданном промежутке. Например, необходимо найти промежутки монотонности функции z(y) = (y^2 + 1) / y. Следует отметить, что она является дифференцируемой. Ее область определения D(z) = (-бесконечность;0) U (0;+бесконечность). Решать ее нужно по алгоритму:
- Производная: [(y^2 + 1) / y]’ = (y^2 – 1) / y.
- Приравнять к 0: (y^2 – 1) / y = 0.
- Найти корни – критические точки (y – 1)(y + 1) / y = 0: y1 не равен 0, y2 = 1 и у3 = – 1.
- Построить таблицу.
| y | (-infinity;-1) | (-1;0) | (0;1) | (1;+infinity) |
| z’ | – | + | – | + |
| z | У | В | У | В |
Таблица 1. Интервалы монотонности.
Если функция является четной, то эта особенность не влияет на результат, поскольку ее производная может быть с отрицательным знаком. Примером является обычный тригонометрический косинус.
Таким образом определение монотонности функции на заданном промежутке является одним из элементов исследования ее поведения. Для осуществления этой операции применяются специальный алгоритм, теоремы и свойства.
Исследование функций должно начинаться с установления области определения и интервалов монотонности. Для этого студент должен обладать хорошими знаниями поведения элементарных функций и последующим теоретическим материалом.
Функция 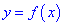
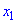
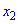
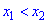
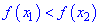
Для того чтобы функция 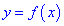
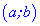
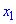
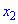
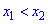
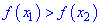
Как возрастающие, так и убывающие функции называются монотонными, а интервалы в которых
функция возрастает или убывает – интервалами монотонности.
Область возрастания и убывания функции 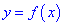
некотором интервале производная больше нуля 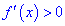
если же наоборот 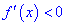
Интервалы монотонности могут прилегать друг к другу или точками, где производная равна нулю
или точками, где производная не существует. Эти точки называются критическими точками.
Для того, чтобы найти интервалы монотонности функции 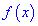
1) найти область определения функции 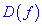
2) вычислить производную данной функции;
3) найти критические точки из условия равенства нулю производной 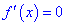
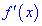
4) разделить критическими точками область определения на интервалы, в каждом из которых определить знак производной.
На интервалах где производная положительная функция возрастает, а где отрицательная – убывает.
———————————–
Примеры.
Рассмотрим задачу из сборника В.Ю. Клепко, В.Л. Голец “Высшая математика в примерах и задачах” на нахождение интервалов монотонности функции.
1. (3.36.10)
Функция существует во всех точках где определен логарифм и он не обращается в нуль, а также где функция под корнем принимает неотрицательные значения. На основе этого находим
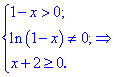
Итак, областью определения будут два интервала
2. (3.36.11)
С подкоренной функцией ведем себя как и в предыдущем примере, а функция 
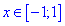
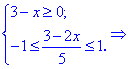
Единственным промежутком, который удовлетворяет эти условия являются следующий
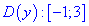
3. (3.36.13)
Область определения функции находим из двух условий
Первое условие дает две точки
в которых функция не существует.
С второго условия получим
Исследуем поведение функции в интервалах монотонности на которые разбивают заданные точки. Для этого
выбираем произвольные точки 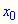
Функция 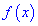
Вместе с первым условием получим следующую область определения
——————————
Рассмотрим примеры исследования монотонности функции из сборника задач Дубовика В.П., Юрика И.И. “Высшая математика” .
І. (5.705) Показать, что функция 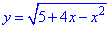
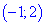
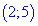
1) Областью определения функции будет множество значений для которых подкоренная функция принимает неотрицательные значения.
Решим квадратное уравнение
Определим знак функции на всем интервале
Таким образом получим следующую область определения
2) Найдем производную
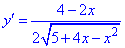
3) Приравняем ее к нулю и найдем критические точки:
Не стоит забывать и о точках, в которых производная не существует. Это корни уравнения в
знаменателе. Итак производная существует на интервале 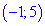
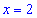
4) Знаки производной: подставляем 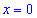
Так что на интервале 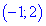
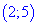
ІІ. (5.715) Найти интервалы монотонности функции
1. Областью определения будет множество точек 
основе этого получим
Итак
2) Найдем производную функции
3) Находим критические точки
Другая точка, где производная не существует это 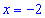
Таким образом получили два интервала монотонности 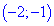
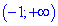
4) Выясним где функция возрастает, а где убывает. Подставим точки 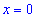
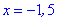
производной
Исследуемая функция на интервале 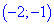
При исследовании функций на монотонность определите все критические точки в которых производная равна нулю или не существует. Также не забывайте при этом учитывать область определения функции. Остальное зависит от Ваших знаний свойств элементарных функции, поскольку именно на их основе построены все задачи, которые Вам задают преподаватели.
———————————————-
Посмотреть материалы:
- Исследования функции и построения графика
- Наибольшее и наименьшее значение функции на отрезке
- Локальный экстремум функции. Примеры
- Выпуклость и вогнутисть графика функции
- Асимптоты функции
- Область определения функции
Е
сли
для всех точек отрезка
при
выполняется равенство
,
то функция
называется возрастающей
на
.
При
выполнении условий
,
функция
называется убывающей
на
.
Интервалы,
в которых функция
только
возрастает или только убывает, называются
интервалами
монотонности
функции.
П
ризнак
возрастания.
Дифференцируемая функция
возрастает на отрезке
тогда и только тогда, когда её производная
.
П
ризнак
убывания.
Дифференцируемая функция
убывает на отрезке
тогда и только тогда, когда её производная
.
В
точках, отделяющих интервалы монотонности
функции, производная функции обращается
в нуль или не существует. Эти точки
называются критическими.
Для
нахождения интервалов монотонности
функции
необходимо
найти все её критические точки и
установить знак производной в каждом
из интервалов, на которые критические
точки разбивают область существования
функции.
Пример
7.13.
Найдите интервалы монотонности функции
.
Ф
ункция
определена на всей числовой оси. Найдём
её производную.
.
Найдём
критические точки, приравняв производную
к нулю.
— критические.
Результаты исследования занесём в
таблицу:
|
|
|
|
|
|
|
|
|
+ |
|
+ |
||
|
|
|
|
|
|
Т
аким
образом, функция
возрастает а интервалах
и
,
а убывает на интервале
.
§ 6. Экстремум функции. Необходимый признак.
Т
очка
называется точкой
максимума
(maximum)
функции
,
если значение функции в этой точке
больше её значений во всех точках
некоторого интервала, содержащего точку
,
т.е.
для любого
(
—
мало
по величине).
Т
очка
называется точкой
минимума
(minimum)
функции
,
если значение функции в этой точке
меньше её значений во всех точках
некоторого интервала, содержащего точку
,
т.е.
.
Точки,
в которых функция достигает максимума
или минимума, называются точками
экстремума
функции, а значения функции в этих точках
называют экстремальными.
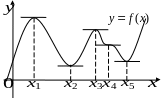
Ф
ункция,
заданная кривой на рисунке выше, в точках
и
достигает максимума, в точках
и
—
минимума, в точке
—
экстремума нет. Очевидно, что функция
имеет производную, равную нулю в
критических точках. Касательная к кривой
в этих точках параллельна оси
.
Необходимый
признак экстремума.
Если дифференцируемая функция достигает
в некоторой точке экстремума, то её
производная в этой точке равна нулю или
не существует.
§ 7. Достаточные признаки экстремума функции.
П
ервый
достаточный признак.
Пусть функция
непрерывна в некотором интервале,
содержащем критическую точку
и дифференцируема во всех точках этого
интервала (кроме, быть может самой точки
).
Тогда, если:
а)
при
,
при
,
то в точке
функция
достигает максимума;
б)
при
,
при
,
то в точке
функция
достигает
минимума.
В
торой
достаточный признак экстремума.
Пусть функция
имеет
в точке
производную
и
непрерывную вторую производную
.
Тогда, если
в точке
будет максимум, а если
в точке
будет минимум.
Пример
7.14. В
примере 7.13 точки
являются точками экстремума. В точке
функция достигает максимума, в точке
функция достигает минимума.
Пример
7.15.
Издержки предприятия выражаются формулой
,
где
—
объём производства. При каком объёме
производства средние издержки будут
минимальными?
С
редние
издержки выражаются формулой
.
Найдем минимум этой функции.
.
.
Найдем
вторую производную функции.
,
значит, по второму достаточному признаку
экстремума при
средние издержки достигают минимума.
Соседние файлы в предмете Высшая математика
- #
- #
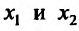
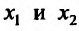 из интервала (а, b), удовлетворяющих условию
из интервала (а, b), удовлетворяющих условию 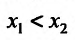 справедливо неравенство
справедливо неравенство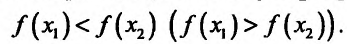 Неубывающие и невозрастающие функции называют монотонными функциями.
Неубывающие и невозрастающие функции называют монотонными функциями.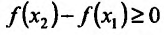
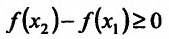
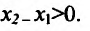
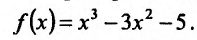
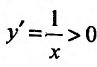
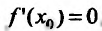
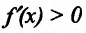 на
на 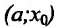 и
и 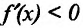 на
на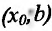 , то точка
, то точка 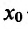 – точка максимума функции f(x);
– точка максимума функции f(x);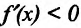 на
на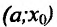 и
и 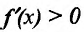 на
на 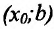 , то точка
, то точка  – точка минимума функции f(x);
– точка минимума функции f(x);