Пример 1.
Найти область сходимости степенного
ряда:
а)
![]() ; б)
; б)![]() ;
;
в)
![]() ; г)
; г)![]() ;
;
д)
![]() .
.
а)
Найдем радиус сходимости R.
Так как
![]() ,
,![]() ,
,
то
 .
.
Итак, ряд сходится
абсолютно для всех x,
удовлетворяющих неравенству
![]() ,
,
то есть интервал сходимости ряда![]() .
.
Исследуем на
сходимость данный ряд на концах интервала
сходимости.
При ![]() получаем
получаем
числовой ряд
![]() .
.
Этот ряд сходится, так как является
обобщенным гармоническим рядом![]() при
при![]() .
.
При ![]() получаем
получаем
числовой ряд
![]() .
.
Этот ряд абсолютно сходящийся, так как
ряд, составленный из абсолютных величин
его членов![]() ,
,
сходящийся.
Итак, область
сходимости данного ряда
![]() .
.
б)
Найдем радиус
сходимости R.
Так как
![]() ,
,
то .
.
Итак, интервал
сходимости ряда
![]() .
.
Исследуем на
сходимость данный ряд на концах интервала
сходимости.
При
![]() имеем числовой ряд
имеем числовой ряд
![]() .
.
Этот ряд расходящийся, так как![]() .
.
При
![]() имеем числовой ряд
имеем числовой ряд
![]() .
.
Этот ряд расходящийся, так как![]()
не существует.
Итак, область
сходимости данного ряда
![]() .
.
в)
Найдем радиус
сходимости R.
Так как
![]() ,
,![]() то
то .
.
Итак, интервал
сходимости
![]() .
.
Область сходимости данного ряда совпадает
с интервалом сходимости, то есть ряд
сходится при любом значении переменнойx.
г)
Найдем радиус сходимости R.
Так как
![]() ,
,![]() то
то![]() .
.
Так как
![]() ,
,
то ряд сходится только в точке![]() .
.
Значит, область сходимости данного ряда
представляет собой одну точку![]() .
.
д)
Найдем радиус сходимости R.
Так как
![]() ,
,![]() ,
,
то
 .
.
Итак, ряд сходится
абсолютно для всех x,
удовлетворяющих неравенству
![]() ,
,
то есть![]() .
.
Отсюда
![]() − интервал сходимости,
− интервал сходимости,![]() − радиус сходимости.
− радиус сходимости.
Исследуем данный
ряд на сходимость на концах интервала
сходимости.
При
![]() получаем числовой ряд
получаем числовой ряд
![]() ,
,
который
расходится (гармонический ряд).
При
![]() получаем числовой ряд
получаем числовой ряд![]() ,
,
который сходится условно (ряд сходится
по признаку Лейбница, а ряд, составленный
их абсолютных величин его членов,
расходится, так как является гармоническим).
Итак, область
сходимости ряда
![]() .
.
2.3. Ряды Тейлора и Маклорена.
Разложение
функций в степенной ряд.
Приложение
степенных рядов к приближенным вычислениям
Примеры решения задач
Пример 1.
Разложить в степенной ряд функции:
а)
![]() ; б)
; б)![]() ;
;
в)
![]() ; г)
; г)![]() .
.
а)
Заменив в формуле
![]() x
x
на
![]() ,
,
получим искомое разложение:
![]() ,
,
где ![]()
или
![]() .
.
б)
Заменяя в равенстве
![]() ,
,
где ![]()
x
на
![]() ,
,
получим искомое разложение:
![]() .
.
в)
Данную функцию можно записать так: ![]() .
.
Чтобы найти искомый ряд, достаточно в
разложение
![]() .,
.,
где ![]()
подставить ![]() .
.
Тогда получим:

или
![]() .
.
г)
Данную функцию можно переписать так:
![]() .
.
Функцию ![]()
можно разложить в степенной ряд, положив
в биномиальном ряде ![]() ,
,
получим ![]() .
.
![]() ,
,
где ![]() .
.
Чтобы получить
искомое разложение, достаточно перемножить
полученные ряды (ввиду абсолютной
сходимости этих рядов).
Следовательно,
![]()
![]() ,
,
где ![]() .
.
Пример 2.
Найти приближенные значения данных
функций:
а) ![]()
с точностью до 0,0001;
б) ![]()
с точностью до 0,00001.
а)
Так как ![]() ,
,
то в разложение функции ![]() ,
,
где ![]() подставим
подставим ![]() :
:
 или
или ![]()
Так как ![]() ,
,
то требуемая точность будет обеспечена,
если ограничиться только первыми двумя
членами полученного разложения.
Итак,
![]() .
.
б)
![]() .
.
Используем
биномиальный ряд
![]() .,
.,
где ![]() .
.
Полагая ![]()
и ![]() ,
,
получим следующее разложение:
![]()
или
![]() .
.
Если в последнем
знакочередующемся ряде учитывать только
первые два члена, а остальные отбросить,
то погрешность при вычислении ![]()
не превысит по абсолютной величине
0,000006. Тогда погрешность при вычислении
![]()
не превысит числа ![]() .
.
Следовательно,
![]() .
.
Пример 3.
Вычислить с точностью до 0,001:
а)  ; б)
; б)
 .
.
а)
 .
.
Разложим
подынтегральную функцию в степенной
ряд. Для этого подставим в биномиальный
ряд ![]()
и заменим x
на ![]() :
:
![]() .
.
Так как отрезок
интегрирования ![]()
принадлежит области сходимости
полученного ряда ![]() ,
,
то будем интегрировать почленно в
указанных пределах:

![]() .
.
В полученном
знакочередующемся ряде четвертый член
по абсолютной величине меньше 0,001.
Следовательно, требуемая точность будет
обеспечена, если учитывать только первые
три члена ряда.
 .
.
Так как первый из
отброшенных членов имеет знак минус,
то полученное приближенное значение
будет с избытком. Поэтому ответ с
точностью до 0,001 равен 0,487.
б)
Предварительно представим подынтегральную
функцию в виде степенного ряда. Заменим
в разложении функции
![]() ,
,
где ![]()
x
на
![]() ,
,
получим:
![]()
Тогда
![]() .
.

![]() .
.
Полученный
знакочередующийся ряд удовлетворяет
условиям признака Лейбница. Четвертый
член ряда по абсолютной величине меньше
0,001. Чтобы обеспечить требуемую точность,
достаточно найти сумму первых трех
членов.
Следовательно,  .
.
Соседние файлы в папке Матаматика
- #
- #
- #
- #
- #
- #
Функциональные и степенные ряды
Возьмем последовательность натуральных чисел n{n} и поставим каждому n{n} в соответствие функцию fn(x)f_n (x). Если функции fn(x)f_n (x) определены на некотором множестве x∈Ex in E, E⊂RE subset R, то на множестве EE определено выражение:
f1(x)+f2(x)+f3(x)+…+fn(x)+…,f_1 (x)+f_2 (x)+f_3 (x)+ ldots +f_n (x)+ ldots,
состоящее из функций fn(x)f_n (x), которое называется функциональным рядом.
В общем виде функциональный ряд записывается как:
∑n=1∞fn(x)sumlimits_{n=1}^{infty} f_n(x)
Примеры функциональных рядов
1+cosx2!+cos2×3!+cos3×4!+…+cosnx(n+1)!+…=∑n=1∞cosnx(n+1)!1+frac{cos x}{2!}+frac{cos 2x}{3!}+frac{cos 3x} {4!} +ldots +frac{cos nx}{(n+1)!}+ldots=sumlimits_{n=1}^{infty}frac{cos nx} {(n+1)!}
ex−ex+13+ex+29−ex+327+…+(−1)nex+n3n+…=∑n=0∞(−1)nex+n3ne^{x}-frac{e^{x+1}}{3}+frac{ e^{x+2}}{9}-frac{e^{x+3}}{27} +ldots +(-1)^nfrac{ e^{x+n}}{3^n}+ldots=sumlimits_{n=0}^{infty} (-1)^n frac{ e^{x+n}}{3^n}
Степенные ряды являются одним из видов функциональных рядов и в общем виде записываются как:
a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…=∑k=0∞ak(x−x0)ka_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n+ldots=sumlimits_{k=0}^{infty} a_k(x-x_0)^k
где a0,a1,…,an,…a_0, a_1, ldots, a_n, ldots – постоянные, коэффициенты ряда,
x0x_0 – центр интервала сходимости ряда ∣x−x0∣<R|x-x_0|<R,
RR – радиус сходимости степенного ряда.
Примеры степенных рядов
12+2!(x−5)4+3!(x−5)28+…+(n+1)!(x−5)n2n+1+…=∑n=0∞(n+1)!(x−5)n2n+1frac{1}{2}+frac{2!(x-5)}{4}+frac{3!(x-5)^2}{8}+ldots +frac{(n+1)!(x-5)^n}{2^{n+1}}+ldots =sum limits_{n=0} ^{infty} frac{(n+1)!(x-5)^n}{2^{n+1}}
ex−ex+13+ex+29−ex+327+…+(−1)nex+n3n+…=∑n=0∞(−1)nex+n3ne^{x}-frac{e^{x+1}}{3}+frac{ e^{x+2}}{9}-frac{e^{x+3}}{27} +ldots +(-1)^nfrac{ e^{x+n}}{3^n}+ldots=sumlimits_{n=0}^{infty} (-1)^n frac{ e^{x+n}}{3^n}
Сходимость степенных рядов
Сумму SnS_n первых nn членов степенного ряда называют nn–й частичной суммой:
Sn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)nS_n(x)= a_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n
Если при определенном значении x∈Ex in E существует конечный предел:
limn→∞Sn(x)=S(x)limlimits_{n to infty } S_n (x) = S (x)
то ряд называется сходящимся, а значение S(x)S(x) называют суммой ряда. Если сходится ряд, составленный из абсолютных величин его членов, то такой ряд называется абсолютно сходящимся.
Если степенной ряд сходится в точке x=x1x=x_1, то он сходится абсолютно и при:
∣x∣<∣x1∣|x|<|x_1 |
Если степенной ряд расходится в точке x=x2x=x_2, то он расходится и при:
∣x∣>∣x2∣|x|>|x_2 |
Интервалом сходимости степенного ряда является:
(x0−R,x0+R)(x_0-R,x_0+R)
Здесь RR – радиус сходимости степенного ряда. Степенной ряд расходится при:
∣x−x0∣>R|x-x_0 |>R
Для граничных точек интервала
∣x−x0∣>R|x-x_0 |>R
степенной ряд может, как сходится, так и расходится, для чего требуется дополнительное изучение.
Основные признаки сходимости
Приведем основные признаки, используемые для определения сходимости степенных рядов.
1-й признак сравнения
Пусть даны два ряда с положительными членами:
∑n=1∞unsum limits_{n=1} ^{infty} u_n и ∑n=1∞vnsum limits_{n=1} ^{infty} v_n
причем, un≤vnu_n le v_n для всех номеров, начиная с некоторого nn. Тогда:
-
Если ряд ∑n=1∞vnsum limits_{n=1} ^{infty} v_n сходится, то сходится и ряд ∑n=1∞unsum limits_{n=1} ^{infty} u_n
-
Если ряд ∑n=1∞unsum limits_{n=1} ^{infty} u_n расходится, то расходится и ряд ∑n=1∞vnsum limits_{n=1} ^{infty} v_n
2-й признак сравнения
Пусть даны два ряда с положительными членами:
∑n=1∞unsum limits_{n=1} ^{infty} u_n и ∑n=1∞vnsum limits_{n=1} ^{infty} v_n
и существует конечный и отличный от нуля предел:
limn→∞unvn≠0limlimits_{n to infty } dfrac{ u_n }{ v_n }ne 0
Тогда ряды
∑n=1∞unsum limits_{n=1} ^{infty} u_n и ∑n=1∞vnsum limits_{n=1} ^{infty} v_n
сходятся или расходятся одновременно.
Признак Лейбница для знакочередующихся рядов
При исследовании степенных рядов на сходимость часто используется признак Лейбница для знакочередующихся рядов. Ряд, содержащий как положительные, так и отрицательные члены, называют знакопеременным.
Ряд вида:
b1−b2+b3−b4+…+(−1)n+1bn+1+…=∑k=1∞(−1)k+1bk+1b_1-b_2+b_3-b_4+ ldots +{(-1)}^{n+1}b_{n+1}+ldots=sumlimits_{k=1} ^ {infty}{(-1)}^{k+1}b_{k+1},
когда любые два соседних члена имеют противоположные знаки, называется знакочередующимся.
Очевидно, каждый знакочередующийся ряд является знакопеременным.
В случае, когда выполняется два условия:
b1>b2>b3>b4>…>bn>…b_1>b_2>b_3>b_4> ldots >b_{n}> ldots, т.е когда члены ряда по модулю монотонно убывают
и
limn→∞an=0limlimits_{n to infty }{a_n}=0, т.е. когда общий член ряда стремится к нулю при n→∞n to infty, ряд сходится. Если, помимо этого, сходится ряд
b1+b2+b3+b4+…+bn+1+…=∑k=1∞bk+1b_1+b_2+b_3+b_4+ ldots + b_{n+1}+ldots=sumlimits_{k=1} ^ {infty} b_{k+1}
составленный из модулей исходного ряда, то такой ряд называют абсолютно сходящимся. Если признак Лейбница выполняется, но, при этом, ряд из абсолютных значений не сходится, то такой ряд называют условно сходящимся.
Признак Даламбера
Пусть дан ряд с положительными членами
∑n=1∞unsum limits_{n=1} ^{infty} u_n
и существует конечный предел
limn→∞un+1un=1limlimits_{n to infty } dfrac{ u_{n+1} }{ u_n }=1
Тогда, если l<1l<1, то данный ряд сходится; если же l>1l>1, то – расходится. Если l=1l=1 , то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов.
Признак Коши
Пусть дан ряд с положительными членами
∑n=1∞unsum limits_{n=1} ^{infty} u_n
такой, что существует конечный предел
limn→∞unn=1limlimits_{n to infty } sqrt [n] { u_n }=1
Тогда, если l<1l<1, то ряд сходится. В случае, если l>1l>1, то ряд расходится. Если же l=1l=1, то вопрос о сходимости рядя требует дополнительного исследования.
Интегральный признак сходимости
Пусть дан ряд с положительными членами
∑n=1∞unsum limits_{n=1} ^{infty} u_n
для которого существует положительная, непрерывная и монотонно убывающая на промежутке [1,+∞)[1, +infty) функция f(x)f(x) такая, что f(n)=an,n=1,2,…f(n)=a_n, n=1,2, ldots
Тогда данный ряд и несобственный интеграл ∫0∞f(x)dxintlimits_0^infty f(x) dx сходятся или расходятся одновременно.
Примеры исследования степенных рядов
Пример 1
Найти область сходимости ряда
∑n=1∞(x−1)n+12n(n+1)sum limits_{n=1} ^{infty} dfrac{(x-1)^{n+1}}{2^n {(n+1)}}
Используем признак Даламбера. Учитывая, что
∣an+1an∣=∣(x−1)(n+1)+12n+1(n+1+1):(x−1)n+12n(n+1)∣=∣(x−1)n+2(x−1)n+1⋅2n2n+1⋅n+1n+2∣=∣x−1∣2⋅n+1n+2Bigl| dfrac{a_{n+1}}{a_n} Bigr|= Bigl| dfrac {(x-1)^{(n+1)+1}}{2^{n+1}(n+1+1)}: dfrac {(x-1)^{n+1}}{2^n(n+1)}Bigr|= Bigl| dfrac {(x-1)^{n+2}}{(x-1)^{n+1}}cdot dfrac {2^n}{2^{n+1}}cdot dfrac {n+1}{n+2}Bigr|=dfrac {|x-1|}{2} cdot dfrac{n+1}{n+2}
находим:
limn→∞∣an+1an∣=limn→∞(∣x−1∣2⋅n+1n+2)=∣x−1∣2⋅limn→∞1+1n1+2n=∣x−1∣2limlimits_{n to infty }Bigl| dfrac{a_{n+1}}{a_n} Bigr|= limlimits_{n to infty} left(dfrac {|x-1|}{2} cdot dfrac{n+1}{n+2}right)= dfrac {|x-1|}{2} cdot limlimits_{n to infty }dfrac{1+dfrac{1}{n}}{1+dfrac{2}{n}}=dfrac {|x-1|}{2}
Для определения требуемых значений xx решаем неравенство:
∣x−1∣2<1⇔−1<x−12<1⇔−2<x−1<2⇔−1<x<3dfrac{|x-1|}{2}<1 Leftrightarrow -1<dfrac{x-1}{2}<1 Leftrightarrow -2<x-1<2 Leftrightarrow -1<x<3
Таким образом, при x∈(−1,3)x in (-1,3) ряд сходится абсолютно, а при $ x notin (-1,3) $ ряд расходится. Это означает, что (−1,3)(-1,3) – интервал сходимости данного ряда.
Для полного решения задачи необходимо исследовать сходимость ряда на концах интервала, при x=−1x=-1 и x=3x=3.
При x=3x=3 получаем ряд
∑n=1∞(x−1)n+12n(n+1)=∑n=1∞(3−1)n+12n(n+1)=∑n=1∞2n+12n(n+1)=∑n=1∞2n+1sum limits_{n=1}^{infty} dfrac{(x-1)^{n+1}}{2^n(n+1)}=sum limits_{n=1} ^{infty} dfrac{(3-1)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{2^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{2}{n+1}
Применим 2-й признак сравнения и проведем сравнение этого ряда с гармоническим:
∑n=1∞1nsum limits_{n=1} ^{infty} dfrac{1}{n}
Получаем:
limn→∞(2n+1:1n)=limn→∞(2nn+1)=limn→∞(21+1n)=2≠0limlimits_{n to infty }left( dfrac{2}{n+1}:dfrac{1}{n}right)= limlimits_{n to infty }left( dfrac{2n}{n+1}right)=limlimits_{n to infty }left( dfrac{2}{1+dfrac{1}{n}}right)=2 ne 0
Как известно, гармонический ряд расходится. Так как полученный предел отличен от нуля, то ряды
∑n=1∞2n+1sum limits_{n=1} ^{infty} dfrac{2}{n+1} и ∑n=1∞1nsum limits_{n=1} ^{infty} dfrac{1}{n}
сходятся или расходятся одновременно. В данном случае, они расходятся, и, следовательно, исходный ряд при x=2x=2 расходится.
При x=−1x=-1 получаем ряд
∑n=1∞(x−1)n+12n(n+1)=∑n=1∞(−1−1)n+12n(n+1)=∑n=1∞(−2)n+12n(n+1)=∑n=1∞(−1)n+1⋅(2)n+12n(n+1)=∑n=1∞(−1)n+1⋅2n+1sum limits_{n=1}^{infty} dfrac{(x-1)^{n+1}}{2^n(n+1)}=sum limits_{n=1} ^{infty} dfrac{(-1-1)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{(-2)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{(-1)^{n+1}cdot (2)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{ (-1)^{n+1}cdot 2}{n+1}
Как было показано, этот ряд не является абсолютно сходящимся, так как ряд, составленный из абсолютных значений:
∑n=1∞∣(−1)n+1⋅2n+1∣=∑n=1∞2n+1sum limits_{n=1} ^{infty}Bigl| dfrac{ (-1)^{n+1}cdot 2}{n+1} Bigl|=sum limits_{n=1} ^{infty} dfrac {2}{n+1}
расходится.
Используя признак Лейбница, выясним сходимость данного знакочередующегося ряда. Очевидно, что неравенство:
bn>bn+1⇔2n+1>2(n+1)+1⇔2n+1>2n+2b_n>b_{n+1} Leftrightarrow dfrac{2}{n+1}>dfrac{2}{(n+1)+1} Leftrightarrow dfrac{2}{n+1}>dfrac{2}{n+2}
выполнено для всех n=1,2,3,…n=1,2,3, ldots
Выполняется и второе условие:
limn→∞an=limn→∞3n+2=0limlimits_{n to infty } a_n = limlimits_{n to infty } dfrac{3}{n+2}=0
Оба условия признака Лейбница выполнены. Это означает, что знакочередующийся ряд
∑n=1∞(−1)n+13n+2sum limits_{n=1} ^{infty} (-1)^{n+1} dfrac {3}{n+2}
сходится. Так как этот ряд не является абсолютно сходящимся, то знакочередующийся ряд сходится условно.
Таким образом, областью сходимости исходного ряда является промежуток:
x∈[−1,3)x in [-1,3)
Пример 2
Найти область сходимости ряда
∑n=2∞(x+3)nnln3nsum limits_{n=2} ^{infty} dfrac{(x+3)^n}{nln^3{n}}
Используем признак Даламбера. Учитывая, что
∣an+1an∣=∣(x+3)n+1(n+1)ln3(n+1):(x+3)nnln3n∣=∣(x+3)n+1(x+3)n⋅nn+1⋅ln3nln3(n+1)∣=∣x+3∣⋅nn+1⋅ln3nln3(n+1)Bigl| dfrac{a_{n+1}}{a_n} Bigr|= Bigl| dfrac {(x+3)^{n+1}}{(n+1)ln^3{(n+1)}}: dfrac {(x+3)^n}{nln^3{n}}Bigr|= Bigl| dfrac {(x+3)^{n+1}}{(x+3)^n}cdot dfrac {n}{n+1}cdot dfrac {ln^3{n}}{ln^3{(n+1)}}Bigr|=|x+3| cdot dfrac{n}{n+1} cdot dfrac{ln^3{n}}{ln^3{(n+1)}}
находим c помощью правила Лопиталя:
limn→+∞∣an+1an∣=limn→+∞(∣x+3∣⋅nn+1⋅ln3nln3(n+1))=∣x+3∣⋅limn→∞11+1n⋅(limn→∞lnnln(n+1))3=∣x+3∣⋅limn→∞1n1n+1=∣x+3∣limlimits_{n to +infty } Bigl| dfrac {a_{n+1}}{a_n}Bigr| = limlimits_{n to +infty } left( |x+3| cdot dfrac {n}{n+1}cdot dfrac{ln^3{n}}{ln^3{(n+1)}} right)=|x+3| cdot limlimits_{n to infty } dfrac {1}{1+dfrac{1}{n}} cdot {left(limlimits_{n to infty } dfrac {ln{n}}{ln{(n+1)}}right)}^3= |x+3| cdot limlimits_{n to infty } dfrac{dfrac{1}{n}}{dfrac{1}{n+1}}=|x+3|
Для определения требуемых значений x решаем неравенство:
∣x+3∣<1⇔−1<x+3<1⇔−4<x<−2|x+3|<1 Leftrightarrow -1<x+3<1 Leftrightarrow -4<x<-2
Таким образом, при x∈(−4,−2)x in (-4,-2) ряд сходится абсолютно, а при x∉(−4,−2)x notin (-4,-2) ряд расходится. Это означает, что (−4,−2)(-4,-2) – интервал сходимости данного ряда.
Для полного решения задачи необходимо исследовать сходимость ряда на концах интервала, при x=−4x=-4 и x=−2x=-2.
При x=−4x=-4 получаем ряд
∑n=2∞(x+3)nnln3n=∑n=2∞(−4+3)nnln3n=∑n=2∞(−1)nnln3nsum limits_{n=2} ^{infty} dfrac{(x+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{(-4+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{(-1)^n}{nln^3{n}}
Воспользуемся интегральным признаком. Возьмем функцию:
f(x)=1xln3xf(x)=dfrac{1}{x ln^3{x}}
Очевидно, что для любых x1>x2>2x_1>x_2>2:
1x2ln3×2>1x1ln3×1⇒f(x2)>f(x1)dfrac{1}{x_2 ln^3{x_2}}>dfrac{1}{x_1 ln^3{x_1}} quad Rightarrow quad f(x_2 )>f(x_1 )
Найдем неопределенный интеграл
∫dxxln3x=∫d(lnx)xln3x=(−12)(lnx)−2+C=−12ln2x+Cint dfrac {dx}{x ln^3 {x}}=int dfrac {d(ln{x})}{x ln^3 {x}}=left( -dfrac{1}{2}right)(ln{x})^{-2}+C= -dfrac{1}{2 ln^2{x}}+C
Далее:
∫2∞f(x)dx=∫2∞dxxln3x=limd→+∞∫2ddxxln3x=limd→+∞(−12ln2x∣2d)=limd→+∞(−12ln2d+12ln22)=12ln22intlimits_2^infty f(x) dx=intlimits_2^infty dfrac {dx}{x ln^3 {x}}=limlimits_{d to +infty }intlimits_2^d dfrac{dx}{xln^3 {x}}=limlimits_{d to +infty }left( -dfrac{1}{2 ln^2{x}}Bigr|_2^d right) = limlimits_{d to +infty } left(-dfrac{1}{2 ln^2{d}}+dfrac{1}{2 ln^2{2}} right) = dfrac{1}{2 ln^2{2}}
Таким образом, несобственный интеграл сходится. Это значит, что ряд
∑n=2∞1nln3nsum limits_{n=2} ^{infty} dfrac{1}{nln^3{n}}
также сходится, а ряд
∑n=2∞(−1)nnln3nsum limits_{n=2} ^{infty} dfrac{(-1)^n}{nln^3{n}}
сходится абсолютно.
При x=−2x=-2 получим ряд
∑n=2∞(x+3)nnln3n=∑n=2∞(−2+3)nnln3n=∑n=2∞1nln3nsum limits_{n=2} ^{infty} dfrac{(x+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{(-2+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{1}{nln^3{n}}
Как было показано, этот ряд сходится абсолютно. Следовательно, область сходимости исходного ряда – промежуток [−4,−2][-4, -2].
Тест по теме “Степенные ряды”
Выпишем общий член и следущий:
$$ u_n = frac{x^n}{n^2} $$
$$ u_{n+1} frac{x^{n+1}}{(n+1)^2} $$
Найдем отношения следующего и предыдущего члена ряда: $$ frac{u_{n+1}}{u_n} = frac{x^{n+1} n^2}{(n+1)^2 x^n} = frac{x n^2}{(n+1)^2} $$
Находим предел модуля полученного выражения:
$$ limlimits_{n to infty} bigg |frac{u_{n+1}}{u_n} bigg | = limlimits_{n to infty} bigg |frac{x n^2}{(n+1)^2} bigg | = $$
Так как $ n $ положительное, то палочки можно убрать. А $ x $ может принимать как положительные, так и отрицательные значения, поэтому его выносить за знак модуля не станем.
$$ = |x| limlimits_{n to infty} frac{n^2}{(n+1)^2} = frac{infty}{infty} = $$
Вынесем $ n^2 $ за скобки и выполним сокращение числителя и знаменателя:
$$ = |x| limlimits_{n to infty} frac{n^2}{n^2 (1+frac{1}{n})^2} = |x| limlimits_{n to infty} frac{1}{(1+frac{1}{n})^2} = $$
Вычисляем предел окончательно:
$$ =|x| cdot 1 = |x| $$
Итак, предел равен:
$$ limlimits_{n to infty} bigg |frac{x n^2}{(n+1)^2} bigg | = |x| $$
Составим строгое неравенство всегда меньшее единицы:
$$ |x|<1 $$
Раскроем модуль и получим, что интервал сходимости:
$$ -1 < x < 1 $$
Итак, интервал найден. Теперь необходимо найти область сходимости степенного ряда. А для этого исследуем поведение ряда на концах полученного интервала:
1) Возьмём левую границу $ x = -1 $
Подставляя $ x = -1 $ в исходный ряд, получаем ряд: $ sum_{n=1}^infty frac{(-1)^n}{n^2} $
Так как ряд знакочередующийся из-за $ (-1)^n $, то исследуем сходимость по признаку Лейбница:
1) Ряд знакочередующийся
2) $ limlimits_{n to infty} bigg | frac{(-1)^n}{n^2} bigg | = limlimits_{n to infty} frac{1}{n^2} = 0 $
Выполнены оба условия, значит ряд сходится и точку $ x=-1 $ можно включить в область сходимости.
2) Возьмём правую границу $ x = 1 $
Подставим $ x = 1 $ в исходный ряд и получим: $ sum_{n=1}^infty frac{1}{n^2} $
Текущий ряд попадает под общий гармонический ряд, в котором $ p = 2 $. А так как $ p>1 $, то ряд сходится. Значит, можно точку $ x = 1 $ записать в область сходимости.
Итого, подведем итог: область сходимости степенного ряда $ sum_{n = 1}^infty frac{x^n}{n^2} $ записывается в виде: $ -1 leqslant x leqslant 1 $
Найдем радиус сходимости $ R = frac{b-a}{2} = frac{1+1}{2} = 1 $
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Назначение сервиса. Онлайн калькулятор предназначен нахождения области сходимости степенного ряда. Результаты вычисления оформляются в формате Word (см. пример).
Например, исходный ряд 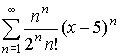 подразделяется на три части: n^n, 2^n*n!, (x-5)^n.
подразделяется на три части: n^n, 2^n*n!, (x-5)^n.
Правила ввода функций:
- Все математические операции выражаются через общепринятые символы (
+,-,*,/,^). Например, (x-4)n, записываем как(x-4)^n. - Число π ≡ pi, корень квадратный √¯ ≡ sqrt. Например, sqrt(n^2+n), en = exp(n)
Пример. 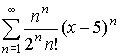 .
.
Решение.
Общий вид степенного ряда 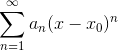 . В нашем случае x0=5,
. В нашем случае x0=5, 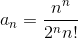 .
.
Известно, что область сходимости степенного ряда определяется величиной радиуса сходимости R:
|x-x0|<R или x0-R<x<x0+R
Сходимость ряда на границах (при x=x0±R) необходимо исследовать дополнительно.
Найдем радиус сходимости ряда, используя формулу Даламбера:
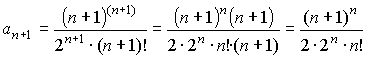 ;
;
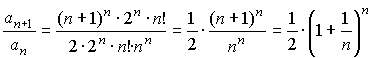 ;
;
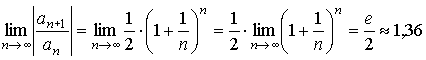 .
.
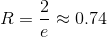
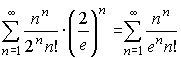 .
.
Для исследования сходимости этого ряда используем формулу Стирлинга 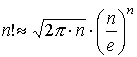 , верную для факториалов больших чисел.
, верную для факториалов больших чисел.
Получим ряд сравнения. Этот ряд расходится.
Проверим сходимость ряда при 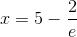 . Подставляя это значение в исходный ряд, получим числовой ряд
. Подставляя это значение в исходный ряд, получим числовой ряд
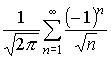 .
.
Этот ряд сходится (по признаку Лейбница).
Итак, мы получили область сходимости исходного ряда:
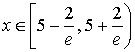 .
.
Содержание:
Степенные ряды:
До сих пор мы рассматривали ряды, членами которых были числа, т.е. числовые ряды. Теперь перейдем к рассмотрению рядов, членами которых являются функции, в частности степенные функции
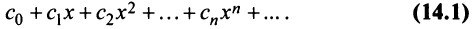
Такие ряды называются степенными, а числа 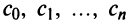
Область сходимости степенного ряда
Совокупность тех значений 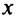 , при которых степенной ряд (14.1) сходится, называется областью сходимости степенного ряда.
, при которых степенной ряд (14.1) сходится, называется областью сходимости степенного ряда.
Пример:
Найти область сходимости степенного ряда
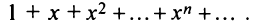
Решение:
Данный ряд можно рассматривать как геометрический ряд со знаменателем 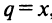 , который сходится при
, который сходится при 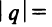
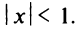 Отсюда
Отсюда 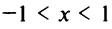 , т.е. областью сходимости является интервал
, т.е. областью сходимости является интервал 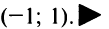
Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.
Теорема Абеля. 1) Если степенной ряд сходится при значении 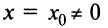 (отличном от нуля), то он сходится и, притом абсолютно, при всех значениях х таких, что
(отличном от нуля), то он сходится и, притом абсолютно, при всех значениях х таких, что 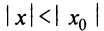 . 2) Если степенной ряд расходится при
. 2) Если степенной ряд расходится при 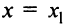 то он расходится при всех значениях х таких, что
то он расходится при всех значениях х таких, что 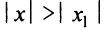 .
.
1) По условию ряд (14.1) сходится при 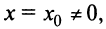 следовательно, выполняется необходимый признак сходимости
следовательно, выполняется необходимый признак сходимости 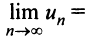
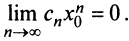 Отсюда следует, что последовательность
Отсюда следует, что последовательность 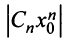 ограничена, т.е. существует такое число
ограничена, т.е. существует такое число 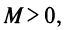 что для всех п выполняется неравенство
что для всех п выполняется неравенство

Рассмотрим ряд, составленный из абсолютных величин членов ряда (14.1) 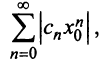 который представим в виде
который представим в виде
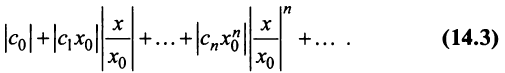
Члены ряда (14.3) согласно неравенству (14.2) меньше соответствующих членов ряда
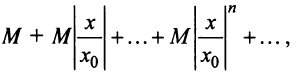
представляющего геометрический ряд, который сходится, когда его знаменатель 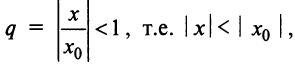 основании признака сравнения ряд (14.1) сходится.
основании признака сравнения ряд (14.1) сходится.
2) По условию ряд (14.1) расходится при 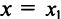 . Покажем, что он расходится для всех
. Покажем, что он расходится для всех 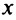 , удовлетворяющих условию
, удовлетворяющих условию 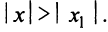 Предположим противное, т.е. при
Предположим противное, т.е. при 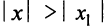 ряд (14.1) сходится. Тогда по доказанному выше он должен сходиться и в точке
ряд (14.1) сходится. Тогда по доказанному выше он должен сходиться и в точке 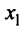 (ибо
(ибо 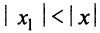 ), что противоречит условию. Таким образом, для всех х таких, что
), что противоречит условию. Таким образом, для всех х таких, что 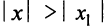 ряд (14.1) расходится. ■
ряд (14.1) расходится. ■
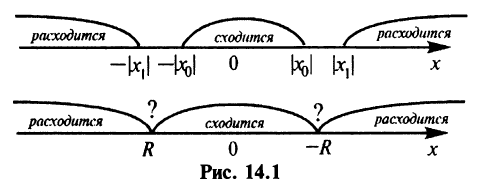
Из теоремы Абеля (см. рис. 14.1) следует, что существует такое число  что при
что при 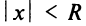 ряд сходится, а при
ряд сходится, а при 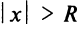 — расходится.
— расходится.
Число 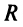 получило название радиуса сходимости, а интервал
получило название радиуса сходимости, а интервал 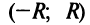 — интервала сходимости степенного ряда. На концах интервала сходимости, т.е. при
— интервала сходимости степенного ряда. На концах интервала сходимости, т.е. при 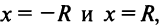 ряд может как сходиться, так и расходиться (см. рис. 14.1).
ряд может как сходиться, так и расходиться (см. рис. 14.1).
Найдем выражение радиуса сходимости степенного ряда (14.1) через его коэффициенты. Рассмотрим ряд, составленный из абсолютных величин его членов
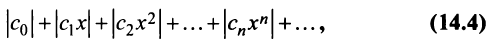
в котором все коэффициенты 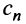 , по крайней мере начиная с некоторого номера
, по крайней мере начиная с некоторого номера 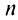 , отличны от нуля. По признаку Даламбера ряд (14.4) сходится, если
, отличны от нуля. По признаку Даламбера ряд (14.4) сходится, если
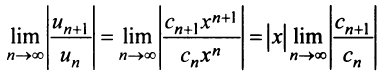 будет меньше 1, т.е.
будет меньше 1, т.е. 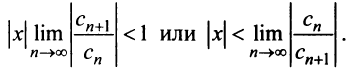 Если этот предел существует, то он и является радиусом сходимости ряда (14.1), т.е.
Если этот предел существует, то он и является радиусом сходимости ряда (14.1), т.е.

Замечание. Следует отметить, что у некоторых рядов интервал сходимости вырождается в точку 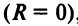 , у других охватывает всю ось
, у других охватывает всю ось 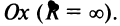
Пример:
Найти область сходимости степенного ряда
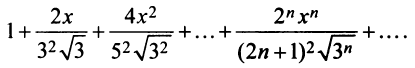
Решение:
Найдем радиус сходимости ряда по формуле (14.5) 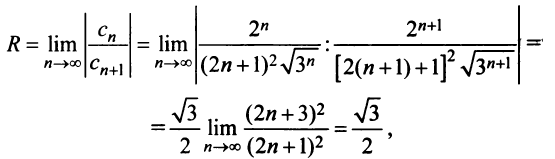 т.е. интервал сходимости ряда
т.е. интервал сходимости ряда 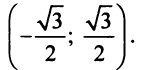
Теперь выясним поведение ряда на концах интервала сходимости. На левом конце при 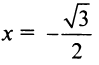 данный степенной ряд принимает вид
данный степенной ряд принимает вид 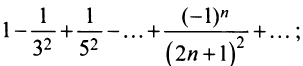 этот ряд сходится по признаку Лейбница. На правом конце при
этот ряд сходится по признаку Лейбница. На правом конце при 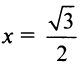 получаем ряд
получаем ряд 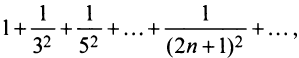 представляющий обобщенный гармонический ряд (13.12) при
представляющий обобщенный гармонический ряд (13.12) при 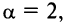 у которого все члены с четными номерами равны нулю. Так как
у которого все члены с четными номерами равны нулю. Так как 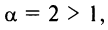 то этот ряд сходится.
то этот ряд сходится.
Следует отметить, что сходимость ряда на левом конце ин-тервала сходимости при 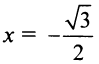 могла быть установлена с помощью достаточного признака сходимости знакопеременного ряда (см. § 13.4), так как ряд, составленный из абсолютных величин его членов, т.е. ряд
могла быть установлена с помощью достаточного признака сходимости знакопеременного ряда (см. § 13.4), так как ряд, составленный из абсолютных величин его членов, т.е. ряд 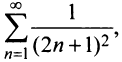 сходится.
сходится.
Итак, область сходимости данного ряда 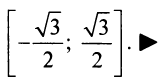
Замечание. При исследовании сходимости на концах интервала сходимости для получающегося ряда с положительными членами применять признак Даламбера не имеет смысла, так как в этом случае всегда будем получать 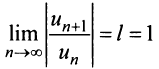 с нерешенным вопросом о сходимости ряда; в этом случае рекомендуется рассматривать другие признаки сходимости (например, признак сравнения, необходимый признак и т.д.).
с нерешенным вопросом о сходимости ряда; в этом случае рекомендуется рассматривать другие признаки сходимости (например, признак сравнения, необходимый признак и т.д.).
Пример:
Найти области сходимости степенных рядов:
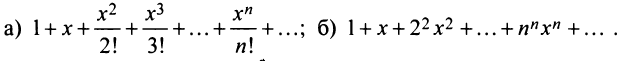
Решение:
а) Радиус сходимости ряда по (14.5)
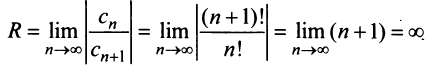 т.е. область сходимости ряда
т.е. область сходимости ряда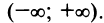
б) Задачу можно решать аналогично предыдущим. Решение упрощается, если заметить, что 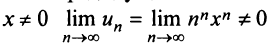 , т.е. необходимый признак сходимости не выполняется, и ряд расходится.
, т.е. необходимый признак сходимости не выполняется, и ряд расходится.
Итак, область сходимости ряда состоит из одной точки 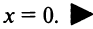
Пример:
Найти область сходимости ряда
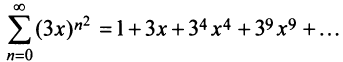
Решение:
Найти радиус сходимости по формуле (14.5) в данном случае не представляется возможным, так как коэффициенты ряда 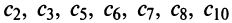 и т.д. равны нулю. Поэтому непосредственно применим признак Даламбера. Данный ряд будет абсолютно сходиться, если
и т.д. равны нулю. Поэтому непосредственно применим признак Даламбера. Данный ряд будет абсолютно сходиться, если  и расходиться, если
и расходиться, если 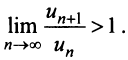 Поэтому найдем
Поэтому найдем
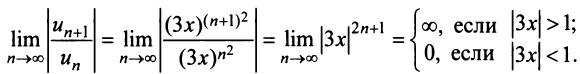 Следовательно, ряд сходится при
Следовательно, ряд сходится при 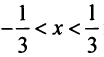 или на интервале
или на интервале 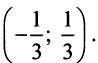
Исследуем сходимость на концах интервала сходимости: при 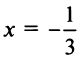 ряд принимает вид
ряд принимает вид 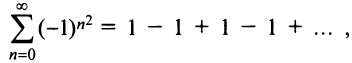 а при
а при 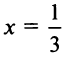 вид
вид 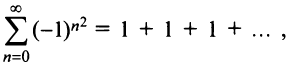 т.е. оба ряда расходятся, так как не выполняется необходимый признак сходимости.
т.е. оба ряда расходятся, так как не выполняется необходимый признак сходимости.
Итак, область сходимости ряда 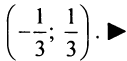
Свойства степенных рядов. Пусть функция 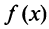 является суммой степенного ряда, т.е.
является суммой степенного ряда, т.е.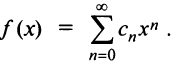 В подобных курсах математического анализа доказывается, что степенные ряды по своим свойствам напоминают конечные суммы (многочлены): на любом отрезке
В подобных курсах математического анализа доказывается, что степенные ряды по своим свойствам напоминают конечные суммы (многочлены): на любом отрезке 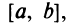 целиком принадлежащем интервалу сходимости
целиком принадлежащем интервалу сходимости 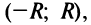 функция
функция 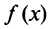 является непрерывной, а следовательно, степенной ряд можно почленно интегрировать на этом отрезке:
является непрерывной, а следовательно, степенной ряд можно почленно интегрировать на этом отрезке:
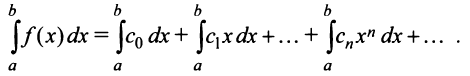
Кроме того, в интервале сходимости степенной ряд можно почленно дифференцировать:
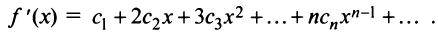
При этом после интегрирования или дифференцирования полученные ряды имеют тот же радиус сходимости 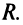
Определение степенного ряда и его сходимости
Понятое функциональной зависимости является одним из важнейших в математике. Всякая функция осуществляет некоторое соответствие между объектами, составляющими область задания этой функции, и объектами, составляющими область её значений. Так можно рассматривать функции, которые ставят в соответствие числам – ряды. Эти функции называются функциональными рядами, т.е. функциональный ряд это выражение

членами которого являются некоторые функции переменной х. Например, ряд
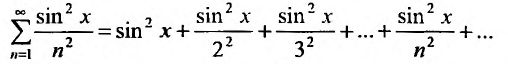
является функциональным рядом.
Придавая в выражении (29.1.1) переменной х некоторые значения 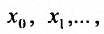 мы будем получать числовые ряды
мы будем получать числовые ряды
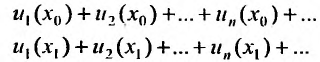
которые могут оказаться, как сходящимися, так и расходящимися.
В простейших случаях для определения сходимости ряда (29.1.1) можно применять к нему известные признаки сходимости числовых рядов, считая х фиксированным.
Определение 29.1.1. Совокупность всех значений переменной х, для которых соответствующие числовые ряды сходятся, называется областью сходимости функционального ряда (29.1.1). Определение 29.1.2. Функциональный ряд вида
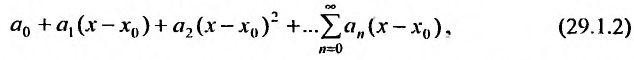
где 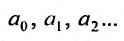 – действительные числа, независящие от переменной х, называется степенным относительно переменной х рядом. Числа
– действительные числа, независящие от переменной х, называется степенным относительно переменной х рядом. Числа 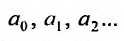 называются коэффициентами этого ряда.
называются коэффициентами этого ряда.
Если в ряде (29.1.2) сделать замену переменного, положив
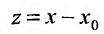 , то получим ряд
, то получим ряд 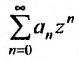 . В дальнейшем будем использовать букву x:
. В дальнейшем будем использовать букву x:

Очевидно, что исследование сходимости ряда (29.1.2) эквивалентно исследованию сходимости ряда (29.1.3). Примером степенного ряда может служить ряд
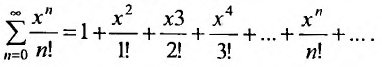
Сумма п первых членов ряда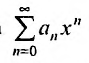 называется n -ой частичноной суммой ряда и обозначается
называется n -ой частичноной суммой ряда и обозначается 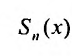 , т.е.
, т.е. 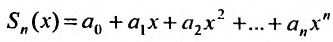
Для степенного ряда можно составить последовательность частичных сумм 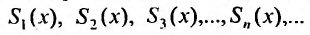 Очевидно, что n-ые частичные суммы
Очевидно, что n-ые частичные суммы 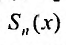 степенного ряда являются функциями.
степенного ряда являются функциями.
Остатком степенного ряда после n -го его члена (или n -ым остатком) называется ряд, полученный из заданного исключением n его первых членов:
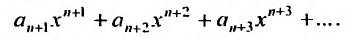
Определение 29.1.3. Степенной ряд называется сходящимся на некотором множестве, если он сходится в любой точке этого множества.
Степенной ряд называется абсолютно сходящимся на некотором множестве, если в каждой точке этого множества сходится ряд из модулей его членов:
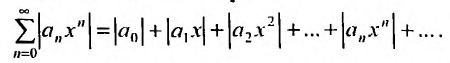 Степенной ряд (29.1.3) при тех или иных конкретных значениях переменной x превращается в числовой ряд; так если
Степенной ряд (29.1.3) при тех или иных конкретных значениях переменной x превращается в числовой ряд; так если 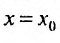 , то получим числовой ряд:
, то получим числовой ряд:
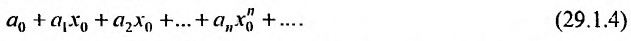
Соответствующий числовой ряд а0 +о,л:0 +… сходится абсолютно, если сходится ряд 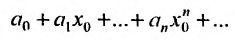 составленный из модулей его членов.
составленный из модулей его членов.
Так как каждой точке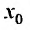 сходимости ряда (29.1.3) ставится в соответствие определенное значение суммы (29.1.4), то сумма сходящегося на некотором множестве степенного ряда является функцией переменной x. Тогда
сходимости ряда (29.1.3) ставится в соответствие определенное значение суммы (29.1.4), то сумма сходящегося на некотором множестве степенного ряда является функцией переменной x. Тогда 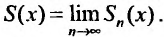 Если обозначить сумму остатка через
Если обозначить сумму остатка через 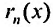 , то в области сходимости степенного ряда справедливо равенство:
, то в области сходимости степенного ряда справедливо равенство: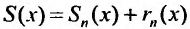
Для сходящегося степенного ряда предел остатка равен нулю: 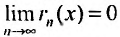
Степенные ряды можно складывать, вычитать, умножать. Пусть заданы два степенных ряда:
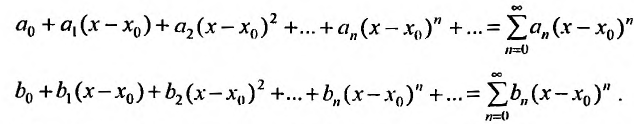
Сумма, разность и произведение заданных степенных рядов определяется формулами:
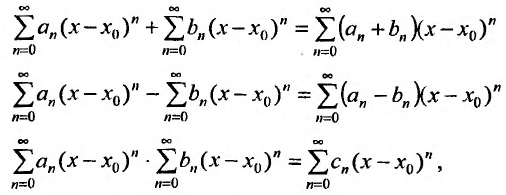
где 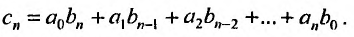
Например, сумма, разность и произведение степенных рядов:
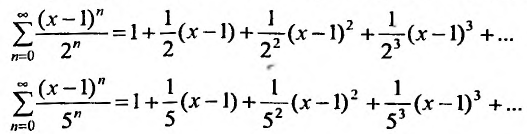
имеет вид: 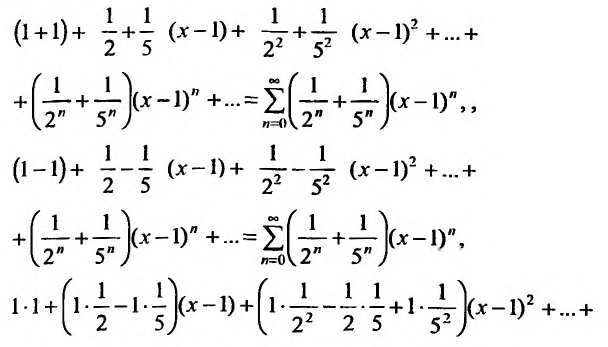
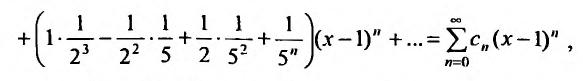
где 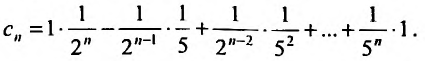
Радиус сходимости, интервал сходимости
Области сходимости степенных рядов устроены довольно просто. Они описываются следующей теоремой.
Теорема 29.2.1 (теорема Абеля). Если степенной ряд

сходится при некотором 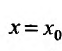 , то он сходится абсолютно при всех значениях х, для которых
, то он сходится абсолютно при всех значениях х, для которых 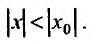
Если же степенной ряд (29.2.1) расходится при 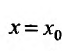 , то он расходится при всех значениях х, для которых
, то он расходится при всех значениях х, для которых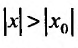 .
.
Доказательство. Предположим сначала, что степенной ряд (29.2.1) сходится в точке 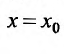 . Это значит, что сходится числовой ряд
. Это значит, что сходится числовой ряд
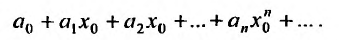
Тогда, в силу необходимого признака сходимости, 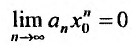 и поэтому члены этого ряда ограничены, т.е. найдется такое К, что при любом номере
и поэтому члены этого ряда ограничены, т.е. найдется такое К, что при любом номере 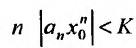 . В силу этого для n -го члена ряда (29.2.1) получаем следующею оценку
. В силу этого для n -го члена ряда (29.2.1) получаем следующею оценку
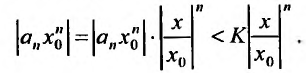
Если 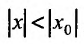 , то ряд
, то ряд 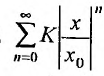 , являясь геометрической прогрессией со знаменателем
, являясь геометрической прогрессией со знаменателем 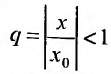 сходится. Поэтому, в силу I признака сравнения и так как
сходится. Поэтому, в силу I признака сравнения и так как 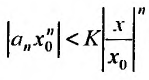 , сходится и ряд
, сходится и ряд 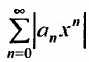 А это означает абсолютную сходимость ряда (29.2.1), при
А это означает абсолютную сходимость ряда (29.2.1), при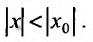
Предположим теперь, что степенной ряд (29.2.1) расходится, при 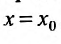 , т.е. расходится числовой ряд:
, т.е. расходится числовой ряд:
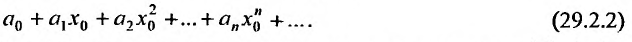
Возьмём тогда некоторое значение х, для которого 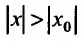 и предположим, что ряд
и предположим, что ряд 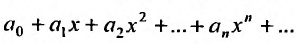 в этой точке
в этой точке
сходится. Но тогда из сходимости этого ряда, в силу первой части доказательства теоремы, вытекает сходимость ряда (29.2.2), что противоречит предположению, о его расходимости. Полученное противоречие означает, что для всех 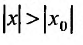 степенной ряд (29.2.1) расходится.
степенной ряд (29.2.1) расходится.
Если ряд (29.2.1) имеет вещественные коэффициенты и переменная х принимает только вещественные значения, то справедливо следующее определение, вытекающее из теоремы Абеля.
Определение 29.2.1. Величина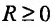 (R-число или символ
(R-число или символ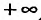 )
)
такая, что при всех х, у которых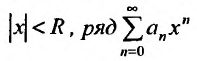 сходится, а при всех X у которых
сходится, а при всех X у которых 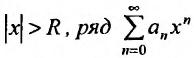 расходится, называется радиусом сходимости степенного ряда (29.2.1).
расходится, называется радиусом сходимости степенного ряда (29.2.1).
Множество точек х удовлетворяющих соотношению 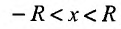 , называется интервалом сходимости.
, называется интервалом сходимости.
Итак, из определения 29.2.1 и теоремы Абеля следует, что областью сходимости степенного ряда – является интервал сходимости. И если значение 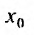 переменной х, принадлежит интервалу сходимости, то можно говорить о сумме степенного ряда (29.2.1) в точке
переменной х, принадлежит интервалу сходимости, то можно говорить о сумме степенного ряда (29.2.1) в точке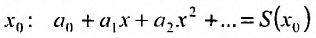 . Таким образом, значение суммы степенного ряда зависит от значения
. Таким образом, значение суммы степенного ряда зависит от значения 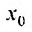 переменной х, т.е. сумма степенного ряда сама является функцией переменной х. Эта функция ничем не отличается от обычной функции и, следовательно, можно говорить о дифференцировании, непрерывности, интегрируемости и других ее свойствах.
переменной х, т.е. сумма степенного ряда сама является функцией переменной х. Эта функция ничем не отличается от обычной функции и, следовательно, можно говорить о дифференцировании, непрерывности, интегрируемости и других ее свойствах.
Свойства степенных рядов
Для степенных рядов справедливы следующие свойства:
1) Степенной ряд сходится равномерно внутри интервала сходимости.
2) Внутри интервала сходимости ряда сумма его является непрерывной функцией.
3) Если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то последовательность интегралов от частичных сумм ряда сходится к интегралу от суммы ряда.
4) Если степенной ряд
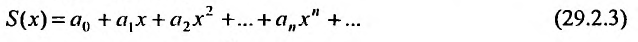
имеет радиус сходимости R , то и ряд
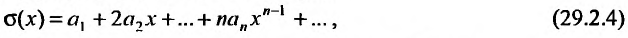
получаемый в результате почленного дифференцирования ряда (29.2.3) также имеет радиус сходимости R. Производная суммы ряда (29.2.3) равна сумме ряда (29.2.4), т.е. 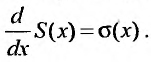
Вычисление интервала сходимости
Как уже было сказано в и. 2 областью сходимости степенного ряда является интервал сходимости. Более того, из теоремы Абеля следует, что областью сходимости степенного ряда является интервал с центром в начале координат (рис 29.1).
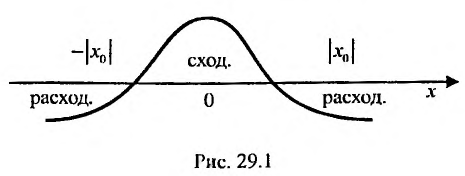
Действительно, если 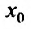 есть точка сходимости, то весь интервал
есть точка сходимости, то весь интервал 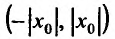 заполнен точками абсолютной сходимости, что следует из теоремы Абеля. Если же
заполнен точками абсолютной сходимости, что следует из теоремы Абеля. Если же 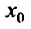 – точка расходимости, то вся бесконечная полупрямая вправо от точки
– точка расходимости, то вся бесконечная полупрямая вправо от точки 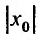 и вся полупрямая влево от точки –
и вся полупрямая влево от точки –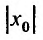 состоят из точек расходимости, в противном случае мы бы получили, что степенной ряд в точке
состоят из точек расходимости, в противном случае мы бы получили, что степенной ряд в точке 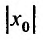 или –
или –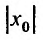 сходится по теореме Абеля.
сходится по теореме Абеля.
Заметим, что на концах интервала вопрос о сходимости или расходимости решается индивидуально в каждом конкретном случае. У некоторых рядов интервал сходимости может вырождаться в точку, у других охватывать всю ось Ох.
Укажем теперь способ вычисления радиуса сходимости степенного ряда.
Пусть задан степенной ряд 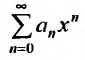 Составим ряд из модулей членов данного ряда
Составим ряд из модулей членов данного ряда 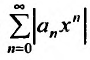 и применим признак Д’Аламбера, т.е.
и применим признак Д’Аламбера, т.е.
вычислим предел
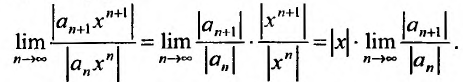
Если этот предел меньше единицы, то, как следует из признака Д’Аламбера, ряд, составленный из модулей членов ряда (29.2.1) сходится, т.е. ряд сходится если 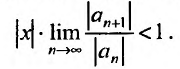
Если же 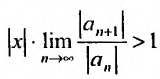 , то ряд (29.2.1) расходится.
, то ряд (29.2.1) расходится.
А это означает, что если 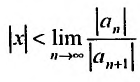 , то степенной ряд (29.2.1) сходится абсолютно, а при
, то степенной ряд (29.2.1) сходится абсолютно, а при 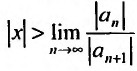 . степенной ряд расходится.
. степенной ряд расходится.
Учитывая определение радиуса сходимости степенного ряда, получим, что радиус сходимости можно вычислить по формуле:

Рассуждая аналогичным образом можно получить еще одну формулу для определения радиуса сходимости:

Если степенной ряд содержит только четные или нечетные степени х, то применяем признак Д’Аламбсра или Коши к ряду, составленному из модулей членов данного ряда.
Пример №1
Найти радиус и интервал сходимости степенного ряда:
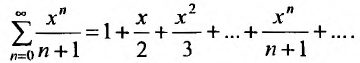
Решение:
Выпишем вначале значения 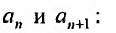
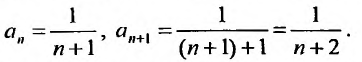
Для определения радиуса сходимости воспользуемся формулой (29.3.1):
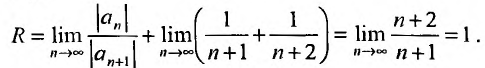
Итак, степенной ряд сходится для |х| 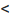 1.
1.
Исследуем сходимость ряда на концах интервала сходимости.
Пусть х =—1. Тогда получим знакочередующийся ряд 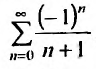 который согласно признаку Лейбница сходится. Пусть х = 1. Получим числовой ряд
который согласно признаку Лейбница сходится. Пусть х = 1. Получим числовой ряд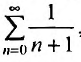 который расходится, так как является гармоническим рядом.
который расходится, так как является гармоническим рядом.
Суммируя вышесказанное, получим интервал сходимости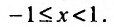
Пример №2
Найти радиус и интервал сходимости степенного ряда 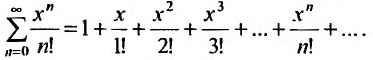
Решение:
Выпишем вначале значения 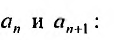
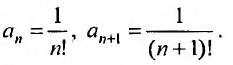
Для определения радиуса сходимости воспользуемся формулой (29.3.2):
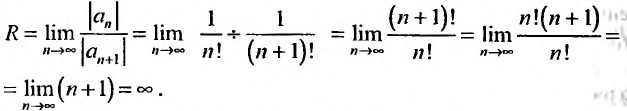
Так как 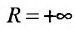 , то исследуемый ряд сходится для всех х.
, то исследуемый ряд сходится для всех х.
Пример №3
Найти радиус и интервал сходимости степенного ряда:
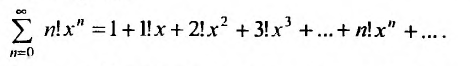
Решение:
Выпишем вначале значения 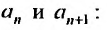
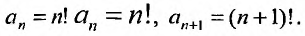
Для определения радиуса сходимости воспользуемся формулой (29.3.1): 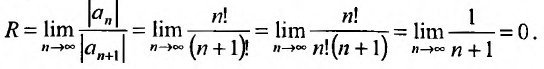
Так как радиус сходимости равен нулю, то ряд сходится только в одной точке x= 0.
Пример №4
Найти радиус и интервал сходимости степенного ряда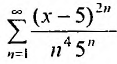
Решение:
Данный ряд содержит только четные степени (а- – 5), коэффициенты при нечетных степенях равны нулю. Поэтому воспользоваться формулами (29.3.1) и (29.3.2) не представляется возможным.
Считая х фиксированным, применим признак Д’Аламбера к ряду, составленному из модулей членов данного ряда. Выпишем значения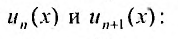
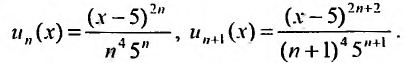
Тогда
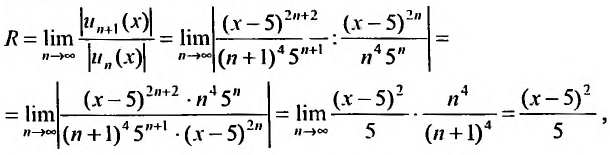
так как 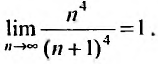
Ряд сходится, если 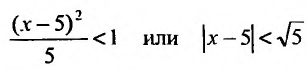 или
или
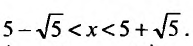 Это значит, что ряд сходится в интервале
Это значит, что ряд сходится в интервале
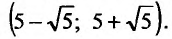
Исследуем сходимость ряда на концах интервала сходимости. Пусть 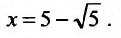 . Подставив это значение х в исследуемый ряд, получим числовой ряд:
. Подставив это значение х в исследуемый ряд, получим числовой ряд:
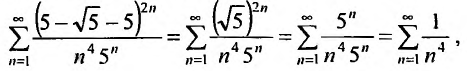
который сходится, как ряд Дирихле, для которого а = 4. При 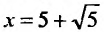 получим тот же сходящийся числовой ряд. Следовательно, данный ряд сходится на отрезке
получим тот же сходящийся числовой ряд. Следовательно, данный ряд сходится на отрезке
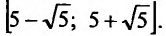
Пример №5
Найти радиус и интервал сходимости степенного ряда 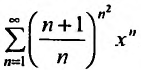
Решение:
Выпишем значение 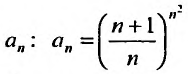 и вычислим радиус сходимости данного ряда по формуле (29.3.2):
и вычислим радиус сходимости данного ряда по формуле (29.3.2):
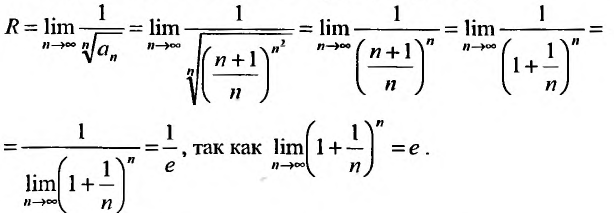 Так как
Так как 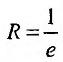 , то данный ряд сходится в интервале
, то данный ряд сходится в интервале
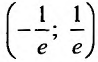
Исследуем его сходимость на концах интервала.
Пусть 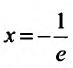 . Подставив это значение х в данный степенной ряд, получим числовой знакочередующийся ряд:
. Подставив это значение х в данный степенной ряд, получим числовой знакочередующийся ряд:
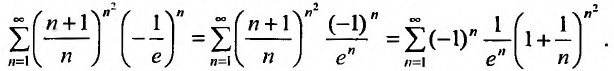 Предел общего члена полученного ряда не стремится к нулю:
Предел общего члена полученного ряда не стремится к нулю:
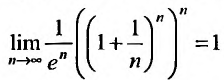
Следовательно, данный ряд расходится. И при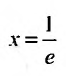 получим расходящийся числовой ряд:
получим расходящийся числовой ряд: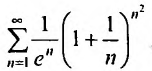 Следовательно,
Следовательно, 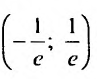 интервал сходимости данного ряда.
интервал сходимости данного ряда.
Ряды Тейлора и Маклорена
Как уже отмечалось, сумма сходящегося степенного ряда является некоторой функцией, определенной внутри интервала сходимости. В связи с этим мы рассмотрим задачу разложения некоторой функции в ряд, т.е. будем по заданной функции искать сходящийся ряд того или иного типа, сумма которого в интервале сходимости равнялась бы заданной функции.
Известно, что если функция f имеет на некотором отрезке производные всех порядков, то можно написать формулу Тейлора для любого значения n:
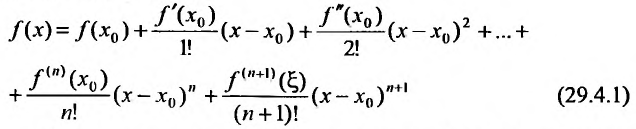
где 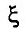 заключено между
заключено между 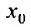 и х. Формула (29.4.1) называется формулой Тейлора с оста точным членом в форме Лагранжа.
и х. Формула (29.4.1) называется формулой Тейлора с оста точным членом в форме Лагранжа.
В формуле Тейлора обозначим:
пункта 27.2 (теорема 27.2.1) следует, что если

то степенной ряд
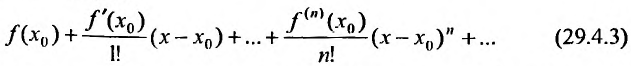
сходится и его суммой будет функция f(х), так как 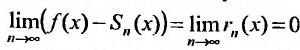 Следовательно,
Следовательно, 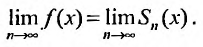
Справедливо и обратное утверждение, что если степенной ряд (29.4.3) сходится, то выполняется (29.4.2).
Определение 29.4.1. Представление функции f в виде ряда
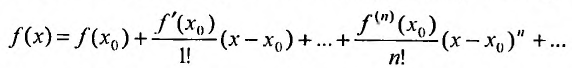
называется разложением этой функции в ряд Тейлора. Если же 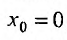 , то разложение в ряд Тейлора называется разложением в ряд Маклорена:
, то разложение в ряд Тейлора называется разложением в ряд Маклорена:
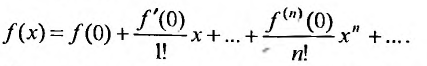
Следует заметить, что остаточный член в формуле Тейлора для функции J не обязательно является остатком ряда Тейлора для этой функции. Поэтому из сходимости ряда Тейлора для функции f , еще не следует сходимость именно к этой функции. При разложении функции в ряд Тейлора необходимо проверять условие (29.4.2). Однако сели разложение функции в какой-либо степенной ряд вообще возможно, то оно является разложением в ряд Тейлора, т.е. справедлива следующая теорема.
Теорема 29.4.1. Пусть
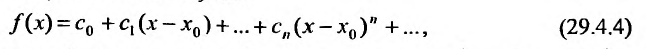
и стоящий справа ряд сходится в интервале 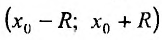 к функции f . Тогда этот ряд является рядом Тейлора, т.е.
к функции f . Тогда этот ряд является рядом Тейлора, т.е.

Доказательство. Так как степенной ряд в интервале сходимости можно почленно дифференцировать, то n-ую производную функции (29.4.4) можно представить в виде:
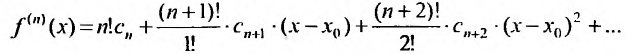
Полагая в последнем тождестве 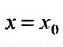 , получим
, получим 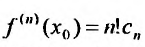 (все другие слагаемые равны нулю). Откуда и следует (29.4.5).
(все другие слагаемые равны нулю). Откуда и следует (29.4.5).
Из доказанной теоремы вытекает, что в одной и той же области, для одной и той же функции существует единственное разложение.
На практике, для разложения функции в ряд Тейлора, удобно пользоваться следующей теоремой.
Теорема 29.4.2. Если при любых х, удовлетворяющих неравенству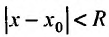 производные функции f(x) для любых п ограничены одним и тем же числом С > 0 т.е.
производные функции f(x) для любых п ограничены одним и тем же числом С > 0 т.е.
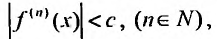
то ряд Тейлора, для этой функции, сходится в интервале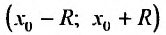 и его сумма равна f(x).
и его сумма равна f(x).
Доказательство. Из условия теоремы следует, что функцию f можно представить формулой Тейлора с остаточным членом в форме Лагранжа, т.е.
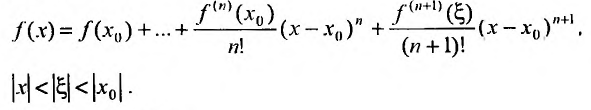 Оценим остаток:
Оценим остаток: 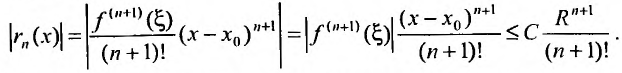
Переходя к пределу при , получим неравенство:
, получим неравенство:

Воспользовавшись асимптотической формулой Стерлинга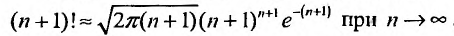 , получим:
, получим:
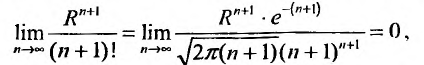
так как стспснно-показательная функция 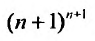 и взрастает быстрее показательных функций
и взрастает быстрее показательных функций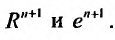
Тогда из неравенства (29.4.6) получим: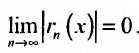 . Слсдова-
. Слсдова-
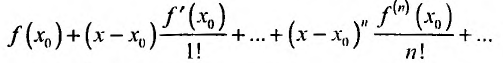 сходится к функции f(х). Теорема доказана.
сходится к функции f(х). Теорема доказана.
Разложение некоторых элементарных функций в ряд Маклорена
Из пункта 29.4 следует, что для того чтобы некоторая функция разлагалась в ряд Тейлора нужно, чтобы она имела производные любого порядка и чтобы либо 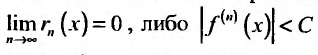 (где С> 0 – произвольная постоянная), для любых n и
(где С> 0 – произвольная постоянная), для любых n и 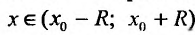 . Рассмотрим разложение некоторых функций в ряд Маклорена.
. Рассмотрим разложение некоторых функций в ряд Маклорена.
1. Разложение функции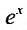 .
.
Находим производные данной функции и их значения при х=0. Так как 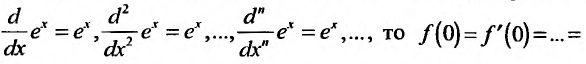
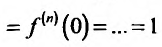 и формула Маклорена для функции
и формула Маклорена для функции 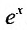 имеет вид:
имеет вид:
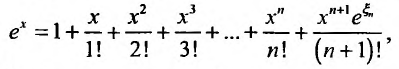
где 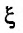 заключено между 0 и х.
заключено между 0 и х.
Вычислим предел остаточного члена, для любого х: 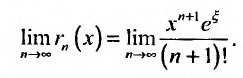
Выражение 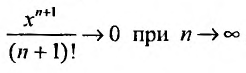 как общий член сходящегося ряда
как общий член сходящегося ряда 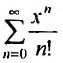 . Множитель
. Множитель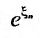 в выражении остаточного члена не превосходит
в выражении остаточного члена не превосходит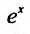 при х > 0 , и единицы при х
при х > 0 , и единицы при х  0. Это означает, что остаточный член стремится к нулю при всех значениях x
0. Это означает, что остаточный член стремится к нулю при всех значениях x 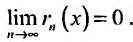
Следовательно, ряд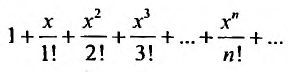 сходится при любом х и суммой его является функция
сходится при любом х и суммой его является функция 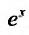 . Итак,
. Итак,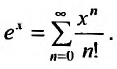 Заменяя х на -x, получим ряд
Заменяя х на -x, получим ряд 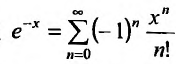 —, интервалом сходимости для которого является вся числовая ось.
—, интервалом сходимости для которого является вся числовая ось.
2. Разложение функций cos х и sin х. Для функции cos x имеем:
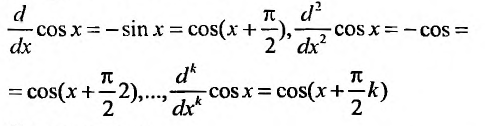
Следовательно,
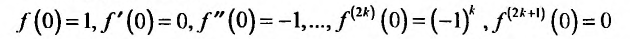 и формула
и формула
Маклорена с остаточным членом в форме Лагранжа для функции cosx имеет вид:
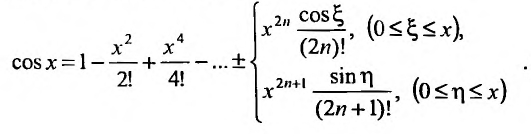
Ясно, что для любого X
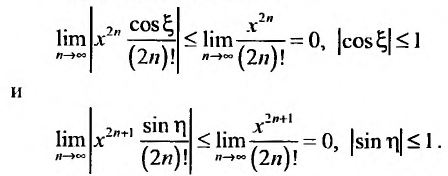
Поэтому, функция cos л- разлагается в ряд Маклорена вида:
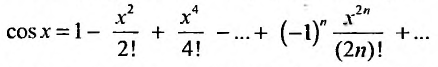
Аналогично получается разложение в ряд Маклорена функции sinx: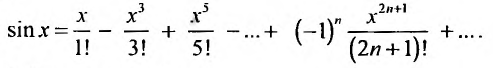
3. Биномиальный ряд.
Найдем разложение в степенной ряд функции

где m -произвольное действительное число.
Дифференцируя равенство (29.5.1) n раз, получим:
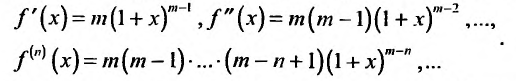
Значения функции и се производных при х = 0 равны: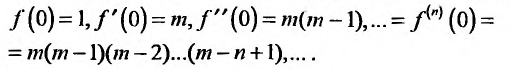
Следовательно, ряд Маклорена имеет вид: 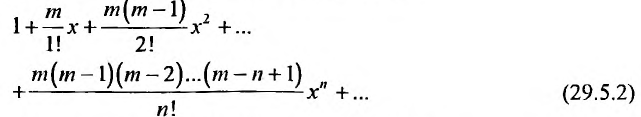
Если m- целое, то выражение (29.5.2) содержит конечное число членов. Если же m- нецелое, то выражение (29.5.2)- бесконечный ряд, называемый биномиальным.
Определим вначале радиус сходимости этого ряда, для чего применим признак Д’Аламбсра к ряду, составленному из модулей его членов:
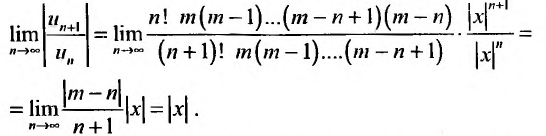
Следовательно, при |х| 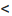 1, биномиальный ряд абсолютно сходится, т.е. существует сумма S(x) этого ряда.
1, биномиальный ряд абсолютно сходится, т.е. существует сумма S(x) этого ряда.
Покажем теперь, что ряд (29.5.2) сходится к функции 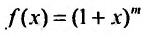 ‘. Для этого продифференцируем ряд (29.5.2) , получим:
‘. Для этого продифференцируем ряд (29.5.2) , получим:
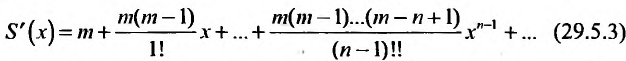
Умножим обе части (29.5.3) на 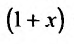 и приведем подобные члены. Получим степенной ряд, в котором коэффициент при
и приведем подобные члены. Получим степенной ряд, в котором коэффициент при 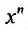 равен сумме двух слагаемых:
равен сумме двух слагаемых:
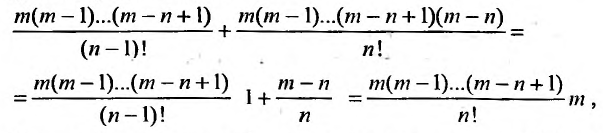
Эта сумма, как показано, равна произведению коэффициента при 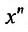 , ряда (29.5.2), на m . Следовательно, в интервале сходимости биномиального ряда, имеем равенство:
, ряда (29.5.2), на m . Следовательно, в интервале сходимости биномиального ряда, имеем равенство:
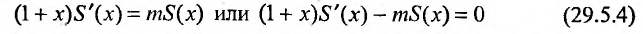
С другой стороны, вычисляя производную отношения
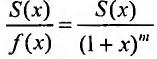 получим:-
получим:-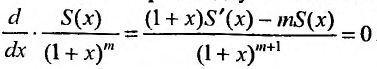 в силу (29.5.4).
в силу (29.5.4).
Решая дифференциальное уравнение 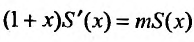 , последовательно получим:
, последовательно получим:
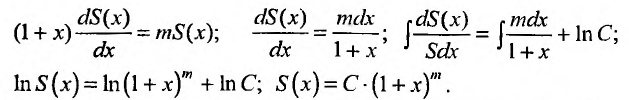
Пусть x = 0, тогда S(0) = С. Из (29.5.2) следует, что S(0) = 1, тогда С = 1.
Следовательно, 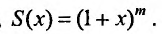
Итак, разложение
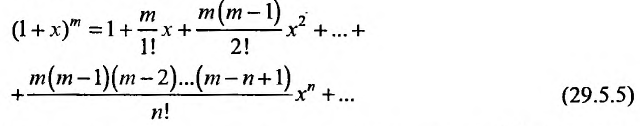
имеет место при всех х, удовлетворяющих условию 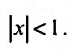 . Придавая m конкретные значения можно получать разложения различных функций в степенные ряды. В общем случае разложение (29.5.5) даст обобщение бинома Ньютона для какого угодно показателя m.
. Придавая m конкретные значения можно получать разложения различных функций в степенные ряды. В общем случае разложение (29.5.5) даст обобщение бинома Ньютона для какого угодно показателя m.
Применение рядов в приближенных вычислениях
Разложения функций в ряд Маклорена позволяют во многих случаях вычислить с большой степенью точности значения этих функций, заменяя ее конечным числом членов разложения. Чем меньше х, тем меньше членов можно брать в этом разложении для вычисления f(х) с желаемой точностью. Если х весьма мало, то достаточно ограничится первыми двумя членами, отбросив все остальные. Например, при х близких к нулю можно пользоваться следующими приближенными формулами:
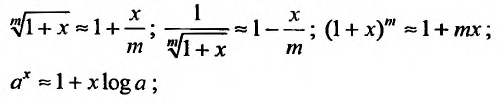
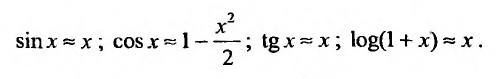
Например, вычислим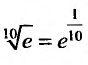 , до пяти знаков.
, до пяти знаков.
Имеем, 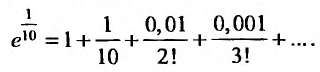 Остаточный член
Остаточный член
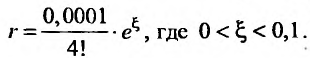 Так как близко к единице, то остальные члены в разложении не повлияют на первые пять знаков после запятой и их можно отбросить. Вычисление приводит к результату:
Так как близко к единице, то остальные члены в разложении не повлияют на первые пять знаков после запятой и их можно отбросить. Вычисление приводит к результату: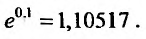
Иногда при вычислении значений функций удобно пользоваться почленным дифференцированием или интегрированием рядов.
Например, известно, что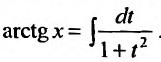
С другой стороны, 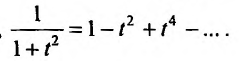
Следовательно,
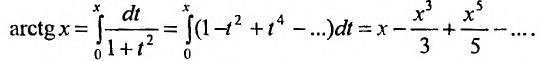 В частности, при x = 0,1, получим:
В частности, при x = 0,1, получим:
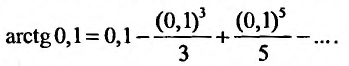
Этот ряд знакочередующийся. Поэтому, его остаток не превосходит первого «отброшенного» члена. Удерживая в разложении первых два слагаемых, получим значение arctg 0,1 = 0,09967 с пятью верными знаками.
При помощи биномиальною ряда можно быстро и довольно точно вычислять значение корней из чисел.
Пример №6
Вычислить 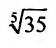 с точностью до 0,0001.
с точностью до 0,0001.
Решение:
Представим, этот корень в виде
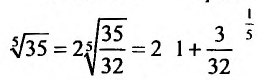 и воспользуемся разложением бинома:
и воспользуемся разложением бинома:
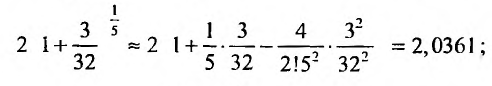
следующим член 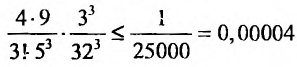 , поэтому точность нужная получена.
, поэтому точность нужная получена.
В общем случае можно записать:
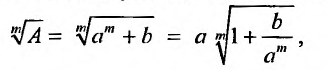
где 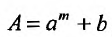 , причем
, причем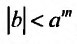 , так как всегда можно подобрать целое число а так, чтобы m -ая степень а была, по возможности, ближе к А.
, так как всегда можно подобрать целое число а так, чтобы m -ая степень а была, по возможности, ближе к А.
Кроме того, биномиальный ряд является основой многих дальнейших разложений функций в ряды. Например, можно найти разложение в ряд Маклорена функции:
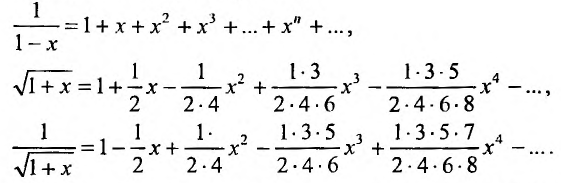
При помощи рядов можно вычислять определенные интегралы.
Например, вычислим интегральный синус: 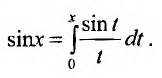
Имеем
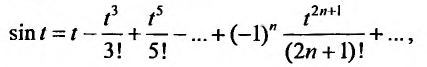
тогда 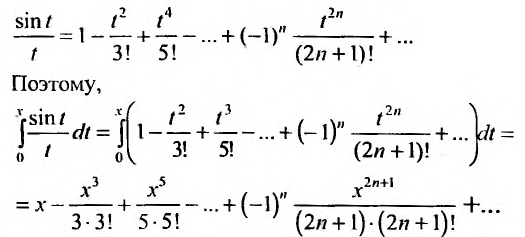
Подставляя вместо x, те или иные конкретные значения переменной, мы можем вычислять интересующие нас значения интегрального синуса.
При помощи разложении в степенные ряды можно приближенно интегрировать разнообразные дифференциальные уравнения.
Например, найдем решение уравнения 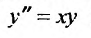 при начальных условиях
при начальных условиях 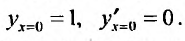
Будем искать решение этого уравнения в виде степенного ряда: 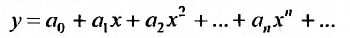 при начальных условиях
при начальных условиях 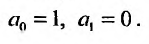 . Тогда получим:
. Тогда получим:
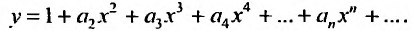
Вычислим первую и вторую производные от этого ряда:
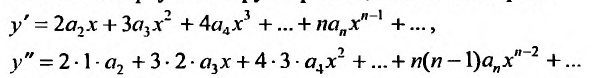
и подставив у, 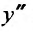 в заданное уравнение:
в заданное уравнение:
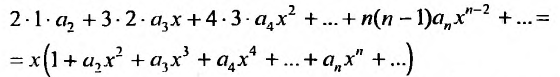
приравняем коэффициенты при равных степенях .г, предварительно умножив правую часть на х: 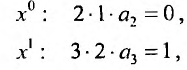
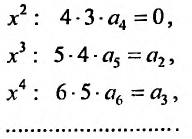
Получаем систему уравнений, из которой находим:
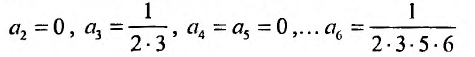
Замечаем, что отличными от нуля будут лишь те коэффициенты, у которых индекс и степень делятся на 3. Получим решение заданного дифференциального уравнения в виде: 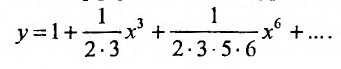
- Заказать решение задач по высшей математике
Ряд Маклорена
Предположим, что функция 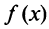 , определенная и
, определенная и 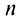 раз дифференцируемая в окрестности точки
раз дифференцируемая в окрестности точки 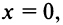 может быть представлена в виде суммы степенного ряда или, другими словами, может быть разложена в степенной ряд
может быть представлена в виде суммы степенного ряда или, другими словами, может быть разложена в степенной ряд
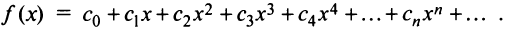
Выразим коэффициенты ряда через 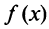 . Найдем производные функции
. Найдем производные функции 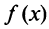 , почленно дифференцируя ряд
, почленно дифференцируя ряд 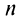 раз:
раз:
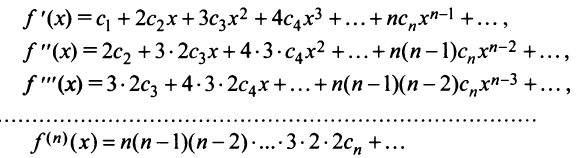
Полагая в полученных равенствах 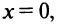 получим
получим 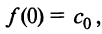
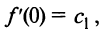
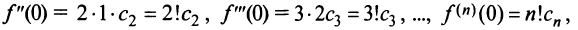 откуда
откуда
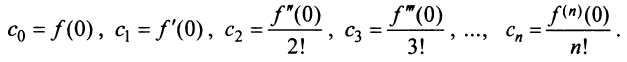
Подставляя значения коэффициентов 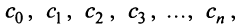 получим ряд
получим ряд
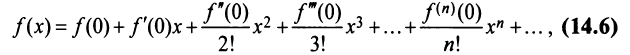
называемый рядом Маклорена.
Следует отметить, что не все функции могут быть разложены в ряд Маклорена. Может оказаться, что ряд Маклорена, составленный формально для функции 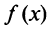 , является расходящимся либо сходящимся не к функции
, является расходящимся либо сходящимся не к функции 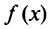 .
.
Так же как и для числовых рядов, сумму 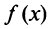 ряда Маклорена можно представить в виде (13.9)
ряда Маклорена можно представить в виде (13.9)
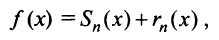
где 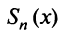 —
— 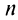 -я частичная сумма ряда;
-я частичная сумма ряда; 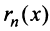 —
— 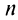 -й остаток ряда.
-й остаток ряда.
Тогда на основании свойства 4 сходящихся рядов (см. §13.1) можно сформулировать теорему.
Теорема. Для того чтобы ряд Маклорена сходился к функции 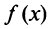 , необходимо и достаточно, чтобы при
, необходимо и достаточно, чтобы при 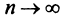 остаток ряда стремился к нулю, т.е.
остаток ряда стремился к нулю, т.е.

для всех значений 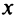 из интервала сходимости ряда.
из интервала сходимости ряда.
Можно доказать, что если функция 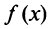 разложима в ряд Маклорена, то это разложение единственное.
разложима в ряд Маклорена, то это разложение единственное.
Замечание. Ряд Маклорена является частным случаем ряда Тейлора:
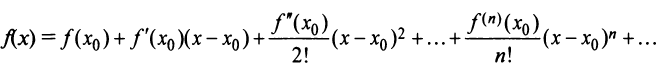
при 
Ряд Тейлора тесно связан с формулой Тейлора.
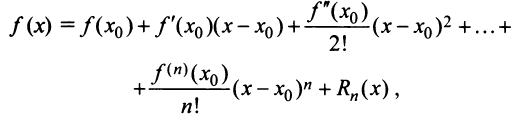
где 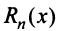 — остаточный член формулы Тейлора:
— остаточный член формулы Тейлора:
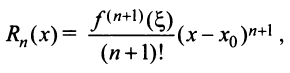
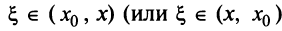 ), записанный в форме Лагранжа.
), записанный в форме Лагранжа.
Очевидно, что при выполнении условия (14.7) остаток 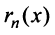 ряда Тейлора равен остаточному члену
ряда Тейлора равен остаточному члену 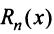 формулы Тейлора.
формулы Тейлора.
Разложение в ряд Маклорена некоторых функций
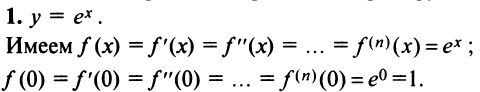
По формуле (13.6)
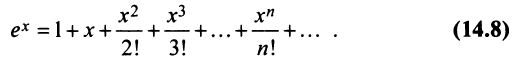
Область сходимости ряда 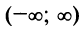 .
.
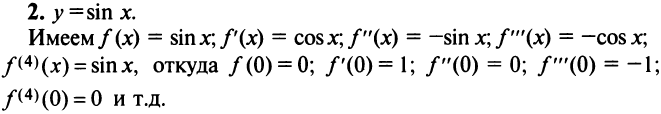
Очевидно, что производные четного порядка 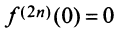 , а нечетного порядка
, а нечетного порядка 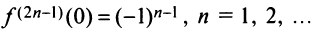 . По формуле (14.6)
. По формуле (14.6)
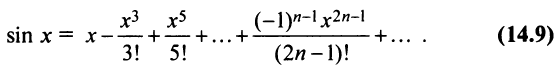
Область сходимости ряда 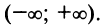
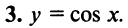 Рассматривая аналогично, получим
Рассматривая аналогично, получим
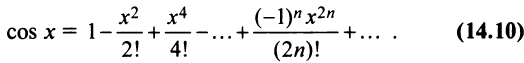
Область сходимости ряда 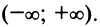
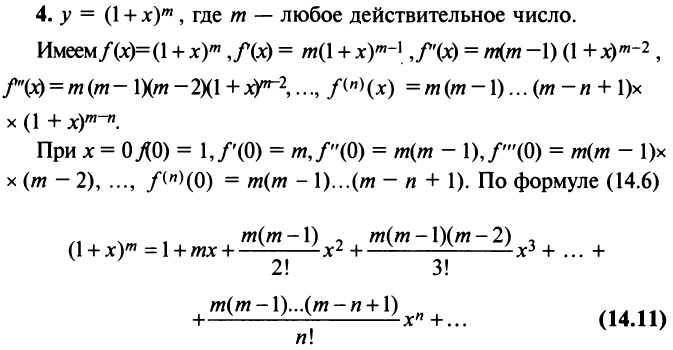
Интервал сходимости ряда 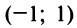 (на концах интервала при
(на концах интервала при 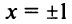 сходимость ряда зависит от конкретных значений от).
сходимость ряда зависит от конкретных значений от).
Ряд (14.11) называется биномиальным. Если 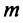 — целое положительное число, то биномиальный ряд представляет формулу бинома Ньютона, так как при
— целое положительное число, то биномиальный ряд представляет формулу бинома Ньютона, так как при 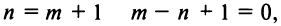
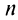 -й член ряда и все последующие равны нулю, т.е. ряд. обрывается, и вместо бесконечного разложения получается конечная сумма.
-й член ряда и все последующие равны нулю, т.е. ряд. обрывается, и вместо бесконечного разложения получается конечная сумма.
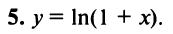
Получить разложение для этой функции можно проще, не вычисляя непосредственно коэффициенты ряда (14.6) с помощью производных.
Рассмотрим геометрический ряд
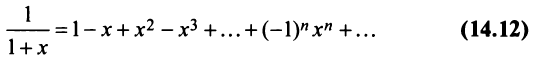
со знаменателем 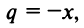 который сходится при
который сходится при 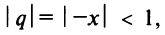 т.е. при
т.е. при 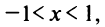 к функции
к функции 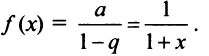
Интегрируя почленно равенство (14.12) в интервале 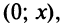 где
где 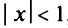 , с учетом того, что
, с учетом того, что 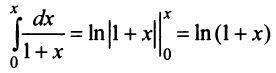 получим
получим
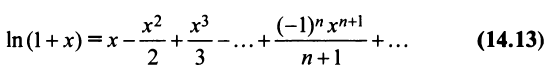
Область сходимости ряда (после выяснения сходимости на концах интервала сходимости) есть 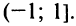
Можно доказать, что ряды, приведенные в формулах (14.8) — (14.13), сходятся к функциям, для которых они составлены.
При разложении более сложных функций используют непосредственно формулу (14.6) либо таблицу простейших разложений (14.8) – (14.13).
Пример №7
Разложить в ряд функции: 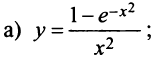
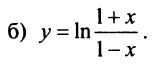
Решение:
а) Так как по (14.8) 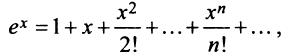
то, заменяя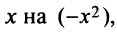 получим
получим
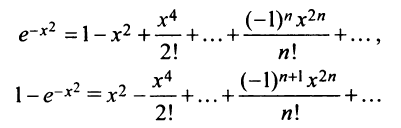
и, наконец,
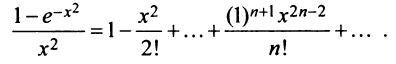
Область сходимости ряда 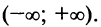
б) В разложении 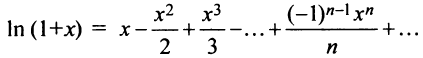 заменим
заменим 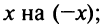 получим
получим
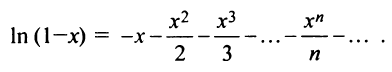
Теперь
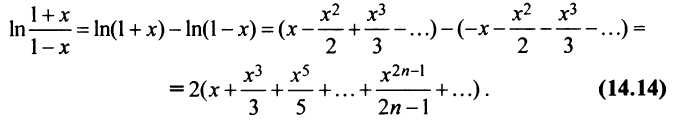
Область сходимости ряда 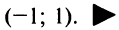
Применение рядов в приближенных вычислениях
Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «неберущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения.
Пример №8
Вычислить приближенно с точностью до 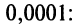
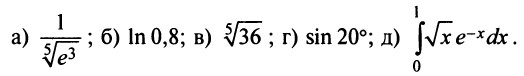
Решение:
а) Для вычисления 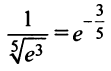 запишем ряд (14.8) при
запишем ряд (14.8) при 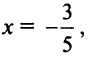 принадлежащем области сходимости
принадлежащем области сходимости 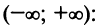
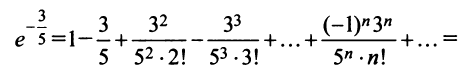
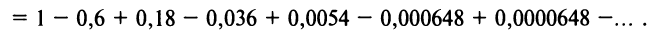
Взяв первые шесть членов разложения, на основании следствия из теоремы Лейбница (см. § 13.4) для сходящегося знакочередующегося ряда мы допустим погрешность 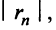 не превышающую первого отброшенного члена (по абсолютной величине), т.е.
не превышающую первого отброшенного члена (по абсолютной величине), т.е.
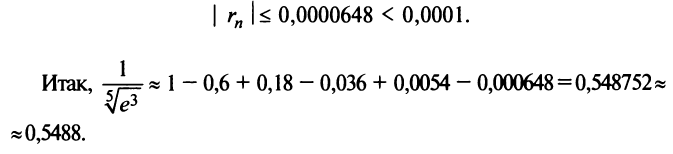
б) Для вычисления 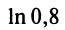 запишем ряд (14.13) при
запишем ряд (14.13) при 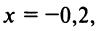 входящем в область сходимости ряда
входящем в область сходимости ряда 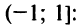
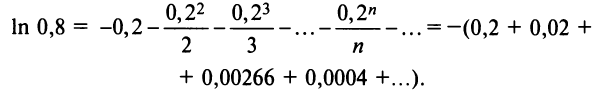
Если в качестве 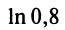 взять первые четыре члена, мы допустим погрешность
взять первые четыре члена, мы допустим погрешность
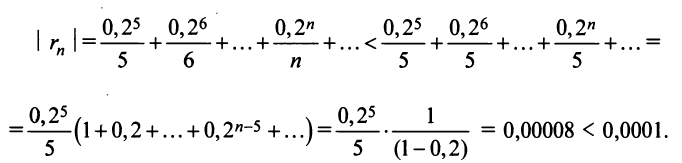
(Мы учли, что сумма сходящегося геометрического ряда в
скобках равна 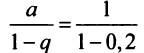 .) Итак, 1 -q 1-0,2
.) Итак, 1 -q 1-0,2
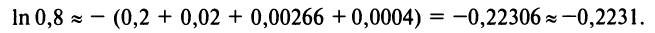
Следует отметить, что для вычисления логарифмов более удобным является ряд (14.14), который сходится быстрее ряда (14.13). Действительно, пусть 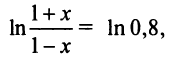 тогда
тогда 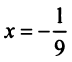 и согласно (14.14)
и согласно (14.14)
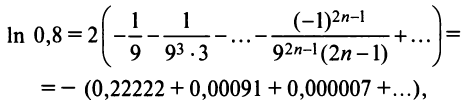
т.е. для вычисления 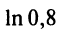 с точностью до
с точностью до 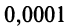 потребуется всего два члена. С помощью ряда (14.14) можно вычислять логарифмы любых чисел, в то время как с помощью ряда (14.13) -лишь логарифмы чисел, расположенных на промежутке
потребуется всего два члена. С помощью ряда (14.14) можно вычислять логарифмы любых чисел, в то время как с помощью ряда (14.13) -лишь логарифмы чисел, расположенных на промежутке 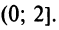
в) Представим 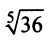 в виде
в виде 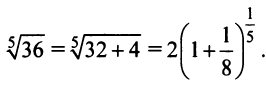
Так как 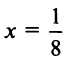 входит в область сходимости степенного ряда
входит в область сходимости степенного ряда  то при
то при 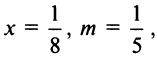 учитывая (14.11), получим
учитывая (14.11), получим
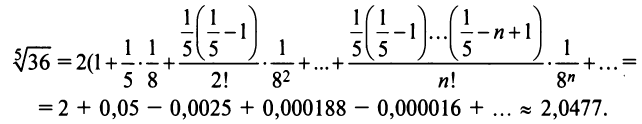
(Для обеспечения данной точности расчета необходимо взять 4 члена, так как по следствию из признака Лейбница для сходящегося знакочередующегося ряда погрешность 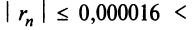
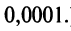 )
)
г) Для вычисления 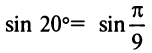 запишем ряд (14.9) при
запишем ряд (14.9) при 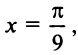 принадлежащем области сходимости
принадлежащем области сходимости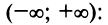
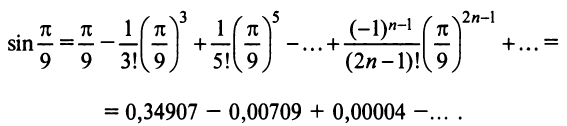
(Необходимо взять два члена, так как при этом погрешность
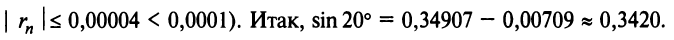
д)«Точное» интегрирование здесь невозможно, так как интеграл «неберущийся». Заменив 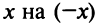 в разложении (14.8), получим
в разложении (14.8), получим
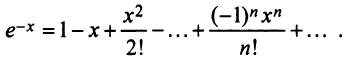
Умножая полученный ряд на 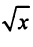
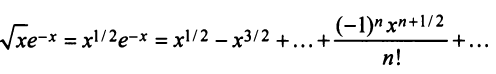
и почленно интегрируя в интервале 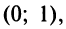 принадлежащем интервалу сходимости ряда
принадлежащем интервалу сходимости ряда  , получим
, получим 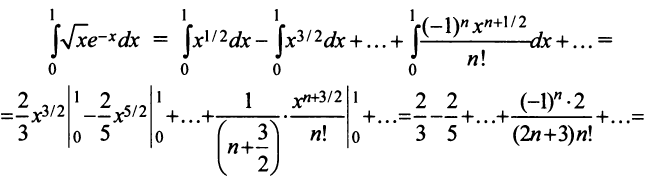
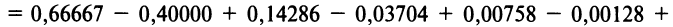
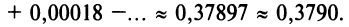 Оценка погрешности вычисления производится так же, как в примерах а), в) и г). ►
Оценка погрешности вычисления производится так же, как в примерах а), в) и г). ►
Пример №9
Исследовать сходимость ряда
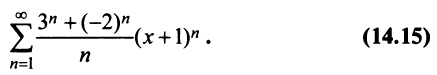
Решение:
Радиус сходимости ряда (14.15), заданного по степеням 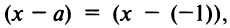 находится по той же формуле (14.5);
находится по той же формуле (14.5);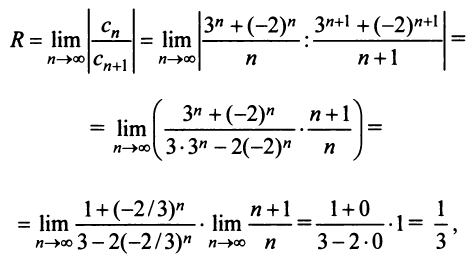
т.е. 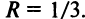 Интервал сходимости ряда (14.15) определяется из условия
Интервал сходимости ряда (14.15) определяется из условия 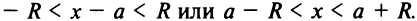 В данном примере интервал сходимости ряда есть
В данном примере интервал сходимости ряда есть 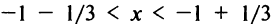 или
или 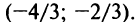
Исследуем сходимость ряда (14.15) на концах этого интервала. При 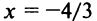 ряд принимает вид
ряд принимает вид 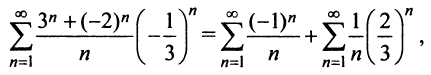 т.е. представляет сумму двух рядов. Первый, знакочередующийся ряд
т.е. представляет сумму двух рядов. Первый, знакочередующийся ряд 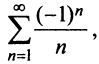 сходится (условно) (см. § 13.4), а второй ряд
сходится (условно) (см. § 13.4), а второй ряд 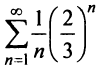 исследуем на сходимость с помощью признака Даламбера:
исследуем на сходимость с помощью признака Даламбера: 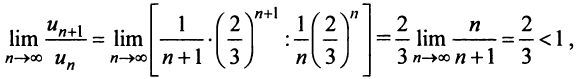 т.е. ряд сходится, а следовательно, сходится и ряд (14.15) при
т.е. ряд сходится, а следовательно, сходится и ряд (14.15) при
При 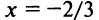 ряд (14.15) имеет вид
ряд (14.15) имеет вид 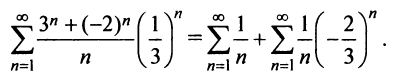 Первый из полученных рядов — гармонический — расходится, а второй — сходится на основании признака абсолютной сходимости, так как выше было показано, что ряд из абсолютных величин его членов сходится. Следовательно, ряд (14.15) при
Первый из полученных рядов — гармонический — расходится, а второй — сходится на основании признака абсолютной сходимости, так как выше было показано, что ряд из абсолютных величин его членов сходится. Следовательно, ряд (14.15) при 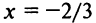 расходится. (Установить расходимость этого ряда с положительными членами
расходится. (Установить расходимость этого ряда с положительными членами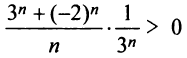 при любом
при любом 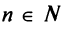 можно было и с помощью признака сравнения, так как его члены при
можно было и с помощью признака сравнения, так как его члены при 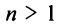 превосходят члены расходящегося гармонического ряда, умноженные на
превосходят члены расходящегося гармонического ряда, умноженные на 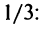
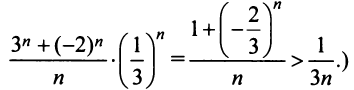
Итак, область сходимости степенного ряда (14.15) 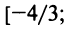
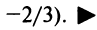
Пример №10
Разложить в ряд Маклорена функцию
Решение:
Первый способ. Применим метод непосредственного разложения по формуле (14.6).
Вначале найдем производные до «-го порядка и вычислим их значения при 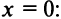
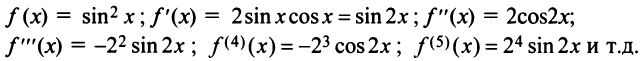
При 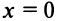 значения функции
значения функции 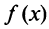 и ее производных:
и ее производных:
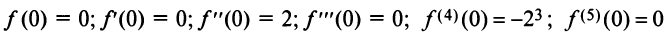
и т.д. Теперь по формуле (14.6) запишем ряд
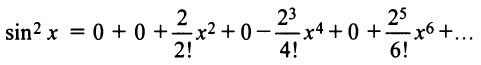
или
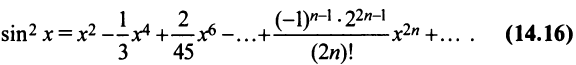
Второй способ. Учитывая, что 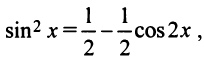 используем готовое разложение (14.10) для функции
используем готовое разложение (14.10) для функции 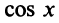 (в котором вместо
(в котором вместо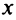 берем
берем 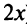 ), умножаем обе части полученного равенства на
), умножаем обе части полученного равенства на 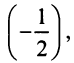 а затем прибавляем к ним
а затем прибавляем к ним 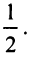 Получим
Получим
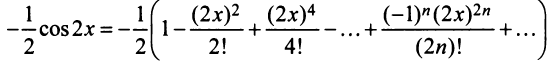 и
и
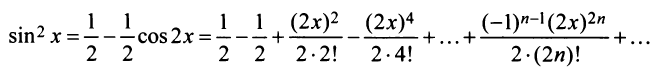 или
или
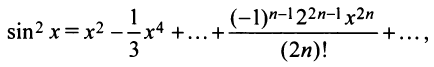
т.е. то же разложение (14.16).
Третий способ. Разложение функции 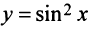 может быть осуществлено с помощью правила перемножения рядов. Если в некоторой окрестности точки
может быть осуществлено с помощью правила перемножения рядов. Если в некоторой окрестности точки 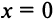 имеют место разложения
имеют место разложения
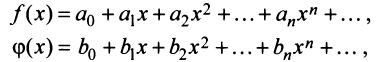
то произведение функций разлагается в той же окрестности в степенной ряд
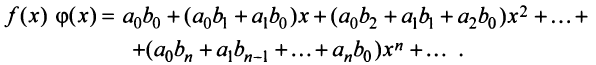
В частности, при 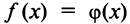 получаем следующее правило возведения в квадрат степенного ряда:
получаем следующее правило возведения в квадрат степенного ряда:
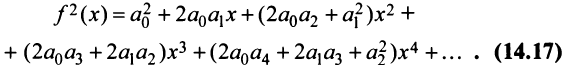
Для функции 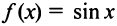 имеющей разложение в ряд (14.9), т.е.
имеющей разложение в ряд (14.9), т.е.
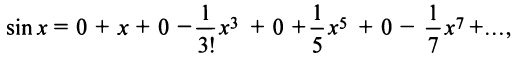
находим по формуле (14.17)
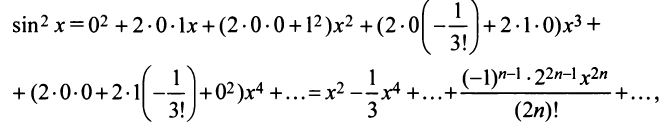
т.е. получили то же разложение (14.16).
Область сходимости ряда, как нетрудно убедиться, есть 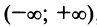 ►
►
Пример №11
Вычислить с точностью до 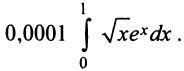
Решение:
Выражение данного интеграла в виде числового ряда находится
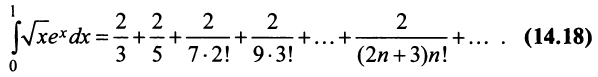
Вычисление интеграла свелось не к нахождению суммы сходящегося знакочередующегося ряда, при вычислении которой погрешность оценивается с помощью следствия из теоремы Лейбница, а к определению суммы ряда с положительными членами с неизвестной оценкой погрешности.
Поступим следующим образом. Предположим, что для оценки суммы ряда мы взяли 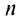 членов (вместе с первым при
членов (вместе с первым при 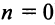 ). Тогда погрешность вычисления суммы ряда будет определяться остатком ряда
). Тогда погрешность вычисления суммы ряда будет определяться остатком ряда
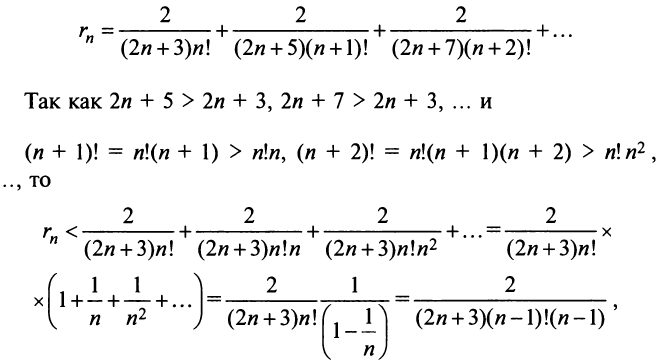
ибо выражение в круглых скобках представляет сумму сходящегося геометрического ряда (13.5) при 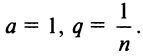
При 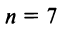
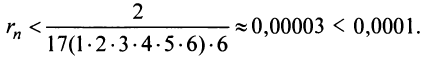
(Легко вычислить, что при любых 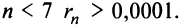 ) Итак, для обеспечения данной в условии точности вычисления интеграла необходимо взять первые 7 членов:
) Итак, для обеспечения данной в условии точности вычисления интеграла необходимо взять первые 7 членов:

- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений
- Числовые ряды
- Знакопеременные ряды
