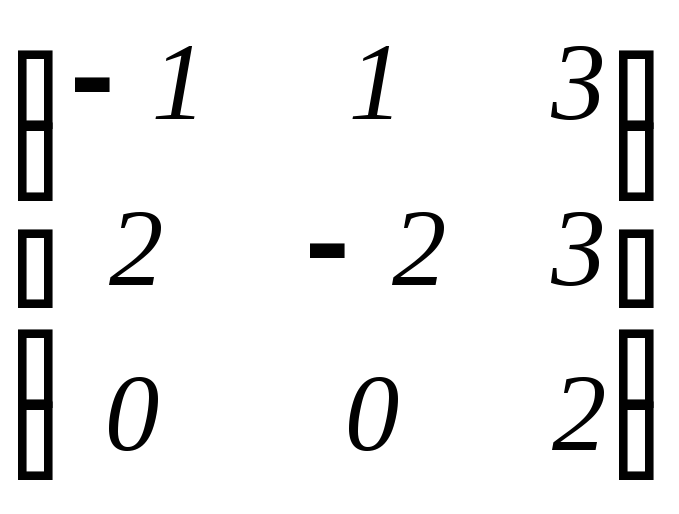Как найти инвариантные подпространства линейного оператора

Как найти инвариантные подпространства линейного оператора

Инвариантные подпространства

Определение инвариантных подпространств

Пусть mathcal{A}colon Vto V — линейное преобразование линейного пространства {V}. Линейное подпространство Ltriangleleft V называется инвариантным относительно преобразования mathcal{A}, если образ любого вектора из L принадлежит подпространству L, т.е. mathcal{A}(mathbf{v})in L~ forall mathbf{v}in L. Другими словами, инвариантное подпространство L включает свой образ mathcal{A}(L)colon, mathcal{A}(L)subset L. Нулевое подпространство {boldsymbol{o}} и все пространство {V} являются инвариантными подпространствами для любого линейного преобразования mathcal{A}colon Vto V.

Пусть L — инвариантное подпространство относительно преобразования mathcal{A}colon Vto V. Линейный оператор mathcal{A}colon Lto L, рассматриваемый как линейное преобразование пространства L в себя, называется сужением (ограничением) линейного преобразования mathcal{A}colon Vto V на инвариантное подпространство Ltriangleleft V и обозначается mathcal{A}_Lcolon Lto L, или Bigl.{mathcal{A}}Bigr|_{L}colon Lto L. Для всех векторов mathbf{v}in L выполняется равенство mathcal{A}_L (mathbf{v})= mathcal{A}(mathbf{v}), т.е. forall mathbf{v}in L образы, порождаемые оператором mathcal{A} и его сужением mathcal{A}_L, совпадают.

Примеры инвариантных подпространств

Рассмотрим инвариантные подпространства линейных операторов (преобразований).

1. Для нулевого преобразования mathcal{O}colon Vto V любое подпространство Ltriangleleft V является инвариантным, так как mathcal{O}(L)= {boldsymbol{o}}subset L. Сужение нулевого преобразования mathcal{O}_{L}colon Lto L является нулевым преобразованием.

2. Для тождественного преобразования mathcal{E}colon Vto V любое подпространство Ltriangleleft V является инвариантным, так как mathcal{E}(L)=L. Сужение тождественного преобразования mathcal{E}_{L} colon Lto L является тождественным преобразованием.

3. Для центральной симметрии mathcal{Z}_{boldsymbol{o}}colon Vto V любое подпространство Ltriangleleft V является инвариантным, так как mathcal{Z}_{boldsymbol{o}}(L)=L. Сужение центральной симметрии Bigl.{mathcal{Z}_{boldsymbol{o}}}Bigr|_{L}colon Lto L является центральной симметрией.

4. Для гомотетии mathcal{H}_{lambda}colon Vto V любое подпространство Ltriangleleft V является инвариантным, так как mathcal{H}_{lambda} (L)=L (при lambdane0). Сужение гомотетии Bigl.{mathcal{H}_{lambda}}Bigr|_{L}colon Lto L является гомотетией.

5. Для поворота mathcal{R}_{varphi}colon V_2to V_2 плоскости (при varphinepi k,~ kinmathbb{Z}) имеются два инвариантных подпространства: нулевое {vec{o}} и вся плоскость V_2. Других инвариантных подпространств нет.

6. Для оператора дифференцирования mathcal{D}colon P_n(mathbb{R})to P_n(mathbb{R}) каждое из подпространств {o(x)}triangleleft P_0(mathbb{R}) triangleleft P_1(mathbb{R})triangleleft ldotstriangleleft P_n(mathbb{R}) является инвариантным, так как при дифференцировании степень многочлена уменьшается.

7. Рассмотрим оператор Pi_{L_1}colon Vto V проектирования на подпространство L_1 параллельно подпространству L_2. Здесь V=L_1oplus L_2, Pi_{L_1}(mathbf{v}_1+ mathbf{v}_2)=mathbf{v}_1 для mathbf{v} =mathbf{v}_1+mathbf{v}_2, mathbf{v}_1in L_1,~ mathbf{v}_2in L_2. Для этого оператора подпространства L_1 и L_2 инвариантные, так как Pi_{L_1}(L_1)=L_1 и Pi_{L_1}(L_2)={boldsymbol{o}}subset L_2. Сужение оператора проектирования на подпространство L_1 является тождественным преобразованием Bigl.{Pi_{L_1}}Bigr|_{L_1}=mathcal{E}, а сужение на подпространство L_2 — нулевым Bigl.{Pi_{L_1}}Bigr|_{L_2}= mathcal{O}.

8. Рассмотрим оператор mathcal{Z}_{L_1}colon Vto V отражения в подпространстве L_1 параллельно подпространству L_2. Здесь V=L_1oplus L_2, mathcal{Z}_{L_1}(mathbf{v}_1+ mathbf{v}_2)=mathbf{v}_1-mathbf{v}_2 для mathbf{v} =mathbf{v}_1+mathbf{v}_2, mathbf{v}_1in L_1,~ mathbf{v}_2in L_2. Для этого оператора подпространства L_1 и L_2 инвариантные, так как mathcal{Z}_{L_1}(L_1)=L_1 и mathcal{Z}_{L_1}(L_2)=L_2. Сужение оператора отражения на подпространство L_1 является тождественным преобразованием Bigl.{mathcal{Z}_{L_1} }Bigr|_{L_1}=mathcal{E}, а сужение на подпространство L_2 — центральной симметрией Bigl.{mathcal{Z}_{L_1} }Bigr|_{L_2}=mathcal{Z}_{boldsymbol{o}}, так как Bigl.{mathcal{Z}_{L_1} }Bigr|_{L_2}(mathbf{v}_2)=-mathbf{v}_2.

9. В пространстве V_3 радиус-векторов пространства, отложенных от фиксированной точки O, рассмотрим поворот на угол varphinepi k,~ kinmathbb{Z}, вокруг оси l, заданной радиус-вектором vec{l}. Подпространство L=operatorname{Lin}(vec{l}) инвариантно относительно этого преобразования, так как любой вектор, принадлежащий L, не изменяется в результате поворота, т.е. отображается в себя. Подпространство Pi=L^{perp} — радиус-векторов, принадлежащих плоскости, перпендикулярной оси вращения, также инвариантное, так как в результате поворота все эти радиус-векторы остаются в той же плоскости.

Свойства инвариантных подпространств

1. Если L — инвариантное подпространство относительно обратимого линейного преобразования mathcal{A}colon Vto V, то его сужение mathcal{A}_Lcolon Lto L также обратимое линейное преобразование.

2. Для любого линейного преобразования mathcal{A}colon Vto V ядро ker mathcal{A} и образ operatorname{im} mathcal{A} являются инвариантными подпространствами, так как

mathcal{A}(ker mathcal{A}) ={boldsymbol{o}}triangleleft ker mathcal{A} и mathcal{A}(operatorname{im} mathcal{A})triangleleft operatorname{im} mathcal{A}

3. Если L — инвариантное подпространство относительно линейного преобразования mathcal{A}colon Vto V, то L — инвариантно относительно любой натуральной степени этого преобразования, причем

mathcal{A}^m(L)triangleleft mathcal{A}^{m-1}(L)triangleleft ldotstriangleleft mathcal{A}(L)triangleleft mathcal{E}(L)=L.

В самом деле, каждое из указанных множеств является линейным подпространством, так как это образы сужений линейных операторов, например, mathcal{A}^m(L)=operatorname{im} (mathcal{A}_L)^m. Докажем, например, включение mathcal{A}^2(L)triangleleft mathcal{A}(L). Для любого mathbf{w}in mathcal{A}^2(L) существует вектор mathbf{v}in mathcal{A}(L)triangleleft L, что mathbf{w}= mathcal{A}(mathbf{v}). Следовательно, mathbf{w}in mathcal{A}(L).

4. Если L — инвариантное подпространство относительно линейного преобразования mathcal{A}colon Vto V, то L — инвариантно относительно любого многочлена от этого преобразования.

Теорема (9.2) о матрицах оператора и его сужения на инвариантное подпространство

Пусть mathcal{A}colon Vto V — линейное преобразование n-мерного пространства V, а L — подпространство, инвариантное относительно преобразования mathcal{A}. Тогда существует базис (mathbf{e})=(mathbf{e}_1,ldots, mathbf{e}_n) пространства V, в котором матрица A преобразования mathcal{A} имеет нулевой угол:

A=begin{pmatrix}B!!&vline!!&C\hline O!!&vline!!& D end{pmatrix}!,

где B — матрица сужения mathcal{A}_L преобразования mathcal{A} на подпространство L, O — нулевая матрица размеров (n-ell)times ell,~ ell=dim{L}. И наоборот, если в некотором базисе (mathbf{e}) матрица A преобразования mathcal{A} имеет нулевой угол (нулевую матрицу O размеров (n-ell)times ell), то преобразование mathcal{A} имеет ℓ-мерное инвариантное подпространство.

В самом деле, возьмем базис mathbf{e}_1,ldots,mathbf{e}_{ell} подпространства L и дополним его векторами mathbf{e}_{ell+1},ldots,mathbf{e}_n до базиса mathbf{e}_1,ldots,mathbf{e}_n всего пространства V. Раскладывая образы первых ell базисных векторов по этому базису, получаем

mathcal{A}(mathbf{e}_i)= a_{1i}mathbf{e}_1+ldots+a_{ell i}mathbf{e}_{ell}+ 0cdot mathbf{e}_{ell+1}+ldots+0cdot mathbf{e}_{n},

так как mathcal{A}(mathbf{e}_i)in L,~ i=1,ldots,ell. Следовательно, последние (n-ell) элементов первых ell столбцов матрицы A преобразования mathcal{A} равны нулю. Обратное утверждение доказывается, проводя аналогичные рассуждения в обратном порядке.

Следствие. Если n-мерное пространство V представлено в виде прямой суммы ненулевых инвариантных относительно преобразования mathcal{A} подпространств V=L_1oplusldotsoplus L_k, то существует базис, в котором матрица преобразования имеет блочно-диагональный вид

A=operatorname{diag}(A_1,ldots,A_k)= begin{pmatrix}A_1&{}&O\ {}&ddots&{}\ O&{}&A_k end{pmatrix}!,

где A_i — матрица сужения mathcal{A}_{L_i} преобразования mathcal{A} на подпространство L_i,~ i=1,ldots,k.

Например, рассмотрим операторы проектирования Pi_{L_1}colon Vto V и отражения mathcal{Z}_{L_1}colon Vto V. Объединяя базисы подпространств L_1 и L_2, получаем базис пространства V=L_1oplus L_2, в котором матрицы преобразований имеют блочно-диагональный вид

Pi_{L_1}= begin{pmatrix}E!!&vline!!&O\hline O!!&vline!!&Oend{pmatrix}!,qquad Z_{L_1}= begin{pmatrix}E!!&vline!!&O\hline O!!&vline!!&-Eend{pmatrix}!.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Пусть

: V

V
– линейный
оператор, W
–
подпространство в V.
Оно называется -инвариантным,
если
w

W
(w)

W.
Будем использовать обозначение W


V.

Примеры.
1. Очевидно,
что {0}


V
и V


V
для любого линейного оператора
: V

V
.

2.
Если
: V

V
– линейный оператор, то Ker()


V
и Im()


V
, т.к.
k

Ker()
(k)
= 0

Ker()
и
v

Im()
(v)

Im().

3.
Пусть линейный оператор
: V
V
имеет в базисе {e1
, e2
, e3}
матрицу

. Тогда
пространство L(e1
, e2)
является
–инвариантным.

Действительно,
по определению матрицы линейного
оператора имеем

(e1)
= (e1
, e2
, e3)= –e1
+ 2e2

L(e1
, e2),
(e2)
= (e1
, e2
, e3)= =e1
– 2e2

L(e1
, e2)
и поэтому

l
= 1e1
+ 2e2

L(e1
, e2)
верно
включение (l)
= 1(e1)
+ 2(e2)

L(e1
, e2).

Оказывается,
пример 3
отражает общую ситуацию, как показывает
следующая

Лемма
(об инвариантных подпространствах
линейного оператора).
Следующие
условия для линейного оператора
: V

V
и подпространства W
в
n-мерном
векторном пространстве V

эквивалентны:

(1)
подпространство W
является -инвариантным,

  1. для
    некоторого базиса (    w1
    , … ,     wk)
    пространства     W
    выполнены
    условия     (wi)

    W
    (1
    i

    k).

Кроме того,
эквивалентны следующие утверждения:

(3)
существует собственное -инвариантное
подпространство W
(т.е. {0}

W

V,
(W)

W),

(4)
в некотором базисе e
= (e1
, … , en)
пространства V
матрица линейного оператора
имеет полураспавшийся вид []e
=
,
гдеA

M(k,
F),
B

M(n
– k,
F),
C

M(k,
n
– k,
F).

Доказательство.
(1)
(2) Если
W
– –инвариантное
подпространство, то
w

W
(w)

W.
В частности, это выполнено и для векторов
любого базиса (w1
, … , wk)
пространства
W.

(2)

(1) Пусть
теперь для векторов некоторого базиса
(w1
, … , wk)
пространства
W
выполнено условие (wi)

W (1

i

k).
Докажем, что
w

W
(w)

W:
если w
= 1w1
+ … + kwk
– разложение
по базису, то (w)
= = 1(w1)+…+k(xk)

W.

(3)

(4) Пусть W
– собственное –инвариантное
подпространство с базисом {e1
, … , ek}
и 0
< dim
W
= k
< dim
V
= n.
Дополним этот базис до базиса всего
пространства V
векторами ek+1
, … , en
и рассмотрим
матрицу линейного оператора

в
расширенном базисе e
= (e1
, … , ek
, ek+1
, … , en
). Имеем
[]e
=
,
где A

M(k, F), B
M(n – k, F), C
M(k, n – k, F) и
D
M(n – k, k, F).
Первые k её
столбцов – это координатные столбцы
[(e1)]e
, … , [(ek)]e
, причём ввиду –инвариантности
подпространства W
= L(e1
, … , ek)
выполнены
включения (ei)

L(e1
, … , ek)
(1
i
k). Таким
образом, (ei)
= a1ie1
+ … + akiek
+ 0ek+1
+ … 0en
, т.е. D
= 0(n–k)k
и матрица оператора полураспавшаяся
в выбранном базисе.

(4)

(3) Пусть в
некотором базисе e
= (e1
, … , ek
, ek+1
, … , en
) пространства
V
матрица []e
полураспавшаяся
[]e
=
.
Докажем, что пространство W
= L(e1
, … , ek)
является
–инвариантным
подпространством в V.
Действительно,

(ei)
= (e1
, … , ek
, ek+1
, … , en)[]e(i)
= (e1
, … , ek
, ek+1
, … , en)=

=
(e1
, … , ek)a(i)
= a1ie1
+ … + akiek

L(e1
, … , ek)
= W.

Таким
образом, подпространство W
является
–инвариантным.

Лемма
доказана.

Упражнения:
1. Найдите
все
инвариантные подпространства линейного
оператора
: V

V
с матрицей []e
=

в некотором базисе {e1
, e2
, e3}.

2.
Найдите все
инвариантные подпространства линейного
оператора
: V

V
с матрицей []e
=

в некотором базисе {e1
, e2
, e3}.

Особенно часто
используются одномерные инвариантные
подпространства, к изучению которых мы
сейчас переходим.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Помогаю со студенческими работами здесь

Понятия линейного многообразия и подпространства
Чем отличаются понятия линейных многообразия и подпространства?
По определениям из статей вики…

Выписать базис линейного подпространства
Добрый день! Дана такая задача:

Выписать базис линейного подпространства
L = left ( 3a -…

Найти все подпространства
В пространстве функций Span{sin(t),cos(t),…,sin(nt),cos(nt)}, n in N, найти все подпространства,…

Найти матрицу линейного оператора
5. Оператор Фи переводит векторы a1,a2,a3 соответственно в векторы b1,b2,b3 . Найти матрицу…

Найти матрицу линейного оператора
найти матрицу линейного оператора переводящего стандартный базис е1=(1,0,0),е2=(0,1,0).е3=(0,0,1)…

Найти матрицу линейного оператора
Может ли кто-нибудь помочь мне с этой задачей, пожалуйста.
Спасибо.

Наитй матрицу линейного…

Искать еще темы с ответами

Или воспользуйтесь поиском по форуму:

8

Источник

Добавить комментарий