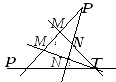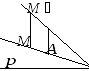Как найти инвариантные точки

Лекция 6

Проективные
преобразования плоскости и прямой,
свойства.

Аналитическое
выражение проективных преобразований.

Гомологии.
Инволюция

Рассмотрим
на проективной плоскости

два проективных репера

и
.

Определение 6.1.
Преобразование проективной плоскости
,
которое каждой точке

ставит в соответствие точку, имеющую
такие же координаты

или
,
где
,
относительно репера
,
называется проективным преобразованием
плоскости.

Свойства
проективного преобразования 6.2.

6.2.1. Всякое
проективное преобразование плоскости
переводит прямую в прямую. (Следует,
что всякое проективное преобразование
плоскости сохраняет коллинеарность
точек. Поэтому проективное преобразование
плоскости называеют еще коллинеацией).

6.2.2. Существует
единственное проективное преобразование,
которое любую упорядоченную четверку
точек общего положения

переводит в любую наперед заданную
упорядоченную четверку точек
.

6.2.3. Всякое
проективное преобразование плоскости
сохраняет сложное отношение четырех
точек прямой.

Аналитическое
выражение проективного преобразования
плоскости.

Пусть
дано проективное преобразование
,
заданное парой реперов

и
.
Точка

– произвольная точка в репере
,
точка

– образ точки

при преобразовании
.

Пусть
,
тогда
.
Обозначим координаты точки

относительно репера
.
Найдем связь координат точки

в двух проективных реперах: для этого
воспользуемся формулами перехода от
репера

к реперу
(лекция
2), причем

– новые координаты точки
,
а

– старые координаты
этой точки. Получим:

Это и есть формулы
проективного преобразования плоскости.

–
матрица проективных преобразований.
Определитель матрицы

отличен от нуля, так как точки

не лежат на одной прямой.

На расширенной
аффинной (или евклидовой ) плоскости
можно ввести неоднородные координаты.
Воспользовавшись формулами
,
имеем:
.
Тогда формулы проективных преобразований
плоскости в неоднородных координатах
примут следующий вид:
,
.

Пусть

– проективное отображение прямой

на прямую
.
–
проективный репер на прямой
,

– проективный репер на прямой
.

Определение
6.3. Отображение

прямой

на прямую
,
которое каждой точке прямой
,
имеющей в репере

координаты
,
ставит в соответствие точку
,
принадлежащую прямой

с теми же координатами

в репере
,
называется проективным.

Если
,
то

– проективное преобразование, то есть
проективное отображение прямой на себя
также называется проективным
преобразованием.

По аналогии с
нахождением формул проективных
преобразований плоскости можно получить
формулы проективных преобразований
прямой:
.
Определитель матрицы, составленной из
коэффициентов правых частей данных
формул проективных преобразований на
прямой, отличен от нуля. На расширенной
аффинной (или евклидовой) прямой, введя
неоднородные координаты, имеем следующую
формулу:
.

Определение
6.4. Проективное
преобразование прямой называется
инволюцией, если оно совпадает со своим
обратным преобразованием.

Свойства
инволюций 6.5.

6.5.1. Инволюция
может иметь либо две инвариантные точки,
либо ни одной.

Если
инволюция имеет две инвариантные точки,
то она называется гиперболической; если
инволюция не имеет инвариантных точек,
то она называется эллиптической.

6.5.2. Если

и

– инвариантные точки гипербоинволюции,
то они гармонически разделяют любую
пару соответствующих при инволюции
точек этой прямой.

Теорема 6.6.
(признак
инволюции)
Если проективное преобразование прямой
какую-нибудь точку

прямой переводит в точку
,
а точку

в точку
,
то оно является инволюцией.

Инвариантные
точки и инвариантные прямые

Пусть дано
проективное преобразование

плоскости:



Определитель матрицы преобразований
отличен от нуля.

Определение 6.7.
Точка

проективной
плоскости

называется инвариантной точкой
проективного преобразования
,
если ее образ совпадает с точкой
.

Найдем
характеристическое уравнение для
нахождения инвариантных точек. Пусть
,
тогда, если

– инвариантная
точка, то
и
.
В формулах проективных преобразований
плоскости заменим

на
:

Выполнив
преобразования, получим:

.

Система уравнений
однородна, имеет ненулевые решения,
если ее определитель равен нулю:
–
характеристическое уравнение для
нахождения инвариантных точек. Оно
имеет по крайней мере один действительный
корень. Решая, находим
,
которое позволяет найти координаты
инвариантной точки. Таким образом,
всякое проективное преобразование
плоскости имеет по крайней мере одну
инвариантную точку.

Определение
6.8. Прямая

называется инвариантной прямой
проективного преобразования
,
если ее образ

совпадает с прямой
.
(Образ любой
точки
прямой
принадлежит
этой же прямой
).

Пусть прямая

задана уравнением

и точка прямой
.
При проективном преобразовании

точка

переходит в точку
.
Так как прямая

инвариантная, то точка

принадлежит прямой
,
и координаты этой точки удовлетворяют
ее уравнению:

(*).

Подставим в
уравнение (*) вместо

их выражения из формул проективных
преобразований при
.
Получим:

(**)

Полученное
уравнение (**) является уравнением прямой
,
так как она инвариантная, то есть
уравнение (**) должно совпадать с уравнением
.
Тогда коэффициенты при неизвестных
будут пропорциональными.

.

Так как

не равны нулю одновременно, то определитель
системы равен нулю. Итак, всякое
проективное преобразование имеет по
крайней мере одну инвариантную прямую.

Гомология

Определение 6.9.
Проективное преобразование плоскости,
которое имеет прямую инвариантных
точек, а значит, и пучок инвариантных
прямых называется гомологией.

Определение
6.10. Центр
пучка инвариантных прямых называется
центром гомологии; прямая

инвариантных точек называется осью
гомологии.

Гомология задается
центром; осью; парой соответственных
точек.

Виды гомологии:

• гиперболическая
  (центр не лежит на оси гомологии)

• параболическая
  (центр лежит на оси гомологии).

Свойства гомологии
6.11.

1. Прямая, проходящая
   через несовпадающие соответственные
   точки гомологии, является инвариантной
   прямой;

2. Прямые, проходящие
   через несовпадающие соответственные
   точки гомологии, принадлежат одному
   пучку, центр которого является
   инвариантной точкой.

3. Точка, ее образ
   и центр гомологии лежат на одной
   прямой.

4. Соответствующие
   прямые пересекаются на оси гомологии.

Способ построения
образа точки при гомологии

Пусть М – любая точка проективной плоскости, – образ точки Ь при гомологии с центром и осью . Построить точку – образ любой точки .
Проведем прямую (искомая точка ); Проведем прямую ; Найдем точку пересечения прямой с осью гомологии : ;	Гиперболическая
Параболическая

Виды гомологии
на расширенной плоскости

Условия определения центра и оси	Чертеж	Название
1. Ось – несобственная прямая, центр – собственная точка.		Гомотетия с центром и коэффициентом
2. Ось – собственная прямая, центр – несобственная точка.	Перспективно-аффинное или родство аффинной плоскости
		Косое сжатие – ось сжатия
		Частный случай родства: сдвиг вдоль оси родства
3. Ось – несобственная прямая, центр – несобственная точка.		Параллельный перенос на вектор

Соседние файлы в папке вопрос 9

• #
• #
• #
• #
• #

Неподвижных точек действительно нет, так как система $%x=y$%; $%y=z$%; $%z=x+1$% решений не имеет.

Рассмотрим уравнение плоскости: $%ax+by+cz+d=0$%, где хотя бы одно из чисел $%a,b,c$% отлично от нуля. Если эта плоскость инвариантна, то для любой её точки после замены координат должно иметь место равенство $%ay+bz+c(x+1)+d=0$%, то есть $%cx+ay+bz+c+d=0$%. Это уравнение той же плоскости, и оно не обязательно совпадает с предыдущим, но пропорционально ему с некоторым коэффициентом $%k$%, то есть $%c=ka$%, $%a=kb$%, $%b=kc$%, $%c+d=kd$%. Легко видеть, что $%a=0Rightarrow c=0Rightarrow b=0Rightarrow a=0$%, поэтому ни одно из чисел $%a,b,c$% нулю не равно. Тогда $%abc=k^3abc$%, и после сокращения на $%abcne0$% получается $%k^3=1$%, то есть $%k=1$%. (Здесь важно, что всё происходит над полем действительных чисел, потому что в комплексной области результат был бы другим.) Теперь из равенства $%c+d=d$% получается противоречие, из которого можно сделать вывод, что инвариантных плоскостей у нас нет.

Теперь рассмотрим вопрос об инвариантных прямых. Рассмотрим на прямой две различные точки с координатами $%(x_1,y_1,z_1)$% и $%(x_2,y_2,z_2)$%. Тогда $%(x_2-x_1,y_2-y_1,z_2-z_1)$% есть направляющий вектор прямой. После замены координат он превратится в $%(y_2-y_1,z_2-z_1,x_2-x_1)$%, и этот вектор пропорционален предыдущему. Как и выше, легко проверяется, что у него нет нулевых координат (в противном случае все нулевые), а произведение координат не изменилось, поэтому коэффициент пропорциональности равен 1, и все координаты равны. Это означает, что (1,1,1) является направляющим вектором инвариантной прямой (если таковая вообще есть).

Таким образом, прямая задаётся параметрически в виде $%x=x_0+t$%, $%y=y_0+t$%, $%z=z_0+t$%. После замены, сумма координат увеличивается на 1, и это значит, что значение параметра $%t$% увеличивается на $%frac13$%. Отсюда можно сделать вывод, что $%(x_0+frac13,y_0+frac13,z_0+frac13)=(y_0,z_0,x_0+1)$%. Точку $%x_0$% можно выбрать произвольно — например, полагая $%x_0=0$%. Тогда $%y_0=frac13$%, $%z_0=frac23$%, и прямая, заданная параметрически в виде $%x=t$%, $%y=frac13+t$%, $%z=frac23+t$% оказывается инвариантной. Точка $%(y,z,x+1)$% будет принадлежать той же прямой при замене значения параметра $%t$% на $%t+frac13$%.

Можно заметить, что эта прямая является пересечением двух плоскостей: $%y=x+frac13$% и $%z=y+frac13$%.