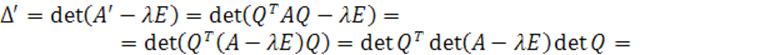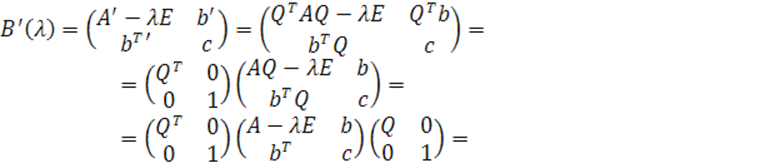Как найти инварианты матрицы - Сайт, где вы сможете решить свои вопросы

Рассматриваются
подобные матрицы
иразмерности,
задающие один и тот же линейный операторA
относительно
различных пар базисов. Для этих матриц
существует невырожденная
– матрица,
связывающая матрицыиматричным соотношением подобия

.
(3.1)

Матричное
соотношение подобия (3.1) имеет два
матричных
аналога

и
.
(3.2)

Возникает
вопрос: какие
характеристики подобных
матриц
ипри преобразованиях подобия вида (3.2)сохраняются,
а
какие –
нет?

Определение
3.1 (О3.1). Характеристики
матриц размерности
,
принадлежащих классу подобных, то есть
задающих один и тот же линейный операторA,
которые сохраняются
неизменными на всем классе подобных
представлений, называются матричными
инвариантами.

Определение
3.2 (О3.2).
Характеристики матриц размерности
,
принадлежащих классу подобных, то есть
задающих один и тот же линейный операторA,
которые для каждой реализации подобной
матрицы оказываются своими,
называются
матричными
неинвариантами.

Рассмотрим
матричные
инварианты
на примере двух подобных матриц
ивида (3.2).

1.
Первым матричным инвариантом
является характеристический полином
иподобных матрици.
В этой связи сформулируем и докажем
следующее утверждение.

Утверждение
3.1 (У3.1). Характеристические
полиномы подобных матриц
исовпадают так, что выполняется соотношение

. □(3.3)

Доказательство.
Подставим
в (3.3) матрицу
с использованием представления (3.2), а
также представление единичной матрицы
в форме,
тогда получим скалярно-матричное
соотношение

(3.4)

Воспользуемся
положением о том, что детерминант
произведения матриц равен произведению
детерминантов, с учетом которого (3.4)
принимает вид

Если
учесть, что детерминант это скаляр, и
воспользоваться свойством детерминанта
произведения матриц в обратном порядке
так, что произведение детерминантов
равняется детерминанту произведения
матриц, согласованных по размерности,
то получим

Таким
образом, установлено равенство
.
■

2.
Вторым матричным инвариантом
являются
алгебраические спектры
и

собственных значений подобных матриц
и,
что записывается в форме

.
(3.5)

3.
Третьим матричным инвариантом являются
детерминанты
иподобных матрици,
определяемые соотношением

(3.6)

4.
Четвертым матричным инвариантом
являются следы
и

подобных матриц
и,
определяемые выражением

,
(3.7)

и вычисляемые с
помощью соотношений

,
(3.8)

(3.9)

Примечание
3.1 (П3.1). Матричным
инвариантом
являются
также ранги
иподобных матрици
,
как число линейно независимых столбцов,
как размерности
и
образов
этих матриц, определяемые числом
ненулевых
собственных значений подобных матриц
и
.

Примечание
3.2 (П3.2). Необходимым,
но недостаточным условием подобия двух
матриц
иявляются равенства (3.6) детерминантов
матриц и (3.7) следов матриц. Достаточным
условием подобия матрициявляются равенства (3.3) характеристических
полиномов матриц и совпадения
алгебраических спектров собственных
значений этих матриц.

Рассмотрим
матричные
неинварианты
на примере двух подобных матриц
ивида (3.2).

1.
Первым матричным неинвариантом являются
геометрические спектры
исобственных векторовиподобных матрици,
задаваемых в форме

,
(3.10)

.
(3.11)

При этом (как
правило) выполняется отношение неравенства

.
(3.12)

2.
Вторым матричным неинвариантом
являются нормы
и
подобных
матриц
и,
которые в зависимости от индекса (*)
нормы задаются в формах.

2.1. Евклидова
(Фробениусова) норма

(3.13)

При этом (как
правило) выполняется отношение неравенства

(3.14)

2.2. Операторные
(индуцированные) нормы

(3.15)

2.2.1.
При
столбцовые нормыи;

2.2.2.
При
строчные нормыи;

2.2.3. При
спектральные нормыи,
вычисляемые в силу соотношений

;

где
и
–
соответственно максимальные сингулярные
числа матриц
и.
Приведенные матричные нормы удовлетворяют
оценочным неравенствам, конструируемые
на примере матрицы:

; ;

При этом (как
правило) выполняется отношение неравенства

при
(3.16)

3.
Третьим матричным неинвариантом
являются алгебраические спектры
и
сингулярных
чисел подобных матриц
и.
С понятием сингулярное число связана
процедура сингулярного разложения
матриц (процедураSVD–разложения),
которую рассмотрим для общего случая.

Определение
3.3 (О3.3).
Сингулярным разложением вещественнозначной
матрицы
N
размерности
называется еефакторизация,
задаваемая в виде

,
(3.17)

где
U
– ортогональная
матрица,V
– ортогональная
матрица, образующие соответственно
левый и правый сингулярные базисы и
обладающие свойствами:

, .
(3.18)

–матрица
сингулярных чисел
,
которая принимает вид

при
,
(3.19)

при
,
(3.20)

при
.
(3.21)

Положим
и транспонируем матричное выражение
(3.17), тогда получим

(3.22)

Умножим (3.17) на
(3.22) тогда с использованием свойства
(3.18) получим цепочку равенств

.
(3.23)

Теперь умножим
(3.22) слева на (3.17), получим:

.
(3.24)

Умножим
матричное уравнение (3.23) на матрицу U
справа, тогда с учетом (3.18) получим
матричное соотношение:

.
(3.25)

Перейдем в (3.25) к
столбцовой форме записи правых матричных
компонентов:

что эквивалентно
матрично-векторному представлению

.
(3.26)

Если
учесть, что столбец
имеет вид

,
(3.27)

то с учетом (3.27)
соотношение (3.26) записывается

.
(3.28)

Векторно-матричное
соотношение (3.28) представляет собой
полное решение проблемы собственных
значений
и собственных векторовматрицы.
В результате чего получаем, чтоищутся как решения характеристического
уравнения

,
(3.29)

а
матрица
оказывается составленной из собственных
векторов

матрицы
единичной нормы в форме

(3.30)

Умножим
теперь матричное уравнение (3.24) на
матрицу
справа, тогда с учетом (3.18) получим:

(3.31)

По
аналогии с (3.26) – (3.29) соотношение (3.31)
запишем в форме
матрично-векторных выражений:

,
(3.32)

которое
представляет собой задачу на собственные
значения
и собственные векторыматрицы.
Последнее позволяет составить
характеристическое уравнение

,
(3.33)

позволяющее
вычислить все
,
знание которых в силу (3.32) позволяет
найти собственные векторыединичной нормы матрицы.
Матрицаправого сингулярного базиса в итоге по
аналогии с (3.30) записывается в форме:

.
(3.34)

Следует
заметить, что в случае
матрицыиобладают одним и тем же спектром
собственных значений так, что.
Если,
то спектрсодержитсобственных значений, а спектрсодержитсобственных значений, причем количествоненулевых
элементов этих спектров оказываются
равными.

Дадим
теперь геометрическую
интерпретацию сингулярного разложения
матрицы
(3.17). Для этой цели умножим (3.17) на матрицусправа и воспользуемся свойствами
(3.18), тогда получим:

.
(3.35)

Запишем (3.35) по
аналогии с (3.28) и (3.32) в столбцовой форме

.
(3.36)

Сконструируем
теперь на векторно-матричном соотношении
(3.36) согласованные тройки
,
которые несут информацию о том, что в
силу (3.36) эффект действия оператора с
матрицейнаi-й
элемент
правого сингулярного базисасостоит в умножении наi-ое
сингулярное число
i-го
элемента

левого сингулярного базиса
.

Если
теперь с помощью матрицы
в силу линейного векторно-матричного
соотношения

(3.37)

отобразить
сферу
,
то она отобразится вэллипсоид,
положение
полуосей которого определяется
элементами

левого сингулярного базиса
,
адлины
этих полуосей в силу (3.36) будут равны
.

В
заключение заметим, что в англоязычной
литературе сингулярное разложение
матриц именуется SVD–разложением
(SVD–процедурой).
Во всех версиях пакета MATLAB
существует функция SVD(N),
которая выводит матричные компоненты
факторизации (3.17).

Возвращаясь
к проблеме матричных неинвариантов,
следует констатировать, что если в
качестве
– матрицывзять подобные матрицыи
,
то, как правило, на спектрах их сингулярных
чисел выполняется отношение неравенства

4.
Четвертым матричным неинвариантом
являются числа обусловленности
подобных матрици.

Дадим
определение числу обусловленности
произвольной
матрице,
первое из них будетгеометрическим,
а второе –алгебраическим.

Определение
3.4 (О3.4).
Числом обусловленности
произвольнойматрицыназывается положительнозначная скалярная
характеристика этой матрицы, задаваемая
в форме

(3.38)

Примечание
3.3 (П3.3).Численно
значение числа обусловленности матрицы
зависит от типа используемой в (3.38)
матричной нормы. Если в (3.38) используется
спектральная норма матриц (),
то выполняется соотношения

(3.39)

Число
обусловленности (3.38), построенное на
спектральных нормах (3.39), принимает вид

(3.40)

Выражение
(3.40) показывает, что число обусловленности
матрицы
линейной алгебраической задачи (3.37)геометрически
характеризует
степень
сплющенности
эллипсоида, получаемого при отображении
сферы
единичного радиуса.

Алгебраическое
определение числа обусловленности
матрицывведем на базе следующего утверждения.

Утверждение
3.2 (У3.2). Число
обусловленности матрицы
,
заданное в форме (3.38), содержательно
представляет собойкоэффициент
усиления относительных погрешностей
задания (знания) компонентов правой
части ЛАЗ (3.37) в относительную погрешность
ee
левой части.
□

Доказательство.
Введем в рассмотрение помимо номинальной
версии ЛАЗ (3.37) ее возмущенную версию

.
(3.41)

Перейдем от задачи
(3.41) к задаче в абсолютных приращениях,
которая с использованием (3.37) и (3.41)
запишется в форме

.
(3.42)

Переход
в (3.42) к согласованным матричным и
векторным нормам позволяет записать

.
(3.43)

Введем
в рассмотрение относительные погрешности
представления компонентов ЛАЗ и ее
решения, определив их следующими
соотношениями:

;

.
(3.44)

Свяжем
относительные погрешности (3.44)
аналитической зависимостью, опираясь
на соотношение (3.43). Для этих целей
представим номинальную версию ЛАЗ
(3.37) в форме

которая
в согласованных матричных и векторных
нормах позволяет записать

.
(3.45)

Деление
левой части неравенства (3.43) на левую
часть второго неравенства (3.45) и
соответственно правой части неравенства
(3.43) на правую часть второго неравенства
(3.45) усиливает выполнение условий
исходного неравенства (3.43) и принимает
вид

.
(3.46)

Если
в (3.46) учесть (3.38), а также выражение для
относительных погрешностей (3.44), то
неравенство (1.8) примет вид

.
■(3.47)

Таким
образом, алгебраическое
определение числа обусловленности
матрицы совпадает с выдвинутым положением
утверждения 3.2 и имеет следующую
формулировку.

Определение
3.5 (О3.5).
Число обусловленности, заданное в форме
(3.38) произвольной квадратной матрицы
,
порождающей линейную алгебраическую
задачу вида (3.37), содержательно представляет
собойкоэффициент
усиления относительных погрешностей
задания (знания) компонентов правой
части ЛАЗ (3.37) в относительную погрешность
ee
левой части. □

В
заключение заметим, что числа
обусловленности
подобных матрици,
являясь матричныминеинвариантами,
как правило, связаны отношением
неравенства

Решение вариантов
задач

Задача
3.1.
Выбрать из приводимых ниже матриц пару
подобных путем вычисление матричных
инвариантов,
в случае положительного исхода выбора
вычислить все матричные инварианты
и неинварианты
этих матриц.

3.1.

3.2.

3.3.

3.4.

3.5.

3.6.

3.7.

3.8.

3.9.

3.10.

3.11.

3.12.

3.13.

3.14.

3.15.

Решение
задачи на примере пары матриц 3.15 и 3.7.
Выдвинем гипотезу,
что матрицы
иподобны. Вычислим матричныеинварианты
этих матриц:

1. Характеристические
полиномы, которые принимают вид

;

Гипотеза
верна, так как
,
поэтому выбранные матрицыи
подобны.

2. Алгебраические
спектры собственных значений матриц

;

3. Определители
(детерминанты) матриц

4. Следы матриц

Вычислим
матричные неинварианты
этих матриц:

1.
Спектры собственных векторов
и

;

2.
Нормы
и
.

2.1. Евклидовы
(Фробениусовы) матричные нормы

2.2.
Операторные
(индуцированные) нормы

2.2.1.
При
столбцовые нормы.

2.2.2.
Пристрочные нормы.

2.2.3.
При
спектральные нормыи,
вычисляемые в силу соотношений

;

;
;

;

3.
Алгебраические спектры
и
сингулярных
чисел подобных матриц
и
вычислены
в предыдущем пункте и имеют представления

4.
Спектральные числа обусловленности
подобных матриц
и
,
вычисляемых в силу соотношений

■

Соседние файлы в папке Книга18_МОСТУ_АМПС_ПослВерстка

#
#
#
#
#
#
21.03.2016101.38 Кб24Обложка_FIN_СУ.vsd

Источник

Инвариантные множители многочленной матрицы (λ-матрицы)

Пусть A(lambda) — λ-матрица n-го порядка. Любой минор этой матрицы представляет собой многочлен переменной lambda . Напомним, что рангом λ-матрицы называется максимальный порядок минора, не равного тождественно нулю, т.е. operatorname{rg} A(lambda)=r , если в матрице имеется отличный от нуля минор r-го порядка, а все миноры большего порядка тождественно равны нулю или не существуют.

Обозначим через d_k(lambda) наибольший общий делитель миноров k-го порядка λ-матрицы A(lambda) . Для определенности будем считать, что старшие коэффициенты многочленов равны единице. Заметим, что в совокупности многочленов

d_1(lambda),~ d_2(lambda),~ ldots,~ d_r(lambda),

где r=operatorname{rg}A(lambda) , каждый последующий многочлен делится на предыдущий.

В самом деле, разложив любой минор k-го порядка по строке, получим сумму миноров (k-1)-го порядка, взятых с некоторыми коэффициентами. Так как каждый минор (k-1)-го порядка делится на $d_{k-1}(lambda)$ , то и вся сумма будет делиться на $d_{k-1}(lambda)$ . Следовательно, любой минор k-го порядка делится на $d_{k-1}(lambda)$ . Поэтому и наибольший общий делитель $d_{k}(lambda)$ также делится на $d_{k-1}(lambda)$ . Многочлены

$e_1(lambda)=d_1(lambda),quad e_2(lambda)= frac{d_2(lambda)}{d_1(lambda)}, quad ldots,quad e_r(lambda)=frac{d_r(lambda)}{d_{r-1}(lambda)},,$

(7.11)

называются инвариантными множителями λ-матрицы A(lambda) . Здесь — ранг λ-матрицы .

Теорема 7.3 об инвариантных множителях. При элементарных преобразованиях λ-матрицы ее инвариантные множители не изменяются.

Достаточно показать, что при элементарных преобразованиях не изменяются многочлены d_1(lambda), d_2(lambda), ldots, d_r(lambda) . Это доказательство почти дословно повторяет доказательство теоремы 3.3. В самом деле, при одном элементарном преобразовании (I, II или III типа) матрицы A(lambda) любой ее минор k-го порядка либо не изменится, либо поменяет знак на противоположный, либо совпадет с другим минором к -го порядка, либо окажется равным сумме двух миноров k-го порядка (взятых с некоторыми множителями). Ни одно из этих действий не может изменить наибольшего общего делителя d_k(lambda) . Отсюда следует, что и отношения (7.11) наибольших общих делителей не изменяются.

Следствие 1. Ранг λ-матрицы не изменяется при элементарных преобразованиях столбцов (строк).

Следствие 2. Инвариантные множители λ-матрицы полностью определяют ее нормальный диагональный вид, т.е. многочлены e_i(lambda),~i=1,ldots,r , в (7.9) совпадают с инвариантными множителями (7.11) λ-матрицы.

В самом деле, все миноры первого порядка матрицы (7.9), т.е. элементы этой матрицы, делятся на e_1(lambda) . Поэтому d_1(lambda)=e_1(lambda) . Все миноры второго порядка матрицы (7.9) делятся на произведение e_1(lambda)e_2(lambda) . Следовательно, d_2(lambda)=e_1(lambda)e_2(lambda) и т.д. Рассматривая миноры r-го порядка получаем, что d_r(lambda)=e_1(lambda)e_2(lambda)ldots e_r(lambda) . Отсюда следуют равенства (7.11). По теореме 7.3 все эквивалентные λ-матрицы имеют одни и те же инвариантные множители, которые, как мы только что убедились, полностью определяют нормальный диагональный вид λ-матрицы.

Следствие 3. Эквивалентные λ-матрицы приводятся к одному и тому оке нормальному диагональному виду.

Способы нахождения инвариантных множителей многочленных матриц

Первый способ. Привести λ-матрицу к нормальному диагональному виду (7.9): $operatorname{diag}(e_1(lambda),ldots,e_r(lambda),,0,ldots,0)$ . Ненулевые многочлены, стоящие на главной диагонали, являются искомыми инвариантными множителями.

Второй способ.

1. Найти наибольший общий делитель d_1(lambda) миноров 1-го порядка λ-матрицы (т.е. ее элементов); найти наибольший общий делитель d_2(lambda) миноров 2-го порядка и т.д. Процесс завершить, если все миноры некоторого порядка (r+1) либо тождественно равны нулю, либо не существуют.

2. Найти инвариантные множители по формулам (7.11).

Пример 7.7. Найти инвариантные множители многочленных матриц

$A(lambda)=begin{pmatrix}lambda-1&0\ 0&lambda-1end{pmatrix}!,quad B(lambda)=begin{pmatrix}lambda-1&0\ 0&lambda-2end{pmatrix}!,quad C(lambda)= begin{pmatrix}lambda&1&0\ 0&lambda&1\ 0&0&lambdaend{pmatrix}!.$

Решение. Матрица A(lambda) . Первый способ. Матрица имеет нормальный диагональный вид. Поэтому e_1(lambda)=lambda-1 и e_2(lambda)=lambda-1 .

Второй способ. 1. Запишем ненулевые миноры первого порядка матрицы A(lambda) . Они равны lambda-1 . Следовательно, их наибольший общий делитель d_1(lambda)=lambda-1 . Минор второго порядка этой матрицы единственный и равен (lambda-1)^2 . Следовательно, d_2(lambda)=(lambda-1)^2 .

2. По определению (7.11) находим инвариантные множители:

$e_1(lambda)=d_1(lambda)=lambda-1,qquad e_2(lambda)= frac{d_2(lambda)}{d_1(lambda)}= frac{(lambda-1)^2}{lambda-1}=lambda-1.$

Матрица B(lambda) . Второй способ. 1. Диагональный вид матрицы не является нормальным, поскольку двучлен (lambda-2) не делится на двучлен (lambda-1) (без остатка). Запишем ненулевые миноры первого порядка: lambda-1,~lambda-2 . Наибольший общий делитель этих многочленов равен единице, т.е. d_1(lambda)=1 . Матрица B(lambda) имеет единственный минор второго порядка, поэтому

d_2(lambda)=(lambda-1)cdot(lambda-2).

2. По формулам (7.11) находим инвариантные множители:

$e_1(lambda)=d_1(lambda)=1,quad e_2(lambda)=frac{d_2(lambda)}{d_1(lambda)}= frac{(lambda-1)(lambda-2)}{1}=(lambda-1)(lambda-2).$

Матрица C(lambda) . Первый способ. Матрица A(lambda) была приведена к нормальному диагональному виду (см. пример 7.6): $C(lambda)sim operatorname{diag}(1;1;lambda^3)$ , поэтому

e_1(lambda)=1,qquad e_2(lambda)=1,qquad e_3(lambda)=lambda^3.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

1. Вы зря раскрыли скобки в минорах. Лучше было бы оставить их в виде произведений одночленов. Вы явно ошиблись при расчетах: степени ненулевых элементов матрицы равны 2, так что миноры третьего порядка должны иметь степени не выше 6. А у вас откуда-то нарисовались и . Распишите ваши вычисления подробно.

2. НОД многочленов определяется так же, как и НОД целых чисел (а все потому, что и то, и то – евклидовы кольца). Для двух многочленов $f$ и $g$ назовем многочлен $h$ со старшим коэффициентом, равным 1, их НОДом, если любой многочлен $k$ , делящий одновременно и $f$ , и $g$ , делит и $h$ . Находится НОД при помощи алгоритма Евклида, применяемого к многочленам. Как действует алгоритм Евклида знаете?

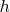
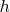
А что значит продолжая таким образом?

Пока применение этого шага не перестанет изменять матрицу, насколько я понял.

И как вообще получит можно полиномы?

Не понял вопроса. Полиномы – это то же, что и многочлены.

Источник

и,
следовательно, определитель матрицы составленной из коэффициентов уравнения квадрики, есть
инвариант этого уравнения. Порядок инварианта равен .

Определение 2: Многочлен

называется
характеристическим многочленом матрицы

Теорема 3. Докажем, что характеристический многочлен
матрицы инвариантен относительно преобразования координат.

Следствия
из теоремы

. Коэффициенты характеристического многочлена являются инвариантами уравнения квадрики. Они представляют собой
суммы главных миноров матрицы соответствующего порядка: инвариант – это сумма миноров -го порядка, ; в частности,. Порядок инварианта равен .

. Корни характеристического многочлена , то есть характеристические числа матрицы , являются инвариантами уравнения квадрики (Известно,
что все вещественные. [19] или [10]). Выясним, каков порядок
этих инвариантов.

С этой целью рассмотрим характеристические
многочлены матриц и , обозначив переменную в первом многочлене через , а во втором –. Эти многочлены таковы: и . Второй многочлен преобразуем:

Таким образом, характеристические числа обеих
матриц могут быть найдены из уравнений и=0. Поэтому
они связаны соотношением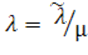. Следовательно, при умножении коэффициентов уравнения
квадрики на соответствующие характеристические числа умножаются тоже на . Это значит, что характеристические числа матрицы являются инвариантами порядка .

Наряду с уже встречавшимися квадратными матрицами
и рассмотрим прямоугольную матрицу, у которой строк и столбцов; соответствующие матрицы, составленные из
коэффициентов преобразованного уравнения будем отличать штрихом: В силу (16)

Так как матрицы и неособенные, то ранги матриц равны соответственно рангам матриц. Это значит, что ранги всех трех матриц не меняются при
преобразовании координат. Не меняются они и при умножении коэффициентов
квадрики на произвольное число. Поэтому ранги матриц являются инвариантами квадрики.

Перечисленных выше инвариантов недостаточно для
полной характеристики квадрики. Квадрика имеет еще один инвариант, не
сводящийся к рассмотренным. Обозначим через определитель -матрицы

Этот определитель представляет собой многочлен
-ой степени относительно :

Здесь
– сумма тех главных миноров го порядка матрицы , которые содержат элемент с, их называют окаймленными
минорами матрицы Очевидно что, , .

Теорема

1.
Многочлен
инвариантен относительно поворотов

2.
Если
, то последних (младших) членов многочлена равны нулю =

3.
Коэффициент
, инвариантен при переносах

Доказательство

1.
Первая
часть теоремы доказывается непосредственным подсчетом многочлена в новых координатах. Имеем в силу (16) при

А
так как

то
.

Инвариантность многочлена относительно поворотов доказана.

2.
Если , то второе утверждение теоремы тривиально, так как членов, про
которые утверждается, что они равны нулю, нет. Поэтому в дальнейшем будем
считать, что . В этом случае имеется нулевых независимых линейных комбинаций из строк матрицы . Поэтому существует квадратная неособенная матрица порядка , такая, что в матрице первые строк будут нулевыми (здесь имеется ввиду, что существует
такое преобразование строк матрицы , что первые будут нулевыми):

Можно положить , если это не так, то вместо матрицы можно взять матрицу . Далее обозначим

и
так как , то . Подсчитываем произведение матриц

(17)

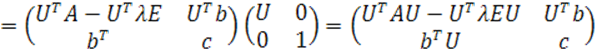
Выделим нулевые блоки в матрицах и . В матрице-столбце первые элементов – нули. Оставшеюся часть обозначим .Так как в матрице первые строк тоже нулевые, то и в матрице первые строк тоже нулевые, а в силу симметричности последней матрицы
у нее будут нулевыми и первые столбцов, оставшуюся часть этой матрицы обозначим .Таким образом, получаем:

На
блоки соответствующих размеров разобьем и матрицу :

При
таких обозначениях из (17) получаем

Поэтому

(18)

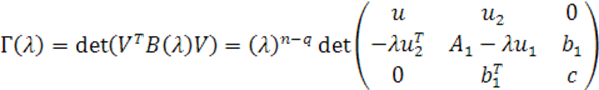
Таким образом, многочлен делится на , поэтому члены многочлена, содержащие — в степенях с показателями, меньшими , равны нулю. Этим доказано утверждение (2) теоремы.

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

Источник

1.
Введем понятие об инвариантных многочленах -матрицы .

Пусть
многочленная матрица имеет ранг , т. е. в этой матрице
имеются не равные тождественно нулю миноры -го порядка, в то время как все миноры
порядка тождественно
относительно равны
нулю. Обозначим через наибольший общий делитель всех
миноров -го-
порядка матрицы . Тогда, как
нетрудно видеть, в ряду

каждый
многочлен делится без остатка на последующий. Соответствующие частные обозначим
через :

. (10)

Определение
4. Многочлены ,
определяемые формулами (10), называются инвариантными многочленами
прямоугольной матрицы .

Термин
«инвариантные многочлены» связан со следующими соображениями. Пусть и – две эквивалентные
многочленные матрицы. Тогда они получаются друг из друга при помощи
элементарных операций. Но нетрудно непосредственно проверить, что элементарные
операции не изменяют ни ранга матрицы , ни самих многочленов . Действительно,
применяя к тождеству (3”) формулу, выражающую минор произведения матриц через
миноры сомножителей (см. стр. 22), мы для произвольного минора матрицы получим выражение

Отсюда
следует, что все миноры порядка матрицы равны нулю и, следовательно, для
ранга матрицы
имеем:

Кроме
того, из этой же формулы вытекает, что – наибольший общий делитель всех
миноров -го
порядка матрицы –
делится на нацело
. Но
матрицы и
можно
поменять ролями. Поэтому , и делится без остатка на . Отсюда

,
, , …, .

Поскольку
элементарные операции не меняют многочленов , то они не изменяют и многочленов , определяемых
формулами (10).

Таким
образом, многочлены остаются неизменными, инвариантными
при переходе от одной матрицы к другой, ей эквивалентной.

Если
многочленная матрица имеет канонический диагональный вид (9), то, как нетрудно
видеть, для этой матрицы

Но
тогда в силу соотношений (10) диагональные многочлены в (9) совпадают с
инвариантными многочленами

. (11)

Здесь
являются
одновременно и инвариантными многочленами исходной матрицы , поскольку эта матрица
эквивалентна матрице (9).

Полученные
результаты мы можем сформулировать в виде следующей теоремы.

Теорема
3. Многоценная прямоугольная матрица всегда эквивалентна канонической
диагональной матрице

(12)

При
этом здесь обязательно – ранг, a – инвариантные многочлены
матрицы ,
определяемые формулами (10).

Следствие
1. Для того чтобы две прямоугольные матрицы одинаковых размеров и были эквивалентны,
необходимо и достаточно, чтобы они имели одни и те же инвариантные многочлены.

Действительно,
необходимость этого условия была выяснена выше. Достаточность следует из того,
что две многочленные матрицы, имеющие одни и те же инвариантные многочлены,
эквивалентны одной и той же канонической диагональной матрице и, следовательно,
эквивалентны между собой.

Таким
образом, инвариантные многочлены образуют полную систему инвариантов -матрицы.

Следствие
2. В ряду инвариантных многочленов

(13)

каждый
многочлен, начиная со второго, является делителем предыдущего.

Это
утверждение не вытекает непосредственно из формул (13). Оно следует из того,
что многочлены совпадают
с многочленами канонической
диагональной матрицы (9).

2.
Укажем методы вычисления инвариантных многочленов для квазидиагональных -матриц, если
известны инвариантные многочлены матриц, стоящих в диагональных клетках.

Теорема
4. Если в квазидиагональной прямоугольной матрице

любой
инвариантный многочлен матрицы является делителем любого
инвариантного многочлена матрицы , то совокупность инвариантных
многочленов матрицы получается объединением инвариантных
многочленов матриц и .

Доказательство.
Обозначим через и
соответственно
инвариантные многочлены -матриц и . Тогда

и,
следовательно,

. (14)

-матрица,
стоящая в правой части этого соотношения, имеет каноническую диагональную
форму. Тогда согласно теореме 3 не равные тождественно нулю диагональные
элементы этой матрицы образуют полную систему инвариантных многочленов матрицы . Теорема доказана.

Для
того чтобы в общем случае при произвольных инвариантных многочленах матриц и определить
инвариантные многочлены , мы воспользуемся важным понятием об
элементарных делителях.

Разложим
инвариантные многочлены на неприводимые в данном числовом
поле множители:

(15)

Здесь
– все
различные неприводимые в поле многочлены (со старшими
коэффициентами, равными единице), входящие в состав .

Определение
5. Все отличные от единицы степени среди в разложении (15) называются
элементарными делителями матрицы в поле .

Теорема
5. Совокупность элементарных делителей прямоугольной квазидиагональной матрицы

всегда
получается объединением элементарных делителей матрицы с элементарными делителями
матрицы .

Доказательство.
Разложим инвариантные многочлены матриц и на неприводимые в поле множители:

Обозначим
через

(16)

все
отличные от нуля числа среди .

Тогда
матрица эквивалентна
матрице (14), а последняя перестановкой строк и столбцов может быть приведена к
«диагональному» виду

, (17)

где
через мы
обозначили многочлены, взаимно простые с , а через – многочлены, взаимно
простые с либо
тождественно равные нулю. Из вида матрицы (17) непосредственно вытекают
следующие разложения многочленов и для матрицы :

и
т. д.,

и
т. д.

Отсюда
следует, что ,
т. е. все не равные единице из степеней

являются
элементарными делителями матрицы .

Аналогично
определяются элементарные делители матрицы , являющиеся степенями и т. д. Теорема
доказана.

Примечание.
Совершенно аналогично предыдущему можно построить теорию эквивалентности для
целочисленных матриц (т. е. матриц, у которых элементы – целые числа). При этом
в 1, 2 (см. стр. 135) , заменяется целым числом, а в формулах
(3), (3′), (3″) вместо и стоят целочисленные матрицы с
определителями, равными .

3.
Пусть дана теперь матрица с элементами из поля . Составим для нее
характеристическую матрицу

. (18)

Характеристическая
матрица является -матрицей
ранга .
Ее инвариантные многочлены

(19)

называются
инвариантными многочленами матрицы , а соответствующие элементарные
делители в поле –
элементарными делителями в поле матрицы . Первый инвариантный многочлен совпадает с
минимальным многочленом матрицы . Знание инвариантных многочленов (а
следовательно, и элементарных делителей) матрицы позволяет исследовать ее структуру.
Поэтому представляют интерес практические способы вычисления инвариантных
многочленов матрицы. Сами формулы (19) дают алгоритм для вычисления этих многочленов,
но этот алгоритм при больших очень громоздок.

Теорема
3 дает другой способ вычисления инвариантных многочленов, основанный на
приведении характеристической матрицы (18) при помощи элементарных операций к каноническому
диагональному виду.

Пример.

, .