Если в результате композиции двух функций
и
получается тождественная функция
, то говорят, что эти две функции являются инверсиями друг друга.
Если применение функции
к входу дает
выход
, то применение другой функции
к
должно вернуть значение
. Следовательно, обратная функция обращает функцию. Область данной функции становится областью обратной функции, а область данной функции становится областью обратной функции.
В общем, обратная функция — это отражение функции начала координат относительно прямой
. Ее можно получить, заменив
на
.
Если даны графики двух функций, можно определить, являются ли они обратными друг другу. Если графики обеих функций симметричны относительно прямой y = x, то мы говорим, что эти две функции являются обратными друг другу. Это объясняется тем, что если
лежит на функции, то
лежит на ее обратной функции:
Обратная функция — это любая функция, которая никогда не принимает одно и то же значение дважды. Другими словами, для каждого значения
существует только одно значение
. Это означает, что каждый элемент кодомена является образом не более чем одного элемента его области.
Кроме того, обратная функция проходит тесты на вертикальную линию и горизонтальную линию:
Никакая горизонтальная линия не пересекает ее график более одного раза. Таким образом, никакие два элемента в домене не соответствуют одному и тому же элементу в диапазоне
Загрузить PDF
Загрузить PDF
Математические функции, обычно обозначаемые как f(x) или g(x), можно представить как порядок выполнения математических операций, которые позволяют прийти от «x» к «y». Обратная функция f(x) записывается как f-1(x).[1]
В случае простых функций найти обратную функцию несложно.
Шаги
-
1
Полностью перепишите функцию, заменив f(x) на y. При этом «у» должна находиться на одной стороне функции, а «x» — на другой. Если вам дана функция вида 2 + y = 3x2, вам необходимо изолировать «у» на одной стороне, а «x» — на другой.
- Пример. Перепишем данную функцию f(x) = 5x – 2 как y = 5x – 2. f(x) и «y» взаимозаменяемы.
- f(x) — это стандартная запись функции, но если вы имеете дело с несколькими функциями, то каждой из них нужно будет присвоить свою букву, чтобы их было легче отличать друг от друга. Например, часто функции обозначают как g(x) и h(x).
-
2
Найдите «x». Другими словами, выполните математические операции, необходимые для изолирования «x» по одну сторону от знака равенства. Основные алгебраические принципы: если «x» имеет числовой коэффициент, то разделите обе стороны функции на этот коэффициент; если к члену с «x» прибавляется некоторый свободный член, вычтите его с обеих сторон функции (и так далее).
- Помните, что вы можете применять любую операцию по отношению к одной из сторон уравнения только в том случае, если вы применяете ту же операцию по отношению ко всем членам по обе стороны от знака равенства.[2]
- В нашем примере добавьте 2 к обеим частям уравнения. Вы получите y + 2 = 5x. Затем разделите обе части уравнения на 5 и получите (y + 2)/5 = x. И, наконец, перепишите уравнение с «x» в левой части: x = (y + 2)/5.
- Помните, что вы можете применять любую операцию по отношению к одной из сторон уравнения только в том случае, если вы применяете ту же операцию по отношению ко всем членам по обе стороны от знака равенства.[2]
-
3
Поменяйте переменные, заменив «x» на «y» и наоборот. Результатом будет функция, обратная исходной. Другими словами, если мы подставим значение «x» в исходное уравнение и найдем значение «у», то, подставив это значение «у» в обратную функцию, мы получим значение «x».
- В нашем примере получим y = (x + 2)/5.
-
4
Замените «у» на f-1(x). Обратные функции обычно записывают в виде f-1(x) = (члены с «x»). Следует отметить, что в данном случае -1 — это не показатель степени; это просто обозначение обратной функции.
- Так как «x» в -1 степени равно 1/x, то f-1(x) — это форма записи 1/f(x), что также обозначает функцию, обратную f(x).
-
5
Проверьте работу, вместо «x» подставив постоянное значение в исходную функцию. Если вы правильно нашли обратную функцию, подставив в нее значение «у», вы найдете подставленное значение «x».
- Например, подставьте x = 4. Вы получите f(x) = 5(4) – 2 или f(x) = 18.
- Теперь подставьте 18 в обратную функцию и получите y = (18 + 2)/5 = 20/5 = 4. То есть у = 4. Это подставленное значение «x», поэтому вы правильно нашли обратную функцию.
Реклама
Советы
- Когда вы выполняете алгебраические операции над функциями, вы можете свободно заменять f(x) = y и f^(-1)(x) = y в обоих направлениях. Но прямая запись обратной функции может привести к путанице, поэтому придерживайтесь записи f(x) или f^(-1)(x), которая поможет вам отличить их друг от друга.
- Обратите внимание, что обратная функция обычно (но не всегда) является функциональной зависимостью.[3]
Реклама
Об этой статье
Эту страницу просматривали 63 367 раз.
Была ли эта статья полезной?
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 июля 2022 года; проверки требуют 13 правок.
Функция 
и обратная ей функция 
. Если 
, то 
Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции обычно обозначается , иногда также используется обозначение 
.
Функция, имеющая обратную, называется обратимой.
Определение[править | править код]
Функция 
называется обратной к функции 
, если выполнены следующие тождества:
Связанные определения[править | править код]
Существование[править | править код]
Чтобы найти обратную функцию, нужно решить уравнение 
относительно 
. Если оно имеет более чем один корень, то функции, обратной к не существует. Таким образом, функция 
обратима на интервале 
тогда и только тогда, когда на этом интервале она взаимно-однозначна.
Для непрерывной функции 
выразить 
из уравнения 
возможно в том и только том случае, когда функция строго монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её строгой монотонности. Например, 
является обратной функцией к 
на 
, хотя на промежутке ![(-infty, 0]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0241c015ef4c611c9c9aeafb395e7c4a16178405)
обратная функция другая: 
.
Для существования обратной функции не являются необходимыми ни непрерывность, ни монотонность исходной функции. Пример: функция 
где 
— функция Дирихле, разрывна и не монотонна, однако обратная для неё существует[2]: 
Примеры[править | править код]
Свойства[править | править код]
Графики функции и обратной ей
или
- ,
- ,
или короче
- ,
- ,
где 
означает композицию функций, а 
— тождественные отображения на 
и 
соответственно.
- .
Теорема. Композиция любых двух обратимых функций является обратимой функцией, то есть 
.
| Доказательство |
|---|
Поскольку  и  для любой обратимой функции  , где  — тождественное преобразование, то можно записать следующие равенства.
Имеем: Подействуем слева функцией |
Это утверждение легко запомнить так: «Пиджак надевают после рубашки, а снимают раньше».
Разложение в степенной ряд[править | править код]
Обратная функция аналитической в некоторой окрестности точки 
функции может быть представлена в виде степенного ряда:
где функции 
задаются рекурсивной формулой:
См. также[править | править код]
- Теорема Лагранжа об обращении рядов
- Обратные тригонометрические функции
- Обратимая функция
Примечания[править | править код]
- ↑ Куликов Л.Я. “Алгебра и теория чисел: Учебное пособие для педагогических институтов”
- ↑ Шибинский В. М. Примеры и контрпримеры в курсе математического анализа. Учебное пособие. — М.: Высшая школа, 2007. — С. 29—30. — 543 с. — ISBN 978-5-06-005774-4.
Понятие обратной функции и ее определение в алгебре
Допустим, что у нас есть некая функция y=f(x), которая является строго монотонной (убывающей или возрастающей) и непрерывной на области определения x∈a; b; область ее значений y∈c; d, а на интервале c; d при этом у нас будет определена функция x=g(y) с областью значений a; b. Вторая функция также будет называться непрерывной и строго монотонной. По отношению к y=f(x) она будет обратной функцией. То есть мы можем говорить об обратной функции x=g(y) тогда, когда y=f(x) на заданном интервале будет либо убывать, либо возрастать.
Две этих функции, f и g, будут взаимно обратными.
Обратная функция – это что такое? Дадим определение взаимно обратимой функции (что такое обратимая функция – определение).
Для чего вообще нам нужно понятие обратных функций?
Это нужно нам для решения уравнений y=f(x), которые записываются как раз с помощью этих выражений. Также понятие особенностей обратных функций помогают в решении операций по извлечению n-ой степени (она обратна возведению в степень).
На самом деле это не является чем-то сложным. Онлайн, как и в нашем материале, вы можете найти много примеров обратной функции, которые помогут в этом убедиться.
Важно знать, что любая функция y = y (x) – это определенное правило, которое определяет соответствие между двумя значениями: x и y. К примеру, функция y = x² ставит соответственно каждому действительному числу его в квадрат. Можно сделать определенную таблицу, в которой будут располагаться значения этой функции для целых аргументов.
| x | -2 | -1 | 0 | 1 | 2 |
| y = x² | 4 | 1 | 0 | 1 | 4 |
Как найти функцию обратную данной
Как найти обратную функцию?
Допустим, нам нужно найти решение уравнения cos(x)=13. Его решениями будут все точки: x=±arсcos13+2π·k, k∈Z
Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.
Разберем несколько задач на нахождение функций, обратных заданным. Вот несколько примеров обратной функции.
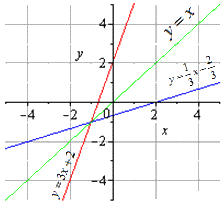
Условие: какая функция будет обратной для y=3x+2?
Решение
Область определений и область значений линейной функции, данной в условии, – это множество всех действительных чисел. Попробуем решить данное уравнение через x, то есть выразив x через y.
Мы получим x=13y-23. Это и есть нужная нам обратная функция, но y здесь будет аргументом, а x – функцией. Переставим их, чтобы получить более привычную форму записи:
y=13x-23
Ответ: функция y=13x-23 будет обратной для y=3x+2.
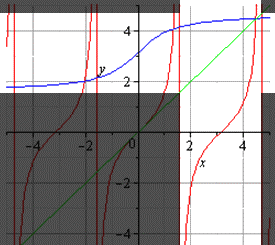
Обе взаимообратные функции можно отобразить на графике следующим образом:
На графике мы находим симметричность обоих графиков относительно y=x (они отображаются симметрично). Эта прямая является биссектрисой первого и третьего квадрантов. Что это позволило нам доказать? Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.
Возьмем онлайн-пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.
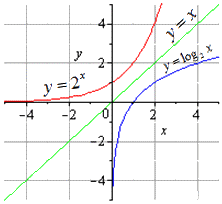
Условие: определите, какая функция будет обратной для y=2x.
Решение
Для заданной функции областью определения являются все действительные числа. Область значений лежит в интервале 0; +∞. Теперь нам нужно выразить x через y, то есть решить указанное уравнение через x. Мы получаем x=log2y. Переставим переменные и получим y=log2x.
В итоге этого примера у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.
Ответ: y=log2x.
Графически обе функции будут выглядеть или иметь следующее отображение:
Также взаимно обратные функции можно рассматривать на примере теорем.
Предположим, мы имеем определенную, с возрастающей или убывающей монотонностью, а также непрерывную в определенном промежутке x функцию y = f(x). Значит, в промежутке значений y этой функции существует и обратная функция. Она также монотонно убывает или возрастает. Также ее можно определить как непрерывную (в промежутке y).
Основные свойства взаимно обратных функций
В этом пункте мы перечислим основные свойства обратимых функций y=f(x) и x=g(y). Какими же свойствами обладают взаимообратные функции?
- Первое (исходное) свойство мы уже вывели ранее: y=f(g(y)) и x=g(f(x)).
- Второе свойство вытекает из первоначального (первого) и означает, что область определения y=f(x) будет совпадать с областью значений обратной функции x=g(y), и наоборот.
- Графики обратных функций будут симметричными (находиться в симметрии) относительно y=x.
- Если y=f(x) является возрастающей, то и x=g(y) будет возрастать, а если y=f(x) убывает, то убывает и x=g(y).
Советуем внимательно отнестись к понятиям области определения и области значения функций и никогда их не путать, так как это не одно и тоже даже исходя из названий. Допустим, что у нас есть две взаимно обратные функции y=f(x)=ax и x=g(y)=logay. Согласно первому свойству, y=f(g(y))=alogay. Данное равенство будет верным только в случае положительных значений y, а для отрицательных логарифмов не определен, поэтому не спешите записывать, что alogay=y. Обязательно проверьте и добавьте характеристику, что это верно только при положительном y.
А вот равенство x=f(g(x))=logaax=x будет верным при любых действительных значениях x.
Не забывайте про этот момент, особенно если приходится работать с тригонометрическими и обратными тригонометрическими функциями. Так, arcsinsin7π3≠7π3, потому что область значений арксинуса -π2; π2 и 7π3 в нее не входит. Верной будет запись
arcsinsin7π3=arcsinsin2π+π3==по формуле привидения=arcsinsinπ3=π3
А вот sinarcsin13=13 – верное равенство, т.е. sin(arcsin x)=x при x∈-1; 1 и arcsin(sin x)=x при x∈-π2; π2. Всегда будьте внимательны с областью значений и областью определений обратных функций!
Графики взаимно обратных функций
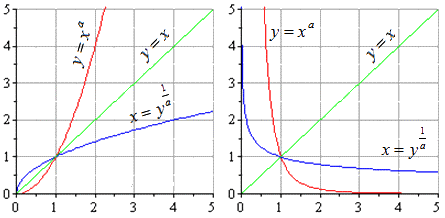
- Основные взаимно обратные функции: степенные
Если у нас есть степенная функция y=xa, то при x>0 степенная функция x=y1a также будет обратной ей. Замена букв будет давать соответственно y=xa и x=y1a.
Сделаем график. На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):
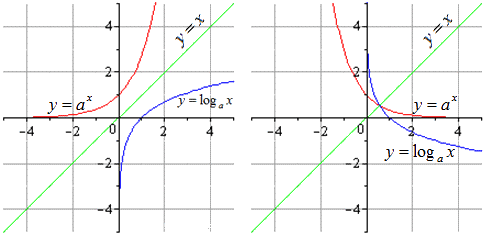
- Основные взаимно обратные функции: показательные и логарифмические
Возьмем a, которое будет положительным числом, не равным 1.
Узнаем, какими будут графики для функций с a>1 и a<1. Они будут выглядеть так:
- Основные взаимно обратные функции: тригонометрические и обратные тригонометрические
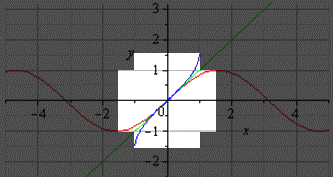
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):
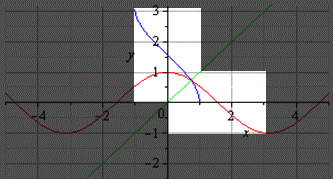
Если построить график главной ветви косинуса и арккосинуса, то он будет выглядеть так:
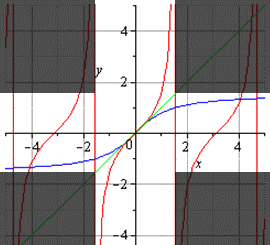
Если строить график главной ветви арктангенса и тангенса, то он будет таким:
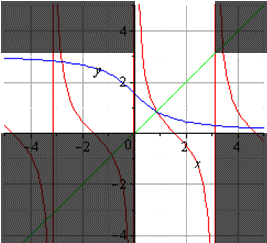
График главной ветви арккотангенса и котангенса будет таким:
В случае построения обратных ветвей, отличные от главных, то обратную тригонометрическую функцию мы сдвигаем вдоль оси Oy на нужное число периодов. Так, если требуется обратная функция для ветви тангенса на π2; 3π2, то мы можем сдвинуть ее на величину π вдоль оси абсцисс. График будет представлять собой ветвь арктангенса, которая сдвинута на π вдоль оси ординат.
Это все свойства обратных функций, о которых мы хотели бы вам рассказать.
Многие приложения в алгебре и исчислении зависят от знания того, как найти обратную функцию, и это тема данного руководства.
Прежде всего, вам нужно понять, что перед тем, как найти инверсию функции, вы должны убедиться, что такая инверсия существует.
Преимущество метода поиска обратного, который мы будем использовать, заключается в том, что мы найдем обратное и выясним, существует ли оно одновременно.
Готовый?? Тогда пристегнитесь.
Как узнать, есть ли у функции инверсия?
Технически функция имеет инверсию, когда она взаимно однозначна (инъективна) и сюръективна.
Однако решающим условием является то, что она должна быть взаимно однозначной, потому что функцию можно сделать сюръективной, ограничив ее диапазон своим собственным изображением.
Как узнать, что функция взаимно однозначна?
Что ж, есть как минимум пара способов. Один из них – алгебраический, а другой – графический (держу пари, я знаю, какой из них вы предпочитаете, да?)
Алгебраический путь
Для алгебраического подхода, чтобы функция (f) была взаимно однозначной, нам нужно доказать, что каждый раз, когда это (f(x) = f(y)), нам нужно иметь это (x = y).
Другими словами, нам нужно доказать, что
[f(x) = f(y) ,,Rightarrow ,, x = y]
Графический способ
Для графического способа нам нужно использовать
проверка горизонтальной линии
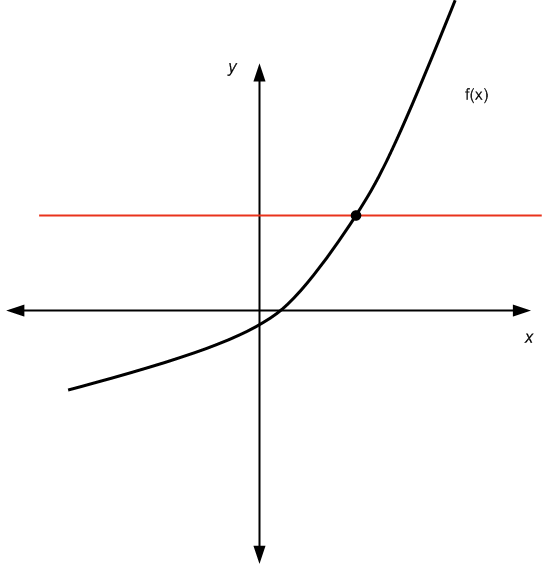
: Для любой горизонтальной линии, которую мы рисуем, график функции не более одного раза пересекает эту горизонтальную линию.
Графически:
Проходит тест горизонтальной линии
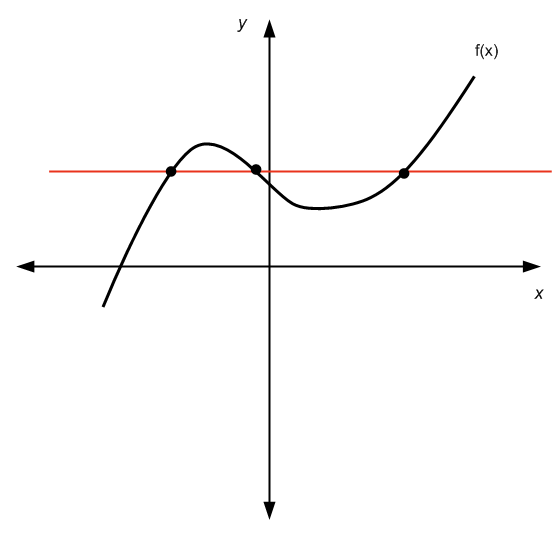
Не проходит тест горизонтальной линии
В поисках обратного
Чтобы найти обратную функцию для заданной функции (f(x)), необходимо решить уравнение.
Действительно, у вас есть уравнение (f(x) = y), вы берете (y) как заданное число, и вам нужно решить его для (x), и вам нужно убедиться, что решение УНИКАЛЬНО.
Это все. Легко, правда ??
Теперь о практических шагах:
Шаг 1:
Для заданного (y) задайте уравнение:
[f(x) = y]
и решите его для (x).
Шаг 2:
Обязательно обратите внимание на то, для какого (y) существует действительно уникальное решение.
Шаг 3:
Как только вы решите (x) в терминах (y), это выражение, которое зависит от (y), будет вашим (f^{-1}(y)).
Шаг 4:
Измените имя переменной с (y) на (x), и у вас будет обратная функция (f^{-1}(x)).
ПРИМЕР 1
Найдите обратную функцию (f(x) = sqrt x)
ОТВЕЧАТЬ:
Итак, мы берем (y) как данное, и нам нужно решить (f(x) = y), что в данном случае соответствует решению
[sqrt x = y]
Обратите внимание, что квадратный корень всегда неотрицателен, поэтому для решения нам понадобится (yge 0).
Применяя квадрат к обеим сторонам, получаем, что
[Rightarrow ,, (sqrt x)^2 = y^2]
[Rightarrow ,, x = y^2]
Итак, (f^{-1}(y) = y^2), переключая имя переменной, мы получаем обратную функцию:
[f^{-1}(x) = x^2]
для (xge 0).
ПРИМЕР 2
Найдите обратную функцию (f(x) = displaystyle frac{x}{x+1}) для (x > -1)
ОТВЕЧАТЬ:
Опять же, мы берем (y) как дано, и теперь нам нужно решить для (x) уравнение (f(x) = y). Итак, у нас есть
[displaystyle frac{x}{x+1} = y]
[Rightarrow ,, x = y(x+1)]
[Rightarrow ,, x = yx + y]
[Rightarrow ,, x – yx = y]
[Rightarrow ,, x(1 – y) = y]
[Rightarrow displaystyle ,, x = frac{y}{1-y}]
Итак, (f^{-1}(y) = displaystyle frac{y}{1-y}), переключая имя переменной, мы получаем обратную функцию:
[f^{-1}(x) = displaystyle frac{x}{1-x}]
Подробнее о поиске обратной функции
Одним из важнейших свойств обратной функции (f^{-1}(x)) является то, что (f(f^{-1}(x)) = x).
Подумайте, о чем это говорит. Что-то вроде: “Функция, вычисленная в обратном порядке, дает вам идентичность”.
Или, другими словами, вычисление инверсии через функцию похоже на бездействие с аргументом.
Или, как некоторые любят говорить: функция может каким-то образом отменить обратное.
Вы выбираете свою версию.
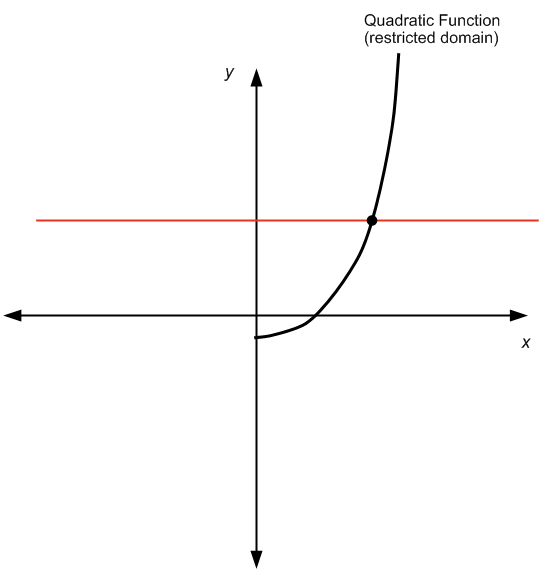
Как найти обратную квадратичную функцию? Ты можешь?
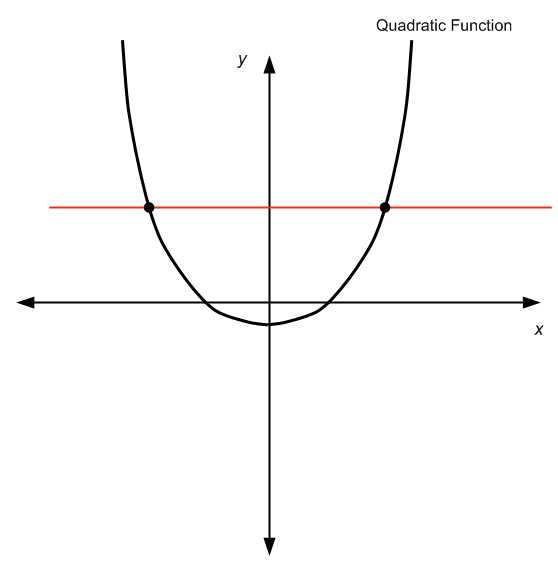
Собственно, ответ таков: это зависит от обстоятельств. Это потому, что если мы рассмотрим квадратичную функцию
по всей реальной линии
, то это не один к одному, поскольку он не проходит тест горизонтальной линии, как вы можете видеть на диаграмме ниже:
Не пройдя тест горизонтальной линии, мы можем увидеть, что для данного (y) существует более одного значения (x), так что (f(x) = y), поэтому мы не можем “решить” для (x), поскольку существует более одного (x).
НО, если вы ограничите домен и рассмотрите, скажем, только положительные числа, мы получим следующее:
который проходит проверку горизонтальной линии, и, следовательно, квадратичная функция обратима.
НРАВСТВЕННОСТЬ ИСТОРИИ: Чтобы проверить, является ли что-то обратимым, речь идет НЕ только о функции. Речь идет о функции И ее
домен и диапазон
.
Как быстро построить график обратных функций
Всегда существует требование оценки, является ли функция (f(x)) обратимой или нет (проверяя, является ли она взаимно однозначной). Но если предположить, что вы знаете, что это обратимо, есть простой способ найти график обратимости.
Сначала изобразите график данной функции (f(x)).
Затем нарисуйте линию под углом 45 градусов (y = x).
Чтобы построить график (f^{-1}(x)), все, что вам нужно сделать, это отразить график (f(x)) через линию (y = x) под углом 45 градусов, как зеркало.
См. Пример ниже с функциями (f(x) = sin x) и (f^{-1}(x) = arcsin x).
Другой способ увидеть это – использовать оригинал
график
и измените значение (x) на значение (y).
Есть ли способ сделать функцию обратной?
Да, это действительно возможно, но это происходит только для функции идентификации, то есть с (f(x) = x).
