Как найти иррациональное число на отрезке

На странице вопроса Найти хотя бы одно иррациональное число, расположенное на отрезке [0 ; 1]? из категории Алгебра вы найдете
ответ для уровня учащихся 5 – 9 классов. Если полученный ответ не
устраивает и нужно расшить круг поиска, используйте удобную поисковую
систему сайта. Можно также ознакомиться с похожими вопросами и ответами
других пользователей в этой же категории или создать новый вопрос. Возможно,
вам будет полезной информация, оставленная пользователями в комментариях, где
можно обсудить тему с помощью обратной связи.

Содержание:

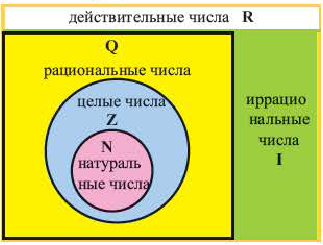
Иррациональные числа

Практическая работа 1. Великий греческий математик, физик, астроном и изобретатель Архимед хотел найти рациональное число, квадрат которого равен 3. С этой целью он выбрал числа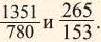

Классификация чисел

Любое рациональное число можно записать в виде дроби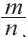

Каждую конечную десятичную дробь можно записать в виде бесконечной десятичной периодической дроби с цифрой 0 в периоде. Но есть такие числа, которые невозможно представить в виде десятичной периодической дроби. Бесконечная десятичная непериодическая дробь выражает число, которое не является рациональным. Такие числа называются иррациональными числами. Иррациональное число невозможно представить в виде 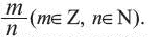Приведём примеры иррациональных чисел:

a) 0,1010010001… (количество нулей после каждой единицы увеличивается на один);

b) 0,123456789101112… (в дробной части записана последовательность натуральных чисел);

c) 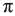= 3,14159265… (выражает отношение длины окружности к диаметру).

Если 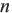не является точным квадратом какого-либо натурального числа, то 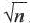является иррациональным числом. Например, 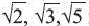иррациональные числа. Множество иррациональных чисел обозначается буквой I. Арифметические действия над иррациональными числами и их свойства аналогичны рациональным числам. Множество, состоящее из рациональных и иррациональных чисел, называется множеством действительных чисел, которое обозначается буквой R.

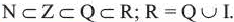
Практическая работа.

1) Начертите квадрат со стороной равной единичному отрезку и проведите диагональ данного квадрата. На диагонали квадрата постройте новый квадрат. Убедитесь, что площадь полученного квадрата в два раза больше площади единичного квадрата. Покажите, что сторона полученного квадрата равна соответственно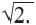

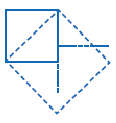
2) Повторите работу по алгоритму, представленному ниже. На координатной оси постройте квадрат, сторона которого равна единичному отрезку. Начертите окружность с центром в точке нуль, радиусом равным диагонали квадрата и отметьте точку пересечения с числовой осью. Объясните связь между соответствующим данной точке числом и длиной диагонали квадрата.

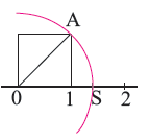
Числовая ось, рациональные, иррациональные числа

Каждой точке на числовой оси соответствует единственное число (рациональное или иррациональное) и каждому числу, на числовой оси соответствует единственная точка. Опираясь на это числа можно сравнивать. Число, соответствующее точке, которая расположена правее, больше числа, соответствующему точке, расположенной левее.

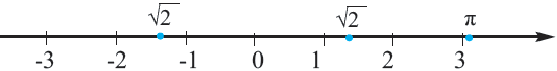
Практическая работа.

1) При помощи калькулятора вычислите значения 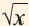при заданных значениях 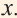Округлите их до десятых и заполните таблицу.

2) На координатной плоскости отметьте точки из таблицы, с соответствующими координатами, и соедините их плавной линией.

3) Может ли 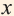принимать отрицательные значения?

4) Как изменяются соответствующие значения 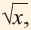при увеличении значений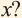

Функция y=√x и её график

Функция 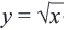и её график

В таблице, которую вы заполнили, показаны некоторые значения аргументов 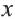в 1-ой строке, соответствующие значению функции 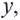заданной формулой, 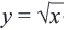во 2-ой строке. Аргумент функции 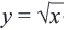определен при всех неотрицательных значениях 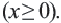Функция также припишет только положительные значения (т.к. не существует квадратного корня из отрицательного числа и арифметический корень припишет только положительные значения).

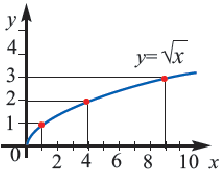
График функции 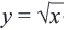похож на ветвь параболы. При 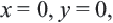т.е. начало координат принадлежит графику. При 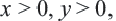т.е. график расположен в I четверти. Большему значению 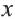соответствует большее значение 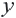. Например, 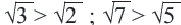и т.д.

Приближенное значение квадратного корня

Практическая работа.

Какова наибольшая длина стороны квадрата, составленного из 14 одинаковых единичных квадратов? Как вы нашли результат? Между какими последовательными натуральными числами, являющимися точными квадратами, расположено число 14?

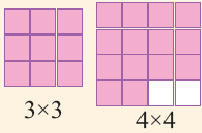
Приближённое значение квадратного корня можно найти при помощи калькулятора, но существуют и другие методы. Вычислить приближённое значение квадратного корня можно при помощи числовой оси и чисел, являющихся точными квадратами. Например, найдём при помощи данного метода,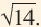

Число 14 расположено между числами 9 и 16. Квадратные корни этих чисел соответственно равны 3 и 4. Целая часть квадратного корня из 14 равна 3. Найдём приближённое значение дробной части: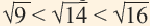

На числовой прямой от 14 до 9-ти 5 единиц, от 9-ти до 16 – 7 единиц.

Дробная часть числа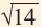

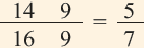
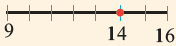
Полученное приближённое значение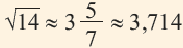

Значение, найденное при помощи калькулятора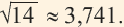

Квадратный корень из произведения и частного

Исследование: Найдите значение выражений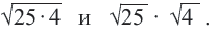

Верно ли равенство?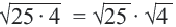

Проверьте, что соответствующее равенство верно для любых двух неотрицательных чисел.

Квадратный корень из произведения и частного

При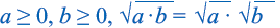

Корень из произведения неотрицательных множителей равен произведению корней из этих же множителей. Это свойство верно и для более двух множителей

Аналогичным образом можно показать, что при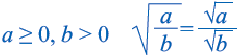

Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.

Пример:

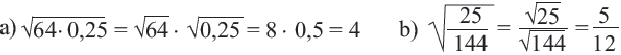
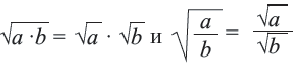при перестановке левой и правой части равенства получим: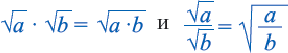

Пример:

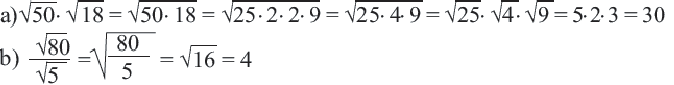
Квадратный корень степени

Из того, что арифметический квадратный корень не может принимать отрицательных значений, следует что равенство 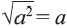не всегда верно. Оно верно только для 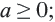при 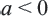верно равенство 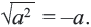Например,

Действительно, при , 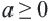по определению арифметического квадратного корня 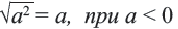имеем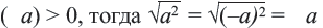

Таким образом,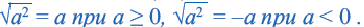

Приняв во внимание, что абсолютное значение числа всегда положительное или равно нулю) и объединив два равенства, приведённых выше получим следующее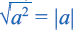

Для извлечения корня чётной степени подкоренное выражение надо записать в виде квадрата идентичного выражения, а затем применить тождество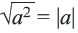

Пример:

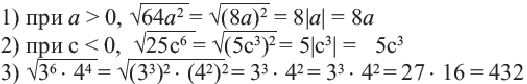
Преобразование выражений, содержащих квадратные корни

Вынесение множителя из-под знака корни

Пример 1. Сравним числа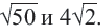

При решении мы заменили 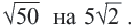Такое преобразование называется вынесением множителя из-под знака корня.

• Заказать решение задач по высшей математике

Пример 2.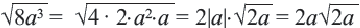

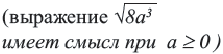
Внесение множителя под знак корня

Пример 3. Сравним числа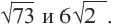

Заменим число 6 на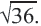

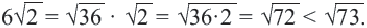Мы заменили 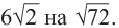Такое преобразование называется внесением множителя под знак корня.

Пример 4.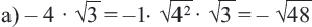

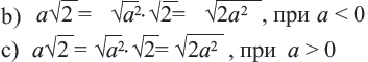
Сложение и вычитание корней, имеющих одинаковое подкоренное выражение вида 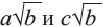выполняется также как сложение и вычитание выражени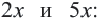й Если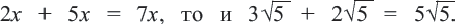

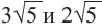называются подобными корнями.

Пример:

Чему равна длина двух досок, если длина одной доски равна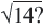

Пример:

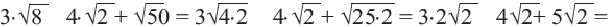
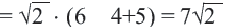
Пример:

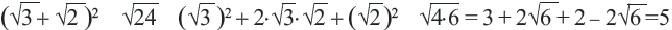
Пример:

Сократите дробь.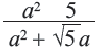

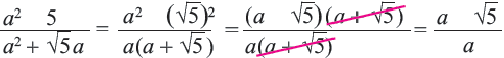
Освобождение знаменателя от иррациональности

Сумма, разность, произведение (кроме умножения на «0» ) и отношение рационального и иррационального чисел является иррациональным числом. А вот сумма, разность, произведение и отношение двух иррациональных чисел может быть рациональным числом.

Пример:

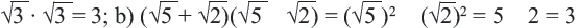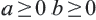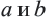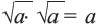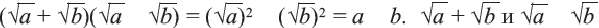а) При При для рациональных выражений верно равенство и называются сопраженными выражениями. Для избавления от иррациональности в знаменателе, надо числитель и знаменатель дроби умножить на выражение, сопраженное знаменателю.

Пример:

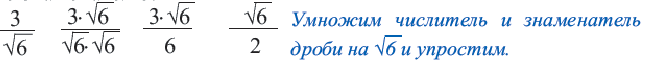
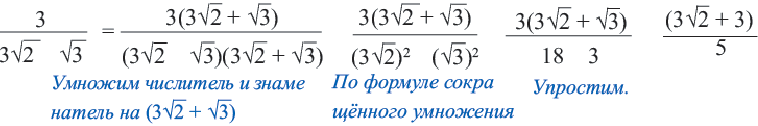
Определение вида треугольника по длинам его сторон

Пусть 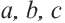стороны треугольника и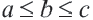

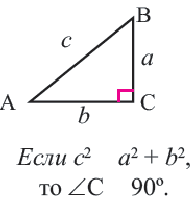
– прямоугольный треугольник.

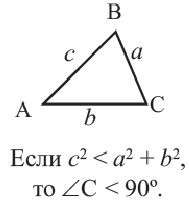
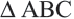– остроугольный треугольник.

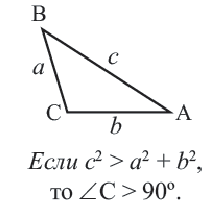
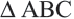– тупоугольный треугольник.

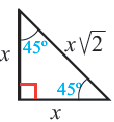
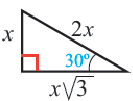
Особые прямоугольные треугольники

Теорема 1. В равнобедренном прямоугольном треугольнике гипотенузы больше любого из катетов в 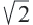раза.

Отношение сторон: 1 : 1 :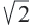

Теорема 2. В прямоугольном треугольнике с острым углом 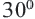гипотенуза в 2 раза больше меньшего катета. Больший катет длиннее меньшего в 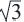раза.

Отношение сторон: 1 : 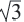: 2