Как найти иррациональное число расположенное между числами – Сайт, где вы сможете решить свои вопросы

Полосатый жираф Алик

Искусственный Интеллект

(310699)

11 лет назад

Ты даже не представляешь, сколько иррациональных чисел находится между 4 и 5!!! Не меньше, чем рациональных, а их (в этом же промежутке) бесконечное количество.

Источник: Математика, однако…

СергеевнаМастер (1112)

11 лет назад

ну какие к примеру?

Владимир БородинМудрец (19215)

11 лет назад

Браво, Алик!

Источник

Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 2. ФУНКЦИЯ у = √x. СВОЙСТВА КВАДРАТНОГО КОРНЯ. § 12. Иррациональные числа. ОТВЕТЫ на упражнения 12.1 — 12.17. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.

§ 12. Иррациональные числа

Задание № 12.1. Является ли данное число иррациональным: a) √9; б) √12; в) √18; г) √25 ?

Смотреть ответы на № 12.1

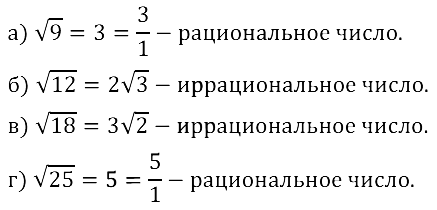
Задание № 12.2. Проверьте справедливость соотношения:
а) 6,1 < √38 < 6,2; б) 10,5 < √111 < 10,6; в) 4,4 < √20 < 4,5; г) 21,5 < √463 < 21,6.

Смотреть ответы на № 12.2

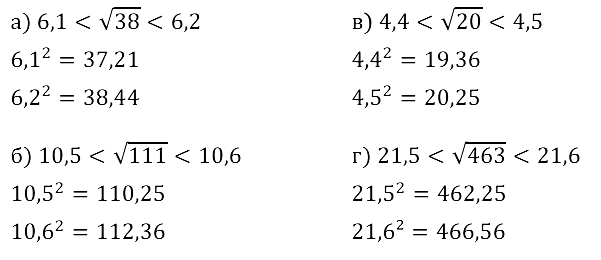
Задание № 12.3. Между какими целыми числами находится число √7 ?

Смотреть ответы на № 12.3

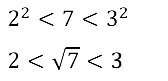
Задание № 12.4. Найдите три иррациональных числа, которые находятся между числами 4 и 5.

Смотреть ответы на № 12.4

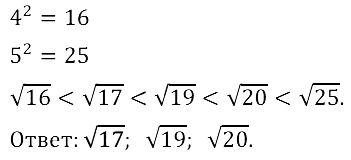
Задание № 12.5. Сравните числа: а) √7 и 3; б) √17,3 и 4; в) √5 и 2; г) √10 и 3,16.

Смотреть ответы на № 12.5

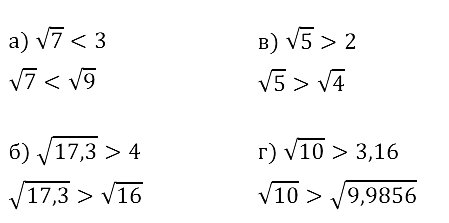
Задание № 12.6. а) –√12 и –4; б) –√25,6 и –5; в) –√l9 и –4,5; г) –√37 и –6,1.

Смотреть ответы на № 12.6

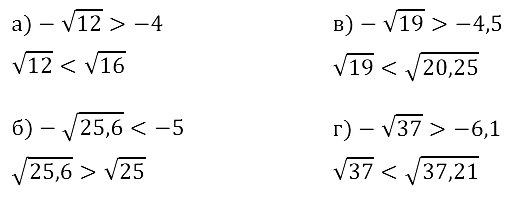
Задание № 12.7. Докажите, что:
а) сумма иррациональных чисел 6 + √2 и 6 – √2 является рациональным числом;
б) произведение иррациональных чисел 2 + √3 и 2 – √3 является рациональным числом;
в) сумма иррациональных чисел 3 + 2√5 и 3 – 2√5 является рациональным числом;
г) произведение иррациональных чисел √7 – √27 и √7 + √27 является рациональным числом.

Смотреть ответы на № 12.7

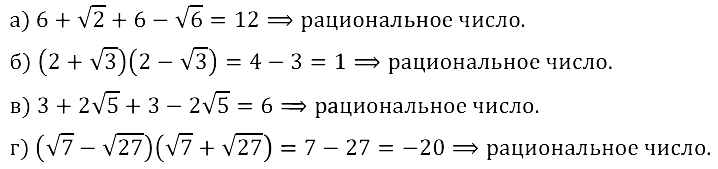
Задание № 12.8. а) Приведите пример двух иррациональных чисел, сумма которых — рациональное число.
б) Приведите пример двух иррациональных чисел, сумма которых — иррациональное число.

Смотреть ответы на № 12.8

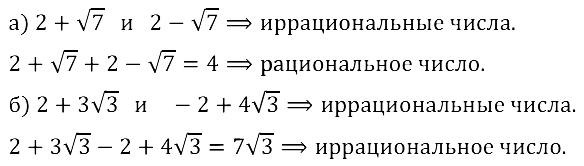
Задание № 12.9. а) Приведите пример двух иррациональных чисел, произведение которых — рациональное число.
б) Приведите пример двух иррациональных чисел, произведение которых — иррациональное число.

Смотреть ответы на № 12.9

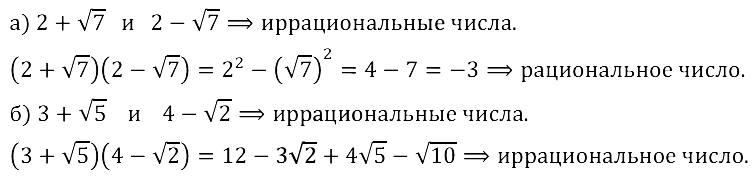
Задание № 12.10.

Смотреть ответы на № 12.10

Задание № 12.11.

Смотреть ответы на № 12.11

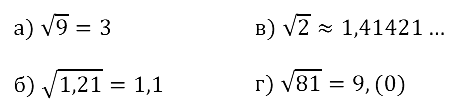
Задание № 12.12.

Смотреть ответы на № 12.12

Задание № 12.13.

Смотреть ответы на № 12.13

Задание № 12.14.

Смотреть ответы на № 12.14

Задание № 12.15.

Смотреть ответы на № 12.15

Задание № 12.16.

Смотреть ответы на № 12.16

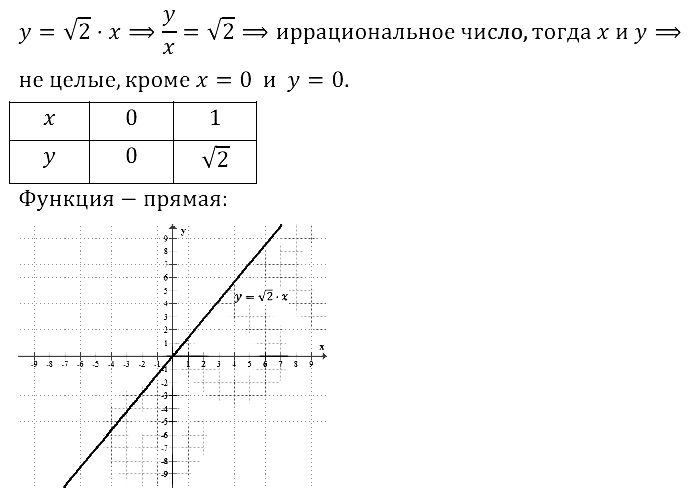
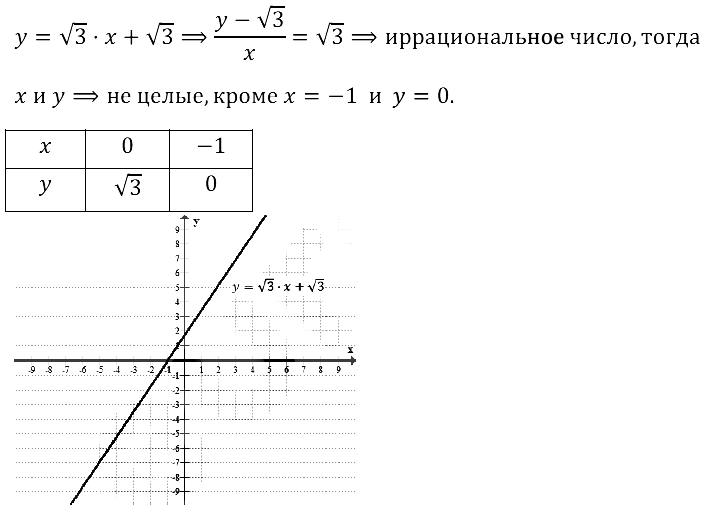
Задание № 12.17.

Смотреть ответы на № 12.17

Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 2. ФУНКЦИЯ у = √x. СВОЙСТВА КВАДРАТНОГО КОРНЯ. § 12. Иррациональные числа. ОТВЕТЫ на упражнения 12.1 — 12.17. Вернуться в ОГЛАВЛЕНИЕ.

Источник

~~gehh~~

Заблокирован

Иррациональное число между двумя рациональными

05.05.2014, 14:37. Показов 9313. Ответов 4

Студворк — интернет-сервис помощи студентам

Даны два рациональных числа A и B.
Требуется доказать, что между ними есть иррациональное число C
Решение:
Пусть
A=a₀,a₁a₂….a_n…
B=b₀,b₁b₂….b_n…
Поскольку первые цифры этих чисел могут совпадать, то
существует такое n, что a_n < b_n
И наше число C приобретет вид:
C=a₀,a₁a₂….a_n…
Иначе говоря C < B
Однако число A может содержать после a_n
лишь конечное число девяток. Значит существует такое
число m, что m > n и a_m < 9.
Теперь наше число C обретет вид:
C=a₀,a₁a₂….a_n9 … 9(a_m+1)…
То есть A < C < B
Остаётся добавить к числу C иррациональный хвост. Имеем:
C=a₀,a₁a₂….a_n9…9(a_m+1)0100100010000 …
Или число C иррациональное, большее A, но меньшее B
Что и требовалось доказать.

Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782	05.05.2014, 14:37
4

3944 / 2858 / 665

Регистрация: 08.06.2007

Сообщений: 9,668

Записей в блоге: 4

05.05.2014, 18:49

Лучший ответ Сообщение было отмечено gehh как решение

Решение

По-моему, можно проще: взять число $https://www.cyberforum.ru/cgi-bin/latex.cgi?A+(sqrt2/2)cdot(B-A)$

~~gehh~~

Заблокирован

05.05.2014, 19:04

[ТС]

Спасибо! Классный ответ!!
Я бы до такого не догадался бы!!
Уверен, что не только я.
Это САМЫЙ ЛУЧШИЙ ОТВЕТ !!
Иного и быть не может!
Ещё раз большое вам Спасибо!

1130 / 789 / 232

Регистрация: 12.04.2010

Сообщений: 2,012

06.05.2014, 00:21

Множество рациональных чисел интервала [a,b] счётно. Имеет меру нуль.

Подробнее. { a_1, a_2, a_3, … a_n, … } множество всех рациональных чисел интервала [a,b].
Выберем к.н. интервалы длины

$https://www.cyberforum.ru/cgi-bin/latex.cgi?frac{varepsilon }{2}, ; frac{varepsilon }{2^2}, ; ... ; frac{varepsilon }{2^n}, ; ...varepsilon leq frac{|a-b|}{2}$

$https://www.cyberforum.ru/cgi-bin/latex.cgi?a_1 in [c_1, d_1], ; a_2 in [c_2, d_2], ; ...$

Сумма длин этих интервалов $https://www.cyberforum.ru/cgi-bin/latex.cgi?leq varepsilon$ . Но это противоречит тому, что они содержат все точки интервала [a,b].