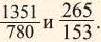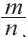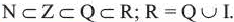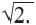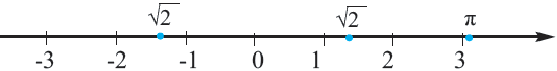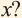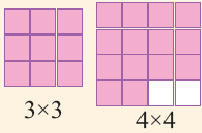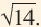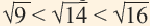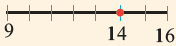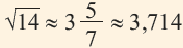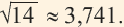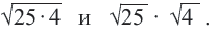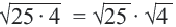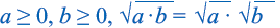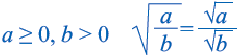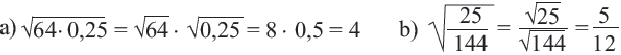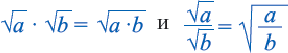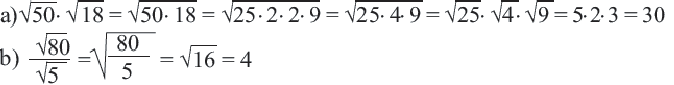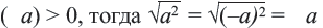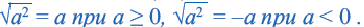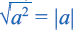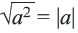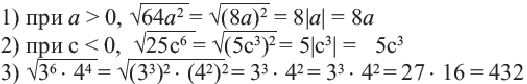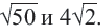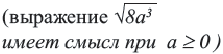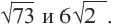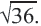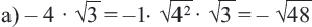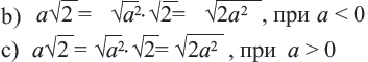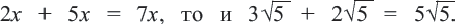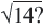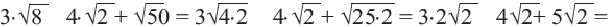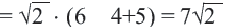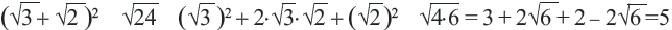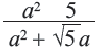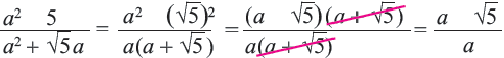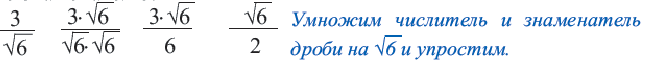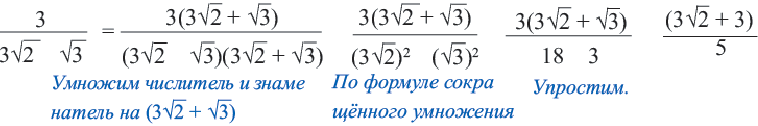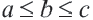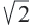Как найти иррациональность числа

Как найти иррациональность числа

Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде обыкновенной дроби {frac {m}{n}}, где m,n — целые числа, nneq 0[1]. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.

Другими словами, множество иррациональных чисел есть разность {displaystyle mathbb {I} =mathbb {R} backslash mathbb {Q} } множеств вещественных и рациональных чисел.

О существовании иррациональных чисел (точнее отрезков, несоизмеримых с отрезком единичной длины), знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа {sqrt {2}}[2].

Иррациональными являются, среди прочих, отношение длины окружности к диаметру круга (число π), основание натурального логарифма e, золотое сечение φ, квадратный корень из двух[3][4][5]. Все квадратные корни натуральных чисел, кроме полных квадратов, иррациональны.

Иррациональные числа также могут рассматриваться через бесконечные непрерывные дроби. Следствием доказательства Кантора является то, что действительные числа не счётны, а рациональные — счётны, отсюда следует, что почти все действительные числа иррациональны[6].

Свойства[править | править код]

  • Сумма двух положительных иррациональных чисел может быть рациональным числом.
  • Иррациональные числа определяют дедекиндовы сечения во множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.
  • Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя различными числами имеется иррациональное число.

Алгебраические и трансцендентные числа[править | править код]

Каждое иррациональное число является либо алгебраическим, либо трансцендентным. Множество алгебраических чисел является счётным множеством. Так как множество вещественных чисел несчётно, то множество иррациональных чисел также несчётно.

Каждое вещественное трансцендентное число является иррациональным; алгебраическое число может быть как рациональным, так и иррациональным..

Множество иррациональных чисел является множеством второй категории[7].

Иррациональные числа и непрерывные дроби[править | править код]

Иррациональное число представляются бесконечной непрерывной дробью. Пример, число e:

{displaystyle e=[2;1,2,1,1,4,1,1,6,1,ldots ,1,2n,1,ldots ].}

Квадратичным иррациональностям соответствуют периодические непрерывные дроби.

{displaystyle phi ={frac {1+{sqrt {5}}}{2}}=[1;1,1,1,1,dots ].}

Примеры[править | править код]

Иррациональными являются:

Примеры доказательства иррациональности[править | править код]

Корень из 2[править | править код]

Допустим противное: {sqrt {2}} рационален, то есть представляется в виде дроби {frac {m}{n}}, где m — целое число, а n — натуральное число.

Возведём предполагаемое равенство в квадрат:

{sqrt {2}}={frac {m}{n}}Rightarrow 2={frac {m^{2}}{n^{2}}}Rightarrow m^{2}=2n^{2}.

В каноническое разложение левой части равенства число 2 входит в чётной степени, а в разложение 2n^{2} — в нечётной. Поэтому равенство {displaystyle m^{2}=2n^{2}} невозможно. Значит, исходное предположение было неверным, и {sqrt {2}} — иррациональное число.

Двоичный логарифм числа 3[править | править код]

Допустим противное: log _{2}3 рационален, то есть представляется в виде дроби {frac {m}{n}}, где m и n — целые числа. Поскольку log _{2}3>0, m и n могут быть выбраны положительными. Тогда

{displaystyle log _{2}3={frac {m}{n}}Rightarrow m=nlog _{2}3Rightarrow 2^{m}=2^{nlog _{2}3}Rightarrow 2^{m}=3^{n}}

Но 2^{m} чётно, а правая часть получившегося равенства нечётна. Получаем противоречие.

e[править | править код]

См. раздел «Доказательство иррациональности» в статье «e».

История[править | править код]

Античность[править | править код]

Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (приблизительно 750—690 года до нашей эры) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены[источник не указан 2764 дня].

Первое доказательство существования иррациональных чисел, а точнее существование несоизмеримых отрезков, обычно приписывается пифагорейцу Гиппасу из Метапонта (приблизительно 470 год до нашей эры)[8]. Нет точных данных о том, иррациональность какого числа была доказана Гиппасом. Согласно легенде он нашёл его, изучая длины сторон пентаграммы[9][10]. Поэтому разумно предположить, что это было золотое сечение, так как это и есть отношение диагонали к стороне в правильном пятиугольнике.

Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения.
Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям».
Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.

Феодор Киренский доказал[11] иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17.
По поводу того, каким могло быть это доказательство, историками математики было высказано несколько различных предположений. Согласно наиболее правдоподобному[12] предположению Жана Итара[fr], оно было основано на теореме о том, что нечётное квадратное число делится на восемь с остатком один[13].

Позже Евдокс Книдский (410 или 408 г. до н. э. — 355 или 347 г. до н. э.) развил теорию пропорций, которая принимала во внимание как рациональные, так и иррациональные отношения. Это послужило основанием для понимания фундаментальной сути иррациональных чисел. Величина стала считаться не числом, но обозначением сущностей, таких как отрезки прямых, углы, площади, объёмы, промежутки времени — сущностей, которые могут меняться непрерывно (в современном понимании этого слова). Величины были противопоставлены числам, которые могут меняться лишь «прыжками» от одного числа к соседнему, например, с 4 на 5[14]. Числа составляются из наименьшей неделимой величины, в то время как величины можно уменьшать бесконечно.

Поскольку никакое количественное значение не сопоставлялось величине, Евдокс смог охватить и соизмеримые, и несоизмеримые величины при определении дроби как отношения двух величин, и пропорции как равенства двух дробей. Убрав из уравнений количественные значения (числа), он избежал ловушки, состоящей в необходимости назвать иррациональную величину числом. Теория Евдокса позволила греческим математикам совершить невероятный прогресс в геометрии, предоставив им необходимое логическое обоснование для работы с несоизмеримыми величинами[15]. Десятая книга «Начал» Евклида посвящена классификации иррациональных величин.

Средние века[править | править код]

Средние века ознаменовались принятием таких понятий как ноль, отрицательные числа, целые и дробные числа, сначала индийскими, затем китайскими математиками. Позже присоединились арабские математики, которые первыми стали считать отрицательные числа алгебраическими объектами (наряду и на равных правах с положительными числами), что позволило развить дисциплину, ныне называемую алгеброй.

Арабские математики соединили древнегреческие понятия «числа» и «величины» в единую, более общую идею вещественных чисел. Они критически относились к представлениям Евклида об отношениях, в противовес ей они развили теорию отношений произвольных величин и расширили понятие числа до отношений непрерывных величин. В своих комментариях на Книгу 10 «Начал» Евклида, персидский математик аль-Махани (ок. 800 года н. э.) исследовал и классифицировал квадратичные иррациональные числа и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами. Он легко оперировал этими объектами, но рассуждал как об обособленных объектах, например[16]:

Рациональной [величиной] является, например, 10, 12, 3%, 6% и так далее, поскольку эти величины произнесены и выражены количественно. Что не рационально, то иррационально, и невозможно произнести или представить соответствующую величину количественно. Например, квадратные корни чисел таких, как 10, 15, 20 — не являющихся квадратами.

В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни — иррациональными. Он также ввёл арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин[16]:

результат сложения иррациональной величины и рациональной, результат вычитания рациональной величины из иррациональной, результат вычитания иррациональной величины из рациональной.

Египетский математик Абу Камил (ок. 850 г. н. э. — ок. 930 г. н. э.) был первым, кто счёл приемлемым признать иррациональные числа решением квадратных уравнений или коэффициентами в уравнениях — в основном, в виде квадратных или кубических корней, а также корней четвёртой степени[17]. В X веке иракский математик Аль-Хашими вывел общие доказательства (а не наглядные геометрические демонстрации) иррациональности произведения, частного и результатов иных математических преобразований над иррациональными и рациональными числами[18]. Аль-Хазин (900 г. н. э. — 971 г. н. э.) приводит следующее определение рациональной и иррациональной величины[19]:

Пусть единична величина содержится в данной величине один или несколько раз, тогда эта [данная] величина соответствует целому числу… Каждая величина, которая составляет половину, или треть, или четверть единичной величины, или, сравнённая с единичной величиной составляет три пятых от неё, это рациональная величина. И в целом, всякая величина, которая относится к единичной как одно число к другому, является рациональной. Если же величина не может быть представлена как несколько или часть (l/n), или несколько частей (m/n) единичной длины, она иррациональная, то есть невыразимая иначе как с помощью корней.

Многие из этих идей были позже переняты европейскими математиками после перевода на латынь арабских текстов в XII веке. Аль Хассар, арабский математик из Магриба, специализировавшийся на исламских законах о наследстве, в XII веке ввёл современную символьную математическую нотацию для дробей, разделив числитель и знаменатель горизонтальной чертой[20]. Та же нотация появилась затем в работах Фибоначчи в XIII веке[21]. В течение XIV—XVI вв. Мадхава из Сангамаграмы и представители Керальской школы астрономии и математики исследовали бесконечные ряды, сходящиеся к некоторым иррациональным числам, например, к pi , а также показали иррациональность некоторых значений тригонометрических функций. Джестадева привёл эти результаты в книге «Йуктибхаза».

Новое время[править | править код]

В XVII—XVIII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667—1754) и Леонард Эйлер (1707—1783). Когда теория комплексных чисел в XIX веке стала замкнутой и чёткой, стало возможным классифицировать иррациональные числа на алгебраические нерациональные и трансцендентные (доказав при этом существование трансцендентных чисел), тем самым переосмыслив работы Евклида по классификации иррациональных чисел. По этой теме в 1872 году были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ начал рассмотрения, схожие с работами Гейне, именно 1872 год принято считать годом рождения теории. Метод Вейерштрасса был полностью изложен Сальваторе Пинкерле в 1880 году[22], а Дедекинд получил дополнительную известность благодаря более поздней работе автора (1888) и одобрению Поля Таннери (1894). Вейерштрасс, Кантор и Гейне обосновывали свои теории при помощи бесконечных рядов, в то время как Дедекинд работал с (ныне так называемыми) дедекиндовыми сечениями множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.

Цепные дроби, тесно связанные с иррациональными числами (цепная дробь, представляющая данное число, бесконечна тогда и только тогда, когда число является иррациональным), были впервые исследованы Катальди в 1613 году, затем снова привлекли к себе внимание в работах Эйлера, а в начале XIX века — в работах Лагранжа. Дирихле также внёс значительный вклад в развитие теории цепных дробей. В 1761 году Ламберт с помощью цепных дробей показал, что pi не является рациональным числом, а также что e^{x} и operatorname {tg}x иррациональны при любом ненулевом рациональном x[23]. Хотя доказательство Ламберта можно назвать незавершённым, принято считать его достаточно строгим, особенно учитывая время его написания. Лежандр в 1794 году, после введения функции Бесселя — Клиффорда, показал, что pi ^{2} иррационально, откуда иррациональность pi следует тривиально (рациональное число в квадрате дало бы рациональное).

Существование трансцендентных чисел было доказано Лиувиллем в 1844—1851 годах. Позже Георг Кантор (1873) показал их существование, используя другой метод, и обосновал, что любой интервал вещественного ряда содержит бесконечно много трансцендентных чисел. Шарль Эрмит доказал в 1873 году, что e трансцендентно, а Фердинанд Линдеман в 1882 году, основываясь на этом результате, показал трансцендентность pi . Доказательство Линдеманна было затем упрощено Вейерштрассом в 1885 году, ещё более упрощено Давидом Гильбертом в 1893 году и, наконец, доведено до почти элементарного Адольфом Гурвицем и Паулем Горданом[24].

См. также[править | править код]

  • Дедекиндово сечение
  • Диофантовы и лиувиллевы числа
  • Конструктивные способы определения вещественного числа
  • Мера иррациональности

Примечания[править | править код]

  1. ↑ Рациональное число // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
  2. ↑ История, 1970, Том 1, с. 73.
  3. ↑ The 15 Most Famous Transcendental Numbers Архивная копия от 24 октября 2007 на Wayback Machine. by Clifford A. Pickover. URL retrieved 24 October 2007.
  4. ↑ Irrational Numbers Архивная копия от 29 августа 2010 на Wayback Machine // mathsisfun.com; URL retrieved 24 October 2007.
  5. ↑ Weisstein, Eric W. Irrational Number (англ.) на сайте Wolfram MathWorld. URL retrieved 26 October 2007.
  6. ↑ Cantor, Georg. Contributions to the Founding of the Theory of Transfinite Numbers (англ.) / Philip Jourdain  (англ.) (рус.. — New York: Dover, 1955. — ISBN 978-0-486-60045-1.
  7. ↑ Ильин, Садовничий, Сендов, 2006, с. 64.
  8. ↑ Kurt Von Fritz, 1945.
  9. ↑ James R. Choike. The Pentagram and the Discovery of an Irrational Number (англ.) // The Two-Year College Mathematics Journal  (англ.) (рус. : magazine. — 1980.
  10. ↑ Kurt Von Fritz, 1945, p. 242—264.
  11. ↑ История, 1970, Т 1. С древнейших времён до начала Нового времени, с. 74.
  12. ↑ А. И. Щетников. Как древнегреческие математики доказывали иррациональность. Архивная копия от 4 марта 2016 на Wayback Machine
  13. ↑ Jean Itard. Les livres arithmétiques d’Euclide. — Paris: Hermann, 1961. Архивировано 22 ноября 2015 года.
  14. ↑ Kline 1990, p.48.
  15. ↑ Kline 1990, p.49.
  16. ↑ 1 2 Matvievskaya, 1987, p. 253–277 [259].
  17. ↑ Jacques Sesiano, «Islamic mathematics», p. 148, in Selin, Helaine; D’Ambrosio, Ubiratan. Mathematics Across Cultures: The History of Non-western Mathematics (англ.). — Springer, 2000. — ISBN 1-4020-0260-2..
  18. ↑ Matvievskaya, 1987, p. 253–277 [260].
  19. ↑ Matvievskaya, 1987, p. 253–277 [261].
  20. ↑ Cajori, Florian (1928), A History of Mathematical Notations (Vol.1), La Salle, Illinois: The Open Court Publishing Company pg. 269.
  21. ↑ (Cajori 1928, pg.89)
  22. ↑ Salvatore Pincherle. Saggio di una introduzione alla teoria delle funzioni analitiche secondo i principii del prof. C. Weierstrass (итал.) // Giornale di Matematiche : diario. — 1880. — P. 178—254,317—320.
  23. ↑ J. H. Lambert. Mémoire sur quelques propriétés remarquables des quantités transcendentes, circulaires et logarithmiques (фр.) // Mémoires de l’Académie royale des sciences de Berlin : magazine. — 1761. — P. 265—322. Архивировано 28 апреля 2016 года.
  24. ↑ Gordan, Paul. Transcendenz von e und π // Mathematische Annalen. — Teubner, 1893. — Т. 43. — С. 222—224. — doi:10.1007/bf01443647.

Литература[править | править код]

  • В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — 672 с. — ISBN 5-482-00445-7.
  • История математики с древнейших времён до начала XIX столетия. В трёх томах / под ред. Юшкевича. — М.: Наука, 1970.
  • Kline, M. (1990). Mathematical Thought from Ancient to Modern Times, Vol. 1. New York: Oxford University Press. (Original work published 1972).
  • Matvievskaya, Galina. The Theory of Quadratic Irrationals in Medieval Oriental Mathematics (англ.) // Annals of the New York Academy of Sciences  (англ.) (рус. : journal. — 1987. — Vol. 500. — doi:10.1111/j.1749-6632.1987.tb37206.x.
  • Kurt Von Fritz. The Discovery of Incommensurability by Hippasus of Metapontum (англ.) // The Annals of Mathematics : journal. — 1945.
Источник

Иррациональные числа: определение, примеры

Иррациональные числа известны людям с глубокой древности. Еще за несколько веков до нашей эры индийский математик Манава выяснил, что квадратные корни некоторых чисел (например, 2) невозможно выразить явно.

Данная статья является своего рода вводным уроком в тему “Иррациональные числа”. Приведем определение и примеры иррациональных чисел с пояснением, а также выясним, как определить, является ли данное число иррациональным.

Иррациональные числа. Определение

Само название “иррациональные числа” как бы подсказывает нам определение. Иррациональное число – это действительное число, которое не является рациональным. Другими словами, такое число нельзя представить в виде дроби mn, где m – целое, а n – натуральное число.

Определение. Иррациональные числа

Иррациональные числа – это такие числа, которые в десятичной форме записи представляют собой бесконечные непериодические десятичные дроби.

Для обозначения множества иррациональных чисел используется символ 

Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Содержание:

Иррациональные числа

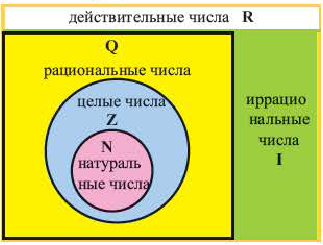
Практическая работа 1. Великий греческий математик, физик, астроном и изобретатель Архимед хотел найти рациональное число, квадрат которого равен 3. С этой целью он выбрал числа Иррациональные числа - определение и вычисление с примерами решения

Классификация чисел

Любое рациональное число можно записать в виде дроби Иррациональные числа - определение и вычисление с примерами решения

Каждую конечную десятичную дробь можно записать в виде бесконечной десятичной периодической дроби с цифрой 0 в периоде. Но есть такие числа, которые невозможно представить в виде десятичной периодической дроби. Бесконечная десятичная непериодическая дробь выражает число, которое не является рациональным. Такие числа называются иррациональными числами. Иррациональное число невозможно представить в виде 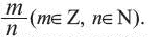Иррациональные числа - определение и вычисление с примерами решения Приведём примеры иррациональных чисел:

a) 0,1010010001… (количество нулей после каждой единицы увеличивается на один);

b) 0,123456789101112… (в дробной части записана последовательность натуральных чисел);

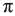
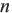
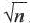
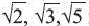
c) Иррациональные числа - определение и вычисление с примерами решения = 3,14159265… (выражает отношение длины окружности к диаметру).

Если Иррациональные числа - определение и вычисление с примерами решения не является точным квадратом какого-либо натурального числа, то Иррациональные числа - определение и вычисление с примерами решения является иррациональным числом. Например, Иррациональные числа - определение и вычисление с примерами решения иррациональные числа. Множество иррациональных чисел обозначается буквой I. Арифметические действия над иррациональными числами и их свойства аналогичны рациональным числам. Множество, состоящее из рациональных и иррациональных чисел, называется множеством действительных чисел, которое обозначается буквой R.

Иррациональные числа - определение и вычисление с примерами решения

Иррациональные числа - определение и вычисление с примерами решения

Практическая работа.

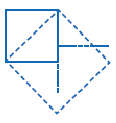
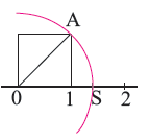
1) Начертите квадрат со стороной равной единичному отрезку и проведите диагональ данного квадрата. На диагонали квадрата постройте новый квадрат. Убедитесь, что площадь полученного квадрата в два раза больше площади единичного квадрата. Покажите, что сторона полученного квадрата равна соответственно Иррациональные числа - определение и вычисление с примерами решения

Иррациональные числа - определение и вычисление с примерами решения

2) Повторите работу по алгоритму, представленному ниже. На координатной оси постройте квадрат, сторона которого равна единичному отрезку. Начертите окружность с центром в точке нуль, радиусом равным диагонали квадрата и отметьте точку пересечения с числовой осью. Объясните связь между соответствующим данной точке числом и длиной диагонали квадрата.

Иррациональные числа - определение и вычисление с примерами решения

Числовая ось, рациональные, иррациональные числа

Каждой точке на числовой оси соответствует единственное число (рациональное или иррациональное) и каждому числу, на числовой оси соответствует единственная точка. Опираясь на это числа можно сравнивать. Число, соответствующее точке, которая расположена правее, больше числа, соответствующему точке, расположенной левее.

Иррациональные числа - определение и вычисление с примерами решения

Практическая работа.

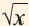
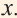
1) При помощи калькулятора вычислите значения Иррациональные числа - определение и вычисление с примерами решения при заданных значениях Иррациональные числа - определение и вычисление с примерами решения Округлите их до десятых и заполните таблицу.

Иррациональные числа - определение и вычисление с примерами решения

2) На координатной плоскости отметьте точки из таблицы, с соответствующими координатами, и соедините их плавной линией.

3) Может ли 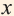Иррациональные числа - определение и вычисление с примерами решения принимать отрицательные значения?

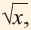
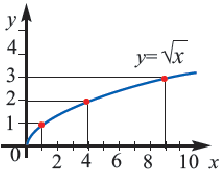
4) Как изменяются соответствующие значения Иррациональные числа - определение и вычисление с примерами решения при увеличении значений Иррациональные числа - определение и вычисление с примерами решения

Функция y=√x и её график

Функция 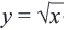Иррациональные числа - определение и вычисление с примерами решения и её график

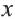
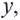
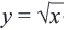
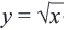
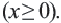
В таблице, которую вы заполнили, показаны некоторые значения аргументов Иррациональные числа - определение и вычисление с примерами решения в 1-ой строке, соответствующие значению функции Иррациональные числа - определение и вычисление с примерами решения заданной формулой, Иррациональные числа - определение и вычисление с примерами решения во 2-ой строке. Аргумент функции Иррациональные числа - определение и вычисление с примерами решения определен при всех неотрицательных значениях Иррациональные числа - определение и вычисление с примерами решения Функция также припишет только положительные значения (т.к. не существует квадратного корня из отрицательного числа и арифметический корень припишет только положительные значения).

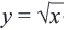
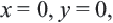
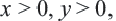
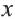
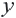
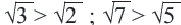
График функции Иррациональные числа - определение и вычисление с примерами решения похож на ветвь параболы. При Иррациональные числа - определение и вычисление с примерами решения т.е. начало координат принадлежит графику. При Иррациональные числа - определение и вычисление с примерами решения т.е. график расположен в I четверти. Большему значению Иррациональные числа - определение и вычисление с примерами решения соответствует большее значение Иррациональные числа - определение и вычисление с примерами решения. Например, Иррациональные числа - определение и вычисление с примерами решения и т.д.

Иррациональные числа - определение и вычисление с примерами решения

Приближенное значение квадратного корня

Практическая работа.

Какова наибольшая длина стороны квадрата, составленного из 14 одинаковых единичных квадратов? Как вы нашли результат? Между какими последовательными натуральными числами, являющимися точными квадратами, расположено число 14?

Иррациональные числа - определение и вычисление с примерами решения

Приближённое значение квадратного корня можно найти при помощи калькулятора, но существуют и другие методы. Вычислить приближённое значение квадратного корня можно при помощи числовой оси и чисел, являющихся точными квадратами. Например, найдём при помощи данного метода, Иррациональные числа - определение и вычисление с примерами решения

Число 14 расположено между числами 9 и 16. Квадратные корни этих чисел соответственно равны 3 и 4. Целая часть квадратного корня из 14 равна 3. Найдём приближённое значение дробной части: Иррациональные числа - определение и вычисление с примерами решения

Иррациональные числа - определение и вычисление с примерами решения

На числовой прямой от 14 до 9-ти 5 единиц, от 9-ти до 16 – 7 единиц.

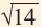
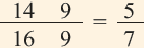
Дробная часть числа Иррациональные числа - определение и вычисление с примерами решения Иррациональные числа - определение и вычисление с примерами решения Иррациональные числа - определение и вычисление с примерами решения

Полученное приближённое значение Иррациональные числа - определение и вычисление с примерами решения

Значение, найденное при помощи калькулятора Иррациональные числа - определение и вычисление с примерами решения

Квадратный корень из произведения и частного

Исследование: Найдите значение выражений Иррациональные числа - определение и вычисление с примерами решения

Верно ли равенство? Иррациональные числа - определение и вычисление с примерами решения

Проверьте, что соответствующее равенство верно для любых двух неотрицательных чисел.

Квадратный корень из произведения и частного

При Иррациональные числа - определение и вычисление с примерами решения

Корень из произведения неотрицательных множителей равен произведению корней из этих же множителей. Это свойство верно и для более двух множителей

Аналогичным образом можно показать, что при Иррациональные числа - определение и вычисление с примерами решения

Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.

Пример:

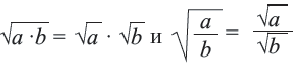
Иррациональные числа - определение и вычисление с примерами решения

Иррациональные числа - определение и вычисление с примерами решения при перестановке левой и правой части равенства получим: Иррациональные числа - определение и вычисление с примерами решения

Пример:

Иррациональные числа - определение и вычисление с примерами решения

Квадратный корень степени

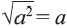
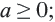
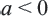
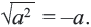
Из того, что арифметический квадратный корень не может принимать отрицательных значений, следует что равенство Иррациональные числа - определение и вычисление с примерами решения не всегда верно. Оно верно только для Иррациональные числа - определение и вычисление с примерами решения при Иррациональные числа - определение и вычисление с примерами решения верно равенство Иррациональные числа - определение и вычисление с примерами решения Например, Иррациональные числа - определение и вычисление с примерами решения

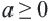
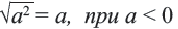
Действительно, при , Иррациональные числа - определение и вычисление с примерами решения по определению арифметического квадратного корня Иррациональные числа - определение и вычисление с примерами решения имеем Иррациональные числа - определение и вычисление с примерами решения

Таким образом, Иррациональные числа - определение и вычисление с примерами решения

Приняв во внимание, что абсолютное значение числа всегда положительное или равно нулю) и объединив два равенства, приведённых выше получим следующее Иррациональные числа - определение и вычисление с примерами решения

Для извлечения корня чётной степени подкоренное выражение надо записать в виде квадрата идентичного выражения, а затем применить тождество Иррациональные числа - определение и вычисление с примерами решения

Пример:

Иррациональные числа - определение и вычисление с примерами решения

Преобразование выражений, содержащих квадратные корни

Вынесение множителя из-под знака корни

Пример 1. Сравним числа Иррациональные числа - определение и вычисление с примерами решения

При решении мы заменили 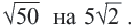Иррациональные числа - определение и вычисление с примерами решения Такое преобразование называется вынесением множителя из-под знака корня.

  • Заказать решение задач по высшей математике

Пример 2. 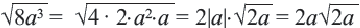Иррациональные числа - определение и вычисление с примерами решения Иррациональные числа - определение и вычисление с примерами решения

Внесение множителя под знак корня

Пример 3. Сравним числа Иррациональные числа - определение и вычисление с примерами решения

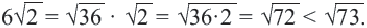
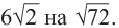
Заменим число 6 на Иррациональные числа - определение и вычисление с примерами решения

Иррациональные числа - определение и вычисление с примерами решения Мы заменили Иррациональные числа - определение и вычисление с примерами решения Такое преобразование называется внесением множителя под знак корня.

Иррациональные числа - определение и вычисление с примерами решения

Пример 4. Иррациональные числа - определение и вычисление с примерами решения

Иррациональные числа - определение и вычисление с примерами решения

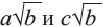
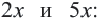
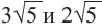
Сложение и вычитание корней, имеющих одинаковое подкоренное выражение вида Иррациональные числа - определение и вычисление с примерами решения выполняется также как сложение и вычитание выражений Иррациональные числа - определение и вычисление с примерами решения Если Иррациональные числа - определение и вычисление с примерами решения

Иррациональные числа - определение и вычисление с примерами решения называются подобными корнями.

Пример:

Чему равна длина двух досок, если длина одной доски равна Иррациональные числа - определение и вычисление с примерами решения

Иррациональные числа - определение и вычисление с примерами решения

Пример:

Иррациональные числа - определение и вычисление с примерами решенияИррациональные числа - определение и вычисление с примерами решения

Пример:

Иррациональные числа - определение и вычисление с примерами решения

Пример:

Сократите дробь. Иррациональные числа - определение и вычисление с примерами решения

Иррациональные числа - определение и вычисление с примерами решения

Освобождение знаменателя от иррациональности

Сумма, разность, произведение (кроме умножения на «0» ) и отношение рационального и иррационального чисел является иррациональным числом. А вот сумма, разность, произведение и отношение двух иррациональных чисел может быть рациональным числом.

Пример:

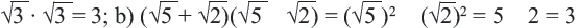
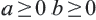
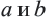
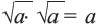
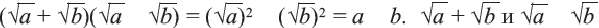
а) При Иррациональные числа - определение и вычисление с примерами решения При Иррациональные числа - определение и вычисление с примерами решения для рациональных выражений Иррациональные числа - определение и вычисление с примерами решения верно равенство Иррациональные числа - определение и вычисление с примерами решенияи Иррациональные числа - определение и вычисление с примерами решения называются сопраженными выражениями. Для избавления от иррациональности в знаменателе, надо числитель и знаменатель дроби умножить на выражение, сопраженное знаменателю.

Пример:

Иррациональные числа - определение и вычисление с примерами решения

Иррациональные числа - определение и вычисление с примерами решения

Определение вида треугольника по длинам его сторон

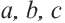
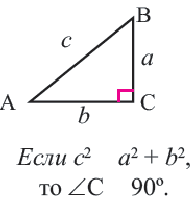
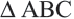
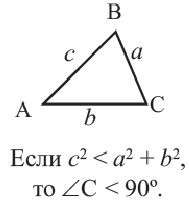
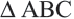
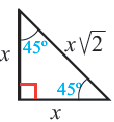
Пусть Иррациональные числа - определение и вычисление с примерами решения стороны треугольника и Иррациональные числа - определение и вычисление с примерами решения

Иррациональные числа - определение и вычисление с примерами решения Иррациональные числа - определение и вычисление с примерами решения – прямоугольный треугольник.

Иррациональные числа - определение и вычисление с примерами решения Иррациональные числа - определение и вычисление с примерами решения – остроугольный треугольник.

Иррациональные числа - определение и вычисление с примерами решения Иррациональные числа - определение и вычисление с примерами решения – тупоугольный треугольник.

Особые прямоугольные треугольники

Теорема 1. В равнобедренном прямоугольном треугольнике гипотенузы больше любого из катетов в 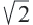Иррациональные числа - определение и вычисление с примерами решения раза.

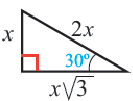
Отношение сторон: 1 : 1 : Иррациональные числа - определение и вычисление с примерами решения

Иррациональные числа - определение и вычисление с примерами решения

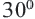
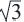
Теорема 2. В прямоугольном треугольнике с острым углом Иррациональные числа - определение и вычисление с примерами решения гипотенуза в 2 раза больше меньшего катета. Больший катет длиннее меньшего в Иррациональные числа - определение и вычисление с примерами решения раза.

Отношение сторон: 1 : 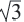Иррациональные числа - определение и вычисление с примерами решения : 2

Иррациональные числа - определение и вычисление с примерами решения

  • Действительные числа
  • Решение уравнений высших степеней
  • Системы неравенств
  • Квадратные неравенства
  • Уравнения и неравенства содержащие знак модуля
  • Уравнение
  • Метод математической индукции
  • Система координат в пространстве
Источник

Иррациональные числа

Содержание:

  • Что такое иррациональные числа
  • Виды, место в общей классификации, как обозначаются

    • Алгебраические и трансцендентные
  • Для чего они используются
  • Как вычислить иррациональное число, действия

Что такое иррациональные числа

Если в ходе решения математической задачи получилась дробь, в которой нельзя полностью разделить числитель на знаменатель, то это иррациональное число.

Существует еще одно условие принадлежности такой дроби к иррациональным величинам. Это отсутствие периодов в наборе цифр после запятой, т.е. нет периодически повторяемой цифровой последовательности.

Иррациональным называется число, которое нельзя представить в виде законченного частного от деления двух целых величин.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

С таким множеством сталкивались еще математики древних веков. Для них, например, было понятно, что диагональ квадрата нельзя разделить на длину его стороны и получить при этом не бесконечную дробь. Аналогичным образом характеризуется соотношение постоянной π выбранной окружности к диаметру.

Говоря простыми словами, если в обычной десятичной дроби после запятой обнаруживается бесконечное количество цифр и в них отсутствует повторяемость периодов, то это представитель иррационального множества.

Пример

Для наглядности можно рассмотреть примеры: √2 = 1,41421356…;  -√11= -3.31662…; π = 3,1415926…

Термин, обозначающий данную категорию цифр, произошел в результате сложение двух частей: ratio, что означает «соотношение» и ir, что означает отрицание. В итоге слово «иррациональный» закрепилось за дробями, не способными дать четкое соотношение.

Например, диагональ квадрата, сторона которого равна 1, не может быть представлена рациональным числом, но она имеет определенное числовое выражение. К таким же случаям можно отнести √5, √7, √10. Именно для выражения таких значений введено множество иррациональных чисел, каждое из которых может быть представлено бесконечной непериодической дробью (в отличие от рационального, которое можно представить периодической десятичной дробью).

Виды, место в общей классификации, как обозначаются

В арифметической классификации иррациональным числам выделено четкое место, наравне с рациональными, которые делятся на целые и дробные.

Действительные числа

Для обозначения множества используют букву I. Его математическое выражение выглядит так: I=R-Q.

Алгебраические и трансцендентные

В алгебре те величины, которые могут являться квадратными корнями с целыми коэффициентами из многочленов, относятся ко множеству алгебраических. Те же, которые не могут выступать в этой роли, образуют другое множество — трансцендентных.

Происхождение термина «трансцендентный» объясняется его переводом с латыни: transcendentis — выходящий за границы. Таким образом, это величины, которые находятся за пределами множества чисел, которые могут стать квадратным корнем с целым коэффициентом из различных многочленов.

О необходимости введения такого множества впервые заговорил в 1775 году Леонард Эйлер. Стоит отметить, что во время его деятельности еще не было известно никаких трансцендентных значений.

Вычислить их пример не удавалось математикам и в последующие много лет. Лишь в 1844 году Ж.Луивилль привел всем их пример. Его теореме досталось лидирующее место в теории диофантовых приближений.

Теорема

Алгебраические числа плохо приближаются рациональными, в частности, если алгебраическое число αn (n — наименьшая степень многочлена P(x) с целыми коэффициентами такого, что P(α)=0), то для любой дроби p/q справедливо выражение: 

Где С — константа, зависящая от α.

Все числа типа m/n, где n отлично от нуля, а m и n представлены целыми значениями, являются алгебраическими. Для них справедливо равенство: nx-m=0.

К понятию «алгебраические», кроме рациональных, отнесены иррациональные, для которых характерна формула n√m. При этом m и n представлены целыми числами, а n больше либо равно 2.

При любых действиях с алгебраическими числами (сложение, вычитание, деление либо умножение) результат решения будет алгебраической величиной. Кроме этого, алгебраическими будут корни многочленов, коэффициенты которых также отнесены к этому множеству.

Для чего они используются

В математике использование иррациональных чисел объясняется списком их свойств. Например, возможность точного определения величины, полученной в результате извлечения квадратного корня из 2-х, не всегда нужна. Так, в геометрии измерения длины гипотенузы часто производят приблизительно (1,4, 1,41 и т.д.). Извлечение точного квадратного корня из 2-х понадобится только при работе с абстрактной математической моделью.

Однако такие ситуации в науке существуют. Поэтому существование множества иррациональных чисел оправданно. С помощью них можно высчитать дедекиндово сечение в рациональных числах, у которых отсутствует самое большое в нижнем сегменте и самое малое — в верхнем.

Представители иррациональных значений позволяют уплотнить числовую прямую с нанесенными рациональными значениями, таким образом, что между каждой такой парой можно записать иррациональное.

Примечание

Бывают случаи, что, складывая два иррациональных значения, получают рациональное.

Например, в результате сложения корня из семи (любой степени) и такого корня из семи, только со знаком минус, получается рациональное число — 0.

Сумма двух положительных иррациональных чисел также может быть рациональным значением. Однако при сложении рационального и иррационального в итоге всегда получается представитель иррациональных. Такое свойство называется отсутствием у множества замкнутости.

Исходя из сказанного, следует сделать вывод, что введение множества иррациональных чисел необходимо для увеличения точности. Например, когда между натуральными числами единицей и двойкой не было промежуточных величин, нужно было ее ввести для расширения диапазона точности.

Иррациональные числа

Как вычислить иррациональное число, действия

Чтобы вычислить иррациональное число проще всего предположить, что оно рациональное и его реально представить в виде дроби p/q, не поддающейся сокращению. В результате преобразующих действий доказывается, что натуральные p и q не являются взаимно простыми. Тогда понятно, что это именно иррациональное значение, а предположение о рациональности взятой дроби ошибочно.

В целом же под понятием «иррациональное» понимается число, записать которое в виде десятичной дроби невозможно. Часть после запятой будет бесконечной:

π =3,14159…;

e =2,7182…;

«золотого сечения» 1,61803398…

При этом степень точности результата зависит от количества знаков, взятых после запятой.

Правда, при описании таких величин чаще используют логарифмы, корни, степени и т.п.

Чтобы в текущий момент определить принадлежность данного числа к категории иррациональных, можно воспользоваться онлайн калькулятором, в котором можно произвести вычисления до оговоренной точности. 

Пример

Задание: рассчитать рациональность заданных значений.

На калькуляторе нужно задать число в виде правильной дроби (по определению, оно рациональное). Исходя из этого, результативным будет определение иррационального компонента для выражений в виде корней (со степенью n).

Получаем:

  •  2√2 = 1,414 (иррациональное);
  •  3√27 = 3 (рациональное);
  •  5√147 = 2,713 (иррациональное).

Видим, что, имея дело с квадратными и кубическими корнями, извлекаемая величина может быть рациональной.

Источник

Слово «рациональный» (по-латински ratio — разум ) переводится как «разумный». Соответственно, слово  «иррациональный» означает «неразумный».

Иррациональным числом называют действительное число, которое не является рациональным (его нельзя записать обыкновенной дробью). Иррациональное число — только бесконечная непериодическая дробь.

Если натуральное число (n) не является точным квадратом, т. е. n≠k2, где k∈ℚ, то  n является иррациональным числом.

Пример:

5=2,23606798…11=3,31662479…

Число π≈ (3,141592…) также является иррациональным. Это доказал в  (1766) году немецкий математик И. Ламберт. Интересно, что для этого числа была взята буква греческого алфавита «пи», так как с этой буквы начинается греческое слово периферия — окружность.

Итак,

1. в результате всякого арифметического действия над рациональными числами (помимо деления на (0)) получаем рациональное число.

2. Любое арифметическое действие над иррациональными числами может привести в итоге к рациональному или к иррациональному числу.

3. Если в арифметическом действии принимают участие рациональное и иррациональное числа, то в итоге будет иррациональное число (исключение — умножение и деление на (0)).

4. Т. к. в результате действий по извлечению корней (квадратного и кубического) из неотрицательного числа получается иррациональное число, определились, что иррациональным выражением считают любое алгебраическое выражение,  где есть действие по извлечению квадратного и кубического корня из переменной.

Источник

Добавить комментарий