Опорные решения системы линейных уравнений.
Рассмотрим систему
из m линейных уравнений с n
неизвестными, причем m<n:
 (2.8)
(2.8)
Базисом системы
линейных уравнений называется максимальное
количество линейно независимых векторов
системы. Для данной системы это количество
равно m . Воспользуемся методом
последовательных исключений неизвестных
и выделим в системе некий исходный
единичный базис:
 (2.9)
(2.9)
В полученной
системе единичные вектора
![]()
называются базисными, а вектора
![]()
— свободными.
О п р е д е л е н и е 5. Базисными
решениями называются решения системы,
получаемые при приравнивании свободных
неизвестных нулю.
О п р е д е л е н и е 6. Базисное
решение называется невырожденным,
если все базисные переменные полученного
решения ненулевые, в противном случае
базисное решение называется вырожденным.
Очевидно, что
базисные решения проще находить, если
система приведена к единичному базису,
поэтому отыскание всех базисных решений
сводится к последовательному преобразованию
системы к всевозможным единичным
базисам. Этого можно достигнуть путем
последовательных преобразований
однократного замещения.
Для выполнения
одного преобразования однократного
замещения нужно выбрать среди не
единичных столбцов коэффициентов
отличный от нуля разрешающий элемент
Aqp и провести одно
преобразование схемы последовательных
исключений. Тогда разрешающий ( p-й )
столбец коэффициентов превратится в
единичный, а, наоборот, единичный столбец,
имеющий координату 1 в разрешающем q-м
уравнении, станет не единичным. Это
соответствует переходу в число базисных
неизвестного xp и, наоборот,
выводу из числа базисных неизвестного,
относительно которого было разрешено
q-е уравнение.
При этом нужно
следить за тем, чтобы в процессе
преобразований не повторялся ранее
встречавшийся базис. Для этого необходимо
систематизировать расчеты.
Важно также
запомнить, что если r — количество
базисов, которые могут быть выделены
из данной системы, то
![]() .
.
Причем равенство достигается только в
том случае, если ни один из векторов ни
при каком из базисов не является
вырожденной комбинацией.
О п р е д е л е н и е 7. Опорными
решениями системы называются те
базисные решения, которые имеют все
неотрицательные значения неизвестных.
Конечно, их можно
выделить, если найдены все базисные
решения, но такой путь ведет к чрезвычайно
сложным расчетам. Если же выбирать
разрешающий элемент из дополнительных
условий, то те же преобразования
однократного замещения обеспечат
переход не просто к базисным, а к опорным
решениям. Эти дополнительные условия
заключаются в следующем:
1) разрешающий
столбец (номер p) выбирается так,
чтобы в нем оказался хотя бы один
положительный элемент Aip >
0;
2) разрешающая
строка (номер q) выбирается из
условия, чтобы отношение
![]()
было наименьшим из значений
![]()
при Aip > 0.
После выбора
разрешающего элемента дальнейшие
вычисления ведутся согласно обычным
правилам преобразований однократного
замещения.
Как и при определении
базисных решений, здесь также необходимо
следить, чтобы на какой либо итерации
не вернуться к ранее найденному опорному
решению. Это условие дополнительно
ограничивает выбор разрешающего
элемента.
Ï ð è ì å ð 3. С
помощью преобразований однократного
замещения найти все базисы и опорные
решения следующей системы уравнений:

Р е ш е н и е
. Количество опорных решений
данной системы линейных уравнений
![]() .
.
|
A1 |
A2 |
A3 |
A4 |
A5 |
A0 |
A0/A1 |
A0/A2 |
Опорные |
||||||
|
-2 |
3 |
1 |
0 |
0 |
9 |
3 |
Базис |
x1 |
x2 |
x3 |
x4 |
x5 |
||
|
1 |
1 |
0 |
1 |
0 |
8 |
8 |
8 |
A3,A4,A5 |
0 |
0 |
9 |
8 |
9 |
|
|
3 |
-2 |
0 |
0 |
1 |
9 |
3 |
A3,A4,A1 |
3 |
0 |
15 |
5 |
0 |
||
|
min |
3 |
A1,A2,A3 |
5 |
3 |
10 |
0 |
0 |
|||||||
|
A1,A2,A5 |
3 |
5 |
0 |
0 |
10 |
|||||||||
|
A1 |
A2 |
A3 |
A4 |
A5 |
A0 |
A0/A2 |
A0/A5 |
Шаг |
A2,A4,A5 |
0 |
3 |
0 |
5 |
15 |
|
0 |
1,667 |
1 |
0 |
0,667 |
15 |
9 |
22,5 |
|||||||
|
0 |
1,667 |
0 |
1 |
-0,33 |
5 |
3 |
||||||||
|
1 |
-0,67 |
0 |
0 |
0,333 |
3 |
9 |
||||||||
|
min |
3 |
|||||||||||||
|
A1 |
A2 |
A3 |
A4 |
A5 |
A0 |
A0/A5 |
A0/A4 |
Шаг |
||||||
|
0 |
0 |
1 |
-1 |
1 |
10 |
10 |
||||||||
|
0 |
1 |
0 |
0,6 |
-0,2 |
3 |
5 |
||||||||
|
1 |
0 |
0 |
0,4 |
0,2 |
5 |
25 |
12,5 |
|||||||
|
min |
10 |
|||||||||||||
|
A1 |
A2 |
A3 |
A4 |
A5 |
A0 |
A0/A4 |
A0/A3 |
Шаг |
||||||
|
0 |
0 |
1 |
-1 |
1 |
10 |
10 |
||||||||
|
0 |
1 |
0,2 |
0,4 |
0 |
5 |
12,5 |
25 |
|||||||
|
1 |
0 |
-0,2 |
0,6 |
0 |
3 |
5 |
||||||||
|
min |
5 |
|||||||||||||
|
A1 |
A2 |
A3 |
A4 |
A5 |
A0 |
A0/A1 |
A0/A3 |
Шаг |
||||||
|
1,667 |
0 |
0,667 |
0 |
1 |
15 |
9 |
22,5 |
|||||||
|
-0,67 |
1 |
0,333 |
0 |
0 |
3 |
9 |
||||||||
|
1,667 |
0 |
-0,33 |
1 |
0 |
5 |
3 |
||||||||
|
min |
3 |
Дальнейший перебор
не приводит к нахождению новых опорных
решений.
В предыдущем
примере заданная система уравнений
имела некоторый выделенный исходный
базис. Если система не приведена к
единичному базису, то для его нахождения
необходимо выполнить следующую
последовательность действий:
1) начинаем с
преобразования системы методом
последовательных исключений, причем
выбор разрешающего элемента на начальном
этапе может быть совершенно произвольным;
2) если после
приведения системы к единичному базису
появились отрицательные свободные
элементы, выберем среди них наибольший
по абсолютной величине и вычтем почленно
выделенное таким образом уравнение
из всех остальных уравнений с отрицательными
свободными членами. Само же выделенное
уравнение перепишем, умножив все
коэффициенты на -1;
3) дальнейшие
преобразования системы будем проводить
согласно правилам однократного замещения,
выбирая разрешающий столбец из условия,
чтобы он имел в выделенной строке
положительный элемент. Для выбора
разрешающей строки вычисляем отношения
Aio к Aip и берем
в качестве разрешающей строку с
минимальным полученным значением;
4) предположим,
что после выполнения некоторого
количества итераций (3) мы все же не
смогли выделить базис полностью и пришли
к таблице, в которой выделенная строка
не имеет ни одного положительного
элемента, кроме свободного члена.
Очевидно, что процесс последовательных
преобразований на этом обрывается, ибо
становится невозможным выбор разрешающего
столбца по указанному выше принципу.
Нетрудно прийти к выводу, что в этом
случае исходная система уравнений не
имеет ни одного решения с неотрицательными
значениями неизвестных, в том числе и
опорного решения, или, как говорят,
несовместна в области неотрицательных
(допустимых) решений.
В случае, если
исходная система имеет хотя бы одно
опорное решение, после конечного числа
описанных выше итераций будет получено
исходное опорное решение.
Ï ð è ì å ð 4. Найти
исходное опорное решение системы
уравнений, приведя ее к единичному
базису при неотрицательных свободных
членах:

Р е ш е н и е
.
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A0 |
A0/Ak |
Исходная |
|
|
1 |
1 |
0 |
-3 |
4 |
1 |
0 |
-6 |
|||
|
1 |
-1 |
1 |
5 |
-4 |
6 |
0 |
8 |
|||
|
0 |
1 |
-1 |
-6 |
5 |
-4 |
0 |
-12 |
|||
|
1 |
0 |
0 |
1 |
3 |
1 |
1 |
-3 |
|||
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A0 |
A0/Ak |
Шаг |
|
|
1 |
1 |
0 |
-3 |
4 |
1 |
0 |
-6 |
|||
|
0 |
-2 |
1 |
8 |
-8 |
5 |
0 |
14 |
|||
|
0 |
1 |
-1 |
-6 |
5 |
-4 |
0 |
-12 |
|||
|
0 |
-1 |
0 |
4 |
-1 |
0 |
1 |
3 |
|||
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A0 |
A0/Ak |
Шаг |
|
|
1 |
1 |
0 |
-3 |
4 |
1 |
0 |
-6 |
|||
|
0 |
-2 |
1 |
8 |
-8 |
5 |
0 |
14 |
|||
|
0 |
-1 |
0 |
2 |
-3 |
1 |
0 |
2 |
|||
|
0 |
-1 |
0 |
4 |
-1 |
0 |
1 |
3 |
|||
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A0 |
A0/Ak |
Шаг |
|
|
1 |
2 |
0 |
-5 |
7 |
0 |
0 |
-8 |
|||
|
0 |
3 |
1 |
-2 |
7 |
0 |
0 |
4 |
|||
|
0 |
-1 |
0 |
2 |
-3 |
1 |
0 |
2 |
|||
|
0 |
-1 |
0 |
4 |
-1 |
0 |
1 |
3 |
|||
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A0 |
A0/A4 |
Шаг |
|
|
-1 |
-2 |
0 |
5 |
-7 |
0 |
0 |
8 |
1,6 |
||
|
0 |
3 |
1 |
-2 |
7 |
0 |
0 |
4 |
|||
|
0 |
-1 |
0 |
2 |
-3 |
1 |
0 |
2 |
1 |
||
|
0 |
-1 |
0 |
4 |
-1 |
0 |
1 |
3 |
0,75 |
||
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A0 |
A0/Ak |
Шаг |
|
|
-1 |
-0,75 |
0 |
0 |
-5,75 |
0 |
-1,25 |
4,25 |
|||
|
0 |
2,5 |
1 |
0 |
6,5 |
0 |
0,5 |
5,5 |
|||
|
0 |
-0,5 |
0 |
0 |
-2,5 |
1 |
-0,5 |
0,5 |
|||
|
0 |
-0,25 |
0 |
1 |
-0,25 |
0 |
0,25 |
0,75 |
Исходная система
уравнений не имеет опорных решений, так
как несовместна в области неотрицательных
(допустимых) решений.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Каноническая задача линейного программирования в векторной форме имеет вид:

Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.
Базисным решением системы называется частное решение, в котором неосновные переменные имеют нулевые значения. Любая система уравнений имеет конечное число базисных решений, равное ![]() , где
, где ![]() – число неизвестных,
– число неизвестных, ![]() – ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются опорными.
– ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются опорными.
Опорным решением задачи линейного программирования называется такое допустимое решение ![]() , для которого векторы условий, соответствующие положительным координатам
, для которого векторы условий, соответствующие положительным координатам ![]() , линейно независимы.
, линейно независимы.
Число отличных от нуля координат опорного решения не может превосходить ранга ![]() Системы векторов условий (т. е. числа линейно независимых уравнений системы ограничений).
Системы векторов условий (т. е. числа линейно независимых уравнений системы ограничений).
Если число отличных от нуля координат опорного решения равно ![]() , то такое решение называется Невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше
, то такое решение называется Невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше ![]() , такое решение называется Вырожденным.
, такое решение называется Вырожденным.
Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.
Теорема. Любое опорное решение является угловой точкой области допустимых решений.
Теорема. Любая угловая точка области допустимых решений является опорным решением.
Пример.
Графический метод решения задачи линейной оптимизации рассмотрим на примере задачи производственного планирования при
![]() = 2.
= 2.
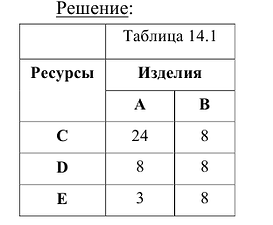
Предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами трех видов С, D и Е в объемах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и представлены в табл. 14.1
Решение:
|
Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В – 50 млн. руб. Требуется найти объемы производства изделий А и В, обеспечивающие максимальную прибыль. |
Построим математическую модель задачи, для чего обозначим ![]() и
и ![]() – объемы производства изделий А и В соответственно.
– объемы производства изделий А и В соответственно.
Тогда прибыль предприятия от реализации ![]() изделий А и
изделий А и ![]() изделий В составит:
изделий В составит:
![]() .
.
Ограничения по ресурсам будут иметь вид:

Естественно, объемы производства должны быть неотрицательными ![]() .
.
Решение сформулированной задачи найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений неравенств запишем в виде уравнений и пронумеруем их:


Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.
Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: при ![]() , а при
, а при ![]() . Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку
. Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку ![]() и, подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка
и, подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка ![]() лежит левее первой прямой, то и полуплоскость будет находиться левее прямой
лежит левее первой прямой, то и полуплоскость будет находиться левее прямой ![]() . На рис. 14.1 расположение полуплоскости относительно первой прямой отмечено стрелками.
. На рис. 14.1 расположение полуплоскости относительно первой прямой отмечено стрелками.
Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенству. Точки, удовлетворяющие ограничениям ![]() , находятся в первом квадранте.
, находятся в первом квадранте.
Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. Такой областью на графике (рис. 14.1) является многоугольник ![]() .
.
Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что эта задача линейной оптимизации имеет множество допустимых решений, т. е. многовариантна. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.
Чтобы найти эту точку, приравняем функцию к нулю и построим соответствующую ей прямую. Вектор–градиент прямой функции ![]() имеет координаты
имеет координаты ![]() .
.
 |
Рис. 14.1
Изобразим вектор на графике и построим прямую функции перпендикулярно вектору на рис. 14.1. Перемещая прямую функции параллельно самой себе в направлении вектора, видим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения. Координаты точки В находим, решая систему уравнений, прямые которых пересекаются в данной точке.

Решив эту систему, получаем, что ![]() .
.
Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную:
![]() (млн. руб.).
(млн. руб.).
Алгоритм решения задачи линейного программирования графическим методом таков:
1. Строится область допустимых решений;
2. Строится вектор нормали к линии уровня с точкой приложении в начале координат;
3. Перпендикулярно вектору нормали проводится одна из линий уровня, проходящая через начало координат;
4. Линия уровня перемещается до положения опорной прямой. На этой прямой и будут находиться максимум или минимум функции.
В зависимости от вида области допустимых решений и целевой функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения.

На рис. 14.3 показан случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции ![]() достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т. к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.
достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т. к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.
![]()
Основные понятия симплексного метода решения задачи линейного программирования.
Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж. Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения рассмотренного выше метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача линейного программирования; направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи.
Симплекс-метод основан на следующих свойствах задачи линейного программирования:
· Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.
· Множество всех планов задачи линейного программирования выпукло.
· Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
· Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.
Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).
Симплекс-метод с естественным базисом
Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью ![]() . В этом случае очевиден начальный опорный план (неотрицательное базисное решение).
. В этом случае очевиден начальный опорный план (неотрицательное базисное решение).
Для определенности предположим, что первые Т Векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план: ![]() .
.
Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.
Полученный опорный план снова проверяется на оптимальность и т. д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.
Признак оптимальности заключается в следующих двух теоремах.
Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:
![]() , где
, где  ,
, ![]()
То можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:
1. Если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;
2. Если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.
Теорема 2. Если для всех векторов выполняется условие ![]() , то полученный план является оптимальным.
, то полученный план является оптимальным.
На основании признака оптимальности в базис вводится вектор ![]() , давший минимальную отрицательную величину симплекс-разности:
, давший минимальную отрицательную величину симплекс-разности: ![]() .
.
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор ![]() Г, Который дает минимальное положительное отношение:
Г, Который дает минимальное положительное отношение:
 ;
; ![]() ,
, ![]() .
.
Строка ![]() Называется Направляющей, Столбец
Называется Направляющей, Столбец ![]() и элемент
и элемент
![]() — Направляющими (последний называют также Разрешающим Элементом).
— Направляющими (последний называют также Разрешающим Элементом).
Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:
 ,
, ![]()
А элементы любой другой ![]() -й Строки пересчитываются по формулам:
-й Строки пересчитываются по формулам:
 ,
,![]() ,
, ![]()
Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:
 для
для ![]() ;
;  ,
, ![]() для
для ![]() .
.
Если наименьшее значение ![]() достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.
достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.
Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение ![]() на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.
на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.
Для использования приведенной выше процедуры симплекс-метода к минимизации линейной формы ![]() следует искать максимум функции
следует искать максимум функции ![]() , затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.
, затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.
Симплексный метод с искусственным базисом (М-метод)
Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.
М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (–М) на сумму искусственных переменных, где М – достаточно большое положительное число.
В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки ![]() теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М – достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М – достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
В процессе решения М–Задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М–Задачи содержит искусственные векторы или М–Задача неразрешима, то исходная задача также неразрешима.
Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.
| < Предыдущая | Следующая > |
|---|
Содержание:
Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т.е. отражения реального процесса через математические соотношения. При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих процессах выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т.д.). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование» или математические методы исследования операций.
Математическое программирование включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование. Сюда же относят и стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.
Математическое программирование – это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных, при наличии ограничений на переменные.
Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразования, транспортные задачи и т.д.
Построение математической модели экономической задачи включает следующие этапы:
- выбор переменных задачи;
- составление системы ограничений;
- выбор целевой функции.
Переменными задачи называются величины 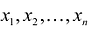
Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например, положительности переменных и т.п.
Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.
Общая задача математического программирования формулируется следующим образом: найти экстремум целевой функции: 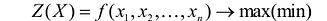 и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений:
и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений:
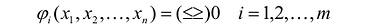
Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования и в общем виде может быть записана следующим образом:
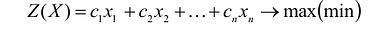
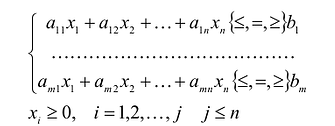
Данная запись означает следующее: найти экстремум целевой функции задачи и соответствующие ему переменные X = (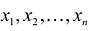 ). при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.
). при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.
Допустимым решением (планом) задачи линейного программирования называется любойX = (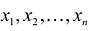 ). удовлетворяющий системе ограничений и условиям неотрицательности. Множество допустимых решений (планов) задачи образует область допустимых решений.
). удовлетворяющий системе ограничений и условиям неотрицательности. Множество допустимых решений (планов) задачи образует область допустимых решений.
Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение задачи, при котором целевая функция достигает экстремума.
Задача линейного программирования
В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Каноническая задача линейного программирования в координатной форме записи имеет вид:
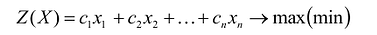
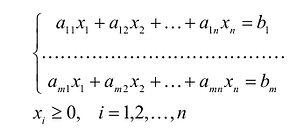
Используя знак суммирования эту задачу можно записать следующим образом:
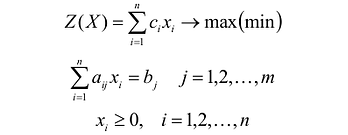
Каноническая задача линейного программирования в векторной форме имеет вид:
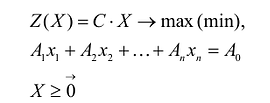
В данном случае введены векторы:
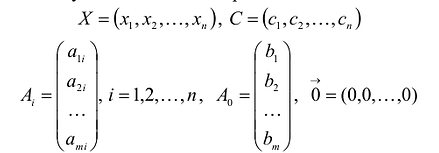
Здесь С – X – скалярное произведение векторов С и X.
Каноническая задача линейного программирования в матричной форме записи имеет вид:
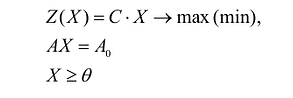
где:
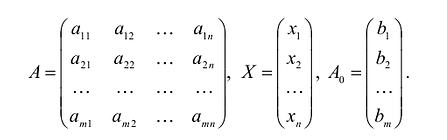
Здесь А – матрица коэффициентов системы уравнений, X -матрица-столбец переменных задачи; 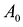 – матрица-столбец правых частей системы ограничений.
– матрица-столбец правых частей системы ограничений.
Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной форме записи имеют вид:
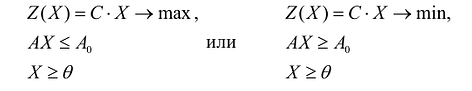
Приведение общей задачи линейного программирования к канонической форме
В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства:
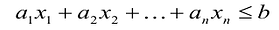 прибавляется величина
прибавляется величина 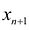 такая, что переводит неравенство в равенство
такая, что переводит неравенство в равенство 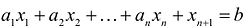 , где:
, где: 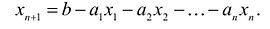
Неотрицательная переменная  называется дополнительной переменной.
называется дополнительной переменной.
Основания для возможности такого преобразования дает следующая теорема.
Теорема. Каждому решению  неравенства
неравенства 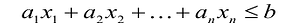 соответствует единственное решение
соответствует единственное решение 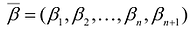 уравнения:
уравнения: 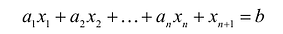 и неравенства
и неравенства 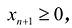 и, наоборот, каждому решению
и, наоборот, каждому решению  уравнения:
уравнения: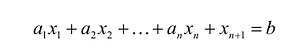 и неравенства
и неравенства  соответствует единственное решение
соответствует единственное решение 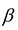 неравенства:
неравенства: 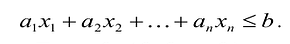
Доказательство. Пусть  – решение неравенства
– решение неравенства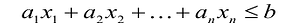 . Тогда:
. Тогда: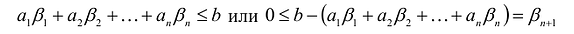
Если в уравнение 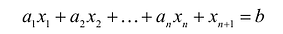 вместо переменных подставить значения
вместо переменных подставить значения 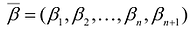 , получится:
, получится:
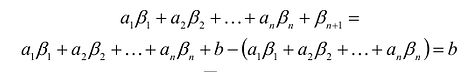
Таким образом, решение  удовлетворяет уравнению:
удовлетворяет уравнению: 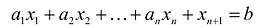 и неравенству
и неравенству  .
.
Доказана первая часть теоремы.
Пусть  удовлетворяет уравнению
удовлетворяет уравнению 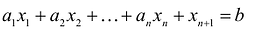 и неравенству
и неравенству  , т.е.
, т.е. 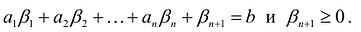 . Отбрасывая в левой части равенства неотрицательную величину
. Отбрасывая в левой части равенства неотрицательную величину 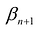 , получим:
, получим: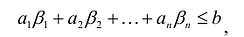
т.е.  удовлетворяет неравенству:
удовлетворяет неравенству: 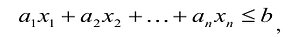 что и требовалось доказать.
что и требовалось доказать.
Если в левую часть неравенств системы ограничений вида 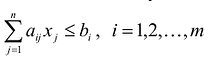
добавить переменную 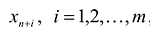 , то получится система ограничений – уравнений
, то получится система ограничений – уравнений 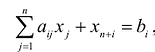
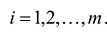 В случае, если система неравенств-ограничений имеет вид
В случае, если система неравенств-ограничений имеет вид 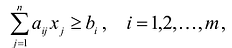 , то из левой части неравенств-ограничений нужно вычесть соответствующую неотрицательную дополнительную переменную
, то из левой части неравенств-ограничений нужно вычесть соответствующую неотрицательную дополнительную переменную 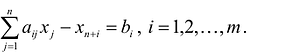
Полученная таким образом система уравнений-ограничений, вместе с условиями неотрицательности переменных, т.е. 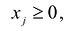
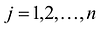 и целевой функцией является канонической формой записи задачи линейного программирования.
и целевой функцией является канонической формой записи задачи линейного программирования.
Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.
В реальных практических задачах дополнительные неизвестные имеют определенный смысл. Например, если левая часть ограничений задачи отражает расход ресурсов на производство продукции в объемах 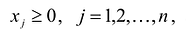 , а правые части – наличие производственных ресурсов, то числовые значения дополнительных неизвестных
, а правые части – наличие производственных ресурсов, то числовые значения дополнительных неизвестных 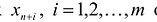 и означают объем неиспользованных ресурсов i-го вида.
и означают объем неиспользованных ресурсов i-го вида.
Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.
Множества допустимых решений
Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит их произвольную выпуклую линейную комбинацию.
Выпуклой линейной комбинацией произвольных точек 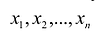 Евклидова пространства
Евклидова пространства 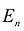 называется сумма
называется сумма 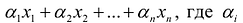 – произвольные неотрицательные числа, сумма которых равна 1.
– произвольные неотрицательные числа, сумма которых равна 1.
Геометрически это означает, что если множеству с любыми двумя его произвольными точками полностью принадлежит и отрезок, соединяющий эти точки, то оно будет выпуклым. Например, выпуклыми множествами являются прямолинейный отрезок, прямая, круг, шар, куб, полуплоскость, полупространство и др.
Точка множества называется граничной, если любая окрестность этой точки сколь угодно малого размера содержит точки, как принадлежащие множеству, так и не принадлежащие ему.
Граничные точки множества образуют его границу. Множество называется замкнутым, если оно содержит все свои граничные точки.
Ограниченным называется множество, если существует шар с радиусом конечной длины и центром в любой точке множества, содержащий полностью в себе данное множество. В противном случае множество будет неограниченным.
Пересечение двух или более выпуклых множеств будет выпуклым множеством, так как оно отвечает определению выпуклого множества.
Точка выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации двух других различных точек этого множества.
Так, угловые точки треугольника – его вершины, круга – точки окружности, ее ограничивающие, а прямая, полуплоскость, плоскость, полупространство, пространство не имеют угловых точек.
Выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек, называется выпуклым многоугольником, а замкнутое выпуклое ограниченное множество в трехмерном пространстве, имеющее конечное число угловых точек, называется выпуклым многогранником.
Теорема. Любая тонка многоугольника является выпуклой линейной комбинацией его угловых точек.
Теорема. Область допустимых решений задачи линейного программирования является выпуклым множеством.
Уравнение целевой функции при фиксированных значениях самой функции является уравнением прямой линии (плоскости, гиперплоскости и т.д.). Прямая, уравнение которой получено из целевой функции при равенстве ее постоянной величине, называется линией уровня.
Линия уровня, имеющая общие точки с областью допустимых решений и расположенная так, что область допустимых решений находится целиком в одной из полуплоскостей, называется опорной прямой.
Теорема. Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении нормали и убывают при перемещении в противоположном направлении.
Теорема. Целевая функция задачи линейного программирования достигает экстремума в угловой точке области допустимых решений; причем, если целевая функция достигает экстремума в нескольких угловых точках области допустимых решений, она также достигает экстремума в любой выпуклой комбинации этих точек.
Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками
Каноническая задача линейного программирования в векторной форме имеет вид:
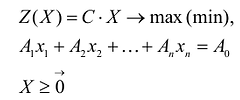
Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.
Базисным решением системы называется частное решение, в котором неосновные переменные имеют нулевые значения. Любая система уравнений имеет конечное число базисных решений, равное 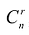 , где n – число неизвестных, r- ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются опорными.
, где n – число неизвестных, r- ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются опорными.
Опорным решением задачи линейного программирования называется такое допустимое решение 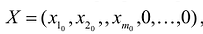 , для которого векторы условий, соответствующие положительным координатам
, для которого векторы условий, соответствующие положительным координатам  линейно независимы.
линейно независимы.
Число отличных от нуля координат опорного решения не может превосходить ранга r системы векторов условий (т.е. числа линейно независимых уравнений системы ограничений).
Если число отличных от нуля координат опорного решения равно m, то такое решение называется невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше т, такое решение называется вырожденным.
Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.
Теорема. Любое опорное решение является угловой точкой области допустимых решений.
Теорема. Любая угловая точка области допустимых решений является опорным решением.
Пример:
Графический метод решения задачи линейной оптимизации рассмотрим на примере задачи производственного планирования при n = 2.
Предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами трех видов С, D и Е в объемах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и представлены в табл. 14.1
Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В – 50 млн.руб. Требуется найти объемы производства изделий А и В, обеспечивающие максимальную прибыль.
Построим математическую модель задачи, для чего обозначим 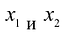 – объемы производства изделий А и В соответственно.
– объемы производства изделий А и В соответственно.
Тогда прибыль предприятия от реализации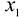 изделий А и
изделий А и 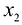 изделий В составит:
изделий В составит:
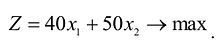
Ограничения по ресурсам будут иметь вид:
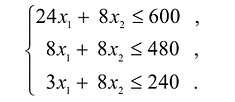
Естественно, объемы производства должны быть неотрицательными 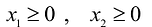
Решение сформулированной задами найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений неравенств запишем в виде уравнений и пронумеруем их:
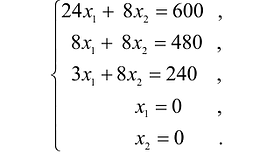
Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.
Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: 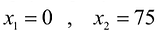 а при
а при 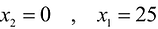 .
.
Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку O(0,0) подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка O(0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой
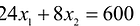 . На рис 14 , расположение полуплоскости относительно первой прямой отмечено стрелками.
. На рис 14 , расположение полуплоскости относительно первой прямой отмечено стрелками.
Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенству. Точки, удовлетворяющие ограничениям 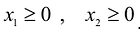 , находятся в первом квадранте. Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. Такой областью на графике (рис. 14.1) является многоугольник ОАВС.
, находятся в первом квадранте. Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. Такой областью на графике (рис. 14.1) является многоугольник ОАВС.
Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что эта задача линейной оптимизации имеет множество допустимых решений, т.е. моговариантпа. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.
Чтобы найти эту точку, приравняем функцию к нулю и построим соответствующую ей прямую. Вектор-градиент прямой функции
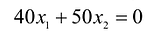 имеет координаты
имеет координаты 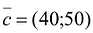
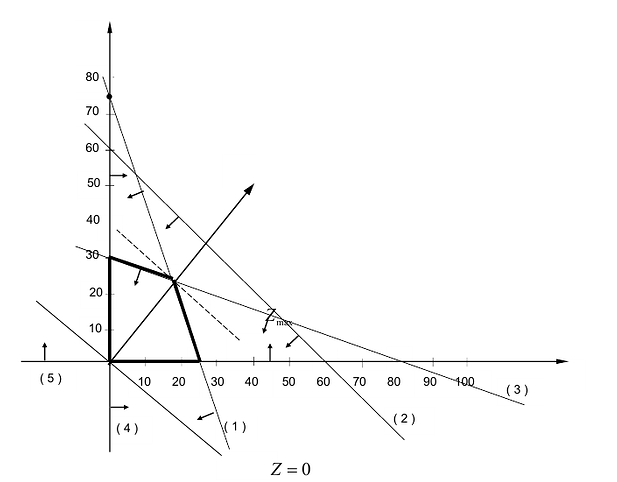
Рис. 14.1
Изобразим вектор на графике и построим прямую функции перпендикулярно вектору на рис. 14.1. Перемещая прямую функции параллельно самой себе в направлении вектора, видим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения. Координаты точки В находим, решая систему уравнений, прямые которых пересекаются в данной точке.
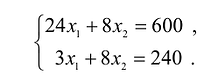
Решив эту систему, получаем, что 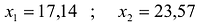
Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную:
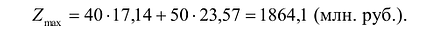
Алгоритм решения задачи линейного программирования графическим методом таков:
- Строится область допустимых решений;
- Строится вектор нормали к линии уровня с точкой приложении в начале координат;
- Перпендикулярно вектору нормали проводится одна из линий уровня, проходящая через начало координат;
- Линия уровня перемещается до положения опорной прямой. На этой прямой и будут находиться максимум или минимум функции.
В зависимости от вида области допустимых решений и целевой функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения. 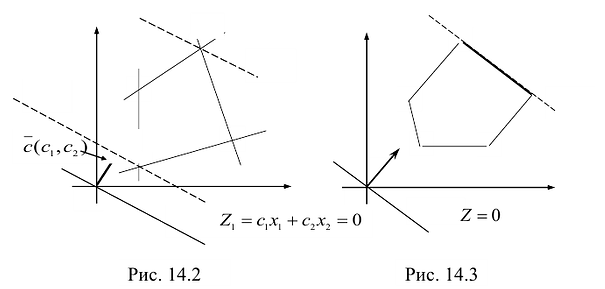
На рис. 14.3 показан случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции Z достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т.к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.
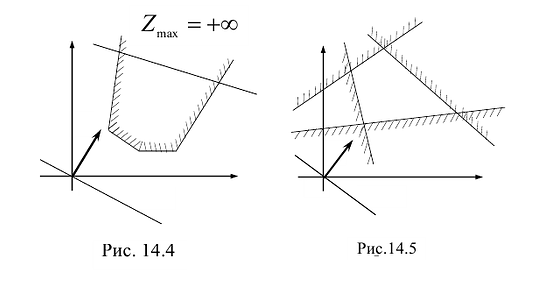
На рисунке 14.4 изображен случай, когда система ограничений образует неограниченное сверху множество. Функция Z в данном случае стремится к бесконечности, так как прямую функции можно передвигать в направлении вектора градиента как угодно далеко, а на рисунке 14.5 представлен случай несовместной системы ограничений.
Основные понятия симплексного метода решения задачи линейного программирования.
Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж.Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения рассмотренного выше метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача линейного программирования; направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи.
Симплекс-метод основан на следующих свойствах задачи линейного программирования:
- Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.
- Множество всех планов задачи линейного программирования выпукло.
- Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
- Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.
Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).
- Заказать решение задач по высшей математике
Симплекс-метод с естественным базисом
Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью mхm. В этом случае очевиден начальный опорный план (неотрицательное базисное решение).
Для определенности предположим, что первые m векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план: 
Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.
Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.
Признак оптимальности заключается в следующих двух теоремах.
Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:
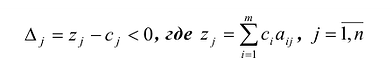
то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:
- если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;
- если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.
Теорема 2. Если для всех векторов выполняется условие 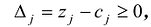 то полученный план является оптимальным.
то полученный план является оптимальным.
На основании признака оптимальности в базис вводится вектор Ак, давший минимальную отрицательную величину симплекс-разности: 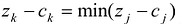
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор  , который дает минимальное положительное отношение:
, который дает минимальное положительное отношение:
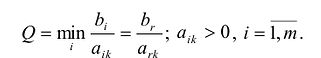
Строка 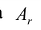 называется направляющей, столбец
называется направляющей, столбец 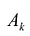 и элемент
и элемент 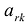 — направляющими (последний называют также разрешающим элементом).
— направляющими (последний называют также разрешающим элементом).
Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:
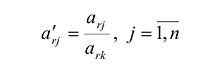
а элементы любой другой i-й строки пересчитываются по формулам:
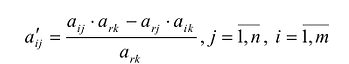
Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:
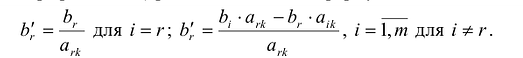
Если наименьшее значение Q достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.
Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение Q на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.
Для использования приведенной выше процедуры симплекс -метода к минимизации линейной формы  следует искать максимум функции
следует искать максимум функции 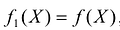 затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.
затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.
Симплексный метод с искусственным базисом (М-метод)
Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.
М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М – достаточно большое положительное число.
В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки А, теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М – достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
В процессе решения M-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.
Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.
Теория двойственности
Любой задаче линейного программирования можно сопоставить сопряженную или двойственную ей задачу. Причем, совместное исследование этих задач дает, как правило, значительно больше информации, чем исследование каждой из них в отдельности.
Любую задачу линейного программирования можно записать в виде:
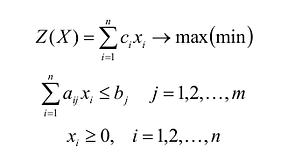
Первоначальная задача называется исходной или прямой.
Модель двойственной задачи имеет вид:
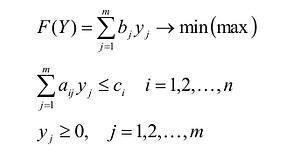
Переменные двойственной задачи 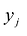 называют объективно обусловленными оценками или двойственными оценками.
называют объективно обусловленными оценками или двойственными оценками.
Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.
Двойственная задача по отношению к исходной составляется согласно следующим правилам:
- Целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи – на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид <, а в задаче на минимум – вид
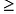
- Матрица
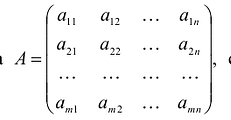 , составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица
, составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица 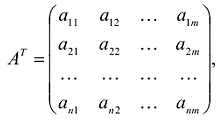 , в двойственной задаче получаются друг из друга транспонированием;
, в двойственной задаче получаются друг из друга транспонированием; - Число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи – числу переменных в исходной задаче;
- Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи – коэффициенты при неизвестных в целевой функции исходной задачи;
- Каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства <, соответствует переменная, связанная условием неотрицательности.
Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.
Математические модели пары двойственных задач могут быть симметричными и несимметричными. В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной – в виде неравенств, причем переменные в двойственной задаче могут быть и отрицательными. В симметричных двойственных задачах система ограничений как исходной, так и двойственной задачи задается в виде неравенств, причем на двойственные переменные налагается условие неотрицательности.

где:
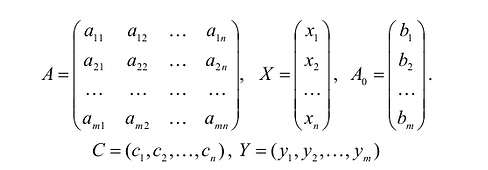
Рассмотрим пример, показывающий, как в реальной экономической ситуации появляются взаимно двойственные задачи линейного программирования.
На некотором предприятии после выполнения годового плана возник вопрос: как поступить с остатками сырья? Из оставшегося сырья можно наладить производство продукции и реализовать его или продать сырье.
Предположим, что имеется два вида сырья 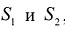 , остатки которого составляют соответственно 35 и 20 единиц. Из этого сырья можно наладить производство трех видов товаров:
, остатки которого составляют соответственно 35 и 20 единиц. Из этого сырья можно наладить производство трех видов товаров: 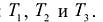
При исследовании первой возможности (наладить выпуск товаров 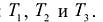 ) возникает вопрос о плане выпуска, который задается тремя переменными
) возникает вопрос о плане выпуска, который задается тремя переменными 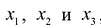 , которые соответствуют количеству произведенного товара. Эти переменные должны удовлетворять условиям:
, которые соответствуют количеству произведенного товара. Эти переменные должны удовлетворять условиям:
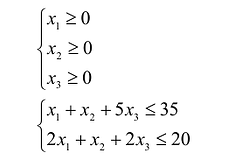
Прибыль, которую получит предприятие от реализации товара, составит:
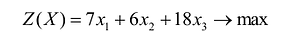
В интересах предприятия эту прибыль максимизировать.
Это прямая задача.
Объективно обусловленными оценками двойственной задачи 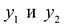 будут цены, по которым целесообразно продавать излишки сырья, т.е. при продаже сырья по ценам ниже
будут цены, по которым целесообразно продавать излишки сырья, т.е. при продаже сырья по ценам ниже 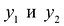 предприятие будет терпеть убытки.
предприятие будет терпеть убытки.
Справедливое требование со стороны продающего предприятия состоит в следующем: если взять сырье, идущее на производство единицы товара 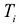 то выручка от его продажи должна быть не меньше, чем прибыль от реализации готового изделия (в противном случае нет смысла продавать сырье – целесообразнее изготовить товар и получить прибыль от его реализации).
то выручка от его продажи должна быть не меньше, чем прибыль от реализации готового изделия (в противном случае нет смысла продавать сырье – целесообразнее изготовить товар и получить прибыль от его реализации).
Это требование можно представить в виде системы неравенств: 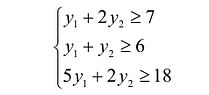
В левой части каждого неравенства предполагаемая выручка от продажи сырья, необходимого для производства единицы товара 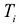 а в правой – прибыль от реализации этой единицы товара.
а в правой – прибыль от реализации этой единицы товара.
Что касается покупателя, то он заинтересован в минимизации расходов на покупку сырья, т.е. величины 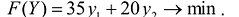
Теоремы двойственности
Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач: можно либо найти оптимальное решение другой задачи, не решая ее, либо установить его отсутствие.
Возможны следующие случаи:
- обе задачи из пары двойственных имеют оптимальные решения;
- одна из задач не имеет решения ввиду неограниченности целевой функции, а другая – ввиду несовместности системы ограничений.
Первая теорема двойственности.
Для двойственных задач линейного программирования имеет место один из взаимоисключающих случаев:
- В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают:
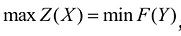
- В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество.
- В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым;
- Обе из рассматриваемых задач имеют пустые допустимые множества.
Вторая теорема двойственностн (теорема о дополняющей нежесткости):
Пусть 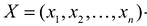 – допустимое решение прямой задачи, а
– допустимое решение прямой задачи, а 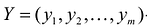 допустимое решение двойственной задачи.
допустимое решение двойственной задачи.
Для того, чтобы они были оптимальными решениями соответствующих взаимодвойственных задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:
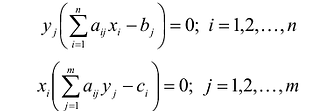
Эти условия устанавливают связь между оптимальными значениями прямой и двойственной задач и позволяют, зная решение одной из них, находить решение другой задачи.
Теорема об оценках:
Значения переменных 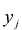 в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов
в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов 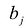 системы ограничений – неравенств прямой задачи на величину
системы ограничений – неравенств прямой задачи на величину 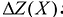 :
:
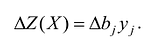
Диапазон изменения компонент вектора В, в котором сохраняется оптимальный базис, называется областью устойчивости оптимальных оценок.
Экономический смысл первой теоремы двойственности следующий. План производства X и набор ресурсов Y оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная при известных заранее ценах продукции 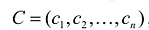 , равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов
, равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов 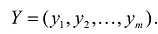 Для всех других планов прибыль от продукции всегда меньше или равна стоимости затраченных ресурсов
Для всех других планов прибыль от продукции всегда меньше или равна стоимости затраченных ресурсов 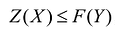 , т.е. ценность выпущенной продукции не превосходит суммарной оценки затраченных ресурсов. Значит, величина Z(X)~ F(Y) характеризует производственные потери в зависимости от рассмотренной производственной программы и выбранных оценок ресурсов.
, т.е. ценность выпущенной продукции не превосходит суммарной оценки затраченных ресурсов. Значит, величина Z(X)~ F(Y) характеризует производственные потери в зависимости от рассмотренной производственной программы и выбранных оценок ресурсов.
- Дифференциальное исчисление функций одной переменной
- Исследование функции
- Пространство R”
- Неопределённый интеграл
- Линейный оператор – свойства и определение
- Многочлен – виды, определение с примерами
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
Обновлено: 22.05.2023
Решение систем линейных алгебраических уравнений (СЛАУ) является одной из основных задач линейной алгебры. Эта задача имеет важное прикладное значение при решении научных и технических проблем. Кроме того, является вспомогательной при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований.
Применяемые на практике численные методы решения СЛАУ делятся на две группы – прямые и итерационные.
Прикрепленные файлы: 1 файл
кур по алгебре.docx
Первые r неизвестные х1,…,хr являются базисными неизвестными. Положив свободные неизвестные хr+1, …, xn равными нулю, получим одно базисное решение
Заметим, что система уравнений может быть системой с базисом относительно какой-то группы из r неизвестных, где r – ранг матрицы системы. При этом каждое базисное неизвестное xк присутствует в одном уравнении, но не обязательно, что в к-ом уравнении. Тогда от такой системы можно перейти к системе вида (1.1) после соответствующей перестановки уравнений и перенумерации неизвестных.
Пусть система линейных уравнений совместна и ранг матрицы этой системы меньше числа неизвестных (r преобразованная система будет содержать уравнение
то она противоречива (противоречива и исходная система); ясно, что в этой ситуации r(A) ≠ r(Ā).
2. Если преобразованная система будет иметь уравнения вида
то их надо отбросить, так как они являются следствиями остальных; ранг расширенной матрицы будет меньше числа min на число исключенных из системы уравнений.
Алгоритм приведения системы к системе с базисом
- Составляется таблица Гаусса.
- Выбирается разрешающий элемент аsk ≠ 0. Тогда s-я строка называется разрешающей, а к-й столбец – разрешающим столбцом.
- Элементы разрешающей строки делятся на разрешающий элемент, т.е. преобразуются по формуле
Коэффициент при хк в s-ом уравнении преобразованной системы будет равен единице.
4. Элементы разрешающего столбца преобразованной таблицы аsk* = 1, заполняются нулями.
5. Элементы остальных строк преобразованной таблицы вычисляются по правилу прямоугольника.
Процесс метода Жордана-Гаусса продолжается, пока хотя бы в одной строке есть коэффициенты при неизвестных, отличные от нуля и не занимающие места разрешающих элементов предыдущих итераций.
Метод Жордана-Гаусса дает другой способ получения базисных решений системы. При этом, приведя систему к системе с базисом, получим только одно базисное решение из всех возможных ее базисных решений.
Система с базисом, у которой свободные члены всех уравнений неотрицательны, называется канонической системой уравнений.
Базисные решения канонической системы с базисными переменными, относительно которых она является системой с базисом, одновременно является опорным решением. Другие базисные решения исходной канонической системы могут и не быть опорными.
Одно опорное решение канонической системы сразу выписывается по виду этой системы (достаточно свободным неизвестным придать нулевые значения). В линейном программировании важной задачей является задача о нахождении всех опорных решений системы или части из них. Чтобы найти какое-нибудь другое опорное решение канонической системы, надо перейти к другой канонической системе, равносильной исходной.
Приведем теорему о возможности перехода от одной канонической системы к эквивалентной канонической системе: если в канонической системе уравнений среди коэффициентов при каком-либо свободном неизвестном имеется хотя бы один положительный, то возможен переход к новой канонической системе. Эквивалентной исходной, в которой указанное свободное неизвестное окажется базисным (при этом одна из базисных неизвестных станет свободной).
Переход от одной канонической системы к равносильной канонической системе называется преобразованием (операцией) однократного замещения.
Алгоритм преобразования однократного замещения
- По данной канонической системе заполняется таблица Жордана-Гаусса с добавлением двух столбцов – столбца из базисных неизвестных и вспомогательного столбца θ.
- Выбирается разрешающий столбец. Это – любой столбец из коэффициентов при свободных неизвестных, имеющий хотя бы один положительный элемент.
- Заполняется столбец θ. Для этого элементы свободного столбца (правые части системы) делятся на элементы разрешающего столбца.
- Выбирается разрешающая строка. Это есть строка, против которой в столбце θ стоит наименьшее неотрицательное число.
- Выбирается разрешающий элемент, которым является элемент, находящийся на пересечении разрешающей строки и разрешающего столбца.
- Заполняется новая таблица по алгоритму привидения системы к системе с базисом.
При этом свободная переменная из разрешающего столбца заместит базисную переменную, которая находится на пересечении разрешающей строки и столбца из базисных переменных (базисная переменная разрешающей строки станет свободной). Остальные базисные неизвестные в новой таблице сохраняются. По данной второй таблице (ее нового базисного столбца и нового столбца из свободных членов) выписывается следующее опорное решение. Легко выписать и новую каноническую систему уравнений.
Аналогичным образом по второй таблице можно осуществлять следующую операцию однократного замещения. Так можно найти все опорные решения или часть из них.
Распределительная таблица фактически является матрицей, с которой можно проводить преобразования и получать новые опорные решения используя метод однократного замещения Жордана-Гаусса, сущность которого сводится к назначению другой базисной переменной, вместо одной из свободных.
При целенаправленном преобразовании начальной таблицы-матрицы можно достигать как минимизации затрат. Рассмотрим методику названного алгоритма.
Циклом называют набор клеток, в котором две и только две клетки расположены в одной строке или в одном столбце, причём, последняя клетка столбца образует первую клетку строки, и так далее, вплоть до замыкания цепочки в цикле (см. рис. 4.1).

Рис. 4.1. Схема циклического преобразования
Целевая функция при этом равна Z0= 1130
С каждым опорным решением можно провести циклическое преобразование, которое всегда начинается в одной из свободных клеток, затем проходит только через занятые клетки, и заканчивается на исходной клетке.
Число вариантов таких преобразований равно числу свободных клеток. Число занятых клеток всегда должно быть равно рангу системы.
В свободной клетке (4-4) размещаем +λ1 (первая нечётная порядковая клетка). Протягиваем далее от неё стрелку до занятой клетки (4-4), где будет размещаться – λ2 . далее поступаем аналогичным образом, чередуя положительные и отрицательные значения λm , размещённые в угловых клетках, согласно последовательности построения цикла. Заметим, что индексы фиксируют только порядковое расположение λ, и к его численному значению никакого отношения не имеет. Численное значение λ определяется после построения цикла. Правила построение циклов всегда обеспечивают равное количество отрицательных и положительных по знаку значений λm..
3начение величины λ определяем (см. рис 4.2) следующим образом:
1) выберем в углах цикла клетку, с наименьшим размером корреспонденции, это будет клетка (1-1) с корреспонденцией λ11= 10;
2) выполним одно преобразование однократного замещения;
4) далее, можно определить ΔZ1 = λ · О1 = (+10)· (+10) = 100.
5) делаем вывод, что выбранная клетка (4-1) не обеспечивает уменьшение целевой функции Z. (Z1 >Z0), и от преобразования с ней надо отказаться. Выбираем следующую клетку. и так далее, пока не найдём клетку с отрицательной оценкой.

Рис. 4.2. Табличная матрица после преобразования № 1
Для того чтобы заранее определить, будет ли вести новое решение, к уменьшению значения целевой функции, мы прибегаем к расчёту оценки свободной клетки на предмет полезности её использования для получения нового опорного решения с уменьшенным численным значением целевой функции.

Для того чтобы найти какой-либо другой единичный базис, возьмём за разрешающий элемент любой неравный нулю коэффициент при каком-либо свободном неизвестном и выполним одну итерацию методом Жордано-Гаусса.
Свободное неизвестное x3 стало базисным, а базисное неизвестно x1 стало свободным. Такое преобразование называется преобразованием однократного замещения, т.к. произошло замещение базисного неизвестного x1 свободным неизвестным x3. Т.о. данная система уравнений преобразована к новому единичному базису, в котором вектор-коэффициенты при x3,x4,x5. Последовательно выполняя преобразования однократного замещения, можно найти все базисы векторов коэффициентов и все базисы решений данной системы.

Для данной системы уравнений нельзя в качестве базисных неизвестных взять набор x1,x2,x4, т.к. им соответствуют вектор-коэффициенты , которые линейно зависимы, т.к. А1-А2-3А4=θ.
§6. Опорные решения. Отыскание исходного опорного решения.
Опорным решением системы линейных уравнений (1, §5) называется базисное допустимое решение (для которого векторы условий, соответствующие положительным координатам, линейно независимы). Отыскание исходного опорного решения рассмотрим на примере.
Найти исходное опорное решение системы уравнений.

Система уравнений приведена к единичному базису.
Выпишем базисное решение:

.

Получили противоречие предположение о существовании такого вектораX неверно.
Систему линейных уравнений (2) запишем в виде таблицы.


10:4=

3:2=






Во втором уравнении системы (2) найдём какой-либо положительный элемент; если такого элемента не существует, то это будет означать в соответствии с утверждением несовместность с ОДР.

Тем самым четвёртый столбец таблицы стал разрешающим.
Определим разрешающую строку. Для этого для положительных элементов четвёртого столбца вычислим отношение свободных членов (стоящих в той же строке) к этим положительным элементам.

Пусть (*)
Теорема: если в системе линейных уравнений (2) выполнить однократное замещение с разрешающим элементом ak4, то все свободные члены уравнений системы останутся неотрицательными.
Возьмём любой свободный член bp и покажем, что он остаётся неотрицательным.
ap4 0 в i-й строке.
Найдём разрешающий элемент, согласно (*), при этом может оказаться:
Разрешающий элемент aks оказался в i-й строке, т.е. k=i.
Выполним однократное замещение с разрешающим элементом ais, тогда i-е уравнение системы станет разрешающим относительно xs, и все свободные члены уравнений системы будут неотрицательными, и мы сможем выписать исходное опорное решение.
Разрешающий элемент i-й строке, , при этомbk>0.
Выполним однократное замещение с разрешающим элементом aks.

При этом свободный член i-го уравнения уменьшится, но i-е уравнение останется неразрешённым, но свободный член уменьшится.
После конечного числа шагов придём к случаю 1., либо в i-м не останется положительных коэффициентов при неизвестных, что означает несовместность системы в ОДР, либо придём к случаю 3.

Поэтому, прежде чем выполнять преобразование однократного замещения с разрешающим элементом aks, нужно попробовать выбрать другой разрешающий столбец по другому положительному элементу в i-й строке. Если это сделать нельзя, то нужно выполнить однократное замещение с разрешающим элементом aks, тогда изменится состав базисных неизвестных, и выбор разрешающего элемента нужно будет начинать сначала. Через конечное число шагов придём к случаям 2. или 1., либо установим несовместность системы уравнений в ОДР.
Этот метод имеет ограниченную область применения. Этим методом можно решать следующие задачи:
- Задачи с двумя переменными, имеющими симметричную форму записи.
- Задачи с n переменными, имеющие каноническую форму записи, если выполняется условие n-r≤2, где n – число неизвестных, r – ранг системы линейных уравнений (1).
Задача типа 2 сводится к задаче типа 1, для чего нужно перейти от канонической к симметричной форме записи.
Рассмотрим решение задач типа 1.
Найти X=(x1,x2), который является решением (1), удовл. (2),
и на котором целевая функция f(X)=c1x1+c2x2 (3) достигает экстремума (максимума или минимума).
Решение задачи содержит два этапа:

ОДР находится в 1-й координатной четверти
система (1) содержит линейные неравенства с двумя переменными
Решением такого неравенства является любая пара чисел (x1;x2), которая при подстановке в (7) обращает его в верное числовое равенство.
На координатной плоскости (x1;x2) – точка .
Множество решений (7) – некоторое множество точек на x1Ox2.
Выясним, какую область на плоскости x1Ox2 образуют точки, которые являются решением ограничений (1) и (2).
Заменим неравенство (7) соответствующим ему равенством.
это уравнение определяет на плоскости x1Ox2 прямую линию. Эта линия делит плоскость x1Ox2 на 2 полуплоскости π1 и π2.
Утверждение. Точки одной из этих полуплоскостей являются решением
а точки другой полуплоскости являются решением неравенства . (**)
Докажем это утверждение.
Выясним знак выражения в зависимости от того, в какой из полуплоскостей (π1,π2) находится данная точка.
Знак выражения зависит от знака
Для того, чтобы определить полуплоскость, в которой выполняются соответствующие неравенства, достаточно подставить в неравенство координаты какой-либо одной точки, не лежащей на граничной прямой.
Если неравенство удовлетворяется, то областью решения будет полуплоскость, в которой находится эта точка; если нет – то в другой.
Чтобы построить ОДР на координатной плоскости x10x2, нужно построить граничные прямые и области решений каждого неравенства системы; пересечение областей решения этих неравенств, взятое в первом квадранте и будет областью решений данной задачи.
II. Нахождение ОДР оптимального решения задачи.
Рассмотрим уравнение (3) При конкретном значении f это уравнение определяет на плоскости прямую линию. При изменении f мы получим семейство параллельных прямых (прямые ||, т.к. они все имеют один угловой коэффициент ). Каждую из этих прямых называют линией уравнения, т.к. согласно равенству (3) на каждой такой прямой функция f сохраняет постоянное значение.
– это вектор, перпендикулярный линиям уровня, и он показывает направление, по которому нужно перемещать линию уровня, чтобы значение f возрастало. Обозначим
Линия уровня, имеющая общие точки с ОДР и расположенная так, что ОДР целиком находится в одной из полуплоскостей, на которые данная линия уровня делит координатную плоскость, называется опорной прямой.
Чтобы найти ОДР оптимального решения, выполним:
1. Строим в начале координат.
2. Перпендикулярно проводим одну из линий уровня, имеющую общие точки с ОДР.
3. Перемещая эту линию уровня в направлении в задаче на max или в противоположном направлении в задаче на min, находим опорную прямую.
4. Совместно решив уравнения прямых, ограничивающих ОДР и имеющих общие точки с опорной прямой, найдем оптимальное решение. В зависимости от вида ОДР и целевой функции задача может иметь единственное решение, бесконечное множество решений, или не иметь решений ввиду несовместности системы ограничений или неограниченности целевой функции ОДР.

Решим совместно уравнения прямых BC и DC, и имеющих общую точку с опорной прямой, найдём оптимальное решение.
§5. Преобразование однократного замещения.
Пусть дана система линейных уравнений
Дана система линейных уравнений, приведённая к единичному базису. Требуется преобразовать её к какому-либо другому единичному базису.
| Базисные неизвестные | x1 | x2 | x3 | x4 | x5 | bi | Базисное решение |
| x1,x4,x5 | -3 | ||||||
| -3 | |||||||
| x3,x4,x5 |
Для того чтобы найти какой-либо другой единичный базис, возьмём за разрешающий элемент любой неравный нулю коэффициент при каком-либо свободном неизвестном и выполним одну итерацию методом Жордано-Гаусса.
Свободное неизвестное x3 стало базисным, а базисное неизвестно x1 стало свободным. Такое преобразование называется преобразованием однократного замещения, т.к. произошло замещение базисного неизвестного x1 свободным неизвестным x3. Т.о. данная система уравнений преобразована к новому единичному базису, в котором вектор-коэффициенты при x3,x4,x5. Последовательно выполняя преобразования однократного замещения, можно найти все базисы векторов коэффициентов и все базисы решений данной системы.
Для данной системы уравнений нельзя в качестве базисных неизвестных взять набор x1,x2,x4, т.к. им соответствуют вектор-коэффициенты , которые линейно зависимы, т.к. А1-А2-3А4=θ.
Этот метод имеет ограниченную область применения. Этим методом можно решать следующие задачи:
- Задачи с двумя переменными, имеющими симметричную форму записи.
- Задачи с n переменными, имеющие каноническую форму записи, если выполняется условие n-r≤2, где n – число неизвестных, r – ранг системы линейных уравнений (1).
Задача типа 2 сводится к задаче типа 1, для чего нужно перейти от канонической к симметричной форме записи.
Рассмотрим решение задач типа 1.
Найти X=(x1,x2), который является решением (1), удовл. (2),
и на котором целевая функция f(X)=c1x1+c2x2 (3) достигает экстремума (максимума или минимума).
Решение задачи содержит два этапа:

ОДР находится в 1-й координатной четверти
система (1) содержит линейные неравенства с двумя переменными
Решением такого неравенства является любая пара чисел (x1;x2), которая при подстановке в (7) обращает его в верное числовое равенство.
На координатной плоскости (x1;x2) – точка .
Множество решений (7) – некоторое множество точек на x1Ox2.
Выясним, какую область на плоскости x1Ox2 образуют точки, которые являются решением ограничений (1) и (2).
Заменим неравенство (7) соответствующим ему равенством.
это уравнение определяет на плоскости x1Ox2 прямую линию. Эта линия делит плоскость x1Ox2 на 2 полуплоскости π1 и π2.
Утверждение. Точки одной из этих полуплоскостей являются решением
а точки другой полуплоскости являются решением неравенства . (**)
Докажем это утверждение.
Выясним знак выражения в зависимости от того, в какой из полуплоскостей (π1,π2) находится данная точка.
Знак выражения зависит от знака
Для того, чтобы определить полуплоскость, в которой выполняются соответствующие неравенства, достаточно подставить в неравенство координаты какой-либо одной точки, не лежащей на граничной прямой.
Если неравенство удовлетворяется, то областью решения будет полуплоскость, в которой находится эта точка; если нет – то в другой.
Чтобы построить ОДР на координатной плоскости x10x2, нужно построить граничные прямые и области решений каждого неравенства системы; пересечение областей решения этих неравенств, взятое в первом квадранте и будет областью решений данной задачи.
II. Нахождение ОДР оптимального решения задачи.
Рассмотрим уравнение (3) При конкретном значении f это уравнение определяет на плоскости прямую линию. При изменении f мы получим семейство параллельных прямых (прямые ||, т.к. они все имеют один угловой коэффициент ). Каждую из этих прямых называют линией уравнения, т.к. согласно равенству (3) на каждой такой прямой функция f сохраняет постоянное значение.
– это вектор, перпендикулярный линиям уровня, и он показывает направление, по которому нужно перемещать линию уровня, чтобы значение f возрастало. Обозначим
Линия уровня, имеющая общие точки с ОДР и расположенная так, что ОДР целиком находится в одной из полуплоскостей, на которые данная линия уровня делит координатную плоскость, называется опорной прямой.
Чтобы найти ОДР оптимального решения, выполним:
1. Строим в начале координат.
2. Перпендикулярно проводим одну из линий уровня, имеющую общие точки с ОДР.
3. Перемещая эту линию уровня в направлении в задаче на max или в противоположном направлении в задаче на min, находим опорную прямую.
4. Совместно решив уравнения прямых, ограничивающих ОДР и имеющих общие точки с опорной прямой, найдем оптимальное решение. В зависимости от вида ОДР и целевой функции задача может иметь единственное решение, бесконечное множество решений, или не иметь решений ввиду несовместности системы ограничений или неограниченности целевой функции ОДР.

Решим совместно уравнения прямых BC и DC, и имеющих общую точку с опорной прямой, найдём оптимальное решение.
§5. Преобразование однократного замещения.
Пусть дана система линейных уравнений
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Папиллярные узоры пальцев рук – маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.


Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Читайте также:
- Структура потребностей их иерархия кратко
- Зарождение жизни в горячей воде кратко
- Пути обогащения словарного состава языка кратко
- Возрастной состав влияние на трудовые ресурсы кратко
- Проблемы европейской интеграции углубление и расширение ес кратко
