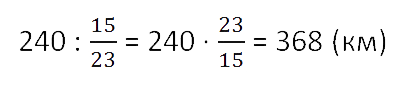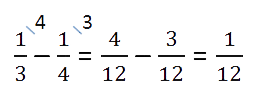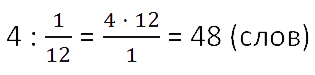Как найти искомое число в математике

В этом уроке мы научимся, зная дробь от числа, находить все число.

Также мы узнаем, как делать аналогичные действия для процентов, то есть по данному количеству процентов находить все число.

Потом применим полученные навыки для решения задач.

Сформулируем, в чем состоит задача нахождения числа по его дроби.

Имеется дробь; она говорит о том, какая часть от числа нам дана.

Имеется число, равное данной дробной части от искомого числа.

Мы уже умеем находить дробь от числа. Вспомним как это делать.

Чтобы найти дробь от числа нам нужно исходное число умножить на эту дробь, тогда получится какое-то значение, обозначающее дробь от числа.

В этой задаче было известно все число и то, какую дробную часть от него необходимо получить. Дробь от числа оставалась неизвестной.

В задаче этого урока дробь от числа нам уже известна, а все число, напротив, только предстоит найти.

Для его нахождения можно составить уравнение, аналогичное тому, которое было на картинке выше. Отличие будет только в том, какие переменные нам известны.

Решая это уравнение, вы переносите известный нам множитель, то есть дробь, в правую часть.

Как делить на дробь мы изучили в прошлом уроке. Напомним, что для этого надо домножить на взаимно обратное число к этой дроби.

Итак, вы получили выражение для неизвестного числа.

Сформулируем правило: чтобы найти дробь от числа необходимо разделить известную часть числа на дробь.

Пример 1

(mathbf{frac{3}{4}}) от числа равны 21-му, найдите исходное число.

Для решения необходимо разделить известную часть на дробь, то есть 21 разделить на (mathbf{frac{3}{4}})

(mathbf{21divfrac{3}{4}=21cdotfrac{4}{3}=frac{21cdot4}{3}=frac{7cdot4}{1}=28})

Пример 2

(mathbf{frac{2}{7}}) от числа равны 12, найдите исходное число.

Для решения надо разделить данную часть числа на данную дробь, то есть 12 разделить на (mathbf{frac{2}{7}})

(mathbf{12divfrac{2}{7}=12cdotfrac{7}{2}=frac{12cdot7}{2}=frac{6cdot7}{1}=42})

Пример 3

Далеко не всегда часть числа делится на числитель данной дроби; в таких случаях мы будем получать в ответе не целые числа, а дроби или смешанные числа.

(mathbf{frac{2}{3}}) от числа равны 11, найдите исходное число.

Во всем остальном решение ничем не будет отличаться- также разделим дробь от числа, равную (mathbf{frac{2}{3}}), на величину дроби, равную 11 и получим результат.

(mathbf{11divfrac{2}{3}=11cdotfrac{3}{2}=frac{11cdot3}{2}=frac{33}{2}=16frac{1}{2}})

Для получения ответа нам понадобилось выделить целую часть.

 Важен еще один случай.

Никто не гарантирует, что данная нам часть числа сама по себе не будет являться дробью.

Такого случая не стоит пугаться, а стоит придерживаться алгоритма, а именно делить часть числа на то, какой дробью она является.

Пример 4

(mathbf{frac{5}{6}}) от числа равны (mathbf{frac{2}{3}}), найдите все число.

Для решения этого примера разделим (mathbf{frac{2}{3}})- часть числа, на (mathbf{frac{5}{6}})- дробь.

(mathbf{frac{2}{3}divfrac{5}{6}=frac{2}{3}cdotfrac{6}{5}=frac{2cdot6}{3cdot5}=frac{2cdot2}{5}=frac{4}{5}})

Все исходное число равняется (mathbf{frac{4}{5}})

Теперь представим, что дан какой-то определенный процент от числа и необходимо найти, от какого числа брали процент.

Вспомним, что процент- это способ записи десятичной дроби.

То есть, чтобы из процента получить десятичную дробь, которую он обозначает, надо величину процента разделить на 100.

Поэтому для решения такого рода задач надо преобразовать процент в десятичную дробь, а дальше сделать все то же самое: разделить число на эту дробь.

Пример 1

Известно, что зарплата работника увеличилась на 2 000 рублей или на 25 процентов. Какая зарплата у работника была изначально?

Решение:

Переведем проценты в дроби: (mathbf{25%=25div100=0.25})

Разделим число на дробь: (mathbf{2000div0.25=8000})

Ответ: изначально зарплата работника была 8000 рублей.

Сформулируем правило.

Чтобы найти число по проценту от него, надо перевести процент в десятичную дробь, а после разделить данную часть числа на полученную дробь.

Пример 2

Сказано, что 9% от числа равны 81. Необходимо найти все число.

Решение:

Первым действием переводим проценты в десятичную дробь.

(mathbf{9%=9div100=0.09})

Вторым действием делим данное число на эту дробь.

(mathbf{81div0.09=900})

Ответ: искомое число 900

Задачи, в которых фигурируют дроби от числа часто встречаются не только в школьных учебниках и задачниках, но и в реальной жизни, поэтому стоит уделить им особое внимание.

Сначала разберем некоторые из таких задач вместе, а дальше вы попробуете свои силы в самостоятельном решении задач.

Часть задач тривиальна, иными словами, их решение очевидно, достаточно лишь увидеть в них формулу, подставить в нее данные значения и получить результат.

Пример:

Айсберг возвышается над водой на (mathbf{frac{1}{11}}) своей высоты.

Капитан корабля заметил, что от воды до макушки айсберга по вертикали 16 метров.

Какова общая высота айсберга?

Решение:

В данном случае мы сразу можем сказать, что все число- это общая высота айсберга, дробь от числа- 16 (метров), а величина дроби- (mathbf{frac{1}{11}}).

Соответственно, по правилу, для получения ответа мы делим 16 на (mathbf{frac{1}{11}}) и получаем результат.

(mathbf{16divfrac{1}{11}=16cdot11=176}) (метр)- общая высота айсберга

Ответ: 176 (метров).

Некоторые задачи для своего решения требуют более глубокого анализа.

Пример:

Магазин продал (mathbf{frac{2}{3}}) пар новых кроссовок специальной партии, после чего на складе осталось 56 пар.

Какого размера была специальная партия?

Решение:

В данной задаче, если не вчитываться в условие, интуитивно хочется просто поделить 56 на (mathbf{frac{2}{3}}) и получить ответ, но ответ не будет правильным.

Если посмотреть внимательно, то 56 пар соответствуют оставшейся части партии, в то время как дробь (mathbf{frac{2}{3}}) описывает проданную часть.

Но мы пока не знаем общего количества пар и не можем сказать, какому числу соответствует (mathbf{frac{2}{3}})

Зато мы можем вычислить размер оставшейся части.

Если вся партия – это 1, и продано (mathbf{frac{2}{3}}), значит осталась (mathbf{frac{1}{3}}) товара.

Эта дробь соответствует 56 оставшимся парам.

Дальнейшие действия аналогичны рассмотренным в предыдущей задаче.

Теперь оформим решение:

1) (mathbf{1-frac{2}{3}=frac{1}{3}}) составляет оставшаяся часть от всего размера партии

2) (mathbf{56divfrac{1}{3}=56cdot3=168}) (пар) кроссовок всего было в партии

Ответ: 168 (пар).

Вам могут встретиться задачи и с более сложными условиями, все их разобрать невозможно, но главное:

• не давать себя запутать
• расписать, какой части какая дробь и какое число соответствует
• понять, где данных достаточно, чтобы узнать что- то новое
• и так постепенно продвигаться к ответу

Задачи математики часто диктуются другими науками, в том числе экономикой.

Существуют поднауки других наук, связанные с математикой. Примерами таких могут служить математическая физика, изучающая, как следует из названия, физические модели, а также математическая экономика, о которой мы вам сейчас расскажем.

Предметом изучения этой теории является математическое описание экономических объектов, явлений и процессов.

В самом деле, интересно применить мощнейший математический аппарат к таким насущным вопросам, как изменение цен и доходов, изменение предпочтений покупателей и пр.

Истоки математической экономики идут с XVII века. Тогда преподаватели германских университетов начали использовать новый стиль преподавания, который включал в себя статистику. Там, где появляется статистика, то есть множество чисел, появляется и математика, которая выявляет какие-то закономерности.

К примеру, расчет среднего дохода крестьян не является сложной задачей и сводится к вычислению среднего арифметического, но тоже является задачей математики.

В это же время группа английских ученых создала метод «численной аргументации государственной политики», который затрагивал темы налогов, сборов, таможенных пошлин, и прочие экономические процессы, в которых участвует государство.

К XIX веку появляется и развивается классическая школа политической экономики, чьим лицом принято считать Адама Смита.

Именно в этот период математика начала активно применяться в экономике.

В дальнейшем все большее количество математических инструментов переходило в экономику, а в наши дни на нее трудятся еще и информационные технологии.

Так что в наши дни великим экономистом может быть не тот, кто изначально учился на экономиста, а успешный математик или программист.