Сейчас меня будут закидывать тапками и тряпками, но всё, что я напишу здесь, более физично и научно, чем вся школьная физика в том виде, в котором её пихают на уроках (пример в конце)
Как это работает в теории
В задаче (расчетной) обычно просят написать в ответе значение какой-то величины. Узнать это значение можно только измерениями – прямыми или косвенными. Как правило, прямые измерения невозможны, поэтому для решения задачи требуется использовать формулы.
Физические формулы из себя представляют связь между физическими величинами через арифметические действия (+-*/…) и отношения порядка (><=) (более подробно в моей статье)
Значит, нам надо найти те формулы, которые устанавливают связь искомой величины с данными.
Тут есть две трудности.
Первая трудность: может не оказаться формулы, которая напрямую связывает искомую величину с данными (уже измеренными). Решается эта проблема “легко” – из всех формул выбираются формулы, которые содержат искомую величину, потом выбираются формулы, которые содержат другие “неизвестные” величины, входящие в первый круг формул, и так далее. Путь длинный, но гарантированно верный.
Есть ещё более “лёгкий” вариант решения этой проблемы: для нахождения каждой величины в каждой ситуации (по всем возможным наборам известных величин) выводится (читай – смотрится в интернете) персональная формула и запоминается.
Вторая трудность: Каждая формула работает только в определённых явлениях, и, например, формулу v=s/t нет смысла применять в явлении равноускоренного движения: числа-то мы туда подставим, вычисления произведём, но результат будет просто числом, никак не связанным с реальностью. Для решения этой проблемы надо определять явления, и выбирать только те формулы, которые подходят под данное явление.
Итак. Схема решения любой физической задачи вырисовывается такая:
1. Определить явления и объекты, которые в этих явлениях участвуют.
2. Определить все величины, характерные для этих объектов в этих явлениях
3. Выбрать все модельные связи и определения величин (формулы), которые совместимы с этими объектами и явлениями, и в которые входят величины (возможно, рекурсивно).
4. Решить задачу. Профит.
Пункт 4 “Решить задачу” сам по себе выглядит довольно дерзко. Расшифровывается он так: во все формулы подставляем числовые значения величин (возможно, придётся использовать одну и ту же формулу несколько раз). В общем случае, получается недоопределённая система уравнений (в которых неизвестных куда больше, чем уравнений). Но задача задана всегда таким образом, чтобы система имела частичное решение (то есть, можно определить не все, а только лишь некоторые величины). В “простых” задачах, система оказывается определённой, в которой есть единственное решение (два, в случае квадратных уравнений).
И вот пример применения этого на практике.
Задача
От станции равноускоренно тронулся поезд и, пройдя путь 500 м, достиг скорости 20 м/с. Определите ускорение поезда.
Решение
Шаг 1. Определяем явления. Оно тут одно – равноускоренное движение. Объект тоже один – поезд.
Шаг 2. Для равноускоренного движения и поезда, принятого за материальную точку, можно выбрать величины и серии величин:
[Мгновенная скорость в каждое мгновение задачи], ускорение, [координата в каждое мгновение задачи], пройденный путь, [текущее время в каждое мгновение задачи], затраченное время, средняя скорость (а почему бы и нет?), и так далее. Это не полный список величин, его можно дополнять и, возможно, нам это потребуется (а искомую я подчеркнул)
Шаг 3. Формулы.
Для этих величин подойдут три формулы:
1. Определение ускорения,
2. определение средней скорости,
3. закон движения при равноускоренном движении;
(формулы только для 9 класса возьмём, так как задача из задачника 9 класса)
*Обратите внимание, что в первой формуле “t” обозначает промежуток времени и вообще-то должно писаться через “Δt”, Во второй это затраченное время, а в последней – текущее, которое показывает секундомер. Буква одна, величины – разные.
Шаг 4. Подставляем числа.
Есть кое-какие правила подстановки чисел в формулы в физике, ибо это вам не математика.
Во-первых, все числа должны быть в одной системе единиц (сделано).
Во-вторых, в одну формулу можно подставлять только числа, соответствующие одному и тому же процессу или моменту времени, а так же одному и тому же объекту или системе объектов.
В-третьих, мы вольны выбирать моменты времени так, как пожелаем, но лучше всего брать те, для которых мы хотя бы одно число можем узнать.
Вот мы и возьмём два момента времени – (1) при старите, когда на секундомере число “00:00”, и (2) когда поезд доехал до отметки 500 м.
*Обратите внимание, что хоть “t” и обозначает разные величины, но их значения будут одинаковыми, так как во втором выбранном моменте время на секундомере в точности совпадает со временем, затраченным на весь путь, а в первом – 0.
Система уравнений решается отлично любым способом. Можно загнать её в вольфрам или маткад, можно попытаться все три неизвестных подобрать. В школьной математике рекомендуют метод подстановки.
По-хорошему, никто не регламентирует метод решения математической задачи (а это уже математическая), важно, что в результате мы найдём числовое значение величины ускорение, которое и надо найти. А если для нахождения этого числа можно решить только одно уравнение, то вообще круто.
А теперь прочитаем требования к развёрнутому ответу на вторую часть ЕГЭ по физике.
(допускается решение «по частям» с промежуточными вычислениями);
Это я написал для тех, кто считает, что решать задачи нужно с обязательным выводом формулы и подстановкой уже в неё.
И да – составление системы с числами считается “по частям”
Перейдем к рассмотрению тестового задания ОГЭ по математике – задания №12. В данном задании нам необходимо поработать с формулами – либо просто подставить значения в формулу и провести вычисления, либо вначале выразить неизвестную величину, а затем произвести подстановку.
Задание 12OM21R
Площадь четырехугольника можно вычислить по формуле S=d1d2sina2, где d1 и d2 длины диагоналей четырехугольника, а – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2=16, sin a=25, a S=12,8
Для выполнения данного задания надо подставить все известные данные в формулу:
12,8=d1×16×252
В правой части можно сократить 16 и 2 на 2: 12,8=d1×8×251
Теперь умножим 8 на дробь 25, получим 3,2: 12,8=d1×3,2
Найдем неизвестный множитель, разделив 12,8 на 3,2: d1=12,8:3,2=4
Ответ: 4
pазбирался: Даниил Романович | обсудить разбор
Задание OM1406o
Площадь четырёхугольника можно вычислить по формуле:
где d1 и d2 – длины диагоналей четырёхугольника, α – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если d1=13, sinα=3/13, а S=25,5.
Так как искомая величина является в формуле частью выражения справа, то ее необходимо выразить через остальные величины. Тогда получим:
В полученную формулу подставим числовые данные из условия и вычислим искомую диагональ:
Ответ: 17
pазбирался: Даниил Романович | обсудить разбор
Задание OM1405o
Закон Кулона описывает взаимодействие между двумя электрическими зарядами. Закон можно записать в виде
где F – сила взаимодействия в ньютонах, q1 и q2 – величины зарядов в кулонах, k – коэффициент пропорциональности в Н·м2/Кл2, а r – расстояние между зарядами в метрах. Пользуясь формулой, найдите величину заряда q1 (в кулонах), если k=9·109 Н·м2/Кл2, q2=0,004 Кл, r=600 м, F=0,4 Н.
Поскольку искомая величина стоит в формуле справа и не является результирующей), необходимо преобразовать эту формулу. Результатом преобразования в данном случае должно стать уравнение, в котором слева будет зафиксировано искомое q1, а справа – все остальные величины, фигурирующие в начальной формуле.
Для удобства преобразования сначала поменяем местами левую и правую части начальной формулы:
Далее r2 из знаменателя слева переносим в числитель справа, а k и q2 из числителя слева – в знаменатель справа. Получим:
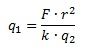
Результат мы получим в кулонах, как и требуется по условию. Основание для этого утверждения таково: т.к. все величины в условии даны в единицах СИ, то и результат будет получен только в СИ, а в этой системе единицей измерения эл.заряда является кулон (Кл).
Подставим в полученную формулу числовые данные из условия и вычислим искомую величину:
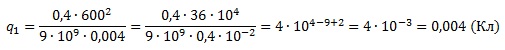Ответ: 0,004
pазбирался: Даниил Романович | обсудить разбор
Задание OM1404o
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой
tF = 1,8 • tC + 32,
где tC — температура в градусах Цельсия, tF — температура в градусах Фаренгейта.
Какая температура по шкале Фаренгейта соответствует -25° по шкале Цельсия?
Подставляем значение -25 в формулу:
tF = 1,8 • (-25) + 32 = -45 + 32 = -13
Ответ: -13
pазбирался: Даниил Романович | обсудить разбор
Задание OM1403o
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле:
T = 2 • √l
где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
Выразим из формулы l, для этого возведем обе части в квадрат, получим:
T ² = 4 • l ,
тогда:
l = T ² / 4
Подставляя значения из условия, получаем:
l = 3 ² / 4 = 9 / 4 = 2,25
Ответ: 2,25
pазбирался: Даниил Романович | обсудить разбор
Задание OM1402o
В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле:
С = 6000 + 4100•n,
где n — число колец, установленных в колодце.
Пользуясь этой формулой, рассчитайте стоимость колодца из 7 колец. Ответ укажите в рублях.
В данном случае выражать из формулы нам ничего не требуется, поэтому подставим в данную формулу значение n = 7:
С = 6000 + 4100•7 = 6000 + 28700 = 34700
Ответ: 34700
pазбирался: Даниил Романович | обсудить разбор
Задание OM1401o
Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 224 Вт, а сила тока равна 4 А.
Выразим сопротивление R:
R = P / I2
Подставим значения в полученную формулу:
R = 224 / 42 = 224 / 16 = 14 ом
Ответ: 14
pазбирался: Даниил Романович | обсудить разбор
Выведение переменной из формулы
Данную статью я начну с общего алгоритма выражения переменной, а затем уже будем разбираться на конкретных примерах.
Пусть дана какая-то формула…
1) Если она содержит скобки, то раскрываем их и приводим подобные слагаемые;
2) Если есть знаменатель, то избавляемся от него, умножив обе части формулы на этот знаменатель (если знаменателей несколько, то умножаем обе части равенства на общий знаменатель);
3) Если есть корни, то обе части возводим в степень, равную показателю корня;
4) Переносим все члены с нужной нам переменной в одну сторону;
5) Если таких членов несколько, то выносим нужную нам переменную за скобку в качестве общего множителя. Если нет, то этот шаг пропускаем.
6) Делим обе части формулы на все сомножители нужной нам переменной.
7) Если нужная переменная возведена в n-ую степень, то нужно из обеих частей формулы извлечь корень n-ой степени.
На самом деле, всё не так ужасно) На ОГЭ так вообще простые задания.
Вот парочка примеров.
1) Центростремительное ускорение при движении по окружности вычисляется по формуле a=ω2R, где ω – угловая скорость, R – радиус окружности. Выразим из этой формулы R и ω.
Выразим радиус R, разделив обе части на его сомножитель ω2:
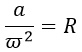
Но обычно пишут так, чтобы искомая переменная была слева:
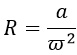
Теперь выразим угловую скорость. Разделим обе части равенства на сомножитель угловой скорости (на R, короче говоря):
Получается вот такая запись:
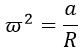
Нужная нам угловая скорость возведена в квадрат. Избавиться от степени нам поможет квадратный корень:
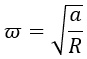
Теперь возьмем формулу с дробью.
2) Площадь четырехугольника можно вычислить по формуле
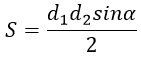
Выразим из нее d1.
Избавляемся от знаменателя, умножив обе части равенства на 2 (т.к. знаменатель равен двум).
Получим:
Чтобы выразить d1 разделим обе части на сомножители d2 и sinα.
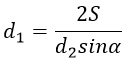
Точно также выражаются d2 и sinα. Можешь даже самостоятельно попробовать.
Еще один пример. Последний.
3) Дана формула
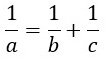
Выразим из нее переменную b.
Формула содержит дроби, поэтому надо избавится от знаменателей. Умножим обе части равенства на общий знаменатель abc.
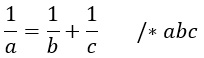
Получится такое выражение:
Перенесем все члены равенства, содержащие переменную b в левую часть.
Вынесем b за скобки как общий множитель.
Разделим обе части равенства на (с – а).
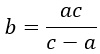
Что-то не выражается? Напиши мне свой пример. Используй функцию “Предложить новость”.
https://vk.com/mymaths
Физика
В каждой задаче по физике требуется из формулы выразить неизвестную, следующим шагом подставить численные значения и получить ответ. Лучше не решать физическую задачу по шагам: найти из одной формулы значение физической величины, затем подставлять ее во вторую формулу. Почему? Во-первых, получается неточный результат в вычислениях после многократного округления. Во-вторых, многие задачи нет возможности решить таким путем, из-за того, что нет значения некоторой физической величины. Но тупик часто заключается в том, что если бы мы подставляли в буквенном виде одну формулу в другую, то та неизвестная физическая величина сократилась бы. Поэтому учимся на примерах выражать из формулы необходимую физическую величину. Главное правило: букву, которую необходимо выразить, представляем в уме за x, остальные буквы представляем известными значениями. В этом случае получим совершенно обычное математическое уравнение.
Выведение переменной из формулы
Данную статью я начну с общего алгоритма выражения переменной, а затем уже будем разбираться на конкретных примерах.
Пусть дана какая-то формула.
1) Если она содержит скобки, то раскрываем их и приводим подобные слагаемые;
2) Если есть знаменатель, то избавляемся от него, умножив обе части формулы на этот знаменатель (если знаменателей несколько, то умножаем обе части равенства на общий знаменатель);
3) Если есть корни, то обе части возводим в степень, равную показателю корня;
4) Переносим все члены с нужной нам переменной в одну сторону;
5) Если таких членов несколько, то выносим нужную нам переменную за скобку в качестве общего множителя. Если нет, то этот шаг пропускаем.
6) Делим обе части формулы на все сомножители нужной нам переменной.
7) Если нужная переменная возведена в n-ую степень, то нужно из обеих частей формулы извлечь корень n-ой степени.
На самом деле, всё не так ужасно) На ОГЭ так вообще простые задания.
Вот парочка примеров.
1) Центростремительное ускорение при движении по окружности вычисляется по формуле a=ω 2 R, где ω — угловая скорость, R — радиус окружности. Выразим из этой формулы R и ω.
Выразим радиус R, разделив обе части на его сомножитель ω 2 :
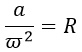
Но обычно пишут так, чтобы искомая переменная была слева:
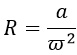
Теперь выразим угловую скорость. Разделим обе части равенства на сомножитель угловой скорости (на R, короче говоря):
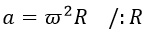
Получается вот такая запись:
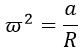
Нужная нам угловая скорость возведена в квадрат. Избавиться от степени нам поможет квадратный корень:
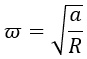
Теперь возьмем формулу с дробью.
2) Площадь четырехугольника можно вычислить по формуле
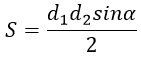
Выразим из нее d1.
Избавляемся от знаменателя, умножив обе части равенства на 2 (т.к. знаменатель равен двум).
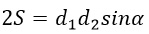
Чтобы выразить d1 разделим обе части на сомножители d2 и sinα.
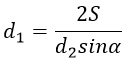
Точно также выражаются d2 и sinα. Можешь даже самостоятельно попробовать.
Еще один пример. Последний.
3) Дана формула
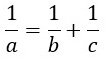
Выразим из нее переменную b.
Формула содержит дроби, поэтому надо избавится от знаменателей. Умножим обе части равенства на общий знаменатель abc.
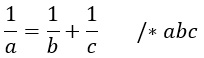
Получится такое выражение:
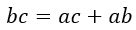
Перенесем все члены равенства, содержащие переменную b в левую часть.
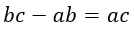
Вынесем b за скобки как общий множитель.
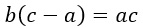
Разделим обе части равенства на (с — а).
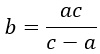
Что-то не выражается? Напиши мне свой пример. Используй функцию “Предложить новость”.
Правила вывода величины из формулы (7-11 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Правила вывода величины из формулы
Формула – это правило вычисления одной величины через другие, записанное при помощи их буквенных обозначений.
Иногда для решения задач необходимо вывести неизвестную величину из формулы. Для этого существуют несколько правил.
Формулы можно преобразовывать по правилам математики. Рассмотрим примеры. В левой колонке таблицы вы видите исходные формулы. В средней колонке каждая из формул преобразована так, что «выражена» величина, обозначенная « b ». В последней колонке выражена величина « с »
Примеры вывода физической величины из формулы
Курс повышения квалификации
Педагогические основы деятельности учителя общеобразовательного учреждения в условиях ФГОС
Курс повышения квалификации
Анализ урока как инструмент развития профессиональных компетенций учителя в соответствии с требованиями ФГОС
- Сейчас обучается 26 человек из 16 регионов
Курс повышения квалификации
Теория и методика преподавания предмета «Астрономия» в условиях реализации ФГОС СОО
- Сейчас обучается 67 человек из 35 регионов
«Домашнее обучение. Лайфхаки для родителей»
- подготовка к ЕГЭ/ОГЭ и ВПР
- по всем предметам 1-11 классов
«Такие разные дети: преимущества тьюторской позиции учителя»
Свидетельство и скидка на обучение каждому участнику
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 909 890 материалов в базе
«Интеграция современного искусства в детское творчество»
Свидетельство и скидка на обучение
каждому участнику
Ищем педагогов в команду «Инфоурок»
- ЗП до 91 000 руб.
- Гибкий график
- Удаленная работа
Другие материалы
- Физика
- 7 класс
- Тесты
- Учебник: «Физика», Перышкин А.В.
- 02.05.2018
- 482
- 0
- Физика
- 7 класс
- Другие методич. материалы
- Учебник: «Физика», Перышкин А.В.
- 02.05.2018
- 8598
- 28
- Физика
- 10 класс
- Презентации
- Учебник: «Физика. Базовый и профильный уровни», Тихомирова С.А., Яворский Б.М.
- Тема: Глава 1. Кинематика
- 02.05.2018
- 3214
- 47
- Физика
- 7 класс
- Тесты
- Учебник: «Физика», Перышкин А.В.
- Тема: Глава 3. Давление твёрдых тел, жидкостей и газов
- 02.05.2018
- 13283
- 149
- Физика
- 9 класс
- Другие методич. материалы
- Учебник: «Физика», Перышкин А.В., Гутник Е.М.
- Тема: § 13 Свободное падение тел
- 02.05.2018
- 340
- 0
- Физика
- 7 класс
- Презентации
- Учебник: «Физика», Перышкин А.В.
- Тема: §55 Механическая работа. Единицы работы
- 02.05.2018
- 258
- 1
- Физика
- 10 класс
- Презентации
- Учебник: «Физика. Базовый и профильный уровни», Тихомирова С.А., Яворский Б.М.
- Тема: § 19. Сила трения
- 02.05.2018
- 2054
- 25
- Физика
- 8 класс
- Конспекты
- Учебник: «Физика», Перышкин А.В.
- Тема: Приложение к Главе 1
- 02.05.2018
- 443
- 0
«Практический подход в работе с утратой смысла жизни: логотерапия»
Свидетельство и скидка на обучение каждому участнику
Вам будут интересны эти курсы:
- Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
- Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
- Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
- Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»
- Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
- Курс повышения квалификации «Организация маркетинга в туризме»
- Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
- Курс повышения квалификации «Психодинамический подход в консультировании»
- Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
- Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»
- Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»
- Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
- Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
- 02.05.2018 2588
- DOCX 186.2 кбайт
- Оцените материал:
Настоящий материал опубликован пользователем Абдуллаева Гульбахор Уришовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 8 месяцев
- Подписчики: 9
- Всего просмотров: 1158579
- Всего материалов: 1214
40%
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
60 минут
«Политическая карта как объект изучения в школьном курсе географии. Объекты и субъекты, уникальные характеристики, динамизм и изменчивость политической карты»
25 минут
«Мозаичный декор из цветного стекла»
64 минуты
«Развитие коммуникативных способностей школьников на уроках и во внеурочной деятельности»
Подарочные сертификаты
- Курсы «Инфоурок»
- Онлайн-занятия с репетиторами на IU.RU
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Правила вывода величины из формулы
Формула – это правило вычисления одной величины через другие, записанное при помощи их буквенных обозначений.
Иногда для решения задач необходимо вывести неизвестную величину из формулы. Для этого существуют несколько правил.
Формулы можно преобразовывать по правилам математики. Рассмотрим примеры. В левой колонке таблицы вы видите исходные формулы. В средней колонке каждая из формул преобразована так, что «выражена» величина, обозначенная «b». В последней колонке выражена величина «с» 
Примеры вывода физической величины из формулы
