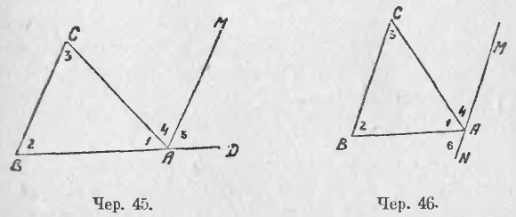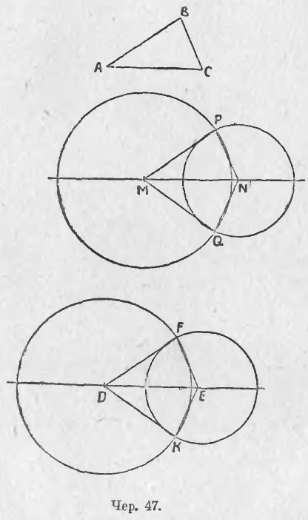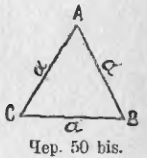Как определить искомый треугольник
Задачи на экстремум в планиметрии
Трейдинг криптовалют на полном автомате по криптосигналам. Сигналы из первых рук от мощного торгового робота и команды из реальных профессиональных трейдеров с опытом трейдинга более 7 лет. Удобная система мгновенных уведомлений о новых сигналах в Телеграмм. Сопровождение сделок и индивидуальная помощь каждому. Сигналы просты для понимания как для начинающих, так и для опытных трейдеров. Акция. Посетителям нашего сайта первый месяц абсолютно бесплатно .
Отсюда следует, что искомый треугольник — это треугольник с вершинами в основаниях высот данного, т.е. ортотреугольник данного треугольника. Действительно, пусть AA», BB» и CC» — высоты треугольника ABC, а точки A1, B1 и C1 расположены на сторонах соответственно BC, AC и AB. Если треугольник A1B1C1 не совпадает с треугольником A»B»C», то по ранее доказанному
P A1B1C1 PA»B1C1 PA»PQ,
где P и Q — точки пересечения прямой MN со сторонами соответственно AB и AC треугольника ABC. При этом хотя бы один из знаков неравенства — строгий. Значит, искомый треугольник минимального периметра — это треугольник A»PQ. Если бы точка P не совпадала с точкой C», то, повторив предыдущие рассуждения, построили бы треугольник, площадь которого меньше площади треугольника A»PQ, что невозможно. Аналогично для точки Q. Таким образом, точка P совпадает с C», а точка Q — с точкой B».
1. Изложенное решение основано на доказательстве Фейера (L.Fejer). Это, а также другие изящные доказательства данного утверждения (Г.А.Шварц, Л.Шрутка, Бюкнер) см. в книге Г.Радемахера и О.Теплица «Числа и фигуры» (М.,1962, с.36-46).
2. Другой способ доказательства того, что точки P и Q пересечения прямой MN со сторонами соответственно AB и AC также будут основаниями высот треугольника ABC.
Поскольку AM = AA» = AN, то точки M, A» и N лежат на окружности с центром A и радиусом AA». Тогда
A»NP = A»AP
(вписанный угол равен половине соответствующего центрального). Поэтому из точек A и N отрезок A»P виден под одним и тем же углом. Значит, точки A, P, A», N лежат на одной окружности.
С другой стороны, треугольники AA»C и ANC симметричны относительно прямой AC, поэтому они равны. Значит, из точек A» и N отрезок AC виден под прямым углом, поэтому эти точки лежат на окружности с диаметром AC. Поскольку через три точки, не лежащие на одной прямой, проходит ровно одна окружность, то все пять точек A, P, A», C и N лежат на окружности с диаметром AC. Тогда из точки P диаметр AC виден под прямым углом, т.е. CP — высота треугольника ABC. Аналогично докажем, что BQ — также высота треугольника ABC.
В этой курсовой работе я изучила некоторые теоремы, позволяющие решать задачи на экстремумы, проиллюстрировала их применение.
В заключение этой работы, на мой взгляд, следует провести однозначную черту под бесспорным фактом целесообразности и полезности применения ряда задач элементарной геометрии на построение некоторых фигур таким образом, чтобы один из параметров получил наибольшее или наименьшее значение. Во многих случаях решение можно получить без применения методов математического анализа.
1. С.И. Зетель, «Задачи на максимум и минимум», Москва
2. С.А. Теляковский, «Алгебра», Москва, 2001г.
3. Ю.Н. Макарычев, «Математика», Москва, 1988г.
4. Г.С.М. Коксетер, С.П. Грейтцер, «Новые встречи с геометрией», 1978г.
Как определить вид треугольника
Онлайн калькулятор поможет узнать по сторонам, является ли треугольник прямоугольным, равнобедренным, равносторонним или разносторонним.
Как определить, что треугольник прямоугольный: по Теорема Пифагора — сумма квадратов длин катетов равна квадрату длины гипотенузы c 2 = a 2 + b 2
Как определить, что треугольник равнобедренный: один из признаков равнобедренного треугольника — две стороны равны.
Как определить, что треугольник равносторонний: все стороны равны.
Принято выделять три типа треугольников:
тупоугольные — один из углов более 90 градусов,
прямоугольные — один из угол равен 90 градусов,
остроугольные — все углы менее 90 градусов.
Это классификация по типу углов.
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).
Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:
Далее, из формулы
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.
Решение. Иcпользуя теорму косинусов найдем сторону c:
Из формулы (3) найдем cosA:
Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.
Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
Задачи на экстремум в планиметрии
Трейдинг криптовалют на полном автомате по криптосигналам. Сигналы из первых рук от мощного торгового робота и команды из реальных профессиональных трейдеров с опытом трейдинга более 7 лет. Удобная система мгновенных уведомлений о новых сигналах в Телеграмм. Сопровождение сделок и индивидуальная помощь каждому. Сигналы просты для понимания как для начинающих, так и для опытных трейдеров. Акция. Посетителям нашего сайта первый месяц абсолютно бесплатно .
Отсюда следует, что искомый треугольник — это треугольник с вершинами в основаниях высот данного, т.е. ортотреугольник данного треугольника. Действительно, пусть AA”, BB” и CC” — высоты треугольника ABC, а точки A1, B1 и C1 расположены на сторонах соответственно BC, AC и AB. Если треугольник A1B1C1 не совпадает с треугольником A”B”C”, то по ранее доказанному
P A1B1C1 PA”B1C1 PA”PQ,
где P и Q — точки пересечения прямой MN со сторонами соответственно AB и AC треугольника ABC. При этом хотя бы один из знаков неравенства — строгий. Значит, искомый треугольник минимального периметра — это треугольник A”PQ. Если бы точка P не совпадала с точкой C”, то, повторив предыдущие рассуждения, построили бы треугольник, площадь которого меньше площади треугольника A”PQ, что невозможно. Аналогично для точки Q. Таким образом, точка P совпадает с C”, а точка Q — с точкой B”.
1. Изложенное решение основано на доказательстве Фейера (L.Fejer). Это, а также другие изящные доказательства данного утверждения (Г.А.Шварц, Л.Шрутка, Бюкнер) см. в книге Г.Радемахера и О.Теплица “Числа и фигуры” (М.,1962, с.36-46).
2. Другой способ доказательства того, что точки P и Q пересечения прямой MN со сторонами соответственно AB и AC также будут основаниями высот треугольника ABC.
Поскольку AM = AA” = AN, то точки M, A” и N лежат на окружности с центром A и радиусом AA”. Тогда
A”NP = A”AP
(вписанный угол равен половине соответствующего центрального). Поэтому из точек A и N отрезок A”P виден под одним и тем же углом. Значит, точки A, P, A”, N лежат на одной окружности.
С другой стороны, треугольники AA”C и ANC симметричны относительно прямой AC, поэтому они равны. Значит, из точек A” и N отрезок AC виден под прямым углом, поэтому эти точки лежат на окружности с диаметром AC. Поскольку через три точки, не лежащие на одной прямой, проходит ровно одна окружность, то все пять точек A, P, A”, C и N лежат на окружности с диаметром AC. Тогда из точки P диаметр AC виден под прямым углом, т.е. CP — высота треугольника ABC. Аналогично докажем, что BQ — также высота треугольника ABC.
В этой курсовой работе я изучила некоторые теоремы, позволяющие решать задачи на экстремумы, проиллюстрировала их применение.
В заключение этой работы, на мой взгляд, следует провести однозначную черту под бесспорным фактом целесообразности и полезности применения ряда задач элементарной геометрии на построение некоторых фигур таким образом, чтобы один из параметров получил наибольшее или наименьшее значение. Во многих случаях решение можно получить без применения методов математического анализа.
1. С.И. Зетель, «Задачи на максимум и минимум», Москва
2. С.А. Теляковский, «Алгебра», Москва, 2001г.
3. Ю.Н. Макарычев, «Математика», Москва, 1988г.
4. Г.С.М. Коксетер, С.П. Грейтцер, «Новые встречи с геометрией», 1978г.
Определить возможность существования треугольника по сторонам
Задача
Треугольник существует только тогда, когда сумма любых двух его сторон больше третьей.
Дано: a , b , c – стороны предполагаемого треугольника.
Требуется сравнить длину каждого отрезка-стороны с суммой двух других. Если хотя бы в одном случае отрезок окажется больше суммы двух других, то треугольника с такими сторонами не существует.
Решение
Ниже приведены решения задачи на языке программирования Паскаль двумя способами. В первом случае все стороны проверяются в одном операторе if; во втором случае каждое условие проверяется отдельно, а программа содержит вложенные операторы if-else.
Программа 1 (предпочтительный способ решения):
В языке Паскаль логический оператор and имеет приоритет над операторам >, if проверяется, что каждая из сторон меньше суммы других. Если хотя бы одна будет больше, то все логическое выражение вернет ложь ( false ). В таком случае сработает ветка else .
В данном случае существование треугольника проверяется по-этапно. Если первое условие возвращает ложь, то программа переходит к последнему else. Если же первое условие соблюдено, то поток выполнения программы оказывается у вложенного if. Здесь проверяется уже второе условие. Если оно возвращает ложь, то программа переходит к предпоследнему else. Если и второе логическое выражение возвращает истину (true), то программа идет к третьему условию. При его соблюдении выполняется тело самого вложенного оператора if. При его несоблюдении сработает самое вложенное else.
Несмотря на то, что данная программа кажется длиннее, в определенных ситуациях она может выполняться быстрее, чем первая. Здесь если внешнее if возвращает ложь, то остальные логические выражения вообще не проверяются. В первой программе могут и проверяться (это зависит от особенностей языка программирования).
[spoiler title=”источники:”]
http://www.refsru.com/referat-3147-5.html
http://pas1.ru/triangle
[/spoiler]
Содержание:
Ранее мы выполняли построения на плоскости при помощи линейки с делениями, чертежного треугольника, транспортира и циркуля.
Математиков всегда интересовали построения геометрических фигур, которые можно выполнить только при помощи циркуля и линейки. В геометрии специально выделяют задачи на построение, которые могут быть решены с помощью этих двух инструментов.
Например, при помощи циркуля и линейки можно построить треугольник, стороны которого равны трем данным отрезкам. Или построить угол, равный данному углу.
Рассмотрим одну из таких задач на построение. На прямой
Найти точку — это значит построить ее при помощи циркуля и линейки. Если перемещать некоторую точку по прямой 
Чтобы построить серединный перпендикуляр, нужно построить две пересекающиеся окружности равных радиусов с центрами в точках А к В (рис. 293, б). Затем провести прямую MN через точки пересечения этих окружностей (ниже мы обоснуем это построение). В пересечении серединного перпендикуляра MN к отрезку АВ и прямой 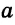
Рассмотренная задача может иметь и практический смысл. Допустим, есть два населенных пункта и шоссе рядом с ними. На шоссе нужно найти место для остановки, чтобы путь для жителей обоих населенных пунктов до остановки был одинаковым. Все построения будут сделаны на карте населенного пункта.
При решении задач на построение линейка считается односторонней и без делений. При помощи такой линейки нельзя построить две параллельные прямые, проведя линии по краям линейки, нельзя измерять и откладывать отрезки, нельзя строить перпендикуляры, используя прямоугольную форму линейки. Рассмотрим, какие операции можно выполнять линейкой, а какие циркулем.
Операции с линейкой
При помощи линейки можно провести (построить):
а) произвольную прямую;
б) прямую, проходящую через две точки (рис. 294).
Операции с циркулем
При помощи циркуля можно:
а) построить произвольную окружность и окружность (дугу окружности) с данным центром и радиусом, равным данному отрезку (рис. 295);
б) отложить отрезок, равный данному отрезку, на некоторой прямой.
Откладывание отрезка
Для откладывания отрезка, равного данному отрезку 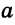
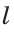
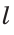
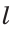
В пересечении дуги и прямой 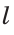
Операция откладывания отрезка на прямой позволяет построить сумму и разность двух отрезков (рис. 297): в первом случае на произвольной прямой откладывают последовательно два отрезка, во втором — на большем отрезке от любого его конца откладывают меньший отрезок.
В дальнейшем при решении задач на построение мы не будем описывать процедуру откладывания отрезка на прямой, считая ее элементарной операцией.
Перечислим 5 основных задач на построение, к которым сводятся другие задачи. Решая сложные задачи, будем ссылаться на эти основные, не описывая ту часть решения, которая связана с одной из основных задач.
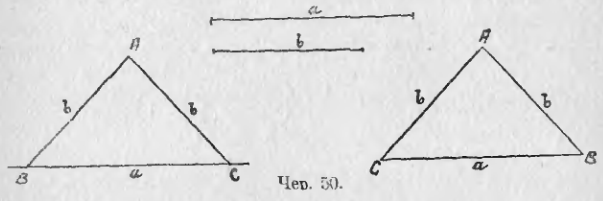
- Задача I. Построение треугольника по трем сторонам.
- Задача II. Построение угла, равного данному.
- Задача III. Построение биссектрисы угла.
- Задача IV. Построение середины отрезка.
- Задача V. Построение прямой, перпендикулярной данной.
В некотором смысле «линейка» и «циркуль» — это два идеальных робота, которые могут выполнять определенный набор операций. И наша задача — составить алгоритм из последовательности таких операций — команд для этих роботов, который приведет к построению необходимой фигуры. Фактически нужно написать программу для «циркуля» и «линейки».
Замечание. В треугольнике ABC стороны, противолежащие углам А, В и С, будем соответственно обозначать 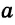
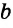
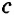
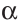
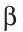
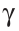
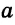
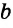
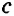
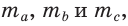
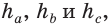
Построение треугольника по трем сторонам. Построение угла, равного данному
Задача №1
Построить треугольник со сторонами 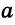
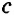
Решение:
Пусть даны отрезки 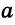
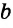
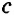
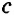
Строим окружность с центром в точке А радиусом 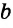
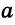
Треугольник ABC — искомый, так как у него ВС = 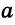
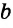
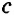
Задача имеет решение, если для данных отрезков 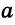
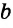
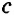
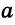
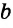
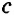
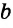
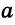
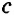
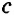
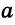
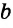
Следствие.
Если для чисел 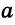
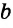
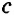
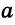
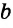
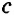
Замечание. При решении задач на построение под числом решений понимается число фигур разной формы, удовлетворяющих условию. В данном случае решение одно.
Задача №2
Построить угол, равный
Решение:
Пусть дан угол А (рис. 301, а).
Нужно построить угол А1, равный углу А. Идея решения состоит в том, чтобы построить некоторый треугольник ABC с углом А и равный ему треугольник A1B1C1.
Строим произвольный луч А1К (рис. 301, б). Произвольным, но одним и тем же радиусом строим дуги с центрами в точках А и А1. Получаем АВ =АС =А1С1. Строим дугу окружности с центром в точке C1 радиусом, равным СВ, до пересечения ее с уже построенной дугой в точке В1. Строим луч А1В1. Угол A1 — искомый. Действительно, так как 

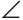
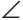
Замечания. Построение угла, равного данному, дает возможность строить сумму и разность двух углов.
Задача №3
Построить треугольник по двум сторонам и углу между ними.
Решение:
Пусть даны отрезки 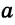
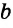
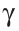
Нужно построить треугольник со сторонами 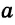
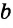
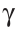
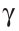
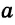
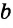
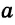
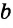
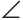
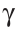
Заметим, что решение существует, если 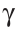
Задача №4
Построить треугольник по стороне и двум прилежащим к ней углам.
Решение:
Пусть дана сторона 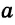
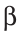
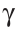
Нужно построить треугольник со стороной 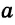
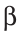
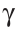
На произвольной прямой 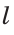
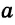
От лучей ВС и СВ в одну полуплоскость откладываем углы, равные углу 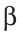
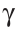
Решение существует, если 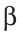
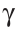
Построение биссектрисы угла. Построение середины отрезка
Задача:
Построить биссектрису данного угла.
Решение:
Пусть дан угол А (рис. 305).
Нужно построить его биссектрису. Произвольным радиусом строим дугу окружности с центром в точке А, которая пересекает стороны угла А в точках В и С. Далее одинаковым радиусом строим две дуги с центрами в точках В и С до их пересечения в точке D. Строим луч AD, который является искомой биссектрисой. Доказательство следует из того, что 

Задача №5
Построить середину отрезка (разделить данный отрезок пополам).
Решение:
Пусть АВ — данный отрезок. Произвольным, но одним и тем же радиусом (большим половины отрезка АВ) проводим две дуги с центрами в точках А и В до их пересечения в точках С и D (рис. 306).
Через точки С и D проводим прямую. В пересечении прямых CD и АВ получаем точку М — середину отрезка АВ. Докажем это. Так как точки С и D равноудалены от концов отрезка АВ (СА = СВ = DA = DB как радиусы), то они лежат на серединном перпендикуляре к этому отрезку. Поскольку две точки задают единственную прямую, то CD — серединный перпендикуляр к отрезку АВ.
Следовательно, AM = MB.
Замечание. Указанный способ построения середины отрезка также является и способом построения серединного перпендикуляра к отрезку.
Задача №6
Построить треугольник по стороне 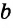
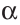
Решение:
Предположим, что задача решена, и сделаем чертеж искомого треугольника АВС (рис. 307).
Пусть AC = 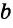
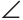
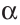
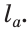
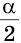
AC = 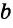
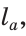
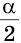
1) Строим 
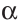
2) Строим биссектрису AG угла EAF (основная задача). Получаем 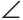
3) Строим треугольник АКС по двум сторонам и углу между ними: на луче AF откладываем отрезок AC = 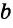
4) Находим точку В пересечения луча СК и луча АЕ. Треугольник ABC — искомый.
Задача №7
Построить центр данной окружности.
Решение:
Мы знаем, что серединный перпендикуляр к хорде проходит через центр окружности. Серединные перпендикуляры к двум хордам окружности будут пересекаться в ее центре. Отсюда построение.
Строим хорду АВ (рис. 309) и к ней серединный перпендикуляр МК (основная задача).
Строим хорду CD (не параллельную АВ) и к ней серединный перпендикуляр EF. Точка О пересечения прямых МК и EF — центр окружности.
Замечание. Вторым способом решения будет построение одного серединного перпендикуляра МК к хорде АВ, нахождение точек Т и Р пересечения МК с окружностью и построение середины О диаметра ТР.
Построение прямой, перпендикулярной данной
Задача:
Построить прямую, перпендикулярную прямой 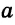
Решение:
Алгоритм построения одинаков для случая, когда точка А не принадлежит прямой 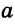
Построение.
Проводим дугу с центром в точке А, которая пересекает прямую 
Доказательство:
Так как точки А и D равноудалены от концов отрезка ВС (АВ=АС, BD = CD как радиусы), то AD — серединный перпендикуляр к отрезку ВС.
Следовательно, AD
Этапы решения задачи на построение
При решении задачи на построение выделяют 4 этапа.
1. Анализ.
На этом этапе предполагают, что задача решена, делают чертеж с изображением искомой фигуры и указывают идею решения задачи.
2. Построение.
На этом этапе дают описание последовательности шагов, приводящих к построению искомой фигуры, то есть алгоритм построения. Иногда на этом этапе проводят и сами операции построения на произвольно взятых отрезках, углах и других фигурах. В сложных задачах обычно указывают лишь шаги построения, ссылаясь на основные и ключевые задачи.
3. Доказательство.
На этом этапе доказывают, что построенная фигура удовлетворяет требованию задачи. Иногда это следует непосредственно из построения.
4. Исследование.
На данном этапе определяют, при какой величине заданных в условии отрезков и углов существует решение и число решений.
При записи решения задачи на построение этапы анализа и исследования в школе необязательны, если в условии задачи нет специальных указаний.
Задача №8
Построить прямоугольный треугольник по катету и прилежащему острому углу.
Решение:
Пусть дан катет 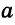
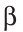
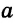
Построение.
1) Строим прямой угол. Для этого проводим произвольную прямую 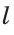
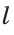
2) На одной стороне прямого угла С от его вершины откладываем отрезок СВ = 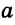
3) Строим 
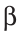
4) В пересечении стороны угла В со стороной прямого угла получим точку А.
Доказательство:
Треугольник АВС — искомый, так как по построению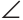
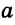
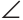
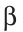
Замечание. Мы не описываем построение прямой, перпендикулярной данной, и построение угла, равного данному, так как это основные задачи. На рисунке 311 построение прямого угла С показано для наглядности.
Задача №9
Построить прямую, параллельную данной прямой, если расстояние между этими прямыми равно заданному отрезку.
Решение:
Пусть дана прямая 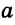
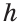
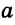
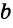
Нужно построить прямую 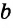
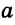
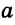
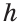
Построение.
1) Отмечаем на прямой 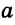
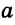
2) Откладываем на прямой 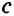
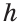
3) Строим прямую 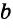
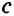
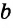
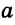
Доказательство:
Так как 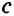
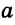
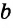
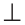
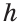
Задача №10
Построить треугольник по основанию 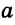
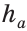
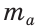
Решение:
Анализ. Пусть у треугольника ABC ВС = 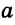
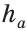
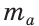
Заметим, что треугольник АНМ может быть построен по катету и гипотенузе, а затем достроен до искомого треугольника ABC путем откладывания от точки М влево и вправо отрезков МС = MB = 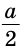
Построение.
1) Строим прямой угол Н (рис. 314).
На одной его стороне откладываем отрезок АН = 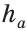
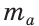
2) Делим отрезок 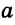
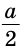
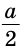
Доказательство:

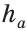
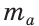
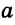
Исследование*. Так как катет меньше гипотенузы, то высота 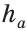
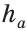
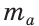
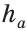
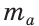
Геометрическое место точек
Определение. Геометрическим местом точек (ГМТ) называется множество всех точек, обладающих общим свойством.
Примеры геометрических мест точек на плоскости
1. Окружность — это геометрическое место точек плоскости, равноудаленных от данной точки.
2. Серединный перпендикуляр — это геометрическое место точек плоскости, равноудаленных от концов отрезка.
3. Биссектриса — геометрическое место точек внутри угла, равноудаленных от сторон угла.
4. Геометрическое место точек, находящихся на заданном расстоянии 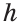
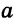
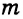
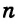
5. Геометрическое место точек, равноудаленных от двух данных параллельных прямых 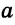
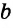
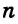
В пространстве геометрическим местом точек, равноудаленных от данной точки, является сфера.
Метод геометрических мест точек
Одним из методов решения задач на построение является метод пересечения двух геометрических мест точек. Суть его состоит в следующем. Пусть искомая точка удовлетворяет, например, некоторым двум условиям: геометрическое место точек, удовлетворяющих первому условию, — это некоторая фигура F1 (окружность, биссектриса угла, серединный перпендикуляр и т. д.), а геометрическое место точек, удовлетворяющих другому условию, — это фигура F2. Искомая точка, принадлежащая и фигуре F1, и фигуре F2, является точкой их пересечения. В частности, методом пересечения двух геометрических мест точек решена основная задача о построении треугольника по трем сторонам.
Задача №11
Построить внутри данного угла точку, которая равноудалена от сторон угла на данное расстояние 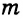
Решение:
Анализ. Пусть дан угол ВАС и отрезок длиной 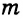
Все точки, равноудаленные от сторон угла, лежат на биссектрисе угла. Поэтому искомая точка лежит на биссектрисе угла. С другой стороны, все точки, удаленные от стороны угла на расстояние 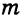
Построение.
1) Строим прямую 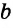
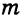
2) Строим биссектрису угла ВАС (основная задача).
3) В пересечении биссектрисы и прямой 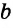
Доказательство:
Расстояние между параллельными прямыми 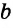
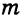
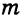
Задача №12
Построить треугольник по двум сторонам 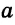
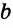
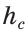
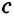
Решение:
Заметим, что в общем случае существует два треугольника со сторонами 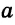
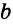
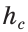
Построение (рис. 320).
1) Строим две параллельные прямые 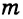
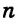
2) Строим дугу с центром в точке С и радиусом 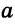
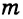
3) Строим дугу с центром в точке С радиусом 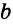
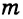
Доказательство:
Следует из построения и теоремы о расстоянии между параллельными прямыми.
Исследование. Так как перпендикуляр меньше наклонной, проведенной из той же точки к одной прямой, то задача может иметь решение, только если 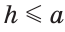
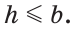
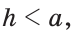
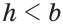
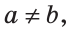
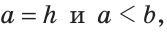
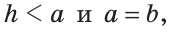
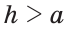
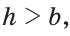
Задачи на построение с решением
С помощью линейки с делениями, циркуля, угольника, транспортира, шаблонов (рис. 312) вам не раз приходилось проводить различные геометрические построения.
А можно ли обходиться меньшим количеством чертежных инструментов? Оказывается, что во многих случаях достаточно использовать только циркуль и линейку без делений. Например, чтобы провести биссектрису угла, совсем не обязательно иметь транспортир, а разделить отрезок пополам можно и тогда, когда на линейку не нанесена шкала.
А стоит ли в наше время, когда созданы точнейшие приборы и совершенные компьютерные программы, позволяющие выполнять сложнейшие измерения и построения, обходиться такими «скудными» средствами, как циркуль и линейка? На практике, конечно, нет. Поэтому, например, конструкторы, строители, архитекторы, дизайнеры не ограничивают себя в выборе инструментов.
Однако при изучении геометрии очень полезно принять участие в игре по таким правилам:
- все построения выполняются только с помощью циркуля и линейки без делений;
- с помощью линейки можно через заданную точку
провести прямую, а также через заданные две точки
и
провести прямую
;
- с помощью циркуля можно построить окружность с данным центром и радиусом, равным заданному отрезку
.
Итак, договоримся, что если в задаче требуется построить какую-то фигуру, то построение выполняется по описанным выше правилам.
Решить задачу на построение — это значит составить план (алгоритм) построения фигуры; реализовать план, выполнив построение; доказать, что полученная фигура является искомой.
Рассмотрим основные задачи на построение.
Задача №13
Постройте угол, равный данному, одна из сторон которого является данным лучом.
Решение:
На рисунке 313 изображены угол 
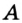
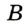
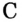
Пусть 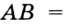
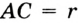
Проведем окружность радиуса 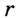
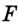
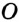
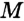
Покажем, что каждый из углов 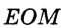
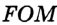
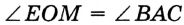
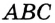
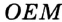
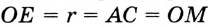
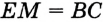
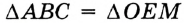
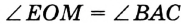
Задача №14
Постройте серединный перпендикуляр данного отрезка.
Решение:
Пусть 
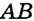
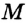
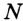
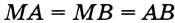
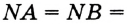
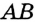
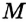
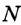
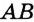
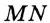
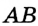
Замечание. Поскольку прямая 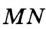
Задача №15
Даны прямая и не принадлежащая ей точка. Через эту точку проведите прямую, перпендикулярную данной.
Решение:
Пусть 
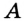
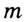
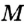
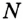
Поскольку 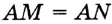
Задача №16
Даны прямая и принадлежащая ей точка. Через эту точку проведите прямую, перпендикулярную данной.
Решение:
Пусть 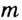
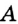
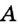
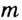
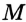
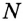
Поскольку 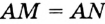
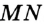
Задача №17
Постройте биссектрису данного угла.
Решение:
Пусть 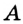
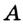
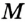
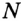
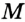
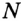
Эти окружности пересекаются в точках 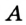
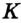
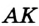
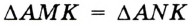
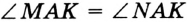
Задача №18
Постройте прямоугольный треугольник по гипотенузе и катету.
Решение:
Проведем две перпендикулярные прямые 
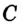
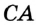
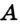
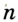
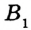
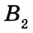
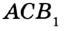
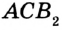
Задача №19
Постройте треугольник по стороне и высотам, проведенным к двум другим сторонам.
Решение:
На рисунке 322 изображен треугольник 
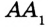
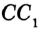
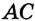
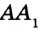
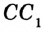
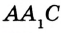
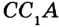
Построим прямоугольный треугольник 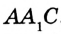
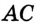
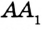
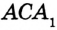
Теперь осталось построить треугольник по стороне и двум прилежащим к ней углам. Выполните это построение самостоятельно.
Задача №20
Постройте треугольник по углу, высоте и биссектрисе, проведенным из вершины этого угла.
Решение:
На рисунке 325 изображен треугольник 
Если известны длины отрезков 
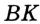
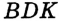
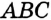
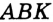
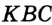
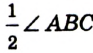
Строим прямоугольный треугольник 
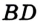
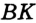
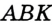
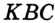
Метод геометрических мест точек в задачах на построение
Известно, что если смешать синий и желтый цвета, то получим зеленый. Пусть на плоскости надо найти точки, обладающие какими-то двумя свойствами одновременно. Если синим цветом покрасить точки, обладающие первым свойством, а желтым — обладающие вторым свойством, то понятно, что «зеленые» точки будут обладать сразу двумя свойствами. В этом и состоит идея метода ГМТ, которую проиллюстрируем следующими задачами.
Задача №21
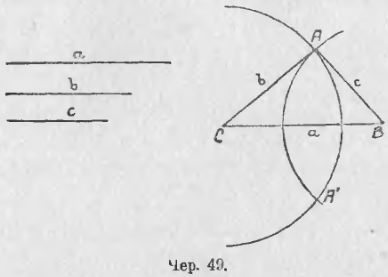
Постройте треугольник по трем данным его сторонам.
Решение:
Пусть даны три отрезка, длины которых равны 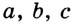
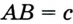
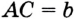
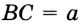
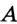
Воспользуемся тем, что точка 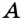
- принадлежит геометрическому месту точек, равноудаленных от точки
на расстояние
с, т. е. «синей» окружности (рис. 328);
- принадлежит геометрическому месту точек, равноудаленных от точки
на расстояние
, т. е. «желтой» окружности (рис. 328).
В качестве точки 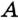
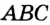
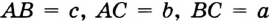
Из описанного построения следует, что если каждый из трех данных отрезков меньше суммы двух других, то эти отрезки могут служить сторонами треугольника.
Задача №22
Постройте фигуру, все точки которой принадлежат данному углу, равноудалены от его сторон и находятся на заданном расстоянии а от его вершины.
Решение:
Искомые точки принадлежат сразу двум геометрическим местам точек: биссектрисе данного угла и окружности с центром в его вершине и радиусом, равным 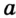
Задача №23
Постройте центр окружности радиуса 
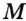
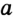
Решение:
Поскольку окружность касается прямой 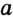
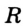
Геометрическое место точек, являющихся центрами окружностей радиуса 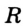
Построение для случая, когда данная точка принадлежит данной прямой, рассмотрите самостоятельно.
Задача №24
Постройте треугольник по стороне, медиане, проведенной к этой стороне, и радиусу описанной окружности.
Решение:
Построим окружность данного радиуса и проведем хорду 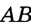
- Угол – определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Неравенство треугольника – определение и вычисление
- Свойства прямоугольного треугольника
- Расстояние между параллельными прямыми
- Задачи на построение циркулем и линейкой
Искомый треугольник
Cтраница 2
Предположим, что искомый треугольник построен и С – вершина его прямого угла. Так как / – АС В – 90, точка С лежит на окружности S с диаметром АВ. Поэтому точка С является точкой пересечения окружности S и данной окружности. Построив точку С и проведя прямые С А и АВ, найдем оставшиеся вершины искомого треугольника.
[16]
По этим данным искомый треугольник ВАС может быть построен.
[17]
Предположим, что искомый треугольник ABC построен.
[19]
Третьей вершиной А искомого треугольника буает, очевидно, точка пересечения этой дуги с большим кругом, перпендикулярным к дуге ВС и проходящим через ее середину. Задача всегда имеет одно решение.
[20]
Вершины А и В искомого треугольника легко построить. Значит, задача сводится к построению вершины С.
[21]
Согласно дополнительному требованию задачи, искомый треугольник должен быть расположен на плоскости так, чтобы он имел общий угол с данным треугольником ABC. Отложим от его вершины на Л С отрезок ACib и проведем прямую CiBi СВ. ДЛС удовлетворяет всем требованиям задачи.
[22]
Пересечение этих призм и дает искомый треугольник составов системы. Схематически это показано на фиг.
[23]
Пересечение этих призм и дяет искомый треугольник составов системы. Схематически это показано на фиг.
[24]
Если данная боковая сторона ВС искомого треугольника меньше квадранта, то задача может иметь два решения, одно решение или не иметь ни одного решения ( черт. Построение треугольника с наибольшей площадью сводится к проведению через точки В и С окружности, касающейся построенной окружности ( упр.
[25]
Если данная боковая сторона ВС искомого треугольника раина квадранту, то задача может иметь одно решение или не иметь ни и i-ного решения ( черт.
[26]
Это соотношение указывает способ построения искомого треугольника ABC.
[27]
Полученный треугольник АгА А3 и есть искомый треугольник. Аналогичное построение можно сделать и в случаях, когда некоторые из углов равны нулю или тт.
[28]
В соответствии с анализом легко построить искомый треугольник и доказать, что он удовлетворяет всем требованиям задачи.
[29]
И опять, если мы возьмем искомый треугольник заданного вида, то придется искать прямоугольный треугольник такой, чтобы полусумма перпендикулярных сторон, умноженная на себя и увеличенная на шестикратную площадь, давала квадрат.
[30]
Страницы:
1
2
3
4
3. Доказательство имеет целью установить, что построенная фигура действительно удовлетворяет условию задачи.
Доказательство проводится в предположении, что каждый шаг построения может быть выполнен.
4. Исследование. При анализе, построении обычно ограничиваются отысканием одного какого-либо решения, предполагая выполнимость шагов построения. Идя полного решения задачи нужно выяснить:
1) всегда ли (т.е. при любом ли выборе данных) можно выполнить построения избранным способом;
2) можно ли и как построить искомую фигуру, если для какого-нибудь выбора данных указанный способ построения не пригоден;
3) сколько решений имеет задача при каждом возможном выборе данных.
Эти вопросы составляют содержание исследования. Итак, исследование ставит цель – установить условия разрешимости и определить число решений.
Практически исследование проводят по ходу построения, рассматривая каждый шаг построения на возможность и единственность.
Однако такое исследование связано с данным способом построения. В этом случае остается открытым вопрос: нет ли других решений при другом способе решения. На этот вопрос отвечают с помощью указанного выше приема: доказывают, что произвольное решение данной задачи совпадает с одним из уже полученных решений.
Для иллюстрации сказанного рассмотрим следующий пример.
Задача. Построить треугольник, если известны: длина основания а, угол при основании α и разность двух других сторон d.
Решение. Заметим, что в условии задачи не указаны инструменты. B таких случаях будем полагать (как и в школе), что задачу надо решить с помощью линейки и циркуля.

А
нализ. Поиск решения задачи проведем, полагая задачу решенной. Пусть ∆ABC – искомый треугольник: AB = a, AC–BC = AD=d,
= α. Замечаем, что ∆АВD = определен по двум сторонам и углу между ними.
Третья вершина С искомого треугольника может быть найдена как точка пересечения луча АD и прямой l – серединного перпендикуляра отрезка ВD). Иначе говоря план решения найден, отроим треугольник ∆АВD, а затем и третью вершину С.
Построение. В этом пункте реализуем план решения.
Строим последовательно:

1)
2) l, l – серединный перпендикуляр отрезка BD;
3) C, C = [AD) ∩ l.
Треугольник АВС – искомый.
Доказательство. Действительно, ∆АВС удовлетворяет всем условиям задачи, т.к. по построению
АВ = а, АС – ВС = АD = d, BAD = α.
Исследование. Проверил каждый шаг построения на осуществимость и единственность. Первый шаг возможен и единственен тогда и только тогда, когда 0<α<π. Второй шаг возможен и единственен всегда. Третий шаг возможен и единственен тогда и только тогда, когда α< а cos α. Действительно, если d < a cos α, то прямая l пересекает луч AD. Если же d = a cos α , то l и AD, поэтому треугольника, удовлетворяющего условию задачи, не существует. В том случае, когда d < a cos α, прямая l пересекает луч DА. В этом случае также задача не имеет решения.
Но вернемся к анализу. У нас задача решена, предполагая, что α лежит против меньшей из двух боковых сторон. Если α лежит против большей стороны, то предыдущий метод построения не проходит. Как быть? По теории мы должны и для этого случая дать решение. Нетрудно убедиться, что ΔABF определен (a,d и угол π – α). Построение, доказательство и исследование провoдятcя так же, как и выше.
Необходимо еще выяснить: вcе ли решения найдены. Да, все, так как если бы каким-то способом построить треугольник по a, d и α то этот треугольник был бы равен одному из указанных треугольников (это легко доказать через ).

Методы решения задач на построение
Основными являются три: метод геометрических мест (ГМТ), метод геометрических преобразований, алгебраический метод.
Метод геометрических мест (пересечения фигур).
Сущность метода: решение задачи сводит к построению некоторой точки (основного элемента построения), подчиненной двум условиям. Отбрасывают одно из этих условий и строят ГМТ Ф1 , удовлетворяющих первому условию, потом Ф2 – ГМТ, удовлетворяющих второму условию. По соответствующей аксиоме конструктивной геометрии можем сказать Ф1∩Ф2 = Ø или нет и если ≠ Ø, то считать построенным пересечение Ф1 ∩ Ф2. Точки Ф1 ∩ Ф2 и только они удовлетворяют обоим условиям одновременно. Точки пересечения и только они дают решение задачи.
Заметим, что успех от применения этого метода полностью зависит от знания конкретных ГМТ. Наиболее часто применяются следующие геометрические места:
ГМТ 1. Множество точек плоскости, каждая из которых равноудалена от двух данных точек А и В, есть серединный перпендикуляр отрезка АВ.
ГMT 2. Множество точек, находящихся на данном расстоянии от данной прямой, есть две прямые, параллельные данной и отстоящие от нее на данном расстоянии.
ГМТ 3. Множество точек, каждая из которых равноудалена от двух данных параллельных прямых, есть прямая, являющаяся их осью симметрии.
ГМТ 4. Множество точек, каждая из которых равноудалена от двух пересекающихся прямых, есть две взаимно перпендикулярные прямые, содержащие биссектрисы углов, образованных данными прямыми,
ГМТ 5. Множества точек плоскости, из которых отрезок АВ виден под прямым углом, есть окружность (без точек А и В ), построенная на отрезке АВ как на диаметре.
ГМТ 6. Множество точек плоскости, из которых отрезок АВ виден под углом α, где α ≠ 90º, α ≠ 180º , есть две дуги с общими концами А и В (без точек А и В), симметричные относительно прямой АВ.
ГМТ 7. Множество точек плоскости, из которых данная окружность видна под углом α, где α ≠ π, есть окружность,- концентрическая с данной, радиус которой больше радиуса данной окружности.
ГМТ 8. Множество точек, делящих всевозможные хорда окружности (O, ОА), проведенные через точку А окружности, в одном и том же отношении λ, где λ > 0, есть окружность (без точки А) с центром на прямой ОА, проходящая через точку А. Если λ = 1, то эта окружность построена на отрезке ОА как на диаметре.
ГМТ 9. Множество точек плоскости, для каждой из которых разность квадратов расстояний от двух данных точек А и В постоянна, есть прямая, перпендикулярная прямой АB.
ГМТ 10. Множество точек плоскости, для каждой из которых сумма квадратов расстояний до двух данных точек А и В равна а2, есть окружность с центром в середине отрезка АВ, если 2а2>AB2; середина отрезка AB, если 2a2 = AB2; и пустое множество, если 2a22.
ГМТ 11. Множество точек плоскости, для каждой из которых отношение расстояний до двух данных точек А и В постоянно и отлично от единицы, есть окружность с центром на прямой АВ (окружность Аполлония).
Для иллюстрации метода ГМТ решим следующую задачу.
Задача. Построить треугольник, если известны: длина основания а, угол при вершине α и отношение боковых сторон λ, λ ≠ 1.
Решим методом ГМТ.
Анализ. Две вершины А и В искомого треугольника легко построить. Задача сводится к построению точки С. Точка С должна удовлетворять следующим двум условиям: 1) точка С принадлежит сегменту, вмещающему данный угол α; 2) точка С принадлежит окружности Аполлония.

ς α
Построение. Строим последовательно: а) отрезок АВ, АВ = 0; б) сегмент А ς В, вмещающий данный угол α; в) окружность Аполлония на отрезке АВ; г) точку С , принадлежащую пересечению сегмента А ς В и окружности Аполлония.
Треугольник АВС – искомый.
Доказательство и исследование предлагаем читателям провести самостоятельно.
Метод геометрических преобразований
Сущность метода: при решении задачи, и прежде всего на первом этапе – анализе, наряду с данными и искомыми фигурами рассматривают другие фигуры, полученные из данных или искомых фигур (или их частей) с помощью некоторого геометрического преобразования (ГП). В зависимости от того, какое (ГП) выбрано, говорят о той или иной разновидности метода ГП (метод параллельного переноса, гомотетии, инверсии и т.д.). Рассмотрим примеры.
1. Параллельный перенос (ПП).
Сущность: наряду с данными и искомыми фигурами рассматривают другие фигуры, полученные из указанных фигур (или частей) с помощью ПП.
Задача. Достроить трапецию так, чтобы ее основания и диагонали были соответственно равны четырем данным отрезкам.

Анализ. Пусть ABCD – искомая трапеция. Сделаем параллельный перенос плоcкости, определяемый вектором ВС: ВС : BD → CF.
Треугольник ACF определен по трем сторонам: AF = a + b, AC = d1, CF = d2.
План решения ясен. Предлагаем читателям завершить решение этой задача.
2. Осевая симметрия.
Задача. Даны прямая l и две точки А и В, принадлежащие одной плоскости, определяемой прямой l. Найти такую точку Х l, чтобы сумма АХ + ХВ была минимальной.

Уклонимся от схемы. Рассмотрим Sе. Пусть A′ = Se (A), X = A′B ∩ l. Покажем, что Х – искомая точка. В самом деле, для любой точки
Y l: AX + XB = A′B < A′Y + YB = AY + YB (Y ≠ X).
Исследование. Задача всегда имеет решение, причем единственное.
3. Поворот.
Задача. Даны: угол АОВ и точка С внутри него. Построить равносторонний треугольник, одна вершина которого совпадает о точкой С, а две другие лежат на сторонах данного угла.
Анализ. Пусть ∆СDE – искомый. Сделаем поворот плоскости вокруг точки С на угол 60°: R60º (D) = E, R60º (OB) = O′B′, причем E = OB ∩ O′B′. Аналогично находим положение точки D: D = OB ∩ Rc-60º(OA).

Построение очевидно. Доказательство и исследование предлагаем провести самостоятельно.
4. Центральная симметрия.

Задача. Построить квадрат, если даны его центр О и две точки А и В на параллельных его сторонах.
Анализ. Пусть искомый квадрат построен. Тогда А’ и В, где лежат на А’ = Z0 (A), лежат на одной стороне квадрата. Аналогично В’ и А, где В’ = Z0 (в), лежат на одной стороне квадрата. Тогда на прямых ВА’ и АВ’ лежат стороны квадрата. Дальнейшее продолжение не вызывает трудностей, предлагаем провести самим.
5. Метод подобия (гомотетии).
Сущность метода строят фигуру, подобную данной, не учитывая какой-нибудь линейный размер или специальное положение искомой фигуры относительно данных. Затем строят искомую (чаще всего гомотетией), учитывая, что коэффициент подобия равен отношению любых двух соответственных отрезков.
Задача. Даны угол и точка внутри него. Построить окружность, проходящую через точку А и касающуюся сторон угла.
Анализ. Центр искомой окружности должен лежать на биссектрисе данного угла. Снимем требование, чтобы окружность ω проходила через А (это подобно тому, что не требуется, чтобы расстояние от точки О до точки окружности равнялось известному отрезку а). Тогда легко построить окружность ω1 , касающуюся сторон утла. Окружности ω и ω1 гомотетичы (с центром в точке 0). Найдем образы точек А и В: А → А’, В→В’ . Очевидно, АВ׀׀А’В’.
Учитывая оказанное, можно наметить следующий план решения:
1) строим окружность СО1 , касающуюся сторон угла;
2) проводам ОА;
3) строим точки пересечения ω и ω1;
4) из точки А проводим прямую, параллельную прямой А’В’. Пусть В – одна из точек пересечения.
Построение и доказательство опускаем (самим).
Исследование. 1.Окружность ω1 можно построить и бесчисленным множеством способов.
2. Пересечением ОА и ω1 всегда являются две точки А’ и А”.
3. Через точку А можно провести две прямые, параллельные соответственно В’А’ или В’А”. Эти две прямые l1 и l2 различны, если А ОВ’; и совпадает, если А
ОВ’.

4. Пересечения l1 ∩ ОВ и l2 ∩ ОВ’ существуют и единственны, если А ОВ’ , т.е. задача в этом случае имеет два решения.
Если же А ОВ’, то этим способом центр искомой окружности не найдем. Для этого принципиально нового случая найдем новое специфичное решение: строим прямую, перпендикулярную ОА-биссектрисе данного угла. Далее проведем биссектрисы углов ОСА и МСА. Точки в1 и в2 – искомые центры.
Задача (наглядная). Построить треугольник по двум углам , β

и медиане, проведенной из какой-нибудь вершины.
1. Строим треугольник АВ1С1
2. Подобным преобразованием получим искомый ΔАBC
6. Метод инверсии
Сущность метода: наряду с данными и искомыми фигурами рассматривают фигуры, инверсные им или их частям. Он применяется в тех случаях, когда построение фигуры, инверсной искомой, является более легкой (доступной). Построив инверсную построенной, получают искомую. Метод инверсии дает возможность решить трудные конструктивные задачи. Недостаток – громоздкость (большое число построений).
Задача. Даны: точка О и прямые а и в, не проходящие через О. Построить луч, выходящий из О, чтобы произведение его отрезков от О до точек пересечения с данными прямыми было равно 2, где
– длина отрезка
.
Анализ. Пусть [ОА) – искомый луч. Тогда ОА*ОВ= 2. Инверсия I относительно окружности ω(o,r) точку B переведет в точку A, прямую в→в’, где b’ – некоторая окружноcть, тогда A = a∩в’.

Построение. Строим последовательно: 1) ω(o,r); 2) в’, где в’ = I (в) окружность, проходящая через О; 3) А, А а ∩ в; 4) [ОА) – искомый.
Доказательство. Через В обозначим пересечение в ∩ [ОА). Тогда В – прообраз А, т.к. А = [ОА) ∩ в’→[ОА) ∩ в = В. По определению инверсии имеем: ОА*ОВ = r2.
Исследование. Если: a ∩ в’ = Ø, то нет решения; – точка касания, то одно решение; a ∩ в’ = {A}, A – точка касания, то одно решение; a ∩ в’ = {A1 A2, A1 ≠ A2, то два решения.
Алгебраический метод.
Сущность: решение задачи сводят к построению отрезка, длину которого можно выразить через длины данных отрезков с помощью формул. Затем строят искомый отрезок по полученной формуле.
З
адача. Даны: угол АОВ и две точки С и D да луче OВ. Найти на луче [ОА) точку X, чтобы величина угла СХD была наибольшей.
Анализ. Пусть точка X найдена. Очевидно, точка X является точкой касания окружности, проходящей через С и D. Обозначим длину отрезка ОХ через х.

И меем:
х2 = |ОС|*|ОD|, |ОС| и |ОD | –
длины известных отрезков ОС и ОD) . План решения состоит из двух шагов: Строим так, чтобы
и х = [OA) ∩ω(O,x),
где – длина отрезка х.
Построение, доказательство, исследование предлагаем провести самим.
Построение отрезков, заданных формулами.
Алгебраический метод решения задач на построение сводится к построению отрезков, заданных формулами.
Полная формулировка задачи: даны отрезки . Пусть а, в, с,…, d – их длина при некоторой единице измерения. Требуется построить с помощью данных инструментов (циркуля и линейки) отрезок
, длина которого x (при той же единице измерения) выражается через длины данных отрезков формулой х = f (a, в2, с,…, d). Будем рассматривать такие значения а, в, с,…,d, при которых f имеет смысл и положительна.
Мы уже знаем, как cтроить выражения
,
,
,
, х = а ± в,(а – в, при а >
в). К рассмотренным построениям можно свести построение более сложных формул:
1) , n = натуральное число; делается так:
, причем
, если n = p·q,
, если n = p2 ± q2;
2)
3)
·
и т.д.
Все построенные выше формулы обладают одним общим cвойcтвом: они являютcя однородными выражениями первой степени. Напоминаем, выражение F(а,…,с) называют однородным степени 11, если
F(ta,…,tc) = tn · F (a,…,c).
Пользуясь понятием однородной функции, мо;но выделить некоторые, классы алгебраичеcких выражений, которые могут быть построены циркулем и линейкой. Например, циркулем и линейкой можно построить:
-
Oтрезок, заданный формулой
,
где Pn+1 (…) и Pn (a,b,…,c) – однородные многочлены с рациональными коэффициентами от длин а,в,…,с отрезков степени соответственно n+1 и n.
Пусть
Pn+1 =
Далее, пусть – произвольный отрезок, d – его длина (в той же единице измерения).
Разделим чиcлитель на dn , знаменатель – на dn-1 .
Выражение представляет сумму одночленов вида
.
Следовательно, можно построить каждое слагаемое, а потому и весь числитель: . Аналогично,
. Наконец строим
– отрезок длины х, где
;
2) отрезок, заданный формулой , где – (
(…) – однородная рациональная функция 2 степени с рациональными коэффициентами. Делается так:
, где (R2(…) – отношение двух однородных многочленов
, тогда
как и выше, строим
3) Замечание. При вычерчивании кривых иногда приходится строить алгебраические выражения, не являющиеся однородными первой степени. Пусть надо построить отрезок , длина которого x = f(a,b,…,c), где f(…) не является однородной первой cтепени, например, y = x3 +1.
Правило: построение произвольного выражения от n аргументов всегда можно свести к построению некоторого однородного выражения первой степени от n+1 аргументов. Достигается это выбором единицы измерения.
Выберем некоторый отрезок в качестве единичного, e =1.
– однородная функция первой степени.
Если сумеем построить отрезок по этой формуле, то он и будет искомым при выбранной, единице масштаба. Ясно, что получим различные неравные отрезки в зависимости от выбора
.
Примеры:
1)
2)
3)
4)
5)
Разрешимость задач на построение с помощью циркуля и линейки.
Для краткости операции «+», «-», «·», «:» и извлечение арифметического квадратного корня» назовем основными действиями.
Теорема. Отрезок, длина которого задается положительной функцией для данных отрезков, может быть построен циркулем и линейкой тогда и только тогда, когда длина искомого отрезка выражается через длины данных отрезков при помощи конечного числа основных действий.
Достаточность. С помощью циркуля и линейки можно построить отрезок , длина которого x равна соответственно:
а
а-в
ав (за счет , е = 1)
(- « -)
Так, как по условию длина искомого отрезка выражается через длины данных отрезков с помощью конечного числа основных действий, то остается единственный возможный случай, когда промежуточный отрезок не сможем построить – это построение разности а-в при а < в.
В таких случаях перейдем к положительной разности с помощью тождества а – в = – (в – а).
Теперь можно последовательно выполнить все построения, соответствующие основным операциям, и через конечное число шагов получим искомый отрезок.
Необходимость. Ясно, что построение отрезка равносилъно построению его концов. Так как
можно построить, то существует конечная последовательность основных построений, в результате выполнения которых на каком-то m -м шаге будет построен один конец (обозначим его через А ), а на к -ом – другой конец (точку в ). На плоскости построим прямоугольную декартовую систему координат.

Пусть А ( ,β), В (γ, δ) – координаты построенных точек. Данные отрезки
построим на положительной полуоси ОХ, тогда длины этих отрезков выражаются числами а1,…,ар ς (А, В) = х =
т.е. длина отрезка
выражается через числа
, β, γ, δ с помощью конечного числа основных действий. Если докажем, что сами числа
, β, γ, δ выражаются через а1,…,ар с помощью конечного числа основных действий, то теорема будет доказана (длина отрезка
выражается с помощью конечного числа основных действий).
Заметим, что любые построенные точки в ходе построения появляются двояко: либо выбираемые произвольно, либо как общие точки двух ранее построенных линий.
В первом случае выберем только такие точки, координаты которых выражаются через а1,…,ар при помощи конечного числа основных действий.
Во втором случае точка получается одним из следующих способов:
а) пересечение прямых (причем каждая прямая проведена через 2 построенные точки):
б) пересечение окружности и прямой (окружность построена через 2 построенные точки);
в) пересечение двух окружностей.
Рассмотрим случай а). Пусть прямая l1 проведена через точки
C1 (x1,y1) и D1 (x2,y2.). Покажем, что числа х1, у1, х2 и у2 могут быть выражены через а1,…,ар с помощью конечного числа основных действий (К4ОД). Действительно, пусть уравнение прямой l1 имеет вид:
в1х + с1у = d1

Легко убедиться, что чиcла в1, с1, d1 выражаются через х1, х2, у1, у2 с помощью конечного числа основных действий. То же самое имеет место относительно коэффициентов прямой l2 : в2х + с2у + d2=0.
Точка пересечения (x0, y0) еcть решение cиcтемы
причем решение выражается через в1, с1,…, d1 с помощью КrОД
В cлучае б) (х0, у0).- точка пересечения – есть решение системы
Числа х0,у0 выражаются через в,с, d, х1, х2, R c помощью КrОД.
В случае в) точка пересечения (х0,у0) является решением системы
Легко убедиться, что решение выражается с помощью КrОД через координаты ранее построенных точек.
Итак, координаты вновь построенных точек получаются через координаты ранее построенных с помощью конечного числа основных действий. Но, к ранее построенным точкам применимы точно такие же рассуждения. В конечном счете (из-за конечности числа построений циркулем и линейкой) получим, что координаты А и В выражаются через а1,…,ар с помощью КrОД.
Следствие. Если даны: отрезок, принимаемый за единичный, и число а, то отрезок длины а может быть построен циркулем и линейкой тогда и только тогда, когда число а может быть получено из «I» посредством лишь конечного числа основных действий.
О задачах, не разрешимых циркулем и линейкой.
Большой интерес представляют такие задачи на построения, когда фигура, удовлетворяющая всем условиям задачи, заведомо существует, но не может быть построена указанными инструментами. Такого рода “доказательства невозможности” даже простых по формулировке задач на построение часто оказываются связанными с наиболее трудными вопросами алгебры, анализа.
Познакомимся с некоторыми классическими задачами на построение, решения которых не могут быть найдены о помощью циркуля и линейки.
1. Задача о квадратуре круга (пользовалась исключительной известностью с древнейших времен).
Построить циркулем и линейкой квадрат, площадь которого бала бы равна площади круга данного радиуса.
Пусть – радиус круга,
, т.е. площадь крута равна площади квадрата со стороной
Иначе говоря, x является средней пропорциональной
и
.
Если бы можно было построить , то легко можно было строить искомый квадрат.
Итак, задача о квадратуре круга свелась к задаче о опрямлении окружности, т.е. построению отрезка длины . При
эта длина равна
.
Ламберт И. (швейцарский математик) доказал, что π – иррациональное число. Но вопрос о возможности спрямления окружности остался открытым, так как согласно следствию из предыдущей теоремы отрезок длины а (при выбранном единичном отрезке) может быть построен циркулем и линейкой, если а получается из I с помощью конечного числа основных действий. Такие числа являются алгебраическими, т.е. служат корнями многочленов с рациональными коэффициентами. Числа, не являющиеся алгебраическими, называются трансцендентными.
В 1882 г. Линдеманн Ф. доказал, что π является трансцендентным числом. Следовательно, проблема о квадратуре крута разрешена, задача о квадратуре крута не разрешима о помощью циркуля и линейки.
2. Задачу удвоения куба: зная ребро куба, построить ребро куба, объем которого был бы вдвое больше объема данного.
Пусть а – длина ребра данного куба, x – искомого. Имеем: х2 = 2а3. Если а = 1, то получим уравнение х3 – 2 = 0. Это уравнение не имеет рациональных корней (т.к. рациональные корни этого уравнения обязательно целые, их надо искать среди делителей свободного члена). Из алгебры известно: если уравнение рациональные числа) не имеет рационального корня, то ни один корень этого уравнения не может быть выражен через I лишь с помощью конечного числа основных действий. Тогда, учитывая указанное выше следствие, получим, что отрезок длины x не может быть построен с помощью циркуля и линейки.
Замечание. Эта задача может быть решена с привлечением двух прямых углов.
3. Задача о трисекции угла: построить угол, в 3 раза меньший данного.
Достаточно рассмотреть эту задачу для острых углов, т.к. при тупом угол
является острым и третья часть равна
Отсюда следует, что
Итак, пусть α – данный острый угол, φ – искомый,

Если отрезок длины x можно построить циркулем и линейкой, то из прямоугольника следует, что можно построить и сам угол φ. Следовательно, задача свелась к построению отрезка длины х, где x – один из корней уравнения (I).
Пусть α = 60º, тогда в = 1. Уравнение (I) приводится к виду:
Легко убедиться (из тех же соображений, что и выше), что у этого уравнения нет рациональных корней, следовательно нет ни одного корня, который выражался бы через I с помощью конечного числа основных действий.
Следовательно, задача о трисекции угла не разрешима циркулем и линейкой в общем виде.
Но, может быть, она никогда не разрешима? Это не так. Пусть α = 90°. Тогда уравнение (I) имеет вид: x3 – зх = 0, Отрезок
можно построить, следовательно, задача в этом случае разрешима.
|
нетрудно построить и угол φ. |
Можно чисто геометрически построить угол в 60° (хорда равна радиусу, см.рис.). |
Замечание 1. Существуют приборы-трисекторы, позволяющие делить угол на три равные части.

АВСD и AB1C1D1 – ромбы, φ = .

Замечание 2. Задачу о трисекции угла легко решить циркулем. Строим последовательно: 1) окружность ω расстояние между отметками на линейке;
2) точку А;
3) прямую, проходящую через А так, чтобы расстояние между второй точкой пересечения с окружностью и точкой пересечения этой прямой с прямой ОN было равно .
Построение правильных многоугольников циркулем и линейкой.
Решение проблемы связано большими трудностями, и решена она полностью великим немецким математиком Гауссом в 1796 году.
Вопрос построения правильного n -угольника равносилен вопросу о возможности деления окружности на n равных частей. Возьмем окружноcть радиуcа и прямоугольную систему координат. Задача деления

окружности на n равных частей состоит в построении точек
т.е, в построении корней уравнения Zn – 1= 0 о тличных – от Z0 = 1. Это равносильно построению корней уравнения Это уравнение называется уравнением деления окружности.
Гаусс доказал следующую замечательную теорему.
Теорема. Построение правильного n – угольника с помощью циркуля и линейки возможно тогда и только тогда, когда (числа Ферма).
Рассмотрим несколько частных случаев:
|
|
Пусть |

Следовательно, правильный пятиугольник можно построить циркулем и линейкой.
Подставим:
Строим , потом
Повторяя дугу АВ 3 раза, получим все точки.
Построения иными инструментами
1. Построения одним циркулем. Во многих случаях построения, проводимые циркулем, оказываются точнее, чем построения, проводимые линейкой.
Итальянский учений Л. Маскерони (1750-1800) и датский ученый Г.Мор (1640-1697) исследовали конструктивные возможности циркуля и доказали следующую теорему.
Теорема (Мора-Маскерони). Любая геометрическая задача на построение фигуры из конечного числа точек, разрешимая циркулем и линейкой может быть решена при наличии только циркуля.
Пояснения: 1) имеется в виду, что фигура состоит из конечного числа точек, окружностей, отрезков, лучей прямых; 2) циркулем конечно, нельзя построить прямую, отрезок, луч, здесь имеется в виду, что циркулем можно сделать их известными (прямая известна, если известны две ее точки; отрезок известен, если известны два его конца; луч известен, если известна начальная точка и точка, через которую проходит луч).
Доказательство опускаем.
2. Построения одной линейкой.
Построения одной линейкой исключительно ограничены. Например, отрезок нельзя разделить пополам. Но если на плоскости задана окружность, возможности увеличиваются.
Справедлива теорема. Всякая геометрическая задача на построение фигуры, состоящей из конечного числа точек, разрешимая циркулем и линейкой, может быть решена одной линейкой, если на плоскости построена окружность и отмечен ее центр (т.е. воли воспользоваться циркулем один раз). Это теорема Штейнера, иногда называют ее теоремой Понселе-Штейнера.
3. Построения двусторонней линейкой
Пример. Разделить данный угол пополам.

Проводим параллели, ОС – биссектриса
Оказывается, справедлива теорема
Всякая геометрическая фигура, состоящая из конечного числа точек, которая может быть построена циркулем и линейкой, может быть построена только двусторонней линейкой.
4. Построения с помощью прямого угла.
Пример. Построить центр начерченной окружности. Всякая геометрическая фигура, состоящая из конечного числа точек, которая может быть построена циркулем и линейкой, может быть построена только прямым углом. Это же верно для любого угла.

Пример 2. Дан ΔАВС; требуется построить три окружности так, чтобы каждая из них касалась двух других окружностей и двух сторон треугольника (задача Мальфатти). Считаем задачу решенной (фиг. 1). Пусть точка О будет центром вписанной в треугольник окружности (радиуса r). Радиусы кругов К и L обозначим соответственно через r1 и r2. Из точек К, О, L опустим перпендикуляры на сторону АВ и таким путем построим точки D, Е, F. Положим AE = s, BE = t, AD = x, BF = y.

Фиг. 2
Если мы проведем KG || AB, то
LG = r2 – r1 и KG =
Из подобия 7) треугольников ADK и AEO следует, что
аналогично этому и , что вытекает из подобия треугольников BFL и ВЕО.
AB = AD + DF + FB,
следовательно:
=
или (подставляя вместо r1 и r2 полученные для них выражения)
=
(1)
Если опустим из точек L, М,О перпендикуляры на сторону ВС и положим РС = и и QC = z, то получится равенство
2) = t + u;
аналогично мы получим равенство и для третьей стороны :
3) = u + s.
Таким образом, мы имеем три уравнения для определения трех неизвестных х, у, z.
Мальфатти сообщает решения этих трех уравнений,:
Если подставить эти значения в вышеприведенные уравнения, то они удовлетворят последним. Путь, которым Мальфатти нашел решения, чрезвычайно сложен, как он сам указывает.
Геометрическое же построение величин х, у, z представляется чрезвычайно простым, ибо
вследствие чего отрезки эти, равно как и отрезки s, t, r, u, r, легко могут быть построены.
Если же теперь построить выражение
x = ОА — m, у = ОБ — m,
z = OC – m (фиг. 2).
Пример 3. Даны три окружности K1, K2, К3, коих центры лежат на одной прямой; радиус каждой из окружностей К1, К2 равен r2. Последние две окружности имеют одно и то же центральное расстояние а от окружности К1{r1). Требуется построить все окружности, которые касаются трех данных (фиг. 3).

Фиг.3.
Для того, чтобы решить эту задачу вычислением, мы кладем в основание прямоугольную систему координат. При этом уравнения данных окружностей таковы:
К1 … х2+у2 = ,
K2 … (x – a)2 + y2 =
K3 … (x + a)2 + y2 =
Уравнение же каждой из искомых окружностей имеет вид:
(x – pi)2 + (y – qi)2 = ρi2.
Для круга О1 (фиг. 3) легко могут быть получены три уравнения, определяющие три неизвестные велиeчины p1, q1, ρ1; именно, из условий
вытекают равенства
Из двух последних следует, что p1 = 0, а отсюда уже непосредственно вытекает:
(1)
ибо радиус круга О2 равен радиусу ρ1 круга О1 (фиг. 3).
Окружность О3 касается окружностей К2 и К3 извне, а окружности К1 — изнутри; таким образом, имеют место равенства
Отсюда получается
(2)
Для окружности О5 имеют место равенства
откуда получается:
Построение может быть выполнено по следующему плану. Строим по порядку (фиг. 3):
AB = r2, BC = a,
тогда
если затем построить
Аналогично построим
1. Весьма удобным методом для решения геометрических задач на построение является метод геометрических мест.
Он основывается на следующем: стараются свести всю задачу к нахождению некоторой точки X, что в большей части случаев сделать не трудно.
Точка X определяется двумя условиями, вытекающими из требования задачи. Если устранить первое из условий, то существует не одна только точка X, но бесчисленное множество таких точек, составляющих в совокупности некоторую линию, некоторое геометрическое место. Если же устранить второе условие и ограничиться первым, то получится другое геометрическое место. Каждая точка пересечения этих двух геометрических мест удовлетворяет требованиям задачи.
2. Является необходимым предварительно изучить некоторые геометрические места. Мы приведем наиболее простые и вместе с тем наиболее употребительные из них.
a) Геометрическое место точек, находящихся от данной точки на данном расстоянии, есть окружность, описанная из данной точки, как из центра, радиусом, равным данному расстоянию.
b) Геометрическое место точек, находящихся на данном расстоянии от данной прямой, состоит из двух прямых, проведенных параллельно данной прямой, на данном от нее расстоянии.
c) Геометрическое место точек, равноотстоящих от двух данных точек А и В, есть прямая, перпендикулярная к отрезку АВ в его середине. (Симметраль точек А и В).
d) Геометрическое место точек, равноотстоящих от двух данных прямых, состоит из двух взаимно перпендикулярных прямых делящих пополам углы между данными прямыми (биссектрисы).
e) Геометрическим местом точек, из которых отрезок АВ виден под данным углом а, является дуга окружности, стягиваемая* отрезком АВ (построение ясно из фиг. 4).

Фиг. 4 Фиг. 5
f) Геометрическое место точек, расстояния которых от двух данных точек находятся в данном отношении m : n, есть некоторая, окружность (фиг. 5)
При этом
Откуда по известной теореме получается , что < APP1 = < P1PB.
Имеет место также пропорция
AP1😛1B = AP2:BP2
Четыре такие точки называются, как известно, четырьмя гармоническими точками.
g) Геометрическое место точек, расстояния которых от двух данных прямых находятся в данном отношении m : n, образуется двумя прямыми линиями х и у, проходящими через точку пересечения данных прямых (фиг. б).
h) Геометрическое место точек, квадраты расстояний которых от двух данных точек А и В сохраняют постоянную разность d2, есть прямая, перпендикулярная к отрезку АВ.

Фиг. 6 Фиг.7
Доказательство: Пусть точка Р1 (фиг. 7) обладает указанным свойством, так что
Если опустить из точки P1 на АВ перпендикуляр и взять на нем произвольную точку Р1 то
Из h) может быть выведено следствие, которое позже для нас будет важно. Мы лишь предпошлем ему краткое замечание:
а) Как известно, справедливо следующее предложение: „Если через точку Р (фиг. 8а, 8Ь) провести секущие к окружности, то постоянно
РА .РА’ = РВ.РВ’ = … “
Эго постоянное произведение называется степенью точки Р в отношении данной окружности; степень равна d2 — r2, где d есть расстояние точки Р от центра (центральное расстояние точки Р), r есть радиус окружности.

Фиг. 8а Фиг. 8б
Е сли точка Р лежит вне окружности, то степень точки также р
авна РТ2.
β) Если даны две окружности с центрами О1 и О2, то точка Р имеет определенную степень по отношению к каждой из них. Если же точка Р по отношению к обеим окружностям (с радиусами r1 и r2) имеет одну и ту же степень, то
так что
следовательно, геометрическое место точек, имеющих одну и ту же степень в отношении обеих окружностей, есть (согласно h) прямая, перпендикулярная к линии центров этих окружностей; прямая мл называется радикальной осью обеих окружностей.
Если окружности пересекаются, то их радикальная ось проходит через точки их пересечения, ибо каждая из точек пересечения имеет в отношении обеих окружностей степень, равную нулю.
Если же окружности не пересекаются, то радикальную ось можно построить (фиг. 9), опустив перпендикуляр на линию центров из середины общей касательной к обеим окружностям; можно при этом следовать и другому пути, пользуясь теоремой: „Если даны на плоскости три окружности, то определяемые ими три радикальные оси проходят через одну и ту же точку (радикальный центр трех окружностей)”; доказательство теоремы основывается на том соображении, что точка пересечения двух каких-либо радикальных осей имеет одну и ту же степень в отношении всех трех окружностей, следовательно, лежит на третьей радикальной оси.

Фиг. 9
3. Мы разъясним метод геометрических мест на двух примерах:
а) Даны две окружности О1, О2 радиусов r1 и r2.
Требуется построить такую окружность К1 которая касалась бы обеих данных окружностей и имела бы данный радиус r.
Если откинуть требование, чтобы окружность К касалась окружности О2, то искомых окружностей существует бесчисленное множество; геометрическое место их центров состоит из двух концентрических с О1 окружностей, радиусы которых соответственно равны r1 + r и r1 — r. Аналогично мы получим для искомого центра X и другое геометрическое место, состоящее из двух окружностей, описанных из точки О2, как из центра, радиусами
Точка X должна совпасть с одной из точек пересечения обоих геометрических мест; существует не больше восьми точек, удовлетворяющих требованиям задачи.
β) Даны три окружности K1, К2, К3; требуется построить все окружности, касающиеся трех данных (Аполлониева задача о касании).
Если (фиг. 10) через центр одной из данных трех окружностей, например, через центр окружности /С3, провести окружность, концентрическую с искомой X, то окажется, что упомянутая выше задача сведется к следующей:
Даны две окружности К΄1, К΄2 и точка Р΄; требуется построить окружности, касающиеся двух данных и проходящие через точку Р΄΄.

Фиг. 10
Геометрическое место центров всех окружностей, которые касаются окружности К1΄΄ и проходят через точку Р, есть эллипс или гипербола, в зависимости от того, лежит ли Р внутри окружности К΄1 или вне ее.
Центр окружности К΄1 и точка Р являются фокусами этих конических сечений; асимптоты гиперболы перпендикулярны к касательным, которые можно провести к окружности К΄1 из точки Р.
Каждая из данных трех окружностей может свестись и к одной точке или перейти в прямую. Геометрическое место центров окружностей, которые касаются прямой l и проходят через точку Р, есть парабола, имеющая прямую l своей директрисой, а фокус — в точке Р.
Вариант 15
-
Построить треугольник ΔАВС по а, с-b,
-
Построить трапецию по отношению боковых сторон, углу между ними и двум основаниям.
-
Даны прямая МN и точки A и В в одной полуплоскости относительно прямой MN. Поcтроить на прямой МN точку X такую, что
.
4. Вписать в данный четырехугольник параллелограмм так, чтобы его центр совпал c данной точкой.
5. В данном круге через данную внутри его точку А провести хорду так, чтобы она в точке А разделилась в отношении m : n.
6. Построить треугольник с данным отношением сторон длин биссектрисы и медианы, проведенных из одной вершины.
7. Построить прямоугольной треугольник по радиусам описанной окружности R и вписанной окружности r.
8. На приведeнных ниже чертежах дано схематичное решение четырех задач на, построение. Сформулировать эти задачи и дать их полное решение.
9. Построить ромб, зная его сторону а и отношение диагоналей р : q, где p и q заданные отрeзки. Решить задачу двумя способами.
10. Рассматриваются всевозможные треугольники c данными основанием a, угол при вершине которых равен φ. Найти множество точек пересечения медиан
54
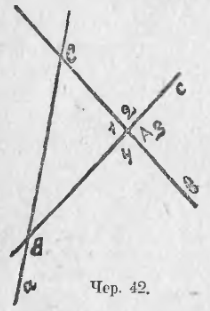
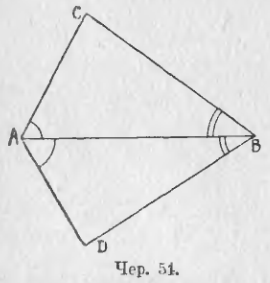
36. Мы уже рассматривали фигуру, состоящую из двух пересекающихся прямых (вертикальные углы, п. 18). Присоединим к ним еще третью прямую, пересекающую каждую из первых двух прямых в отдельно точке. Получим фигуру, данную на чер. 42: прямая a и прямая b пересекаются в точке C, прямые b и c – в точке A и прямые c и a – в точке B (мы называем для сокращения письма и речи каждую прямую одною малою буквою). Построенная фигура называется треугольником. Слово «треугольник» обозначается знаком Δ; обыкновенно треугольник обозначают тремя буквами, которыми названы три точки пересечения прямых. На чер. 42 имеем ΔABC.
Прямые a, b и с называют сторонами треугольника, точки A, B и C – его вершинами. Треугольник разделяет плоскость на 7 областей, из которых 6 бесконечны, а одна конечная. Эта последняя ограниченна сторонами треугольника и называется площадью треугольника. При каждой вершине треугольника образуется по 4 угла меньших выпрямленного, например, ∠1, ∠2, ∠3 и ∠4 при точке A; внутренняя область одного из них, а именно ∠1, захватывает площадь треугольника (или: площадь треугольника лежит внутри ∠1) – этот угол называется внутренним углом треугольника, а остальные три (∠2, ∠3 и ∠4) – внешними. Среди внешних углов рассматривают обыкновенно лишь один при каждой вершине: при точке A ∠2 или ∠4, которые равны между собою как вертикальные, а ∠3 = внутреннему ∠1 на том же основании. Всего имеем в треугольнике 3 внутренних угла, которые часто называются просто углами треугольника.
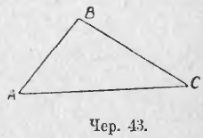
Название «сторона треугольника» употребляется в двух смыслах: 1) этим именем называют, как указано выше, одну из трех прямых, напр., прямую a, неопределенно продолженную, 2) этим же именем называют отрезок этой прямой между двумя вершинами, напр., отрезок BC. Если вопрос таков, что приходится рассматривать только отрезки наших трех прямых, то треугольник изображают так, как на чер. 43.
В треугольнике обыкновенно рассматривают 6 элементов: три стороны (отрезки) AB, BC и CA и 3 внутренних угла – ∠A, ∠B и ∠C.
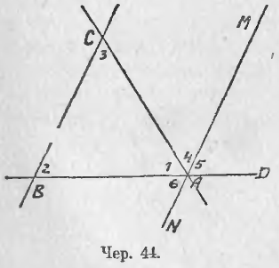
37. Рассматривая ΔABC (чер. 42), мы видим, что здесь является возможным применить построение п. 29. Именно в конце п. 29 мы пришли к заключению, что если дана прямая и вне ее точка, то через эту точку можно построить прямую, параллельную данной. На чер. 42 мы можем, например, счесть прямую a за данную прямую и точку A за данную точку (либо: прямую b и точку B, либо прямую c и точку C). Построим же через точку A прямую, параллельную стороне BC (или прямой a). Получим фигуру, данную на чер. 44, где MN || BC. Назовем внутренние углы ΔABC нумерами 1, 2, 3 и занумеруем еще нумерами 4, 5 и 6 некоторые углы при точке A, полученные после построения прямой MN (см. чер. 44). Мы видим, что при точке A выполнено сложение нескольких углов. Например, мы видим, что
∠1 + ∠4 + ∠5,
причем сумма равна выпрям. углу BAD, т. е.
∠1 + ∠4 + ∠5 = выпрям. углу.
Но ∠4 = ∠3, так как это внутренние накрест-лежащие углы при параллельных BC и MN и секущей AC; также ∠5 = ∠2 как соответственные углы при параллельных BC и AM и секущей BD. Поэтому в предыдущем равенстве мы можем заменить ∠4 и ∠5 углами 3-м и 2-м; тогда получим
∠1 + ∠3 + ∠2 = выпр. углу,
т. е. оказывается, что во всяком треугольнике сумма внутренних углов (если их сложить) равна выпрямленному углу.
К тому же результату мы придем, если обратим внимание, что при точке A выполнено сложение ∠6, ∠1 и ∠4, причем сумма равна выпрям. углу NAM. Здесь, следовательно, мы видим:
∠6 + ∠1 + ∠4 = выпр. углу.
Но мы знаем, что ∠6 = ∠2, как внутр. накр.-леж. при параллельных BC и NM и секущей BD и ∠4 = ∠3, как внутр. накр.-леж. при тех же параллельных и секущей CA. Поэтому заключаем, что
∠2 + ∠1 + ∠3 = выпр. углу.
Обратим еще внимание на ∠CAD, являющийся внешним для ΔABC. Мы видим, что лучом AM он разбит на 2 слагаемых, на ∠4 и ∠5, т. е.
∠CAD = ∠4 + ∠5.
Но, как мы уже выяснили, ∠4 = ∠3 и ∠5 = ∠2; следовательно.,
∠CAD = ∠3 + ∠2.
Эти 2 угла (∠3 и ∠2) являются внутренними углами ΔABC, не смежными с ∠CAD (с ∠CAD смежен ∠1). Поэтому мы заключаем:
Внешний угол треугольника (образованный одною его стороною и продолжением другой) равен сумме двух внутренних углов с ним не смежных.
Мы можем из чертежа 44 выделить только те элементы, которые необходимы для выяснения полученных свойств, и удалить все остальное, не нужное, тогда получим упрощенный чертеж. На чертежах 45 и 46 даны 2 таких упрощенных чертежа. Для чер. 45 имеем:
1) ∠1 + ∠4 + ∠5 = выпр. углу, но ∠4 = ∠3 и ∠5 = ∠2; след., ∠1 + ∠3 + ∠2 = выпр. углу.
2) ∠CAD = ∠4 + ∠5, но ∠4 = ∠3 и ∠5 = ∠2. Следов, ∠CAD = ∠3 + ∠2.
Для чер. 46 имеем: ∠6 + ∠1 + ∠4 = выпр. углу, но ∠6 = ∠2 и ∠4 = ∠3, следов., ∠2 + ∠6 + ∠3 = выпр. углу.
38. Задача. Построить Δ с такими же сторонами, как у данного треугольника. Пусть дан ΔABC (чер. 47). Строим где-либо прямую и на ней при помощи циркуля откладываем отрезок MN = AC. Таким образом мы получили две вершины искомого треугольника M и N. Чтобы найти третью вершину, воспользуемся задачею п. 27: надо найти такую точку, чтобы отрезок, соединяющий ее с точкой M, был равен AB и отрезок, соединяющий ее с точкою N, был = CB. Эти круги пересекутся в двух точках P и Q; соединив эти точки прямыми с M и N, получим два искомых треугольника: один ΔMPN и другой ΔMQN (MN = AC; MP = MQ = AB; NP = NQ = CB). Примем, что два круга не могут пресекаться более, чем в двух точках (впоследствии этот вопрос будет разъяснен в п. 128). Согласно п. 26 точки пересечения наших кругов P и Q расположены симметрично относительно линии центров MN. Поэтому при перегибании всей фигуры по оси симметрии MN точка P должна совместиться с точкою Q, а, следовательно, ΔMPN совместиться с ΔMQN. Согласно п. 2, мы можем назвать эти треугольники равными или конгруэнтными.
Если мы повторим где-либо на ином месте плоскости предыдущее построение, то получим еще 2 треугольника DEF и DEK с такими же сторонами, как у ΔABC (DE = AC; DF = DK = AB, EF = EK = CB). Также в силу того, что прямая DE есть ось симметрии всей фигуры, мы заключим, что эти два треугольника равны или конгруэнтны между собою. Возникает теперь вопрос: можно ли добиться того, чтобы какой-либо из треугольников второй пары (напр., ΔDEF) совпал с каким-либо треугольником первой пары (напр., с ΔMPN)?
Круги позволят решить этот вопрос. Передвинем нижнюю фигуру чертежа 47 так, чтобы точка D совпала с точкой M и точка E с точкой N (этого добиться можно потому, что MN = DE, – каждый из этих отрезков = AC). Тогда круги фигуры DFEK совпадут соотв. с кругами фигуры MPNQ (ибо радиусы этих кругов соотв. равны между собою и центры их совместились). Поэтому и точки пересечения этих двух пар кругов должны совместиться, т. е., напр., точка F совместится с точкою P и точка K с Q. Отсюда заключаем, что и ΔDEF должен совместиться с ΔMNP, что принято записывать в виде ΔDEF = ΔMNP. Мы также могли бы к ΔABC пристроить два круга, принимая точки A и C за центры и отрезки AB и CB за радиусы, и также при помощи этих кругов пришли бы к заключению, что
ΔABC = ΔMPN = ΔMQN = ΔDFE = ΔDKE.
Итак, если построить два треугольника с попарно равными сторонами, то эти треугольники конгруэнтны (или равны).
(Следует помнить, что для геометрических фигур слова «конгруэнтны» или «равны» означают, что эти фигуры совпадают при наложении).
39. В предыдущем п. мы научились строить равные треугольники. Пусть ΔA’B’C’ = ΔABC (чер. 48) и при наложении сторона A’B’ совпадает с AB, B’C’ – с BC и A’C’ – с AC. Тогда и углы этих треугольников совпадают, а именно ∠C’ с ∠C, ∠A’ с ∠A и ∠B с ∠B, т. е. ∠C’ = ∠C, ∠A’ = ∠A и ∠B = ∠B. Ясно, что в равных треугольниках равные углы лежат против равных сторон и обратно: равные стороны против равных углов.
40. Задача. Построить треугольник по трем данным сторонам.
Пусть даны три отрезка a, b и c (чер. 49); требуется построить треугольник так, чтобы его стороны были соответственно равны данным отрезкам.
Строим где-либо один из данных отрезков a; тогда определяется две вершины треугольника B и C. Третья вершина должна расположиться так, чтобы отрезок, соединяющий ее с точкою B, был = с и отрезок, соединяющий ее с точкою C, был = b; поэтому нахождение ее сведется к задаче п. 27: надо, принимая B за центр, построить круг радиусом = c, и принимая C за центр, – круг радиусом = b и точку пересечения этих кругов, напр., точку A, соединить с точками B и C – тогда ΔABC и есть искомый. Соединив другую точку пересечения окружностей A’ с точками B и C, получим другой такой же Δ, расположенный симметрично с первым относительно оси BC.
Для того, чтобы задача была возможна, надо, чтобы: 1) a – b < c или c > a – b и 2) a + b > c или c < a + b, т. е. чтобы один из данных отрезков был больше разности двух других и меньше их суммы.
41. Пусть теперь даны 2 отрезка a и b (чер. 50). Требуется построить треугольник так, чтобы его стороны были a, b и b (задача возможна, если a < b + b или a < 2b).
Согласно предыдущему п., построение легко выполняется и получим, напр., ∆ABC, у которого две стороны (AB и AC) равны между собой. Такой ∆ называется равнобедренным; та его сторона, которая не имеет себе равных (в ∆ABC сторона BC = a), называется основанием равнобедренного треугольника, а противоположная вершина A называется «вершиною равнобедренного треугольника», причем этим названием эта вершина A как бы выделяется из остальных вершин.
Вообразим, что ∆ABC повернут другою стороною, то новый ∆ABC (чер. 50 — справа) можно простым передвижением совместить с прежним: сторона BC левого треугольника равна стороне CB правого, сторона AB левого = стороне AC правого и сторона AC левого = стороне AB правого, а мы уже знаем, что если стороны двух треугольников попарно равны, то эти треугольники равны, т. е. при наложении совмещаются (п. 38) и ∠B левого треугольника равен, следовательно, углу C правого, или, что то же самое, углу C тоже левого треугольника. Итак, в равнобедренном ∆ABC, у которого AB = AC, ∠B также = ∠C. Это свойство выразим словами:
В равнобедренном треугольнике углы при основании равны
или
В треугольнике, у которого две стороны равны, против равных сторон лежат равные углы.
42. Построим, наконец, ∆, у которого все 3 стороны равнялись бы данному отрезку a. Построение легко выполнить (чер. 50 bis). Этот ∆ называется равносторонним. Легко видеть, что этот ∆ можно счесть за равнобедренный с основанием CB; тогда ∠C = ∠B. Но его можно принять и за равнобедренный с основанием AB и тогда ∠A = ∠B, откуда приходим к заключению, что в равностороннем треугольнике все 3 угла равны между собою.
43. В п. 38 мы получили признак равенства треугольников: если стороны двух треугольников попарно равны, то и треугольники равны. Теперь мы можем, накладывая один треугольник на другой, получить еще другие признаки.
Построим какой угодно ∆ABC (чер. 51); затем построим ∠O = ∠A (п. 28) и на сторонах этого угла отложим отрезки OD > AB и OE < AC). На чер. 51 даны пунктиром те дуги, которые необходимы для построения ∠O = ∠A. Соединив точки D и E, получим ∆ODE. Наложим ∆ODE на ∆ABC так, чтобы ∠O совпал с ∠A (ведь ∠O = ∠A). В силу неравенств OD > AB и OE < AC, ∆ODE при этом наложении не совместится с ∆ABC (следует нарисовать, как именно расположится ∆ODE при этом наложении). Построим еще ∆O’D’E’ так, чтобы 1) ∠O’ = ∠A, 2) ∠O’D’ = ∠AB и 3) O’E’ < AC. Тогда при наложении треугольника O’D’E’ на ∆ABC так, чтобы ∠O’ совместился с ∠A, легко уясним, что и вершина D’ должна также совместиться с точкою B (в силу равенства O’D’ = AB), но точка E’ не совпадет с точкою C, – треугольники опять не совместятся (нарисовать их расположение при указанном наложении!). Теперь легко ответить на вопрос: как надо изменить сторону O’E’ треугольника O’D’E’, чтобы быть убежденным, что этот ∆ совместится с ∆ABC?
Надо, ответим мы, увеличить сторону O’E’ так, чтобы она сделалась равною стороне AC.
Итак, если мы построим ∆O”D”E” так, чтобы 1) ∠O” = ∠A, 2) O”D” = AB и 3) O”E” = AC, то мы можем быть убеждены, что ∆O”D”E” = ∆ABC. Замечая, что ∠O” и ∠A составлены попарно равными сторонами (на чертеже равные стороны и равные углы отмечены одинаковыми значками), мы можем сделать заключение:
Если построены два треугольника так, что у них по две равных стороны и углы, составляемые этими сторонами, также равны, то эти треугольники равны.
44. Построим два вертикальных угла при точке A – они, мы знаем, равны (чер. 52) и на сторонах этих углов отложим попарно равные отрезки AB = AD и AC = AE (это можно сделать двумя способами, почему на чер. 52 даны две фигуры I и II). Равны ли полученные треугольники? Как надо переместить ∆AED, чтобы он совпал с ∆ABC? Указать, какой угол одного из каждой пары треугольников равен какому-либо углу другого (можно воспользоваться п. 39 или выяснить, как именно расположится ∆AED при совмещении его с ∆ABC).
45. Построим какой-либо ∆ABC (чер. 53); затем построим ∆ODE так, чтобы сторона DE = стороне BC, чтобы ∠D был больше ∠B, но ∠E был меньше ∠C. Наложим ∆ODE на ∆ABC так, чтобы DE совпала с BC (точка D с B и точка E с C); этого добиться можно, так как эти стороны равны по построению.
Тогда, в силу того, что ∠D > ∠B и ∠E < ∠C, ∆ODE не совместится ∆ABC (следует нарисовать, как именно при этом наложении расположится ∆ODE). Построим еще ∆O’D’E’ так, чтобы D’E’ = BC, а также ∠E = ∠C, но, по-прежнему, ∠D’ был больше ∠B. Тогда при наложении ∆O’D’E’ на ∆ABC так, чтобы точки D’ и E’ совпали соответственно с точками B и C, увидим, что сторона E’O’ пойдет вне угла B (∠D’ > ∠B) и точка O’ не совпадет с точкою A (следует нарисовать расположение этих треугольников при рассматриваемом наложении). ∆O’D’E’ опять не совместиться с ∆ABC.
Теперь не трудно ответить на вопрос: как надо изменить ∠D’, чтобы добиться совпадения ∠O’D’E’ с ∆ABC? Надо, ответим мы, уменьшить ∠D’ так, чтобы он сделался равен ∠B.
Итак, если мы построим ∆O”D”E” так, чтобы 1) D”E” = BC, 2) ∠E” = ∠C и 3) ∠D” = ∠B, то мы можем быть убеждены, что ∆O”D”E” = ∆ABC. Замечая, что равные стороны D”E” и BC этих треугольников расположены между соответственно равными углами (на чертеже равные стороны и равные углы отмечены одинаковым знаками), мы можем установить еще признак равенства треугольников:
Если построены 2 треугольника так, что они имеют по два равных угла и по равной стороне между этими углами, то такие треугольники равны.
46. Построим какой-либо ∆ABC (чер. 54) и при концах стороны AB построим ∠BAD = ∠CAB и ∠ABD = ∠ABC. Тогда получим ∆ABD.
Равны ли треугольники ACB и ABD? Как можно добиться совмещения этих треугольников? Указать равные стороны в этих треугольниках (можно воспользоваться п. 39).
47. Имея в виду пп. 38, 43 и 45, мы можем теперь свести вместе признаки равенства треугольников:
1) Если три стороны одного треугольника равны соответственно трем сторонам другого, то эти треугольники равны.
2) Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого, то эти треугольники равны.
3) Если два угла и сторона между ними одного треугольника равны соответственно двум углам и стороне между ними другого, то эти треугольники равны.
Прибавим сюда еще заключение п. 39: в равных треугольниках равные углы расположены против равных сторон и равные стороны против равных углов.
Для совмещения равных треугольников иногда бывает необходимо один из них перевернуть другою стороною.
48. Задача. Построить треугольник по двум данным сторонам и углу между ними.
Пусть даны 2 отрезка a и b и угол m (чер. 55). Требуется построить ∆ так, чтобы данные отрезки были его сторонами и угол, ими составленный, был = ∠m.
Строим: 1) при точке C угол, равный ∠m, 2) на сторонах построенного угла откладываем CB = a и CA = b, 3) соединяем точки A и B. Получим искомый ∆ABC.
49. Задача. Построить треугольник по данной стороне и двум прилегающим к ней углам.
Дан отрезок a и 2 угла m и n (чер. 56); требуется построить ∆ так, чтобы одна из его сторон = a и углы, к ней прилегающие, были равны ∠m и ∠n.
Строим: 1) отрезок BC = a, 2) при точке B угол = ∠m и при точке C угол = ∠n так, чтобы одна сторона каждого из этих углов шла по BC; точка пересечения A других сторон построенных углов даст вершину A искомого треугольника.
Может случиться, что стороны построенных углов или вовсе не пересекаются (параллельны между собою – это случится, если ∠m + ∠n = выпр. углу) или пересекутся по другой стороне от BC; в последнем случае получится треугольник, у которого к стороне a прилегают углы не m и не n, а дополняющие их до выпрямленного.
Мы знаем, что сумма всех трех внутренних углов треугольника равна выпрямленному углу, а сумма двух внутренних его углов должна быть, следовательно, меньше выпрямленного. Поэтому для возможности данной задачи необходимо, чтобы было: ∠m + ∠n < выпрямленного угла.
Упражнения
- Построить равнобедренный треугольник по углу при его вершине и по боковой стороне.
- Построить равнобедренный треугольник по основанию и по углу при основании.
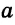
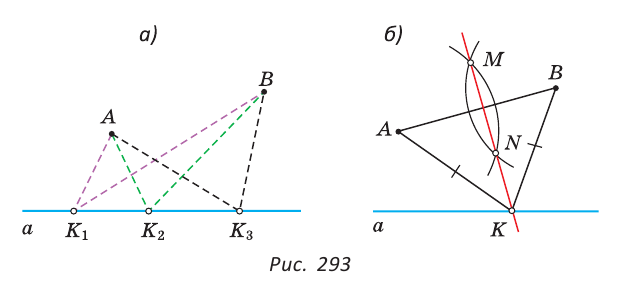

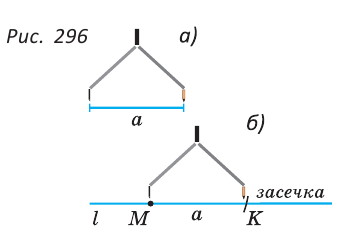
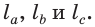
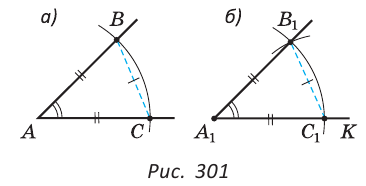
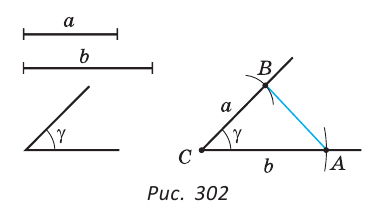
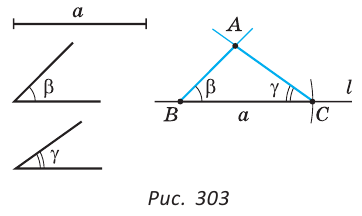
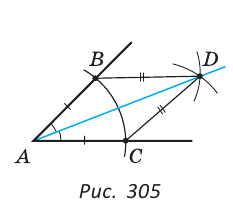
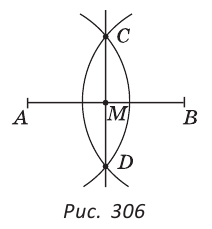
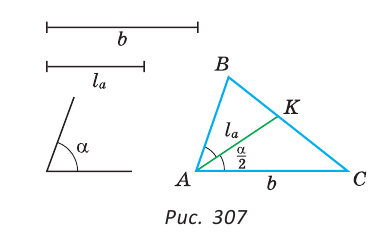
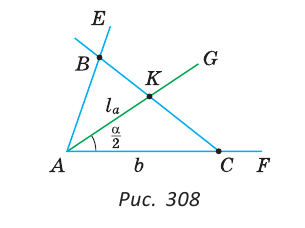
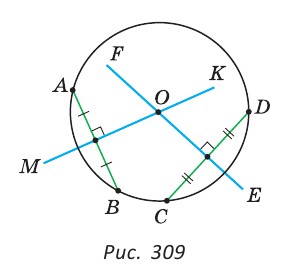
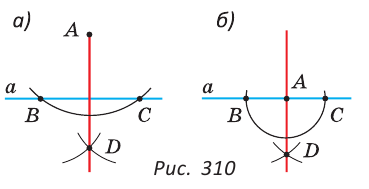
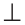
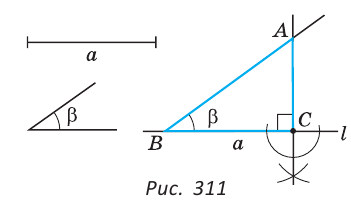
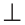
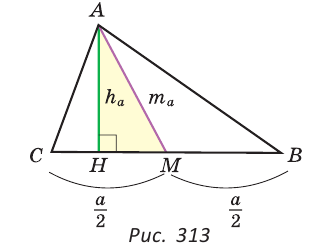
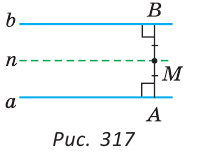
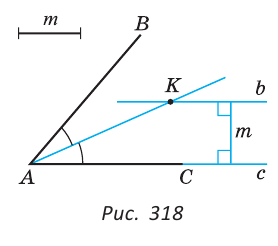
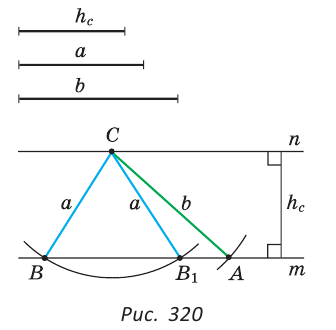

 провести прямую, а также через заданные две точки
провести прямую, а также через заданные две точки  и
и  провести прямую
провести прямую  ;
;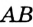 .
.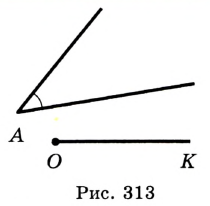
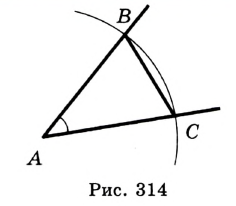
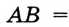
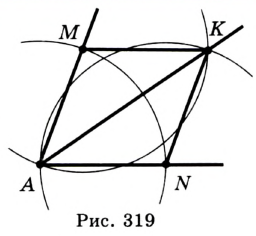
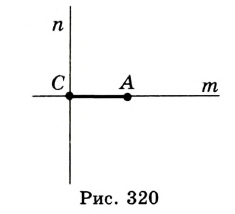
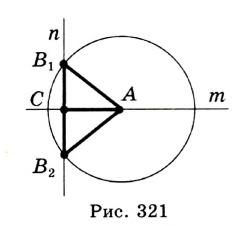
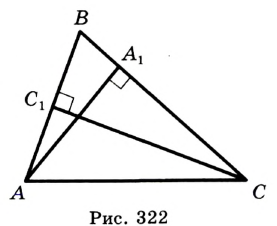
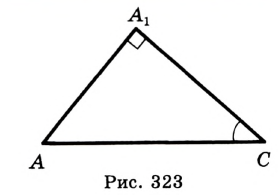
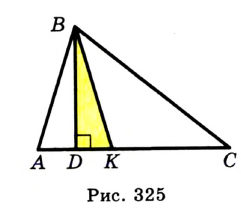
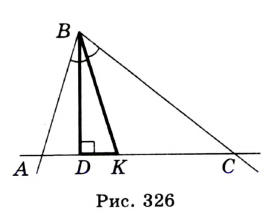
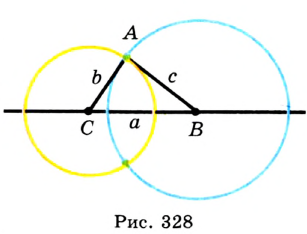
 на расстояние
на расстояние  с, т. е. «синей» окружности (рис. 328);
с, т. е. «синей» окружности (рис. 328); на расстояние
на расстояние  , т. е. «желтой» окружности (рис. 328).
, т. е. «желтой» окружности (рис. 328).