Угол между скрещивающимися прямыми : определение, примеры нахождения
В статье рассматриваются определения угла между скрещивающимися прямыми с приведением графических иллюстраций. При имеющихся координатах направляющих векторов заданных прямых научимся находить искомый угол. В заключительной части решим задачи на нахождение угла.
Угол между скрещивающимися прямыми – определение
Для нахождения искомого угла необходимо пройти несколько этапов.
Две прямые в трехмерном пространстве называются скрещивающимися в случае, если они не находятся в одной плоскости.
Из определения о скрещивающихся прямых следует, что они не являются параллельными или пересекающимися и не совпадают, тогда они находились бы в одной и той же плоскости.
Рассмотрим рисунок, приведенный ниже.

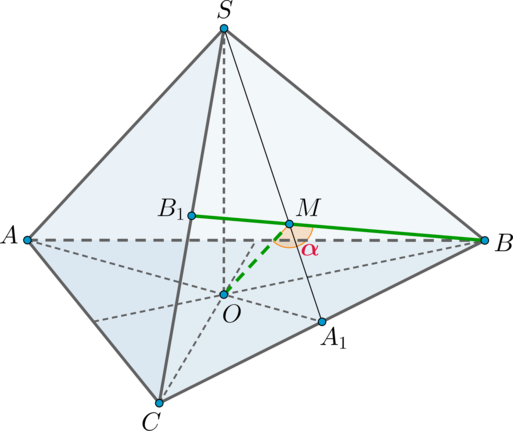
В трехмерном пространстве имеются скрещивающиеся прямые a и b . Проведем прямые а 1 и b 1 параллельные скрещивающимся a и b . Точка М1 является точкой пространства, через которую они проходят. Отсюда получаем, что а1 и b 1 являются пересекающимися прямыми.
Обозначим угол между a 1 и b 1 равным значению α . Построение прямых a 2 и b 2 параллельно скрещивающимися относительно a и b в точке М 2 отличной от М 1 приводит к тому, что значение угла между ними обозначим как α . То есть угол между прямыми a 1 и b 1 равен углу между a 2 и b 2 . В этом можно убедиться, если про/извести параллельный перенос. Тогда точки М 1 и М 2 совпадают.
Углом между скрещивающимися прямыми называют угол, который образуется между двумя параллельными заданными скрещивающимися прямыми.
Отсюда следует, что угол не зависит от точки M и ее выбора. Поэтому точка M может быть любой. Рассмотрим рисунок, приведенный ниже.

Нахождение угла между скрещивающимися прямыми
Угол между скрещивающимися прямыми определяется через угол пересекающихся прямых. Поиск угла сводится к его нахождению между пересекающимися прямыми пространства. Школьные методы решения основываются на необходимости построения на основе подобия фигур или теоремах косинуса, что позволит определить синус, косинус, тангенс угла прямоугольного треугольника.
Удобным способом решения считается нахождение угла методом координат. Рассмотрим его.
Трехмерное пространство имеет прямоугольную систему координат О х у z . Имеется задача, в которой необходимой найти угол α , образованный скрещивающимися прямыми a и b с заданными уравнениями прямых в пространстве.
Для решения необходимо взять произвольную точку в трехмерном пространстве и обозначить буквой M , что дает понять, через нее проходят прямые a 1 и b 1 , которые параллельны скрещивающимся a и b . Угол α , образованными прямыми a и b , из этого определения получится равным пересекающимся a 1 и b 1 .
Для нахождения искомого угла между a 1 и b 1 необходимо использовать формулу для нахождения угла между пересекающимися прямыми, а для этого нужно знать значение координат направляющих векторов у прямых a 1 и b 1 .
Для их получения необходимо применить определение направляющего вектора, которое говорит о том, что множества векторов совпадают. Направляющие векторы прямых обозначают a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) .
Векторы a → и b → имеют координаты, определяющиеся из условия по уравнению или по координатам точек пересекающихся прямых. Тогда получаем, что угол между двумя скрещивающимися прямыми a и b вычисляется из формулы α = a r c cos a → , b → a → · b → = a r c cos a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2 , а a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b .
Использование формулы для нахождения косинуса угла между скрещивающимися прямыми а и b дает выражение вида cos α = a → , b → a → · b → = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2 .
При помощи основного тригонометрического тождества можно найти синус угла между этими прямыми при известном косинусе из формулы sin α = 1 – cos 2 α .
Найти угол между скрещивающимися прямыми a и b , которые заданы уравнениями x 2 = y – 4 0 = z + 1 – 3 и x = 1 + λ y = 1 – λ z = – 3 + 4 · λ , λ ∈ R и определяются в системе координат О х у z .
Для определения координат необходимо использовать каноническое уравнение прямой в плоскости. необходимо обратить внимание на знаменатель дробей. Отсюда видно, что a → = ( 2 , 0 , – 3 ) является направляющим вектором прямой x 2 = y – 4 0 = z + 1 – 3 . При наличии параметрического уравнения можно определить координаты направляющего вектора, так как она равняются коэффициентам, тогда получаем, что b → = ( 1 , – 1 , 4 ) является направляющим вектором для прямой вида x = 1 + λ y = 1 – λ z = – 3 + 4 · λ , λ ∈ R .
Отсюда получаем, что имеются все необходимые формулы и данные для того, чтобы произвести вычисление угла между скрещивающимися прямыми. Имеем, что
α = a r c cos a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2 = a r c cos 2 · 1 + 0 · ( – 1 ) + ( – 3 ) · 4 2 2 + 0 2 + ( – 3 ) 2 · 1 2 + ( – 1 ) 2 + 4 2 = = a r c cos 10 13 · 18 = a r c cos 10 3 26
Ответ: угол между скрещивающимися прямыми равен a r c cos 10 3 26 .
Найти значение синуса и косинуса угла между скрещивающимися прямыми, где имеются ребра A D и В С , принадлежащие пирамиде A B C D , с известными вершинами с координатами A ( 0 , 0 , – 1 ) , B ( 5 , 7 , – 5 ) , C ( 3 , 7 , – 5 ) , D ( 1 , 3 , 1 ) .
A D → и B C → являются векторами соответствующих сторон заданной фигуры. Необходимо вычислить координаты с помощью имеющихся данных начала и конца.
Получаем, что A D → = ( 1 – 0 , 3 – 0 , 1 – ( – 1 ) ) ⇔ A D → = ( 1 , 3 , 2 ) B C → = ( 3 – 5 , 7 – 7 , – 5 – ( – 3 ) ) ⇔ B C → = ( – 2 , 0 , – 2 )
Из формулы cos α = a r c cos A D → , B C → A D → · B C → находим косинус угла между заданными скрещивающимися прямыми. Получаем выражение вида
cos α = 1 · ( – 2 ) + 3 · 0 + 2 · ( – 2 ) 1 2 + 3 2 + 2 2 · ( – 2 ) 2 + 0 2 + ( – 2 ) 2 = 6 14 · 8 = 3 2 7
Перейдем к вычислению синуса угла между этими прямыми. Подставляем значения и получаем, что sin α = 1 – cos 2 α = 1 – 3 2 7 2 = 19 2 7 .
Ответ: sin α = 19 2 7 , cos α = 3 2 7 .
В заключительном этапе рассмотрим задачу, в которой нужно найти угол между скрещивающимися прямыми с самостоятельно введенной системой координат.
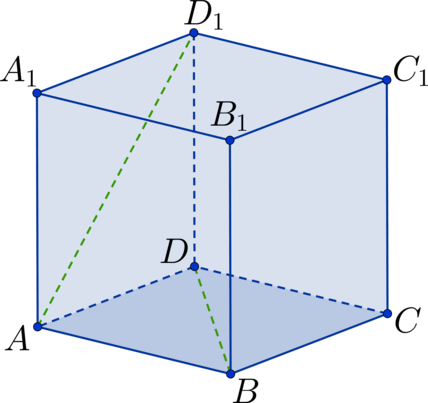
Имеется прямоугольный параллелепипед A B C D A 1 B 1 C 1 D 1 со сторонами А В = 3 , А D = 2 и A A 1 = 7 единиц. Точка E делит прямую А А 1 как 5 : 2 . Определить угол между скрещивающимися прямыми В Е и А 1 С .
Ребра заданного параллелепипеда являются взаимно перпендикулярными, поэтому необходимо ввести прямоугольную систему координат для определения угла между указанными скрещивающимися прямыми с помощью метода координат.
Для начала вводится прямоугольная система координат О х у z . Получаем, что начало координат является совпадающим с вершиной A , а О х совпадает с прямой A D , О у с A B , а О z с А А 1 . Рассмотрим рисунок, приведенный ниже.

Отсюда имеем, что точка B с координатами ( 0 , 3 , 0 ) , E – ( 0 , 0 , 5 ) , A А – ( 0 , 0 , 7 ) , C – ( 2 , 3 , 0 ) . Исходя из координат, мы можем получить координаты векторов B E → и A 1 C → , необходимые для дальнейшего решения задачи. Получаем, что B E → = ( 0 , – 3 , 5 ) , A 1 C → = ( 2 , 3 , – 7 ) .
Применим формулу для нахождения угла, образованного скрещивающимися прямыми, при помощи координат направляющих векторов. Получаем выражение вида
α = a r c cos B E → , A 1 C → B E → · A 1 C → = a r c cos 0 · 2 + ( – 3 ) · 3 + 5 · ( – 7 ) 0 2 + ( – 3 ) 2 + 5 2 · 2 2 + 3 2 + ( – 7 ) 2 = = a r c cos 44 34 · 62 = a r c cos 22 527
Математика для блондинок
Математика – это очень просто, даже проще, чем мы можем себе представить. Сложной математику делают сами математики.
Страницы
четверг, 14 марта 2013 г.
Куб и угол между прямыми
Сейчас решим задачу про куб и угол между прямыми. Задача звучит так:
Точка Е – середина ребра АА1 куба ABCDA1B1C1D1. Найдите угол между прямыми DE и BD1.
Для начала нужно соорудить конструкцию куба и разукрасить её буквами обозначений. Затем попробуем разобраться, чего надобно этим старцам от математики. Рисуем куб и прямые линии.
Получилось, что одна прямая линия совпадает с диагональю куба, вторая прямая линия проходит через боковую грань куба. Математики такие лини называют скрещивающиеся прямые. Угол между скрещивающимися прямыми определяется (не в смысле математическое определение типа “бла-бла-бла”, а когда конкретное дело делается) как угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым. Это не я такой умный, это у меня книжка умная есть, там и вычитал.
Возьмем ту прямую, которая на боковой грани и проведем параллельную ей прямую линию, проходящую через вершину D1. В этом случае мы получили две пересекающиеся прямые, для которых уже можно определить угол.
| Скрещивающиеся и пересекающиеся прямые |
Для определения угла нам нужны размеры куба. Без этого математика бессильна. Поскольку, по условию задачи, размеры куба нам не заданы, мы можем сами выбрать любой, благо все три размера у куба одинаковы. Примем длину ребра нашего куба за единицу. Получился куб в собственном соку, то есть в собственных единицах измерения. Весь этот математический фокус заключается в том, что угол между заданными нам прямыми совершенно не зависит от размеров куба. И в большом кубе, и в маленьком кубике углы между этими прямыми будут одинаковы.
Дальше всё просто, как в реанимации. Назначаем пациенту, то есть кубу:
1. Две теоремы Пифагора для двухмерного пространства.
2. Одну теорему Пифагора для трехмерного пространства.
3. Одну теорему косинусов.
4. Одну таблицу косинусов.
Теперь разберемся, к каким местам на теле куба всё это нужно прикладывать.
| Два прямоугольных треугольника, диагональ куба, искомый угол в треугольнике |
Рассуждаем от конца к началу. По таблице косинусов мы можем найти значение угла в градусах. Значение косинуса угла можно найти по теореме косинусов, если знать размеры сторон синенького треугольника из рисунка выше. По теореме Пифагора для трехмерного пространства мы можем найти диагональ куба – это одна из сторон треугольника. Две другие стороны треугольника можно найти на гранях куба по обычной (двухмерной) теореме Пифагора. А вот для применения теоремы Пифагора нам необходимы числовые размеры куба. Ведь просто слово “ребро” во вторую степень возвести не возможно. Вот для этого мы и приняли в самом начале размер ребра равным единице.
Мы проутюжили наше решение от начала к концу и от конца к началу. Лично у меня оно где-то по середине и срослось, на теореме Пифагора. Что бы там не утверждали наши современные математики, а математических инструментов мощнее тригонометрии и теоремы Пифагора они так и не создали.
Для полного счастья нам нужно ещё рассмотреть теорему косинусов. Ведь тупо записать её могут многие, а вот применять на практике этот калейдоскоп символов нужно ещё уметь. Посмотрите, как буковки в формулах переливаются! Это и есть первозданная красота математики.
Что такое математическая функция арккосинус? Это очень умное выражение, которым нас пугают математики. А фактически это наша голова и таблица косинусов перед глазами. Или специальная кнопочка на калькуляторе. Только вместо команды “Бобик, фас!” ( косинус – найти число по значению угла), нужно выполнять команду “Фас, покусай Бобика!” (арккосинус – найти значение угла по числовому значению косинуса).
Пусть у нас неизвестный угол будет по кличке “гамма”, а диагональку куба мы обзовем “а”. Отрезок прямой, что расположен на грани куба прямо перед нами, будет именоваться “с”, а на грани слева – “b”. Вот теперь можно погонять циферки и получить числовое решение задачи.
Как найти угол между параллельными прямыми в кубе
В кубе найдите углы между прямыми AB и
Так как CC1||BB1, достаточно найти угол между AB и BB1. ABB1A1 — квадрат, все углы которого равны 90°, это и будет ответ.
Ответ:
Аналоги к заданию № 410: 411 Все
В кубе найдите углы между прямыми и
Ответ:
Аналоги к заданию № 410: 411 Все
В кубе найдите углы между прямыми и
Так как AC||A1C1, достаточно найти угол между прямыми B1D1 и A1C1. ABCD — квадрат, в котором диагонали AC и BD пересекаются под углом 45°, это и будет ответ.
Ответ:
Аналоги к заданию № 412: 413 Все
В кубе найдите углы между прямыми и
Ответ:
Аналоги к заданию № 412: 413 Все
В кубе найдите углы между прямыми и
Заметим, что прямая D1C1 перпендикулярна плоскости BB1C, а прямая C1B перпендикулярна прямой B1C. Так как D1C1 перпендикулярна плоскости BB1C, C1B — наклонная от прямой D1C1 к этой плоскости, а C1B — её проекция, DC1 перпендикулярна B1C по теореме о трёх перпендикулярах. Таким образом, искомый угол равен 90°.
Ответ:
[spoiler title=”источники:”]
http://geom10_11-urok.sdamgia.ru/test?theme=57
[/spoiler]
Начнем разбирать это задание с самых легких задач. Необходимо найти угол между двумя прямыми в кубе.
В кубе много параллельных ребер, поэтому задачи решаются просто. Если прямые скрещивающиеся, то используем определение угла между скрещивающимися прямыми: “Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым”.
В треугольной призме так же можно найти параллельные прямые.
В треугольной призме можно выполнить дополнительные построения, выходящие за пределы многогранника.
Из треугольника КАС легко можно найти угол КАС.
Вот еще случай, когда точка пересечения прямых лежит вне многогранника
Угол между двумя прямыми
Скачать материал

Скачать материал


- Сейчас обучается 390 человек из 62 регионов




- Сейчас обучается 269 человек из 65 регионов


Описание презентации по отдельным слайдам:
-

1 слайд
Угол между двумя прямыми
Учитель математики
ГБОУ гимназии №1 города Похвистнево
Самарской области
Антонова Галина ВасильевнаГЕОМЕТРИЯ
Задачи на готовых чертежах для подготовки к ЕГЭ
10 – 11 классы27.12.2020
Антонова Г.В.
1 -

2 слайд
27.12.2020
Антонова Г.В.
ГЕОМЕТРИЯ
Задачи на готовых чертежах для подготовки к ЕГЭ
В презентации использована книга Э.Н.Балаян «Геометрия: задачи на готовых чертежах для подготовки к ЕГЭ:
10 – 11 классы»
2 -

3 слайд
27.12.2020
Антонова Г.В.
𝐴 1
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 1
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми AC и BD.
Угол между двумя прямыми. Куб
Ответ: 𝟗𝟎 ° .
ABCD – квадрат ⇒
AC ⊥ BD
Решение:
3 -

4 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
Задача 2
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑪𝑪 𝟏 и 𝑨𝑫.
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
𝐴 1
Ответ: 𝟗𝟎 ° .
Решение:
𝐶𝐶 1 ⊥ (ABCD) ⇒ 𝐶𝐶 1 ⊥ AD
4 -

5 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 3
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑨𝑨 𝟏 и 𝑩 𝟏 𝑪.
𝐴 1
Ответ: 𝟒𝟓 ° .
Решение:
𝐴𝐴 1 ∥ 𝐵𝐵 1 ⇒
∠( 𝐴𝐴 1 ; 𝐵 1 𝐶)=∠( 𝐵𝐵 1 ; 𝐵 1 𝐶)
= 45 °
5 -

6 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 4
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑩 𝑩 𝟏 и 𝑨 𝟏 𝑪.
𝐴 1
Ответ: 𝒂𝒓𝒄𝒄𝒐𝒔 𝟑 𝟑 .
Решение:
𝐵𝐵 1 ∥ 𝐴𝐴 1 ⇒
∠(𝐵 𝐵 1 , 𝐴 1 𝐶)=∠( 𝐴𝐴 1 ; 𝐴 1 𝐶);
𝜶
6
𝑐𝑜𝑠𝛼= 𝐴𝐴 1 𝐴 1 𝐶 = 1 3 . -

7 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 5
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑨 𝟏 𝑪 и 𝑫 𝑪 𝟏 .
𝐴 1
Ответ: 𝟗𝟎 ° .
Решение:
7
O
𝑁 1
N
Проведём через середину AD (NM M 1 N 1 )∥(DC C 1 D 1 ),
M
𝑀 1
N M 1 ∥ D C 1 ⇒ искомый угол – ∠ 𝐴 1 𝑂𝑁
𝐴 1 𝑂= 3 2 ; NO= 2 2 ; 𝐴 1 𝑁= 5 2 ; по Т., обратной теореме Пифагора 𝐴 1 𝑁 2 = 𝐴 1 𝑂 2 + 𝑁𝑂 2 , поэтому ∠ 𝐴 1 𝑂𝑁 = 90 ° . -

8 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 6
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑨 𝑫 𝟏 и 𝑨 𝟏 𝑩.
𝐴 1
Ответ: 𝟔𝟎 ° .
Решение:
𝐴 𝐷 1 ∥𝐵 𝐶 1 ⇒ ∠ 𝐴 𝐷 1 , 𝐴 1 𝐵 =∠ 𝐵 𝐶 1 , 𝐴 1 𝐵 = 60 °
8 -

9 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 7
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑫 𝑪 𝟏 и 𝑫 𝟏 𝑩 𝟏 .
𝐴 1
Ответ: 𝟔𝟎 ° .
Решение:
𝐷 1 𝐵 1 ∥DB ⇒ ∠(𝐷 𝐶 1 , 𝐷 1 𝐵 1 ) = =∠(𝐷 𝐶 1 ,𝐷𝐵)
Искомый угол находим в равностороннем ∆𝐷𝐵 𝐶 1
9 -

10 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 8
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑨 𝑫 𝟏 и BD.
𝐴 1
Ответ: 𝟔𝟎 ° .
Решение:
BD ∥ 𝐵 1 𝐷 1 ⇒ ∠(𝐴 𝐷 1 , BD) = =∠(𝐴 𝐷 1 , 𝐷 1 𝐵 1 )∠A 𝐷 1 𝐵 1 = 60 ° (как угол правильного треугольника)
10 -

11 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐶 1
𝐷 1
𝐵 1
Задача 9
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑨 𝟏 𝑪 𝟏 и 𝑩 𝟏 C.
𝐴 1
Ответ: 𝟔𝟎 ° .
Решение:
Решение аналогично решению задач № 7 – 8
11 -

12 слайд
𝜶
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 10
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑨 𝟏 𝑪 и 𝑨𝑫.
𝐴 1
Ответ: 𝒂𝒓𝒄𝒄𝒐𝒔 𝟑 𝟑 .
Решение:
12
AD∥BC ⇒ ∠( 𝐴 1 𝐶;𝐴𝐷) = ∠( 𝐴 1 𝐶;𝐵𝐶)=𝛼
𝑐𝑜𝑠𝛼= 𝐵𝐶 𝐴 1 𝐶 = 1 3 = 3 3 ;
𝛼=𝑎𝑟𝑐𝑐𝑜𝑠 3 3 . -

13 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 11
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑨 𝟏 𝑩 и 𝑨𝑪.
𝐴 1
Ответ: 𝟔𝟎 ° .
Решение:
13
𝐴 1 𝐶 1 ∥AC, ⇒ ∠( 𝐴 1 𝐵;𝐴𝐶)=∠( 𝐴 1 𝐵; 𝐴 1 𝐶 1 )
∆ 𝐴 1 𝐶 1 𝐵- равносторонний ⇒ ∠( 𝐴 1 𝐵; 𝐴 1 𝐶 1 )= 60 ° . -

14 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 12
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑨𝑪 и 𝑩 𝟏 𝑫 𝟏 .
𝐴 1
Ответ: 𝟗𝟎 ° .
Решение:
14
∠( 𝐷 1 𝐵 1 ;𝐴𝐶)=∠D𝐵;𝐴𝐶)= 90 ° .𝐷 1 𝐵 1 ∥ DB ⇒
-

15 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐶 1
𝐷 1
𝐵 1
Задача 13
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑨 𝟏 𝑩 и 𝑪 𝑩 𝟏 .
𝐴 1
Ответ: 𝟔𝟎 ° .
Решение:
15
𝐴 1 𝐵∥ 𝐷 1 𝐶 ⇒
∠( 𝐴 1 𝐵;𝐶 𝐵 1 )=∠D𝐵;𝐶 𝐷 1 )= 60 ° ,т.к. ∆𝐶 𝐵 1 𝐷 1 – равносторонний -

16 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 14
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑩 𝟏 𝑪 и 𝑩 𝑫 𝟏 .
𝐴 1
Ответ: 𝟗𝟎 ° .
Решение:
16
Решение задачи аналогично решению задачи №5 презентации -

17 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 15
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑨𝑩 и 𝑪 𝑨 𝟏 .
𝐴 1
Ответ:𝒂𝒓𝒄𝒄𝒐𝒔 𝟑 𝟑 .
Решение:
17
AB∥DC ⇒
∠(𝐴𝐵;𝐶 𝐴 1 )=∠D𝐶;𝐶 𝐴 1 )
∠𝐶𝐷 𝐴 1 )= 90 ° (по Т. О трёх перпендикулярах)
cos ∠𝐷𝐶 𝐴 1 = 𝐶𝐷 𝐶 𝐴 1 = 3 3 . -

18 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 16
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑩 𝑨 𝟏 и 𝑩 𝟏 𝑫 𝟏 .
𝐴 1
Ответ: 𝟔𝟎 ° .
Решение:
18
B 1 D 1 ∥ BD, искомый угол найдём из равностороннего ∆BD 𝐴 1 . -

19 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 17
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑨 𝑩 𝟏 и 𝑩 𝑫 𝟏 .
𝐴 1
Ответ: 𝟗𝟎 ° .
Решение:
19
Решение задачи аналогично решению задачи №5 презентации -

20 слайд
27.12.2020
Антонова Г.В.
Угол между двумя прямыми. Куб
A
C
B
D
𝐵 1
𝐶 1
𝐷 1
Задача 18
В единичном кубе 𝑨𝑩𝑪𝑫 𝑨 𝟏 𝑩 𝟏 𝑪 𝟏 𝑫 𝟏 найдите угол между прямыми 𝑨𝑩 и 𝑫 𝑩 𝟏 .
𝐴 1
Ответ: 𝒂𝒓𝒄𝒕𝒈 𝟐 .
Решение:
20
𝐷𝐶∥AB ⇒ ∠(AB; D 𝐵 1 )=
∠(DC; D 𝐵 1 )
𝑡𝑔 𝐵 1 𝐷𝐶= 𝐵 1 𝐶 𝐷𝐶 = 2 -

21 слайд
1. Источник шаблона:Ранько Елена Алексеевна, учитель начальных классов МАОУ лицей №21 г. Иваново,
Сайт: http://elenaranko.ucoz.ru/
2. Геометрия: задачи на готовых чертежах для подготовки к ЕГЭ: 10 – 11 классы / Э.Н.Балаян. – Ростов н/Д: Феникс, 2013. – 217 с. : ил. – (Большая перемена).27.12.2020
Антонова Г.В.
21 -

22 слайд
http://www.bg2001.ru/upload/iblock/616/4034-7.jpg
грамота (для создания рамки)http://lenagold.narod.ru/fon/clipart/s/svit/svitolk101.png
перо, чернильница, бумагаhttp://megasklad.ru/data/photoes/s194064.jpg
ручка – 1http://www.segment.ru/img_hits/4946015_1_small.jpg
ручка – 2Интернет – ресурсы:
27.12.2020
Антонова Г.В.
22
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 261 106 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
-
Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 27.12.2020
- 3412
- 1
- 27.12.2020
- 4789
- 2
- 27.12.2020
- 5014
- 12
- 27.12.2020
- 5837
- 13
- 27.12.2020
- 5068
- 9
- 27.12.2020
- 4074
- 1
- 27.12.2020
- 3903
- 0
- 27.12.2020
- 3921
- 1
Вам будут интересны эти курсы:
-
Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»
-
Курс повышения квалификации «Введение в сетевые технологии»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС технических направлений подготовки»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»
-
Курс повышения квалификации «Финансы: управление структурой капитала»
-
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
-
Курс профессиональной переподготовки «Управление сервисами информационных технологий»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Курс профессиональной переподготовки «Организация системы менеджмента транспортных услуг в туризме»
-
Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»
-
Курс профессиональной переподготовки «Техническая диагностика и контроль технического состояния автотранспортных средств»
-
Курс профессиональной переподготовки «Организация маркетинговой деятельности»
-
Курс профессиональной переподготовки «Гражданско-правовые дисциплины: теория и методика преподавания в образовательной организации»
-
Настоящий материал опубликован пользователем Доржиева Людмила Юрьевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-

- На сайте: 2 года и 4 месяца
- Подписчики: 0
- Всего просмотров: 64064
-
Всего материалов:
235
Тема 2.
Геометрия в пространстве (стереометрия)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
геометрия в пространстве (стереометрия)
Решаем задачи
Дан куб . Найдите угол между прямыми
и
. Ответ дайте в
градусах.
Показать ответ и решение
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота
падает в точку пересечения медиан основания.
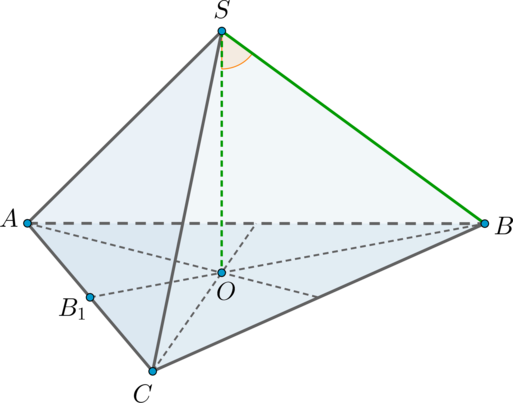
Пусть – медиана, а значит, и высота. По теореме Пифагора
так
как медианы точкой пересечения делятся в отношении , считая от вершины.
Следовательно, прямоугольный является равнобедренным (
), значит, острые
углы равны по .
Показать ответ и решение
Пусть – высота грани
. Так как тетраэдр правильный, то все его грани – равные правильные
треугольники, то есть также является и медианой, значит,
. Также у правильного
тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот)
противоположной грани. Следовательно, если – высота, то
– точка пересечения медиан
треугольника , а значит и высот, так как
правильный. Следовательно,
— медиана
и высота.
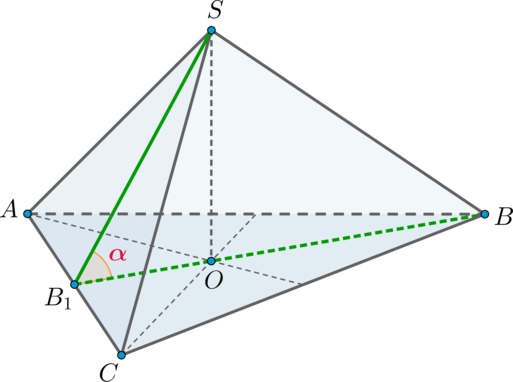
Таким образом, необходимо найти .
Пусть – ребро тетраэдра. Тогда
, следовательно, по теореме Пифагора
Так
как – точка пересечения медиан, а медианы точкой пересечения делятся в отношении
, считая
от вершины, то .
Так как , то
. Следовательно, из прямоугольного
:
Показать ответ и решение
Докажем, что содержит биссектрису угла
. Выберем на
точку
, а на
точку
так, чтобы . Построим прямую, проходящую через точку
и точку
– середину
.
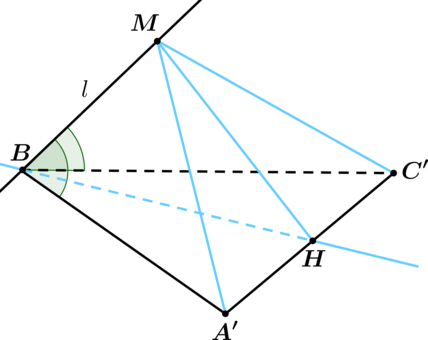
Отметим на точку
. Треугольник
– равнобедренный, тогда
– высота.
Рассмотрим треугольники и
: они равны по двум сторонам и углу между ними, тогда
и треугольник
– равнобедренный, тогда
– его высота.
В итоге и
, следовательно,
. Если предположить, что
–
проекция точки на
, не попадает на прямую, содержащую
, то получим, что
и
, откуда следует, что
. Но тогда плоскости
и
перпендикулярны к одной прямой, пересекаются, но не совпадают, чего быть не
может.
Таким образом, лежит на прямой, содержащей
, но тогда
совпадает с прямой,
содержащей . В итоге,
.
Показать ответ и решение
Пусть – высота грани
. Так как тетраэдр правильный, то все его грани – равные
правильные треугольники, то есть также является и медианой, значит,
. Также у
правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис,
высот) противоположной грани. Следовательно, если – высота, то
– точка пересечения медиан
треугольника , а значит и высот, так как
правильный. Следовательно,
медиана и
высота.
Рассмотрим . Проведем
, следовательно,
.
Заметим также, что будет лежать на
.
Действительно, так как медианы точкой пересечения делятся в отношении , считая от вершины, то
. Следовательно,
(по теореме Фалеса, так как
). Но
и – медианы в
, следовательно, они пересекаются и точкой пересечения тоже делятся в
отношении . А так как
делит
в отношении
, считая от вершины
, то
и есть
точка пересечения медиан и
.
Таким образом, нужно найти .
Пусть – ребро тетраэдра. Тогда
По
теореме Пифагора
Так
как грани тетраэдра равны, то
Следовательно, по теореме косинусов из :
План урока:
Понятие двугранного угла и угла между плоскостями
Перпендикулярность плоскостей
Прямоугольный параллелепипед
Трехгранный угол
Многогранный угол
Типичные задачи на углы между плоскостями
Понятие двугранного угла и угла между плоскостями
Напомним, что в планиметрии углом называют фигуру, состоящую из точки и двух лучей, выходящих из нее. Сама точка именуется вершиной угла, а лучи – сторонами угла.
По аналогии в стереометрии рассматривается схожая фигура – двугранный угол. Он состоит из двух полуплоскостей, которые исходят из одной прямой. Каждая из этих полуплоскостей именуется гранью двугранного угла, а их общая прямая – это ребро двугранного угла.

Для обозначения двугранного угла достаточно указать две точки на его ребре, а также ещё по одной точке на каждой грани. Например, на следующем рисунке показан угол САВD:

Двугранные углы часто встречаются в обычной жизни. Например, его образуют двухскатные крыши домов. В стереометрии двугранные угла можно найти в любом многограннике.
Двугранные углы можно измерять. Для этого надо выбрать произвольную точку на ребре угла и на каждой грани построить перпендикуляр, проходящий через эту точку. Через эти два перпендикуляра можно построить единственную плоскость. Угол между двумя перпендикулярами и принимается за величину двугранного угла.

Отдельно отметим, что плоскость, проходящая через перпендикуляры (на рисунке выше это γ) перпендикулярна ребру угла АВ. Это вытекает из признака перпендикулярности прямой и плоскости. Действительно, АВ⊥ВС и АВ⊥BD, поэтому и АВ⊥γ. Построенный угол ∠СBD называют линейным углом двугранного угла.
Понятно, что в каждом двугранном угле можно построить сколько угодно линейных углов:

Здесь помимо ∠ВСD построены линейные углы ∠В’С’D’ и ∠В’’С’’D’’. Однако все эти углы имеют одинаковую градусную меру. Сравним, например, ∠ВСD и ∠В’С’D’. Так как BD⊥AB и B’D’⊥АВ, то BD||B’D’. Аналогично можно прийти к выводу, что ВС||B’C’. Получаем, что стороны углов ∠ВСD и ∠В’С’D’ – это сонаправленные лучи, а потому ∠ВСD и ∠В’С’D’ одинаковы.
Двугранные углы, как и обычные углы, можно разделить на острые (их градусная мера меньше 90°), прямые (они в точности равны 90°) и тупые (которые больше 90°).

Если две плоскости пересекаются, то они образуют сразу 4 двугранных угла. Если среди них есть острый угол, то его величина считается углом между плоскостями. Если же все образуется 4 прямых двугранных угла, то угол между плоскостями принимается равным 90°.

Перпендикулярность плоскостей
В частном случае, когда угол составляет 90°, говорят, что пересекающиеся плоскости перпендикулярны.

Перпендикулярны друг другу пол и стены в доме, смежные грани кубика, стенки коробки. Существует особый признак перпендикулярности плоскостей.

Действительно, пусть плоскости α и β пересекаются по линии n, и в β есть такая прямая m, что m⊥α. Тогда m и n должны пересекаться в какой-нибудь точке К. Проведем в плоскости α через К прямую р, перпендикулярную n. Ясно, что m⊥р, ведь m⊥α. Получается, угол между m и р как раз и является углом между плоскостями α и β, ведь m⊥n и р⊥n. И этот угол равен 90°, ведь m⊥p, ч т. д.
Из доказанного признака вытекает следующее утверждение:

Прямоугольный параллелепипед
Ранее мы уже узнали про параллелепипед. Это фигура с 6 гранями, каждая из которых представляет собой параллелограмм. Особый интерес представляет его частный случай – прямоугольный параллелепипед.

Такую форму имеют многие шкафы, другие предметы мебели, коробки для обуви, небоскребы. Изображают прямоугольный параллелепипед так:

Для обозначения вершин параллелепипеда применяют латинские буквы. Очень часто для вершин одной грани используют 4 буквы без индекса (на рисунке выше это А, В, С, D), а другие 4 вершины обозначают такими же буквами, но с нижним индексом 1: А1, B1, C1 и D1. При этом одноименные вершины (например, А и А1) находятся на одном ребре, которое располагается на рисунке вертикально.
Докажем некоторые свойства прямоугольного параллелепипеда.

Например, ребро АD пересекается с гранями АВВ1А1 и CDD1C1. Значит, оно перпендикулярно этим граням (точнее говоря, оно перпендикулярно плоскостям, проходящим через эти грани). Действительно, AD⊥DC, ведь ∠ADC является углом в прямоугольнике АВСD и потому он прямой. Аналогично и AD⊥DD1, ведь и ADD1A1 – прямоугольник. Получается, что ребро AD перпендикулярно 2 прямым в грани CDD1C1 (которые при этом пересекаются), и потому оно перпендикулярно и всей грани. То же самое можно продемонстрировать для любого ребра прямоугольного параллелепипеда и любой грани, которую она пересекает.


Эти грани пересекаются по ребру А1D1. Этому ребру в свою очередь перпендикулярны ребра АА1 и А1В1, лежащие в гранях ADD1A1 и A1D1C1B1. Значит, ∠АА1В1 и будет углом между этими гранями. Но он составляет 90°, то есть грани перпендикулярны, ч. т. д.
Хотя у прямоугольного параллелепипеда есть 12 граней, многие из них имеют одинаковую длину. Поэтому для описания размеров этой фигуры достаточно указать только три параметра. Обычно их называют длиной, шириной и высотой:

Эти параметры также называют измерениями прямоугольного параллелепипеда. Зная их, можно вычислить длину диагонали прямоугольного параллелепипеда. Для этого используется следующая теорема:

Действительно, пусть есть прямоугольный параллелепипед АВСDA1B1C1D1. Назовем ребро AD его длиной, АВ – шириной, а ВВ1 – высотой. Пусть необходимо найти длину диагонали В1D:

Сначала построим отрезок BD и рассмотрим ∆ABD. Он прямоугольный, и потому для него верна теорема Пифагора:

Теперь перейдем к ∆В1ВD. Так как ребро BB1 перпендикулярно грани ABCD, то ∠В1ВD – прямой. Тогда и ∆В1ВD – прямоугольный, а потому и для него можно записать теорему Пифагора:

Дополнительно отметим уже известный нам факт, что тот прямоугольный параллелепипед, у которого все стороны одинаковы, именуется кубом. Можно дать и такое определение куба:

Трехгранный угол
Выберем в пространстве произвольную точку K. Далее из нее проведем три луча КА, КВ и КС так, чтобы они не находились в одной плоскости:

В результате мы получили фигуру, которую именуют трехгранным углом. Она состоит их трех плоских углов: ∠АКС, ∠АКВ и ∠ВКС. Эти углы так и называются – плоские углы трехгранного угла. Сам же трехгранный угол обозначают четырьмя буквами: КАВС. Обратите внимание, что через каждую пару лучей КА, КВ и КС можно провести плоскость. Таким образом, название «трехгранный» угол показывает, что в точке К сходятся три грани. Чаще всего в стереометрии такой угол возникает при рассмотрении вершин тетраэдра, в котором есть сразу четыре трехгранных угла:

Доказательство. Пусть в пространстве из точки D выходят лучи AD, BD и CD. Важно понимать, что мы можем свободно «передвигать» точки А, В и С по лучам, и величина плоских углов при этом меняться не будет. Если среди плоских углов нет наибольшего, то теорема очевидно выполняется. Поэтому надо рассмотреть лишь случай, когда один из углов – наибольший. Пусть им будет ∠BDC:

Это возможно сделать, ведь ∠BDC > AD, поэтому внутри ∠BDC можно провести луч DK. Далее «сместим» точку А на луче АD так, чтобы DK = AD. Естественно, что при этом плоские углы трехгранного угла никак не изменятся, также как останется верным равенство

Сравним ∆ADC и ∆DKC. У них есть общая сторона DC, одинаковы стороны DK и AD, а также совпадают углы между ними. Значит, эти треугольники равны, и тогда можно записать, что:

Теперь сравним ∆ABD и ∆DBK. У них BD – общая сторона, а DK = AD. При этом BK < AB. В таком случае против меньшей стороны будет лежать меньший угол (смотри примечание после доказательства), то есть

Именно это неравенство и необходимо было доказать.
Примечание. В ходе доказательства было использовано утверждение, что если у двух треугольников две стороны одинаковы, в третьи стороны отличаются, то против меньшей третьей стороны будет располагаться меньший угол:

Это утверждение часто не рассматривается в курсе планиметрии, поэтому есть смысл доказать его отдельно. Действительно, пусть есть ∆АВС и ∆А’B’C’, АС = А’C’ и АВ = A’B’, а СВ < C’B’. Надо показать, что ∠А <∠A’. Для этого выразим стороны СВ и C’B’ (а точнее говоря, их квадраты) с помощью теоремы косинусов:

Из последнего неравенства на основе определения косинуса для углов из интервала от 0° до 180° вытекает, что и

Многогранный угол
Возможен случай, когда из одной точки в пространстве выходят не три, а большее количество лучей, причем образуемые ими углы не располагаются в единой плоскости. Такая фигура именуется многогранным углом. Трехгранный угол можно считать его частным случаем. Также его частными случаями будут четырехгранный угол, пятигранный угол, шестигранный угол и т. д.
Более наглядна следующая демонстрация многогранного угла. Построим на плоскости α произвольный многоугольник. Далее выберем какую-нибудь точку вне плоскости α и соединим ее с вершинами многоугольника с помощью лучей. При этом у нас как раз получится многогранный угол. Если, например, в качестве многоугольника мы использовали пятиугольник, то и получим мы пятигранный угол:

Важно отметить, что в данном случае состоит многогранный угол именно из лучей КА1, КА2, КА3…, а не из одноименных отрезков. То есть многогранный угол – это ни в коем случае не многогранник КА1А2А3А4А5, у него есть только одна вершина – точка К. Многогранник КА1А2А3А4А5 – это пирамида, такая фигура изучается в курсе стереометрии чуть позже. Многоугольник А1А2А3А4А5 – это сечение многогранного угла. Углы ∠А1КА2, ∠А2КА3, ∠А3КА4… – это плоские углы многогранного угла.
Заметим, что на исходный многоугольник на плоскости может быть как выпуклым, так и невыпуклым. Соответственно и многогранный угол может быть как выпуклым, так и невыпуклым:

Так как любой треугольник – это выпуклый многоугольник, то и любой трехгранный угол является выпуклым. В выпуклом угле все его точки лежат по одну сторону от любой плоскости, проходящей, через какие-нибудь два смежных луча угла. Вообще любое сечение многогранного угла представляет собой выпуклый многоугольник.
Докажем важное утверждение:

Для доказательства возьмем произвольный многогранный угол и проведем в нем сечение А1А2А3…Аn, которое будет являться выпуклым многоугольником:



В последнем равенстве в каждой скобке стоят по два плоских угла в тех трехгранных углах, вершины которых совпадают с вершинами многоугольника А1А2А3…Аn. В предыдущей теореме мы выяснили, что эта сумма меньше третьего плоского угла, то есть

В правой части в скобках стоит сумма углов выпуклого n-угольника А1А2А3…Аn. Она, как мы знаем, составляет 180°•(n – 2), то есть

Последнее неравенство и необходимо было доказать.
Типичные задачи на углы между плоскостями
В школьной практике почти не встречаются задачи с многогранными углами, поэтому достаточно понимания и двугранного угла.
Задание. У тетраэдра ABCD все ребра одинаковы. Найдите величину двугранного угла между плоскостями АВС и АСD.
Решение. Отметим на ребре АС точку М, которая является его серединой:

Заметим, что плоскости АВС и АСD пересекаются по прямой АС. Раз все ребра тетраэдра одинаковы, то ∆АВС и ∆АСD – равносторонние. DM и BM – это медианы в ∆АВС и ∆АСD соответственно, ведь M – середина АС. Но раз треугольники равносторонние, то они одновременно являются и высотами, то есть BM⊥AC и DM⊥АС. Тогда ∠DMB как раз и представляет собой линейный угол двугранного угла BАСD. То есть именно его значение нам и надо вычислить (если, конечно, он окажется не больше 90°).
Пусть ребра тетраэдра имеют длину а. Тогда АМ вдвое короче. Найдем из прямоугольного ∆АМD длину MD:


Задание. Двугранный угол равен φ, меньший 90°. На одной из его граней отмечена точка К, которая находится на расстоянии d от другой грани. Каково расстояние между точкой К и ребром двугранного угла?
Решение. Пусть угол образован плоскостями α и β. Опустим из K два перпендикуляра – один на плоскость β в точку Н, а другой на линию пересечения плоскостей в точку Р:

По условию задачи ∠НРК = φ, а HK = d. Нам же надо найти РК. Это можно сделать, применив определение синуса к ∆РНК:

Задание. Верно ли, что плоскость, пересекающая две параллельные плоскости, образует с ними одинаковые углы?
Решение. Пусть есть параллельные друг другу плоскости α и β, а пересекает их плоскость γ. Линию пересечения α и γ обозначим как n, и такую же линию для β и γ обозначим как m:

Заметим, что m и n располагаются в одной плоскости γ и при этом не пересекаются, в противном случае у α и β нашлась бы общая точка, которой быть не должно. Значит, m||n.
Далее проведем в γ прямую р, перпендикулярную n. Раз m||n и р⊥n, то и р⊥m. То есть р – общий перпендикуляр для m и n.
Далее в α через точку пересечения n и p проведем прямую k, перпендикулярную n. Ясно, что k||β. После уже через точку пересечения m и p построим такую прямую k’, что k||k’:

Так как k||β и k||k’, то прямая k’ будет принадлежать плоскости β (по теореме 6 из этого урока). Так как k||k’, m||n и n⊥k, то по теореме о сонаправленных лучах можно утверждать, что и m⊥k’. Тогда углы, отмеченные на рисунке синим цветом – это и есть линейные углы двугранных углов. Они одинаковы, так как являются соответственными при секущей р и параллельных прямых k и k’. Если же двугранные углы равны, то одинаковы и углы между плоскостями, ч. т. д.
Примечание. Доказанный факт можно сформулировать в виде теоремы:

Она может быть использована при решении некоторых сложных задач.
Задание. В прямоугольном ∆АВС АВ и АС – катеты с длиной 7 и 24 соответственно. Через гипотенузу проведена плоскость β, образующая с плоскостью АВС угол 30°. Каково расстояние между точкой А и плоскостью β?
Решение.

Опустим из А перпендикуляр АН на β. Это и будет искомое нами расстояние. Также в ∆АВС построим высоту AD. Заметим, что раз АН⊥β, то по определению и АН⊥HD. Можно сказать, что HD – это проекция AD на β. Раз прямая ВС перпендикулярна наклонной AD, то она одновременно будет перпендикулярна и наклонной HD по обратной теореме о трех перпендикулярах.
Плоскости АВС и β пересекаются по прямой ВС, АD⊥ВС и HD⊥BC. Получается, что ADH – это как раз угол между АВС и β, и по условию он составляет 30°.
По теореме Пифагора вычислим гипотенузу ВС:

Теперь перейдем к ∆AHD. Он также прямоугольный (∠Н = 90°). Используем для него тригонометрию:

Задание. Известны измерения прямоугольного параллелепипеда. Его длина составляет 90 см, ширина – 20 см, а высота – 60 см. Какова длина диагонали такого параллелепипеда?
Решение. Обозначим измерения буквами а, b, с, а диагональ буквой d. Достаточно просто воспользоваться формулой:

Далее рассмотрим несколько задач, в которых надо найти угол между плоскостями, находящимися в кубе с ребром, чья длина составляет единицу.
Задание. Вычислите угол между гранью ADHЕ и сечением АBGН:

Решение. Заметим, что сечение АВGH содержит прямую АВ. Но АВ – это перпендикуляр к АЕНD. Если АВGH содержит перпендикуляр к ADH, то эти две плоскости перпендикулярны, и угол между ними составляет 90°.
Ответ: 90°.
Задание. Определите угол между гранью ADHE и сечением ADGF:

Решение. Две рассматриваемые плоскости пересекаются по ребру AD. Ребра DH и AD перпендикулярны как стороны квадрата. Так как AD – это перпендикуляр к грани СDHG, то AD⊥DG. Получается, что ∠HDG – это и есть искомый угол. Его величина равна 45°, ведь это угол между диагональю квадрата и его стороной.
Ответ: 45°.
Задание. Вычислите угол между сечениями АВGH и EFCD:

Решение. Пересекаются эти две плоскости по прямой KP, где K и P – точки пересечения диагоналей квадратов BFGH и AEHD. Докажем, что отрезки KG и KC перпендикулярны KP.
Действительно, рассмотрим четырехугольник АВGH. Ребра АВ и GH перпендикулярны граням AEHD и BFGH, поэтому все углы в АВGH – прямые, то есть это прямоугольник и BG||AH. Теперь рассмотрим четырехугольник АВKP. Стороны BK и AP параллельны и равны как половины равных отрезков BG и AH. Значит, BKAP – параллелограмм. Но в нем есть прямые углы ∠В и ∠А, поэтому BKAP – прямоугольник. Аналогично можно показать, что и KGHP – прямоугольник. Это и приводит к выводу о том, что KG⊥KP и PH⊥KP. Поэтому ∠СKG и является искомым углом между сечениями. Он является углом между диагоналями квадрата, то есть равен 90°.
Ответ: 90°.
Задание. Найдите угол между сечением AFH и гранью AEHD:

Решение. Обозначим середину диагонали AH буквой K. Докажем ∠EKF – искомый нами угол:

Действительно, плоскости AHD и AFH пересекаются по прямой AH. EK – медиана в равнобедренном ∆AEH с основанием AH, поэтому она также является и высотой, то есть EK⊥AH. AF и FH – диагонали в равных квадратах ABFE и EFGH, поэтому эти диагонали одинаковы. Значит, ∆AFH – равнобедренный, и поэтому его медиана FK также перпендикулярна основанию AH. Получается, что ∠EKF и является искомым. Вычислить его можно из ∆EKF.
Сначала найдем длину EK. В прямоугольном ∆AEK ∠KAE составляет 45° (угол между диагональю и стороной квадрата), поэтому

Задание. Вычислите угол между гранью BCGF и сечением AFH:

Решение. Вспомним, что в предыдущей задаче мы уже вычислили угол между гранью АЕHD и тем же сечением АFH. Но грани AEHD и BCFG параллельны, поэтому АFH должна пересекаться их под одним и тем же углом. Поэтому ответ этой задачи совпадает с ответом к предыдущей задаче.
Ответ: ≈ 54,74°.
Задание. Чему равен угол между сечениями АСH и AFGH?

Решение. Пусть диагонали СН и DG пересекаются в точке К. Точка K будет принадлежать обоим сечениям, как и точка А. Значит, сечения пересекаются по линии АК. Проведем в сечении AFGH через точку K прямую, перпендикулярны АК и пересекающую FG в какой-то точке Р (позже мы убедимся, что прямая действительно должна пересекать отрезок FG):

Докажем, что ∠CPK и является углом между сечениями. Мы специально провели РК так, что РК⊥АК. Теперь посмотрим на ∆АСН. Он равносторонний, ведь его стороны АС, СН и DH – это диагонали равных квадратов (граней куба). Прямая АК – медиана, ведь K – точка пересечения диагоналей квадрата СDHG, которая делит диагонали пополам. Но раз ∆АСН равносторонний, то его медиана – это ещё и высота, то есть АК⊥РК. Итак, АК⊥СК и АК⊥РК, поэтому ∠CPK – это угол между сечениями. Для его вычисления необходимо найти все стороны в ∆РСК и далее применить теорему косинусов.
Проще всего найти СК. ∆СKD – прямоугольный (∠К = 90°), а ∠СDK составляет 45° (угол между стороной и диагональю в квадрате). Тогда можно записать, что

Отдельно отметим, что отрезки GK и KD имеют такую же длину, ведь диагонали в квадрате (а значит и их половины) одинаковы.
Для нахождения РК покажем отдельно плоскость AFG, то есть красное сечение:

Обозначим ∠KAD как φ. Тогда ∠АКD будет составлять 90 – φ. Углы ∠АКD, ∠АKP и ∠PKG в сумме дают 180°, что позволяет найти ∠PKG:

Получилось, что у ∆АКD и ∆PKG есть по два одинаковых угла (φ и 90°). Значит, они подобны. Составим такую пропорцию:

Теперь можно вернуться ко всему кубу и найти отрезок РС. Здесь снова можно применить теорему Пифагора, но уже к ∆PCG:

Теперь для ∆PCK мы можем записать теорему косинусов

Неожиданно мы доказали, что два построенных сечения перпендикулярны друг другу. Прийти к этому выводу можно было и иначе. Достаточно было бы показать, что прямая CH – это перпендикуляр к сечению AFGD. Попробуйте сделать это самостоятельно.
Ответ: 90°.
Задание. Вычислите угол между сечениями BDHF и ADGF:

Решение. У сечений общими являются точки F и D. Значит, именно по прямой FD они пересекаются.
Опустим в синей сечении BDHF перпендикуляр на FD, который упадет в некоторую точку K:

Докажем, что отрезок GK также перпендикулярен FD. Действительно, BK – это высота в ∆BDF. Но ∆BDF и ∆GDF равны, ведь они одинаковы все три стороны (FD – общая сторона, BF и FG – ребра куба, BD и DG – диагонали на гранях куба). В равных треугольниках высоты должны делить стороны на равные отрезки, поэтому высота, опущенная из G на FD, также разделит FD на отрезки FK и KD. То есть она просто упадет в точку K. Это и значит, что KG – высота. Получается, что нам надо вычислить ∠BKG.
Сначала найдем длину диагоналей BD и BG. Можно применить теорему Пифагора для ∆BFG:

KG имеет ту же длину, ведь KG и BK – одинаковые высоты в равных треугольниках ∆BDF и ∆GDF.
Теперь используем теорему косинусов для ∆BKG:

Мы вычислили двугранный угол, но он оказался больше 90°. Это значит, угол между плоскостями равен не 120°, а 180° – 120°, то есть 60°.
Ответ: 60°.
Сегодня мы познакомились с понятием двугранного угла, научились вычислять углы между плоскостями. В частном случае вместо вычисления угла можно просто доказать перпендикулярность плоскостей.
