Как найти исправленную дисперсию ошибок прибора

Как найти исправленную дисперсию ошибок прибора

Выборочная дисперсия, описание

Выборочная дисперсия является сводной характеристикой для наблюдения рассеяния количественного признака выборки вокруг среднего значения.

Определение

Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).

Связь выборочной и генеральной дисперсии

Генеральная дисперсия представляет собой среднее арифметическое квадратов отступлений значений признаков генеральной совокупности от их среднего значения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Определение

Генеральная совокупность – это комплекс всех возможных объектов, относительно которых планируется вести наблюдение и формулировать выводы.

Выборочная совокупность или выборка является частью генеральной совокупности, выбранной для изучения и составления заключения касательной всей генеральной совокупности.

Как вычислить выборочную дисперсию

Выборочная дисперсия при различии всех значений варианта выборки находится по формуле:

({widehat D}_В=frac{displaystylesum_{i-1}^n{(x_i-{overline x}_В)}^2}n)

Для значений признаков выборочной совокупности с частотами n1, n2,…,nk формула выглядит следующим образом:

({widehat D}_В=frac{displaystylesum_{i-1}^kn_i{(x_i-{overline x}_В)}^2}n)

Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика называется выборочным средним квадратическим отклонением и имеет вид:

({widehatsigma}_В=sqrt{{widehat D}_В})

Упрощенный способ вычисления выборочной или генеральной дисперсии производят по формуле:

(D=overline{x^2}-left[overline xright]^2)

Если вариационный ряд выборочной совокупности интервальный, то за xi принимается центр частичных интервалов. 

Пример

Найти выборочную дисперсию выборки со значениями:

  • xi: 1, 2, 3, 4;
  • ni: 20, 15, 10, 5.

Решение

Для начала необходимо определить выборочную среднюю:

({overline x}_В=frac1{50}(1cdot20+2cdot15+3cdot10+4cdot5)=frac1{50}cdot100=2)

Затем найдем выборочную дисперсию:

(D_В=frac1{50}({(1-2)}^2cdot20+{(2-2)}^2cdot15+{(3-2)}^2cdot10+{(4-2)}^2cdot5)=1)

Исправленная дисперсия

Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:

(Mleft[D_Bright]=frac{n-1}nD_Г)

В данной формуле DГ – это истинное значение дисперсии генеральной совокупности.

Исправить выборочную дисперсию можно путем умножения ее на дробь:

(frac n{n-1})

Получим формулу следующего вида:

(S^2=frac n{n-1}cdot D_В=frac{displaystylesum_{i=1}^kn_i{(x_i-{overline x}_В)}^2}{n-1})

Исправленная дисперсия используется для несмещенной оценки генеральной дисперсии и обозначается S2. 

Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:

(S=sqrt{S^2})

При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах. Различия в этих характеристиках при больших n незначительны. Применение исправленной дисперсии целесообразно при объеме выборки меньше 30.

Для чего применяют исправленную выборочную дисперсию

Исправленную выборочную используют для точечной оценки генеральной дисперсии.

Пример

Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины: 92 мм, 94 мм, 103 мм, 105 мм, 106 мм. Задача найти выборочную среднюю длину предмета и выборочную исправленную дисперсию ошибок измерительного прибора.

Решение

Сначала вычислим выборочную среднюю:

({overline x}_В=frac{92+94+103+105+106}5=100)

Затем найдем выборочную дисперсию:

(D_В=frac{displaystylesum_{i=1}^k{(x_i-{overline x}_В)}^2}n=frac{{(92-100)}^2+{(94-100)}^2+{(103-100)}^2+{(105-100)}^2+{(106-100)}^2}5=34)

Теперь рассчитаем исправленную дисперсию:

(S^2=frac5{5-1}cdot34=42,5)

Источник
Автор статьи

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Генеральная дисперсия

Пусть нам дана генеральная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 1

Генеральная совокупность — совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.

Определение 2

Генеральная дисперсия — среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:

Логотип iqutor

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Бесплатное пробное занятие

*количество мест ограничено

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:

С этим понятием также связано понятие генерального среднего квадратического отклонения.

Определение 3

Генеральное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:

[{sigma }_г=sqrt{D_г}]

Выборочная дисперсия

Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 4

Выборочная совокупность — часть отобранных объектов из генеральной совокупности.

Определение 5

Выборочная дисперсия — среднее арифметическое значений вариант выборочной совокупности.

«Дисперсия: генеральная, выборочная, исправленная» 👇

Пусть значения вариант $x_1, x_2,dots ,x_k$ имеют, соответственно, частоты $n_1, n_2,dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1, x_2,dots ,x_k$ различны. В этом случае $n_1, n_2,dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:

С этим понятием также связано понятие выборочного среднего квадратического отклонения.

Определение 6

Выборочное среднее квадратическое отклонение — квадратный корень из генеральной дисперсии:

[{sigma }_в=sqrt{D_в}]

Исправленная дисперсия

Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $frac{n}{n-1}$, то есть

С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:

!!! В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$

Пример задачи на нахождение дисперсии и среднего квадратического отклонения

Пример 1

Выборочная совокупность задана следующей таблицей распределения:

Рисунок 1.

Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.

Решение:

Для решения этой задачи для начала сделаем расчетную таблицу:

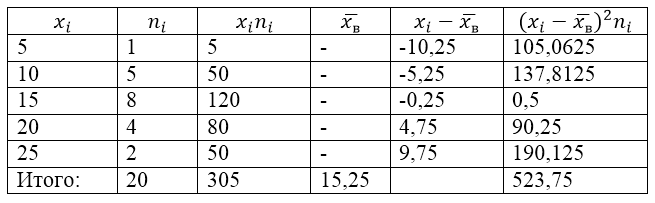
Рисунок 2.

Величина $overline{x_в}$ (среднее выборочное) в таблице находится по формуле:

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}]

То есть

[overline{x_в}=frac{sumlimits^k_{i=1}{x_in_i}}{n}=frac{305}{20}=15,25]

Найдем выборочную дисперсию по формуле:

[D_в=frac{sumlimits^k_{i=1}{{{(x}_i-overline{x_в})}^2n_i}}{n}=frac{523,75}{20}=26,1875]

Выборочное среднее квадратическое отклонение:

[{sigma }_в=sqrt{D_в}approx 5,12]

Исправленная дисперсия:

[{S^2=frac{n}{n-1}D}_в=frac{20}{19}cdot 26,1875approx 27,57]

Исправленное среднее квадратическое отклонение:

[S=sqrt{S^2}approx 5,25]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Можно доказать, что при достаточно большом объеме выборки и при достаточно мелком делении интервалов с практической достоверностью близка к истинной функции распределения F (x).

4.1. Параметры распределения

Одна из задач математической статистики: по имеющейся выборке оценить значения числовых характеристик исследуемой случайной величины. Основными числовыми характеристиками выборки явля-

ются выборочное среднее хв и выборочная дисперсия Dв .

n

Иn

Определение. Выборочным средним

называется среднее арифме-

тическое значений случайной величины, принимаемых в выборке:

l

∑ x n

x

в

=

x1 + … + xn

или

x

в

=

i=1 i i

.

(3.3)

Аn

Выборочное среднее xв служит для точечной оценки математи-

l

б l

ческого ожидания М (Х )

исследуемойДслучайной величины

x =

x1

+ … + xn

.

Определение. Выборочной дисперсией называется

∑ (x − x

в

)2

n

∑ x 2

n

i

i

i

i

Dв (Х ) =

i=и1

=

i=1

− xв 2 .

(3.4)

n

n

Выборочная дисперсия Dв (Х )

служит для точечной оценки дис-

персии D(Х ) .С

4.2. Несмещенность, состоятельность, эффективность параметров распределения

Получив статистические оценки параметров распределения (выборочное среднее, выборочную дисперсию и т.д.), нужно убедиться, что они в достаточной степени служат приближением соответствующих характеристик генеральной совокупности. Определим требования, которые должны при этом выполняться.

110

Пусть θ − статистическая оценка неизвестного параметра θ теоретического распределения. Извлечем из генеральной совокупности несколько выборок одного и того же объема n и вычислим для каждой

из них оценку параметра θ : θ1 ,θ2 ,θ3 , ,θn .

Тогда оценку θ можно рассматривать как случайную величину, принимающую возможные значения θ1 ,θ2 ,θ3 , ,θn .

1. Если математическое ожидание θ не равно оцениваемому параметру, мы будем получать при вычислении оценок систематические

ошибки одного знака (с избытком, если М (θ ) > 0 , и с недостатком, если М (θ ) < 0). Следовательно, необходимым условием отсутствия

2.Определение. Оценка θ называетсяДИэффективной, если она несмещенная и при этом имеет наименьшую дисперсию (наименьший разброс относительно θ ) по сравнениюА с другими несмещенными оценками параметра θ .

3.Определение. Оценкабθ называется состоятельной, если при неограниченном увеличенииио ъема выборки θ сходится по вероят-М (θ ) = 0 .математическое-Ссистематических ошибок является требование

В отличие от выборочного среднего, выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности. Пользуясь оценкой Dв вместо D , мы будем совершать некоторую систе-

матическую ошибку, так как её математическое ожидание несколько меньше истинного значения. Чтобы её ликвидировать, достаточно

ввести поправку, умножив D

на

n

. Таким образом, можно пред-

в

n −1

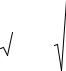
ложить другую оценку дисперсии – исправленную дисперсию s², вы-

111

l

(x

− x

)2 n

n

∑

числяемую по формуле s2 =

D

=

i=1

i

в

i

. Эта оценка яв-

n −1

n −1

в

ляется состоятельной несмещенной оценкой дисперсии D.

Такая оценка будет являться несмещенной. Ей соответствует ис-

правленное среднее квадратическое отклонение (СКО)

l

(x − x

)2 n

∑

i

в

i

s =

s2 =

i=1

.

(3.5)

n

n −1

При больших n поправка

становится близкой к единице и её

n −1

применение теряет смысл.

И

Пример 1. Оптический пирометр установлен на светящуюся нить

накала,

различными операторами было произведено несколько изме-

рений температуры. Получены следующие результаты (табл. 9).

Д

Таблица 9

Температура, °С

925

950

975

1000

1025

500

Число измерений

1

9

6

18

10

2

б

Требуется найти среднюю квадратическую и вероятную ошибки

и

Аорка взята из нормально распределен-

в предположении, что эта вы

ной совокупности.

С

Решение. Найдем сначала выборочное среднее значение

х

в .

Проще наход ть среднее для 1000 – х, а не для х (табл. 10).

Таблица 10

1000–хi

Число измере-

n·(1000–хi)

(1000–хi) 2

n· (1000–хi) 2

ний n

75

1

75

5625

5625

50

9

450

2500

22500

25

6

150

625

3750

0

18

0

0

0

-25

10

-250

625

6250

-50

2

-100

2500

5000

l

46

325

–

43125

∑

i=1

112

l

∑ x n

1000 − x

=

i=1

i i

= 325 = 7,1 или х

=1000 − 7,1 = 992,9°.

в

n

46

в

l

n

∑ x 2

D (Х ) =

i=1

i

i

− x

2

= 43125

− 7,12 = 887 .

в

n

в

46

Найдем исправленную дисперсию

s2 =

n

D =

46

887 = 906,7 С .

n −1

в

45

4.3.Интервальные оценки математического ожидания

исреднего квадратического отклонения

оценками, то есть указывать интервал, в которыйИс заданной вероятностью попадает истинное значение оцениваемого параметра. Разу-

При выборке малого объема точечная оценка может значительно

отличаться от оцениваемого параметра, что приводит к грубым ошиб-

кам. Поэтому в таком случае лучше пользоваться интервальными

меется, чем меньше длина этого интервала, тем точнее оценка пара-

метра.

Д

Поэтому, если для оценки θ* некоторого параметра θ справедли-

во неравенство | θ* – θ | < δ, число δ > 0 характеризует точность

А

оценки (чем меньше δ, тем точнее оценка). Но статистические методы

С

б

позволяют говорить только о том, что это неравенство выполняется с

некоторой вероятностью.

Определение. Доверительными

интервалом называется интервал

θ* – δ < θ < θ* + δ, в котором с заданной вероятностью γ заключено

истинное значение неизвестного параметра θ. Величина γ называется доверительной вероятностью или надежностью. Из определения доверительной вероятности следует, что

γ =Р ( θ* – δ < θ < θ* + δ ).

На практике обычно берут γ=0,95 или γ=0,99.

Рассмотрим построение доверительных интервалов для математического ожидания и среднего квадратического отклонения нормально распределенной случайной величины.

1. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестной дисперсии.

Если известно, что исследуемая случайная величина Х распреде-

113

лена по нормальному закону с неизвестным средним квадратическим отклонением, то для поиска доверительного интервала для ее математического ожидания а построим новую случайную величину

T =

xв − a

,

n

s

где хв – выборочное среднее; s2 – исправленная дисперсия; n – объем выборки. Эта случайная величина, возможные значения которой будем обозначать через t, имеет распределение Стьюдента с k = n – 1 степенями свободы. Плотность распределения Стьюдента явным образом не зависит от а и σ ( неизвестное СКО), а зависит только от n.

По определению доверительного интервала с заданной надежно-

стью γ имеем

γ = P(хв −δ < а < хв + δ )= Р(

хв − а

< δ )=

И

хв − а

n

< δ n

= Р(

< tγ ),

= Р

T

(3.6)

s

Д

s

где tγ =

δ

n

.

А

s

(к)называется критерием Стьюдента для уровня значи-

Число tγ

б

мости α и числа степеней сво оды k = n – 1. Его определяем по табли-

це для распределения Стьюдента (прил. 3). При определении довери-

n

и

s

тельных интервалов задаются о ычно надежностями γ=1–α, равными

0,9;

0,95;

0,99. Затем з

выражения (3.6)

определяем величину

s tγ

С

δ

δ =

,

которую наход м

з соотношения

tγ =

n

. Таким обр а-

зом, доверительный интервал с надежностью γ для математического ожидания а при неизвестном s есть интервал вида

xв − tγ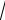ns < а < xв + tγ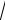ns .

При больших n (n >30) распределение Стьюдента практически совпадает с нормальным. В этом случае tγ можно найти из уравнения

2Ф(tγ )=1−α = γ .

Пример 2. По 25-ти деталям выборочные характеристики прочности Х составили: хв = 3; s = 1,5. Найти доверительный интервал для математического ожидания нормально распределенной случайной величины Х и точность оценки δ при γ= 0,99.

114

Решение. Из таблицы распределения Стьюдента (см. прил. 3) на-

ходим, что tγ (n = 25; к=25–1; α = 1–γ=1–0,99=0,01) = 2,80.

Тогда

3 −

2,8 1,5

< а < 3 +

2,8 1,5

,

25

25

или 2,16< a < 3,84 – доверительный интервал, в который попадает а с

вероятностью 0,99. Точность оценки δ = 0,84.

2. Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения.

Пусть по выборке объёма n получено исправленное среднее

квадратическое отклонение s =

n

D

, которое является точечной

n −1

в

И

оценкой среднего квадратического отклонения σ случайной величины

Х. Будем искать для s нормально распределенной случайной величины доверительный интервал вида (s − δ;s + δ ), где s – исправленное выборочное среднее квадратическое отклонение. По определению,

доверительный интервал с заданной надежностью Р( |σ – s| < δ ) = γ имеет вид s − δ < σ < s + δ .

δ

δ

или обо-

Запишем это неравенство в видеДs 1−

< σ < s 1+

s

s

значим δ

= q и, подставив q в Арассмотренное выше неравенство, по-

s

б

лучим

s(1− q)< σ < s(1+ q) при q<1;

и0 < σ < s(1+ q)

при q>1,

где q = q(n,γ ).

С

Существуют таблицы, из которых можно найти q по заданным n

и γ (прил. 5). Случайная величина q имеет распределение, зависящее только от n.

Для дисперсии оценка имеет вид

s2 (1− q)2 < D < s2 (1+ q)2 при q<1;

0 < D < s2 (1+ q)2 при q>1.

Пример 3. Произведено 20 измерений одним прибором некоторой случайной величины, имеющей нормальное распределение. Исправленное выборочное среднее квадратическое отклонение случайных ошибок измерений равно 1,3. Найти точность прибора с надежностью 0,95.

115

Решение. Точность прибора – это среднее квадратическое отклонение σ случайных ошибок измерений. По условию задачи, n = 20; s = 1,3. Найдем доверительный интервал для σ при заданной надежно-

сти γ = 0,95. По прил. 5 находим q (n = 20; γ = 0,95 ) = 0,37. Следовательно, границы доверительного интервала: 1,3(1–0,37) = 0,819 и 1,3(1+0,37) = 1,781. Итак, 0,819 < σ < 1,781 с вероятностью 0,95.

3. Доверительные интервалы для оценки дисперсии.

Считаем, что, вообще говоря, математическое ожидание неиз-

вестно, а известна только точечная несмещенная оценка дисперсииs2 . Тогда доверительный интервал для дисперсии, соответствующий доверительной вероятности γ = 1−α , имеет вид

(n −1)s2

(n −1)s2

.

(3.7)

≤ D ≤

χ

2

χ 2

И

2

γ

1

Так как по заданной вероятности

можно построить множество

Д

χ 2 выби-

доверительных интервалов для дисперсии, то принято χ 2 и

рать так, чтобы

1

2

А

P(χ 2 > χ 2 )

= 1−

α

, а P(χ 2 < χ 2 )

= α

,

1

2

2

2

2

2

б

где числа χ1 и

χ2 находят по прил. 4 при числе степеней свободы

и

α

и р =

α .

k = n –1 и соответственно при р = 1−

2

2

Пример 4. Пользуясь 90%-ным доверительным интервалом, оце-

С

зменение прочности деталей во всей ге-

ните в условиях пр мера 2

неральной совокупности.

Решение. По условию, п=25; s=1,5; γ=0,9. Найдем доверительный

интервал для оценки дисперсии.

Согласно формуле (3.7)

(n −1)s

2

≤ σ ≤

(n −1)s

2

, а так как при

χ22

χ12

k=n–1=25–1=24 верхняя доверительная граница равна

χ22 (р;к) = χ22

1− γ

;к

2

= χ22 (0,05;24) = 36,4,

нижняя определяется как

1−

γ

χ12 (р;к) =

−

χ12 1

2

;к = χ12 (0,95;24) = 13,8(см. прил. 4),

116

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #

    07.01.2021201.85 Кб018.pdf

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

В Excel имеются функции, отдельно вычисляющие исправленную дисперсию s 2 по формуле (2.6) и исправленное стандартное отклонение s по формуле (2.8), генеральные и выборочные дисперсию Dг и по формуле (2.6) и стандартное отклонение sг и sв по формуле (2.7). Поэтому, прежде чем вычислять дисперсию и стандартное отклонение, следует четко определиться, являются ли ваши данные генеральной совокупностью или выборочной, а также какую дисперсию необходимо вычислить: исправленную или обычную.

Использование стандартных функций Excel возможно только при обработке несгруппированных данных. Если исходные данные уже сгруппированы, то вычисление дисперсий и стандартных отклонений следует производить по указанным выше формулам, используя функции суммирования и извлечения корня.

Для вычисления исправленной дисперсии s 2 по формуле (2.6) и исправленного стандартного отклонения s по формуле (2.8) имеются функции ДИСП (или VAR) и СТАНДОТКЛОН (или STDEV). Аргументом этих функций является набор чисел, как правило, заданный диапазоном ячеек, например, =ДИСП(В1:В48), если данные содержатся в интервале ячеек от В1 до В48.

Для вычисления выборочной (или генеральной) дисперсии по формуле (2.3) и стандартного отклонения по формуле (2.7) имеются функции ДИСПР (или VARP) и СТАНДОТКЛОНП (или STDEVP), соответственно.

Аргументы этих функций такие же как и для исправленной дисперсии.

Поделиться:

Воспользуйтесь поиском по сайту:

studopedia.org — Студопедия.Орг — 2014-2023 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.01 с) .

Источник

Дисперсия и стандартное отклонение в EXCEL

history 4 октября 2016 г.

Вычислим в MS EXCEL дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.

Сначала рассмотрим дисперсию , затем стандартное отклонение .

Дисперсия выборки

Дисперсия выборки ( выборочная дисперсия, sample variance ) характеризует разброс значений в массиве относительно среднего .

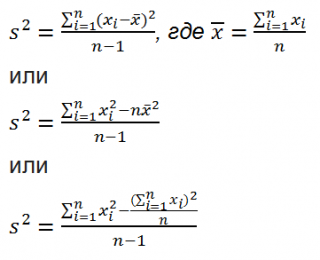
Все 3 формулы математически эквивалентны.

Из первой формулы видно, что дисперсия выборки это сумма квадратов отклонений каждого значения в массиве от среднего , деленная на размер выборки минус 1.

В MS EXCEL 2007 и более ранних версиях для вычисления дисперсии выборки используется функция ДИСП() , англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог ДИСП.В() , англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция ДИСП.Г(), англ. название VARP, т.е. Population VARiance, которая вычисляет дисперсию для генеральной совокупности . Все отличие сводится к знаменателю: вместо n-1 как у ДИСП.В() , у ДИСП.Г() в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция ДИСПР() .

Дисперсию выборки можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ) =КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) – обычная формула =СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1 ) – формула массива

Дисперсия выборки равна 0, только в том случае, если все значения равны между собой и, соответственно, равны среднему значению . Обычно, чем больше величина дисперсии , тем больше разброс значений в массиве.

Дисперсия выборки является точечной оценкой дисперсии распределения случайной величины, из которой была сделана выборка . О построении доверительных интервалов при оценке дисперсии можно прочитать в статье Доверительный интервал для оценки дисперсии в MS EXCEL .

Дисперсия случайной величины

Чтобы вычислить дисперсию случайной величины, необходимо знать ее функцию распределения .

Для дисперсии случайной величины Х часто используют обозначение Var(Х). Дисперсия равна математическому ожиданию квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X)) 2 ]

Если случайная величина имеет дискретное распределение , то дисперсия вычисляется по формуле:

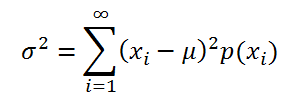
где x i – значение, которое может принимать случайная величина, а μ – среднее значение ( математическое ожидание случайной величины ), р(x) – вероятность, что случайная величина примет значение х.

Если случайная величина имеет непрерывное распределение , то дисперсия вычисляется по формуле:

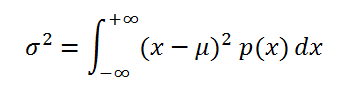
Для распределений, представленных в MS EXCEL , дисперсию можно вычислить аналитически, как функцию от параметров распределения. Например, для Биномиального распределения дисперсия равна произведению его параметров: n*p*q.

Примечание : Дисперсия, является вторым центральным моментом , обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно математического ожидания .

Примечание : О распределениях в MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .

Размерность дисперсии соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг 2 . Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из дисперсии – стандартное отклонение .

Некоторые свойства дисперсии :

Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.

Var(Х)=E[(X-E(X)) 2 ]=E[X 2 -2*X*E(X)+(E(X)) 2 ]=E(X 2 )-E(2*X*E(X))+(E(X)) 2 =E(X 2 )-2*E(X)*E(X)+(E(X)) 2 =E(X 2 )-(E(X)) 2

Это свойство дисперсии используется в статье про линейную регрессию .

Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.

Если случайные величины независимы (independent), то их ковариация равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе стандартной ошибки среднего .

Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1) 2 Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения доверительного интервала для разницы 2х средних .

Примечание : квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).

Стандартное отклонение выборки

Стандартное отклонение выборки — это мера того, насколько широко разбросаны значения в выборке относительно их среднего .

По определению, стандартное отклонение равно квадратному корню из дисперсии :

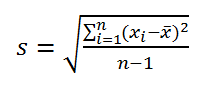
Стандартное отклонение не учитывает величину значений в выборке , а только степень рассеивания значений вокруг их среднего . Чтобы проиллюстрировать это приведем пример.

Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется Коэффициент вариации (Coefficient of Variation, CV) — отношение Стандартного отклонения к среднему арифметическому , выраженного в процентах.

В MS EXCEL 2007 и более ранних версиях для вычисления Стандартного отклонения выборки используется функция =СТАНДОТКЛОН() , англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог =СТАНДОТКЛОН.В() , англ. название STDEV.S, т.е. Sample STandard DEViation.

Кроме того, начиная с версии MS EXCEL 2010 присутствует функция СТАНДОТКЛОН.Г() , англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет стандартное отклонение для генеральной совокупности . Все отличие сводится к знаменателю: вместо n-1 как у СТАНДОТКЛОН.В() , у СТАНДОТКЛОН.Г() в знаменателе просто n.

Стандартное отклонение можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ) =КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))

Другие меры разброса

Функция КВАДРОТКЛ() вычисляет с умму квадратов отклонений значений от их среднего . Эта функция вернет тот же результат, что и формула =ДИСП.Г( Выборка )*СЧЁТ( Выборка ) , где Выборка — ссылка на диапазон, содержащий массив значений выборки ( именованный диапазон ). Вычисления в функции КВАДРОТКЛ() производятся по формуле:

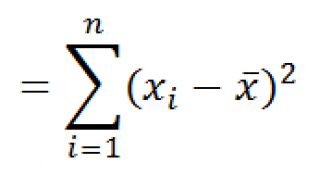
Функция СРОТКЛ() является также мерой разброса множества данных. Функция СРОТКЛ() вычисляет среднее абсолютных значений отклонений значений от среднего . Эта функция вернет тот же результат, что и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка) , где Выборка — ссылка на диапазон, содержащий массив значений выборки.

Вычисления в функции СРОТКЛ () производятся по формуле:

Источник

Выборочная дисперсия. Исправленная дисперсия

Оценка параметров генеральной совокупности

Выборочное среднее

Пусть имеется случайная выборка объема n, представленная вариационным рядом <(xj, nj)>, где xj — варианты, nj — частоты, j = 1, 2, …, m. Если мы имеем дело с интервальным вариационным рядом, то xj — середины интервалов.

Выборочное среднее значение определяется по формуле

(3.1)

Если выборка не сгруппирована, то выборочная средняя определяется по формуле

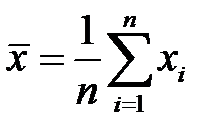(3.2)

Выборочное среднее 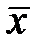является случайной величиной. Её математическое ожидание равно генеральной средней, т.е. выборочное среднее является несмещенной оценкой генеральной средней.

Если у генеральной совокупности генеральная средняя равна a и среднеквадратическое отклонение равно σ, то среднеквадратическое отклонение выборочной средней для повторной выборки вычисляется по формуле

. (3.3)

Среднеквадратическое отклонение выборочной средней для бесповторной выборки вычисляется по формуле

. (3.4)

где N — объем генеральной совокупности.

Для вычисления выборочной средней для не сгруппированной выборки в программе Excel можно воспользоваться следующей функцией (которая вычисляет среднее арифметическое):

Число1, число2, . — это от 1 до 30 аргументов, для которых вычисляется среднее.

  • Аргументы должны быть либо числами, либо именами, массивами или ссылками, содержащими числа.
  • Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.

Если выборка представлена вариационным рядом, то для вычисления выборочного среднего можно воспользоваться функцией СУММПРОИЗВЕД(массив1;массив2;…), которая вычисляет сумму произведений соответствующих элементов массивов массив1, массив2 и т.д.

Пример 3.1. Найти выборочное среднее для выборки из 10 числовых значений, записанных в ячейках А2:А11 (см. рис. 3.1).

Решение. Введите в ячейку А12 формулу =СРЗНАЧ(А2:А11). Получим значение 1,9.

Пример 3.2. Найти выборочное среднее для выборки, представленной вариационным рядом из 10 числовых значений вариант, записанных в ячейках С2:С11, и 10 значений частот, записанных в ячейках D2:D11 .

Решение. Введите в ячейку C12 формулу

Получим значение 3,571429.

Выборочная дисперсия. Исправленная дисперсия

Выборочная дисперсия s 2 для сгруппированной в вариационный ряд выборки определяется по формуле

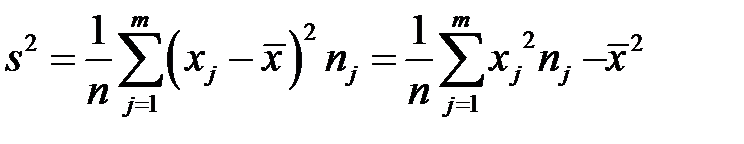(3.5)

Исправленная дисперсия вычисляется по формуле

(3.6)

Если выборка не сгруппирована, то выборочная дисперсия s 2 определяется по формуле

, (3.7)

а исправленная дисперсия — по формуле

(3.8)

Исправленная дисперсия является несмещенной оценкой генеральной дисперсии, т.е. математическое ожидание исправленной дисперсии равно генеральной дисперсии.

В программе Excel для вычисления выборочной дисперсии для выборки, не сгруппированной в вариационный ряд, предназначена функция

Число1, число2. — от 1 до 30 числовых аргументов, соответствующих выборке (числа или диапазоны ячеек).

ДИСПР предполагает, что аргументы представляют всю генеральную совокупность. Если данные представляют только выборку из генеральной совокупности, то дисперсию следует вычислять, используя функцию ДИСП.

Формула для ДИСПР имеет вид (3.7).

Для вычисления исправленной дисперсии предназначена функция

Формула для ДИСП имеет вид (3.8).

Обратите внимание на имена этих функций, можно подумать, что ДИСПР() вычисляет исправленную дисперсию, а ДИСП() — выборочную, тогда как на самом деле функция ДИСП() вычисляет исправленную дисперсию, а ДИСПР() — выборочную.

Источник

Adblock
detector

Источник

Добавить комментарий