Как найти испускательную способность тела

Как найти испускательную способность тела

Энергетическая
светимость тела
RТ,
численно равна энергии W, излучаемой
телом во всем диапазоне длин волн (0<<)
с единицы поверхности тела, в единицу
времени, при температуре тела Т,
т.е.

(1)

Испускательная
способность тела
r,Т
численно равна энергии тела dW,
излучаемой телом c единицы поверхности
тела, за единицу времени при температуре
тела Т, в диапазоне длин волн от
до +d,
т.е.



(2)

Эту
величину называют также спектральной
плотностью энергетической светимости
тела.

Энергетическая
светимость связана с испускательной
способностью формулой

(3)

Поглощательная
способность
тела ,T
– число, показывающее, какая доля энергии
излучения, падающего на поверхность
тела, поглощается им в диапазоне длин
волн от
до +d,
т.е.

.
(4)

Тело,
для которого ,T
= 1
во всем диапазоне длин волн, называется
абсолютно
черным телом (АЧТ).

Тело,
для которого ,T=const<1
во всем
диапазоне длин волн называют серым.

7.3. Закон Кирхгофа

Отношение
испускательной способности тела r,Т
к его
поглощательной способности
,T
не зависит
от природы тела и является для всех тел
универсальной функцией длины волны и
температуры, равной испускательной
способности АЧТ, т.е.

.
(5)

Отсюда
следует, что тело, которое сильнее
поглощает какие-либо лучи, будет сильнее
эти лучи и испускать.

7.4. Распределение энергии в спектре абсолютно черного тела

Абсолютно
черных тел в природе не существует. Его
функции может выполнять малое отверстие
в почти замкнутой полости (см. рис. 1).
Излучение, прошедшее внутрь этого
отверстия, прежде чем выйти обратно из
отверстия претерпевает многократные
отражения и практически полностью
поглощается. Поэтому поглощательная
способность для него,T
= 1
 и по закону
Кирхгофа (5) испускательная способность
r,Т
 такого
устройства очень близка к испускательной
способности АЧТ
.

Таким образом,
если стенки полости поддерживать при
некоторой температуре Т, то из отверстия
выйдет излучение, весьма близкое к
излучению AЧТ.

Разлагая полученное
излучение в спектр с помощью дифракционной
решетки и измеряя интенсивность разных
участков спектра, можно найти
экспериментально вид функции
от
(рис. 2).
Площадь, охватываемая кривой, дает
энергетическую светимость АЧТ [см.
формулу (3)]. Из рис. 2 следует, что
энергетическая светимость АЧТ сильно
возрастает с ростом температуры, а длина
волны, соответствующая максимуму
испускательной способности АЧТ, с ростом
температуры сдвигается в сторону более
коротких волн.

7.5. Закон Стефана-Больцмана

Энергетическая
светимость АЧТ пропорциональна четвертой
степени термодинамической температуры

,
(6)

где =5.6710-8
Вт/(м2К4)
– постоянная Стефана-Больцмана.

7.6. Закон смещения Вина

Длина
волны, соответствующая максимальному
значению испускательной способности
АЧТ, с ростом температуры смещается в
сторону меньших длин волн:

, (7)

где b=2.910-3
мК
– постоянная Вина.

Соседние файлы в папке Методичка Беланов А.С.

  • #
  • #
  • #
  • #
Источник

Фо́рмула Пла́нка (зако́н Пла́нка) — формула, описывающая спектральную плотность излучения, которое создаётся абсолютно чёрным телом определённой температуры. Формула была открыта Максом Планком в 1900 году и названа по его фамилии. Её открытие сопровождалось появлением гипотезы о том, что энергия может принимать только дискретные значения. Эта гипотеза некоторое время после открытия не считалась значимой, но, как принято считать, дала рождение квантовой физике.

Формула[править | править код]

Формула Планка — выражение для спектральной плотности излучения, создаваемого абсолютно чёрным телом определённой температуры. Встречаются различные формы записи этой формулы[1][2].

Энергетическая яркость[править | править код]

Формула, выражающая спектральную плотность энергетической яркости, выглядит следующим образом[3]:

{displaystyle B_{nu }(nu ,T)={frac {2hnu ^{3}}{c^{2}}}{frac {1}{e^{frac {hnu }{kT}}-1}},}

где nu  — частота излучения, T — температура абсолютно чёрного тела, h — постоянная Планка, c — скорость света, k — постоянная Больцмана. В системе СИ величина {displaystyle B_{nu }} в этой формуле имеет размерность Вт·м−2·Гц−1·ср−1. Её физический смысл — энергетическая яркость в малом диапазоне частот {displaystyle (nu ;nu +dnu )}, делённая на {displaystyle dnu }. Можно использовать аналогичную формулу, в которой энергетическая яркость будет функцией длины волны lambda , а не частоты[3][4]:

{displaystyle B_{lambda }(lambda ,T)={frac {2hc^{2}}{lambda ^{5}}}{frac {1}{e^{frac {hc}{lambda kT}}-1}}}.

В этом случае {displaystyle B_{lambda }} имеет размерность Вт·м−2·м−1·ср−1 и соответствует энергетической яркости в малом диапазоне длин волн {displaystyle (lambda ;lambda +dlambda )}, делённой на {displaystyle dlambda }[3][4].

Излучательная способность[править | править код]

Излучательная способность на частоте nu или длине волны lambda  — это мощность излучения на единицу площади в интервале частот {displaystyle (nu ;nu +dnu )} или длин волн {displaystyle (lambda ;lambda +dlambda )}, делённая, соответственно, на {displaystyle dnu } или {displaystyle dlambda }. Она может быть выражена формулами[5]:

{displaystyle varepsilon _{nu }(nu ,T)={frac {2pi hnu ^{3}}{c^{2}}}{frac {1}{e^{frac {hnu }{kT}}-1}}},
{displaystyle varepsilon _{lambda }(lambda ,T)={frac {2pi hc^{2}}{lambda ^{5}}}{frac {1}{e^{frac {hc}{lambda kT}}-1}}}.

Таким образом, излучательная способность тела численно в pi раз больше яркости, если телесный угол в ней измеряется в стерадианах. Величины {displaystyle varepsilon _{nu }} и {displaystyle varepsilon _{lambda }} имеют размерности, соответственно, Вт·м−2·Гц−1 и Вт·м−2·м−1[5].

Спектральная плотность энергии[править | править код]

Ещё одна форма записи описывает спектральную объёмную плотность энергии излучения абсолютно чёрного тела. По аналогии с предыдущими формулами, она равна плотности энергии в малом диапазоне частот или длин волн, делённой на ширину этого диапазона[1][2]:

{displaystyle u_{nu }(nu ,T)={frac {8pi hnu ^{3}}{c^{3}}}{frac {1}{e^{frac {hnu }{kT}}-1}}},
{displaystyle u_{lambda }(lambda ,T)={frac {8pi hc}{lambda ^{5}}}{frac {1}{e^{frac {hc}{lambda kT}}-1}}}.

В системе СИ величины {displaystyle u_{nu }} и {displaystyle u_{lambda }} имеют размерности, равные, соответственно, Дж·м−3·Гц−1 и Дж·м−3·м−1[1][2]. Кроме того, спектральная плотность энергии связана с излучательной способностью соотношением {textstyle varepsilon ={frac {c}{4}}u}[6].

Применимость[править | править код]

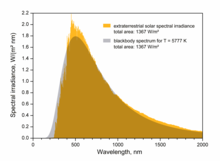
Спектр Солнца (жёлтый цвет) и спектр абсолютно чёрного тела температурой 5777 K (серый цвет)

Формула Планка применима для излучения, которое находится в тепловом равновесии с веществом при определённой температуре[2]. Она применима для абсолютно чёрных тел любой формы вне зависимости от состава и структуры при условии, что размеры излучающего тела и деталей его поверхности гораздо больше длин волн, на которых тело в основном излучает[3][7].

В случае если тело не является абсолютно чёрным, то спектр его равновесного теплового излучения не описывается законом Планка, но связан с ним законом излучения Кирхгофа. Согласно этому закону, отношение излучательной и поглощательной способностей тела одинаково для всех длин волн и зависит только от температуры[8]. Так, например, при одной температуре распределение энергии в спектре абсолютно серого тела будет таким же, как и в спектре абсолютно чёрного, но суммарная энергетическая яркость излучения будет меньше[9].

Формула Планка также используется и для описания реальных тел, спектр излучения которых отличается от планковского. Для этого вводится понятие эффективной температуры тела: это та температура, при которой абсолютно чёрное тело излучает столько же энергии на единицу площади, что и данное тело. Аналогичным образом определяется яркостная температура, равная температуре абсолютно чёрного тела, излучающего столько же энергии на единицу площади на определённой длине волны, и цветовая температура, равная температуре абсолютно чёрного тела с таким же распределением энергии в определённом участке спектра[2][10][11]. Например, для Солнца эффективная температура составляет около 5780 K, а яркостная температура, в зависимости от длины волны, принимает различные значения: на длине волны 1500 Å она достигает минимального значения в 4200 K, а в видимом диапазоне на длине волны 5500 Å составляет около 6400 K, в то время как для абсолютно чёрного тела температуры, определяемые таким образом, совпадают[12].

История открытия[править | править код]

Предыстория[править | править код]

Определение закона теплового излучения представляло интерес с 1859 года, когда Густав Кирхгоф открыл закон излучения Кирхгофа, согласно которому отношение излучательной и поглощательной способностей универсально для всех тел. Следовательно, функция излучения абсолютно чёрного тела, поглощательная способность которого равна единице для всех длин волн, должна совпадать с функцией этого отношения[13][14].

К концу XIX века спектр излучения абсолютно чёрного тела уже был известен экспериментально. В 1896 году Вильгельм Вин эмпирически описал его законом излучения Вина, однако получить ни его теоретическое обоснование, ни какой-либо вывод физикам на тот момент не удавалось. Хотя Вин в своей работе приводил обоснование закона, оно было недостаточно строгим, чтобы эта проблема считалась решённой[6][15][16].

Макс Планк был одним из тех, кто пытался теоретически обосновать закон излучения Вина. Он исходил из того, что излучатели являются линейными гармоническими осцилляторами, у которых установилось равновесие между испусканием и поглощением; определив связь между энтропией и энергией осцилляторов, он смог подтвердить закон излучения Вина[17].

Однако дальнейшие эксперименты показали, что закон излучения Вина неточно описывает спектр теплового излучения в длинноволновой области. В октябре 1900 года Планк представил формулу, которая с точностью до констант совпадала с современным законом Планка. В тот же день было выяснено, что формула хорошо описывает экспериментальные данные, но при этом она не имела под собой теоретической основы. Планк вывел её лишь на основании того, что в предельном случае для коротких волн она должна переходить в закон Вина, но, в отличие от него, согласовываться с экспериментальными данными для длинных волн[18].

Открытие[править | править код]

Менее чем через два месяца после сообщения о получении формулы Планк представил её теоретический вывод на заседании Немецкого физического общества. В нём использовалось соотношение для энтропии, введённое Людвигом Больцманом, в котором рассматривается число возможных микроскопических состояний системы. Планк, чтобы иметь возможность использовать методы комбинаторики и оценить таким образом энтропию, сделал допущение, что полная энергия состоит из целого числа конечных элементов энергии — квантов[15][19].

Несмотря на то, что в этом выводе появились кванты и была введена и впервые использована постоянная Планка, ни сам Планк, ни его коллеги не поняли всей глубины открытия. Например, Планк считал, что дискретность энергии не имеет никакого физического смысла и является лишь математическим приёмом. Другие физики также не придали этому значения и не считали, что это предположение противоречит классической физике. Лишь после публикации Хендрика Лоренца в 1908 году научное сообщество пришло к мнению, что кванты действительно имеют физический смысл. Сам Планк впоследствии называл ввод квантов «актом отчаяния», вызванным тем, что «теоретическое объяснение должно быть найдено любой ценой, сколь высокой она ни была бы». Несмотря на всё это, день, когда формула Планка была обоснована, — 14 декабря 1900 года — считается днём рождения квантовой физики[15][20].

Пользуясь соображениями классической физики, в 1900 году лорд Рэлей, а в 1905 году Джеймс Джинс вывели закон Рэлея — Джинса. К такому же результату, независимо от них, приходил в своих работах и сам Планк. Вывод этого закона мало отличался от вывода закона Планка (см. ниже[⇨]), за исключением того, что средняя энергия излучения {displaystyle langle varepsilon rangle } была принята равной kT, согласно теореме о равном распределении энергии по степеням свободы. С точки зрения классической физики ход вывода не вызывал сомнений, однако закон Рэлея — Джинса не только серьёзно расходился с экспериментальными данными везде, кроме длинноволновой области, но и предсказывал бесконечно большую мощность излучения на коротких волнах. Этот парадокс указал на то, что в классической физике всё же имеются фундаментальные противоречия, и стал дополнительным аргументом в пользу квантовой гипотезы. Пауль Эренфест в 1911 году впервые назвал его ультрафиолетовой катастрофой[6][15][21].

В 1918 году Макс Планк стал лауреатом Нобелевской премии по физике, и хотя официально он был награждён за открытие квантов, это открытие было тесно связано с выводом закона Планка[22].

Вывод формулы Планка[править | править код]

Вывод через распределение Больцмана[править | править код]

Формула Планка выводится следующим образом[6].

При выводе рассматривается абсолютно чёрное тело малых размеров с температурой T, расположенное внутри куба с ребром длины l, внутренние стенки которого идеально отражают излучение. В результате испускание и поглощение света уравновесятся, а излучение будет распределено равномерно по всему внутреннему пространству куба. Внутри куба будет поддерживаться некоторая плотность энергии u(T). Тогда спектральной плотностью энергии будет называться величина {displaystyle u_{omega }(omega ,T)}, равная плотности энергии на единичный интервал угловых частот вблизи omega .

При выборе малой площади Delta S на поверхности абсолютно чёрного тела можно рассчитать, сколько энергии на неё падает. Плотность энергии, падающей под углом theta к нормали из телесного угла dOmega , равна {textstyle d{tilde {u}}=u(T){frac {dOmega }{4pi }}}, так как излучение равномерно распределено по всем направлениям в телесном угле 4pi стерадиан. Свет движется со скоростью c, а значит, за время Delta t на поверхность падает энергия {displaystyle dw}:

{displaystyle dw=c,d{tilde {u}},Delta t,Delta Scos theta ={frac {c}{4pi }}u(T)cos theta sin theta ,dtheta ,dvarphi ,Delta S,Delta t}.

Суммой энергии, приходящей со всех направлений, будет поток Phi :

{displaystyle Phi ={frac {c}{4pi }}u(T)int _{0}^{2pi }dvarphi int _{0}^{pi /2}cos theta sin theta ,dtheta ={frac {c}{4}}u(T)}.

Такое же количество энергии будет излучать та же единица площади абсолютно чёрного тела, а значит, как для всего потока, так и для любого диапазона частот или длин волн будет справедливо соотношение {textstyle varepsilon ={frac {c}{4}}u}.

Так как внутри куба одновременно присутствуют и излучаемые, и отражённые волны, поле теплового излучения должно представлять собой их суперпозицию, то есть иметь вид стоячих электромагнитных волн. Для определения их параметров вводятся декартова система координат вдоль рёбер куба и соответствующие орты {textstyle {vec {e}}_{x},{vec {e}}_{y},{vec {e}}_{z}}. Для волны, которая распространяется строго вдоль оси x, должно выполняться {textstyle l=n_{x}{frac {lambda }{2}}}, где {displaystyle n_{x}} — натуральное число: то есть полуцелое число волн должно иметь суммарную длину ровно {textstyle l}. Волновой вектор такой волны равен {textstyle {vec {k}}=k_{x}{vec {e}}_{x}}, где {textstyle k_{x}={frac {2pi }{lambda }}} — волновое число, ограничение для которого принимает вид {textstyle k_{x}=n_{x}{frac {pi }{l}}}.

Для волн, распространяющихся вдоль осей y и z, рассуждения аналогичны; волну, которая распространяется в любом другом направлении, можно представлять в виде суперпозиции волн, которые распространяются вдоль осей: {displaystyle {vec {k}}=k_{x}{vec {e}}_{x}+k_{y}{vec {e}}_{y}+k_{z}{vec {e}}_{z}}. Следовательно, {textstyle k_{x}=n_{x}{frac {pi }{l}},k_{y}=n_{y}{frac {pi }{l}},k_{z}=n_{z}{frac {pi }{l}}}, где {displaystyle n_{x},n_{y},n_{z}} — независимые друг от друга натуральные числа либо нули. Тогда волновое число любой волны представляется как {textstyle k={sqrt {k_{x}^{2}+k_{y}^{2}+k_{z}^{2}}}={frac {pi }{l}}{sqrt {n_{x}^{2}+n_{y}^{2}+n_{z}^{2}}}}, а частота как {textstyle omega ={frac {pi c}{l}}{sqrt {n_{x}^{2}+n_{y}^{2}+n_{z}^{2}}}}. Каждой тройке этих параметров соответствует одна стоячая волна.

С помощью безразмерной величины {textstyle R={frac {omega l}{pi c}}} можно определить число стоячих волн частотой не более omega . Это число {displaystyle {tilde {N}}} равно числу комбинаций {displaystyle n_{x},n_{y},n_{z}}, для которых {displaystyle R^{2}geq n_{x}^{2}+n_{y}^{2}+n_{z}^{2}}. Тогда можно оценить {displaystyle {tilde {N}}} как восьмую часть объёма шара с радиусом {textstyle R}:

{displaystyle {tilde {N}}={frac {1}{8}}cdot {frac {4}{3}}pi R^{3}={frac {1}{6}}cdot {frac {omega ^{3}l^{3}}{pi ^{2}c^{3}}}={frac {1}{6}}cdot {frac {omega ^{3}}{pi ^{2}c^{3}}}V,}

где V — пространство, в котором заключено излучение. Так как электромагнитные волны — поперечные, в каждом направлении могут распространяться по две волны, поляризованных взаимно перпендикулярно, и реальное число волн N увеличивается ещё в два раза:

{displaystyle N=2{tilde {N}}={frac {1}{3}}cdot {frac {omega ^{3}}{pi ^{2}c^{3}}}V}.

Если продифференцировать это выражение по частоте, получится число стоячих волн с длинами волн в интервале {displaystyle (omega ;omega +domega )}:

{displaystyle dN={frac {omega ^{2}domega }{pi ^{2}c^{3}}}V}.

Можно взять за {displaystyle langle varepsilon rangle } среднюю энергию стоячей электромагнитной волны с частотой omega . Если умножить количество стоячих волн dN на {displaystyle langle varepsilon rangle } и разделить полученное значение на V и на {displaystyle domega }, получится спектральная плотность энергии излучения:

{displaystyle u_{omega }={frac {omega ^{2}}{pi ^{2}c^{3}}}langle varepsilon rangle }.

Для дальнейшего вывода закона Планка необходимо учитывать эффекты квантовой физики, а именно — то, что энергия излучается конечными по величине порциями, по величине равными E = hbar omega ({textstyle hbar ={frac {h}{2pi }}} — постоянная Дирака); соответственно, возможные значения энергии излучения равны {displaystyle varepsilon _{n}=nhbar omega }, где n — любое натуральное число. Таким образом, средняя энергия излучения {displaystyle langle varepsilon rangle } равна:

{displaystyle langle varepsilon rangle =sum _{n=0}^{infty }P_{n}varepsilon _{n},}

где P_{n} — вероятность того, что излучение будет иметь энергию, равную varepsilon _{n}. Вероятность описывается распределением Больцмана по энергиям  (англ.) (рус. с некоторой константой A:

{displaystyle P_{n}=Ae^{-{frac {varepsilon _{n}}{kT}}}}.

С учётом {textstyle sum _{n=0}^{infty }P_{n}=1}, для A верно:

{displaystyle A=left(sum _{n=0}^{infty }e^{-{frac {varepsilon _{n}}{kT}}}right)^{-1}}.

Таким образом, {displaystyle langle varepsilon rangle } выражается как:

{displaystyle langle varepsilon rangle ={frac {sum _{n=0}^{infty }nhbar omega e^{-{frac {nhbar omega }{kT}}}}{sum _{n=0}^{infty }e^{-{frac {nhbar omega }{kT}}}}}=hbar omega {frac {sum _{n=0}^{infty }ne^{-nxi }}{sum _{n=0}^{infty }e^{-nxi }}}}.

Здесь {textstyle xi ={frac {hbar omega }{kT}}}. Знаменатель раскладывается по формуле суммы геометрической прогрессии, а числитель представляется как производная знаменателя по {textstyle xi }:

{displaystyle S=sum _{n=0}^{infty }e^{-nxi }={frac {1}{1-e^{-xi }}}},
{displaystyle sum _{n=0}^{infty }ne^{-nxi }=-{frac {dS}{dxi }}={frac {e^{-xi }}{(1-e^{-xi })^{2}}}}.

Получается выражение для средней энергии:

{displaystyle langle varepsilon rangle ={frac {hbar omega }{e^{frac {hbar omega }{kT}}-1}}}.

Если подставить {displaystyle langle varepsilon rangle } в формулу для спектральной плотности энергии излучения, получится один из окончательных вариантов формулы Планка:

{displaystyle u_{omega }={frac {hbar omega ^{3}}{pi ^{2}c^{3}}}{frac {1}{e^{frac {hbar omega }{kT}}-1}}}.

Соотношение {textstyle varepsilon ={frac {c}{4}}u} позволяет получить формулу для излучательной способности[6]:

{displaystyle varepsilon _{omega }={frac {hbar omega ^{3}}{4pi ^{2}c^{2}}}{frac {1}{e^{frac {hbar omega }{kT}}-1}}}.

Если разделить на pi , получится выражение для спектральной плотности яркости[23]:

{displaystyle B_{omega }={frac {hbar omega ^{3}}{4pi ^{3}c^{2}}}{frac {1}{e^{frac {hbar omega }{kT}}-1}}}.

Эти величины можно выразить через другие параметры — например, циклическую частоту nu или длину волны lambda . Для этого нужно учесть, что по определению выполняются соотношения {displaystyle B_{omega }domega =B_{nu }dnu }, {displaystyle B_{nu }dnu =-B_{lambda }dlambda } (минус появляется из-за того, что про росте длины волны уменьшается частота) и аналогичные формулы для излучательной способности и плотности энергии. Так, для перехода к циклическим частотам нужно заменить {displaystyle omega =2pi nu } (при этом {textstyle hbar ={frac {h}{2pi }}}, так что {displaystyle hnu =hbar omega }) и домножить на {textstyle {frac {domega }{dnu }}=2pi }, тогда формулы примут вид[3][23]:

{displaystyle u_{nu }={frac {8pi hnu ^{3}}{c^{3}}}{frac {1}{e^{frac {hnu }{kT}}-1}}},
{displaystyle varepsilon _{nu }={frac {2pi hnu ^{3}}{c^{2}}}{frac {1}{e^{frac {hnu }{kT}}-1}}},
{displaystyle B_{nu }={frac {2hnu ^{3}}{c^{2}}}{frac {1}{e^{frac {hnu }{kT}}-1}}}.

Аналогичным образом получаются формулы для длин волн. После замены {textstyle nu ={frac {c}{lambda }}} и домножения на {textstyle {frac {dnu }{dlambda }}=-{frac {c}{lambda ^{2}}}}[3][23]:

{displaystyle u_{lambda }={frac {8pi hc}{lambda ^{5}}}{frac {1}{e^{frac {hc}{lambda kT}}-1}}},
{displaystyle varepsilon _{lambda }={frac {2pi hc^{2}}{lambda ^{5}}}{frac {1}{e^{frac {hc}{lambda kT}}-1}}},
{displaystyle B_{lambda }={frac {2hc^{2}}{lambda ^{5}}}{frac {1}{e^{frac {hc}{lambda kT}}-1}}}.

Вывод через статистику Бозе — Эйнштейна[править | править код]

Если рассматривать равновесное излучение как фотонный газ, к нему можно применить статистику Бозе — Эйнштейна. Она определяет среднее число частиц {displaystyle langle n_{i}rangle } в i-м квантовом состоянии с энергией E_{i}[24]:

{displaystyle langle n_{i}rangle ={frac {1}{e^{frac {E_{i}-mu }{kT}}-1}}}.

В этой формуле mu  — химический потенциал газа. Для фотонного газа он равен нулю, поэтому формула для него представима в следующем виде[24]:

{displaystyle langle nrangle ={frac {1}{e^{frac {hbar omega }{kT}}-1}}}.

Если умножить среднее число фотонов {displaystyle langle nrangle } на их энергию hbar omega , получится та же средняя энергия {displaystyle langle varepsilon rangle }, что и выведенная из распределения Больцмана. При подстановке её в формулу для спектральной плотности энергии {textstyle u_{omega }={frac {omega ^{2}}{pi ^{2}c^{3}}}langle varepsilon rangle } получится закон Планка[24].

Вывод через спонтанное и вынужденное излучения[править | править код]

Формула Планка также может быть выведена из рассмотрения механизмов спонтанного и вынужденного излучений атомов[25].

В этом выводе, предложенном Эйнштейном в 1916 году, рассматриваются N_{m} и N_{n} атомов на уровнях с энергией E_m и E_{n} соответственно. Тогда количество переходов с высшего уровня E_{n} на низший E_m в единицу времени пропорционально N_{n} и может быть записано как {displaystyle A_{n}^{m}N_{n}}. При вынужденном излучении количество переходов в единицу времени пропорционально N_{n} и спектральной плотности излучения на частоте перехода {displaystyle u(omega _{mn})}, то есть может быть записано как {displaystyle B_{n}^{m}N_{n}u(omega _{mn})}. Количество же переходов в единицу времени из-за поглощения пропорционально N_{m} и {displaystyle u(omega _{mn})} и записывается как {displaystyle B_{m}^{n}N_{m}u(omega _{mn})}[25].

Величины {displaystyle A_{n}^{m},B_{n}^{m},B_{m}^{n}} — характеристики только самого атома и выбранных энергетических уровней, называемые коэффициентами Эйнштейна. Если поле излучения равновесное и имеет температуру T, то условие детального равновесия выглядит следующим образом[25]:

{displaystyle A_{n}^{m}N_{n}+B_{n}^{m}N_{n}u(omega _{mn})=B_{m}^{n}N_{m}u(omega _{mn})}.

В пределе Trightarrow infty можно пренебречь спонтанным излучением по сравнению с вынужденным, и тогда условие равновесия примет вид {displaystyle B_{n}^{m}N_{n}=B_{m}^{n}N_{m}}. Так как при Trightarrow infty будет выполняться {displaystyle N_{n}=N_{m}}, а коэффициенты Эйнштейна не зависят от температуры, будет верно равенство {displaystyle B_{n}^{m}=B_{m}^{n}}, что справедливо для простых уровней; для кратных уровней нужно дополнительно учитывать коэффициенты кратности. В дальнейшем можно рассматривать только простые уровни, так как плотность энергии излучения не зависит от деталей строения вещества[25].

Можно воспользоваться распределением Больцмана[25]:

{displaystyle {frac {N_{n}}{N_{m}}}=e^{left({frac {E_{n}-E_{m}}{kT}}right)}}.

При применении его к условию равновесия получается[25]:

{displaystyle u(omega _{mn})={frac {alpha (omega _{mn})}{e^{left({frac {hbar omega _{mn}}{kT}}right)}-1}},}

где {textstyle alpha (omega _{mn})={frac {A_{n}^{m}}{B_{n}^{m}}}}. Эта величина не зависит от температуры и может быть найдена из условия, что для высоких температур должна быть справедлива формула Рэлея — Джинса[25]:

{displaystyle u(omega _{mn})={frac {alpha (omega _{mn})kT}{hbar {omega _{mn}}}}},
{displaystyle alpha (omega _{mn})={frac {hbar omega _{mn}^{3}}{pi ^{2}c^{3}}}}.

Энергетические уровни могут быть взяты произвольным образом, поэтому индексы m и n можно убрать и использовать формулу для произвольных частот. При подстановке {displaystyle alpha (omega )} в исходную формулу для {displaystyle u(omega )} получается формула Планка. Таким образом, важным следствием справедливости формулы Планка является существование вынужденных переходов, которые необходимы для реализации лазерной генерации[25].

Связь с другими формулами[править | править код]

Закон Рэлея — Джинса[править | править код]

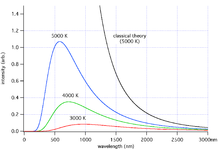
Синим и чёрным цветами обозначены спектры, соответствующие закону Планка и закону Рэлея — Джинса при одной температуре. Видно, что во втором случае наблюдается неограниченный рост мощности при уменьшении длины волны

Закон Рэлея — Джинса — приближение закона Планка, хорошо работающее при {displaystyle hcll lambda kT} (то есть в диапазоне больших длин волн и малых частот), но сильно расходящееся с ним при {displaystyle hc}, сравнимых или больших {displaystyle lambda kT}. В законе Рэлея — Джинса используется приближение {textstyle e^{frac {hc}{lambda kT}}approx 1+{frac {hc}{lambda kT}}}, справедливое при малых {textstyle {frac {hc}{lambda kT}}}, поэтому приближение выглядит следующим образом[26][27]:

{displaystyle B_{lambda }={frac {2hc^{2}}{lambda ^{5}}}{frac {lambda kT}{hc}}={frac {2ckT}{lambda ^{4}}}}.

В рамках классической физики в результате вывода закона излучения получается именно закон Рэлея — Джинса. Однако при малых длинах волн закон Рэлея — Джинса не только расходится с экспериментом, но и предсказывает неограниченный рост мощности излучения при приближении длины волны к нулю. Этот парадокс получил название ультрафиолетовой катастрофы (см. выше[⇨])[6][27].

Закон излучения Вина[править | править код]

Спектры излучения по закону Планка (зелёный), в приближении Рэлея — Джинса (красный) и в приближении Вина (синий). Оси имеют логарифмический масштаб; температура тела — 0,008 К

Закон излучения Вина — приближение закона Планка, хорошо работающее при {displaystyle hcgg lambda kT} — в области малых длин волн и больших частот. Закон излучения Вина предполагает, что при {displaystyle hcgg lambda kT} единицей в знаменателе формулы Планка можно пренебречь и считать {textstyle e^{frac {hc}{lambda kT}}-1approx e^{frac {hc}{lambda kT}}}. Тогда формула принимает вид[26][27]:

{displaystyle B_{lambda }={frac {2hc^{2}}{lambda ^{5}}}e^{-{frac {hc}{lambda kT}}}}.

Закон Стефана — Больцмана[править | править код]

Плотность потока энергии соответствует площади под графиком функции. По закону Стефана — Больцмана она пропорциональна четвёртой степени температуры

Закон Стефана — Больцмана — выражение, описывающее излучение абсолютно чёрного тела во всём электромагнитном диапазоне. Оно выводится из закона Планка интегрированием по частоте или, в зависимости от формы записи, по длине волны[28]:

{displaystyle B(T)=int _{0}^{infty }{B_{nu }}dnu =int _{0}^{infty }{B_{lambda }}dlambda },
{displaystyle B(T)={frac {2h}{c^{2}}}int _{0}^{infty }{frac {nu ^{3}dnu }{e^{frac {hnu }{kT}}-1}}}.

Заменим {textstyle x={frac {hnu }{kT}}}, тогда {textstyle dnu ={frac {kT}{h}}dx}[28]:

{displaystyle B(T)={frac {2h}{c^{2}}}{frac {k^{4}}{h^{4}}}T^{4}int _{0}^{infty }{frac {x^{3}dx}{e^{x}-1}}}.

Этот определённый интеграл равен {textstyle {frac {pi ^{4}}{15}}}. Можно выразить {displaystyle B(T)=AT^{4}}, где A — константа[28]:

{displaystyle A={frac {2k^{4}}{c^{2}h^{3}}}{frac {pi ^{4}}{15}}}.

Плотность потока энергии при этом в pi раз больше энергетической яркости, поэтому для вычисления первой используется коэффициент {displaystyle sigma =pi A}, называемый постоянной Стефана — Больцмана, равный 5,67⋅10−8 Вт·м−2·K−4. Мощность излучения с единичной площади F в таком случае может быть выражена как {displaystyle F=sigma T^{4}}. Это выражение и называется законом Стефана — Больцмана[28].

Закон смещения Вина[править | править код]

По закону смещения Вина длина волны, на которой достигается максимальная излучательная способность, обратно пропорциональна температуре

Закон смещения Вина связывает длину волны, на которой излучательная способность абсолютно чёрного тела максимальна, с его температурой. Он выводится из закона Планка дифференцированием его по частоте или длине волны, в зависимости от формы записи, и приравниванием производной к нулю, который достигается в максимуме функции. При этом получается соотношение {displaystyle lambda _{max}T=b}, где b — константа, равная 0,0029 м·K. Таким образом, при увеличении температуры длина волны максимума уменьшается[29].

Хотя для частот можно проделать аналогичную процедуру, частоту максимума спектральной плотности нельзя рассчитать по формуле {textstyle nu _{max}={frac {c}{lambda _{max}}}}, так как связь между частотой и длиной волны нелинейна, а излучательная способность рассчитывается по излучению на единичном интервале частот или длин волн[29].

Применение[править | править код]

Для абсолютно чёрного тела спектр описываемый законом Планка однозначно связан с его температурой. Поэтому закон находит применение в пирометрии, то есть дистанционном определении температуры горячих тел. В случае отличия спектра тела от излучения абсолютно чёрного тела пирометр измеряет эффективную температуру, которая называется радиационной T_{r}. Зная отношение испускательной способности исследуемого тела к испускательной способности абсолютно чёрного тела {displaystyle Q_{T}=E_{T}/varepsilon _{T}<1}, которая показывает отличие от формулы Планка, можно найти реальную температуру {displaystyle T=T_{r}/(Q_{T})^{1/4}}. Для многих практических важных материалов значения {displaystyle Q_{T}} известны[30].

Примечания[править | править код]

  1. ↑ 1 2 3 Planck’s radiation law (англ.). Encyclopedia Britannica. Дата обращения: 18 декабря 2020. Архивировано 13 декабря 2020 года.
  2. ↑ 1 2 3 4 5 Масалов А. В. Планка закон излучения // Большая российская энциклопедия. — Издательство БРЭ, 2014. — Т. 26. — 767 с. — ISBN 978-5-85270-363-7.
  3. ↑ 1 2 3 4 5 6 Karttunen et al., 2007, p. 103.
  4. ↑ 1 2 Кононович, Мороз, 2004, с. 170.
  5. ↑ 1 2 Кононович, Мороз, 2004, с. 181.
  6. ↑ 1 2 3 4 5 6 1.2. Квантовая теория излучения. Кафедра физики МГТУ им. Баумана. Дата обращения: 18 декабря 2020. Архивировано 28 сентября 2015 года.
  7. ↑ Juan Carlos Cuevas. Thermal radiation from subwavelength objects and the violation of Planck’s law (англ.) // Nature Communications. — Nature Research, 2019. — 26 July (vol. 10). — P. 3342. — ISSN 2041-1723. — doi:10.1038/s41467-019-11287-6. Архивировано 12 марта 2022 года.
  8. ↑ 1.1. Законы теплового излучения. Кафедра физики МГТУ им. Баумана. Дата обращения: 24 января 2021. Архивировано 8 августа 2020 года.
  9. ↑ Серое тело. Энциклопедия физики и техники. Дата обращения: 24 января 2021. Архивировано 17 апреля 2021 года.
  10. ↑ Karttunen et al., 2007, p. 104.
  11. ↑ Кононович, Мороз, 2004, с. 193—194.
  12. ↑ Кононович, Мороз, 2004, с. 239—240.
  13. ↑ Джеммер, 1985, с. 14—16.
  14. ↑ Сивухин, 2002, с. 681—682.
  15. ↑ 1 2 3 4 Max Planck: the reluctant revolutionary (англ.). Physics World (1 декабря 2000). Дата обращения: 19 декабря 2020. Архивировано 6 июля 2022 года.
  16. ↑ Джеммер, 1985, с. 21.
  17. ↑ Джеммер, 1985, с. 22—27.
  18. ↑ Джеммер, 1985, с. 27—30.
  19. ↑ Джеммер, 1985, с. 30—33.
  20. ↑ Джеммер, 1985, с. 30—34.
  21. ↑ Сивухин, 2002, с. 697.
  22. ↑ The Nobel Prize in Physics 1918 (англ.). NobelPrize.org. Nobel Foundation. Дата обращения: 19 декабря 2020. Архивировано 7 июня 2020 года.
  23. ↑ 1 2 3 Different Formulations of Planck’s Law. www.physics-in-a-nutshell.com. Дата обращения: 19 декабря 2020. Архивировано 14 декабря 2020 года.
  24. ↑ 1 2 3 Сивухин, 2002, с. 703—704.
  25. ↑ 1 2 3 4 5 6 7 8 Сивухин, 2002, с. 704—706.
  26. ↑ 1 2 Кононович, Мороз, 2004, с. 182.
  27. ↑ 1 2 3 Karttunen et al., 2007, p. 105.
  28. ↑ 1 2 3 4 Karttunen et al., 2007, pp. 103—104.
  29. ↑ 1 2 Karttunen et al., 2007, pp. 104—105.
  30. ↑ Ландсберг, 2003, с. 639.

Литература[править | править код]

  • Кононович Э. В.; Мороз В. И. Общий курс астрономии / Под ред. В. В. Иванова. — 2-е, испр. — М.: Едиториал УРСС, 2004. — 544 с. — ISBN 5-354-00866-2.
  • Сивухин Д. В. Общий курс физики. — М.: Физматлит МФТИ, 2002. — Т. 4. Оптика. — 792 с. — ISBN 5-9221-0228-1.
  • Джеммер М. Эволюция понятий квантовой механики. — М.: Наука, 1985. — 384 с.
  • Ельяшевич М. А. Планка закон излучения // Физическая энциклопедия. — М.: БРЭ, 1992. — Т. 3. — С. 625—626.
  • Karttunen H., Kroger P., Oja H., Poutanen M., Donner K. J. Fundamental Astronomy. — 5th Edition. — Berlin: Springer, 2007. — 510 p. — ISBN 978-3-540-34143-7.
  • Ландсберг Г. С. Оптика: учебное пособие для вузов. — 6-е изд. стереот.. — М.: Физматлит, 2003. — 848 с. — ISBN 5-9221-0314-8.
Источник

Теплонадзор

17.10.2012

Законы теплового излучения

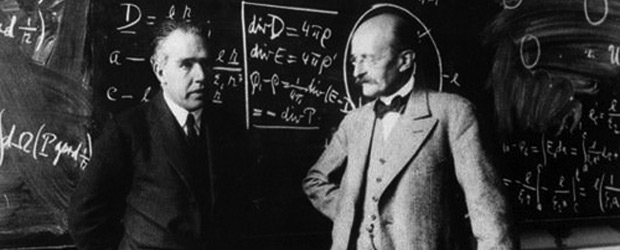
Bohr and Planck

Приведенные ниже законы теплового излучения являются основой бесконтактного измерения температуры тепловиорами и пирометрами. Эти законы теплового излучения не применяются термографистами для расчетов в повседневной работе. Вместе с тем, на этих законах излучения основан пересчет температур в программном обеспечении тепловизоров, процедуры калибровки пирометров и тепловизоров, расчет лучистого теплообмена в строительных и промышленных объектах. Знание законов теплового излучения поможет Вам сдать экзамен при аттестации по тепловому контролю на 1 или 2 уровень. Эти законы теплового излучения довольно часто встречаются в вопросах экзаменов по тепловому контролю.

Закон Стефана — Больцмана

Австрийский физик и математик Йозеф Стефан (Joseph Stefan) в 1879 году путём измерения теплоотдачи платиновой проволоки при различных температурах установил пропорциональность излучаемой ею энергии четвертой степени абсолютной температуры. Теоретическое обоснование этого закона было дано в 1884 году учеником Стефана Людвигом Больцманом (Ludwig Boltzmann).

Энергетическая светимость (q) абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры (T).

q = σ ⋅ T4

εКонстанта в этой формуле называется постоянной Стефана-Болъцмана, σ = 5.67⋅10-8 (Вт/м2)/К4. Энергетическая светимость — это мощность излучения на всех длинах волн с единицы поверхности (Вт/м2). Из этого следует, что все окружающие нас объекты испускают тепловое излучение, так как всегда имеют температуру выше абсолютного нуля 0 К или выше минус 273ºС. При повышении абсолютной температуры в два раза, мощность излучения увеличится в 16 раз. Но так можно говорить только про температуру в абсолютной шкале Кельвина, в градусах Цельсия температура не меняется в разы или на проценты никогда! Закон теплового излучения справедлив для абсолютно черного тела.

Для перехода к реальным объектам (серым телам) необходимо умножить результат на коэффициент излучения (степень черноты) объекта ε, который всегда меньше 1. Важно отметить два момента, о которых часто забывают. Во-первых, этот закон теплового излучения говорит только об общей излучаемой энергии суммарно на всех длинах волн. Тепловизор воспринимает только часть спектра, например, для LWIR камеры рабочий участок 7-14 мкм. Сколько излучения приходится на разные участки длин волн описывается формулой Планка, о которой далее. Во-вторых, приведенная формула показывает только собственное излучение, которое испускает нагретый объект. В случае с поверхностью реального объекта (не АЧТ) к этому излучению добавится некоторое отражение окружающих объектов. Поэтому невозможно узнать фактическую температуру, настраивая только значение коэффициента излучения ε. В некоторых источниках встречается очевидно ошибочная формула для расчета фактической температуры поверхности Tфакт = Tрад / (корень 4 степени из ε).

Закон излучения Кирхгофа

Немецкий физик Густав Кирхгоф (Gustav Kirchhoff), работая работая над основами спектрального анализа, в 1859 году опубликовал статью «О связи между излучением и поглощением света и теплоты», в которой установил общее положение, «что для лучей одной и той же длины волны, при одной и той же температуре, отношение лучеиспускательной способности к поглощательной для всех тел одинаково». В более подробной работе 1861 года Кирхгоф детально и строго обосновал это положение, известное в настоящее время как закон Кирхгофа. Закон получен на основании второго начала термодинамики и затем подтвержден опытным путём.

Отношение излучательной способности (E) к поглощательной способности (A) одинаково для всех тел при данной температуре (T) для данной длины волны (λ) и не зависит от формы тела, его химического состава и проч.

E(λ,T) / A(λ,T) = e(λ,T)

Закон излучения Кирхгофа является одним из основных законов теплового излучения и не распространяется на другие виды излучения. Из закона следует — чем тело больше поглощает при температуре T на длине волны λ, тем оно больше излучает при данных температуре и длине волны. Таким образом, поверхности с высокой степенью черноты (коэффициентом излучения) хорошо поглощают падающее излучение и сами являются хорошими излучателями. Блестящие зеркальные поверхности с низким коэффициентом излучения мало излучают и плохо поглощают падающее на них излучение. Эта связь очень важна в инфракрасной термографии.

Реальные тела имеют поглощательную способность меньше единицы, а значит, и меньше чем у абсолютно чёрного тела излучательную способность. Тела, поглощательная способность которых одинакова для всех длин волн, называются «серыми телами». Их спектр имеет такой же вид, как и у абсолютно чёрного тела. В общем же случае поглощательная способность тел зависит от длины волны и температуры, и их спектр может существенно отличаться от спектра абсолютно чёрного тела. Изучение излучательной способности разных поверхностей впервые было проведено шотландским ученым Лесли при помощи его же изобретения — куба Лесли (Leslie cube).

Формула Планка

Выдающийся немецкий физик Макс Планк (Max Planck), изучая тепловое излучение, открыл его атомный характер. Он рассматривал модель черного тела, представлявшую собой совокупность электромагнитных осцилляторов, излучающих и поглощающих электромагнитную энергию каждый определенной частоты. Планк принял гипотезу, что каждый осциллятор излучает и поглощает энергию конечными порциями — квантами. В 1900 году Планк доложил Берлинскому физическому обществу о своей гипотезе и новой формуле излучения.

Закон теплового излучения Планка

Распределение энергии по спектру излучения описывается формулой Планка, в соответствии с которой в спектре имеется единственный максимум, положение которого определяется законом Вина. Площадь под кривой соответствует суммарной мощьности излучения по закону Стефана-Больцмана. Открытие Планка заложило основу развития квантовой физики.

Закон Вина

Важные результаты в термодинамике излучения были получены немецким физиком Вильгельмом Вином (Wilhelm Wien). В 1893 году Вин на основе термодинамических соображений впервые вывел закон, определяющий положение максимума в распределении энергии в спектре излучения АЧТ. Закон показывает, как смещается максимум распределения энергии в спектре излучения абсолютно чёрного тела при изменении температуры.

Длина волны (λмакс), на которую приходится максимум энергии в спектре равновесного излучения, обратно пропорциональна абсолютной температуре (Т) абсолютно черного тела.

λмакс = b / T

В приведенной формуле постянная b = 2,897⋅10-3 м·К, чтобы получить результат вычисления λмакс в мкм следует взять значение b = 2897 мкм·К. Например, при температуре 36°С (309 К) максимум излучения приходится на 9,4 мкм. При температуре порядка 6000 К (темература поверхности Солнца) максимум излучения приходится на 0,47 мкм (соответствует желтовато-белому).

Законы теплового излучения Планка и Вина объясняют, почему вещество при нагреве начинает светиться в видимом спектре. Как видно из формул, при повышении температуры объекта, все больше излучения испускается с короткими длинами волн. Начиная с температуры около 500°С это излучение уже можно наблюдать невооруженным глазом. Вместе с тем, при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение (например, переход белого каления в красное при остывании металла).

2 Comments on “Законы теплового излучения”

macabre-daydream

26.12.2020 в 09:41

Тепловое излучение абсолютно чёрного тела описывается законом излучения Закон Стефана-Больцмана устанавливает связь между интегральной Закон Кирхгофа устанавливает связь между способностями излучать и Для смеси, содержащей эти газы, степень черноты определяется формулой.

Ответить

Григорий

18.09.2021 в 11:42

Тз формулы Планка определим размерность постлянной Планка при размерности испускательной способности в вт / м^2
вт. / м^2 = h м^2 / cек.^:2* м^5. откуда h = вт.сек^.2 м.

Ответить

Добавить комментарий

© 2014-2023 ООО “Теплонадзор”

Источник

Добавить комментарий