Как найти истинную глубину

Условие задачи:

Кажущаяся глубина водоема (h=4) м. Определить истинную глубину (h_0) водоема, если показатель преломления воды (n=1,33).

Задача №10.3.42 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(h=4) м, (n=1,33), (h_0-?)

Решение задачи:

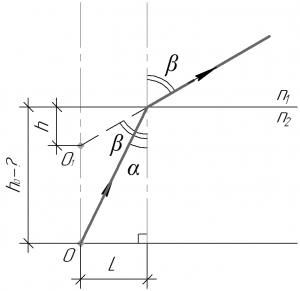Для решения задачи сделаем рисунок. При этом для решения этой задачи нам нужно рассмотреть ход параксиального луча, то есть луча, который распространяется под малым углом к оси OO₁. На рисунке углы (alpha) и (beta) не являются малыми, это сделано исключительно для наглядности рисунка.

Запишем закон преломления света (также известен как закон преломления Снеллиуса):

[{n_2}sin alpha = {n_1}sin beta]

Здесь (alpha) и (beta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Показатель преломления воздуха (n_1) равен 1, показатель преломления воды (n_2) равен 1,33.

Так как углы (alpha) и (beta) являются малыми, тогда можно воспользоваться тем, что в таком случае (sin alpha approx alpha) и (sin beta approx beta) (здесь углы, разумеется, выражены в радианах). Тогда:

[{n_2}alpha = {n_1}beta ]

[beta = frac{{{n_2}}}{{{n_1}}}alpha ;;;;(1)]

Также из прямоугольных треугольников можно получить следующее:

[left{ begin{gathered}
tgalpha = frac{L}{h_0} hfill \
tgbeta = frac{L}{h} hfill \
end{gathered} right.]

Имеем:

[left{ begin{gathered}
L = {h_0} cdot tgalpha hfill \
L = h cdot tgbeta hfill \
end{gathered} right.]

[{h_0} cdot tgalpha = h cdot tgbeta ]

Опять же, если углы (alpha) и (beta) являются малыми, тогда можно воспользоваться тем, что в таком случае (tg alpha approx alpha) и (tg beta approx beta) (здесь углы, разумеется, выражены в радианах).

[{h_0} cdot alpha = h cdot beta ]

В полученное уравнение подставим выражение (1):

[{h_0} cdot alpha = h cdot frac{{{n_2}}}{{{n_1}}}alpha ]

[{h_0} = frac{{{n_2}}}{{{n_1}}}h]

Задача решена в общем, подставим данные задачи в полученную формулу и посчитаем численный ответ:

[{h_0} = frac{{1,33}}{1} cdot 4 = 5,32;м]

Ответ: 5,32 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

10.3.41 Какова истинная глубина водоема, если камень, лежащий на дне его, при рассматривании
10.3.43 На расстоянии 1,5 м от поверхности воды в воздухе находится точечный источник света
10.3.44 Угол падения луча на пластинку толщиной 6 мм и показателем преломления, равным

Спрятать решение

Источник: Кирик Л. А. Са­мо­сто­я­тель­ные и кон­троль­ные ра­бо­ты для 8 клас­са, Х.: «Гим­на­зия», 2001 (№ 1 (высок.) стр. 102)

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Примеры решения задач. Геометрическая оптика

Подробности

Обновлено 28.11.2018 14:23

Просмотров: 1102

«Физика – 11 класс»

1.
Плоское зеркало повернули на угол α = 17° вокруг оси, лежащей в плоскости зеркала.
На какой угол β повернется отраженный от зеркала луч, если направление падающего луча осталось неизменным?

Р е ш е н и е.

Пусть φ — первоначальный угол падения луча.
По закону отражения угол отражения также равен φ, и, следовательно, угол между падающим лучом и отраженным лучом равен 2φ.
При повороте зеркала на угол α перпендикуляр I к зеркалу, восставленный в точке падения, также повернется на угол α и займет положение II.
Значит, новый угол падения будет равен φ + α.
Таким же будет и новый угол отражения.

Поэтому угол, на который повернется отраженный луч β = (φ + α) + α – φ = 2α = 34°.

2.
Определите, на какой угол θ отклоняется световой луч от своего первоначального направления при переходе из воздуха в воду, если угол падения а = 75°.

Р е ш е н и е.

Из рисунка видно, что θ = α – β.

Согласно закону преломления

где n — показатель преломления воды.

Отсюда

Из таблицы синусов находим: β ≈ 46°33′.
Следовательноб

β ≈ 75° — 46°33′ = 28°27′.

3.
Начертите ход лучей сквозь треугольную стеклянную призму, основанием которой является равнобедренный прямоугольный треугольник.
Лучи падают на широкую грань перпендикулярно этой грани.
Показатель преломления стекла равен 1,5.

Р е ш е н и е.

Проходя через широкую грань, лучи не изменяют своего направления, так как угол падения равен нулю.
На узкой грани АВ лучи полностью отражаются, так как угол падения равен 45° и, следовательно, больше предельного угла полного отражения для стекла, равного 42°.
После полного отражения от левой грани лучи падают на правую грань, снова полностью отражаются и выходят из призмы по направлению, перпендикулярному широкой грани.
Таким образом, направление пучка света изменяется на 180°.
Такой ход лучей используется, например, в призматических биноклях.

4.
Определите, во сколько раз истинная глубина водоема больше кажущейся, если смотреть по вертикали вниз.

Р е ш е н и е.

Построим ход лучей, вышедших из точки S на дне водоема и попавших в глаз наблюдателя.
Так как наблюдение ведется по вертикали, один из лучей SA направим перпендикулярно поверхности воды, другой SB — под малым углом α к перпендикуляру, восставленному в точке В (при больших углах а лучи не попадут в глаз).
Точка S₁ пересечения луча SA и продолжения преломленного луча SB — мнимое изображение точки S.

Угол ASB равен углу падения а (внутренние накрест лежащие углы), а угол AS₁B равен углу преломления Р (соответственные углы при параллельных прямых).
Прямоугольные треугольники ASB и AS₁B имеют общий катет АВ, который можно выразить через истинную глубину водоема SA = Н и через кажущуюся глубину S₁A = h:

АВ = Н tg α = htg β.

где n — показатель преломления воды.

Следовательно,

Истинная глубина водоема больше кажущейся в n = 1,3 раза.

5.

На рисунке показано расположение главной оптической оси MN линзы, светящейся точки S и ее изображения S₁.

Найдите построением оптический центр линзы и ее фокусы.
Определите, собирающей или рассеивающей является эта линза, действительным или мнимым является изображение.

Р е ш е н и е.

Луч, проходящий через оптический центр линзы, не отклоняется от своего направления.
Поэтому оптический центр О совпадает с точкой пересечения прямых SS₁ и MN.

Проведем луч SK, параллельный главной оптической оси.
Преломленный луч KS₁ пройдет через фокус.
Зная, что луч, падающий на линзу через фокус, после преломления идет параллельно главной оптической оси, находим другой фокус.
Линза является собирающей, а изображение — действительным.

6.

Изображение предмета имеет высоту Н = 2 см.
Какое фокусное расстояние F должна иметь линза, расположенная на расстоянии ƒ = 4 м от экрана, чтобы изображение данного предмета на экране имело высоту h = 1м?

Р е ш е н и е.

Из формулы линзы

находим фокусное расстояние:

Увеличение линзы можно выразить так:

Источник: «Физика – 11 класс», учебник Мякишев, Буховцев, Чаругин