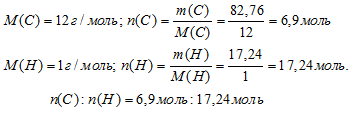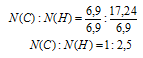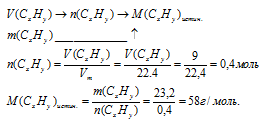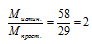Как найти истинную молекулярную массу

Вычисление истинной молярной массы газообразного вещества

Задача 1.28. 
В емкости объемом 9 л содержится 23,2 г некоторого углеводорода в газообразном состоянии (н.у.). Определите формулу этого вещества, если известно, что массовая доля углерода в нем составляет 82,76%.
Дано:
объем газообразного углеводорода (н.у.): V = 9 л;
масса 9 литров углеводорода: m = 23,2 г;
массовая доля углерода: 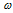(С) = 82,76%.
Найти: молекулярную формулу углеводорода.
Решение:
Шаг 1. В состав углеводорода входит только углерод и водород. Обозначим формулу как СхНу. Следовательно, требуется определить неизвестные индексы х, у.

Шаг 2. В условии нет указаний на химическую реакцию.

Шаг 3. Сначала определим массовую долю водорода. Так как в состав углеводорода входит только углерод и водород, сумма их массовых долей составит 100%:

(С) + m(Н) – 100%
(Н) = 100%  –  (С) =100% – 82,76% = 17,24%.

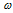
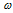
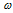
Теперь необходимо произвольно выбрать некоторый образец, в котором мы будем определять соотношение количеств веществ элементов. В условии указана информация о массовой доле, поэтому удобно выбрать образец массой 100 г. В этом случае числовые значения массовой доли каждого элемента совпадут с его массой в этом стограммовом образце.

Итак, в 100 г искомого вещества содержится 82,76 г углерода и 17,24 г водорода.

Далее вычислим соотношение количеств вещества (n) углерода и водорода. Используем соотношение m = n ^. М.

Шаг 4. Находим простейшую формулу.

N(С) : N(Н) = 6,9 : 17,24

Выбираем наименьшее значение (в данном случае «6,9») и делим на него оба числа:

Значения вновь получились не целые. Пробуем их умножать на целые числа от «2» до «5». Видим, что при умножении на «2» получается набор наименьших целых чисел:

N(С) : N(Н) = 2 : 5

Это дает возможность записать простейшую формулу: С₂Н₅.

Шаг 5. Выявление истинной формулы.

Вещества с формулой С₂Н₅ не существует. В истинной формуле индексы будут в некоторое число раз больше, чем в простейшей. Для определения, во сколько раз необходимо увеличить индексы в простейшей формуле, сравним истинную молярную массу искомого вещества с молярной массой простейшей формулы. Молярную массу истинной формулы можно определить, используя данные об объеме порции вещества, известной массы. В данном случае алгоритм определения истинной молярной массы вещества будет следующим:

Определим значение молярной массы для простейшей формулы:

М_прост = 2 ^.1 2 + 5 ^. 1 = 29 г/моль.

Истинная молярная масса больше молярной массы простейшей формулы, следовательно, индексы в простейшей формуле необходимо увеличивать.

Умножаем индексы в простейшей формуле на «2» и получаем истинную формулу: С₄Н_10. М(С₄Н₁₀) = 58 г/моль. Это формула бутана.

Ответ: С₄Н_10.

x:y=n(C):n(H).

По массовым долям определяем, что в (100) г углеводорода содержится (85,71) г углерода и (14,29) г водорода.

Найдём количества этих элементов:

x=m(C)Ar(C)=85,71 г12 г/моль=7,1425 моль;

y=m(H)Ar(H)=14,29г1г/моль=14,29моль;

x:y=7,1425:14,29=7,14257,1425:14,297,1425=1:2.

Mr(CxHy)=Dвозд.(CxHy)⋅Mr(возд.)=0,966⋅29=28,014≈28.

Mr(CxHy)Mr(CH2)=2814=2.

Второй вариант решения

1. Определим относительную молекулярную массу углеводорода:

Mr(CxHy)=Dвозд.(CxHy)⋅Mr(возд.)=0,966⋅29=28,014≈28.

2. Найдём число атомов углерода и водорода в молекуле:

x=Mr(C)⋅w(C)Ar(C)⋅100%=28⋅85,71%12⋅100%=2;

y=Mr(CxHy)⋅w(H)Ar(H)⋅100%=28⋅14,29%1⋅100%=4.

Подготовка к ЕГЭ:

• выполнение заданий высокого уровня
  сложности, задачи на вывод формул.

Задачи на вывод формул соединений –
это задания С5 из 3 части экзаменационной
работы ЕГЭ.

При выводе формул нужно различать
простейшую и
истинную
формулы.

Простейшая формула показывает соотношение
числа атомов каждого элемента.

Истинная формула показывает точный
количественный состав. Например,
простейшая формула бензола СН, она
показывает, что на один атом углерода
в молекуле бензола приходится один атом
водорода. Истинная формула бензола,
показывающая точный количественный
состав молекулы – С₆Н₆.
Чтобы установить истинную формулу,
нужно знать истинную молекулярную
(молярную) массу, она в целое число раз
больше массы, найденной по простейшей
формуле. На это число нужно умножить
индексы в простейшей формуле, чтобы
получить истинную формулу. Если в условии
задачи нет данных для нахождения истинной
молярной массы, а найденная простейшая
формула явно не соответствует истинной,
то полученные индексы нужно увеличить
в два раза. Например, получилась простейшая
формула С₃Н₇, значит истинная
будет С₆Н₁₄

При всём многообразии задач на вывод
формул можно выделить несколько основных
типов. Рассмотрим алгоритмы решений
этих задач наиболее простыми способами.

1. Написать формулу вещества, обозначив
   индексы через x, y,
   z.

2. Если неизвестна массовая доля одного
   из элементов, то её находят, отняв от

100 % известные массовые доли.

3. Найти соотношение индексов, для
этого массовую долю каждого элемента
(лучше в %) разделить на его атомную массу
(округлить до тысячных долей)

x : y: z
= ω₁ / Ar₁
: ω₂ / Ar₂
: ω₃ / Ar₃

4. Полученные числа
привести к целым. Для этого разделить
их на наименьшее из полученных чисел.
При необходимости (если опять получилось
дробное число) после этого домножить
до целого числа на 2, 3, 4 … .

5. Получится простейшая формула.
Для большинства неорганических веществ
она совпадает с истинной, для органических,
наоборот, не совпадает.

Задача № 1.

Массовая доля азота в оксиде азота равна
36,84 % . Найти формулу данного оксида.

Дано:

ω
(N)
= 36,84 % Решение:

1. Напишем формулу:
N_xO_y

М.Ф. = ? 2. Найдём
массовую долю кислорода:

ω(О) = 100 % – 36,84 % =
61,16 %

3. Найдём соотношение
индексов:

x : y
= 36,84 / 14 : 61,16 / 16 = 2,631: 3,948 =

2,631 / 2,631: 3,948 / 2,631 = 1:
1,5 =

= 1 ∙ 2 : 1,5 ∙ 2 = 2 : 3 
N₂O₃

Ответ: N₂O₃.

Задача № 2.

Установите формулу неорганического
соединения, содержащего 20 % магния, 53,33
% кислорода и 26,67 % некоторого элемента.

Дано:

ω
(Mg)
= 20 % Решение:

ω(O) = 53,33 %
1. Напишем формулу: Mg_x
Э_y О_z.

ω(э) = 26,67 % 2. Найдём
соотношение индексов магния и кислорода:

х : у = 20 / 24 : 53,33 / 16 =
0,83 : 3,33 = 1 : 4.

М.Ф. = ? 3. Найдём молекулярную
массу вещества, исходя из значения

массовой доли магния:

ω(Mg) = Ar(Mg)
∙ индекс / Mr 

 Mr = Ar(Mg) ∙
индекс / ω
= 24 ∙ 1 / 0,2 = 120.

4. Найдём
атомную массу неизвестного элемента:

ω(Э) = Ar(Э)
∙ индекс / Mr 
Ar(Э) ∙ индекс =

= ω(Э) ∙ Мr
= 0,2667 ∙ 120 = 32  элемент
– сера.

Ответ: MgSO₄.

Задача № 3.

Массовая доля углерода в углеводороде
равна 83,72 %. Найти молекулярную формулу
углеводорода.

Д
ано:
Решение:

ω(С) = 83,72 % 1. Напишем формулу –
С_хН_у

2. Найдём массовую
долю водорода:

М.Ф. = ? ω(Н) = 100 % – 83,72 % = 16,28 %

3. Найдём соотношение
индексов:

х : у = 83,72 / 12 : 16,28 / 1
= 6,977 : 16,28 = 1 : 2,333 = 3 : 7

4. Простейшая
формула – С₃Н₇, но
она не соответствует истинной.

Выход – увеличить
индексы в 2 раза 
С₆Н_14.

Ответ: С₆Н_14.

Задача № 4.

Массовая доля фосфора в его оксиде
равна 43,66 %. Какова формула оксида?

Ответ: Р₂О₅.

Задача № 5.

Определить формулу вторичного
амина, массовые доли углерода, водорода
и азота, в котором составляют 61; 15,3 и
23,7 % соответственно.

Ответ: CH₃
– NH – C₂H₅.

Задача № 6.

Массовая доля углерода в диеновом
углеводороде составляет 88,89 %. Найти
молекулярную формулу диена.

Ответ: С₄Н₆.

II. Вывод формул
веществ по массовым долям элементов и
данным для нахождения истинной молярной
массы (плотности,
массе и объёму газа или относительной
плотности).

1. Найти истинную молярную массу:

• если известна плотность:

 = m / V = M
/ V_m
 M
=  ∙
V_m
=  _г/л
∙ 22,4 _л/моль

 если известна масса и объём
газа, молярную массу можно найти двумя
способами:

– через плотность 
= m / V, M
=  ∙ Vm;

– через количество вещества: 
= V / Vm, M
= m / .

• если известна относительная плотность
  первого газа по другому:

D₂¹
= M₁
/ M₂

M₁
= D₂
∙ M₂

M =
D_H2
∙ 2 M = D_O2
∙ 32

M
= D_возд. ∙
29 M = D_N2
∙ 28 и т.д.

2. Найти простейшую формулу вещества
(см. предыдущий алгоритм) и его молярную
массу.

3. Сравнить истинную молярную массу
вещества с простейшей и увеличить
индексы в нужное число раз.

Задача № 1.

Найти формулу углеводорода, в котором
содержится 14,29 % водорода, а его
относительная плотность по азоту равна
2.

Дано:

ω
(Н)
= 14,29 % Решение:

D(N₂)
= 2 1. Найдём истинную молярную
массу С_хН_у :

М = DN₂
∙ 28 = 2 ∙ 28 = 56 _г/моль.

М.Ф. = ? 2. Найдём массовую
долю углерода:

ω(С) = 100 % – 14,29 % = 85,71 %.

3. Найдём простейшую
формулу вещества и его молярную массу:

х : у = 85,7 / 12 : 14,29 / 1 = 7,142 : 14,29 = 1 :
2  СН₂

М(СН₂) = 12 + 1 ∙ 2 = 14 _г/моль

4. Сравним молярные
массы:

М(С_хН_у)
/ М(СН₂) = 56 / 14 = 4 
истинная формула – С₄Н_8.

Ответ: С₄Н_8.

Задача № 2.

Массовая доля углерода в углеводороде
– 87,5 %, а относительная плотность
углеводорода по воздуху равна 3,31.
Определить формулу вещества.

Ответ: C₇H_12.

Задача № 3.

Определить молекулярную формулу амина,
массовые доли углерода, азота и водорода
в котором составляют 38,7; 45,15 и 16,15 %
соответственно. Относитель-

ная плотность его паров по воздуху равна
1,069.

Ответ: CH₃NH_2.

Задача № 4.

Определите формулу углеводорода,
массовая доля водорода в котором
составляет 14,3 %. Относительная плотность
этого вещества по водороду равна 21.

Ответ: С₃Н_6.

Задача № 5.

Относительная плотность паров
углеводорода по воздуху равна 3,31, а
массовая доля водорода в нём равна 12,5
%. Определите молекулярную формулу
углеводорода.

Ответ: С₇Н_12.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #

  12.02.2015398.43 Кб275.pdf

• #
• #
• #
• #
• #
• #
• #
• #

Решение задач на вывод формул в соединении

Ключевые слова конспекта: решение задач на вывод формул в соединении, простейшая формула соединения, эмпирическая формула, истинная формула, молекулярная формула, вывод формулы, установление формулы, рассчитать количество вещества элементов.

---

При определении формул химических соединений необходимо различать простейшую (или эмпирическую) формулу соединения и его истинную (или молекулярную) формулу.

Простейшая формула (эмпирическая формула) показывает соотношение числа атомов каждого элемента в молекуле (формульной единице) вещества. Например, простейшая формула оксида фосфора (V) Р₂O₅. Она показывает, что на каждые 2 атома фосфора в молекуле данного оксида приходится 5 атомов кислорода.

Истинная формула (молекулярная формула) показывает точный качественный и количественный состав одной молекулы данного соединения. Так, истинная формула оксида фосфора (V) Р₄О₁₀. Она показывает, что одна молекула данного оксида образована четырьмя атомами фосфора и десятью атомами кислорода.

При выводе простейшей формулы соединения необходимо помнить, что индексы в ней пропорциональны количествам вещества элементов, образующих данное соединение и содержащихся в определенной порции данного вещества. Например, 1 моль воды содержит 2 моль атомов водорода и 1 моль атомов кислорода (т. е. v(H) : v(O) = 2:1, а формула воды — Н₂О). Таким образом, чтобы определить простейшую формулу вещества, необходимо рассчитать количество вещества элементов, образующих данное соединение.

Чтобы установить истинную формулу, необходимо знать относительную молекулярную (или молярную) массу данного соединения. Молекулярная масса в целое число раз больше массы, которая отвечает простейшей формуле. На это число нужно умножить индексы в простейшей формуле, чтобы получить молекулярную формулу. Например, простейшая формула глюкозы СН₂О, относительная молекулярная масса, отвечающая этой формуле, равна 30. Истинная относительная молекулярная масса глюкозы равна 180, т. е. в 6 раз больше. Таким образом, истинная формула глюкозы (СН₂О)₆, или С₆Н₁₂О₆.

Цитаты из пособия «Задачи по химии 8-9 кл.» (авт. О.С. Габриелян и др.) использованы в учебных целях. Ссылка на покупку книги указана в конце конспекта.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

 Задача № 1.
Массовые доли железа и серы в соединении равны соответственно 46,67 и 53,33%. Определите формулу этого соединения.

Ответ. FeS₂.

 Задача № 2.
Массовая доля азота в оксиде азота равна 36,84%. Выведите простейшую формулу данного оксида.

Ответ. N₂О₃.

 Задача № 3.
Массовая доля серы в ее оксиде в 1,5 раза меньше массовой доли кислорода. Определите простейшую формулу оксида.

Ответ. SО₃.

 Задача № 4.
Элемент образует оксид состава ЭO₂. Плотность оксида по воздуху равна 1,586. Определите неизвестный элемент.

Ответ. Э — азот.

 Задача № 5.
Азот образует оксид, плотность паров которого по гелию равна 19, а массовая доля кислорода в нем — 63,16%. Определите молекулярную формулу неизвестного оксида.

Ответ. N₂О₃.

 Задача № 6.
Плотность по водороду смеси оксида серы (IV) и одного из оксидов азота равна 20,1, массовая доля оксида азота в смеси 52,24%, а массовая доля азота в оксиде — 46,67%. Определите молекулярную формулу оксида азота.

Ответ. NО.

 Задача № 7.
Из 185,6 г оксида железа при восстановлении было получено 134,4 г железа. Какова формула данного оксида?

Ответ. Fe₃О₄.

 Задача № 8.
Массы углерода и водорода, входящие в состав газа, занимающего объем 16,8 л (н. у.), равны соответственно 18 и 4,5 г. Определите истинную формулу газа.

Ответ. С₂Н₆.

 Задача № 9.
Отношение молярных масс хлорида и оксида металла (М), в которых металл проявляет степень окисления +2, равно 1,679. Определите неизвестный металл.

Ответ. Цинк.

Задача № 10.
 Элементы X и Y образуют с хлором соединения состава ХYСl₂ и XY₂Cl₂. Массовые доли хлора в этих соединениях равны соответственно 59,66 и 52,59%. Определите формулы неизвестных соединений.

Ответ. SOCl₂ и SO₂Cl₂.

---

Решение задач на вывод формул в соединении. Выберите дальнейшие действия:

• Перейти к: Решение задач на расчет исходных веществ и продуктов реакции
• Вернуться к списку конспектов по Химии.
• Проверить знания по Химии.
• Купить книгу Задачи по химии и способы их решения. 8-9 кл. / О.С. Габриелян и др. — М.: Дрофа.

    Необходимо отметить, что уравнение Дебая применимо только для сильно разбавленных растворов полимеров, когда с < 0,1 %. При этом оно выполняется только в том случае, если размеры макромолекуляр-ных клубков не превышают 40—50 нм, т. е. меньше 1/10Х. При больших размерах рассеиваюш,их частиц в них возникает внутримолекулярная интерференция и суммарная интенсивность светорассеяния системой уменьшается. В результате при расчете по уравнению (V. 32) получаются заниженные значения молекулярной массы. Для определения истинных значений М в таких системах необходимо учесть зависимость интенсивности рассеянного света от угла 0 [см. уравнение (IV. 1)] и в уравнение Дебая ввести соответствующую поправку. [c.147]

    Криоскопический метод определения молекулярной массы, однако, не свободен от погрешностей, и в ряде случаев пользоваться им не рекомендуется. Во-первых, в основу этого метода положен закон Рауля, применимый лишь к разбавленным растворам поэтому с повышением концентрации исследуемого вещества в растворителе наблюдается отклонение от действия этого закона. Кроме того, в применяемых растворителях многие вещества, например ароматические УВ, соединения кислого характера, проявляют склонность к ассоциации, которая тем сильнее, чем выше концентрация раствора. Поэтому истинную молекулярную массу можно определить только в сильно разбавленных растворах, т. е. при бесконечно большом разведении, иначе говоря, при нулевой концентрации. На практике, однако, работа с очень разбавленными растворами влечет за собой другую ошибку, так как при небольших навесках получаемая депрессия слишком мала и возможны ошибки при отсчете. [c.127]

    Определение истинных молекулярных масс [c.204]

    Химическая формула выражает качественный и количественный состав вещества и показывает соотношение между атомами этого вещества. Для определения формулы необходимо проанализировать соединение, установить, какие элементы и в каком количестве входят в его состав. Зная атомные массы этих элементов, можно найти соотношение атомов в молекуле и определить формулу. Такую формулу называют простейшей, или эмпирической, а соответствующую ей молекулярную массу — формульной. Она не отражает истинного состава молекулы. [c.51]

    Ме называют эффективной относительной молекулярной масСой. Разность АМе между эф ктивной и истинной относительными молекулярными массами — важная величина, так как выражает соотношение между временем удерживания некоторого вещества и его структурой. В пределах одного гомологического ряда значения АМ постоянны и проявляют незначительную линейную зависимость от температуры. Для соединений, которые не содержат функциональных групп, взаимодействующих друг с другом, общая величина АМе складывается из величин для отдельных структурных групп. Таким образом, значения АМе, приведенные в таблицах для этих функциональных групп, могут быть использованы при расчете значения АМе для некоторого анализируемого компонента, если принять для него определенную структуру. Из вычисленных значений и истинной молекулярной массы получают значение эффективной молекулярной массы и затем значение Ях а- Таким образом, можно без газохроматографического анализа находить значения Ях 9 для комнонентов, присутствие которых предполагается в анализируемой смеси. [c.235]

    Таким образом, при данном ходе решения задачи можно определить истинную формулу вещества, не прибегая к определению его молекулярной массы. [c.166]

    Одной из важнейших характеристик смолисто-асфальтено-вых веществ является молекулярная масса, сложность определения которой основана на бесконечном разнообразии химического состава, отсутствии возможности четкого фракционирования и методологической трудности определения истинной молекулярной массы из-за ассоциации даже в разбавленных растворах, о чем уже говорилось выше. Все перечисленные факторы особенно сказываются на определении мол. массы асфальтенов [53, 73, 82, 88]. В зависимости от использованного метода были получены самые различные значения. Так, ультрацентрифугирование дало величины молекулярных масс до 300 000, метод молекулярной пленки — 80 000—140000 [88, 115]. Способы, в которых используется перемешивание или подогрев, показывают более низкие значения мол. масс. [c.48]

    Полученное значение является приближенным, так как измерение скорости истечения газов осуществляется с определенными погрешностями. Поскольку эмпирической формуле неизвестного газа СН соответствует формульная масса 13,02 г, нетрудно видеть, что истинная молекулярная масса этого газа должна в шесть раз превышать его формульную массу и, стало быть, равна 6 – 13,02 = 78,12, откуда следует, что молекулярная формула газа-С Нб- [c.149]

    Как видно из данных таблицы, определение молекулярной массы подтверждают формулы четыреххлористого углерода и глицерина, а для этана правильной оказывается удвоенная формула — СгНе. Следовательно, простейшие формулы только тогда действительно выражают атомный состав соединения, когда они подтверждаются определением его молекулярной массы. Иными словами, для установления истинной формулы соединения, кроме процентного состава и атомных масс, необходимо знать и молекулярную массу. [c.26]

    Вопрос об истинных значениях массы молекул асфальтенов, или об их молекулярном весе, имеет принципиальное научное значение для понимания важнейших физических свойств самых сложных по химическому составу и наиболее высокомолекуляр-ных по размерам молекул неуглеводородных составляющих нефти. Не менее важное значение имеет и знание истинных величин их молекулярных весов для решения вопроса о химической структуре и физическом строении этих твердых аморфных компонентов нефти. Неудивительно поэтому, что разработкой методов определения молекулярных весов асфальтенов и установлением связи между размерами их молекул и рядом фундаментальных физических их свойств, прежде всего реологическими свойствами и растворимостью, с образованием как истинных, так и коллоидных растворов, занимались многие исследователи на протяжении более 50 лет. Накоплен большой экспериментальный материал по изучению молекулярных весов смол и асфальтенов, выделенных из сырых нефтей, из тяжелых остатков продуктов переработки, из природных асфальтов. Если для нефтяных смол нет существенного расхождения в значениях молекулярных весов, полученных разными исследователями (обычно значения молекулярных весов лежат в пределах 400—1200), то для асфальтенов уже можно наблюдать большие расхождения. Данные, полученные различными методами, лежат в весьма широких пределах от 2000—3000 до 240 000—300000. Совершенно ясно, что самые низкие значения должны быть отнесены к собственно молекулам асфальтенов, т. е. истинным молекулярным их величинам. Значения же молекулярных весов в пределах от 10000 до 300 ООО соответствуют надмолекулярным частицам асфальтенов, т. е. ассоциатам молекул асфальтенов различной степени сложности. Значения молекулярных весов этих ассоциатов, или мицелл, зависят от многих факторов, но прежде всего от растворяющей способности и избирательности применяемых растворителей и концентрации асфальтенов в растворах. Весьма существенно на значениях найденных молекулярных весов частиц сказываются чистота и степень разделения по размерам молекул [c.69]

    Кроме того, выделен в чистом виде [94] 7-глиадин (глиадин 50), который по молекулярной массе явно превосходит все другие, обнаруженные ранее 7-глиадины. Таким образом, еще остается определенная неясность в отношении истинных молекулярных масс у разных 7-глиадинов, которая может очень отчетливо отражать гетерогенность 7-глиадинов, намного более сильную, чем та, что выявляет анализ с помощью электрофореза в кислой среде. Впрочем, выявлено существование, по крайней мере, 9 7-глиадинов [134], а некоторые исследователи на основе анализа N-концевых последовательностей полагают, что фракция, обозначаемая 72 в действительности, включает не менее двух главных и трех минорных белков и что фракция 73 также гете-рогенна [19]. По молекулярной массе ш-глиадины превосходят а-, Р- и 7-глиадины, но они также образованы одной — единственной полипептидной цепью. Совокупность результатов, полученных разными авторами, указывает на существование двух групп ш-глиадинов — с молекулярными массами соответственно около 65 000 и 75 000—80 000 (табл. 6Б.7). [c.191]

    ОПРЕДЕЛЕНИЕ ИСТИННОЙ ФОРМУЛЫ ХИМИЧЕСКОГО СОЕДИНЕНИЯ ПО ПРОЦЕНТНОМУ СОДЕРЖАНИЮ ЭЛЕМЕНТОВ И МОЛЕКУЛЯРНОЙ МАССЕ [c.32]

    Метод применим для определения средней молекулярной массы алкилсульфатов, алкиларилсульфонатов, алкилсульфонатов. Перед определением из исследуемого вещества должны быть тщательно удалены минеральные соли (во избежание понижения истинной средней молекулярной массы), несульфированные и несульфируемые вещества и влага (для предотвращения повышения средней молекулярной массй). [c.83]

    Определение истинных формул химических соединений по процентному составу и молекулярной массе [c.16]

    Авогадро закон — равные объемы любых газоь при одинаковых условиях (температура, давление) содержат одинаковое число молекул (1811 г., итальянский физик А. Авогадро). А. з. строго справедлив только для идеального газа, Из А. з. следует, что моль любого вещесгва в газообразном состоянии при нормальных условиях (О °С и 10 Па) занимает обьем 22,4 л. А. з. позволил установить истинные атомные массы элементов. А. з. использую при расчетах по химическим формулам и уравнениям химических реакций, для определения относительных молекулярных масс га.зов. См. Авогадро число. [c.4]

    Пример. При определении молекулярной массы газа в шести параллельных опытах были получены следующие результаты 44,7 44,3 43,4 44,5 43,4 43,9. Требуется вычислить доверительный интервал для истинного значения молекулярной массы. [c.19]

    Последовательность выполнения работы. Подготовленный термометр Бекмана вставить в прибор и начать наблюдать за температурой. Для равномерного охлаждения жидкость медленно помешивают вставленной в прибор мешалкой. Помешивание прекратить, когда температура на 0,5° станет выше ожидаемой температуры кристаллизации. После этого внимательно следить за понижением температуры. Без помешивания жидкость легко переохлаждается, о чем свидетельствуют показания термометра. Для чистого растворителя переохлаждение допустимо на 0,5—Г. Возобновление перемешивания переохлажденной жидкости вызывает кристаллизацию. При кристаллизации выделяется теплота и температура начинает заметно повышаться. Не прекращая равномерного помешивания, следить за температурой, отмечая максимальную температуру подъема (из переохлажденного состояния), которая и будет истинной температурой кристаллизации данной жидкости. После этого пробирку вынуть из воздушной рубашки и, подогревая ее рукой, растворить образовавшиеся кристаллы. Затем пробирку вновь опустить в стеклянную рубашку, оставленную в охлаждающей смеси, и повторить переохлаждение с последующей кристаллизацией. Опыт следует повторить несколько раз, пока последние два определения температуры кристаллизации будут отличаться не более чем на 0,01°. Записав температуру кристаллизации растворителя, открыть боковой тубус (если его нет, приподнять пробку) и всыпать навеску исследуемого вещества. Навеска определяется по массе бюкса с исследуемым веществом и без него. После этого вынуть пробирку из рубашки, подогреть рукой раствор, вызывая расплавление кристаллов растворителя и растворение в нем навески. Вставить пробирку вновь в рубашку и провести процесс охлаждения, как и с растворителем. Надо помнить, что раствор переохлаждать более чем на 0,2° нельзя. Температуру кристаллизации раствора определять три-четыре раза из полученных данных рассчитать среднюю температуру кристаллизации, а также разность средних температур кристаллизации растворителя и раствора. Рассчитать молекулярную массу по уравнению (УП1.19). [c.180]

    Хотя в настоящее время известно несколько методов определения молекулярных масс, имеется много веществ, к которым ни один из этих методов неприменим (примером могут служить оба окисла меди). В таких случаях приводится ограничиваться простейшими формулами, условно принимая их за истинные.  [c.26]

    Если соединение построено из молекул, то обычно можно найти способ определения молекулярной массы и, следовательно, можно установить истинную формулу соединения. [c.33]

    Определение молекулярпой массы асфальтенов и смол. Определение молекулярных масс асфальтенов сопряжено с определенными трудностями, которые базируются на бесконечном разнообразии химического состава, отсутствии возможности четкого фракционирования и методологической сложности определения истинной молекулярной массы из-за ассоциации даже в разбавленных растворах. [c.86]

    Криоскопический метод определения молекулярной мас сы в растворах электролитов приводит не к истинной моле кулярной массе, а к меньшей по величине кажущейся молекулярной массе Mi. Через истинную молекулярную массу М и кажущуюся Mi определяют степень диссоциа” [c.117]

    Итак, для строгого суждения о стехиометрии взаимодействия в жидкой системе необходимо пользоваться псевдомольными свойствами (точнее, отклонениями этих свойств от аддитивности). Лишь в этом случае строгое определение стехиометрии может быть проведено без учета точного значения константы равновесия. Мольно-аддитивные свойства, применяемые в физико-химическом анализе, обычно являются псевдомольными, поскольку для определения истинной молекулярной массы жидкой смеси (XXVI.4) необходимы данные о равновесной концентрации компонентов и продукта (продуктов) присоединения. Определение же этих величин в двойных жидких системах, как будет показано в разделе 5 этой главы, представляет весьма сложную задачу. Далее под термином мольные свойства , за исключением оговоренных случаев, будем принимать именно псевдомольные свойства. [c.381]

    Реализация условий кросс-хроматографии технически сложна, поэтому обычно для определения молекулярной и композиционной неоднородности сополимера используют мультидетек-торную ГПХ. Особенно перспективно применение таких детекторов, как проточный фотометр малоуглового рассеяния света или проточный вискозиметр, наряду с традиционными—дифференциальным рефрактометром и УФ-, ИК-снектрофотометра-ми. С помощью первых детекторов можно определить истинную молекулярную массу ГПХ-фракций сополимера, а с помощью последних — их средний состав. [c.230]

    Молекулы ПАВ имеют тенденцию к ассоциации как в полярных, так и в неполярных растворителях. Это накладывает отпечаток на определение их молекулярной массы, поскольку для нахождения истинного значения искомой величины необходимо иметь показания измерений при различных концентррапи-ях с четкой их интерпретацией и учетом возможности молекулярной и коллоидной ассоциаций, а также диссоциации в растворах. Наиболее подходящими для молекул ПАВ являются методы, основанные на изучении коллегативных свойств веществ— свойств, не зависящих от структуры молекулы, а являющихся функцией только числа частиц. Такие свойства определяются кинетической энергией молекул. Это осмотическое [c.80]

    Устойчивость пен оценивается временем жизни пузырька пены или определенного ее объема. Установлено, что при использо-ваннн ПАВ в качестве пенообразователей с ростом нх молекулярной массы стабильность пен увеличивается до определенного предела, а затем при дальнейшем ее увеличении снижается. Максимум стабильности пен наблюдается и с увеличением концентрации таких пенообразователей, как истинно растворимые ПАВ (низкомолекулярные). Подобные вещества относят к пенообразователям первого рода. Пены, полученные с применением таких пенообразователей, быстро разрушаются по мере истечения междупленочной жидкости. [c.350]

    Перед определением средней молекулярной массы из исследуемого вещества должны быть тщательно удалены минеральные соли, несульфированные и не-сульфируемые вещества. Содержание в испытуемом веществе минеральных солей ведет к понижению истинной средней молекулярной массы, а содержание несульфированны.х и несульфируемых веществ и влаги — к повышению средней молекулярной массы. [c.339]

    Описан метод разделения фульвокислот на сефадексе с получением хроматографически однородных фракций, отличающихся друг от друга средней молекулярной массой, содержанием азота, числом карбоксильных и фенольных гидроксильных групп, а также ИК- и ЯМР-спектрами [29]. Низкомолекулярные фракции характеризовались свойствами, близкими к свойствам так называемой зеленой гуминовой кислоты. Молекулярные массы фульвокислот, определенные с помощью гель-проникающей хроматографии на сефадексе от двух до десяти раз превышали молекулярные массы, определенные осмометрически [29]. Ладд [30] критически проанализировал соотношение между истинной молекулярной массой и молекулярной массой, определяемой методом гель-проникающей хроматографии. [c.278]

    Некоторое распространение имеет химический метод. Супщость его заключается в количественном определении в составе белка элемента или аминокислоты, содержащихся в нем в наименьшем количестве. Затем проводят расчет минимальной молекулярной массы, исходя из того, что в молекуле белка не может быть менее одного атома элемента или одного аминокислотного остатка. Однако об истинной молекулярной массе белка этот метод не всегда дает правильное представление. Например, гемоглобин (белок крови человека и животных) содержит 0,34% железа. Так как в гемоглобине не может содержаться менее одного атома Ре, то минимальная молекулярная масса гемоглобина рассчитывается по пропорции 0,34 части Ре соответствует 100 частям белка, 56 частей Ре (один атом) соответствуют х частям белка, отсюда л =(56-100)/ 0,34 = 16 500. Истинная молекулярная масса гемоглобина равна 66 ООО—68 ООО, т. е. учетверенной минимальной молекулярной массе. Это естественно, так как молекула гемоглобина содержит. 4 атома Ре. Таким образом, химический метод определения молекулярной массы белков в определенной мере условен. [c.37]

    Основной причиной этих противоречий является способность асфальтенов, как и смол, образовывать молекулярные соединения — ассоциаты. Поэтому молекулярная масса смолисто-асфаль-теновых веществ в очень большой степени зависит от принятого метода анализа и условий эксперимента. Большое значение имеют также тип растворителя, его полярность, концентрация асфальтенов в растворе, температура и т. п. Надежные и хорошо воспроизводимые значения молекулярной массы асфальтенов получаются, например, при использовании криоскопнческого метода в растворе нафталина при температуре 80 °С (температуре плавления нафталина) и выше при концентрации асфальтенов в растворе от 1 до 16%. При этом молекулы асфальтенов практически не ассоциируют, и молекулярная масса стабильно равна от 2000 до 2500. Это значение подтверждено многими исследованиями последнего времени [42]. Определение молекулярной массы тех же асфальтенов методом мономолекулярной пленки бензольного раствора асфальтенов на воде приводит к значениям 50 000— 100 000 и более [19, с. 501 и сл.]. Вероятно, истинно мономолеку-лярного слоя асфальтенов при этом не получается и основную роль здесь играют крупные ассоциаты молекул. Таким образом, такие высокие значения характеризуют не молекулярную массу асфальтенов, а степень ассоциации их молекул в принятых условиях. [c.33]

    Зависимость с = с(х, I) позвох[яет определить коэффициент диффузии В и затем по формуле Эйнштейна (V. 3) рассчитать размер диффундирующих частиц. Так, диффузионный метод был применен Герцогом для определения эффективного размера молекулы тростникового сахара в водном растворе. Экспериментальное значение коэффихщента диффузии составило X) = 0,384 см /сут. Применяя уравнение (V. 3) и полагая, что молекулы имеют сферическую форму и плотность, равную плотности сахара в кристаллическом состоянии (р= 1,588), получаем для молекулярной массы значения Л/= /з рЛ л = 332, лишь немного отличающегося от истинного — 342. [c.175]

    Важным этапом, способствовавшим выработке единых взглядов на многие важнейшие вопросы химии, была международная встреча химиков в Карлсруэ в 1860 г. Химики собрались для того, чтобы прийти к единому мнению по главным спорным вопросам химии точное определение понятий атома, молекулы, эквивалента, атомности, основности определение истинного эквивалента тел и их формул установление одинакового обозначения и рациональной номенклатуры. Получила наконец признание гипотеза А. Авогадро, создавшая основу для определения правильных атомных и молекулярных масс, эквивалентов. В результате вступили в свои права старые атомные массь Я. Берцелиуса и был наведен некоторый порядок в написании формул органических соединений, хотя бы в отношении их состава. Благодаря работам Э. Франкланда в области металлоорганических соединений возникло ученее о постоянном валентности элементов, о присуш,ей им способности постоянно удовлетворять свое сродство путем сочетания со строго определенными весовыми количествами других элементов. [c.13]

    Весовым методом в одном опыте можно исследовать зависимость р = ДТ), а также неограниченное число раз повторить опыт с одной и той же ампулой (если соблюдаются условия, близкие к равновесным) и тем самым повысить точность определения. В однотемпературную печь помещается ампула с исследуемым веществом, находящимся в одном ее конце (рис. 15, а). С противоположйой стороны ампулы лри-варен кварцевый шток, выходящий за пределы нагретой зоны. Конец штока подвешивается к одной из чашек аналитических весов. Вся система уравновешивается на специально изготевлениой кварцевой призме, находящейся в печи при этом на ампуле делается насечка, фиксирующая ее положение на вершине этой призмы. Пар летучего компонента при данной температуре равномерно распределяется по объему ампулы, а соответствующая потеря массы твердой фазы регистрируется на аналитических весах. Далее с учетом объема ампулы и молекулярной массы пара по уравнению состояния идеальных газов рассчитывают давление. В данной схеме “показания весов не соответствуют истинному изменению массы при диссоциации. Расчет изменения массы вещества следует вести по правилу моментов (рис. 15. б). Введем следующие обозначения Ат — истинное изменение массы при диссоциации Ат и Ат.2 — массы пара соответственно в левой и правой частях ампулы (относительно оси равновесия) Атз — изменение показаний весов /1, и /3 — плечи V — общий объем ампулы  [c.29]

    Например, для определения теплоты образования циклогексана с помощью сжигания в калориметре необходимо определить разность между теплотой сгорания циклогексана и теплотой сгорания шести атомов углерода и шести молекул водорода. Это значит, что для определения теплоты образования (—123 кДж/моль) необходимо определить теплоту реакции (—3920 кДж/моль). Для того чтобы ошибка определения теплоты образования составила 1 кДж/моль или около 1%, теплота сгорания должна быть определена с точностью 1 кДж/моль или около 0,026%. Проблема становится все более острой по мере возрастания молекулярной массы углеводорода для определения АЯ с точностью 1% для алкана С20Н42 необходимо определить теплоту сгорания с точностью до 0,007%. Особую важность приобретают такие факторы, как чистота образца. Так, при сжигании алкана с примесью 0,01% воды точность определения теплоты сгорания составляет 1,5 кДж/моль. Для получения надежных результатов важно правильно установить тип реакции сгорания путем тщательного анализа исходных состояний и продуктов. Еще одна проблема возникает в связи с жидким или твердым состоянием углеводородов. Если соединение является жидким или твердым при 25 С, стандартная теплота образования АЯ° (которую относят к 298,15 К) включает энергию межмолекулярного взаимодействия конденсированного состояния (которая не имеет отношения к обсуждению энергии связи) или соотношения структура — энергия. Для такого обсуждения необходимо знать теплоту образования соединения в гипотетическом состоянии идеального газа. Эту величину можно получить из экспериментального значения АЯ , введя поправку на теплоту испарения (сублимации) до состояния идеального газа при 25 °С. Энергия межмолекулярного взаимодействия может значительно изменяться даже в ряду близко родственных соединений, что маскирует истинную величину термохимической устойчивости. [c.97]

    Что же еще, кроме массовых долей элементов, необходимо знать для установления молекулярной (истинной) форп1улы вещества Нужно знать его молекулярную массу В химии существуют различные экспериментальные способы определения молекулярных масс веществ. Что касается задач, в которых требуется установить молекулярные формулы, то в их условиях молекулярная масса либо просто указывается, либо приводятся данные, позволяющие рассчитать ее. [c.58]

    Выбор истинного числа делался на основании закона Авогадро, Так как в молекуле любого углеродного соединения не может содержаться меньше одного атома углерода, наименьшая доля этого элемента в молекулярной массе и должна соответствовать его атомной массе. Нужно было, следовательно, определить молекулярные массы различных летучих углеродных соединений, вычислить по их процентному составу в каждом случае долю углерода и выбрать из всех полученных чисел наименьшее. Такие определения давали число 12. Поэтому атомную массу углерода и следовало принять равной двенадцати. В качестве примера привв дены расчетные данные для метана, эфира, спирта и диоксида углерода  [c.22]

    Гель-фпльтрацию широко используют для определения молекулярных масс биополимеров, особенно белков. Чем меньше белок, тем больше объем элюции его с колонки (Fr) это, как мы видели,— основной закон гель-фильтрации. Графики селективности ясно указывают иа наличие линейной связи между логарифмом молекулярной массы белка (log М) и величиной Ка (или К ) в определенном интервале значений М для каждого типа геля. Казалось бы, задача этим решается. Достаточно определить в эксперименте значение для данного белка — и с помощью фирменного графика селективности можно будет найти log М, а следовательно, и М. Если довольствоваться весьма приближенным результатом, то можно так и поступить. Однако при более пристальном изучении этой проблемы с целью получить относптельно точные значения М она оказывается значительно слояшее. Прежде всего, фирменные графики селективности носят ориентировочный характер, и для разных партий одного и того же геля истинные зависимости log М от Кдч отличаются друг от друга. Это можно обойти, если построить самому такой график (калибровочную прямую) с помошью набора белков известной массы. Но тут-то и возникает главная трудность. Какие белки выбрать для такого построения Ответа на этот вопрос поищем сначала для случая нативньсх белков. [c.145]

    Экспериментальные графики [47], приведенные на рис. 4.3, отражают общую картину протекания поликонденсации. Как видно из рисунка, молекулярная масса полиэфира, о которой судили по относительной вязкости его раствора (в опытах Кабаяси вязкость определяли в растворе фенола и тетрахлорэтана в соотношении 1 1, при концентрации 0,5 г/100 мл и 20 °С), вначале возрастает, а после истечения определенного времени начинает падать. Максимумы на кривых отражают состояние кажущегося равновесия, поскольку истинное равновесие недостижимо из-аа одновременного прохождения деструктивных процессов. После достижения максимума кривые отражают преобладающее влияние необратимой термодеструкции. [c.67]

---