Алгебра логики
Алгебра логики
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Основоположником алгебры логики является английский математик и логик Дж. Буль (1815–1864), положивший в основу своего логического учения аналогию между алгеброй и логикой. Любое высказывание он записывал с помощью символов разработанного им языка и получал «уравнения», истинность или ложность которых можно было доказать, исходя из определенных логических законов, таких как законы коммутативности, дистрибутивности, ассоциативности и др.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Например, «3 умножить на 3 равно 9», «Архангельск севернее Вологды» — истинные высказывания, а «Пять меньше трех», «Марс — звезда» — ложные.
Очевидно, что не всякое предложение может быть логическим высказыванием, т. к. не всегда есть смысл говорить о его ложности или истинности. Например, высказывание «Информатика — интересный предмет» неопределенно и требует дополнительных сведений, а высказывание «Для ученика 10-А класса Иванова А. А. информатика — интересный предмет» в зависимости от интересов Иванова А. А. может принимать значение «истина» или «ложь».
Кроме двузначной алгебры высказываний, в которой принимаются только два значения — «истинно» и «ложно», существует многозначная алгебра высказываний. В такой алгебре, кроме значений «истинно» и «ложно», употребляются такие истинностные значения, как «вероятно», «возможно», «невозможно» и т. д.
В алгебре логики различаются простые (элементарные) высказывания, обозначаемые латинскими буквами (A, B, C, D, …), и сложные (составные), составленные из нескольких простых с помощью логических связок, например таких, как «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний.
Обозначим как А высказывание «Алгебра логики успешно применяется в теории электрических схем», а через В — «Алгебра логики применяется при синтезе релейно-контактных схем».
Тогда составное высказывание «Алгебра логики успешно применяется в теории электрических цепей и при синтезе релейно-контактных схем» можно кратко записать как А и В; здесь «и» — логическая связка. Очевидно, что поскольку элементарные высказывания А и В истинны, то истинно и составное высказывание А и В.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
1. Логическое отрицание, инверсия (лат. inversion — переворачивание) — логическая операция, в результате которой из данного высказывания (например, А) получается новое высказывание (не А), которое называется отрицанием исходного высказывания, обозначается символически чертой сверху ($A↖{-}$) или такими условными обозначениями, как ¬, ‘not’, и читается: «не А», «А ложно», «неверно, что А», «отрицание А». Например, «Марс — планета Солнечной системы» (высказывание А); «Марс — не планета Солнечной системы» ($A↖{-}$); высказывание «10 — простое число» (высказывание В) ложно; высказывание «10 — не простое число» (высказывание B ) истинно.
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
| A | ¬A |
| истина | ложь |
| ложь | истина |
или
Высказывание $A↖{-}$ ложно, когда А истинно, и истинно, когда А ложно.
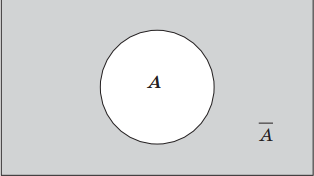
Геометрически отрицание можно представить следующим образом: если А — это некоторое множество точек, то $A↖{-}$ — это дополнение множества А, т. е. все точки, которые не принадлежат множеству А.
2. Конъюнкция (лат. conjunctio — соединение) — логическое умножение, операция, требующая как минимум двух логических величин (операндов) и соединяющая два или более высказываний при помощи связки «и» (например, «А и В»), которая символически обозначается с помощью знака ∧ (А ∧ В) и читается: «А и В». Для обозначения конъюнкции применяются также следующие знаки: А ∙ В; А & В, А and В, а иногда между высказываниями не ставится никакого знака: АВ. Пример логического умножения: «Этот треугольник равнобедренный и прямоугольный». Данное высказывание может быть истинным только в том случае, если выполняются оба условия, в противном случае высказывание ложно.
Таблица истинности операции имеет вид
| A | B | A ∧ B |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
| истина | истина | истина |
или
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∧ В истинно только тогда, когда оба высказывания — А и В истинны.
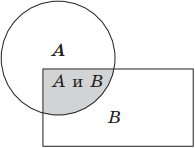
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ∧ В есть пересечение множеств А и В.
3. Дизъюнкция (лат. disjunction — разделение) — логическое сложение, операция, соединяющая два или более высказываний при помощи связки «или» (например, «А или В»), которая символически обозначается с помощью знака ∨ (А ∨ В) и читается: «А или В». Для обозначения дизъюнкции применяются также следующие знаки: А + В; А or В; А | B. Пример логического сложения: «Число x делится на 3 или на 5». Это высказывание будет истинным, если выполняются оба условия или хотя бы одно из условий.
Таблица истинности операции имеет вид
| A | B | A ∨ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | истина |
или
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∨ В ложно только тогда, когда оба высказывания — А и В ложны.
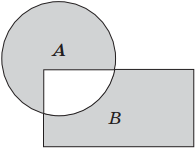
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ∨ В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.
4. Дизъюнкция строго-разделительная, сложение по модулю два — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле, которая символически обозначается с помощью знаков ∨ ∨ или ⊕ (А ∨ ∨ В, А ⊕ В) и читается: «либо А, либо В». Пример сложения по модулю два — высказывание «Этот треугольник тупоугольный или остроугольный». Высказывание истинно, если выполняется какое-то одно из условий.
Таблица истинности операции имеет вид
| А | В | А ⊕ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | ложь |
или
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
5. Импликация (лат. implisito — тесно связываю) — логическая операция, соединяющая два высказывания при помощи связки «если…, то» в сложное высказывание, которое символически обозначается с помощью знака → (А → В) и читается: «если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяется также знак ⊃ (A ⊃ B). Пример импликации: «Если полученный четырехугольник квадрат, то около него можно описать окружность». Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием. Результат операции ложен только тогда, когда предпосылка есть истина, а следствие — ложь. Например, «Если 3 * 3 = 9 (А), то Солнце — планета (В)», результат импликации А → В — ложь.
Таблица истинности операции имеет вид
| А | В | А → В |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
| истина | истина | истина |
или
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
6. Эквивалентность, двойная импликация, равнозначность (лат. aequalis — равный и valentis — имеющий силу) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В, которое читается: «А эквивалентно B». Для обозначения эквивалентности применяются также следующие знаки: ⇔, ∼. Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Примером эквивалентности является высказывание: «Треугольник будет прямоугольным тогда и только тогда, когда один из углов равен 90 градусам».
Таблица истинности операции эквивалентности имеет вид
| А | В | А ∼ В |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
| истина | истина | истина |
или
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Операция эквивалентности противоположна сложению по модулю два и имеет результат «истина» тогда и только тогда, когда значения переменных совпадают.
Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | А ⊕ В | $(A↖{-} ∧B) ∧ (A ∧ B↖{-})$ |
| Импликация | А → В | $A↖{-} ∨ B$ |
| Эквивалентность | А ∼ В | $(A↖{-} ∧ B↖{-}) ∨ (A ∧ B)$ |
Приоритет выполнения логических операций следующий: отрицание («не») имеет самый высокий приоритет, затем выполняется конъюнкция («и»), после конъюнкции — дизъюнкция («или»).
С помощью логических переменных и логических операций любое логическое высказывание можно формализовать, т. е. заменить логической формулой. При этом элементарные высказывания, образующие составное высказывание, могут быть абсолютно не связаны по смыслу, но это не мешает определять истинность или ложность составного высказывания. Например, высказывание «Если пять больше двух (А), то вторник всегда наступает после понедельника (В)» — импликация А → В, и результат операции в данном случае — «истина». В логических операциях смысл высказываний не учитывается, рассматривается только их истинность или ложность.
Рассмотрим, например, построение составного высказывания из высказываний А и В, которое было бы ложно тогда и только тогда, когда оба высказывания истинны. В таблице истинности для операции сложения по модулю два находим: 1 ⊕ 1 = 0. А высказывание может быть, например, таким: «Этот мяч полностью красный или полностью синий». Следовательно, если утверждение А «Этот мяч полностью красный» — истина, и утверждение В «Этот мяч полностью синий» — истина, то составное утверждение — ложь, т. к. одновременно и красным, и синим мяч быть не может.
Примеры решения задач
Пример 1. Определить для указанных значений X значение логического высказывания ((X > 3) ∨ (X < 3)) → (X < 4) :
1) X = 1; 2) X = 12; 3) X = 3.
Решение. Последовательность выполнения операций следующая: сначала выполняются операции сравнения в скобках, затем дизъюнкция, и последней выполняется операция импликации. Операция дизъюнкции ∨ ложна тогда и только тогда, когда оба операнда ложны. Таблица истинности для импликации имеет вид
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Отсюда получаем:
1) для X = 1:
((1 > 3) ∨ (1 < 3)) → (1 < 4) = ложь ∨ истина → истина = истина → истина = истина;
2) для X = 12:
((12 > 3) ∨ (12 < 3) → (12 < 4) = истина ∨ ложь → ложь = истина → ложь = ложь;
3) для X = 3:
((3 > 3) ∨ (3 < 3)) → (3<4) = ложь ∨ ложь → истина = ложь → истина = истина.
Пример 2. Указать множество целых значений X, для которых истинно выражение ¬((X > 2) → (X > 5)) .
Решение. Операция отрицания применена ко всему выражению ((X > 2) → (X > 5)) , следовательно, когда выражение ¬((X > 2) → (X > 5)) истинно, выражение ((X > 2) →(X > 5)) ложно. Поэтому необходимо определить, для каких значений X выражение ((X > 2) → (X > 5)) ложно. Операция импликации принимает значение «ложь» только в одном случае: когда из истины следует ложь. А это выполняется только для X = 3; X = 4; X = 5.
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ∧ третья буква гласная) ⇔ строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 — высказывание ложно.
Логические выражения и их преобразование
Под логическим выражением следует понимать такую запись, которая может принимать логическое значение «истина» или «ложь». При таком определении среди логических выражений необходимо различать:
- выражения, которые используют операции сравнения («больше», «меньше», «равно», «не равно» и т. п.) и принимают логические значения (например, выражение а > b , где а = 5 и b = 7, равно значению «ложь»);
- непосредственные логические выражения, связанные с логическими величинами и логическими операциями (например, A ∨ В ∧ С, где А = истина, B = ложь и C = истина).
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
- вычисление существующих функциональных зависимостей;
- выполнение алгебраических операций (вначале умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в произвольном порядке);
- выполнение логических операций (вначале операции отрицания, затем операции логического умножения, логического сложения, последними выполняются операции импликации и эквивалентности).
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
$1 ≤ a ∨ A ∨ sin(π/a – π/b) < 1 ∧ ¬B ∧ ¬(b^a + a^b > a + b ∨ A ∧ B)$ для а = 2, b = 3, A = истина, В = ложь.
Решение. Порядок подсчета значений:
1) ba + ab > a + b, после подстановки получим: 32 + 23 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ∧ B = истина ∧ ложь = ложь.
Следовательно, выражение в скобках равно (ba + ab > a + b ∨ A ∧ B) = истина ∨ ложь = истина;
3) 1≤ a = 1 ≤ 2 = истина;
4) sin(π/a – π/b) < 1 = sin(π/2 – π/3) < 1 = истина.
После этих вычислений окончательно получим: истина ∨ А ∧ истина ∧ ¬В ∧ ¬истина.
Теперь должны быть выполнены операции отрицания, затем логического умножения и сложения:
5) ¬В = ¬ложь = истина; ¬истина = ложь;
6) A ∧ истина ∧ истина ∧ ложь = истина ∧ истина ∧ истина ∧ ложь = ложь;
7) истина ∨ ложь = истина.
Таким образом, результат логического выражения при заданных значениях— «истина».
Примечание. Учитывая, что исходное выражение есть, в конечном итоге, сумма двух слагаемых, и значение одного из них 1 ≤ a = 1 ≤ 2 = истина, без дальнейших вычислений можно сказать, что результат для всего выражения тоже «истина».
Тождественные преобразования логических выражений
В алгебре логики выполняются основные законы, позволяющие производить тождественные преобразования логических выражений.
| Закон | Для ∨ | Для ∧ |
| Переместительный | A ∨ B = B ∨ A | A ∧ B = B ∧ A |
| Сочетательный | A ∨ (B ∨ C) = (B ∨ A) ∨ C | A ∧ (B ∧ C) = (A ∧ B) ∧ C |
| Распределительный | A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) | A ∨ B ∧ C = (A ∨ B) ∧ (A ∨ C) |
| Правила де Моргана | ${A ∨ B}↖{-}$ = $A↖{-} ∧ B↖{-}$ | ${A ∧ B}↖{-}$ = $A↖{-} ∨ B↖{-}$ |
| Идемпотенции | A ∨ A = A | A ∧ A = A |
| Поглощения | A ∨ A ∧ B = A | A ∧ (A ∨ B) = A |
| Склеивания | (A ∧ B) ∨ (A↖{-} ∧ B) = B | (A ∨ B) ∧ (A↖{-} ∨ B) = B |
| Операция переменной с ее инверсией | $A ∨ A↖{-}$ = 1 | $A ∧ A↖{-}$ = 0 |
| Операция с константами | A ∨ 0 = A A ∨ 1 = 1 |
A ∧ 1 = A A ∧ 0 = 0 |
| Двойного отрицания | $A↖{=}$ = A |
Доказательства этих утверждений производят на основании построения таблиц истинности для соответствующих записей.
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определенному виду путем использования основных законов алгебры логики. Под упрощением формулы, не содержащей операций импликации и эквивалентности, понимают равносильное преобразование, приводящее к формуле, которая содержит либо меньшее по сравнению с исходной число операций, либо меньшее число переменных.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т. п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Рассмотрим на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1) X1 ∧ X2 ∨ X1 ∧ X2 ∪ ¬X1 ∧ X2 = X1 ∧ X2 ∨ ¬X1 ∧ X2 = (X1 ∨ ¬X1) ∧ X2 = 1 ∧ X2 = X2 .
Для преобразования здесь можно применить закон идемпотенции, распределительный закон; операцию переменной с инверсией и операцию с константой.
2) X1 ∨ X1 ∧ X2 = X1 ∨ (1 ∨ 1 ∧ X2) = X1 ∨ (1 ∨ X2) = X1 .
Здесь для упрощения применяется закон поглощения.
3) ¬(X1 ∧ X2) ∨ X2 = (¬X1 ∨ ¬X2) ∨ X2 = ¬X1 ∨ ¬X2 ∨ X2 = ¬X1 ∨ 1 = 1 .
При преобразовании применяются правило де Моргана, операция переменной с ее инверсией, операция с константой
Примеры решения задач
Пример 1. Найти логическое выражение, равносильное выражению A ∧ ¬(¬B ∨ C) .
Решение. Применяем правило де Моргана для В и С: ¬(¬B ∨ C) = B ∧ ¬C .
Получаем выражение, равносильное исходному: A ∧ ¬(¬B ∨ C) = A ∧ B ∧ ¬C .
Ответ: A ∧ B ∧ ¬C.
Пример 2. Указать значение логических переменных А, В, С, для которых значение логического выражения (A ∨ B) → (B ∨ ¬C ∨ B) ложно.
Решение. Операция импликации ложна только в случае, когд а из истинной посылки следует ложь. Следовательно, для заданного выражения посылка A ∨ B должна принимать значение «истина», а следствие, т. е. выражение B ∨ ¬C ∨ B , — «ложь».
1) A ∨ B — результат дизъюнкции — «истина», если хотя бы один из операндов — «истина»;
2) B ∨ ¬C ∨ B — выражение ложно, если все слагаемые имеют значение «ложь», т. е. В — «ложь»; ¬C — «ложь», а следовательно, переменная С имеет значение «истина»;
3) если рассмотреть посылку и учесть, что В — «ложь», то получим, что значение А — «истина».
Ответ: А — истина, В — ложь, С — истина.
Пример 3. Каково наибольшее целое число X, при котором истинно высказывание (35 < X · X) → (X < (X – 3)) ?
Решение. Запишем таблицу истинности для операции импликации:
| A | B | A → B |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Выражение X < (X – 3) ложно при любых положительных значениях X. Следовательно, для того чтобы результатом импликации была «истина», необходимо и достаточно, чтобы выражение 35 < X · X также было ложно. Максимальное целое значение X, для которого 35 < X · X ложно, равно 5.
Ответ: X = 5.
Использование логических выражений для описания геометрических областей
Логические выражения могут быть использованы для описания геометрических областей. В этом случае задача формулируется так: записать для заданной геометрической области такое логическое выражение, которое принимает значение «истина» для значений x, y тогда и только тогда, когда любая точка с координатами (x; y) принадлежит геометрической области.
Рассмотрим описание геометрической области с помощью логического выражения на примерах.
Пример 1. Задано изображение геометрической области. Записать логическое выражение, описывающее множество точек, принадлежащих ей.
1) 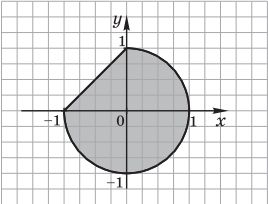 .
.
Решение. Заданную геометрическую область можно представить в виде набора следующих областей: первая область — D1 — полуплоскость ${x}/{-1} +{y}/{1} ≤ 1$, вторая — D2 — круг с центром в начале координат $x^2 + y^2 ≤ 1$. Их пересечение D1 $∩$ D2 представляет собой искомую область.
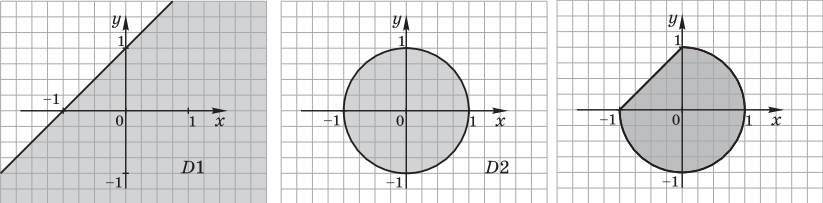
Результат: логическое выражение ${x}/{-1}+{y}/{1} ≤ 1 ∧ x^2 + y^2 ≤ 1$.
2) 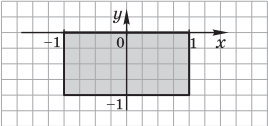
Эту область можно записать так: |x| ≤ 1 ∧ y ≤ 0 ∧ y ≥ -1 .
Примечание. При построении логического выражения используются нестрогие неравенства, а это значит, что границы фигур также принадлежат заштрихованной области. Если использовать строгие неравенства, то границы учитываться не будут. Границы, не принадлежащие области, обычно изображаются пунктиром.
Можно решить обратную задачу, а именно: нарисовать область для заданного логического выражнения.
Пример 2. Нарисовать и заштриховать область, для точек которой выполняется логическое условие y ≥ x ∧ y + x ≥ 0 ∧ y < 2 .
Решение. Искомая область представляет собой пересечение трех полуплоскостей. Строим на плоскости (x, y) прямые y = x; y = –x; y = 2. Это границы области, причем последняя граница y = 2 не принадлежит области, поэтому ее наносим пунктирной линией. Для выполнения неравенства y ≥ x нужно, чтобы точки находились слева от прямой y = x, а неравенство y = –x выполняется для точек, которые находятся справа от прямой y = –x. Условие y < 2 выполняется для точек, лежащих ниже прямой y = 2. В результате получим область, которая изображена на рис.:
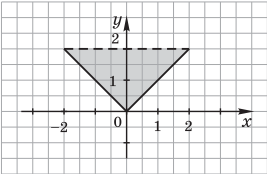
Использование логических функций для описания электрических схем
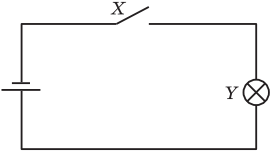
Логические функции очень удобны для описания работы электрических схем. Так, для схемы, представленной на рис., где значение переменной X — это состояние выключателя (если он включен, значение X — «истина», а если выключен — «ложь»), это значение Y — это состояние лампочки (если она горит — значение «истина», а если нет — «ложь»), логическая функция запишется так: Y = X . Функцию Y называют функцией проводимости.
Для схемы, представленной на рис., логическая функция Y имеет вид: Y = X1 ∪ X2, т. к. достаточно одного включенного выключателя, чтобы горела лампочка. В схеме на рис., для того чтобы горела лампочка, должны быть включены оба выключателя, следовательно, функция проводимости имеет вид: Y = X1 ∧ X2 .
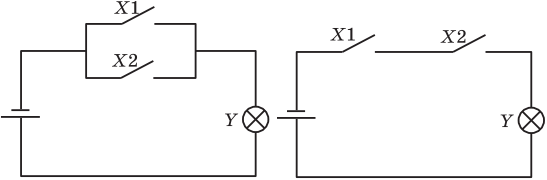
Для более сложной схемы функция проводимости будет иметь вид: Y = (X11 ∨ (X12 ∧ X13)) ∧ X2 ∧ (X31 ∨ X32).

Схема также может содержать контакты на замыкание. В этом случае размыкаемый контакт как выключатель обеспечивает загорание лампочки, когда кнопка отпущена, а не нажата. Для таких схем размыкающий выключатель описывается отрицанием.
Две схемы называются равносильными, если через одну из них ток проходит тогда, когда он проходит и через другую. Из двух равносильных схем более простой считается схема, функция проводимости которой содержит меньшее число элементов. Задача нахождения наиболее простых схем среди равносильных очень важна.
Использование аппарата алгебры логики при проектировании логических схем
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера. Любая информация при обработке на компьютере представляется в двоичной форме, т. е. кодируется некоторой последовательностью 0 и 1. Обработку двоичных сигналов, соответствующих 0 и 1, выполняют в компьютере логические элементы. Логические элементы, которые выполняют основные логические операции И, ИЛИ, НЕ, представлены на рис.

Условные обозначения логических элементов являются стандартными и используются при составлении логических схем компьютера. С помощью этих схем можно реализовать любую логическую функцию, описывающую работу компьютера.
Технически компьютерный логический элемент реализуется в виде электрической схемы, которая представляет собой соединение различных деталей: диодов, транзисторов, резисторов, конденсаторов. На вход логического элемента, который называют также вентилем, поступают электрические сигналы высокого и низкого уровней напряжения, на выход выдается один выходной сигнал также либо высокого, либо низкого уровня. Эти уровни соответствуют одному из состояний двоичной системы: 1 — 0; ИСТИНА — ЛОЖЬ. Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических схем описывают с помощью таблиц истинности. Условное обозначение на схеме ИЛИ знак «1» — от устаревшего обозначения дизъюнкции как «>=1» (значение дизъюнкции равно 1, если сумма двух операндов больше или равна 1). Знак «&» на схеме И является сокращенной записью английского слова and.
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Удобной формой записи при нахождении значений функции является таблица, содержащая, кроме значений переменных и значений функции, также значения промежуточных вычислений. Рассмотрим пример построения таблицы истинности для формулы ${X1}↖{-} ∧ X2 ∨ {X1 ∨ X2}↖{-} ∨ X1$.
| X1 | X2 | ${X1}↖{-}$ | ${X1}↖{-}$ X2 | X1 ∧ X2 | ${X1 ∨ X2}↖{-}$ | ${X1}↖{-}$ ∧ X2 ∨ ${X1 ∨ X2}↖{-}$ | ${X1}↖{-}$ ∧ X2 ∨ ${X1 ∨ X2}↖{-}$ ∨ X1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
- в таблице истинности функции выбирают наборы аргументов, для которых логические формы равны 1 («истина»);
- все выбранные логические наборы как логические произведения аргументов записывают, последовательно соединив их между собой операцией логической суммы (дизъюнкции);
- для аргументов, которые являются ложными, в построенной записи проставляют операцию отрицания.
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
Записываем логические произведения аргументов этих наборов, объединив их логической суммой: X1 ∧ X2 ∨ X1 ∧ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих ложное значение (четвертая строка таблицы; второй набор в формуле; первый и второй элементы): X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
Ответ: F(X1, X2) = X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
- в таблице истинности выбирают наборы аргументов, для которых логические формы равны 0 («ложь»);
- все выбранные логические наборы как логические суммы аргументов записывают последовательно, соединив их между собой операцией логического произведения (конъюнкции);
- для аргументов, которые являются истинными, в построенной записи проставляют операцию отрицания.
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Записываем логические суммы аргументов этих наборов, объединив их логическим произведением: X1 ∨ X2 ∧ X1 ∨ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих истинное значение (вторая строка таблицы, первый набор формулы, второй элемент; для третьей строки, а это второй набор формулы, первый элемент): X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2.
Таким образом, получена запись логической функции в КНФ.
Ответ: X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2.
Полученные двумя методами значения функций являются эквивалентными. Для доказательства этого утверждения используем правила логики: F(X1, X2) = X1 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ X2 = X1 ∧ ${X1}↖{-}$ ∨ X1 ∧ X2 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ ${X2}↖{-}$ ∧ X2 = 0 ∨ X1 ∨ X2 ∨ ${X2}↖{-}$ ∧ ${X1}↖{-}$ ∨ 0 = X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ ${X2}↖{-}$.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Используем алгоритм ДНФ для построения исходной функции:
| X1 | X2 | F(X1, X2) | ||
| 1 | 1 | 1 | • | X1 ∧ X2 |
| 1 | 0 | 0 | ||
| 0 | 1 | 1 | • | ${X1}↖{-}$ ∧ X2 |
| 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ X2 .
Ее можно упростить: X1 ∧ X2 ∨ ${X1}↖{-}$ ∧ X2 = X2 ∧ (X1 ∨ ${X1}↖{-}$) = X2 ∧ 1 = X2.
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
| X1 | X2 | X3 | F(X1, X2, X3) | ||
| 1 | 1 | 1 | 1 | • | X1 ∧ X2 ∧ X3 |
| 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | • | ${X1}↖{-}$ ∧ X2 ∧ X3 |
| 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | • | X1 ∧ X2 ∧ ${X3}↖{-}$ |
| 1 | 0 | 0 | 1 | • | X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$ |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∧ X ∨ ${X1}↖{-}$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ ${X3}↖{-}$ ∪ X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$.
Формула достаточно громоздка, и ее следует упростить:
X1 ∧ X2 ∧ X3 ∨ ${X1}↖{-}$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ ${X3}↖{-}$ ∨ X1 ∧ ${X2}↖{-}$ ∧ ${X3}↖{-}$ = X2 ∧ X3 ∧ (X1 ∨ ${X1}↖{-}$) ∨ X1 ∧ ${X3}↖{-}$ ∧ (X2 ∨ ${X2}↖{-}$) = X2 ∧ X3 ∨ X1 ∧ ${X3}↖{-}$.
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
Решение. Очевидно, что результатом решения будет таблица, в которой искомая функция Y(X1, X2, X3) будет иметь значение «истина», если какие-либо две переменные имеют значение «истина».
| X1 | X2 | X3 | Y(X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
| 1-й урок | 2-й урок | 3-й урок | |
| Информатика | 1 | 1 | 0 |
| Математика | 1 | 0 | 1 |
| Физика | 0 | 1 | 1 |
Из таблицы видно, что существуют два варианта искомого расписания:
- математика, информатика, физика;
- информатика, физика, математика.
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
- Борис — самый старший;
- играющий в футбол младше играющего в хоккей;
- играющие в футбол и хоккей и Петр живут в одном доме;
- когда между лыжником и теннисистом возникает ссора, Борис мирит их;
- Петр не умеет играть ни в теннис, ни в бадминтон.
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
Из условия 4 следует, что Борис не увлекается ни лыжами, ни теннисом, а из условий 3 и 5, что Петр не умеет играть в футбол, хоккей, теннис и бадминтон. Следовательно, любимые виды спорта Петра — лыжи и плавание. Занесем это в таблицу, а оставшиеся клетки столбцов «Лыжи» и «Плавание» заполним нулями.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | |||
| Алексей | 0 | 0 |
Из таблицы видно, что в теннис может играть только Алексей.
Из условий 1 и 2 следует, что Борис не футболист. Таким образом, в футбол играет Алексей. Продолжим заполнять таблицу. Внесем в пустые ячейки строки «Алексей» нули.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | 0 | ||
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 1 | 0 | 0 | 1 | 0 |
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.
На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
Содержание:
- Объяснение задания 2 ЕГЭ по информатике
- Таблицы истинности и порядок выполнения логических операций
- Решение заданий 2 ЕГЭ по информатике
- Задания для тренировки
2-е задание: «Таблицы истинности»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
Типичные ошибки и рекомендации по их предотвращению:
“Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению”
ФГБНУ “Федеральный институт педагогических измерений”
Таблицы истинности и порядок выполнения логических операций
Для логических операций приняты следующие обозначения:
| операция | пояснение | в программировании |
|---|---|---|
| ¬ A, A | не A (отрицание, инверсия) | not(A) |
| A ∧ B, A ⋅ B | A и B (логическое умножение, конъюнкция) | A and B |
| A ∨ B, A + B | A или B (логическое сложение, дизъюнкция) | A or B |
| A → B | импликация (следование) | A <= B |
| A ↔ B, A ≡ B, A ∼ B | эквиваленция (эквивалентность, равносильность) | A==B (python) A=B(pascal) |
| A ⊕ B | строгая дизъюнкция | A != B (python) A <> B (pascal) |
Егифка ©:

Отрицание (НЕ):

Таблица истинности операции НЕ
Конъюнкция (И):

Таблица истинности операции И (конъюнкция)
Дизъюнкция (ИЛИ):

Таблица истинности операции ИЛИ (дизъюнкция)
Импликация (если…, то…):

Таблица истинности операции Импликация (если…, то…)
Эквивалентность (тогда и только тогда, …):

Таблица истинности операции Эквивалентность (тогда и только тогда, …)
Сложение по модулю 2 (XOR):
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Порядок выполнения операций:
- если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность
Еще о логических операциях:
- логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
- логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)
О преобразованиях логических операций читайте здесь.
Егифка ©:

Решение заданий 2 ЕГЭ по информатике
Задание 2_11: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
✎ Способ 1. Электронные таблицы Excel + Логические размышления:
- Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 24=16:
- Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:




xwzy
-
✎ Способ 2. Программирование:
- В результате будут выведены значения для
F=0:
Язык python:
print('x y z w') for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
x y z w 0 0 1 1 0 1 1 1 1 0 0 0 1 0 0 1
xwzy
Язык pascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
F=0:x y z w False False True True False True True True True False False False True False False True
false = 0, True = 1Ответ:
xwzy
-
✎ Способ 3. Логические размышления:
- Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w) = 1 когда: 1. (¬x ∨ y ∨ z) = 1 И 2. (x ∨ ¬z ∨ ¬w) = 1
| x | y | z | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | z | w | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |

| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | w | z | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_12: Разбор 2 задания ЕГЭ:
Миша заполнял таблицу истинности функции:
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
Подобные задания для тренировки
✍ Решение:
✎ Способ 1. Логические размышления (бескомпьютерный вариант):
- Решим задание методом построения полной таблицы истинности.
- Посчитаем общее количество строк в таблице истинности и построим ее:
4 переменных -> 24 = 16 строк

(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w) 1. Избавимся от импликации: ¬(¬z ∧ ¬(x ≡ y)) ∨ ¬(y ∨ w) 2. Внесем знак отрицания в скобки (закон Де Моргана): (z ∨ (x ≡ y)) ∨ (¬y ∧ ¬w) = 0 1 часть = 0 2 часть = 0 * Исходное выражение должно быть = 0. Дизъюнкция = 0, когда оба операнда равны 0.

(z ∨ (x ≡ y)) = 0 когда z = 0 и x ≡ y = 0 ¬y ∧ ¬w = 0 когда: 1. ¬y = 0 ¬w = 0 2. ¬y = 1 ¬w = 0 3. ¬y = 0 ¬w = 1
| x | y | w | z | F |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| y | w | x | z | F |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
Результат: ywxz
✎ Способ 2. Программирование:
- В результате будут выведены значения для F=0:
Язык PascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) <= not(y or w)) then writeln(x:7, y:7, z:7,w:7); end.
x y z w False True False False False True False True True False False True
false = 0, True = 1Сопоставив их с исходной таблицей, получим результат: ywxz
Язык Python:
print ('x y z w') for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y))<=(not(y or w)) if not F: print (x,y,z,w)
F=0:x y z w 0 1 0 0 0 1 0 1 1 0 0 1
Сопоставив их с исходной таблицей, получим результат:
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
🎦 Видео (решение 2 ЕГЭ в Excel):
📹 здесь
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)
Задание 2_10: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
¬a ∧ b ∧ (c ∨ ¬d)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_3: Решение задания 2. Демоверсия ЕГЭ 2018 информатика:
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Подобные задания для тренировки
✍ Решение:
-
✎ Логические размышления (бескомпьютерный вариант):
- Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:
¬x ∨ y ∨ (¬z ∧ w)
| x1 | x2 | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0).¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
y = 0. Значит четвертый столбец соответствует переменной y. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | y | F |
| 1 | 1 | 1 | 0 | 0 |
¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (=1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w. | x | z | w | y | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln('x ','y ','z ','w '); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_13: Разбор досрочного егэ по информатике 2019
Логическая функция F задаётся выражением
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
✍ Решение:
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задания для тренировки
Задание 2_2: Задание 2 ЕГЭ по информатике:
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
Подобные задания для тренировки
✍ Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 25=32, т.е. 32 строки.
- Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
- Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
- В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
- Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:
- Соответственно, истинными будут все остальные строки:
| № | F | G | F ∨ G |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| … | … | … | 1 |
| 32 | … | … | 1 |
32 - 1 = 31
Результат: 31
Подробное объяснение данного задания смотрите на видео:
📹 здесь
Задание 2_6: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 27 = 128 строк.
- В четырех из них результат равен единице, значит в остальных — 0.
- A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
- Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:
- Итого получаем 8 строк.
- Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.
| A | B |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 0 |
| … | … |
Результат: 8
Задание 2_7: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 28 = 256 строк.
- В шести из них результат равен единице, значит в остальных — 0.
- A ∧ B ложно в том случае, когда:
A ∧ B = 0 если: 1. A = 0, B = 1 2. B = 0, A = 1 3. A = 0 и B = 0
- Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0
- Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0
| A | B | F |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| … | … | … |
Результат: 256
Задание 2_4: 2 задание:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
- В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
- Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:
- Но проверим на всякий случай остальные.
- Второй пункт проверяем по первой и третьей строке, так как основная операция — дизъюнкция — ложна только в том случае, если все аргументы ложны (см. таб. истинности для дизъюнкции). Проверяя по первой строке, сразу видим, что x1 в ней равен 1. В таком случаем функция будет = 1. Т.е. этот пункт не подходит:
- Третий пункт проверяем по второй строке, так как основная операция — конъюнкция — возвратит истину только тогда, когда все операнды равны 1. Видим, что x1 = 0, соответственно функция будет тоже равна 0. Т.е. выражение нам не подходит:
- Четвертый пункт проверяем по первой и третьей строкам. В первой — x1 = 1, т.е. функция должна быть равна 1. Т.е. пункт тоже не подходит:
- Таким образом, ответ равен 1.




Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
📹 здесь
Задание 2_8: Решение 2 задания ЕГЭ по информатике:
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
1) 0
2) 30
3) 31
4) 32
Подобные задания для тренировки
✍ Решение:
- Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 25 = 32 строк.
- Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
- Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
- Найдем сколько нулей существует для таб. истинности:
A B F 1. 0 0 0 2. 0 1 0 3. 1 0 0
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
32 - 2 = 30, что соответствует номеру 2
Результат: 2
Подробное решение задания смотрите в видеоуроке:
📹 здесь
Задание 2_5: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
Подобные задания для тренировки
✍ Решение:
- Полная таблица истинности будет иметь 26 = 64 строк (т.к. 6 переменных).
- 4 из них нам известны: в них x3 два раза не совпадает с F.
- Неизвестных строк:
64 - 4 = 60
60 + 2 = 62
Результат: 62
Задание 2_9: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
- Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).
1 пункт:
(((x1 ∧ (x2 → x3) ∧ ¬x4) ∧ x5) ∧ x6) ∧ ¬x7

2 пункт:
(((x1 ∨ (¬x2 → x3) ∨ ¬x4) ∨ ¬x5) ∨ x6) ∨ ¬x7

3 пункт:
(((¬x1 ∧ (x2 → ¬x3) ∧ x4) ∧ ¬x5) ∧ x6) ∧ x7

Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
📹 здесь
Задание 2_1: Задание 2 ЕГЭ по информатике:
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| ??? | ??? | ??? | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
- Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:
(y → x) ∧ (y → z) ∧ z
(y → x) ∧ (y → z) ∧ z = 1 если: 1. (y → x) = 1 2. (y → z) = 1 3. z = 1
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| 3 | 0 | 1 | 0 | 1 |
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| _ | ??? | z | ??? | F |
| № | Перем. 1 | z | Перем. 3 | F |
|---|---|---|---|---|
| 4 | 0 | 1 | 1 | 1 |
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:
📹 здесь
Привет, меня зовут Елена и на канале TeachYou мы разбираемся, как решать задачи из ЕГЭ по информатике. Цель канала я вижу в том, чтобы собрать в одном месте теорию по заданиям базового и продвинутого уровня, а также разобрать типовые задания.
Если вы дочитываете мои публикации до конца, то знаете, что я делаю подборки задач с разными формулировками, которые обязательно нужно прорешать до экзамена.
Логические выражения
Сегодня мы разберем мою любимую тему – алгебру логики (опять передаю привет преподавателю по дискретной математике. Павел Александрович, не ругайте за неакадемическое изложение материала 🙈).
Введение. Высказывания
Высказыванием в алгебре логики называется выражение, относительно которого можно сказать, истинно оно или ложно. Говорят, что высказывание принимает значение “истина” (еще обозначается 1) или “ложь” (обозначается 0).
“На улице идет дождь” – высказывание. Можно выглянуть в окно и проверить, капает там или нет. Высказывания обычно обозначаются заглавными латинскими буквами (A, B, C, X, Y, Z…).
Некоторые логические операции. Таблица истинности
Часто требуется составить комбинацию высказываний. К примеру, в разговоре с другом вы можете сказать, что “если не будет дождя и я найду мяч, то пойдем играть в волейбол“. От чего зависит, пойдете ли вы играть? От значения двух высказываний: “если не будет дождя” и “если я найду мяч“. Если оба высказывания будут истинными – отличной вам игры!
Для составления комбинации высказываний используются логические операции, результат которых может принимать бинарные значения – 0 или 1, ложь или истина.
Основные логические операции:
- отрицание (инверсия, читается “не А”). Обозначается ¬А или чертой над А (как вектор, но без стрелочки. Когда пойму, как вставить этот символ в Дзен, поправлю)). Если высказывание А истинно, то ¬А ложно, и наоборот.
- логическое сложение (дизъюнкция, читается “А или В”). Обозначается A ∨ B. Результат логического сложения будет истинным, когда хотя бы одно из входящих в него высказываний истинно, и ложно, когда все входящие в него высказывания ложны.
- логическое умножение (конъюнкция, читается “А и В”). Обозначается A ∧ B. Результат логического умножения будет истинным, когда все входящие в него высказывания истинны, и ложным в остальных случаях.
- равнозначность (эквиваленция, “А эквивалентно В”, “А то же самое, что и В”). Обозначается А≡В. Результат эквиваленции будет истинным, если значения А и В одинаковы, и ложным, если они различны.
- следование (импликация, читается “из А следует В”). Обозначается А⇒В. Результат импликации будет ложным только тогда, когда А равно истине, а В ложно, в остальных случаях результат принимает значение истины.
Для значений логических операций можно построить таблицу истинности. Чтобы ее построить, переберем возможные комбинации высказываний А и В и запишем соответствующие им значения операций.
Значения логических функций хорошо бы запомнить. Я знаю, у вас есть режим программиста в калькуляторе и вы можете посчитать конкретное значение в питоне или чем там планируете пользоваться. Но произведение 7*8 тоже можно не помнить, а вычислять каждый раз через сумму. Только зачем, если на это тратится время?
Если обычно у школьников со значениями операций конъюнкции-дизъюнкции возникает лишь легкая путаница, то таблицу истинности для импликации запомнить сложнее – она какая-то на первый взгляд неочевидная.
Попытаюсь кинуть вам якорь для запоминания: фразу, перечисляющую значения А и В, для которых импликация истинна. “Из правды может следовать только правда, а из лжи – все, что угодно“. Проговариваем эту фразу, смотря на таблицу истинности:
- когда А=1 и В=1 (из правды следует правда), результат импликации равен истине;
- если А=0, то чему бы не было равно В, результат импликации будет истинным (из лжи следует все, что угодно).
Когда я сдавала ЕГЭ, эта фраза существенно облегчила мне запоминание, при каких значениях А и В импликация принимает значение 1.
И еще один якорек) Представьте, что вы решаете какую-то задачу и получаете ответ. Вы можете:
- ошибиться или решать все правильно;
- получить верный или неверный ответ.
Рассмотрим варианты:
- Если вы ошибетесь, то получите неправильный ответ . Может такое быть? Чаще, чем хотелось бы. Значит, 0⇒0 = 1.
- Если вы ошибетесь, то получите правильный ответ. Такое случается, но реже. Получается, 0⇒1 = 1.
- Если вы будете решать правильно, то получите неправильный ответ. Давайте представим, что мы живем в мире без опечаток на заветных последних страничках задачника. Такого быть не может. Значит, 1⇒0 = 0.
- Если вы будете решать правильно, то получите правильный ответ. Это возможно, и желаю, чтобы на всех экзаменах с вами так и произошло. 1⇒1 = 1.
Нужны ли вам такие фишечки для запоминания или они кажутся странными и лишними?
Есть и другие логические функции, но на данный момент они не встречаются в егэшных задачах. Если вам попадется что-то необычное, напишите в комментариях, обсудим и добавим в статью.
Логические функции. Пример с РешуЕГЭ
Давайте посмотрим, как выглядят задачи 2 типа на ЕГЭ по информатике.
Что тут происходит?
Видим логическую функцию, заданную длинным выражением с инверсиями, дизъюнкциями и конъюнкциями. Так как это функция, у нее есть переменные x, y и z. Для каждого набора значений переменных известно значение логической функции F (в таблице приведены наборы переменных, для которых F истинна, следовательно, для остальных наборов F ложна).
Что нужно понимать на этом этапе?
- Сколько наборов аргументов существует для функции F(x,y,z)? Давайте ответ (предположение/сомнения/непонимания) вы напишете в комментариях. Кстати, на понимание этого момента несколько лет назад предлагались к решению задачи на РешуЕГЭ (пройдите по ссылочке, там две задачи. Их не будет в ЕГЭ-2023, и если вам нужно “натаскивание” на экзамен, ни в коем случае не заглядывайте туда! Задания только для тех, кто хочет понимания того, с чем он работает).
- В каком порядке выполняются логические действия в выражении для функции F? Вспоминаем, что конъюнкция это логическое умножение, дизъюнкция – логическое сложение; инверсия действует на аргумент, стоящий после нее, или на выражение в скобках, если после символа отрицания сразу идет скобка. Остальное все, как в математике – сначала вычисляются значения в скобках, потом выполняется умножение и в самом конце сложение.
Решение задач “ручками”
ЕГЭ по информатике уже два года сдается на компьютерах, и многие задачи, изначально предлагаемые к решению на листочке, теперь можно решить с использованием ЭВМ (так еще говорят вообще?))
Несмотря на это, я за то, чтобы уметь решать задачи по-старинке ручками на листочке. Зачем?
Во-первых, если вы сразу лезете программировать, скорее всего, вы не “чувствуете” задачу и не можете определить, насколько адекватен ответ, полученный программно.
Во-вторых, на экзамене случается всякое. Ваша ЭВМ (простите 😂) может зависнуть, и вы будете сидеть и ждать ее возвращения в строй, тратя драгоценное время, в то время как могли бы решить за это время задачу ручками.
Поэтому – решим эту задачку ручками! Сразу оговорюсь – она простая, точно не уровня ЕГЭ-2023, но подходит для того, чтобы разобраться с темой.
Дублирую условие:
Решение:
Смотрим на вопрос – нужно определить, при каких значениях аргументов функция истинна. Смотрим на выражение. Последнее действие (два последних действия) – дизъюнкция. То есть, у нас есть логическая сумма трех скобок, которая должна быть равна 1. По правде говоря, когда мы дошли до этого утверждения, мы уже почти решили задачу.
Когда логическая сумма (т.е. результат логического сложения) будет истинной? Когда хотя бы одно слагаемое равно 1. У нас таких слагаемых три – три скобки. Выходит, нужно посмотреть, при каком наборе аргументов значение каждой скобки получается истинным.
Итак, ¬x ∧ y ∧ z = 1. Что это за выражение? Это логическое произведение трех аргументов. Когда результат конъюнкции будет истинным? Когда каждый логический множитель равен 1. Получается, ¬x=1 (то есть x=0), y=1, z=1. Нашли первый набор аргументов: x=0, y=1, z=1.
Аналогичным образом находим еще два набора аргументов: x=0, y=0, z=1 и x=0, y=0, z=0.
Теперь нужно сопоставить наши решения (наборы аргументов, при которых функция истинна) приведенным в таблице. Смотрим на картинку:
Еще раз пропишу алгоритм действий:
- Выясняем, какое действие выполняется последним (как в математике, читаем выражение по типу “сумма/произведение синуса и косинуса”).
- Отвечаем на вопрос – когда это выражение будет истинно/ложно (Когда сумма будет равна 0? – Когда все слагаемые равны 0. Когда произведение равно 0? – Когда хотя бы один множитель равен 0. И т.п.)
- Смотрим, при каком наборе аргументов наши скобки будут принимать значение, которое мы определили в п.2.
- Выписываем наборы аргументов, определенные в п.3, в табличку. Сопоставляем нашу табличку таблице из условия.
Формулировки заданий и выражения для логических функций могут быть разными, алгоритм решения, в общем-то, одинаков.
Для тех, кто не хочет решать ручками, даю ссылку на это задание на сайте РешуЕГЭ, там в решении есть пример написания программы для поиска удовлетворяющих заданию аргументов на Python (обратите внимание, как заботливо я проставляю для вас все ссылочки: знаю, что многие поленятся сразу искать сами и оставят это на никогда не наступящее “потом”). Оговорюсь, что на экзамене я рекомендую искать наборы аргументов именно таким, программным, образом. Но мне нужно, чтобы, если программа выдала четыре решения вместо трех, ученик сразу понял, что допустил в коде опечатку, а не продолжил решать задачу дальше.
Несколько примеров (“на И”, дерево решений, лишние строки)
Продолжим решать задачи второго типа ручками. Задачу “на или” (мое название) мы рассмотрели выше. Дальнейшие названия задач тоже будут “авторскими”, они нужны для понимания специфики решения конкретного задания.
Задача “на И”
Рассмотрим задачу №1620 с сайта Полякова:
Такие задачи я называю “задачами на И”, так как конъюнкция – последнее действие в выражении, задающем логическую функцию F.
Нам нужно определить, при каких наборах аргументов функция F будет ложна. Вспоминаем, когда результат логического умножения будет ложным – когда хотя бы один из множителей равен 0 (как и в обычной математике).
Наше выражение представляет собой логическое произведение двух скобок. Приравняем к нулю каждую из них.
Первая скобка ¬x ∨ y ∨ z = 0. Перед нами логическая сумма трех слагаемых. Когда результат дизъюнкции будет ложным? Тогда, когда все слагаемые будут равны 0. Находим набор аргументов, обращающих первую скобку в 0: x=1, y=0, z=0.
Вторая скобка ¬x ∨ ¬z = 0. Это логическая сумма трех слагаемых. Определяем, при каком наборе значений переменных она будет ложной: x=1, z=1. А чему должен быть равен y? Так как y не входит в эту скобку, то значение выражения в ней не зависит от значения y, и оно может быть любым: и 0, и 1. Получается, из второй скобки мы получили два набора аргументов: x=1, y=0, z=1 и x=1, y=1, z=1.
Теперь выписываем полученные наборы значений аргументов (их еще можно называть решениями уравнения F=0) в табличку и сопоставляем их с приведенными в условии. Получаем ответ yzx.
Задача с лишними строками. Дерево решений
Мы все еще абстрагируемся от возможности находить наборы значений переменных программно) На примере следующей задачи покажу, как еще можно решать задачи второго типа.
Смотрим на выражение. Это логическое произведение двух множителей. Чтобы результат конъюнкции был истинным, нужно, чтобы каждый множитель был равен 1. Пока все, как обычно. Дальше нужно смотреть на скобки.
В первой скобке стоит импликация. Таблица истинности для импликации содержит три набора значений аргументов, при которых ее результат будет истинным. Их, конечно, можно перечислить. Но одновременно с этим должна быть равна 1 вторая скобка.
Во второй скобке – отрицание конъюнкции. Чтобы оно было равно 1, результат конъюнкции z ∧ x должен быть равен 0. Вспоминаем, что конъюнкция равна 0 тоже при трех наборах аргументов.
Наборы аргументов, обращающие первую и вторую скобки в 1, нужно как-то пересечь.
Как это можно делать?
- В лоб. Выписать три набора y и z, при которых первая скобка обращается в 1. Вспомнить, что каждое из этих решений порождает два (х в скобку не входит, так что он может быть любым). Получим шесть наборов значений переменных из первой скобки и аналогичным образом шесть наборов из второй. Некоторые наборы будут повторяться. Так как нам нужно, чтобы скобки одновременно были истинными, в таблицу решений включаем те наборы переменных, которые являются одинаковыми. И ищем соответствие между таблицей из условия и нашими решениями.
- Построить дерево решений. Строго говоря, мы делаем то же самое, что и при решении “в лоб”, просто неподходящие варианты будем отбрасывать сразу. Решение приведено в галерее.
Домашнее задание
Я буду приучать вас использовать для подготовки к экзамену сайт К. Полякова. Да, там бывают задачи, близкие к олимпиадным, которые никогда никому не попадутся на ЕГЭ. Зато банк заданий на этом сайте своевременно пополняется новыми задачами и вы не встретите там устаревших формулировок заданий (по крайней мере, не в таком количестве, как на РешуЕГЭ).
Переходим по ссылочке, заботливо ведущей в раздел с задачами второго типа (хотя бы кто мне сердечко за это поставил, для вас же стараюсь) и решаем задачи №№ 5361, 5362, 5293, 5109, 5020, 4441, 3647.
Понимаете, что вам нужна помощь с подготовкой к экзамену?
У меня ещё есть окна для офлайн занятий. Я провожу уроки с использованием графического планшета, записи с занятия высылаю в виде pdf-файла. Пишите в личку или отметьтесь в комментариях, договоримся о первом занятии.
Нравится вам такой формат – теория, разбор задач? В каком виде удобнее читать решение – текстовом или на картинках в галерее? Напишите в комментариях, чтобы я могла делать материал удобным для изучения. И подписывайтесь на мой канал – при подготовке к экзамену все источники будут полезны.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 ноября 2022 года; проверки требуют 7 правок.
Таблица истинности — таблица, описывающая логическую функцию.
Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность.
Например, в двузначной логике они могут принимать значения «истина» либо «ложь» (



Табличное задание функций встречается не только в логике, но и в логических функциях. Таблицы оказались довольно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре.
Таблицы истинности для основных двоичных логических функций[править | править код]
В программировании:
- Конъюнкция = AND = И =
= &
- Дизъюнкция = OR = ИЛИ =
= |
- Сложение по модулю 2 = XOR = ИСКЛЮЧАЮЩЕЕ ИЛИ =
= ~
- Отрицание = NOT = НЕ =
= !
Таблицы истинности для некоторых троичных логических функций[править | править код]
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| min(x,y) | 2 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| max(x,y) | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 1 | 0 |
| x | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| y | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 |
| F2TN22310 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 2 | 1 |
См. также[править | править код]
- Двоичные функции (Булевы)
- Троичные функции
- Алгебра логики
- Битовые операции
- Троичная логика
- Карта Карно
Примечания[править | править код]
Литература[править | править код]
- Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста. — М.: Наука, 1966. — (Математическая логика и основания математики).
Ссылки[править | править код]
- Построение таблиц истинности онлайн
- Онлайн инструменты по математической логике
Сегодня мы поговорим о предмете под названием информатика. Таблица истинности, разновидности функций, порядок их выполнения – это наши основные вопросы, на которые мы постараемся найти ответы в статье.

Обычно данный курс преподается еще в средней школе, но большое количество учеников является причиной недопонимания некоторых особенностей. А если вы собрались посвятить этому свою жизнь, то просто не обойтись без сдачи единого государственного экзамена по информатике. Таблица истинности, преобразование сложных выражений, решение логических задач – это все может встретиться в билете. Сейчас мы рассмотрим более подробно данную тему и поможем вам набрать больше балов на ЕГЭ.
Предмет логики
Что же это за предмет – информатика? Таблица истинности – как ее строить? Зачем нужна наука логика? На все эти вопросы мы сейчас с вами ответим.
Информатика – это довольно увлекательный предмет. Он не может вызывать затруднения у современного общества, ведь все, что нас окружает, так или иначе, относится к компьютеру.
Основы науки логики даются преподавателями средней школы на уроках информатики. Таблицы истинности, функции, упрощение выражений – все это должны объяснять учителя информатики. Эта наука просто необходима в нашей жизни. Приглядитесь, все подчиняется каким-либо законам. Вы подбросили мяч, он подлетел вверх, но после этого упал опять на землю, это произошло из-за наличия законов физики и силы земного притяжения. Мама варит суп и добавляет соль. Почему когда мы его едим, нам не попадаются крупинки? Все просто, соль растворилась в воде, подчиняясь законам химии.

Теперь обратите внимание на то, как вы разговариваете.
- «Если я отвезу своего кота в ветеринарную клинику, то ему сделают прививку».
- «Сегодня был очень тяжелый день, потому что приходила проверка».
- «Я не хочу идти в университет, потому что сегодня будет коллоквиум» и так далее.
Все, что вы говорите, обязательно подчиняется законам логики. Это относится как к деловой, так и к дружеской беседе. Именно по этой причине необходимо понимать законы логики, чтобы не действовать наугад, а быть уверенным в исходе событий.
Функции
Для того чтобы составить таблицу истинности к предложенной вам задаче, необходимо знать логические функции. Что это такое? Логическая функция имеет некоторые переменные, которые являются утверждениями (истинными или ложными), и само значение функции должно дать нам ответ на вопрос: «Выражение истинно или ложно?».
Все выражения принимают следующие значения:
- Истина или ложь.
- И или Л.
- 1 или 0.
- Плюс или минус.
Здесь отдавайте предпочтение тому способу, который для вас является более удобным. Для того чтобы составить таблицу истинности, нам нужно перечислить все комбинации переменных. Их количество вычисляется по формуле: 2 в степени n. Результат вычисления – это количество возможных комбинаций, переменной n в данной формуле обозначается количество переменных в условии. Если выражение имеет много переменных, то можно воспользоваться калькулятором или сделать для себя небольшую таблицу с возведением двойки в степень.
Всего в логике выделяют семь функций или связей, соединяющих выражения:
- Умножение (конъюнкция).
- Сложение (дизъюнкция).
- Следствие (импликация).
- Эквиваленция.
- Инверсия.
- Штрих Шеффера.
- Стрелка Пирса.
Первая операция, представленная в списке, имеет название «логическое умножение». Ее графически можно отметить в виде перевернутой галочки, знаками & или *. Вторая в нашем списке операция – логическое сложение, графически обозначается в виде галочки, +. Импликацию называют логическим следствием, обозначается в виде стрелки, указывающей от условия на следствие. Эквиваленция обозначается двухсторонней стрелкой, функция имеет истинное значение только в тех случаях, кода оба значения принимают либо значение «1», либо «0». Инверсию называют логическим отрицанием. Штрих Шеффера называют функцией, которая отрицает конъюнкцию, а стрелку Пирса – функцией, отрицающей дизъюнкцию.
Основные двоичные функции
Логическая таблица истинности помогает найти ответ в задаче, но для этого необходимо запомнить таблицы двоичных функций. В этом разделе они будут предоставлены.
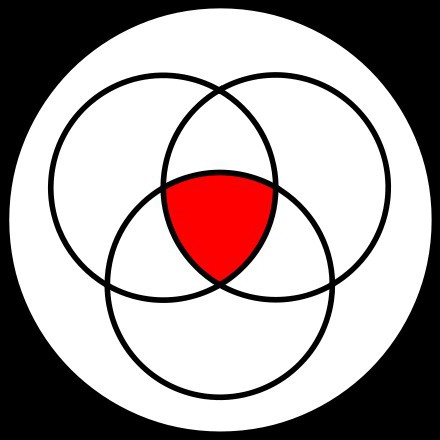
Конъюнкция (умножение). Если два выражения истинны, то в результате мы получаем истину, во всех остальных случаях мы получаем ложь.
|
+ |
+ |
+ |
|
+ |
– |
– |
|
– |
+ |
– |
|
– |
– |
– |
Как выглядит таблица, вы узнали, далее нет необходимости приводить ее ко всем формулам. На картинке выше вы можете увидеть, в каких случаях результат равен единице.
Результат – ложь при логическом сложении мы имеем только в случае двух ложных входных данных.
Логическое следствие имеет ложный результат только тогда, когда условие является истиной, а следствие – ложью. Здесь можно привести пример из жизни: «Я хотел купить сахар, но магазин был закрыт», следовательно, сахар так и не куплен.
Эквиваленция является истиной только в случаях одинаковых значений входных данных. То есть при парах: «0;0» или «1;1».

В случае инверсии все элементарно, если на входе есть истинное выражение, то оно преобразуется в ложное, и наоборот. На картинке видно, как она обозначается графически.
Штрих Шиффера будет на выходе иметь ложный результат только при наличии двух истинных выражений.
В случае стрелки Пирса, функция будет истинной только в том случае, если на входе мы имеем только ложные выражения.
В каком порядке выполнять логические операции
Обратите внимание на то, что построение таблиц истинности и упрощение выражений возможно только при правильной очередности выполнения операций. Запомните, в какой последовательности их необходимо проводить, это очень важно для получения верного результата.
- логическое отрицание;
- умножение;
- сложение;
- следствие;
- эквиваленция;
- отрицание умножения (штрих Шеффера);
- отрицание сложения (стрелка Пирса).
Пример №1
Сейчас мы предлагаем рассмотреть пример построения таблицы истинности для 4 переменных. Необходимо узнать в каких случаях F=0 у уравнения: неА+В+С*D
|
А |
В |
С |
D |
неА |
С*D |
F |
|
– |
– |
– |
– |
+ |
– |
+ |
|
– |
– |
– |
+ |
+ |
– |
+ |
|
– |
– |
+ |
– |
+ |
– |
+ |
|
– |
– |
+ |
+ |
+ |
+ |
+ |
|
– |
+ |
– |
– |
+ |
– |
+ |
|
– |
+ |
– |
+ |
+ |
– |
+ |
|
– |
+ |
+ |
– |
+ |
– |
+ |
|
– |
+ |
+ |
+ |
+ |
+ |
+ |
|
+ |
– |
– |
– |
– |
– |
– |
|
+ |
– |
– |
+ |
– |
– |
– |
|
+ |
– |
+ |
– |
– |
– |
– |
|
+ |
– |
+ |
+ |
– |
+ |
+ |
|
+ |
+ |
– |
– |
– |
– |
+ |
|
+ |
+ |
– |
+ |
– |
– |
+ |
|
+ |
+ |
+ |
– |
– |
– |
+ |
|
+ |
+ |
+ |
+ |
– |
+ |
+ |
Ответом на это задание будет являться перечисление следующих комбинаций: «1;0;0;0», «1;0;0;1» и «1;0;1;0». Как видите, составлять таблицу истинности довольно просто. Еще раз хочется обратить ваше внимание на порядок выполнения действий. В конкретном случае он был следующий:
- Инверсия первого простого выражения.
- Конъюнкция третьего и четвертого выражения.
- Дизъюнкция второго выражения с результатами предыдущих вычислений.
Пример №2

Сейчас мы рассмотрим еще одно задание, которое требует построения таблицы истинности. Информатика (примеры были взяты из школьного курса) может иметь и логические задачи в качестве задания. Коротко рассмотрим одну из них. Виновен ли Ваня в краже мяча, если известно следующее:
- Если Ваня не крал или Петя крал, то Сережа принял участие в краже.
- Если Ваня не виновен, то и Сережа мяч не крал.
Введем обозначения: И – Ваня украл мяч; П – Петя украл; С – Сережа украл.
По данному условию мы можем составить уравнение: F=((неИ+П) импликация С)*(неИ импликация неС). Нам нужны те варианты, где функция принимает истинное значение. Далее необходимо составить таблицу, так как данная функция имеет целых 7 действий, то мы их опустим. Будем вносить только входные данные и результат.
|
И |
П |
С |
F |
|
– |
– |
– |
– |
|
– |
– |
+ |
– |
|
– |
+ |
– |
– |
|
– |
+ |
+ |
– |
|
+ |
– |
– |
+ |
|
+ |
– |
+ |
+ |
|
+ |
+ |
– |
– |
|
+ |
+ |
+ |
+ |
Обратите внимание на то, что в данной задаче мы вместо знаков «0» и «1» использовали плюс и минус. Это также приемлемо. Нас интересуют комбинации, где F=+. Проанализировав их, мы можем сделать следующий вывод: Ваня участвовал в краже мяча, так как во всех случаях, где F принимает значение +, И имеет положительное значение.
Пример №3

Сейчас предлагаем вам найти количество комбинаций, когда F=1. Уравнение имеет следующий вид: F=неА+В*А+неВ. Составляем таблицу истинности:
|
А |
В |
неА |
неВ |
В*А |
F |
|
Л |
Л |
И |
И |
Л |
И |
|
Л |
И |
И |
Л |
Л |
И |
|
И |
Л |
Л |
И |
Л |
И |
|
И |
И |
Л |
Л |
И |
И |
Ответ: 4 комбинации.
