
 |
ПРОБЛЕМА ИСТИНЫ В
МАТЕМАТИКЕ
Главная
цель познания — достижение
научной истины.
Применительно
к философии истина является не только целью познания, но и предметом
исследования. Можно сказать, что понятие истины выражает сущность науки.
Философы давно пытаются выработать такую теорию познания, которая позволила бы
рассматривать его как процесс добывания научных истин. Основные противоречия на
этом пути возникали в ходе противопоставления активности субъекта и возможности
выработки им знания, соответствующего объективному реальному миру. Но истина
имеет множество аспектов, она может быть рассмотрена с самых различных точек
зрения: логической, социологической, гносеологической, наконец, богословской.
Что же такое
истина? Истоки так называемой классической философской концепции истины
восходят к эпохе античности. Например, Платон считал, что “тот, кто говорит о вещах в соответствии с тем,
каковы они есть, говорит истину, тот же, кто говорит о них иначе, — лжет”.
Долгое время классическая концепция истины доминировала в теории познания. В главном
она исходила из положения: что утверждается мыслью, действительно имеет место.
И в этом смысле понятие соответствия мыслей действительности совпадает с
понятием “адекватность”. Иными словами, истина — это свойство субъекта,
состоящее в согласии мышления с самим собой, с его априорными (доопытными)
формами. Так, в частности, полагал И. Кант. Впоследствии под истиной стали
подразумевать свойство самих идеальных объектов, безотносительных к
человеческому познанию, и особый вид духовных ценностей. Августин развивал
учение о врожденности истинных идей. Не только философы, но и представители
частных наук сталкиваются с вопросом, что понимать под действительностью, как
воспринимать реальность или реальный мир? Материалисты и идеалисты понятие
действительности, реальности отождествляют с понятием объективного мира, т.е. с
тем, что существует вне и независимо от человека и человечества. Однако и сам
человек — часть объективного мира. Поэтому, не учитывая этого обстоятельства,
прояснить вопрос об истине просто невозможно.
С учетом
имеющихся в философии направлений, принимая во внимание своеобразие
индивидуальных высказываний, выражающих субъективное мнение того или иного
ученого, истину можно определить как адекватное отражение
объективной реальности познающим субъектом, в ходе которого познаваемый предмет
воспроизводится так, как он существует вне и независимо от сознания.
Следовательно, истина входит в объективное содержание человеческого знания. Но
коль скоро мы убедились, что процесс познания не прерывается, то возникает
вопрос и о характере истины.
Ведь если человек воспринимает
объективный мир чувственным образом и представления о нем формирует в процессе
индивидуального познания и своей мыслительной деятельности, то естественен
вопрос — каким образом он может удостовериться в соответствии его утверждений
самому объективному миру? Таким образом, речь идет о критерии истины, выявление
которого составляет одну из главнейших задач философии. И в данном
вопросе среди философов согласие отсутствует. Крайняя точка зрения сводится к
полному отрицанию критерия истины, ибо, по мнению ее сторонников, истина либо
отсутствует вообще, или же она свойственна, кратко говоря, всему и вся.
Идеалисты — сторонники рационализма — в качестве критерия истины
полагали само мышление, поскольку оно обладает способностью ясно и отчетливо
представить предмет. Такие философы, как Декарт, Лейбниц исходили из
представления о самоочевидности первоначальных истин, постигаемых с помощью
интеллектуальной интуиции. Их доводы опирались на возможности математики
объективно и беспристрастно в своих формулах отображать многообразие реального
мира. Правда, при этом возникал другой вопрос: как, в свою очередь, убедиться в
достоверности их ясности и отчетливости? На помощь здесь должна была прийти
логика с ее строгостью доказательства и его неопровержимостью.
Так, И.
Кант допускал только формально-логический критерий истины, в
соответствии с которым познание должно согласовываться со всеобщими формальными
законами рассудка и разума. Но и опора на логику не избавила от трудностей в
поисках критерия истины. Оказалось не так-то просто преодолеть внутреннюю
непротиворечивость самого мышления, выяснилось, что порой невозможно добиться и
формально-логической согласованности суждений, выработанных наукой, с исходными
или вновь вводимыми утверждениями (конвенциализм).
Даже
стремительное развитие логики, ее математизация и разделение на множество
специальных направлений, а также попытки семантического (смыслового) и
семиотического (знакового) объяснения природы истины не устранили противоречий
в ее критерии.
Субъективные
идеалисты — сторонники сенсуализма
— усматривали критерий истины в непосредственной очевидности самих ощущений, в
согласованности научных понятий с чувственными данными. Впоследствии был введен
принцип верифицируемости, получивший свое название от понятия верификация
высказывания (проверка его истинности). В соответствии с этим принципом всякое
высказывание (научное утверждение) только тогда является осмысленным или
имеющим значение, если возможна его проверка. Главный упор при этом делается
именно на логическую возможность уточнения, а не на фактическую. К примеру, в
силу неразвитости науки и техники мы не можем наблюдать физические процессы,
идущие в центре Земли. Но посредством предположений, опирающихся на законы
логики, можно выдвинуть соответствующую гипотезу. И если ее положения окажутся
логически непротиворечивы, то ее следует признать истинной. Нельзя не принять
во внимание и другие попытки выявить критерий истины с помощью логики,
характерные в особенности для философского направления, именуемого логическим
позитивизмом.
Сторонники
ведущей роли активности человека в познании пытались преодолеть
ограниченность логических методов в установлении критерия истины. Была
обоснована прагматическая концепция истины, согласно которой сущность истины
следует усматривать не в соответствии ее с реальностью, а в соответствии с так
называемым “конечным критерием”. Его же предназначение — в установлении
полезности истины для практических поступков и действий человека. Важно
отметить, что с точки зрения прагматизма сама по себе полезность не является
критерием истины, понимаемой как соответствие знаний действительности. Иными
словами, реальность внешнего мира недоступна человеку, поскольку человек
непосредственно имеет дело именно с результатами своей деятельности. Вот почему
единственное, что он способен установить — не соответствие знаний
действительности, а эффективность и практическая польза знаний. Именно
последняя, выступая в качестве основной ценности человеческих знаний, достойна
именоваться истиной. И все же философия, преодолевая крайности и избегая
абсолютизации, приблизилась к более или менее верному пониманию критерия
истины. Иначе и быть не могло: окажись человечество перед необходимостью
поставить под сомнение не только последствия сиюминутной деятельности того или
иного человека (в отдельных, и нередких, случаях весьма далеких от истины), но
и отрицать собственную многовековую историю, жизнь невозможно было бы
воспринимать иначе, как абсурд. Только понятие объективной истины, опирающееся
на понятие объективной реальности, позволяет успешно развивать философскую
концепцию истины. Подчеркнем еще раз, что объективный или реальный мир
существует не просто сам по себе, но только когда речь идет о его познании.
Относительная
и абсолютная истины
Ограниченность
практических возможностей человека выступает одной из причин и ограниченности
его знаний, т.е. речь идет об относительном характере истины. Относительная истина — это знание, воспроизводящее объективный мир приближенно,
неполно. Поэтому признаками или чертами относительной истины выступают
приближенность и неполнота, которые связаны между собой. Действительно, мир
представляет собой систему взаимосвязанных элементов, любое неполное знание о
нем как целом всегда будет неточным, огрубленным, фрагментарным.
Вместе с тем
в философии используется и понятие абсолютная истина. С его помощью
характеризуется важная сторона развития процесса познания. Отметим, что понятие
абсолютной истины в философии разработано недостаточно (за исключением
метафизической, идеалистической ее ветви, где абсолютная истина, как правило,
соотносится с представлением о Боге как исходной творящей и созидающей
силе). Понятие абсолютной истины употребляется для
характеристики того или иного специфического аспекта всякого истинного знания и
в этом смысле оно аналогично понятиям “объективная истина” и “относительная
истина”. Понятие “абсолютной истины” следует рассматривать в
неразрывной связи с самим процессом познания. Этот же процесс представляет
собой как бы движение по ступеням, означающим переход от менее совершенных
научных представлений к более совершенным, однако при этом старое знание не
отбрасывается, а хотя бы частично включается в систему нового знания. Вот
это-то включение, отражающее преемственность (в историческом смысле),
внутреннюю и внешнюю целостность знания и представляющее истину как процесс,
составляет содержание понятия абсолютной истины. Еще раз напомним, что прежде
всего материальная деятельность человека оказывает воздействие на материальный
мир. Но когда речь заходит о научном познании, то имеется в виду, что из всего
многообразия свойств, присущих объективному миру, выделяются лишь те, что
составляют исторически обусловленный предмет познания. Вот почему практика,
впитавшая в себя знания, является формой непосредственного их соединения с
объективными предметами и вещами. В этом и проявляется функция практики как
критерия истины.
Истина и ее критерии
Для того
чтобы доказать истинность того или иного утверждения, необходимо каким-то
образом проверить его. Средство такой проверки называется критерием
истины (от греч. kriterion — мерило для оценки).
Основные концепции истины
|
Концепция истины |
Определение истины |
Критерий истины |
|
Классическая |
Истина есть соответствие мыслей и высказывании действительности |
Чувственный опыт и/или ясность и отчетливость |
|
Когерентная |
Истина есть согласованность знаний |
Согласованность с общей системой знаний |
|
Прагматическая |
Истина есть практически полезное знание |
Эффективность, практика |
|
Конвенциональная |
Истина есть соглашение |
Всеобщее согласие |
Учеными
предложены различные критерии того, как отличить истинное от ложного:
§ Сенсуалисты опираются на данные чувств и критерием истины считают чувственный
опыт. По их мнению, реальность существования чего-либо проверяется
только чувствами, а не абстрактными теориями.
§ Рационалисты считают, что чувства способны вводить нас в
заблуждение, и видят основы для проверки высказываний в разуме. Для них основным
критерием истины выступают ясность и отчетливость. Идеальной
моделью истинного знания считается математика, где каждый вывод требует четких
доказательств.
§ Дальнейшее развитие рационализм находит в концепции когерентности
(от лат. cohaerentia — сцепление, связь), согласно которой критерием истины
является согласованность рассуждений с общей системой знаний.
Например, «2х2 = 4» истинно не потому, что совпадает с реальным фактом, а
потому, что находится в согласии с системой математических знаний.
§ Сторонники прагматизма (от греч. pragma — дело) считают критерием
истины эффективность знаний. Истинное знание — это знание
проверенное, которое успешно «работает» и позволяет добиться успеха и
практической пользы в ежедневных делах.
§ В марксизме критерием истины объявляется практика (от
греч. praktikos — деятельный, активный), взятая в самом широком смысле как
всякая развивающаяся общественная деятельность человека по преобразованию себя
и мира (от житейского опыта до языка, науки и т.д.). Истинным признается только
проверенное практикой и опытом многих поколений утверждение.
§ Для сторонников конвенционализма (от лат. convcntio — соглашение)
критерием истины является всеобщее согласие по поводу утверждений.
Например, научной истиной считается то, с чем согласно подавляющее большинство
ученых.
Некоторые
критерии (согласованность, эффективность, согласие) выходят за пределы
классического понимания истины, поэтому говорят о неклассической
(соответственно когерентной, прагматической и конвенциональной) трактовке
истины. Марксистский принцип практики пытается соединить воедино прагматизм и
классическое понимание истины.
Поскольку у каждого критерия
истины имеются свои недостатки, все критерии можно рассматривать и как
взаимодополняющие. В таком случае истиной однозначно можно назвать только то,
что удовлетворяет всем критериям.
Имеются и
альтернативные трактовки истинности. Так, в религии говорится о сверхразумной истине,
основанием которой является Священное Писание. Многие современные течения
(например, постмодернизм) вообще отрицают существование какой-либо объективной
истины.
Современная
наука придерживается классической трактовки истины и считает, что истина всегда объективна (не
зависит от желаний и настроений человека), конкретна (не
бывает истины «вообще», вне четких условий), процессуальна(находится
в процессе постоянного развития). Последнее свойство раскрывается в понятиях
относительной и абсолютной истины.
Понятие истины является одним из наиболее важных в философии математики.
Хорошо известны три традиционных теории, раскрывающих природу истины: истина
как соответствие (корреспонденция), истина как согласованность (когеренция) и
истина как полезность. У каждой из этих теорий есть разнообразные модификации.
Согласно представлению о корреспонденции высказывание является истинным, если
оно соответствует описываемой ситуации, т.е. представляет ее такой, какой она
является на самом деле. Истолкование истинности как соответствия
мысли действительности восходит еще к Античности и обычно называется
классической концепцией истины. Все иные понимания истины именуются
неклассическими.
В соответствии с концепцией когеренции истина представляет собой
систематическое согласие выдвинутого положения с уже принятыми утверждениями.
Такое согласие сильнее логической непротиворечивости: не всякое высказывание,
не противоречащее ранее принятым высказываниям, может быть отнесено к истинным.
Истинно только положение, являющееся необходимым элементом систематической,
целостной концепции. «Целостность» обычно понимается так, что из нее нельзя
удалить, без ее разрушения, ни одного элемента. Истолкование истины как
когеренции развивалось П. Дюэмом, У.В.О. Куайном, Т. Куном, Л. Лауданом и др.
Строго говоря, при таком истолковании истины, если оно проводится
последовательно, истина оказывается характеристикой, прежде всего, самой
«целостности», а не ее отдельных элементов. «Целостность» приобретает при этом
абсолютный характер: она не оценивается с точки зрения соответствия ее чему-то
иному, например, внешней реальности, но придает входящим в систему
высказываниям ту или иную степень истинности. При этом степень истинности
высказывания зависит только от его вклада в систематическую согласованность
элементов «целостности».
В противопоставлении внутренней согласованности (когеренции) и соответствия
опыту (корреспонденции) можно подчеркнуть слова «в конечном счете». Опыт
действительно является источником научного знания. Но далеко не всегда новую, и
тем более абстрактную, естественнонаучную гипотезу удается непосредственно
сопоставить с эмпирическими данными. В этом случае ее согласие с другими
утверждениями теории, в рамках которой она выдвинута, значение гипотезы в
систематизации и прояснении связей этой теории с другими, хорошо обоснованными
теориями, вполне может играть роль вспомогательного определения истины.
В формальных науках, математике и логике, не имеющих непосредственной связи с
опытом, истина как согласование нового положения с уже принятыми утверждениями
является основным рабочим инструментом. Большинство «математических» и
«логических истин» никогда не выходит за пределы согласования их с уже
принятыми математическими и логическими теориями и теми критериями, по которым
оцениваются последние. В качестве вспомогательного используется определение
истины как полезности, как того, что приводит к успеху.
Особенно наглядно сложность проблемы математической истины проявляется в случае
математических идей, относительно которых вообще сложно представить способы
сопоставления их с реальностью даже в рамках содержательных научных теорий.
В
качестве характерного примера можно сослаться на две аксиомы теории множеств: аксиому
выбора (1904) и аксиому детерминированности (1964). Эти аксиомы чересчур
абстрактны, чтобы сопоставить их с эмпирическими данными. Аксиомы не входят в
состав более частных математических теорий, которые могли бы быть использованы
в конкретных научных теориях, допускающих сопоставление с опытом. Это
заставляет предположить, что понятие истины как соответствия не применимо к
данным аксиомам. Вместе с тем два других истолкования истины – истины как
согласованности и истины как полезности – могут использоваться для оценки
аксиом. При этом согласованность и полезность являются взаимно поддерживающими
друг друга свойствами рассматриваемых математических утверждений.
Обоснованный
выбор между аксиомой выбора и аксиомой детерминированности возможен, вероятно,
только путем сравнения красоты и богатства математических теорий, построенных с
использованием данных аксиом, а также путем сравнения согласованности следствий
аксиомы выбора и аксиомы детерминированности с математической интуицией и
практикой приложения математики. В частности, решающим аргументом в пользу
аксиомы детерминированности может оказаться построение топологической теории,
сравнимой по красоте и богатству следствий с созданной к настоящему времени
топологией на основе аксиомы выбора.
Истина как когеренция – наиболее частое, а иногда и единственно возможное
понимание истины как в математике, так и в абстрактных, далеких от опыта
областях математического естествознания. Согласие вновь вводимого положения с
системой утверждений, принятых в конкретной области естественнонаучного знания,
обычно определяется степенью полезности этого положения для данной области и
смежных с нею отраслей знания. Согласованность и полезность оказываются, таким
образом, тесно связанными друг с другом.
Cоответствие
опыту некоторой математической теории не устанавливается непосредственно. Оно
может быть лишь результатом сопоставления с эмпирическими данными тех
содержательных научных концепций, в структуре которых используется эта теория
(«ослабленный критерий истинности Куайна»). Именно поэтому в математике, не
связанной непосредственно с опытом, истина понимается чаще всего не как
соответствие реальности, а как согласованность математических идей между
собой.
В
математике используется, таким образом, все три разные истолкования истины,
взаимно дополняющие друг друга: истина как согласованность, истина как
средство, ведущее к успеху, и истина как соответствие.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Все могли слышать о физике и математике, об их особенностях. Их научная истинна, характеризующаяся точностью и неопровержимостью, особенно хороша.
Научная истина математики заключается в том, что, её результаты можно проверить экспериментально. В отличие от других наук, таких как, например филология и археология.
Истина – одна из самых важных понятий в философии. Адекватное отражение объекта познающим субъектом, знание, соответствующее своему предмету, совпадающее с ним. Процесс постижения истины – это движение от неполного знания к полному.
В новое время, когда математические понятия не соотносятся с реальными объектами, а модели математических теорий строятся внутри самой математики, сходное по форме понятие истинности изменилось по существу. Отсылка на подлинное значение основных понятий и их свойств уже не является гарантом непротиворечивости даже интуитивно построенной содержательной теории. Так как в противоречивой теории доказуемы и ложные мнения, то доказательство непротиворечивости теории стало важным пунктом правдивости её теорем.
Аристотель заложил основы для понимания истины как формы познания, т. е. в качестве гносеологической категории. «Истину говорит тот, кто считает разъеденное разъединённым и связанное связанным, а – ложное тот, кто думает, обратно тому как дело обстоит с вещами …. Так вот, не потому, ты бледен, что мы правильно считаем тебя бледным, а наоборот, именно потому, что ты бледен, говорят, что это говорит правду» [1].
Такое понятие истины теперь называют классическим или корреспондентом. Такое понимание истины также развивается в трудах Фрэнсиса Бэкона, К. Гельвеция, П. Д. Гольбаха, Дидро, Спиноза.
В классическом определении истины один недостаток: как определить соответствие познания действительности? Для получения любой информации о реальности, данной нам в виде знания о нем. Сама же реальность дана нам как феномен сознания в виде образов, мыслей, фактов. Решение этой проблемы привело к формированию конвенциалистской (когерентной) концепции истины. В наиболее явном виде она представлена в работе А. Пуанкаре «О науке». Она основывается на принципе непротиворечивости, самосогласованности знания. В этом случае под истиной понимается знание о предмете, не противоречащее другим знаниям о нем. Например, если знание, полученное теоретическим путем, подтверждается чувственным опытом человека, знаниями, полученными при помощи органов чувств, то это знание и есть истина [2].
Таким образом, мы приходим к следующему определению истины, которая характеризует всю философию позитивизма: «Истина – это знание, в соответствии с другими знаниями». Русская философия соответствует определению истины как знания, подтвержденный практикой. Действительно, в этом случае речь идет о соблюдении требований концептуальных знаний на практике. В объяснении природы истины, как правило, выделяют больше прагматик понятие истинного знания. Часто это трактуется упрощенно: это правда, что полезно. Между тем, представители прагматизма предлагают переключить внимание от проблем истинности знаний о ее эффективности. Проблема станет намного легче, если вместо того, чтобы сказать, что вы хотите знать правду, просто сказать, что вы хотите достичь состояния веры. Истина – это то, что мы считаем, что дает уверенность
Возникает вопрос, который волновал исследователей всех времен. Почему возможно такое превосходное соответствие математики с реальными предметами, если сама она является произведением только человеческой мысли, не связанной ни с каким опытом? Эйнштейн понимал, что аксиомы математики и принципы логики выведены из опыта, но его интересовало, почему следствия, вытекающие из созданных человеком аксиом и принципов, так хорошо согласуются с опытом [3].
Математика является замкнутой в себе наукой, она нуждается в каких-либо критериях истинности её теорем. Математика с большим успехом используется для решения естественнонаучных задач. Это служит поводом считать математику естественной наукой, предназначенной для изучения реального мира, и критерий истинности её теорем был выведен за пределы математики и поставлен в зависимость от «реальных фактов» [1].
В математике истинность теоремы отождествляется с выводимостью (доказуемостью) её из непротиворечивой системы посылок (аксиом). Вывод или доказательство представляет собой дедуктивную цепочку, каждый шаг которой обосновывается каким-либо логическим правилом, принадлежащим формальной математической логике.
Таким образом, резюмируя сказанное, можно определить понятие истинности предложений в математике как формальную доказуемость в непротиворечивой теории. Тем самым не игнорируется семантическое понимание истинности теорем в той модели, для изучения которой предназначена данная теория, поскольку при непротиворечивой логике формальное доказательство теоремы гарантирует её истинность в модели.
В заключение следует отметить, что математика не вписывается в принятое деление наук на естественные и гуманитарные, и ей более подходит особый статус универсальной науки [1].
Список используемых источников
-
Янов, Ю.И. Математика, метаматематика и истина [Электронный ресурс] – Режим доступа: http://terme.ru/termin/filosofija-matematiki.html
-
Клайн, М. Математика. Поиск истины / М. Клайн. – М.: Мир, 1988. – С.40-55.
-
Непостижимая эффективность математики. [Электронный ресурс] – Режим доступа: http://www.telenir.net/matematika/matematika_poisk_istiny/p15.php
Содержание:
- Небольшой исторический экскурс
- Построение фундамента для математики в ХХ веке
- Об интуиции в математике
- О математике вообще
- Что есть истина в математике
| Предмет: | Философия |
| Тип работы: | Реферат |
| Язык: | Русский |
| Дата добавления: | 10.03.2019 |
- Данный тип работы не является научным трудом, не является готовой работой!
- Данный тип работы представляет собой готовый результат обработки, структурирования и форматирования собранной информации, предназначенной для использования в качестве источника материала для самостоятельной подготовки учебной работы.
Если вам тяжело разобраться в данной теме напишите мне в whatsapp разберём вашу тему, согласуем сроки и я вам помогу!
По этой ссылке вы сможете найти рефераты на любые темы и посмотреть как они написаны:
Посмотрите похожие темы возможно они вам могут быть полезны:
Введение:
Если вы спросите кого-то, кто далек от науки об истинности математических теорем, он скажет, что они абсолютно истинны. Напротив, многие высказывания людей науки на эту тему утверждают, что однозначного ответа на этот вопрос нет. Причиной такого расхождения является прежде всего расхождение взглядов на природу математических понятий, что приводит к различному пониманию истинности математических теорем. С другой стороны, понятие истинности теоремы является метаматематическим, поэтому до тех пор, пока соответствующий раздел метаматематики не будет формализован и, следовательно, частью математики, обсуждение этой проблемы носит философский характер, но если выбор философского понятия является в первую очередь вопросом предпочтения, то математика требует объективности решения.
Может показаться странным, что человечество накапливает большой опыт, с одной стороны это подтверждает устойчивость математических знаний, а с другой-непрекращающиеся успехи применения математики в различных областях науки и техники, но в свете внутреннего развития математики этот вопрос является новейшим вариантом интерпретации некоторых важных математических явлений.
С древнейших времен и до недавнего времени существуют ученые, рассматривающие математику как естественную науку, призванную изучать свойства реального мира. Последнее является основной причиной пессимизма, поскольку вопрос об адекватности математических моделей реальным ситуациям всегда выходит за пределы математики и даже за пределы достоверного знания. В то же время математика отличается от других наук своей абстрактностью и идеальностью своих понятий, поэтому она считает свои теоремы абсолютно истинными.
Цель данной работы: дать как можно более объективный ответ на проблему истинности математических теорем, требующих уточнения понятия истинности в математике, мы попытаемся сделать это , но сначала мы должны рассмотреть эволюцию некоторых математических понятий.
Математика, как и наука, представляет собой систему понятий и предложений (предложений, теорем, формул) определенного языка. Однако, в отличие от всех других наук, семантика математического языка-это не фрагмент реального мира, а элемент самой математики. Поэтому можно сказать, что математика-это замкнутая наука сама по себе. Но важная часть математики используется для решения задач, возникающих при изучении реального мира, что дало основание рассматривать математику как естественную науку.
Проблема истинности математических теорем во многом зависит от понятий доказательств и других математических и метаматических понятий, с точки зрения самой природы математики. Эти понятия в научной и философской среде имеют разные перспективы. XX век стал поворотным пунктом в трактовке многих математических и философских проблем в математике, и эти достижения позволяют взглянуть на проблему истинности математических текстов с совершенно новой точки зрения, поскольку важная часть метаматикса количественно определена и сконструирована. В то же время пессимистические утверждения о математике появились в основном в конце XIX-начале XX веков, когда атеизм, обнаруженный в традиционно построенных теориях множеств, стал основой математической интуиции.
В древности существовали различные взгляды на природу и назначение математики. В зависимости от отношений с реальным миром их можно разделить на два типа, которые они называют условными, практическими и идеальными. С практической точки зрения математика-это естественная наука, понимающая законы материального мира и черпающая из него свои понятия и задачи, а главное для истинности математических допущений и теорем. он подходит для описания вещей, которые несовместимы с вещами. Поэтому неразумно говорить об особом соответствии математического языка реальному миру. Как мы обсудим позже, существуют и другие трудности при сравнении математических закономерностей с реальными фактами.
С идеальной точки зрения математика-это самостоятельная наука, развивающаяся по своим собственным законам и не имеющая прямого отношения к материальному миру.
Но здесь возникает вопрос о том, почему математические теоремы успешно применяются к реальному миру, причем с разными ответами. С древнейших времен до XIX века было широко распространено мнение, что мир был создан по математическим законам. В трудах Коперника, Кеплера, Декарта, Галилея и Паскаля некоторые природные явления были все математическими, и не только потому, что эти явления были глубоко убеждены, что Бог создал Вселенную с математическим планом, но также и в том, что математическое мышление человека было совместимо с Божьим планом, и что современное мышление согласуется с Божьим, однако более подходящих альтернатив не было предложено.
В настоящей работе мы предлагаем конкретный взгляд на понятие истины в (мета) математике и рассматриваем возможность убедительного доказательства истинности математической теоремы. Несмотря на то, что в научной среде обычно преобладает прагматический подход к математике, всегда существует и идеальная точка зрения на математику, без которой математика превратилась бы в теоретические разделы различных естественных наук. Именно благодаря абстрактной математике человечество получило универсальный аппарат изучения самых различных явлений реального мира. Иногда говорят, что есть две математики-теоретическая и прикладная, но невозможно отделить прикладную математику от теоретической математики, равно как и математическую теорию.
Небольшой исторический экскурс
Наиболее отчетливо различия во взглядах на природу математики проявились у Платона (IV век до н. э.) и его ученика Аристотеля. Сначала, согласно его философской концепции, он считал, что математика принадлежит к миру чистых идей, поэтому ее истина идеальна, абсолютна и неизменна, и наоборот, ее применение к несовершенному миру условно и временно, и в то же время понять свойства материального мира можно только с помощью идеальной математики, а Аристотелю отводилась роль вспомогательного средства, наглядно демонстрировавшего прагматическое отношение к математике. В позднейших научных хрониках эти две точки зрения всегда сохраняются и сохраняются до наших дней, изменяясь лишь в соответствии с изменениями их взглядов на такие понятия, как логика, доказательства, реальный мир и т. д.
Естественно, что взгляды на понятие истины в математических теоремах с этих точек зрения могут быть различными. Как уже говорилось, некоторые сторонники практической точки зрения утверждают, что критерием истинности математических предложений является факт описываемого им материального мира, то есть наше наблюдение. Что касается идеальной точки зрения, то вопрос об истинности математических теорем приобрел в наше время преимущественно формальный характер, который будет обсуждаться в дальнейшем.
Основные принципы математики были четко провозглашены в древние времена. Аристотель, несомненно, говорил о необходимости дедуктивного построения математических доказательств. В то же время он считал, что истинность аксиомы всегда устанавливается не индуктивным опытом, а абсолютной интуицией, и шаг дедукции также определяется интуицией. Это считается началом сознательной замены логических выводов интуитивными доказательствами.
Этот процесс был отложен более чем на два тысячелетия, и в то время как большинство других математических теорий все еще строятся на интуиции, более подробные сведения об этом затем становятся аксиомой геометрии, которая долгое время служила моделью для построения аксиоматической теории, хотя и не с современной точки зрения, Евклида (III век до н. э.). Развитие, с конца XIX века до начала XX века, никогда не снимало вопроса о «правильных» средствах построения математических понятий и доказательств того, что математика является эффективным инструментом для решения физических, астрономических и других прикладных задач. Учитывая отсутствие самого понятия математической логики, главным инструментом доказательства была интуиция. Сегодня, несмотря на появление формальных понятий логики и доказательства, большая часть доказательств построена на интуиции. Поэтому проблема природы и роли интуиции в математике требует особого рассмотрения.
Хорошо известно, что многие важные отрасли математики родились в связи с необходимостью решения прикладных задач, но без должного развития абстрактной математики, приверженцы прагматического подхода к вопросу-математики, строго говоря, ничего не говорят в свою пользу, а опираются на первые факты, опираются на свою точку зрения.
Хотя математика выступает как инструмент для естественных наук, но в своем развитии математический интерес приобретает для нас самостоятельное значение. Помимо простых средств, математика начинает развиваться совершенно свободно под влиянием только внутренних потребностей. Тогда никакие посторонние соображения уже не могут влиять на развитие математики и математика становится вполне автономной. Критерием ценности всех математических теорий является уже не та польза, которую они приносят познанию внешнего мира, а та внутренняя работа, которая достигается с их помощью в нашем собственном сознании.
Построение фундамента для математики в ХХ веке
Вопрос о построении прочного фундамента для математики был поставлен некоторыми математиками еще до XIX века, но причина этой надежды на открытие противоречий в теории множеств Канторова заключается в том, что, с одной стороны, теория множеств основана на интуитивно очень простом и ясном понятии более простого множества, чем понятие чисел, а с другой-она была найдена в нем (называемом доками).
Самый простой из них-так называемый парадокс Рассела. Все множества можно разделить на два вида: множества, содержащие самого себя в качестве своего элемента и множества, не содержащие себя в качестве элемента. Нетрудно привести примеры тех и других. В связи с этим канторовская теория множеств как основа математики была отвергнута.
Другие попытки решить проблему основ математики предпринимались главным образом с трех различных позиций или направлений, которые называются интуиционизмом, логицизмом и формализмом. Схематически эти направления описаны ниже.
Интуитивизм, как определенное направление в математике, в первую очередь принадлежит Л. Брауэру и А. Гейтингу, появившимся в начале XX века. Она основана на номинальной тенденции ограничивать математику понятиями, которые могут дать «реальный смысл». Для реализации этой идеи интуитивисты рассматривают только такие объекты, где есть потенциально жизнеспособные шаги по их постройке, получившие название структуры. Чтобы не выходить за рамки конструктивного объекта, интуитивист должен был сузить логику и отказаться от исключенного третьего закона. Сужая принятые понятия, интуитивист стремится достичь достоверной истинности математических теорем, а следовательно, и непротиворечивости такой математики, поскольку вместо ясности интуитивистские понятия и теоремы в большинстве случаев сложнее классических аналогов, как показывают дальнейшие исследования человеческой интуиции, чем последняя. это снижает согласованность основной математики.

Кроме того, исключение из математики всех понятий, не поддающихся конструктивному определению, и, в частности, концепции фактической бесконечности, привело к устранению важнейших достижений классической математики. В связи с этим высказывания Д. Гильберта, сделанные в 1927 году, вполне разумны: «… закон исключенного третьего ни в коей мере не виновен в появлении хорошо известных парадоксов теории множеств; эти парадоксы встречаются чаще, потому что они используют неприемлемые и бессмысленные образования понятий, которые в моей теории доказательств сами по себе исключены. Убрать закон исключенного среднего из математики – это то же самое, что взять телескоп у астрономов или запретить боксеру использовать кулаки. Запрещение теорем существования и закона исключенного третьего почти эквивалентно полному отказу от математической науки. Действительно, какое значение имеют жалкие остатки, те немногие, неполные, несвязанные отдельные результаты, которые были получены без использования ε-аксиомы интуиционистами, по сравнению с мощной областью современной математики! Все это, естественно, мешало интуиционизму стать основой всей математики. По нашему мнению, главная причина этого провала – наложение искусственных ограничений, основанных на философских соображениях идеальных математических концепций. Утверждение интуиционистов об исключительной истинности их взглядов и требовании строить всю математику на конструктивной основе лишь служило определенной изоляцией этого направления от базовой математики, хотя в некоторых ее разделах (и особенно в метаматематике) использование конструктивного подхода оправдан, а иногда и необходим. На самом деле концепция конечности Гильберта – не что иное, как форма конструктивности. В своем развитии интуиционизм пошел по пути формализма и, можно сказать, стал тенью классической математики, брошенной на неровную поверхность.
Теория логики появилась в XIX и XX веках в связи с построением математической логики. Ее основатель г. Фреге и Б. Рассел хотели «вывести» всю математику из логики. Для этого необходимо определить основное математическое понятие в рамках чистой логики,и все математические теоремы получаются как логический результат. Фреге определил натуральные числа, так много математических понятий, что они казались ему редуцированными, и построил их арифметические операции. Рассел, хотя и находил противоречия в этой арифметике, но продолжал пытаться реализовать идею логики.
Несостоятельность этой идеи воспринимается почти повсеместно, после провала всех попыток ее реализации и признания содержания и природы логики. На самом деле логика основана на слишком широком понимании логики. Согласно общепринятому определению логики, сформулированному Лейбницем, одним из главных создателей консенсуса Рассела–логика-теоретика, тот факт, что многие математические понятия могут быть выражены на языке логики предикатов при определенной интерпретации, состоит в том, что эти понятия, обладающие всеми признаками, принадлежат логике, это означает, что он не входит в комплект поставки. Именно потому, что существуют противоречивые теории, ясно, что математическая истина не обладает этим свойством. Такое понимание логики не позволяет включить в нее определенные отношения, даже если они определены логическими средствами. Однако логики рассматривали всю логику, которая может быть выражена на языке логики предикатов. Мнение Гильберта таково: напротив, в качестве предпосылки для применения логической дедукции и выполнения логических операций существуют определенные нелогичные конкретные объекты, которые существуют визуально, то есть всевозможные объекты.
Однако следует сказать, что окончательные задачи о границах логики еще не решены, но в отношении логики высших уровней предикатов, которые приняты в классической логике предикатов первого порядка в современной математике, они не являются аксиоматическими рекурсивно и недостаточно изучены далее. Поскольку позиция логиков не была четко очерчена, варианты логицизма обсуждались до недавнего времени.
Формализм (или формальная ориентация в математике), в модернизированном виде прописанный в так называемой «программе Гильберта», был опровергнут результатами Гильбертовой программы Геделя якобы, несмотря на древний факт полной аксиомизации математики, являющейся фактически (в некоторых поправках) основным подходом к основам математики.
В наше время такое утверждение не является нежелательным, но в начале XX века преобладала другая точка зрения, согласно которой математические понятия и теоремы с самого начала должны иметь осмысленное значение в виде аналогов в реальном мире или точнее, среди человеческих представлений о нем. Поэтому идеология Гильберта вызвала неприятие со стороны прагматичных коллег.
Древние греки уже понимали роль дедуктивного подхода к математике и важность четких логических правил для построения дедуктивных цепочек. Об этом свидетельствуют попытки Аристотеля описать такие правила, а также попытки Евклида и его предшественников аксиоматизировать математику, но долгое время не было технической возможности для формулировки логики, и поэтому математики не существовало. Это требует четкого разграничения синтаксиса, как возможного содержания теории, как средства конкретизации внешних форм и семантики теории, поэтому само понятие логики именно все это стало ясно только в XX веке(аналогичные идеи были высказаны уже Лейбницем, 1646-1716).
Начало систематическому построению математической логики, в частности, ее языка положили Д. Буль (1815-1864), Г.Ф. Л. Фреге(1848-1925), Д. Пеано (1858-1932). Современная форма математической логики в виде Аксиоматизированной теории была разработана главным образом для работ Рассела и Уайтхеда, особенно Гильберта и Бернейса. Несколько позже была разработана общая концепция формальной системы.
После нахождения в теории множеств, интуитивно построенной Г. Кантором (1845 – 1918), были выявлены противоречия, главной задачей в основах математики было создание методов построения математических теорий, которые гарантировали бы их непротиворечивость. Интуиционизм фактически не давал и не мог дать никаких гарантий согласованности математики, несмотря на сужение класса объектов и логики, поскольку он не вносил фундаментальных изменений в методы доказательства. Осуществимость логистического подхода с самого начала была очень проблемный и остановился на уровне идей. Единственный жизнеспособный способ дальнейшего развития математики-это использовать путь, очерченный Гильбертом в его программе.
В то время в сознании математиков синтаксис математического языка не мог быть отделен от содержания, но Гильберт действительно понимал, что доказывать непротиворечивость теории своими средствами не имеет смысла, чисто конечно, в форме аксиоматического вычисления он дал бы понятие «конечное», чтобы доказать правильность однако, судя по отдельным примерам, это довольно сильная композиционная форма. В то время эта идея Гилберта была слишком необычной и вызвала критику у многих его коллег. Однако дальнейшее развитие основ математики обусловлено тем, что Гедель оказывает такое негативное влияние на достаточно богатые формальные теории, как неполнота и несуществование непротиворечивых теорий доказательства непротиворечивости.
Идея отделения синтаксиса от семантики была очень важна для развития математики. Кроме того, подход Гильберта привел к появлению метаматикса для математизированного типа.
Об интуиции в математике
Проблеме роли интуиции в науке, особенно в математике, посвящены в основном многие работы философского характера. Рассматривая различные философские воззрения, многие работы лишь запутывают основные вопросы о сущности интуиции. Сразу заметим, что нас интересует только своего рода интуиция, называемая «интеллектуальной», которая также является математической интуицией. Поэтому в дальнейшем мы опустим слово «интеллектуальный». Следует сказать, что до XX века, когда была создана математическая логика и стало возможным построить чисто логическое доказательство, интуиция считалась законным средством доказательства. Этот взгляд на интуицию был очень ясно сформулирован Декартом в его правиле для руководства разумом, которое он писал: «интуицией я неустойчив к чувствам» – сказал он. Надо сказать, что такой точки зрения на интуицию вплоть до XX века придерживались все математики, несмотря на различия в философских концепциях.
Единство этого взгляда, а главное, то, что интуитивно доказанные теоремы остаются верными и в наше время, после обнаружения противоречий в построенной интуитивно теории множеств, которая показывает объективную основу интуиции, понятие интуиции сильно меняется, и если оно строится только по закону логики, то только по формальному числу, по сути, отношение понятия доказательства в математике остается прежним, то есть оно строится с опорой на логику, в этом случае критерием объективности (а следовательно, и точности) такого доказательства является утверждение коллективом других математики. Таким образом, понятие неформального доказательства все еще основано на интуиции, и его объективность оправдывается обращением к определенной группе людей. Этот, казалось бы, субъективный критерий всегда действителен, давая миру бесконечное число математических теорем, не подверженных влиянию времени, в отличие от достижений эмпирической науки. Поэтому естественно предположить, что для этого есть объективные причины, а именно способность человеческого разума непосредственно воспринимать определенные истины (по крайней мере, теоретически).
Отсутствие до XX века полного описания логики, а следовательно, и общепринятого понятия доказательства, в большинстве случаев затрудняло построение логически правильного доказательства, оно сопровождалось общей концепцией доказательства, которое не является истинным. В связи с этим изменились и требования к неофициальной аттестации: теперь они обязаны выполнять каждый шаг дедукции по правилам математической логики. Нельзя сказать,что это требование соблюдается во всей математике, но в теории, связанной с основами математики, это условие необходимо.
Возникает вопрос: Может ли интуитивно построенное доказательство превратиться в формальное логическое доказательство? Поскольку интуитивные доказательства, такие как формальные доказательства, строятся в форме дедуктивных цепочек, поставленные проблемы могут быть активно решены, если говорить о некой логике интуитивных доказательств–интуитивной и содержательной логике-устанавливающей эквивалентность формальной и содержательной логики. В наше время, основываясь на опыте построения формальной теории, содержательная логика представляет собой развернутое правило, соответствующее производному (то есть проверяемому) формальному правилу. Это означает, что для любого существенного доказательства существует эквивалентный формальный аналог, построенный в рамках классической логики предикатов и завершающий интуитивное доказательство. Принятие этого утверждения в качестве рабочего тезиса не менее оправдано, чем принятие церковного тезиса для вычислимых функций. Фактически этот тезис уже принят в современной математике и его иногда называют «тезис Гильберта».
Если вы посмотрите на историю науки в целом, а также на математику, вы легко увидите, что большинство фундаментальных научных открытий произошло с неожиданными «озарениями». Сама «интуиция», что в русском языке означает «усмотрение» или «видение», то есть непосредственное восприятие объекта, дает человеку существование определенных способностей «интеллектуального умозрения», таких как чувственное зрение, что также доказывается всей историей попыток «научить» компьютер доказывать математическую теорему хотя бы на человеческом уровне.
Поскольку теперь ясно, что ряд различных программ не приносят ожидаемых результатов, очевидно, что этот факт в сильной технологии (также в долгосрочной перспективе) заставляет человека осознать, что он обладает особой способностью воспринимать логические истины, отличные от обычного логического мышления.
Эта способность, в силу своей базовой информативности, не может быть смоделирована с помощью автоматов, и поэтому искусственный интеллект ущербен по сравнению с человеческим интеллектом, поэтому интуиция не теряет своей ценности как важный инструмент познания.
Содержательный взгляд на интуицию в математике связан с интуитивизмом, который обсуждался в предыдущем параграфе.
О математике вообще
Можно отметить некоторые особенности, отличающие математику от естествознания. Одна из них заключается в том, что математический объект (по крайней мере, в современной математике) не претендует на то, чтобы быть надлежащим аналогом реального объекта. Кроме того, существование реальной (то есть материальной) модели в формальной теории может быть правильно соотнесено только с идеальными математическими объектами и отношениями, поэтому все понятия и описания не должны зависеть от внешних моделей, поскольку математика фактически является замкнутой системой. В этом свете возражения неофиналистов против использования некоторых теоретико-множественных понятий в математике были полностью отвергнуты на том основании, что они не имеют реальных аналогий.
В то же время математические теории используются для решения многих задач в реальном мире и прогнозирования развития в нем тех или иных процессов. Этот факт свидетельствует о специфической объективности абстрактных математических построений, но не доказывает зависимости математики от реальных понятий. Это также свидетельствует об объективности классической логики, которая лежит в основе всех математических теорий (кроме интуитивистских, логика которых является фрагментом классических). В подтверждение этой точки зрения, оспариваемой некоторыми математиками, приводится высказывание известного математика и физика.
«Математика – это самостоятельный микрокосм, который, однако, обладает мощной способностью отражать и моделировать любые мыслительные процессы и, возможно, всю науку в целом. Она всегда приносила большую пользу и продолжает приносить ее еще больше сейчас. »
Другая гипотеза предполагает, что существует общая логика, присущая как человеческому мышлению, так и структуре реального мира.
Мы думаем, что большинство математиков в целом согласны с этими описаниями, но о необъяснимой эффективности математики в описании реальных явлений, ответ на этот вопрос заключается в том, является ли математика полезным языком, является ли она более глубокой в связи с реальным миром или древней ролью математики в познании реального мира, в таком виде эта гипотеза не объясняет сути самого явления, поэтому она не имеет большого смысла. Эта гипотеза имеет косвенное подтверждение, основанное на предположении об уникальности логики, что представляется весьма правдоподобным, поскольку понятие логики есть истина во всех мирах. Тот факт, что логика (по крайней мере ее основная часть) получила в наше время полное формальное описание, объясняется тем, что логика, то есть самый общий закон реального мира.
Отметим некоторые особенности современной математики. В настоящее время математические теории делятся на формализованные(то есть формальные системы)и неформализованные, называемые содержательными или интуитивными. Последнее традиционно строится интуитивно, исходя из смысловых качеств основного объекта. Построение математической теории в формальном исчислении, во-первых, дает точное описание всех постулатов-аксиом, а во-вторых, формальное доказательство любого предложения, исходя из аксиом теорий, более того, появляется все большая возможность для формальной теории доказать ее метатеоретические свойства, особенно непротиворечивость. В то же время формулировка теории, предназначенной для изучения значимых объектов, в ряде случаев имеет отношение к полноте описания свойств этого объекта, оно может быть сделано, но применимо только к теории языка первой ступени. Для более богатых языков этот вопрос еще недостаточно изучен. Например, в языке второго этапа формальная арифметика семантически завершена.
Что есть истина в математике
В естественных науках истинность предложения(на языке этой науки) – это признак природы или языка, который используется для описания результатов наблюдений или экспериментов в определенной области реального мира. В этом случае имплицитно предполагается, что описание фактов уместно для самой действительности, поскольку познавательная ценность науки утрачивается. Понимание этой научной истины критически зависит от тезауруса, то есть от ранее накопленных знаний и базовых языковых структур, технических достижений в экспериментальных областях и т. д. Нам приходится мириться с этим, потому что другого выхода нет. Но естественным и общепринятым свойством истины является ее постоянство, то есть независимость от времени и других условий.
Практический подход к математике ставит математику в один ряд с естественными науками, поэтому мы не можем говорить о достоверной истинности этой теоремы. На самом деле ситуация в математике принципиально иная: как свидетельствует исторический опыт, положения раз доказанные-теоремы остаются навсегда доказанными. Утверждается, что: в известном смысле математика далека от других наук: результат ее доказывается один раз в дальнейшем развитии науки, теорема никогда не ошибается, но впоследствии выясняется, что она является тривиальным частным случаем более общего математического знания, не подлежащего пересмотру, и общая инвентаризация только увеличивается. Одного этого достаточно, чтобы убедиться, что математическая структура сильна и что доказанная математическая истина очень объективна. Однако в свете современной формализации метаматикса необходимо рассмотреть этот вопрос с более формальной точки зрения.
Что означает истинность теорем в идеальной математике? С древних времен и до сравнительно недавнего времени математические понятия рассматривались как идеализированный объект реального мира, а математические аксиомы-как очевидные свойства таких объектов. Доказательства в этом утверждении представляют собой цепочку выводов, каждый из которых содержит истину, исходящую из очевидной предпосылки. Таким образом, эти понятия были просто отождествлены, так как считалось, что доказательство теоремы гарантирует ее истинную истинность. С этой точки зрения проблема непротиворечивости системы посылок не возникала. В наше время, когда математические понятия не соотносятся с реальными объектами, а математические теоретические модели строятся внутри самой математики, понятие истины, сходное по форме прежде всего, с отсылкой к содержанию исходных понятий и их свойствам (реальным), является противоречивым суждением, которое уже не гарантирует интуитивно построенной теории содержания. следует отметить, что в формальной теории понятие доказательства имеет строгое формальное определение, так как доказательство непротиворечивости теории (или той же системы аксиом) становится непременным условием истинности ее теоремы.
В этом случае вопрос о том, является ли какая-либо цепь уравнений доказательством, является алгоритмически, то есть объективно, и поэтому набор доказательств разрешим. (Заметим, что это не означает, что набор теорем может быть решен. Это не может быть решено из-за чистой логики предикатов). Что касается неофициальных свидетельств действительного большинства нашего времени, то современные стандарты говорят, что логический тезис Гильберта уже не гипотеза, а требование, чтобы математические доказательства были выполнены, чтобы они могли быть переведены в формальные. Поэтому один элемент доказательства понятия истинности в математических теоремах представляется вполне достоверно обоснованным. Он будет подробно описан ниже. Это не последовательный случай, как мы также объясним ниже.
Таким образом, можно констатировать, что проблема истинности теорем сводится к проблеме правильности доказательства и непротиворечивости теории:
- Математика-это самодостаточная наука, которая не требует никаких внешних критериев для истинности своей теоремы. В то же время она достигла больших успехов в решении естественнонаучных задач. Это обстоятельство породило представление о том, что математика-это естественная наука, направленная на изучение реального мира, а критерий истинности теоремы взят из математики, и в ней говорится, что в наше время не только математика, но и многие метаматические понятия приобретают точный формальный смысл, это несоответствие в точке зрения не имеет никакого значения.
- В математике истинность теоремы отождествляется с ее выводимостью (проверяемостью) из непротиворечивой системы (аксиомы). Вывод или доказательство-это дедуктивная цепочка, каждый шаг которой обосновывается несколькими логическими правилами, принадлежащими формальной математической логике. На самом деле, подавляющее большинство доказательств содержит шаги дедукции, основанные на интуитивных доказательствах. Поэтому интуитивно очевидные шаги должны быть логически эквивалентны. Как правило, интуитивные доказательства удовлетворяют этому требованию и позволяют принять соответствующую диссертацию, называемую диссертацией Гильберта, за эквивалентность интуитивных и логических доказательств.
- Вопрос о непротиворечивости математической теории не возникал до XIX века, поскольку считалось, что математические понятия отражают неупорядоченную природу реального мира. Кроме того, не было никакого другого способа доказать согласованность, кроме ссылки на фактическую модель. К концу XIX века этот вопрос созрел, и в XX веке, благодаря формулировке математических теорий, стало возможным решить его математическими средствами.
В то же время признается, что ссылки на реальные модели не являются доказательством непротиворечивости, поскольку между идеальными математическими понятиями и реальными объектами нет должного соответствия.
В хорошо развитой математике, которая является современной математикой, обязательно должны быть противоречивые теории, так что проблема непротиворечивости в математике вообще не имеет смысла, поэтому можно говорить только о непротиворечивости отдельных теорий, таких как формальная арифметика или формальная теория множеств.
Это происходит потому, что теория содержания предстает перед нами не как целое, а лишь как фрагмент, построенный в этой точке, и поэтому ее непротиворечивость непротиворечива, проблема непротиворечивости наиболее актуальна для формальной теории и связана главным образом с общей проблемой основ математики. В этом направлении в XX веке было получено много кардинальных результатов, которые значительно расширили и углубили понимание математики. Конечно, многие важные проблемы в области математической логики и в области фундаментальной математической теории (например, теории множеств) остаются нерешенными, но это явление можно отнести к любой теории.
В заключение следует отметить, что математика не вписывается в принятые факультеты естественных и гуманитарных наук, она подходит для особого статуса универсальной науки.
План урока:
Алгебра логики и решение задач
Основные операции
Сравнение операций, первоочередность
Диаграммы Эйлера-Венна
Законы алгебры логики
Электросхемы и таблицы истинности
Универсальный подход помогает решать разнотипные задачи, даже не вникая в условие детально. Именно для этого нужны логические задачи и универсальные способы решения. Существует множество подходов, но наиболее распространены 3 основных:
- Способ рассуждений.
- Табличный способ.
- Решение при помощи средств логики.
Первый позволяет находить правильный ответ, обдумывая каждый пункт задачи, делая выводы из каждого условия. Этим методом мы пользуемся постоянно, в обычной жизни, решая простые бытовые примеры. Он простой, но для сложных задач не подходит.
Табличный метод сокращает форму записи примера и позволяет перебрать все возможные значения исходных данных, анализируя результат, полученный при каждой комбинации. Это очень наглядно, компактно и позволяет использовать обычные слова или же логические обозначения.
Поиск правильного решения средствами логики выводит решение примеров на новый уровень, позволяя абстрагироваться от лишней информации, выделяя только переменные, их взаимосвязи. Это позволяет решать задачи из любой сферы, не вникая в те данные, которые не важны для самого решения. Логическая основа задачи – своеобразный «скелет», а вся сопутствующая информация – «одежда».
Алгебра логики и решение задач
Несмотря на то, что логика, как наука о размышлении, существовала еще 5 в. До н.э., теперь это важная часть многих наук, а не только философии и риторики. Также логика существует, как отдельная наука уже более 200 лет.
Инструменты алгебры логики позволяют переводить словесные высказывания в сухие, объективные выражения, а с их помощью выполнять различные логические операции.Появился этот раздел математики 200 лет назад.
Стоит остановиться на базовых понятиях алгебры логики:
- константы (0,1);
- переменные;
- формула;
- знаки операций;
- скобки.
Логическая переменная – обозначение логического выражения, которое может быть true (t, правда, истина, да, 1) – false (f, ложь, нет, 0).
Формула– символьный способ выражения операции между переменными при помощи специальных знаков и скобок ().
Логическое высказывание – утверждение, в котором говорится только правда или только ложь.
Образец таких предложений: «Луна – вертится вокруг Марса» – ложно, а «После зимы всегда приходит весна» – истинно.
Частицы «не», «или», если», «и» и другие, которые являются связующими элементами в обычной речи, позволяют создавать элементарные логические выражения.
Элементарные высказывания – те, к которым нельзя применить понятие истинности или ложности. Их обозначают различными символами (латинские буквы, цифры), знаками. Ими занимаются те сферы, к которым они относятся. Они входят в состав высказываний логики.
Из одних высказываний можно образовывать другие, в результате получая составные высказывания. И от того, являются исходные элементы составного конечного высказывания правдивыми или неправдивыми, а также какие логические связки использовались, будет правдой или ложью все высказывание в целом.
Чтобы образовать такое составное предложение в обычной жизни, используют связки И, ИЛИ, НЕ. А научный подход заменил их на конъюнкцию, дизъюнкцию, инверсию и более сложные операции. Все эти процессы выражают словесно, таблично (таблицы истинности) или графически (диаграммы Эйлера-Венна).
Простые выражения содержат лишь одно выражение (правдивое или нет), и не содержит никаких логических операций.
Сложные могут содержать от 2 и больше аргументов (простых выражений), которые между собой связаны логическими операциями.
Еще используют понятие «предикат» – содержит любое количество переменных без перечисления всех составляющих данных. Это предикат простых, отрицательных P(x)=(x<0) чисел.
Чтобы исключить лишнюю информацию, оставив только логические связи, используют таблицы истинности, наглядно демонстрирующие, правдиво или неправдиво конечное предложение, если учесть все значения входящих в его состав простейших частей.
Такая форма оформления и решения задач используется в построении электросхем, для решения различных логических задач, в булевой алгебре, программировании.
Основные операции
Количество логических операций, которыми обычно оперирует логика 6:
- Отрицание.
- Умножение.
- Сложение
- Следование.
- Дизъюнкция.
- Равнозначность.
Остановимся на каждом из них детальнее, выясним как правильно они называются в алгебре логики, есть ли у них аналоги в обычной речи, в математике, и как их можно использовать в обычной жизни.
Отрицание или инверсия
Операция отрицания или НЕлогическое, корректнее будет название инверсия.Конечное высказывание будет противоположным первоначальному (исходному). Применяется для одного выражения, которое может быть как сложным, так и элементарным.
На примере этой простейшей операции удобно показывать, насколько лаконичны и информативны таблицы истинности. Обозначим исходное высказывание буквой А, соответственно, окончательное будет не А (или НЕ, ‾, ˥ not А). А их ложность или правдивость напишем при помощи цифр 0 и 1.

Получается, если исходное значение правда, то новое будет ложь, и наоборот.
Умножение или конъюнкция &
Логическое И или умножение еще называют конъюнкцией. Финальное высказывание будет правдивым, только если его составляющие тоже правдивы. Во всех остальных случаях оно будет ложным. Применяется для двух и более аргументов, элементарных или сложных. Обозначение А и В; А ^ В; А &В; A and В.
Как видно, при помощи таблицы истинности из 15 ячеек можно описать то, на описание чего при помощи слов пришлось бы потратить минимум 5 полноценных предложений.

Логическое И в обычной жизни:
- Хорошая певица должна быть талантливой и упорной (наличие только одного качества не позволит проявить миру свой талант).
- По условиям задачи А – число меньше 30, В – число делиться на 3. Нужно найти решение А ˄ В.
Решение: Первое множество содержит числа 1,2,3….29. Второе – 3,6,9,…27. Решением будет множество на пересечении множеств А и В, что хорошо покажут диаграммы Эйлера-Венна. А ˄ В будет истинным для множества чисел 3,6,9,….27.
Сложение или дизъюнкция V
Логическое ИЛИ, сложение по-другому называют дизъюнкцией. Оно истинно всегда, кроме случая, если ложны все составные высказывания. Функция распространяется на простые и сложные исходные аргументы. Обозначение А или В; A v В; А ог В.

В обычной жизни нас окружает логическое ИЛИ:
- «Чтобы сдать тесты на «отлично», нужно старательно готовиться ИЛИ должно повезти с билетом».
- Есть задача с 2-мя условиями: А – число делится на 5, В – число делится на 2.
Решение: Первое множество чисел включает в себя 5, 10, 15…Второе – 10, 20, 30…Решение, при котором истинно Аv В – совокупность обеих множеств (5, 10, 15, 20, 25, 30…).
Следование или импликация
Для этого случая важно значение каждого выражения и даже его очередность, потому что первый аргумент считается условием, второй – следствием. Импликация будет ложной лишь в одном случае – если первое составляющее правдиво, а второе нет.

Такое логическое следование имеет аналог в обычной речи «если.. то», то есть одно событие зависит от другого. Символьно связи выражают следующим образом:

Логическое следование в обычной жизни:
- Если пойти к врачу, можно выздороветь (но можно выздороветь и без похода к врачу, а можно и после визита в больницу не выздороветь).
- По условию задачи, А – если число делится на 10, то В делится на 5.
Строгая дизъюнкция
Такая логическая операция выдаст истину, если любое из составляющих высказываний будет истинным, независимо очередности.

Это пример исключающей функции. Аналог в словесном выражении – «либо». Разница от простой дизъюнкции в том, что конечное выражение будет истинным, только если будет правдой одна переменная.

Эквиваленция или равнозначность
Операция, выдающая истину в случае, если обе исходные переменные истины или неправдивы.Обозначают А ~В, А ↔ В.

Словесная аналогия – «тогда и только тогда, когда», математическая – «необходимо и достаточно». Если сравнить таблицы истинности для предыдущих операций, очевидно, что она противоположна «исключающему ИЛИ», то ее можно посчитать так:

Пример эквивалентности из обычной жизни:
- Если вечером на горизонте солнце темно-красного цвета, значит, завтра будет ветреный день.
- В задаче 2 условия: А – сумма цифр числа равно 9, В – число делится на 9. АВ означает, что число делится на 9, если сумма цифр равна 9.
Сравнение операций, первоочередность
Приведены результаты основных логических функций для 2-х переменных:

Если выражение громоздкое, состоящее из нескольких основных, анализ выполняют по приоритетности функций, по очереди написания, от начала:

Но скобки делают операцию внутри них самой приоритетной.
Законы алгебры логики
Операции логики подчиняются законам, которые во многом напоминают математические законы. Другими словами, операции обладают определенными свойствами, которые упрощают решение и позволяют преобразовывать одни операции в другие.
Таблица законов алгебры логики

Диаграммы Эйлера-Венна
Тем, кто лучше воспринимает информацию в виде изображений, понравятся диаграммы Эйлера-Венна, которые показывают, как пересекаются множества между собой.
Число пересечений (областей) можно посчитать сразу, оно равно n = 2N, где N – число множеств. Так как значение двойки в степени растет очень быстро (4,8,16), обычно диаграммы используют для 2-3 множеств. Далее области пересечения будут сливаться, образуя неразличимые участки. Если множеств 2-3, то рисуют круги, если больше 4 – эллипсы. Этот «цветок» помещают в прямоугольную конструкцию, которую называют универсум U (универсальное множество).
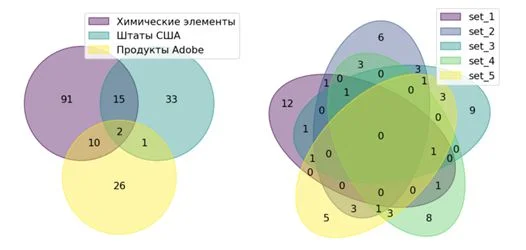
Источник

Источник
Диаграммы позволяют наглядно увидеть результат большинства логических функций:
Конъюнкция множеств А и В:

Отрицание Ā:

Сложное выражение (Ā)∨(A∧B), составленное из элементарных Ā, A∧B и их комбинации, графическое выражение:

Примеры использования диаграмм Эйлера-Венна
Пример №1:
Есть 2 множества цифр и универсум:
А={4,5,6,7}
В={6,7,8,9}
U={0,4,5,6,7,8,9}
Пустой области ничего не принадлежит, опишем в табличном виде, какие цифры какой области принадлежит:

Электросхемы и таблицы истинности
При помощи «0» и «1» можно обозначить, светится ли лампочка, идет ли ток при параллельном или последовательном соединении проводов. Это настолько удобно, что у разных логических функций есть стандартные обозначения при построении электрических схем:

Переменными являются переключатели, а результат (горит лампа/идет ток) будет «1» – истина или «0» – ложь.
Для конъюнкции и инверсии подходит последовательное соединение, но во втором случае переключатель один, для дизъюнкции – параллельное.

Это примеры простейших электросхем. Понимание простейших логических взаимосвязей, умение быстро строить и анализировать электроцепи позволяет строить, паять более сложные, многоуровневые схемы. Для автоматизации применяют различные программы, самый простой вариант – таблицы Excel.

Математическая логика — это раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики.

Алгебра высказываний
Под высказыванием понимаем всякое утверждение (повествовательное предложение), про которое всегда определенно и объективно можно сказать, является оно истинным или ложным. Например, «5-3 = 2» или «В неделе семь дней» — истинные высказывания, а «5 > 8» или «В русском языке 35 букв» — ложные высказывания. Синонимами слова «высказывания» можно считать: логическое высказывание, булевское выражение, суждение, утверждение и т.п. Фразы: «Ура!», «Который час?» — не являются высказываниями.
Если высказывание истинное, то ему предписывается значение «истина» (другие обозначения: «1», «ДА» , «И», «+», «true»). Ложному высказыванию предписывается значение «ложь» (другие обозначения: «О», «НЕТ», «Л», «-«, «false»). Совокупность возможных значений высказывания образует множество истинности {0,1} и {И,Л}.
Есть два вида высказываний: простые и составные (сложные). Под простым будем понимать высказывание, которое не может быть разбито на более простые высказывания. Про него всегда однозначно можно сказать, что оно истинно или ложно, не интересуясь его структурой. Из простых высказываний при помощи логических операций можно строить сложные высказывания, которые всегда только истинны или только ложные. Высказывания обозначаются заглавными латинскими буквами: 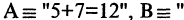 сегодня вторник
сегодня вторник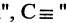 если студент успешно сдал сессионные экзамены, то переводится на следующий курс и будет получать стипендию».
если студент успешно сдал сессионные экзамены, то переводится на следующий курс и будет получать стипендию».
Логические операции
Операции над высказываниями задают в виде таблиц, называемых таблицами истинности.
Отрицание высказывания
Для каждого высказывания А может быть сформировано новое высказывание 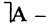 отрицание высказывания А, которое истинно, когда А ложно, и ложно, когда А истинно. Символ
отрицание высказывания А, которое истинно, когда А ложно, и ложно, когда А истинно. Символ 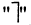 соответствует логическому союзу «не».
соответствует логическому союзу «не». 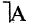 читается «не А» или «не верно, что А». Отрицание — одноместная (или унарная) операция. Последующие операции — двухместные (или бинарные). Например, если
читается «не А» или «не верно, что А». Отрицание — одноместная (или унарная) операция. Последующие операции — двухместные (или бинарные). Например, если 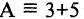
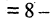 истинное высказывание, то
истинное высказывание, то 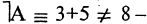 ложное высказывание (отрицание А), или если
ложное высказывание (отрицание А), или если 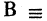 в комнате холодно»,
в комнате холодно», 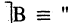 в комнате не холодно». Отметим, что высказывание «в комнате жарко» не является отрицанием В.
в комнате не холодно». Отметим, что высказывание «в комнате жарко» не является отрицанием В.
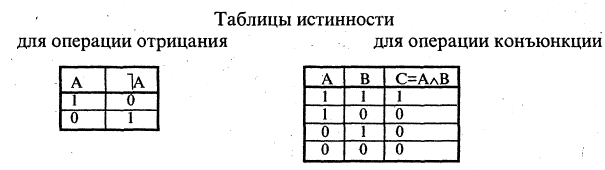
Конъюнкция высказываний
Конъюнкцией высказываний А и В называется высказывание 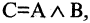 которое истинно только в том случае, когда и А, и В одновременно истинны. Выражение
которое истинно только в том случае, когда и А, и В одновременно истинны. Выражение  читается «А и В». Пример: пусть
читается «А и В». Пример: пусть 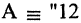 делится на
делится на 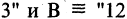 делится на 4″. Тогда формула
делится на 4″. Тогда формула  имеет смысл: «12 делится на 3 и на 4».
имеет смысл: «12 делится на 3 и на 4».
Операцию конъюнкции можно определить и для нескольких высказываний как связку высказываний, объединенных союзом «и». Конъюнкция из п высказываний — новое высказывание, причем высказывание
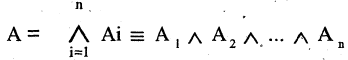
имеет значение «истина», если 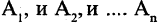 истинны. Во всех других случаях эта конъюнкция имеет значение «ложь». Пусть, например,
истинны. Во всех других случаях эта конъюнкция имеет значение «ложь». Пусть, например, 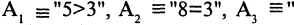 отец старше сына
отец старше сына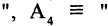 Мурманск севернее Смоленска». Тогда высказывание
Мурманск севернее Смоленска». Тогда высказывание 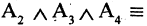 («8=3 и отец старше сына, и
(«8=3 и отец старше сына, и
Мурманск севернее Смоленска») — ложное высказывание. В то время как 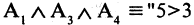 и отец старше сына, и Мурманск севернее Смоленска» — истинное высказывание.
и отец старше сына, и Мурманск севернее Смоленска» — истинное высказывание.
Дизъюнкция высказываний
Дизъюнкцией высказываний А и В называется высказывание 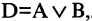 которое ложно только тогда, когда и А, и В ложны одновременно. Дизъюнкция имеет значение «истина», если хотя бы одно из высказываний, входящее в дизъюнкцию, является истинным. Выражение
которое ложно только тогда, когда и А, и В ложны одновременно. Дизъюнкция имеет значение «истина», если хотя бы одно из высказываний, входящее в дизъюнкцию, является истинным. Выражение  читается «А или В». Пусть
читается «А или В». Пусть 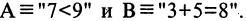 Тогда
Тогда 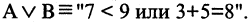
Операцию дизъюнкции можно определить для нескольких высказываний как связку высказываний, объединенных союзом «или»,
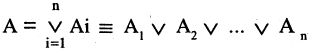
В этом случае высказывание А истинно, если истинно хотя бы одно из высказываний, входящих в связку.
Импликация высказываний
Импликацией высказываний А и В называется высказывание 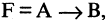 которое ложно только в том случае, когда А — истинно, а В — ложно. Во всех других случаях импликация
которое ложно только в том случае, когда А — истинно, а В — ложно. Во всех других случаях импликация 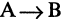 имеет значение «истина». Символ
имеет значение «истина». Символ 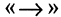 соответствует логическому союзу: «если А, то В». Например, А — «целое число делится на 4, то оно делится на 2». Для иллюстрации содержательного смысла импликации рассмотрим следующий пример: А
соответствует логическому союзу: «если А, то В». Например, А — «целое число делится на 4, то оно делится на 2». Для иллюстрации содержательного смысла импликации рассмотрим следующий пример: А  «папа завтра получит премию», В
«папа завтра получит премию», В  «папа завтра купит сыну велосипед». Тогда импликация
«папа завтра купит сыну велосипед». Тогда импликация 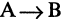 может быть сформулирована так: «если папа завтра получит премию, то купит сыну велосипед».
может быть сформулирована так: «если папа завтра получит премию, то купит сыну велосипед».

Пусть А и В истинны. Тогда папа, получив премию, покупает сыну велосипед. Естественно считать это истинным высказыванием. Когда же папа не купит сыну велосипед (В — ложно), получив премию (А — истинно), то это, мягко говоря, не логичный поступок, а импликация имеет значение «ложь». Если же папа не получит премию (А — ложно), но купит велосипед (В -истинно), то результат положителен. В том случае, если, не получив премии (А ложно), папа не купит велосипед (В — ложно) -обещание не нарушено, результат можно считать истинным.
Эквивалентность высказываний
Эквивалентностью высказываний А и В называется высказывание 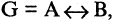 которое истинно, когда высказывания и А, и В оба истинны или оба. ложны. Символ логической эквивалентности
которое истинно, когда высказывания и А, и В оба истинны или оба. ложны. Символ логической эквивалентности  соответствует связке «тогда и только тогда». Пример. Пусть А
соответствует связке «тогда и только тогда». Пример. Пусть А  «число З
«число З является четным», В
является четным», В  «число
«число  является четным». Высказывание «число З
является четным». Высказывание «число З является четным тогда и только тогда, когда
является четным тогда и только тогда, когда  -четное число» есть эквивалентность высказываний А и В. Эквивалентность высказываний может быть задана следующей таблицей истинности:
-четное число» есть эквивалентность высказываний А и В. Эквивалентность высказываний может быть задана следующей таблицей истинности:
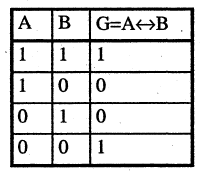
Замечание. Характерной особенностью операций над высказываниями является введение логических союзов с точно определенным смыслом, не допускающим никакой двусмысленности в толковании этих символов. Таким образом, математическая логика применима не для любых высказываний, а только для таких, которые допуск кают четкую оценку в двоичной системе «истина — ложь». Для преодоления такого рода ограничений в рамках нечеткой математики разрабатывается нечеткая логика.
Если в выражении встречаются различные логические операции, то в качестве естественного порядка (выполняемого поочередно слева направо) используется следующая последовательность: 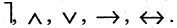 Это означает, что сначала выполняются операции отрицания, затем конъюнкции и т. д. Для нарушения порядка служат скобки. Рассмотрим пример. Пусть высказывания А и В имеют значения «истина», а высказывания С и Б — «ложь». Тогда формула
Это означает, что сначала выполняются операции отрицания, затем конъюнкции и т. д. Для нарушения порядка служат скобки. Рассмотрим пример. Пусть высказывания А и В имеют значения «истина», а высказывания С и Б — «ложь». Тогда формула 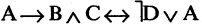 имеет значение «ложь», т.к.:
имеет значение «ложь», т.к.:
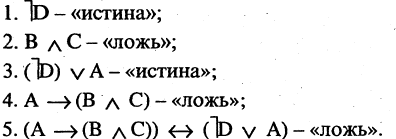
Введя скобки, получим формулу 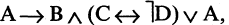 которая уже имеет другое значение — «истина». Действительно:
которая уже имеет другое значение — «истина». Действительно:
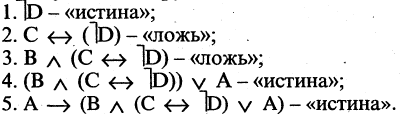
Если в выражении присутствуют арифметические операции, операции сравнения и логические операции, то порядок старшинства операций следующий:
Использование различных операций позволяет в удобной аналитической форме задавать различные множества.
Например, множество точек А, заштрихованное на рис. 1.16, может быть задано следующей формулой:
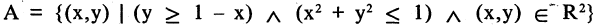
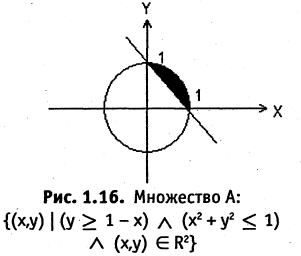
Система операций  называется полной, если всякая формула эквивалентна некоторой формуле, в которую входят только операции из системы
называется полной, если всякая формула эквивалентна некоторой формуле, в которую входят только операции из системы  . Система введенных пяти операций (отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности) полная, хотя вообще говоря, избыточна, так как одни логические операции могут быть выражены через другие. Например, импликация и эквивалентность можно выразить через отрицание, конъюнкцию и дизъюнкцию следующим образом:
. Система введенных пяти операций (отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности) полная, хотя вообще говоря, избыточна, так как одни логические операции могут быть выражены через другие. Например, импликация и эквивалентность можно выразить через отрицание, конъюнкцию и дизъюнкцию следующим образом:
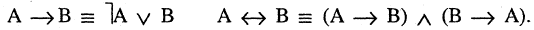
Булевы функции
Всякую формулу логики высказываний можно рассматривать как некоторую функцию: каждая буква (высказывание) может принимать одно из двух значений — «истина» или «ложь», при этом сложное высказывание, заданное этой формулой, также может быть истинным или ложным. Так формула
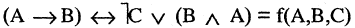
выражает функцию от переменных А, В и С.
Такого рода функции называются булевыми, а их аргументы — булевыми переменными. Аргументы булевых функций могут представлять собой, сокращенные обозначения некоторых конкретных высказываний. Тогда функция обозначает сокращенную запись некоторого сложного высказывания. Например, 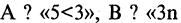 делится на 3», С ? «Мурманск севернее Смоленска». В этом случае
делится на 3», С ? «Мурманск севернее Смоленска». В этом случае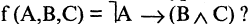 «если
«если 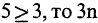 делится на 3 и Мурманск севернее Смоленска». Сравните с известной формулой физики
делится на 3 и Мурманск севернее Смоленска». Сравните с известной формулой физики 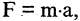 где m — масса тела, а — его ускорение, а F — сила, вызвавшая это ускорение. Буквы в булевых функциях могут выступать в качестве переменных. Подставляя вместо них любые высказывания, можно по формуле вычислить соответствующее значение функции. Действительно, если в формуле
где m — масса тела, а — его ускорение, а F — сила, вызвавшая это ускорение. Буквы в булевых функциях могут выступать в качестве переменных. Подставляя вместо них любые высказывания, можно по формуле вычислить соответствующее значение функции. Действительно, если в формуле 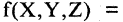
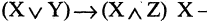 «истина», Y — «ложь», Z — «истина», то
«истина», Y — «ложь», Z — «истина», то 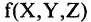 — «истина». Если же Z будет иметь ложное значение, то
— «истина». Если же Z будет иметь ложное значение, то 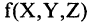 поменяет значение на противоположное и будет «ложью».
поменяет значение на противоположное и будет «ложью».
Целый ряд булевых функций обладает тем свойством, что они принимают одни и те же значения при любых значениях истинности аргументов. Такие формулы называются тождественно истинными. Например, при любых X и Y истинны формулы 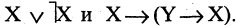 Тождественно ложные функции при любых значениях аргументов имеют значение «ложь». Так формулы
Тождественно ложные функции при любых значениях аргументов имеют значение «ложь». Так формулы 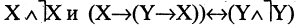 всегда имеют значение «ложь».
всегда имеют значение «ложь».
Наиболее важные тождественно истинные формулы получили название Основные законы математической логики.
Основные законы математической логики
1.Коммутативность
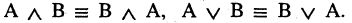
2.Ассоциативность
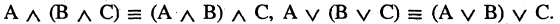
3.Дистрибутивность
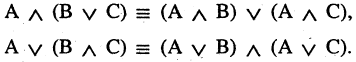
4.Законы де Моргана
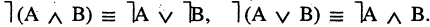
5.Закон поглощения
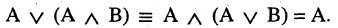
6.Закон идемпотентности
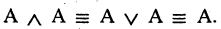
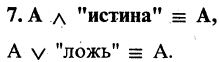
8.Закон противоречия
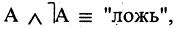
9.Закон исключения третьего
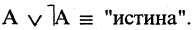
10.Закон двойного отрицания
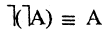
Пример:
Упростить выражение, используя тождественны преобразования
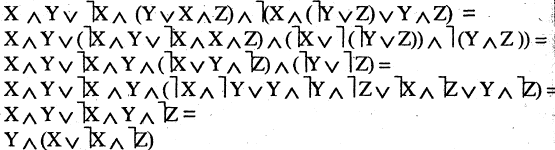
Существует бесконечное множество тавтологий. Некоторы из них легли в основу методов доказательства.
Основные методы доказательств
При построении любой теории выделяется некоторый набор высказываний, так называемых аксиом, истинность которых постулируется. Из аксиом чисто логическим путем может был установлена истинность некоторых других высказываний называемых теоремами. Последовательность высказываний рассматриваемой теории, каждое из которых либо является аксиомой, либо выводится из одного или более предыдущих высказываний этой последовательности по логическим правилам вывода, называется доказательством. Высказывание, которое можно доказать, называется теоремой.
Формально каждая теорема может быть выражена в форме импликации 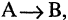 где посылка А называется условием теоремы, а следствие В — заключением. Теорема верна, если выражающая ее импликация тождественно истинна, т. е. является тавтологией. Тавтологии рассматривают как некоторые логически истинные схемы рассуждений. В этой связи тавтологии играют роль законов, определяющих построение правильных умозаключений. Существует бесконечное множество тавтологий. Некоторые из них легли в основу методов доказательства. Основные методы доказательств.
где посылка А называется условием теоремы, а следствие В — заключением. Теорема верна, если выражающая ее импликация тождественно истинна, т. е. является тавтологией. Тавтологии рассматривают как некоторые логически истинные схемы рассуждений. В этой связи тавтологии играют роль законов, определяющих построение правильных умозаключений. Существует бесконечное множество тавтологий. Некоторые из них легли в основу методов доказательства. Основные методы доказательств.
Метод цепочек импликаций
Метод цепочек импликаций состоит в том, что из посылки А страивается цепочка из  -импликаций, последним высказыванием в которой является заключение теоремы В, т. е.
-импликаций, последним высказыванием в которой является заключение теоремы В, т. е.
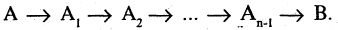
В основе этого метода лежит закон цепного высказывания или закон силлогизма 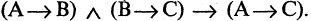
Метод от противного
Метод от противного. Используя этот метод, вместо доказательства прямого следствия «из А следует В» доказывают, что из «не В» следует «не А». Этот метод основан на законе контрапозиций, имеющем следующий вид:
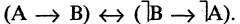
Метод необходимого и достаточного
Метод необходимого и достаточного. Теорема формулируется так: «Чтобы имело место А, необходимо и достаточно выполнение В». Доказательство такого вида теоремы распадается на две части:
а) доказывается, что если имеет место А, то справедливо В (В необходимо для А);
б) если имеет место В, то имеет место и А (В достаточно для А).
Доказательство таким методом базируется на законе тавтологии:
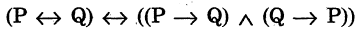
Алгебра предикатов
Предикатом 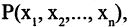 заданным на множествах
заданным на множествах 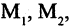
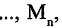
называется функция Р, отображающая их прямое произведение на двоичное множество, т. е. 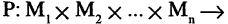
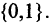 Множество М называется предметной областью предиката,
Множество М называется предметной областью предиката, 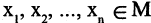 называются предметными переменными или термами. Предикат представляет собой логическую функцию, принимающую, как и булевская функция, значение «истина» или «ложь», когда ее предметные переменные принимают определенные значения.
называются предметными переменными или термами. Предикат представляет собой логическую функцию, принимающую, как и булевская функция, значение «истина» или «ложь», когда ее предметные переменные принимают определенные значения.
Рассмотрим примеры, 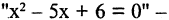 одноместный предикат на множестве комплексных чисел, при этом, например, если
одноместный предикат на множестве комплексных чисел, при этом, например, если 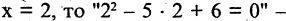 истинное высказывание, а
истинное высказывание, а
положив 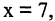 получим
получим 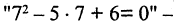 «ложь». Выражение «X — брат Y» — двухместный предикат, заданный на множестве людей. Здесь термы X и Y указывают места, на которые нужна поставить имена двух людей, чтобы получить правильно построенное высказывание. Очевидно, что X — лицо мужского пола, а Y может выбираться из всего множества людей.
«ложь». Выражение «X — брат Y» — двухместный предикат, заданный на множестве людей. Здесь термы X и Y указывают места, на которые нужна поставить имена двух людей, чтобы получить правильно построенное высказывание. Очевидно, что X — лицо мужского пола, а Y может выбираться из всего множества людей.
Всякий предикат  определяет отношение R, такое, что
определяет отношение R, такое, что  тогда и только тогда, когда
тогда и только тогда, когда 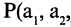
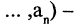 «истина». В этом случае говорят, что отношение R задается областью истинности предиката
«истина». В этом случае говорят, что отношение R задается областью истинности предиката  . Например, отношение
. Например, отношение 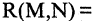 «расстояние на плоскости между точками
«расстояние на плоскости между точками 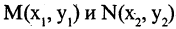 больше величины 1″ можно задать предикатом
больше величины 1″ можно задать предикатом 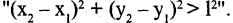
Если в  -местный предикат на место одного из термов подставить определенный элемент из соответствующего множества, то предикат станет
-местный предикат на место одного из термов подставить определенный элемент из соответствующего множества, то предикат станет 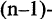 местным. Заменив все термы на конкретные значения из предметной области предиката, получим 0 — местный предикат, т. е. высказывание. Например, «Х- брат Y» — двухместный предикат, «X — брат Маши» — одноместный предикат, «Саша — брат Маши» — высказывание.
местным. Заменив все термы на конкретные значения из предметной области предиката, получим 0 — местный предикат, т. е. высказывание. Например, «Х- брат Y» — двухместный предикат, «X — брат Маши» — одноместный предикат, «Саша — брат Маши» — высказывание.
Логические операции над предикатами
Отрицание предиката
Пусть предикат  задан на множествах
задан на множествах 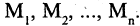 Предикат
Предикат  называется отрицанием предиката
называется отрицанием предиката  тогда и только тогда, если при одних и тех же кортежах
тогда и только тогда, если при одних и тех же кортежах 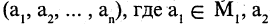
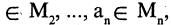 высказывание
высказывание 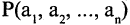 истинно, когда
истинно, когда 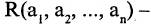 ложно и наоборот. Обозначение
ложно и наоборот. Обозначение
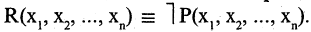
Например, предикат « — четное число» есть отрицание предиката «
— четное число» есть отрицание предиката « — нечетное число» на множестве целых чисел.
— нечетное число» на множестве целых чисел.
Конъюнкция предикатов
Пусть на множествах 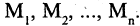 заданы два
заданы два  — местных предиката
— местных предиката 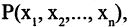 и
и  . Конъюнкцией этих предикатов называется предикат
. Конъюнкцией этих предикатов называется предикат
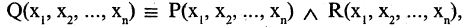
который истинен для одних и тех же кортежей только тогда, когда оба предиката — и  и
и 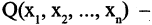 истинны.
истинны.
Например, конъюнкция предикатов 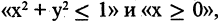 где
где 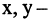 вещественные числа, определяет предикат «точки правой половины единичного круга» (см. рис. 1.17а).
вещественные числа, определяет предикат «точки правой половины единичного круга» (см. рис. 1.17а).
Дизъюнкция предикатов
Дизъюнкция предикатов  и
и  есть новый предикат
есть новый предикат  который имеет значение «ложь» для тех и только тех кортежей из
который имеет значение «ложь» для тех и только тех кортежей из 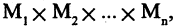 для которых оба предиката — и
для которых оба предиката — и  и
и  — имеют значение «ложь». На рис. 1.17 6 иллюстрируется дизъюнкция предиката
— имеют значение «ложь». На рис. 1.17 6 иллюстрируется дизъюнкция предиката 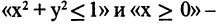 (заштрихованная область).
(заштрихованная область).
Импликация предикатов
Импликация предикатов  и
и  есть новый предикат
есть новый предикат 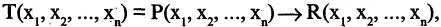 который имеет значение «ложь» для тех и только тех кортежей из
который имеет значение «ложь» для тех и только тех кортежей из 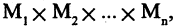 для которых предикат
для которых предикат  имеет значение «истина», а предикат
имеет значение «истина», а предикат  имеет значение «ложь».
имеет значение «ложь».
Например, импликация « делится на 4″ —» »
делится на 4″ —» »  делится на 2″ есть предикат: «если
делится на 2″ есть предикат: «если  делится на 4, то
делится на 4, то  делится на 2″.
делится на 2″.
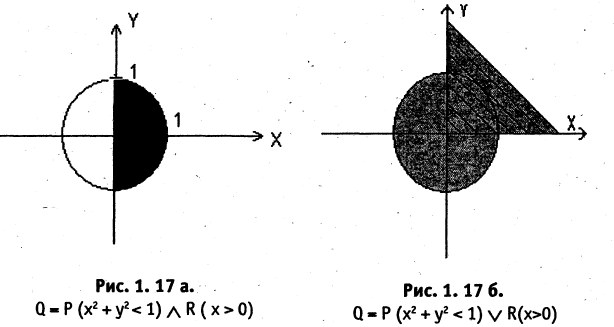
Эквивалентность предикатов
Эквивалентность предикатов  и
и  есть новый предикат
есть новый предикат 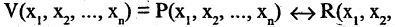
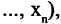 который имеет значение «истина» для тех и только тех кортежей из
который имеет значение «истина» для тех и только тех кортежей из  для которых предикат
для которых предикат  и предикат
и предикат  имеют одинаковые значение или оба «истина» или оба «ложь». Два предиката, заданные на одних и тех же множествах, называются равносильными, если при всех наборах входящих в них предметных переменных эти предикаты принимают одинаковые значения. Равносильность называют также логической эквивалентностью. Например, эквивалентность предикатов
имеют одинаковые значение или оба «истина» или оба «ложь». Два предиката, заданные на одних и тех же множествах, называются равносильными, если при всех наборах входящих в них предметных переменных эти предикаты принимают одинаковые значения. Равносильность называют также логической эквивалентностью. Например, эквивалентность предикатов 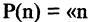 делится на 6» и
делится на 6» и 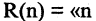 делится на 2 и
делится на 2 и  делится на 3» есть предикат
делится на 3» есть предикат 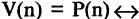
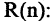 «если
«если  делится на 6, то
делится на 6, то  делится на 2 и на 3». Предикаты
делится на 2 и на 3». Предикаты 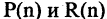 логически эквивалентны.
логически эквивалентны.
Наряду с логическими операциями важную роль играют операции, называемые кванторами. Квантор всеобщности есть операция, которая предикат  превращает в высказывание: «все
превращает в высказывание: «все  обладают свойством
обладают свойством  ». Знак квантора всеобщности
». Знак квантора всеобщности 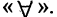 Он заменяет фразы: «для всех», «каждый», «любой» и т.п. Обозначение
Он заменяет фразы: «для всех», «каждый», «любой» и т.п. Обозначение  читается так: «для всех
читается так: «для всех  таких, что Р от
таких, что Р от  ». Например,
». Например, 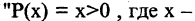 вещественное число», есть предикат «
вещественное число», есть предикат « — положительное число». Тогда
— положительное число». Тогда  есть высказывание «каждое число — положительно». Это ложное высказывание. Если же
есть высказывание «каждое число — положительно». Это ложное высказывание. Если же  — любое натуральное число
— любое натуральное число 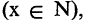 то
то  есть выражение: «каждое натуральное число — положительно» — истинное высказывание. Квантор всеобщности есть обобщение серии конъюнкций единичных высказываний. Пусть М — множество очков, которое может выпасть при бросании игральной кости, т. е.
есть выражение: «каждое натуральное число — положительно» — истинное высказывание. Квантор всеобщности есть обобщение серии конъюнкций единичных высказываний. Пусть М — множество очков, которое может выпасть при бросании игральной кости, т. е. 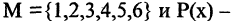 предикат: «при бросании игральной кости один раз выпадает
предикат: «при бросании игральной кости один раз выпадает  очков», где
очков», где 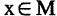 . Применение квантора всеобщности позволяет вместо сложного высказывания
. Применение квантора всеобщности позволяет вместо сложного высказывания 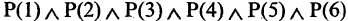 записать равносильное ему компактное высказывание
записать равносильное ему компактное высказывание 
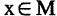 : «при бросании игральной кости один раз может выпасть любое из шести первых натуральных чисел».
: «при бросании игральной кости один раз может выпасть любое из шести первых натуральных чисел».
Квантор существования
Квантор существования есть операция, которая предикат  превращает в высказывание: «существует хотя бы один
превращает в высказывание: «существует хотя бы один 
из М, обладающий свойством  ». Знак квантора существования
». Знак квантора существования 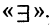 Он заменяет фразы: «существует хотя бы один», «найдется», «некоторый» и т.п. Обозначение
Он заменяет фразы: «существует хотя бы один», «найдется», «некоторый» и т.п. Обозначение  читается так: «существует хотя бы один
читается так: «существует хотя бы один  такой, что Р от
такой, что Р от  ». Например,
». Например,  — предикат: «
— предикат: « — студент», где
— студент», где  — элемент множества жителей Москвы. Тогда выражение
— элемент множества жителей Москвы. Тогда выражение  есть высказывание «хотя бы один житель Москвы является студентом». Квантор существования есть обобщение серии дизъюнкций единичных высказываний. Если задано множество
есть высказывание «хотя бы один житель Москвы является студентом». Квантор существования есть обобщение серии дизъюнкций единичных высказываний. Если задано множество 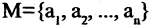 и на нем определен предикат
и на нем определен предикат 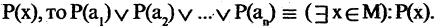
Кванторы обладают свойствами, являющимися аналогами законов де Моргана:
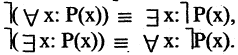
С помощью кванторов можно выражать ряд часто используемых на практике отношений между множествами. Например, высказывание «все объекты  из данного множества, обладающие свойством
из данного множества, обладающие свойством  , обладают также и свойством
, обладают также и свойством 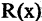 » формально можно записать —
» формально можно записать — 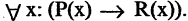
Переход от 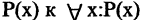 или
или  называется квантификацией или связыванием переменной
называется квантификацией или связыванием переменной  . Связанная переменная фактически не является переменной, т. е. переход от
. Связанная переменная фактически не является переменной, т. е. переход от 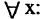
 или от
или от 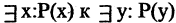 не меняет истинности выражений. Навешивание переменной на многоместный предикат уменьшает в нем число свободных переменных и превращает его в предикат от меньшего числа переменных
не меняет истинности выражений. Навешивание переменной на многоместный предикат уменьшает в нем число свободных переменных и превращает его в предикат от меньшего числа переменных
Рассмотрим пример. На множестве чисел задан двухместный предикат 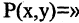 число
число  делится на число
делится на число  ». Связывая одну переменную, можно получить следующие одноместные предикаты:
». Связывая одну переменную, можно получить следующие одноместные предикаты:
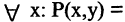 «каждое число делится на
«каждое число делится на  » — ложь;
» — ложь;
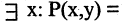 «существует число, которое делится на
«существует число, которое делится на  » — истина;
» — истина;
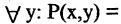 «число
«число  делится на любое число» — ложь;
делится на любое число» — ложь;
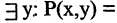 «существует число, на которое делится
«существует число, на которое делится  » — истина.
» — истина.
Связывая обе переменные данного предиката, получим высказывания:
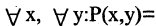 «каждое число делится на любое число» -ложное высказывание,
«каждое число делится на любое число» -ложное высказывание,
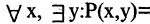 «существует число, на которое делится любое число» — истина, т.к. такое число есть 1,
«существует число, на которое делится любое число» — истина, т.к. такое число есть 1,
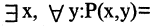 «существует число, которое делится на любое число» — ложное высказывание,
«существует число, которое делится на любое число» — ложное высказывание,
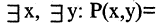 «существует число, которое делится на какое-нибудь число» — истинное высказывание.
«существует число, которое делится на какое-нибудь число» — истинное высказывание.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

