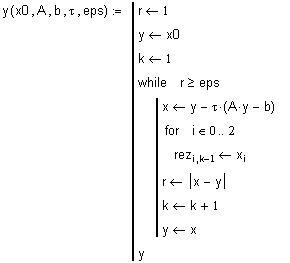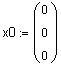Как найти итерацию матрицы

Итерационные методы решения системы линейных алгебраических уравнений

В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.

Общие сведения об итерационных методах или методе простой итерации

Метод итерации — это численный и приближенный метод решения СЛАУ.

Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x0.

Рассмотрим систему Ax=b.

Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x=Bx+d. Затем выбираем начальное приближение к решению СЛАУ x(0)=(x10, x20,…xm0)  и находим последовательность приближений к корню. 

Для сходимости итерационного процесса является достаточным заданное условие В<1. Окончание итерации зависит от того, какой итерационный метод применили.

Метод Якоби

Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x1, из 2-го выражаем неизвестное x2 и т.д.

Результатом служит матрица В, в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:

bij=-aij/aii, i,j=1, 2…, n

Элементы (компоненты) вектора d вычисляются по следующей формуле:

di=bi/aii, i=1, 2,…, n

Расчетная формула метода простой итерации:

x(n+1)=Bx(x)+d

Матричная запись (координатная):

xi(n+1)=bi1xn1+bi2x(n)2+…+b

Критерий окончания в методе Якоби:

x(n+1)-x(n)<ε1, где ε1=1-BBε

В случае если B<1/2, то можно применить более простой критерий окончания итераций:

x(n+1)-x(n)<ε

Решить СЛАУ методом Якоби:

10×1+x2-x3=11×1+10×2-x3=10-x1+x2+10×3=10

Как решить?

Необходимо решить систему с показателем точности ε=10-3.

Приводим СЛАУ к удобному виду для итерации:

x1=-0,1×2+0,1×3+1,1×2=-0,1×1+0,1×3+1×3=0,1×1-0,1×2+1

Выбираем начальное приближение, например: x(0)=1,111 — вектор правой части.

В таком случае, первая итерация имеет следующий внешний вид:

x1(1)=-0,1×1+0,1×1+1,1=1,1×2(1)=-0,1×1,1+0,1+1=0,99×3(1)=0,1×1,1-0,1×1+1=1,01

Аналогичным способом вычисляются приближения к решению:

x(2)=1,1020,9911,011, x(3)=1,1020,99091,0111, x(4)=1,102020,990911,01111

Находим норму матрицы В, для этого используем норму B∞.

Поскольку сумма модулей элементов в каждой строке равна 0,2, то B∞=0,2<1/2, поэтому можно вычислить критерий окончания итерации:

x(n+1)-x(n)<ε

Далее вычисляем нормы разности векторов:

x(3)-x(2)∞=0,002, x(4)-x(3)∞=0,00002.

Поскольку x(4)-x(3)∞<ε, то можно считать, что мы достигли заданной точности на 4-ой итерации.

Ответ:

x1=1,102; x2=0,991; x3=1,011.

Метод Зейделя

Метод Зейделя — метод является модификацией метода Якоби.

Суть: при вычислении очередного (n+1)-го приближения к неизвестному xi при i >1 используют уже найденные (n+1)-е приближения к неизвестным x1, x2, …, xi —1, а не n-ое приближение, как в методе Якоби.

Матричная запись:

xi(n+1)=bi1x1(n+1)+bi2x2(n+1)+…+bi,i-1xi-2(n+1)+bi,i+1xi+1(n)+

+…+bimxm(n)+di

i=1, 2,…m…

За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.

Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.

Как решать?

Решим 3 системы уравнений:

2×1+x2=3×1-2×2=1, x1+2×2=32×1-x2=1, 2×1-0,5×2=32×1+0,5×2=1

Приведем системы к удобному для итерации виду:

x1(n+1)=-0,5×2(n)+1,5×2(n+1)=0,5×1(n+1)+0,5, x1(n+1)=-2×2(n)+3×2(n+1)=2×1(n+1)-1, 2×1-0,5×2=32×1+0,5×2=1.

Отличительная особенность, условие сходимости выполнено только для первой системы:

B<1

Вычисляем 3 первых приближения к каждому решению:

1-ая система: x(0)=1,5-0,5, x(1)=1,750,375, x(2)=1,31250,1563, x(3)=1,42190,2109

Решение: x1=1,4, x2=0,2. Итерационный процесс сходится.

2-ая система: x(0)=3-1, x(1)=59, x(2)=-15-31, x(3)=65129

Итерационный процесс разошелся.

Решение: x1=1, x2=2

3-я система: x(0)=1,52, x(1)=2-6, x(2)=02, x(3)=02

Итерационный процесс зациклился.

Решение: x1=1, x1=2

Метод простой итерации

Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:

x=x-τ(Ax-b), τ – итерационный параметр.

Расчетная формула имеет следующий внешний вид:

x(n+1)=x(n)-τ(Axn-b).

Здесь B=E-τA и параметр τ>0 выбирают таким образом, чтобы по возможности сделать максимальной величину B2.

Пусть λmin и λmax – максимальные и минимальные собственные значения матрицы А.

τ=2/(λmin+λmax) – оптимальный выбор параметра. В этом случае B2 принимает минимальное значение, которое равняется (λmin+λmax)/(λmin-λmax).

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Методы решения задач о собственных
значениях и векторах матриц

Постановка задачи

Пусть [math]A[/math] — действительная числовая квадратная матрица размера [math](ntimes n)[/math]. Ненулевой вектор [math]X= bigl(x_1,ldots,x_nbigr)^T[/math] размера [math](ntimes1)[/math], удовлетворяющий условию

[math]Acdot X= lambdacdot X,qquad mathsf{(2.1)}[/math]

называется собственным вектором матрицы [math]A[/math]. Число [math]lambda[/math] в равенстве (2.1) называется собственным значением. Говорят, что собственный вектор [math]X[/math] соответствует (принадлежит) собственному значению [math]lambda[/math].

Равенство (2.1) равносильно однородной относительно [math]X[/math] системе:

[math](A-lambda E)cdot X=0quad (Xne 0).qquad mathsf{(2.2)}[/math]

Система (2.2) имеет ненулевое решение для вектора [math]X[/math] (при известном [math]lambda[/math]) при условии [math]|A-lambda E|=0[/math]. Это равенство есть характеристическое уравнение:

где [math]P_n(lambda)[/math] — характеристический многочлен n-й степени. Корни [math]lambda_1, lambda_2,ldots,lambda_n[/math] характеристического уравнения (2.3) являются собственными (характеристическими) значениями матрицы [math]A[/math], а соответствующие каждому собственному значению [math]lambda_i,~ i=1,ldots,n[/math], ненулевые векторы [math]X^i[/math], удовлетворяющие системе

являются собственными векторами.

Требуется найти собственные значения и собственные векторы заданной матрицы. Поставленная задача часто именуется второй задачей линейной алгебры.

Проблема собственных значений (частот) возникает при анализе поведения мостов, зданий, летательных аппаратов и других конструкций, характеризующихся малыми смещениями от положения равновесия, а также при анализе устойчивости численных схем. Характеристическое уравнение вместе с его собственными значениями и собственными векторами является основным в теории механических или электрических колебаний на макроскопическом или микроскопическом
уровнях.

Различают полную и частичную проблему собственных значений, когда необходимо найти весь спектр (все собственные значения) и собственные векторы либо часть спектра, например: [math]rho(A)= max_{i}|lambda_i(A)|[/math] и [math]min_{i}|lambda_i(A)|[/math]. Величина [math]rho(A)[/math] называется спектральным радиусом.

Замечания

1. Если для собственного значения [math]lambda_i[/math] — найден собственный вектор [math]X^i[/math], то вектор [math]mu X^i[/math], где [math]mu[/math] — произвольное число, также является собственным вектором, соответствующим этому же собственному значению [math]lambda_i[/math].

2. Попарно различным собственным значениям соответствуют линейно независимые собственные векторы; k-кратному корню характеристического уравнения соответствует не более [math]k[/math] линейно независимых собственных векторов.

3. Симметрическая матрица имеет полный спектр [math]lambda_i,~ i=overline{1,n}[/math], действительных собственных значений; k-кратному корню характеристического уравнения симметрической матрицы соответствует ровно [math]k[/math] линейно независимых собственных векторов.

4. Положительно определенная симметрическая матрица имеет полный спектр действительных положительных собственных значений.

---

Метод непосредственного развертывания

Полную проблему собственных значений для матриц невысокого порядка [math](nleqslant10)[/math] можно решить методом непосредственного развертывания. В этом случае будем иметь

Уравнение [math]P_n(lambda)=0[/math] является нелинейным (методы его решения изложены в следующем разделе). Его решение дает [math]n[/math], вообще говоря, комплексных собственных значений [math]lambda_1,lambda_2,ldots,lambda_n[/math], при которых [math]P_n(lambda_i)=0~ (i=overline{1,n})[/math]. Для каждого [math]lambda_i[/math] может быть найдено решение однородной системы [math](A-lambda_iE)X^i=0,~ i=overline{1,n}[/math]. Эти решения [math]X^i[/math], определенные с точностью до произвольной константы, образуют систему [math]n[/math], вообще говоря, различных векторов n-мерного пространства. В некоторых задачах несколько этих векторов (или все) могут совпадать.

Алгоритм метода непосредственного развертывания

1. Для заданной матрицы [math]A[/math] составить характеристическое уравнение (2.5): [math]|A-lambda E|=0[/math]. Для развертывания детерминанта [math]|A-lambda E|[/math] можно использовать различные методы, например метод Крылова, метод Данилевского или другие методы.

2. Решить характеристическое уравнение и найти собственные значения [math]lambda_1, lambda_2, ldots,lambda_n[/math]. Для этого можно применить методы, изложенные далее.

3. Для каждого собственного значения составить систему (2.4):

[math](A-lambda_iE)cdot X^i=0,quad i=1,2,ldots,n[/math]

и найти собственные векторы [math]X^i[/math].

Замечание. Каждому собственному значению соответствует один или несколько векторов. Поскольку определитель [math]|A-lambda_iE|[/math] системы равен нулю, то ранг матрицы системы меньше числа неизвестных: [math]operatorname{rang}(A-lambda_iE)=r<n[/math] и в системе имеется ровно [math]r[/math] независимых уравнений, а [math](n-r)[/math] уравнений являются зависимыми. Для нахождения решения системы следует выбрать [math]r[/math] уравнений с [math]r[/math] неизвестными так, чтобы определитель составленной системы был отличен от нуля. Остальные [math](n-r)[/math] неизвестных следует перенести в правую часть и считать параметрами. Придавая параметрам различные значения, можно получить различные решения системы. Для простоты, как правило, попеременно полагают значение одного параметра равным 1, а остальные равными 0.

Пример 2.1. Найти собственные значения и собственные векторы матрицы [math]Ain mathbb{R}^{2times 2}[/math], где [math]A=begin{pmatrix}3&-2\-4&1end{pmatrix}[/math].

Решение

Пример 2.2. Найти собственные значения и собственные векторы матрицы [math]A= begin{pmatrix}2&-1&1\-1&2&-1\0&0&1end{pmatrix}[/math].

Решение

---

Метод итераций для нахождения собственных значений и векторов

Для решения частичной проблемы собственных значений и собственных векторов в практических расчетах часто используется метод итераций (степенной метод). На его основе можно определить приближенно собственные значения матрицы [math]A[/math] и спектральный радиус [math]rho(A)= max_{i}bigl|lambda_i(A)bigr|[/math].

Пусть матрица [math]A[/math] имеет [math]n[/math] линейно независимых собственных векторов [math]X^i,~ i=1,ldots,n[/math], и собственные значения матрицы [math]A[/math] таковы, что

[math]rho(A)= bigl|lambda_1(A)bigr|> bigl|lambda_2(A)bigr|geqslant ldotsgeqslant bigl|lambda_n(A)bigr|.[/math]

Алгоритм метода итераций

1. Выбрать произвольное начальное (нулевое) приближение собственного вектора [math]X^{1(0)}[/math] (второй индекс в скобках здесь и ниже указывает номер приближения, а первый индекс без скобок соответствует номеру собственного значения). Положить [math]k=0[/math].

2. Найти [math]X^{1(1)}=AX^{1(0)},~ lambda_1^{(1)}= frac{x_i^{1(1)}}{x_i^{1(0)}}[/math], где [math]i[/math] — любой номер [math]1leqslant ileqslant n[/math], и положить [math]k=1[/math].

3. Вычислить [math]X^{1(k+1)}=Acdot X^{1(k)}[/math].

4. Найти [math]lambda_1^{(k+1)}= frac{x_i^{1(k+1)}}{x_i^{1(k)}}[/math], где [math]x_i^{1(k+1)}, x_i^{1(k)}[/math] — соответствующие координаты векторов [math]X^{1(k+1)}[/math] и [math]X^{1(k)}[/math]. При этом может быть использована любая координата с номером [math]i,~ 1leqslant ileqslant n[/math].

5. Если [math]Delta= bigl|lambda_1^{(k+1)}- lambda_1^{(k)}bigr|leqslant varepsilon[/math], процесс завершить и положить [math]lambda_1cong lambda_1^{k+1}[/math]. Если [math]Delta>varepsilon[/math], положить [math]k=k+1[/math] и перейти к пункту 3.

---

Замечания

1. Процесс последовательных приближений

[math]begin{aligned}&X^{1(1)}= AX^{1(0)},quad X^{1(2)}= AX^{1(1)}= A^{2}X^{1(0)},quad ldots,\ &X^{1(k)}= AX^{1(k-1)}= AA^{k-1}X^{1(0)}= A^kX^{1(0)},quad ldots end{aligned}[/math]

сходится, т.е. при [math]xtoinfty[/math] вектор [math]X^{1(k)}[/math] стремится к собственному вектору [math]X^1[/math]. Действительно, разложим [math]X^{1(0)}[/math] по всем собственным векторам: [math]textstyle{X^{1(0)}= sumlimits_{i=1}^{n} c_iX^i}[/math]. Так как, согласно (2.4), [math]AX^i= lambda_iX^i[/math], то

[math]begin{aligned}& AX^{1(0)}= X^{1(1)}= sumlimits_{i=1}^{n} c_i lambda_iX^i,quad AX^{1(1)}= A^2X^{1(0)}= X^{1(2)}= sumlimits_{i=1}^{n} c_i lambda_i^2X^i,quad ldots\ &A^kX^{1(0)}= X^{1(k)}= sumlimits_{i=1}^{n} c_i lambda_i^kX^i= lambda_1^k! left[c_1X^1+ c_2{left(frac{lambda_2}{lambda_1}right)!}^k X^2+ ldots+ c_n{left(frac{lambda_n}{lambda_1}right)!}^k X^nright]!. end{aligned}[/math]

При большом [math]k[/math] дроби [math]{left(frac{lambda_2}{lambda_1}right)!}^k, ldots, {left(frac{lambda_n}{lambda_1}right)!}^k[/math] малы и поэтому [math]A^kX^{1(0)}= c_1lambda_1^kX^1[/math], то есть [math]X^{1(k)}to X^1[/math] при [math]ktoinfty[/math]. Одновременно [math]lambda_1= limlimits_{ktoinfty} frac{x_{i}^{1(k+1)}}{x_{i}^{1(k)}}[/math].

2. Вместо применяемой в пункте 4 алгоритма формулы для [math]lambda_1^{(k+1)}[/math] можно взять среднее арифметическое соответствующих отношений для разных координат.

3. Метод может использоваться и в случае, если наибольшее по модулю собственное значение матрицы [math]A[/math] является кратным, т.е.

[math]lambda_1= lambda_2= ldots= lambda_s[/math] и [math]bigl|lambda_1bigr|> bigl|lambda_kbigr|[/math] при [math]k>s[/math].

4. При неудачном выборе начального приближения [math]X^{1(0)}[/math] предел отношения [math]frac{x_i^{1(k+1)}}{x_i^{1(k)}}[/math] может не существовать. В этом случае следует задать другое начальное приближение.

5. Рассмотренный итерационный процесс для [math]lambda_1[/math] сходится линейно, с параметром [math]c=frac{lambda_2}{lambda_1}[/math] и может быть очень медленным. Для его ускорения используется алгоритм Эйткена.

6. Если [math]A=A^T[/math] (матрица [math]A[/math] симметрическая), то сходимость процесса при определении [math]rho(A)[/math] может быть ускорена.

7. Используя [math]lambda_1[/math], можно определить следующее значение [math]lambda_2[/math] по формуле [math]lambda_2= frac{x_i^{1(k+1)}- lambda_1 x_i^{1(k)}}{x_i^{1(k)}- lambda_1 x_i^{1(k-1)}}~ (i=1,2,ldots,n)[/math]. Эта формула дает грубые значения для [math]lambda_2[/math], так как значение [math]lambda_1[/math] является приближенным. Если модули всех собственных значений различны, то на основе последней формулы можно вычислять и остальные [math]lambda_j~(j=3,4,ldots,n)[/math].

8. После проведения нескольких итераций рекомендуется “гасить” растущие компоненты получающегося собственного вектора. Это осуществляется нормировкой вектора, например, по формуле [math]frac{X^{1(k)}}{|X^{1(k)}|_1}[/math].

Пример 2.3. Для матрицы [math]A=begin{pmatrix}5&1&2\ 1&4&1\ 2&1&3 end{pmatrix}[/math] найти спектральный радиус степенным методом с точностью [math]varepsilon=0,,1[/math].

Решение

Пример 2.4. Найти максимальное по модулю собственное значение матрицы [math]A=begin{pmatrix}2&-1&1\ -1&2&-1\ 0&0&3 end{pmatrix}[/math] и соответствующий собственный вектор.

Решение

---

Метод вращений для нахождения собственных значений

Метод используется для решения полной проблемы собственных значений симметрической матрицы и основан на преобразовании подобия исходной матрицы [math]Ainmathbb{R}^{ntimes n}[/math] с помощью ортогональной матрицы [math]H[/math].

Напомним, что две матрицы [math]A[/math] и [math]A^{(i)}[/math] называются подобными ([math]Asim A^{(i)}[/math] или [math]A^{(i)}sim A[/math]), если [math]A^{(i)}=H^{-1}AH[/math] или [math]A=HA^{(i)}H^{-1}[/math], где [math]H[/math] — невырожденная матрица.

В методе вращений в качестве [math]H[/math] берется ортогональная матрица, такая, что [math]HH^{T}=H^{T}H=E[/math], т.е. [math]H^{T}=H^{-1}[/math]. В силу свойства ортогонального преобразования евклидова норма исходной матрицы [math]A[/math] не меняется. Для преобразованной матрицы [math]A^{(i)}[/math] сохраняется ее след и собственные значения [math]lambda_icolon[/math]

[math]operatorname{tr}A= sum_{i=1}^{n}a_{ii}= sum_{i=1}^{n} lambda_i(A)= operatorname{tr}A^{(i)}.[/math]

При реализации метода вращений преобразование подобия применяется к исходной матрице [math]A[/math] многократно:

Формула (2.6) определяет итерационный процесс, где начальное приближение [math]A^{(0)}=A[/math]. На k-й итерации для некоторого выбираемого при решении задачи недиагонального элемента [math]a_{ij}^{(k)},~ ine j[/math], определяется ортогональная матрица [math]H^{(k)}[/math], приводящая этот элемент [math]a_{ij}^{(k+1)}[/math] (а также и [math]a_{ji}^{(k+1)}[/math]) к нулю. При этом на каждой итерации в качестве [math]a_{ij}^{(k+1)}[/math] выбирается наибольший по модулю. Матрица [math]H^{(k)}[/math] называемая матрицей вращения Якоби, зависит от угла [math]varphi^{(k)}[/math] и имеет вид

В данной ортогональной матрице элементы на главной диагонали единичные, кроме [math]h_{ii}^{(k)}= cosvarphi^{(k)}[/math] и [math]h_{jj}^{(k)}=cosvarphi^{(k)}[/math], а остальные элементы нулевые, за исключением [math]h_{ij}^{(k)}=-sinvarphi^{(k)}[/math], [math]h_{ji}^{(k)}=sinvarphi^{(k)}[/math] ([math]h_{ij}[/math] -элементы матрицы [math]H[/math]).

Угол поворота [math]varphi^{(k)}[/math] определяется по формуле

где [math]|2varphi^{(k)}|leqslant frac{pi}{2},~ i<j[/math] ([math]a_{ij}[/math] выбирается в верхней треугольной наддиагональной части матрицы [math]A[/math]).

В процессе итераций сумма квадратов всех недиагональных элементов [math]sigms(A^{(k)})[/math] при возрастании [math]k[/math] уменьшается, так что [math]sigms(A^{(k+1)})< sigma(A^{(k)})[/math]. Однако элементы [math]a_{ij}^{(k)}[/math] приведенные к нулю на k-й итерации, на последующей итерации немного возрастают. При [math]ktoinfty[/math] получается монотонно убывающая ограниченная снизу нулем последовательность [math]sigma(A^{(1)})> sigma(A^{(2)})> ldots> sigma(A^{(k)})>ldots[/math]. Поэтому [math]sigma(A^{(k)})to0[/math] при [math]ktoinfty[/math]. Это и означает сходимость метода. При этом [math]A^{(k)}to Lambda= operatorname{diag}(lambda_1,ldots,lambda_n)[/math].

Замечание. В двумерном пространстве с введенной в нем системой координат [math]Oxy[/math] с ортонормированным базисом [math]{vec{i},vec{j}}[/math] матрица вращения легко получается из рис. 2.1, где система координат [math]Ox’y'[/math] повернута на угол [math]varphicolon[/math]

[math]begin{cases}vec{i},’= vec{i}cos varphi+ vec{j}sin varphi,\[2pt] vec{j},’=-vec{i}sin varphi+ vec{j}cos varphi. end{cases}[/math]

Таким образом, для компонент [math]vec{i},’,, vec{j},'[/math] будем иметь [math]bigl(vec{i},’,vec{j},’bigr)= bigl(vec{i},vec{j}bigr)cdot! begin{pmatrix} cos varphi&-sin varphi\ sin varphi& cos varphiend{pmatrix}[/math]. Отсюда следует, что в двумерном пространстве матрица вращения имеет вид [math]H= begin{pmatrix} cos varphi&-sin varphi\ sin varphi& cos varphiend{pmatrix}[/math]. Отметим, что при [math]n=2[/math] для решения задачи требуется одна итерация.

---

Алгоритм метода вращений

1. Положить [math]k=0,~ A^{(0)}=A[/math] и задать [math]varepsilon>0[/math].

2. Выделить в верхней треугольной наддиагональной части матрицы [math]A^{(k)}[/math] максимальный по модулю элемент [math]a_{ij}^{(k)},~ i<j[/math].

Если [math]|a_{ij}^{(k)}|leqslant varepsilon[/math] для всех [math]ine j[/math], процесс завершить. Собственные значения определяются по формуле [math]lambda_i(A^{(k)})=a_{ii}^{(k)},~ i=1,ldots,n[/math].

Собственные векторы [math]X^i[/math] находятся как i-e столбцы матрицы, получающейся в результате перемножения:

[math]nu_k= H^{(0)}cdot H^{(1)}cdot H^{(2)}cdot ldotscdot H^{(k-1)}= bigl( X^1,X^2,X^3,ldots,X^nbigr).[/math]

Если [math]bigl|a_{ij}^{(k)}bigr|>varepsilon[/math], процесс продолжается.

3. Найти угол поворота по формуле [math]varphi^{(k)}= frac{1}{2} operatorname{arctg} frac{2a_{ij}^{(k)}}{a_{ii}^{(k)}-a_{jj}^{(k)}}[/math].

4. Составить матрицу вращения [math]H^{(k)}[/math].

5. Вычислить очередное приближение [math]A^{(k+1)}= bigl(H^{(k)}bigr)^T A^{(k)} H^{(k)}[/math].Положить [math]k=k+1[/math] и перейти к пункту 2.

Замечания

1. Используя обозначение [math]overline{P}_k= frac{2a_{ij}^{(k)}}{a_{ii}^{(k)}-a_{jj}^{(k)}}[/math], можно в пункте 3 алгоритма вычислять элементы матрицы вращения по формулам

[math]sinvarphi^{(k)}= operatorname{sign}overline{P}_kcdot sqrt{frac{1}{2}!left(1-frac{1}{sqrt{1+overline{P}_{k}^{;2}}}right)},,qquad cosvarphi^{(k)}= sqrt{frac{1}{2}!left(1+ frac{1}{sqrt{1+overline{P}_{k}^{;2}}}right)},.[/math]

2. Контроль правильности выполнения действий по каждому повороту осуществляется путем проверки сохранения следа преобразуемой матрицы.

3. При [math]n=2[/math] для решения задачи требуется одна итерация.

Пример 2.5. Для матрицы [math]A=begin{pmatrix} 2&1\1&3 end{pmatrix}[/math] методом вращений найти собственные значения и собственные векторы.

Решение

Пример 2.6. Найти собственные значения и собственные векторы матрицы [math]A=begin{pmatrix}5&1&2\ 1&4&1\ 2&1&3 end{pmatrix}[/math].

Решение

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Лекция Итерационные методы решения
системы алгебраических линейных
уравнений.

Условие
сходимости итерационного процесса.
Метод
Якоби. Метод
Зейделя

Метод
простой итерации

Рассматривается система линейных
алгебраических уравнений

Ax = b

Для применения итерационных методов
система должна быть приведена к
эквивалентному виду

x=Bx+d.

Затем выбирается начальное приближение
к решению системы уравнений

и находится последовательность
приближений к корню.

Для сходимости итерационного процесса
достаточно, чтобы было выполнено условие

(норма матрицы). Критерий окончания
итераций зависит от применяемого
итерационного метода.

Метод Якоби.

Самый простой способ приведения системы
к виду, удобному для итерации, состоит
в следующем:

Из первого уравнения системы выразим
неизвестное x₁, из второго
уравнения системы выразим x₂,
и т. д.

В результате получим систему уравнений
с матрицей B, в которой на главной
диагонали стоят нулевые элементы, а
остальные элементы вычисляются по
формулам:

Компоненты вектора d вычисляются по
формулам:

Расчетная формула метода простой
итерации имеет вид:

или в покоординатной форме записи
выглядит так:

Критерий окончания итераций в методе
Якоби имеет вид:

Если
,
то можно применять более простой критерий
окончания итераций

Пример 1. Решение системы линейных
уравнений методом Якоби.

Пусть дана система уравнений:

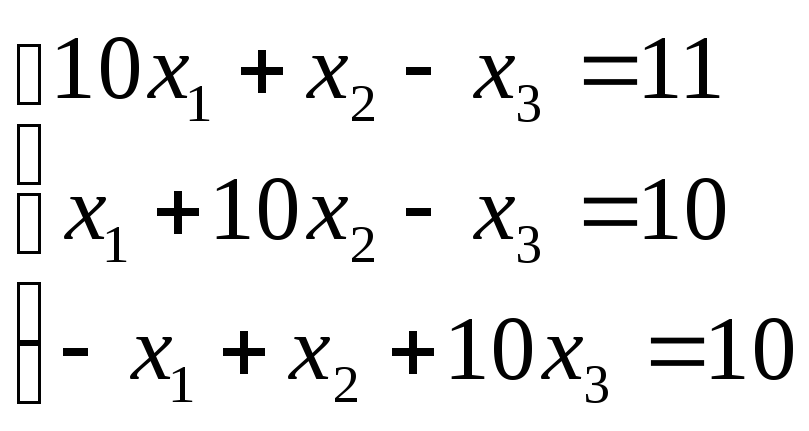
Требуется найти решение системы с
точностью

Приведем систему к виду удобному для
итерации:

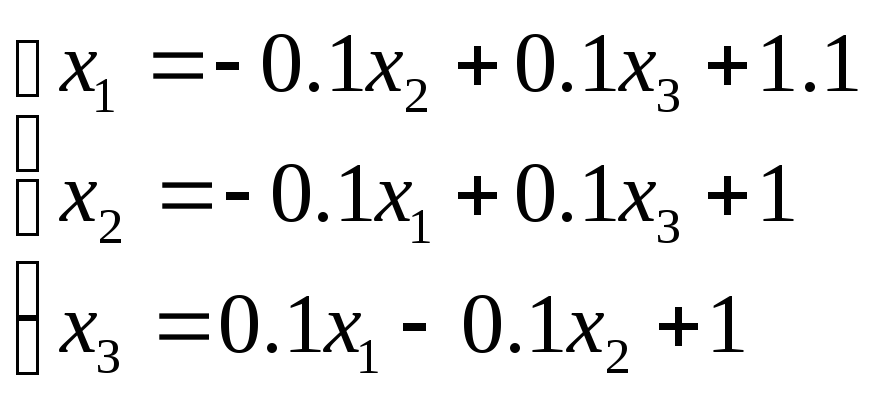
Выберем начальное приближение, например,

– вектор правой части.

Тогда первая итерация получается так:

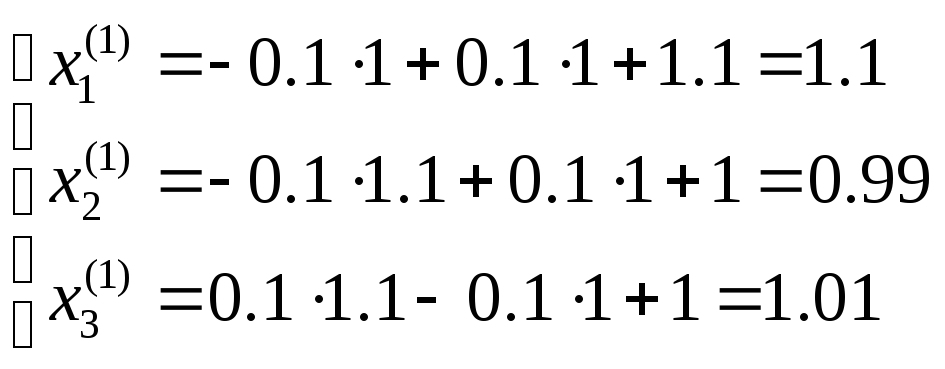
Аналогично получаются следующие
приближения к решению.

Найдем норму матрицы B.

Будем использовать норму

Так как сумма модулей элементов в каждой
строке равна 0.2, то
,
поэтому критерий окончания итераций в
этой задаче

Вычислим нормы разностей векторов:

Так как

заданная точность достигнута на четвертой
итерации.

Ответ: x₁
= 1.102, x₂ =
0.991, x₃ =
1.011

Метод Зейделя.

Метод можно рассматривать как модификацию
метода Якоби. Основная идея состоит в
том, что при вычислении очередного
(n+1)-го приближения к неизвестному
x_i при
i >1 используют
уже найденные (n+1)-е приближения к
неизвестным x₁, x₂,
…, x_{i – 1}, а не n-ое приближение,
как в методе Якоби.

Расчетная формула метода в покоординатной
форме записи выглядит так:

Условия сходимости и критерий окончания
итераций можно взять такими же, как в
методе Якоби.

Пример 2. Решение систем линейных
уравнений методом Зейделя.

Рассмотрим параллельно решение 3-х
систем уравнений:

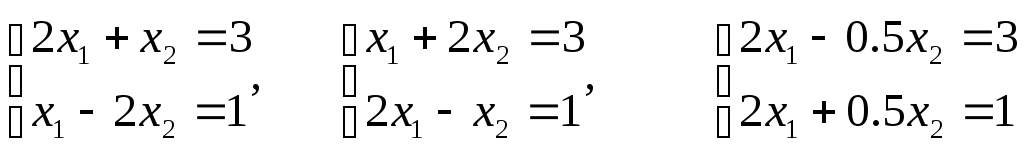
Приведем системы к виду удобному для
итераций:

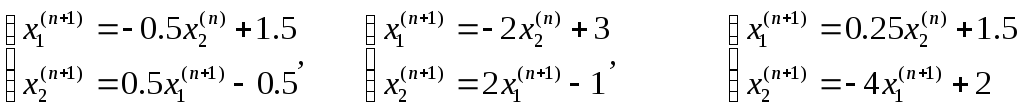
Заметим, что условие сходимости

выполнено только для первой системы.
Вычислим 3 первых приближения к решению
в каждом случае.

1-ая система:

Точным решением будут значения: x₁
= 1.4, x₂ = 0.2.
Итерационный процесс сходится.

2-ая система:

Видно, что итерационный процесс
расходится.

Точное решение x ₁ =
1, x ₂ = 0.2.

3-я система:

Видно, что итерационный процесс
зациклился.

Точное решение x ₁ =
1, x ₂
= 2.

Пусть матрица системы уравнений A –
симметричная и положительно определенная.
Тогда при любом выборе начального
приближения метод Зейделя сходится.
Дополнительных условий на малость нормы
некоторой матрицы здесь не накладывается.

Метод простой итерации.

Если A – симметричная и положительно
определенная матрица, то систему
уравнений часто приводят к эквивалентному
виду:

x = x -τ (Ax – b), τ – итерационный
параметр.

Расчетная формула метода простой
итерации в этом случае имеет вид:

x ⁽ⁿ⁺¹⁾ = x
ⁿ – τ (Ax ⁽ⁿ⁾
– b).

Здесь

B = E – τ A

и параметр τ > 0 выбирают так, чтобы по
возможности сделать минимальной величину

Пусть λ_min
и λ_max
– минимальное и максимальное
собственные значения матрицы A. Оптимальным
является выбор параметра

В этом случае

принимает минимальное значение равное:

Пример
3. Решение систем линейных уравнений
методом простой итерации. (в MathCAD)

Пусть дана система уравнений Ax = b

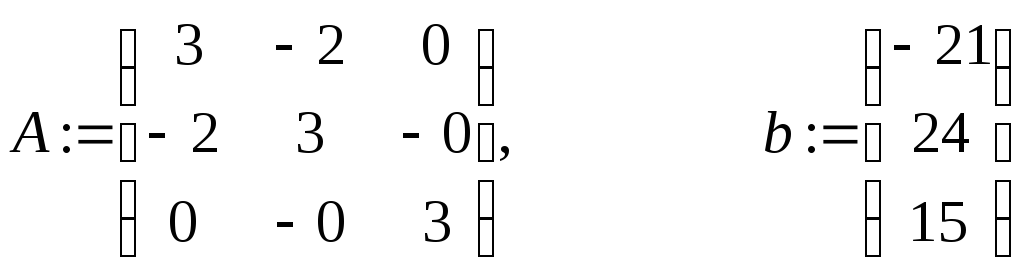
1. Для построения итерационного процесса
   найдем собственные числа матрицы A:

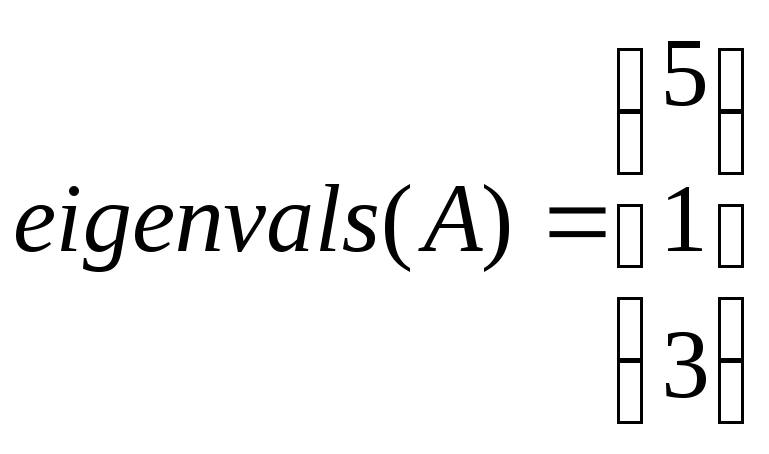
– используется встроенная функция для
нахождения собственных чисел.

1. Вычислим итерационный параметр и
   проверим условие сходимости

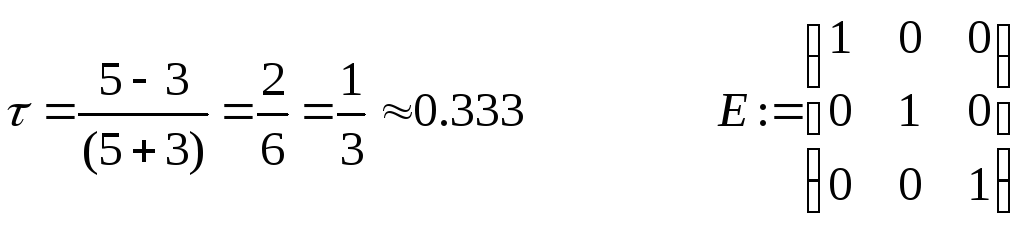
– условие сходимости выполнено.

1. Возьмем начальное приближение – вектор
   x0, зададим точность 0.001 и найдем начальные
   приближения по приведенной ниже
   программе:

Точное решение

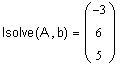
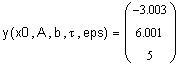
Замечание. Если в программе возвращать
матрицу rez, то можно просмотреть все
найденные итерации.

6

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Для решения систем линейных алгебраических уравнений (СЛАУ) большой размерности, а также систем, имеющих разреженные матрицы, применение точных методов (например, метод Гаусса) не является целесообразным, так как сказывается ограниченность разрядной сетки и накапливается погрешность округления.

Система с разреженной матрицей получается, например, при составлении системы уравнений теплового баланса технологической схемы или же при численном расчете потенциалов из дифференциального уравнения Гельмгольца на равномерной сетке. Есть и другие примеры, которые приводят нас к необходимости решать СЛАУ с разряженной матрицей.

Рассмотрим здесь простейший метод решения линейных систем – метод простых итераций.

Так как я не люблю сложные теоретические усложнения, то начну с простого примера системы с тремя неизвестными.

Допустим, у вас есть следующая система уравнений:

В матричном виде эту систему можно было бы записать так:

Выразим из 1-го уравнения системы первую неизвестную x1
Выразим из 2-го уравнения системы вторую неизвестную x2
Выразим из 3-го уравнения системы третью неизвестную x3

Заметим, что элементы, лежащие на главное диагонали матрицы не должны быть нулевые. Ну а если такое случается, то надо переставлять местами уравнения, так, чтобы выполнялось условие неравенства нулю диагональных элементов.

Итак, все эти три уравнения мы можем записать общей формулой, если перейдем к индексам: первый индекс будет пробегать по строкам, а второй по столбцам. В нашей теории нумерация начинается с 1.

Обратите внимание, что в скобках, где находится сумма произведений, не встречается элемента с совпадающими индексами (тот а[k][k] который лежит на диагонали), поэтому при суммировании мы должны его пропустить.

В принципе, этот пропуск можно реализовать конструкцией continue при программировании алгоритма. Но если вам это не нравится, то общую формулу суммы можно переписать в другом виде:

Постараюсь сделать схему решения еще более понятной для программирования:

Важные уточнения:

columns – количество столбцов
k – текущий корень системы, совпадает с номером строки матрицы
i – номер столбца, индекс, по которому проводится суммирование
x[i] – старые корни, полученные на предыдущей итерации
x[k] – новый корень, которые считается на базе корней, полученных на предыдущей итерации

Ещё хочется обратить ваше внимание на то, что во многих языках программирования принято начинать нумерацию с нуля (!). Поэтому в наших формулах произойдет сдвиг индекса, это нужно не забыть исправить, чтобы не выйти за диапазон изменения допустимых значений индекса при записи решения в массив / список / вектор.

Иногда, в книгах по численным методам еще используется верхний индекс (чаще всего в скобках, чтоб не спутали со степенью), чтобы разграничить где решение на новой итерации, а где решение на предыдущей итерации.

У нас получается рекуррентная формула:

На мой взгляд, не нужно особо обращать внимание на верхние индексы, показывающие где новая итерация, а где старая. Так как начинающих это только сбивает с толку. В реальной программе это будет перезапись одной и той же переменной, БЕЗ как либо верхних индексов.

Приведу очень простой пример, почему на практике не нужны загромождения верхними индексами для рекуррентной формулы:

Теперь опять вернемся к нашей задаче. Итерационный процесс можно запустить до бесконечности и далее… Шучу, нельзя. Компилятор быстро спустит вас с небес на землю! Но когда останавливаться? Теория говорит нам, что можно остановиться при достижении необходимой точности.

Точность часто обозначается буквой экспилон ε, ну а в программировании взяли за правило обозначать eps ( сокращение от epsilon ), так как греческими буквами нам нельзя пользоваться при написании названий переменных.

Для остановки и проверки точности, а также завершения вычислений на основе вычисления расстояния между соседними элементами в последовательности итераций можно воспользоваться Евклидовой метрикой.

В этом случае, условие завершения вычислений следующее:

По сути, это что-то вроде относительной погрешности, учитывающий все решения, а именно среднеквадратичные отклонения, чтобы исключить влияние знака. Потому что при сложении абсолютных разниц у нас могла произойти иллюзия достижения необходимой точности и иллюзия маленького разброса, если бы одна разница была бы большой со знаком “+”, а другая разница примерно такой же большой, но со знаком “-“. Они бы просто друг друга аннигилировали и дали бы нам ложный результат. Именно поэтому используются квадраты отклонений, а потом уже накладывается корень.

Для того, чтобы мы могли считать Евклидову метрику на каждой итерации, нам необходимо сохранять вектор решения на предыдущей итерации. То есть считая новый набор корней на новой итерации, мы должны сохранить старый набор корней на предыдущей итерации, чтобы было потом с чем сравнивать.

На практике же, я бы посоветовал помимо погрешности ограничивать выполнения цикла каким-либо предельным количеством итераций. Например, чтобы максимальное число итераций было 100~500. Для адекватной сходимости этого достаточно за глаза. Так как, если метод сходится, то система достигает нужной точности примерно за 20-50 итераций (чаще всего, если точность eps = 0.0001).

Уже совсем другое дело, если решение расходится. Именно тогда вас спасает ограничение по числу итераций, чтобы не войти в бесконечный цикл.

Следует отметить, что скорость сходимости итерационного процесса выше для матриц, у которых элементы главной диагонали велики по сравнению с внедиагональными элементами. В связи с этим, перед началом численного решения задачи желательно преобразовать систему уравнений так, чтобы преобладали диагональные элементы.

Также, чтобы запустить рекуррентную формулу и начать любой метод итераций, нам нужно начальное приближение корней. Можно взять любое, но в разумных пределах. К примеру, можно использовать столбец свободных коэффициентов в матричном представлении системы. Или просто обнулить начальное приближение. Или везде поставить единицы. Если метод будет сходиться, то он в любом случае придет к корням с нужным приближением.

Порядок решения СЛАУ методом Якоби такой:
● Приведение системы уравнений к виду, в котором на каждой строчке выражено какое-либо неизвестное значение системы.
● Произвольный выбор нулевого решения, в качестве него можно взять вектор-столбец свободных членов.
● Производим подстановку произвольного нулевого решения в систему уравнений, полученную под пунктом 1.
● Осуществление дополнительных итераций, для каждой из которых используется решение, полученное на предыдущем этапе.

Итак, теперь всё сказано и можно приступать к реализации.

Я набросаю алгоритм на Python:

https://pastebin.com/PhemwtGX

Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram

Тема  3.  Решение  систем  линейных  алгебраических  уравнений  итерационными  методами.

Описанные  выше  прямые  методы  решения  СЛАУ  не  очень  эффективны  при  решении  систем  большой  размерности  (т.е.  когдо  значение  n  достаточно  велико).  Для  решения  СЛАУ  в  таких  случаях  больше  подходят  итерационные  методы

Итерационные  методы  решения  СЛАУ  (их  второе  название  –  методы  последовательного  приближения  к  решению)  не  дают  точного  решения  СЛАУ,  а  дают  только  приближение  к  решению,  причем  каждое  следующее  приближение  получается  из  предыдущего  и  является  более  точным,  чем  предыдущее   (при  условии,  что  обеспечена  сходимость  итераций).  Начальное  (или,  так  называемое,  нулевое)  приближение  выбирается  вблизи  предполагаемого  решения  или  произвольно  (в  качестве  его  можно  взять  вектор  правой  части  системы).  Точное  решение  находится  как  предел  таких  приближений  при  стремлении  их  количества  к  бесконечности.  Как  правило,  за  конечное  число  шагов  (т.е.  итераций)  этот  предел  не  достигается.  Поэтому,  на  практике,  вводится  понятие  точности  решения,  а  именно  задается  некоторое  положительное  и  достаточно  малое  число  e  и  процесс  вычислений  (итераций)  проводят  до  тех  пор,  пока  не  будет  выполнено  соотношение    .

Здесь   –  приближение  к  решению,  полученное  после  итерации  номер  n,   а  –  точное  решение  СЛАУ  (которое  заранее  неизвестно).  Число  итераций  n=n(e),   необходимое  для  достижения  заданной  точности  для  конкретных  методов  можно  получить  из  теоретических  рассмотрений  (т. е.  для  этого  имеются  расчетные  формулы).  Качество  различных  итерационных  методов  можно  сравнить  по  необходимому  числу  итераций  для  достижения  одной  и  той  же  точности.

            Для  исследования  итерационных  методов  на  сходимость  необходимо  уметь  вычислять  нормы  матриц.   Норма  матрицы  –  это  некая  числовая  величина,  характеризующая  величину  элементов  матрицы  по  абсолютной  величине.   В  высшей  математике  имеется  несколько  различных  видов  норм  матриц,  которые,  как  правило,  являются  эквивалентными.  В  нашем  курсе  мы  будем  пользоваться  только  одной  из  них.  А  именно,  под  нормой  матрицы  мы  будем  понимать  максимальную  величину  среди  сумм  абсолютных  величин  элементов  отдельных  строк  матрицы.  Для  обозначения  нормы  матрицы  –  ее  название  заключается  в  две  пары  вертикальных  черточек.  Так,  для  матрицы  A  под  ее  нормой  будем  понимать  величину

                                          .                                                      (3.1)

Так,  к  примеру,  норма  матрицы  А  из  примера  1  находится  следующим  образом :

            .

Рекомендуемые материалы

Наиболее  широкое  применение  для  решения  СЛАУ  получили  три  итерационных  метода

– метод  простой  итерации

– метод  Якоби

– метод  Гуасса-Зейделя.

Метод  простой  итерации  предполагает  переход  от  записи  СЛАУ  в  исходном  виде  (2.1)  к  записи  ее  в  виде 

                                        (3.2)

или,  что  тоже,  в  матричном  виде, 

                                               x = С×x + D,                                                                                    (3.3)

где  :

   C  –  матрица  коэффициентов  преобразованной  системы  размерности  n´n

    x  –  вектор  неизвестных,  состоящий  из  n  компонент

   D  –   вектор  правых  частей  преобразованной  системы,  состоящий  из  n  компонент.

Система  в  виде  (3.2)  может  быть  представлена  в  сокращенном  виде

                    

Исходя  из  этого  представления  формула  простой  итерации  будет  иметь  вид

                                                          (3.4)

где  m  –  номер  итерации,   а      –  значение  x_j  на  m-ом  шаге  итерации.  Тогда,  если  процесс  итераций  сходится,  с  увеличением  количества  итераций  будет  наблюдаться 

             

Доказано,  что  процесс  итераций    сходится,  если  норма  матрицы  D  будет  меньше  единицы.

            Если  за  начальное  (нулевое)  приближение  взять  вектор  свободных  членов,  т.е.  x⁽⁰⁾  = D,  то  величина  погрешности  имеет  вид

                                                                                   (3.5)

здесь под  x^*  понимается  точное  решение  системы.   Следовательно, 

если   ,  то  по  заданной  точности  e  можно  заранее  расчитать  необходимое  количество  итераций.  А  именно,  из  соотношения 

                                         

после  небольших  преобразований  получим

                                      .                                                              (3.6)

При  выполнении  такого количества  итераций  гарантировано  будет  обеспечена  заданная  точность  нахождения  решения  системы.  Эта  теоретическая  оценка  необходимого  количества  шагов  итерации  несколько  завышена.  На практике  необходимая  точность  может  быть  достигнута  за  меньшее  количество  итераций.

            Поиск  решений  заданной  СЛАУ  методом  простой  итерации  удобно  производить  с  занесением  полученных  результатов  в  таблицу  следующего  вида :

Следует  особо  отметить,  что  в  решении  СЛАУ  этим  методом  наиболее  сложным  и  трудоемким  является  выполнение  преобразования  системы  из  вида  (2.1)  к  виду  (3.2).  Эти  преобразования  должны  быть  эквивалентными,  т.е.  не  меняющими  решения  исходной  системы,  и  обеспечивающие  величину  нормы  матрицы  C  (после  выполнения  их) меньшей  единицы.   Единого  рецепта  для  выполнения  таких  преобразований  не  существует.  Здесь  в  каждом  конкретном  случае  необходимо  проявлять  творчество.  Рассмотрим  примеры,  в  которых  будут  приведены  некоторые  способы  преобразования  системы  к  необходимому  виду.

Пример 1.  Найдем  решение  системы  линейных  алгебраических  уравнений  методом  простой  итерации  (с  точностью  e=0.001)

    

Эта  система  приводится  к  необходимому  виду  простейшим  способом.  Перенесем  все  слагаемые  из  левой  части  в  правую,   а  затем  к  обоим  частям  каждого  уравнения  прибавим  по  x_i  (i=1, 2, 3, 4).  Получим  преобразованную  систему  следующего  вида

                  .

            Матрица  C  и  вектор  D  в  этом  случае  будут  следующими

                  C =  ,        D =  .

Вычислим  норму  матрицы C.  Получим

                

Так  как  норма  оказалась  меньшей  единицы  –  сходимость  метода  простой  итерации  обеспечена.   В  качестве  начального  (нулевого)  приближения  примем  компоненты  вектора  D.   Получим

                     ,   ,   ,   .

По  формуле  (3.6)  вычислим  необходимое  число  шагов  итерации.   Определим  сначала  норму  вектора  D.  Получим

                                   

Тогда

                             .

Следовательно,  для  достижения  заданной  точности  необходимо  выполнить  не  менее  17  итераций.  Выполним  первую  итерацию.  Получим

                             

или

                            

    Выполнив  все  арифметические  операции,  получим 

                                                   .

Продолжая  аналогично,  выполним  дальнейшие  шаги  итераций.  Результаты  их  сведем  в  следующую  таблицу   (D –  наибольшая  величина  изменения   компонент  решения  между  текущим  и  предыдущим  шагами)

            Так  как  уже  после  десятого  шага  разность  между  значениями  на  двух  последних  итерациях  стала  меньше  заданной  точности  –  процесс  итераций  прекратим.   В  качестве  найденного  решения  примем  значения,  полученные  на  последнем  шаге.

Пример 2.   Преобразуем  систему  уравнений

к  виду,  который  позволил  бы  использовать  при  ее  решении  метод  простой  итерации.

            Поступим  сначала  аналогично  предыдущему  примеру.  Получим

Матрица  C  такой  системы  будет

                                                    C =.

Вычислим  ее  норму.  Получим

                                                   

Очевидно,  что  итерационный  процесс  для  такой  матрицы  сходящимся  не  будет.  Необходимо  найти  иной  способ  преобразования  заданной  системы  уравнений. 

            Переставим  в  исходной  системе  уравнений  отдельные  ее  уравнения  так,  чтобы  третья  строка  стала  первой,  первая  –  второй,  вторая  –  третьей.  Тогда,  преобразуя  ее  тем  же  способом,  получим

Матрица  C  такой  системы  будет

                                                   C =.

Вычислим  ее  норму.   Получим

                                                  

Так  как   норма  матрицы C  оказалась  меньшей  единицы,  преобразованная  таким  образом  система  пригодна  для  решения  методом  простой  итерации.

Пример 3.   Преобразуем  систему  уравнений

к  виду,  который  позволил  бы  использовать  при  ее  решении  метод  простой  итерации.

            Поступим  сначала  аналогично  примеру  1.  Получим

Матрица  C  такой  системы  будет

                                       C =.

Вычислим  ее  норму.   Получим

                                      

Очевидно,  что  итерационный  процесс  для  такой  матрицы  сходящимся  не  будет.  

            Для  преобразования  исходной  матрицы  к  виду,  удобному  для  применения  метода  простой  итерации  поступим  следующим  образом.  Сначала  образуем  “промежуточную”  систему  уравнений,  в  которой 

– первое  уравнение  является  суммой  первого  и  второго  уравнений  исходной  системы

– второе  уравнение  –  суммой  удвоенного  третьего  уравнения  со  вторым  за  вычетом  первого

– третье  уравнение  –  разность  третьего  и  второго  уравнений  исходной  системы.

В  результате  получим  эквивалентную  исходной  “промежуточную”  систему  уравнений

Из  нее  несложно  получить  еще  одну  систему  “промежуточную”  систему

      ,

а  из  нее  преобразованную

         .

Матрица  C  такой  системы  будет

                                              C =.

Вычислим  ее  норму.   Получим

                                      

Итерационный  процесс  для  такой  матрицы  будет  сходящимся.

Метод  Якоби  предполагает,  что  все  диагональные  элементы  матрицы    A  исходной  системы  (2.2)  не  равны  нулю.  Тогда  исходную  систему  можно  переписать  в  виде

                                                                    (3.7)

Из  такой  записи  системы  образована  итерационная  формула  метода  Якоби

                       .                   (3.8)

Условием  сходимости  итерационного  процесса  метода  Якоби  является  так  называемое  условие  доминирования  диагонали  в  исходной  системе  (вида  (2,1)).  Аналитически  это  условие  записывается  в  виде

               .                                                       (3.9)

Следует  отметить,  что   если  в  заданной  системе  уравнений  условие  сходимости  метода  Якоби  (т.е.  условие  доминирования  диагонали)  не  выполняется,  во  многих  случаях  можно  путем  эквивалентных  преобразований  исходной  СЛАУ  привести  ее  решение  к  решению  эквивалентной  СЛАУ,  в  которой  это  условие  выполняется. 

Пример 4.   Преобразуем  систему  уравнений

к  виду,  который  позволил  бы  использовать  при  ее  решении  метод  Якоби. 

            Эту  систему  мы  уже  рассматривали  в  примере  3,  поэтому  перейдем  от  нее  к  полученной  там  “промежуточной”  системе  уравнений.  Легко  установить,  что  у  нее  условие  доминирования  диагонали  выполняется,  поэтому  преобразуем  ее  к  виду,  необходимому  для  применения  метода  Якоби.  Получим

Из  нее  получаем  формулу  для  выполнения  вычислений  по  методу  Якоби  для  заданной  СЛАУ

                            

Взяв  за  начальное,  т.е.  нулевое,  приближение  вектор  свободных  членов  выполним  все  необходимые  вычисления.  Результаты  сведем  в  таблицу

Довольно  высокая  точность  полученного  решения  достигнута  за  шесть  итераций.

Метод  Гаусса-Зейделя  является  усовершенствованием  метода  Якоби  и  также  предполагает,  что  все  диагональные  элементы  матрицы    A  исходной  системы  (2.2)  не  равны  нулю.  Тогда  исходную  систему  можно  переписать  в  виде  аналогичном  методу  Якоби,  но  несколько  отличном  от  него

                               .    

Здесь  важно  помнить,  что  если  в  знаке  суммирования  верхний  индекс  меньше  нижнего,  то  никакого  суммирования  не  производится.

Идея  метода  Гаусса-Зейделя  заключается  в  том,  что  авторы  метода  усмотрели  возможность  ускорить  процесс  вычислений  по  отношению  к  методу  Якоби  за  счет  того,  что  в  процессе  очередной  итерации  найдя  новое  значение  x₁  можно  сразу  же  использовать  это  новое  значение  в  этой  же  итерации  для  вычисления  остальных  переменных.  Аналогично  этому,  дальше,  найдя  новое  значение  x₂  можно его  также  сразу  использовать  в  этой  же  итерации  и  т.д.

            Исходя  из  этого,  формула  итераций  для  метода  Гаусса-Зейделя  имеет  следующий  вид

               .         (3.10)

Достаточным  условием  сходимости  итерационного  процесса  метода  Гаусса-Зейделя  является  все  то  же  условие  доминирования  диагонали  (3.9).   Скорость  сходимости  этого  метода  несколько  выше,  чем  в  метода  Якоби.

Пример 5.   Решим  методом  Гаусса-Зейделя  систему  уравнений

            Эту  систему  мы  уже  рассматривали  в  примерах  3  и  4,  поэтому  сразу  перейдем  от  нее  к  преобразованой  системе  уравнений  (см.  пример  4),  в  которой  условие  доминирования  диагонали  выполняется.  Из  нее  получаем  формулу  для  выполнения  вычислений  по  методу  Гаусса-Зейделя 

Взяв  за  начальное  (т.е.  нулевое)  приближение  вектор  свободных  членов,  выполним  все  необходимые  вычисления.  Результаты  сведем  в  таблицу

Довольно  высокая  точность  полученного  решения  достигнута  за  пять  итераций.