 Рис.2.8.
Рис.2.8.
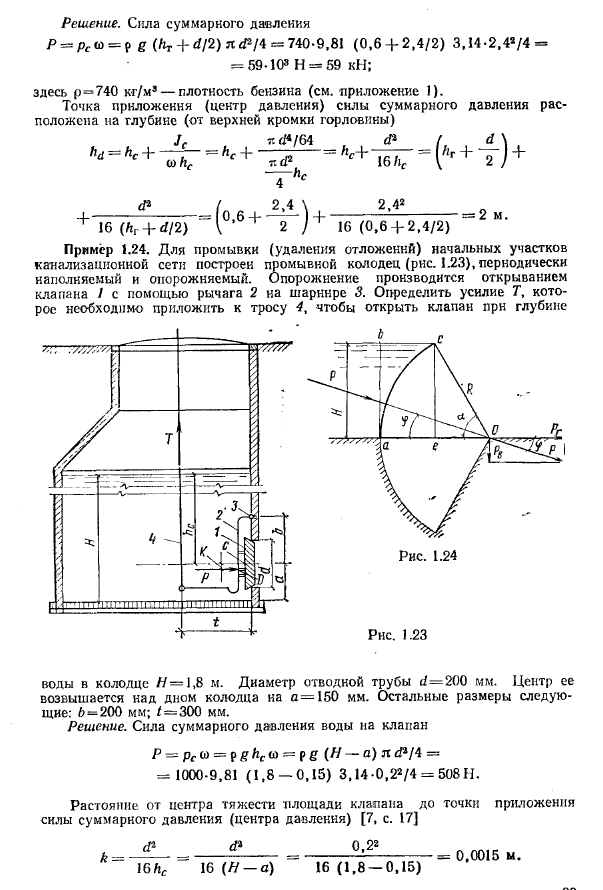
Пример
1.
Определить абсолютное и избыточное
гидростатическое давление
в точке А
(рис. 2.8), расположенной в воде на глубине
![]() ,
,
и пьезометрическую высоту для точки А,
если абсолютное гидростатическое
давление на поверхности![]()
![]() .
.
Решение:
Согласно
основного уравнения гидростатики
абсолютное гидростатическое давление
в точке А определится:
![]() .
.
Избыточное
давление в точке А равно:
![]()
Пьезометрическая
высота для точки А равна:

Можно
отметить, что пьезометром удобно измерять
только относительно малые давления, в
противном случае требуется большая
высота пьезометра, что неудобно в
эксплуатации.
Определить
эти же величины U – образным манометром,
заполненным ртутью. По поверхности
раздела
![]() ртути
ртути
и воды давления со стороны резервуара
и открытого конца манометра будут
одинаковы:
![]()
Следовательно,
избыточное давление в точке А
уравновешивается весом столба ртути
высотой
![]() над
над
поверхностью раздела![]() :
:

Находим
высоту ртутного столба
![]() :
:
 ,
,
где
![]() –
–
плотность ртути.
 Рис.2.9.
Рис.2.9.
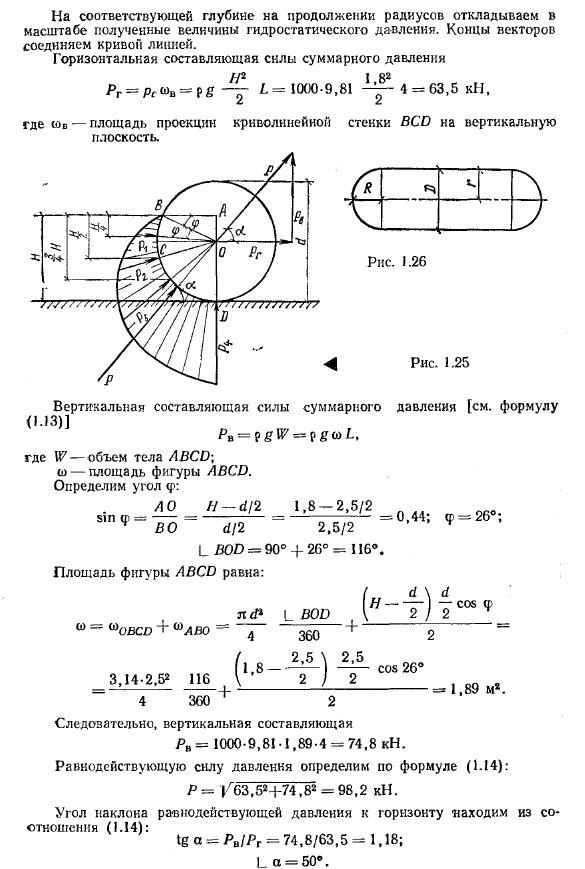
Пример
2.
Определить давление в резервуаре
![]() (рис.
(рис.
2.9) и высоту подъема уровня![]() в
в
трубке 1, если показания ртутного
манометра![]()
![]()
![]()
![]() .
.
Решение:
Запишем
условия равновесия для ртутного манометра
для плоскости
а)
со стороны резервуара
![]()
б)
со стороны манометра
![]() ,
,
тогда
![]()

Таким
образом, в резервуаре – вакуум, величина
которого равна:
![]()
Условия
равновесия трубки 1
![]()

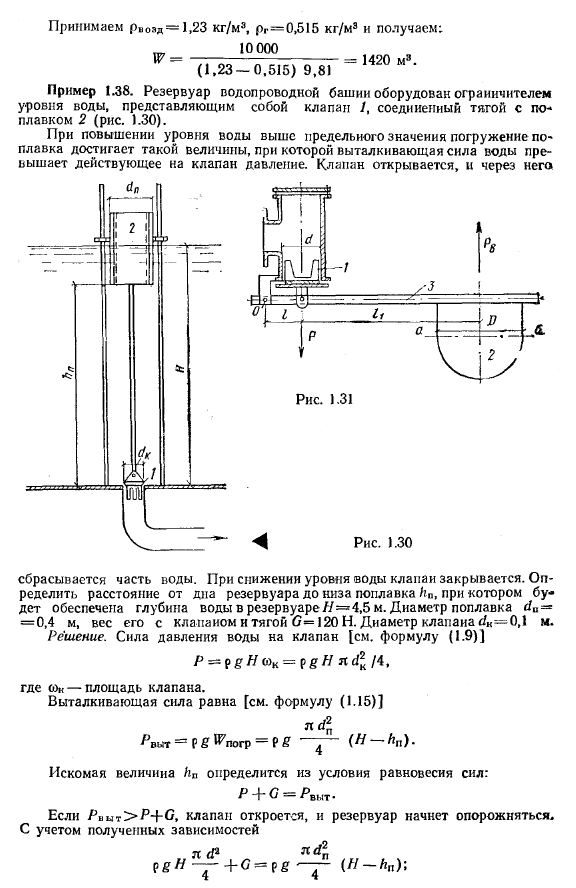
Пример
3.
 Рис.2.10.
Рис.2.10.
Определить
манометрическое давление в трубопроводе
А (рис. 2.10),
если
высота столба ртути по пьезометру
![]() 25
25
см. Центр трубопровода расположен на![]() 40
40
см ниже линии раздела между водой и
ртутью.
Решение:
Находим давление в точке В. Точка В
расположена выше точки А на величину
![]() ,
,
следовательно, давление в точке В будет
равно
![]() .
.
В
точке С давление будет такое же, как в
точке В, то есть
![]() .
.
Определим
давление в точке C, подходя, справа
![]() .
.
Приравнивая
оба уравнения, получаем
![]()
![]()
![]() .
.
Отсюда
манометрическое давление
![]() .
.
![]()

Пример
4.
 Рис.2.11.
Рис.2.11.
Определить
все виды гидростатического давления в
баке с нефтью на глубине
![]() (рис.
(рис.
2.11), если давление на свободной поверхности
нефти![]() .
.
Плотность нефти![]() .
.
Решение:
1. Абсолютное гидростатическое давление
у дна
![]()

2.
Избыточное (манометрическое) давление
у дна
![]()
![]()
3.
Избыточное давление создаваемое столбом
жидкости
![]()
4.
Избыточное давление на свободной
поверхности
![]()
Пример
5.
Определить избыточное давление воды в
трубе по показаниям батарейного ртутного
манометра (рис. 2.12).
 Рис.2.12.
Рис.2.12.
Отметки
уровней ртути от оси трубы:
![]()
![]()
![]()
![]() Плотность
Плотность
ртути![]() ,
,
плотность
воды
![]() .
.
Решение:
Батарейный ртутный манометр состоит
из двух последовательно соединенных
ртутных манометров. Давление воды в
трубе уравновешивается перепадами
уровней ртути, а так же перепадами
уровней воды в трубках манометра.
Суммируя, показания манометра от
открытого конца до присоединения его
к трубе получим:


3. Относительный покой жидкости
3.1. Сведения из теории
Под
относительным покоем понимается такое
состояние, при котором в движущейся
жидкости отдельные частицы не смещаются
одна относительно другой. При этом
жидкость перемещается как твердое тело.
Само движение жидкости в этом случае
можно назвать переносным движением.
Для этого состояния характерно постоянство
формы объема жидкости. Очевидно, что
рассматриваемая масса жидкости будет
неподвижна в координатной системе,
связанной с движущимся резервуаром.
На
жидкость, находящуюся в относительном
покое, действуют массовые силы (силы
тяжести и силы инерции переносного
движения), а из поверхностных – силы
давления.
Рассмотрим
два частных случая относительного
покоя: покой при переносном прямолинейном
движении и покой при переносном
вращательном движении вокруг вертикальной
оси.
3.1.1.
Относительный покой при прямолинейном
движении на наклонной плоскости
Рассмотрим
движение резервуара с жидкостью с
постоянным ускорением a
по наклонной плоскости, образующей угол
a с горизонтальной плоскостью (рис. 3.1).
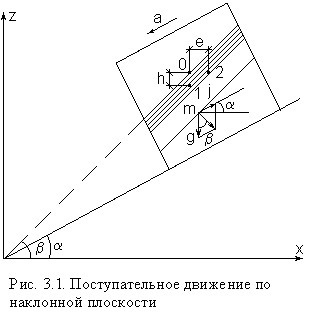 Жидкость
Жидкость
в движущемся резервуаре находится под
действием силы давления, силы тяжести
и силы инерции переносного движения.
Ускорение силы инерции
![]() и
и
направлено в сторону, обратную ускорению
резервуараa.
Результирующий вектор массивных сил
определяется диагональю параллелограмма,
построенного на ускорениях сил тяжести
g
и инерции j.
Элемент
поверхности равного давления
перпендикулярен к диагонали параллелограмма
и образует с горизонтом угол b , тангенс,
которого равен
 (3.1)
(3.1)
Таким
образом, поверхности равного давления,
образуют семейство параллельных
плоскостей с углом наклона к горизонту
b .
Необходимо
учесть, что если резервуар движется
равномерно
![]() ,
,
то![]() и
и
следовательно![]() и
и![]() .
.
В этом случае поверхности равного
давления представляют семейство
горизонтальных плоскостей.
Если
резервуар перемещается под действием
силы тяжести (сила трения резервуара о
плоскость равна 0), то
![]() ,
,![]() ,
,![]() ,
,
а поверхности равного давления образуют
семейство плоскостей, параллельных
плоскости скатывания.
Если
резервуар перемещается с ускорением,
но вертикально (![]() ),
),
то![]() ,
,
а поверхности равного давления образуют
семейство горизонтальных плоскостей.
Найдем
закон распределения давления в
вертикальной плоскости
![]() .
.
Учитывая, что система координат
перемещается вместе с резервуаром,![]() ,
,
а для выбранной плоскости и![]() ,
,
уравнение (2.6) примет вид:
![]() .
.
(3.2)
В
этом случае
![]() .
.
Тогда
![]()
 (3.3)
(3.3)
После
интегрирования имеем:
![]()
 (3.4)
(3.4)
Для
двух точек 0 и 1 с координатами![]() и
и![]() имеем:
имеем:
 (3.5)
(3.5)
или
![]() .
.
(3.6)
По
аналогии получаем распределение давления
в горизонтальной плоскости:
![]() ,
,
(3.7)
если
![]() ,
,
то имеем
![]() ,
,
(3.8)
а
свободная поверхность имеет угол наклона
к горизонту (3.1)
 .
.
(3.9)
При
свободном падении резервуара
![]() и
и![]() ,
,
то есть во всем объеме давление одинаково.
3.1.2
Относительный покой при вращении вокруг
вертикальной оси
В
этом случае на жидкость действуют силы
давления, силы тяжести и силы инерции
переносного вращательного движения
ускорения массовых сил будут равны:
![]()
Дифференциальное
уравнение (2.8) примет вид:
![]() (3.10)
(3.10)
После
интегрирования, с учетом, что
![]() получим:
получим:
 (3.11)
(3.11)
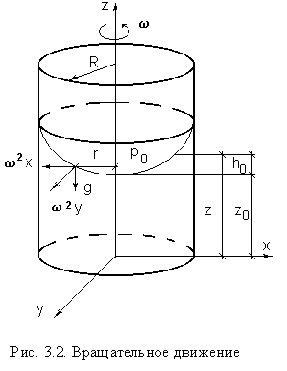
Уравнение
(3.11) является уравнением параболоида
вращения, а поверхности равного давления
образуют семейство параболоидов
вращения, сдвинутых вдоль вертикальной
оси. Каждый параболоид характеризуется
некоторым значением постоянной С. Для
параболоида свободной поверхности
принимаем, что при
![]() (рис.
(рис.
3.2)![]() ,
,
поэтому![]() .
.
Тогда уравнение свободной поверхности
примет вид:
 (3.12)
(3.12)
или
 (3.13)
(3.13)
Закон
распределения давления по объему
жидкости получим из уравнения (2.6),
подставив в него соответствующие
значения X,
Y
и Z.
После интегрирования получаем:
 .
.
(3.14)
Постоянную
интегрирования
![]() определим
определим
из условия, что при![]() и
и![]() ,
,
т.е.![]() .
.
После подстановки в (3.14) окончательно
имеем:
 .
.
(3.15)
Для
частиц жидкости расположенных на одной
вертикали можем записать:
![]() (3.16)
(3.16)
где
![]() ,
,
т.е.
существует обычный гидростатический
закон распределения давления.






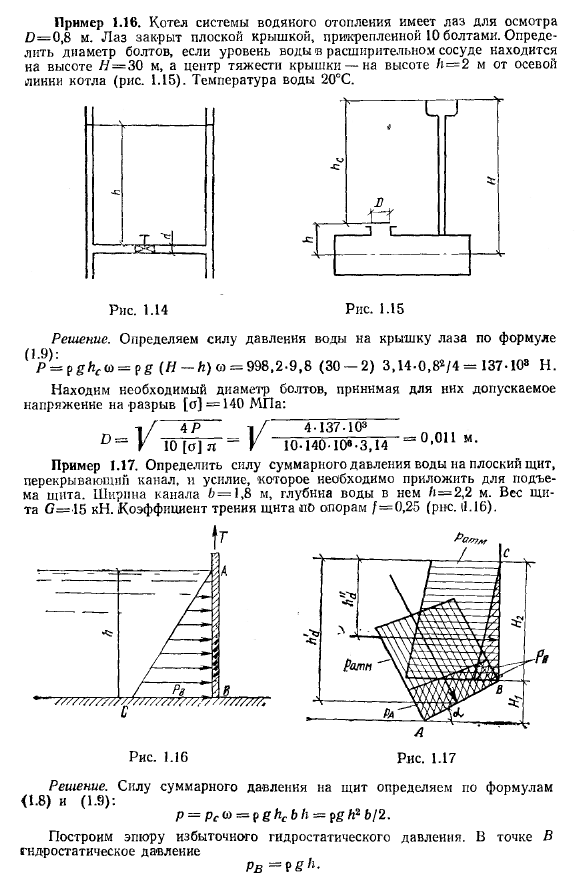












Примеры
Примеры. Пример 1. 1. Определите избыточное давление забоя по глубине скважины Н-85 м, заполненный глинистым раствором с плотностью Р = 1250 кг / м3. Решение. Избыточное давление определяется по формуле (1. 4). Р = ПГХ = 1250-9. 81 −85-1. 04・io6 Па»1 МПа. Пример 1. 2 Определите избыточное давление воды в трубе согласно инструкции* Аккумулятор ртутного манометра. Уровень ртути от оси трубы.
Смотрите также:
- Предмет гидравлика
Манометр ртутного элемента состоит из 2 частей последовательно Подключен ртутный манометр. Давление воды в трубе сбалансировано Различия в уровнях ртути и различия в уровнях воды в трубках Число. Манометр подводится от открытого конца к соединительной детали При нанесении на трубу, она выглядит так: Р = 9 промилле (Р * — Р3) — ПБ 8 (р * — Зет8 Где rv = 1000 кг / м3-плотность воды. РРт = 13 600 кг / м3-плотность ртути. 19.
Смотрите также:
- Закон Архимеда и его приложение.
Присваивает указанное значение для получения следующего. С. С. = 13600-9. 81(2. 5-1. 5 -1000 * 9. 81(3-1. 5 + + 13 600-9. 81(3-1. 75 + 1000-9. 81-1. 75 = 0. 3-10・Па = 0, 3 МПа. Пример 1. 3 в водном пути, ведущем воду к очистной установке, устье Обновлен пневматический уровнемер с записывающей аппаратурой (рис. 1. 3). Нижний край трубки 1 погружают в воду на глубину дна Н2 Уровень воды в реке canal.
В жидкостных манометрах чувствительным элементом является столб жидкости, уравновешивающий измеряемое давление.
Людмила Фирмаль
- Верхний конец трубки 1 подается в трубку 2 Небольшое количество воздуха под достаточным давлением для выпуска воздуха От нижнего края трубки мы кладем внутрь water. To определите глубину канала i По показаниям самописца 3, давление воздуха в трубке 1 i ’= 80 мм, равный рт. Ст. И я » = 29 мм рт. Расстояние от дна канала до дна Конец трубы i 1 = 0, 3 м. Решение. Избыточное давление воздуха в трубке.
В то же время, избыточное давление воды в нижнем конце Трубка Глубина i определяется из условия равного давления. Пример 1 .4 нижняя часть рабочего помещения кессона расположена сзади От свободной поверхности воды λ= 3 0 м .определить избыточное давление Воздух, а значит и вода должны создаваться в рабочей камере кессона Со стороны реки войти в камеру не удалось .
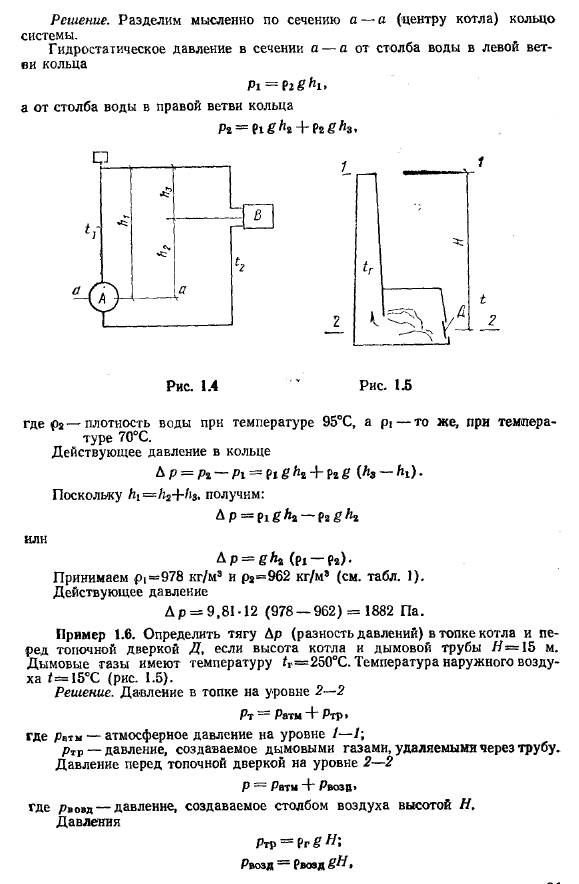
Избыточное давление воздуха в рабочей комнате Больше, чем гидростатическое давление на заданной глубине, то есть [справочная форма Лу (1 .4 ] П> т г ч> 1000 .9 .8-30 = 294000 па =2 .94 .10 па = 294 кПа .Абсолютное давление в рабочей камере кессона по формуле (1 .3) Lä= 9 .81-IO4 + 2 .94-105 = 3 .92-105pa = 392 кПа .Пример 1 .5 определите эффективное давление в кольце системы отопления (Рис . 1 .4), вода в котле а нагревается до температуры 95°C.
Нагреватель B охлаждается до 70°€. Расстояние Между центром котла и нагревательным устройством Я2= 12 м . 20 .Решение .Мысленно разделите кольцо а-а (центр котла) на кольца Система .Секция а гидростатического давления-от левого ветрового столба воды ви кольцо Пи = ч г ч я От водяного столба на правой ветке кольца Р2 = ?ИГ ч 2 + ?2г, Н3 . 1 1 .— у .Два т .Два Рисунок 1 .5 Где p2-плотность воды при температуре 95°C, а pi-то же самое при температуре Круглый 70°C.
Смотрите также:
- Основные понятия о движении жидкости.
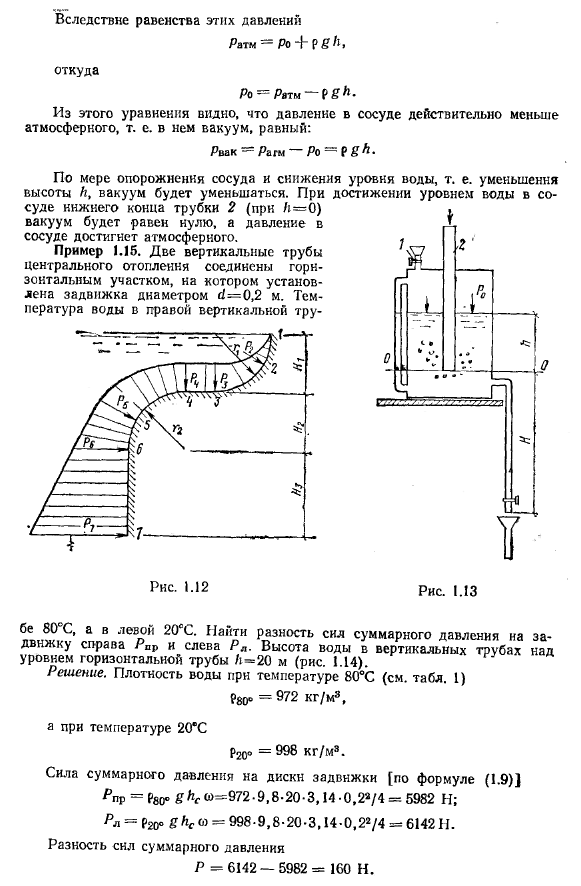
Эффективное давление в кольце. Рабочее давление Δρ= 9 .81 ~ 12 (978-962) = 1882 Па .Пример 1 .Определить осадку Δρ (разность давлений) топки котла 6 Если высота котла и дымохода составляет 15 м, то он составляется дверцей топки D . Температура дымовых газов составляет/ г = 250°С . Температура наружного воздуха xa t = 15°C (рис . 1 .5) .Решение .Давление в печи на уровне.
Для избыточного давления нолем является давление атмосферного воздуха, таким образом, его значение равно абсолютному давлению минус атмосферное давление.
Людмила Фирмаль
- Где атмосферное давление на уровне крыс/-/; РПП-давление, создаваемое дымовой газ удаляется из трубы.Давление в передней части на уровне 2-2 дверь внутреннего сгорания Р-РАТМ 4 ″ Рвозд» Где ρ-давление, создаваемое газовым столбом высотой N . Давление РТР-пр г н я Сброс=Сброс г ч » 21 .Где PR-плотность газа при температуре 250°С . Плотность воздуха при температуре разд-15°C
Разница давлений в топке котла и перед дверцей топки выглядит следующим образом. Мы принимаем rg = 0 . .Рассчитайте разность давлений. Пример 1 .7 вентиляция для уличных и внутренних канализационных сетей Из-за разницы в весе теплого газа в сети и весе атмосферы Воздушный шар .Газ заменяется через стояк 1 .Воздушные потоки от крыши здания, и зазор между крышкой 2 .

2016-11-22
Калькулятор доступен на полной версии сайта, с помощью него вы можете узнать давление жидкости на глубине 1, 5, 10, 20, 50, 100, 500, 1000 метров.
Вычисления осуществляются по избыточной шкале давления, в которой за 0 принято давление атмосферы.
Результат расчета давления на глубине
Вычислить давление на другой глубине
Расчет давления на глубине
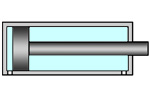
Расчетная схема показана на рисунке:
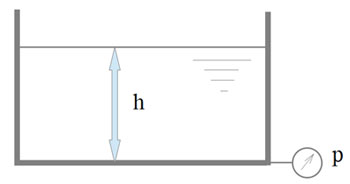
Для расчета используется формула:
P=ρ × g × h
- ρ – плотность жидкость
- h – глубина погружения
- g – ускорение свободного падения
- P – величина давления на глубине h
Пример расчета давления воды на глубине 10 метров
Для расчета давления воды на глубине 10 м, введите в графу глубина (h) – 10, выберите жидкость – вода, нажмите кнопку рассчитать.
Каждые 10 метров воды создают давление в 1 атмосферу
Полученное значение давления воды на 10 метрах равно 98,1 кПа, что примерно равно атмосферному давлению 101 кПа. Поэтому в приблизительных расчетах принимают давление в воде на глубине 10 метров равным 1 атмосфере про избыточной шкале.
Администрация сайта за результаты онлайн вычислений ответственности не несет.
Читайте также:

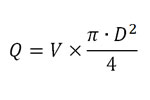
Все новости
Глубина оказывает прямое воздействие на давление воды. Между ними прямая зависимость. Данное значение рассчитывается по специальной формуле. На различных участках глубоководья указанная величина заметно отличается.
Рассмотрим в статье особенности расчет и составляющие формулы, а также отличается ли давление на участках с разной глубиной.
Содержание
- Влияние глубины
- Зависимость двух физических показателей
- Формула для расчета
- Сколько составляет на различных глубоководных участках?
- Заключение
Влияние глубины
 Чем глубже происходит погружение в водную толщу, тем больше становится ее сила. Глубина прямо влияет на увеличение давление. Это значение возрастает пропорционально.
Чем глубже происходит погружение в водную толщу, тем больше становится ее сила. Глубина прямо влияет на увеличение давление. Это значение возрастает пропорционально.
Чем глубже, тем больше плотность водной толщи. С каждым последующим опусканием тела возникает все большая разница между внешним и внутренним водным давлением.
На поверхности действует атмосферное давление. При опускании в воду помимо него тела начинают испытывать еще и гидростатическое сдавливание.
Даже на мелководье на тело оказывается суммарное влияние, состоящее из атмосферного и гидростатического. При нырянии внешнее воздействие на тело возрастает. Возникает разница из-за увеличения плотности среды.
Верхние слои давят на нижние. За счет этого возникает сдавливающая сила на глубоководье. При этом ее показатель на одной глубине один и тот же по всем направлениям.
Зависимость двух физических показателей
С каждым последующим опусканием на 10 м воздействие становится больше на 1 атмосферу. Уже при погружении на 100 метров тела испытывают давление, соизмеримое с тем, что создается в паровом котле.
С погружением общее давление как на человека, так и на любой другой объект, возрастает. На 10 м оно становится больше вдвое.
 Прирост давления на глубоководье неодинаков:
Прирост давления на глубоководье неодинаков:
- На 10 м прирост составляет 100%.
- На 20 м он уже уменьшается вдвое (50%).
- На 40 он падает до 25%.
- На 60 он уже меньше 20% и составляет 17%.
В воде помимо атмосферного давления возникает еще гидростатический прессинг. Он также называется избыточным. При нахождении в воде любой объект будет испытывать уже сумму двух давлений: атмосферного и избыточного.
Зависимость двух величин напрямую прослеживается при изучении состояния человека, находящегося в условиях глубоководья. Если поместить человека в глубоководную среду, то он не сможет сделать полноценный вдох.
Возникшая разница между двумя давлениями, одно из которых оказывается на грудную клетку водой, а второе воздухом, что создается в легких, не позволит человеку нормально дышать. При большем погружении грудная клетка разорвется.
Формула для расчета
Данный показатель повышается пропорционально погружению. Он рассчитывается по специальной формуле:
P = p * g * h, где
- p — плотность среды. Примерно равна 1000 кг/м2.
- g — это ускорение, которое придается телу силой тяжести. Это значение называется ускорением силы тяжести или свободного падения. На Земле данная величина примерно равняется 9,81 м/с2.
- h — глубина, на которую погружается какой-либо объект. Высчитывается в метрах.
Формула является выражением закона Паскаля. По ней высчитывается значение гидростатического прессинга. Он напрямую зависит от высоты водного столба.
Произведение плотности (p) и ускорения (g) приблизительно равняется 0,1 атм. С каждым метром опускания на дно воздействие в водной среде повышается на 0,1 атм. Данное правило подтверждает тот факт, что чем глубже происходит опускание в толщу, тем выше становится показатель воздействия.
Сколько составляет на различных глубоководных участках?
 Если какой-либо объект поместить в воду на один метр, то он будет испытывать на себе силу, равную 0,1 атм.
Если какой-либо объект поместить в воду на один метр, то он будет испытывать на себе силу, равную 0,1 атм.
Предмет, погруженный на 2 м, уже станет испытывать прессинг величиной около 0,2.
С каждым последующим метром показатель будет возрастать на 0,1 атм. При 5 м значение равняется 0,5. При 10 оно будет уже равняться 1. Более точное число равняется 0,97 атмосферы.
На глубоководье водная толща становится сжатой. Ее плотность увеличивается. Уже на 100 м сила будет практически равняться 10. Более точное число составляет 9,7.
На глубинном участке в 1 км водная среда будет сдавливать находящиеся в ней объекты примерно со значением в 97 атм. Поскольку при 100 м величина равна 9,7, то на 1000 м она увеличивается в 10 раз.
Изменение показателя на разных глубоководных участках представлено в таблице.
| Глубина, на которую объект погружается в воду, в метрах | Давление в атмосферах. |
| 1 | 0,10 |
| 2 | 0,19 |
| 3 | 0,29 |
| 4 | 0,39 |
| 5 | 0,49 |
| 10 | 0,97 |
| 15 | 1,46 |
| 25 | 2,43 |
| 50 | 4,85 |
| 100 | 9,70 |
| 200 | 19,40 |
| 250 | 24,25 |
| 500 | 48,50 |
| 1000 | 97 |
При первых 10 метрах прирост невысокий и составляет 0,1 атмосферы. Дальше его показатель увеличивается.
Заключение
Глубина влияет на давление воды. С каждым метром движения объекта вглубь его показатель увеличивается на 0,1 атм. Уже на 10 м сдавливающая сила воды составляет почти 1 атмосферу. Зависимость обеих величин обусловлена плотностью воды, которая возрастает по мере движения тела в ней на дно.
Также на глубоководье происходит увеличение внешнего силового воздействия на объект. Если на поверхности тела испытывают воздействие только атмосферного давления, то в воде помимо него на них еще оказывается и гидростатическое.
При этом прирост воздействия на разных глубинных участках неодинаков. Особенно он высок при первых 10 м погружения. Дальше он начинает довольно быстро снижаться.
Решение задач по гидравлике
Решение задач с использованием закона Архимеда
Задача
Баркас массой mб = 250 кг изготовлен в форме параллелепипеда шириной b = 1 м, длиной l = 3 м, высота бортов h = 0,3 м.
Определить, сколько человек могут разместиться в баркасе, не потопив его.
Средняя масса человека mч = 70 кг, плотность воды ρ = 1000 кг/м3.
Правильное решение:
Определим водоизмещение баркаса Мmax, которое равно массе воды, вытесненной им при полном погружении (по обрез бортов).
Для этого определим объем корпуса баркаса и умножим полученный результат на плотность воды:
Мmax = b×l×h×ρ = 1×3×0,3×1000 = 900 кг.
Чтобы найти грузоподъемность Мгр баркаса, необходимо из полученного результата вычесть массу самого баркаса:
Мгр = Мmax – mб = 900 – 250 = 650 кг.
Разделив полученную максимальную грузоподъемность на среднюю массу человека, и округлив результат до целого числа, получим допустимое количество пассажиров баркаса:
n = Мгр/mч = 650/70 = 9 человек.
Ответ: баркас может принять на борт не более 9 человек.
***
Задача

Медный шар диаметром d = 100 мм весит в воздухе G1 = 45,7 Н, а при погружении в жидкость его вес стал равен G2 = 40,6 Н.
Определить плотность жидкости.
Правильное решение:
Вес шара в жидкости меньше, чем его вес в воздухе, поскольку в жидкости на него действует выталкивающая архимедова сила, равная весу вытесненной шаром жидкости.
Очевидно, что вес вытесненной шаром жидкости будет равен разности между весом шара в воздухе и его весом в жидкости:
Gж = G1 – G2 = 45,7 – 40,6 = 5,1 Н.
Чтобы определить плотность жидкости, необходимо ее массу разделить на объем, который равен объему шара, определяемого по формуле:
Vш = πd3/6 = 3,14×0,13/6 = 0,00052 м3.
Массу жидкости можно определить, зная ее вес:
mж = Gж/g = 5,1/9,81 ≈ 0,52 кг.
Определив массу и объем, находим плотность жидкости:
ρ = mж/Vш = 0,52/0,00052 = 1000 кг/м3.
Ответ: плотность жидкости равна 1000 кг/м3 (судя по плотности, жидкость – вода).
***
Задача
Баржу, имеющую форму параллелепипеда, загрузили песком в количестве 18 тонн. Ее осадка (глубина погружения) составила h0 = 0,5 м.
Определить массу пустой баржи, если ее размеры: длина l = 12 м; ширина b = 4 м.
Какова полная грузоподъемность баржи, если высота ее бортов h = 1 м.
Плотность воды принять равной 1000 кг/м3.
Правильное решение:
В соответствии с законом Архимеда, на баржу со стороны воды действует выталкивающая сила, равная весу воды, вытесненной погруженной частью баржи. Этот вес (обозначим его GВ) можно определить, зная ширину, длину и осадку баржи, а также плотность воды:
GВ = mg = b×l×h0×ρ×g = 4×12×0,5×1000×9,81 = 235400 Н.
Итак, на баржу действует выталкивающая сила, равная 235400 Н, удерживая ее в равновесном состоянии на поверхности воды. Следовательно, вес GБГ баржи с грузом тоже равен 235400 Н, тогда масса баржи с грузом равна:
mБГ = GБГ/g = 235400/9,81 ≈ 24000 кг.
Чтобы найти массу пустой баржи, необходимо из массы груженой баржи вычесть массу груза:
mБ = mБГ – mГ = 24000 – 18000 = 6000 кг.
Очевидно, что при полном погружении баржи в воду (по самые борта), выталкивающая архимедова сила увеличится в два раза по сравнению с рассмотренным нами случаем, т. е. составит 2×235400 = 470800 Н.
Данная сила характеризует водоизмещение баржи, т. е. максимальное количество вытесняемой ее корпусом воды.
Однако, эта величина не характеризует полную грузоподъемность баржи, поскльку она сама имеет вес.
Исходя из этого, полная грузоподъемность баржи может быть подсчитана, как разница между массой вытесненной баржой воды и массой баржи:
Мmax = mВ – mБ = 47080 – 6000 = 41080 кг.
Ответ: пустая баржа весит 6 тонн, а ее полная грузоподъемность – 41 тонна.
***
Задача
Для переправы грузов через реку построен плот из 25 штук пустых железных бочек.
Размеры бочек: диаметр d = 0,8 м, высота h = 1,3 м.
Масса одной бочки m = 50 кг.
Определить грузоподъемность плота Мmax при условии его полного погружения.
Плотность воды принять равной ρ = 1000 кг/м3.
Правильное решение:
Определим объем бочек, из которых изготовлен плот:
V = 25 h πd2/4 = 25×1,3×3,14×0,82/4 = 16,33 м3.
Масса этих бочек: mБ = 25m = 25 × 50 = 1250 кг.
Масса воды, вытесняемой бочками при полном погружении плота, равна произведению плотности воды на объем бочек:
mВ = ρVБ = 1000×1,664 = 16330 кг.
Грузоподъемность плота равна массе вытесняемой бочками воды с учетом массы самих бочек:
Мmax = mВ – mБ = 16330 – 1250 = 15080 кг.
Ответ: максимальная грузоподъемность плота равна 15080 кг.
***
Решение задач с применением основного уравнения гидростатики
Задача
На рисунке изображены три сосуда разной формы, в каждый из которых налита вода на одинаковую высоту Н.
Площадь свободной поверхности в сосуде а больше площади свободной поверхности в сосуде в в два раза, но в два раза меньше площади свободной поверхности в сосуде б.

Площадь дна во всех трех сосудах одинакова и равна S.
Во сколько раз сила давления на дно в сосуде а будет отличаться от силы давления на дно в сосуде в?
Ответ обоснуйте основным уравнением гидростатики.
Решение:
В соответствии с основным уравнением гидростатики p = p0 + γ(z0 – z), т. е. давление в любой точке объема жидкости зависит от внешнего давления p0 и глубины погружения рассматриваемой точки.
Поскольку внешнее давление для всех трех сосудов равно атмосферному давлению, т. е. одинаково, то давление на каждую из точек поверхности дна зависит только от уровня Н (т. е. глубины, равной z0 – z). Очевидно, что для всех трех сосудов, уровень жидкости в которых одинаков, давление на дно тоже будет одинаково.
Тогда и сила давления на дно, определяемая, как произведение площади дна на величину давления, во всех трех сосудах будет одинакова, несмотря на то, что они имеют разную форму.
***
Задача
Определить избыточное давление в забое скважины глубиной h = 85 м, которая заполнена глинистым раствором плотностью ρ = 1250 кг/м3.
Правильное решение:
Избыточное давление – это давление, которое оказывает столб жидкости на единицу площади на данной глубине без учета внешнего давления (атмосферы) на поверхности жидкости, и определяется, как произведение удельной плотности жидкости на высоту столба (глубины погружения).
Удельная плотность жидкости определяется, как произведение абсолютной плотности на ускорение свободного падения.
Тогда избыточное давление в скважине исходя из условий задачи можно записать так:
pизб = γh = ρgh = 1250×9,81×85 = 1040000 Па ≈ 1 МПа.
Ответ: избыточное давление в забое скважины составляет примерно 1 МПа.
***
Задача
Водолазы при подъеме затонувшего судна работали в море на глубине h = 50 м.
Определите давление воды на этой глубине и силу давления на скафандр водолаза, если площадь поверхности S скафандра равна 2,5 м2.

Атмосферное давление считать равным p0 = 1,013×105 Па, плотность воды ρ = 1000 кг/м3.
Правильное решение:
Давление воды на глубине 50 м складывается из атмосферного давления p0 и избыточного давления, обусловленного столбом воды высотой 50 м:
p = p0 + ρgh = 1,013×105 + 1000×9,81×50 = 5,918×105 Па.
Сила давления воды на скафандр водолаза равна произведению площади скафандра на избыточное давление (внутри скафандра давление равно атмосферному, поэтому p0 не учитывается) и определяется по формуле:
F = ρgh×S = 1000×9,81×50×2,5 = 1226250 Н ≈ 1226 кН.
Ответ: давление воды на глубине 50 м равно 591 МПа, а сила давления на скафандр равна 1226 кН.
***
Задача
После сжатия воды в цилиндре под поршнем давление в ней увеличилось на 3 кПа.
Необходимо определить конечный объем V2 воды в цилиндре, если ее первоначальный объем составлял V1 = 2,55 л.
Коэффициент объемного сжатия воды βV = 4,75 • 10-10 Па-1.
Правильное решение:
Приведем исходные данные задачи к системе единиц СИ: V1 = 2,55л = 2,25х10-3 м3, Δp = 3 кПа = 3000 Па.
Тогда конечный объем воды в цилиндре будет равен сумме первоначального объема V1 и уменьшения объема ΔV в результате сжатия:
V2 = V1 + ΔV = (2,25×10-3) + (2,25×10-3×3000×4,75×10-10) = 2,25000320625×10-3 м3 = 2,2500032625 л.
Ответ: конечный объем воды 2,2500032625 л, т. е. изменился ничтожно мало.
***
Задачи по гидродинамике и определению параметров насосов
Скачать задачи по гидравлике с вариантами решений
(в формате Word, размер файла 324 кБ – 27 задач с решениями и вопросы по насосам)
Скачать теоретические вопросы к экзаменационным билетам по дисциплине “Основы гидравлики и теплотехники”
(в формате Word, размер файла 68 кБ)
