☰
Приближение по недостатку и по избытку
Проводя различные измерения, решая уравнения графическим способом, выполняя арифметические вычисления, часто получают приближенные значения, а не точные. Например, при вычислении корня числа может получиться бесконечная непериодическая дробь (т. е. иррациональное число). Кроме того, существуют бесконечные периодические дроби, использовать которые в вычислениях также неудобно.
Поэтому числа, являющиеся бесконечными десятичными дробями или конечными, но имеющими множество знаков после запятой, принято округлять.
Когда округление выполняется в большую сторону, то говорят о приближении по избытку. Когда округление выполняется в меньшую сторону, то говорят о приближении по недостатку.
Полученное при округлении число называют приближенным по недостатку или избытку с определенной точностью. Рассмотрим несколько примеров приближения.
Число π является бесконечной дробью 3,1415926535… Обычно его округляют с точностью до 0,01. Это значит, что после запятой оставляют только два знака. При приближении по избытку получится 3,15. При приближении по недостатку получится 3,14.
Для числа π обычно используют приближение по недостатку, так как согласно правилу округления положительные числа округляются в большую сторону, если первая отбрасываемая цифра 5 или больше пяти. Так как у числа π третья цифра после запятой — это 1, то округление выполняется в меньшую сторону, то есть для расчетов выполняется приближение по недостатку.
Однако, несмотря на правила округления, имеют право быть приближения как по недостатку, так и по избытку.
Если выполнять приближение числа π с точностью до 0,0001, то по избытку получим π ≈ 3,1416, а по недостатку π ≈ 3,1415.
Рассмотрим иррациональное число √2, которое равно 1,414213… . Вычислим его приближение по недостатку и по избытку с точностью до 0,001. Поскольку приближение выполняется до тысячных долей, то у числа надо оставить три знака после запятой. При приближении по недостатку просто отбрасываются все цифры после третьей после запятой. При приближении по избытку цифры после третьей после запятой отбрасываются, а третья цифра увеличивается на 1. Таким образом, приближение по недостатку будет √2 ≈ 1,414, а по избытку √2 ≈ 1,415.
Но примеры, рассмотренные выше, это положительные числа. А так ли обстоит дело при приближении отрицательных чисел. Если взять число –√2 = –1,414213…, то его приближением по избытку до тысячных долей будет –1,414, так как это число больше, чем –√2. А вот приближением по недостатку будет –1,415, так как это число меньше, чем –√2.

На практике, а также при решении задач ЕГЭ, очень часто во избежание ненужных вычислений удобно выполнить округление чисел до необходимой степени точности, то есть заменить данные числа их приближениями.
Существует три вида округления чисел: по недостатку, по избытку и с поправкой.
Округление по недостатку
- При округлении данного положительного числа до n-го разряда по недостатку все его цифры до n-го разряда включительно сохраняют без изменения, а остальные отбрасывают.
- При округлении данного отрицательного числа до n-го разряда по недостатку до его цифры n-го разряда прибавляют единицу, а все последующие цифры отбрасывают.
Округление по избытку
- При округлении данного положительного числа до n-го разряда по избытку до цифры n-го разряда его округления по недостатку прибавляют единицу.
- При округлении данного отрицательного числа до n-го разряда по избытку все его цифры до n-го разряда включительно сохраняют без изменения, а остальные отбрасывают.
Округление с поправкой
При округлении данного числа с поправкой до n-го разряда последняя сохраняемая цифра (цифра n-го разряда) не меняется, если цифра, следующая за ней, меньше 5, и увеличивается на 1, если цифра, следующая за ней, не меньше 5.
Правило округления такое:


Рекомендую познакомиться с примерами задач ЕГЭ, в которых часто встречается округление чисел. Это задачи на вычисление и задачи на округление с недостатком.
Спасибо, что поделились статьей в социальных сетях
Содержание:
- § 1 Понятие о приближенном значении чисел
- § 2 Округление чисел
- § 3 Правило округления чисел
§ 1 Понятие о приближенном значении чисел
В жизни человека встречается два вида чисел: точные и приближённые.
Например, у квадрата четыре стороны, число 4 является точным.
Другая ситуация, на вопрос, сколько вам лет вы отвечаете 12, это приближенная величина, мы ведь не говорим 12 лет 7 месяцев 26 дней.
На практике мы часто не знаем точных значений величин. Никакие весы, как бы хорошо они ни были настроены, не могут показать абсолютно точный вес. Любой термометр показывает температуру с той или иной погрешностью. Наш глаз не в состоянии увидеть четко показания прибора, поэтому вместо того, чтобы иметь дело с точным значением величины, мы вынуждены оперировать с ее приближённым значением
Однако знание о приближённом числе уже даёт понимание о сути дела, и к тому же не всегда точное значение бывает необходимо.
Приближенные значения чисел в математике разделяют на:
1. приближенные значения с избытком;
2. приближенные значения с недостатком.

Например, про арбуз, который весит 9 кг 280 г, мы можем сказать, что его вес примерно равен 9 кг. Это приближенное значение с недостатком. А если бы его вес составлял 9 кг 980 грамм, мы бы сказали 10 кг – это приближенное значение с избытком.
Другой пример – если длина отрезка равна 25 см 3 мм, то 25 см – это приближенное значение длины отрезка с недостатком, а 26 см – это приближенное значение длины отрезка с избытком.
Итак, если число Х больше числа А, но меньше числа В, тогда А – является приближенным значением числа Х с недостатком, а число В – приближенным значением числа Х с избытком.
§ 2 Округление чисел
Давайте рассмотрим такие примеры:
1)число 58,79 больше чем 58, но меньше 59. Число 58,79 ближе расположено к натуральному числу 59;
2)число 181, 123 больше, чем 181, но меньше, чем 182. Число 181,123 расположено ближе к натуральному числу 181. То натуральное число, к которому дробь ближе называют округленным значением этого числа.
Округление чисел – это математическое действие, которое позволяет уменьшить количество цифр в числе, заменяя его приближенным значением.
Под округлением числа понимают отбрасывание одной или нескольких цифр в десятичном представлении числа. Замену числа ближайшим к нему натуральным числом или нулем называют округлением этого числа до целых.
Например, число 58,79 округляется до 59, так как число 59 расположено ближе, а число 181,123 округляется до 181.
§ 3 Правило округления чисел
А что делать, если расстояния до приближенного значения числа с недостатком и избытком равны, например, 23,5? Оказывается, округляют в большую сторону! Т.е. получится 24
Наверняка у вас возник вопрос: «А можно ли округлять не до целого?» Конечно! Округлять можно и до других разрядов, например, до десятых, сотых, тысячных или же до десятков, сотен, тысяч и так далее.
Существует четкое правило для округления чисел:
Чтобы округлить число до какого-либо разряда – подчеркнем цифру этого разряда, а затем все цифры, стоящие за подчеркнутой, заменяем нулями, а если они стоят после запятой – отбрасываем. Если первая замененная нулем или отброшенная цифра равна 0, 1, 2, 3 или 4, то подчеркнутую цифру оставляем без изменения. Если за подчеркнутой цифрой стоит цифра 5, 6, 7, 8 или 9, то подчеркнутую цифру увеличиваем на 1.
Теперь стало понятно, почему число 23,5 округлили до 24.
Т.к. отбрасываемая цифра равна 5.
Пример 1.
Округлим число 86,275 до десятых.
Решение.
Подчеркнем цифру 2, отбрасываем цифры 7 и 5, которые следуют за разрядом десятых. За подчеркнутой цифрой 2 стоит цифра 7, поэтому цифру 2 увеличиваем на 1. Получаем 86,3. Записывают это так:
![]()
Пример 2.
Округлим число 6,6739 до сотых.
Решение.
Подчеркиваем цифру 7, отбрасываем цифры 3 и 9, которые следуют за разрядом сотых. За подчеркнутой цифрой 7 стоит цифра 3, поэтому цифру 7 оставляем без изменения. Получаем 6,67.
Записывают это так:
![]()
Таким образом, можно убедиться, что если десятичную дробь округляют до какого-нибудь разряда, то все следующие за этим разрядом цифры отбрасывают.
Пример 3.
Округлим число 8 154 до сотен.
Решение:
Подчеркиваем цифру 1, за ней следует цифра 5, значит 1 заменяем цифрой 2, а все последующие цифры нулями, то есть получится 8200.
Записывают это так:
![]()
Делаем вывод, что при округлении натурального числа до некоторого разряда все цифры последующих разрядов заменяются нулями.
Итак, перед вами несложный алгоритм, который позволяет правильно выполнить округление любого числа:
Первое: найти нужный разряд и подчеркнуть стоящую в нем цифру.
Второе: переписать все цифры, стоящие до нее.
Третье: заменить все цифры, стоящие после выделенной, нулями до конца целой части или отбросить все цифры, имеющиеся после выделенной, если они стоят после запятой.
Четвертое: увеличить выделенную цифру на единицу, если за этой цифрой стоит цифра 5,6,7,8,9 или переписать выделенную цифру без изменений, если за ней стоит цифра 0,1,2,3,4.
Таким образом, в ходе этого урока Вы узнали, что такое приближенные значения чисел с недостатком и избытком округление чисел, а также приобрели четкий алгоритм, который позволяет правильно выполнить округление любого числа!
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. – М: 2013.
- Дидактические материалы по математике 5 класс. Автор – Попов М.А. – 2013 год
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор – Минаева С.С. – 2014 год
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010 год
- Контрольные и самостоятельные работы по математике 5 класс. Авторы – Попов М.А. – 2012 год
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009
Макеты страниц
Возьмем иррациональное число  Имеем:
Имеем:

Числа 1; 1,4; 1,41; 1,414; 1,4142 называются десятичными приближениями числа  по недостатку с точностью соответственно до 1, до 0,1, до 0,01, до 0,001, до 0,0001. Числа 2; 1,5; 1,42; 1,415: 1,4143 называются десятичными приближениями числа
по недостатку с точностью соответственно до 1, до 0,1, до 0,01, до 0,001, до 0,0001. Числа 2; 1,5; 1,42; 1,415: 1,4143 называются десятичными приближениями числа  по избытку соответственно с той же точностью.
по избытку соответственно с той же точностью.
Для числа  используют представление в виде бесконечной десятичной дроби:
используют представление в виде бесконечной десятичной дроби:  Вообще любое действительное
Вообще любое действительное
число представимо в виде бесконечной десятичной дроби, причем периодической, если число рациональное  непериодической, если число иррациональное.
непериодической, если число иррациональное.
Например,  (см. п. 17). Десятичное приближение числа с точностью до 0,001 по недостатку равно 0,254, а по избытку равно 0,255.
(см. п. 17). Десятичное приближение числа с точностью до 0,001 по недостатку равно 0,254, а по избытку равно 0,255.
Число  имеет вид
имеет вид  Десятичное приближение числа
Десятичное приближение числа  с точностью до 0,0001 по недостатку равно 3,1415, а по избытку —3,1416.
с точностью до 0,0001 по недостатку равно 3,1415, а по избытку —3,1416.
Все числа представимые бесконечными
десятичными дробями , образуют множество
действительных чисел. Познакомимся
с одним из способов построения теории
действительных чисел в общих чертах.
-
Принимают:
а) каждому действительному числу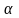
соответствует (в качестве его записи)
бесконечная десятичная дробь:

;
б) каждая бесконечная десятичная дробь
является записью действительного числа.
Но при этом естественно считать десятичную
дробь, заканчивающуюся бесконечной
последовательностью девяток, лишь
второй записью числа, выражающегося
десятичной дробью, заканчивающейся
бесконечной последовательностью нулей:

Такое соглашение поясним примером:

.
Только исключив из рассмотрения
десятичные дроби с девяткой в периоде,
получаем взаимно однозначное соответствие
между множеством действительных чисел
и множеством бесконечных десятичных
дробей.
-
Вводят правило сравнения двух
действительных чисел х и у
.
Если целая часть числа х меньше
целой части числа у, то сам о число
х меньше числа у. Для сравнения
двух чисел, целые части которых равны,
приходится обращаться к их дробным
частям.
Например,

, так как у этих чисел равны целые части
и три первых десятичных знака после
запятой, а четвертый знак после запятой
у числа в левой части меньше:
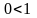
.
Правило сравнения действительных
чисел, записанных в виде бесконечных
десятичных дробей, можно сформулировать
так:

.
-
Принимают определения арифметических
действий ( операций) над действительными
числами: сложения и умножения, вычитания
и деления. ( см. следующий пункт) -
Показывают, что неравенства и
арифметические операции, определенные
в множестве действительных чисел,
сохраняют основные свойства, присущие
им в множестве рациональных чисел. -
Модуль действительного числа определяется
так же ,как и модуль рационального
числа:

.
Например, если

,
то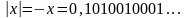
.
3. Десятичные приближения действительного числа по недостатку и по избытку. Арифметические действия с действительными числами.
Для числа

число
называют десятичным приближением по
недостатку с точностью до

( или с точностью до n
знаков), а число
десятичным приближением по избытку
с точностью до
.
Из правил сравнения действительных
чисел следует, что

.
Пример 1. Запишем десятичные приближения
числа

по недостатку и избытку с точностью до
1, до 0,1, до 0,01, …, до 0,00001:

С помощью десятичных приближений
определяются операции сложения и
умножения действительных чисел. Эти
определения даются, исходя из следующих
соображений.
Если

и

рациональные числа, то сумма

уже определена, причем для любого n
выполнены неравенства
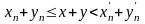
.
Это свойство суммы должно быть сохранено
и для произвольных действительных чисел
(хотя бы для того, чтобы их сумму можно
было находить приближенно). В курсах
математического анализа доказывается,
что для любой пары действительных чисел
и
существует единственное число
такое, что при любом

выполняется
неравенство

Это число
называется суммой чисел
и
(обозначается

).
Пример 2. Найдем первые четыре десятичных
знака суммы
,
где

.
Здесь многоточием отмечены следующие
десятичные знаки, которые для решения
не нужны. Для заданных чисел выпишем
десятичные приближения с точностью до
пяти знаков. Тогда

.
Вы видите, что слева и справа совпадают
четыре десятичных знака. Следовательно

.
Ответ:
.
Произведение неотрицательных
действительных чисел определяется
аналогично. Можно доказать, что для
любой пары неотрицательных действительных
чисел
и
существует единственное число
действительное число
такое, что при любом
выполняется
неравенство

.
Это число
называется произведением чисел
и
(обозначается

).
Для действительных чисел разных знаков,
воспользовавшись тем, что произведение
неотрицательных чисел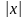
и

уже определено, полагают:
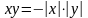
; в остальных случаях

.
Вычитание определяется, как действие
обратное сложению, деление – как
действие, обратное умножению.
Пользуясь определениями арифметических
операций, получаем основные свойства
модуля :

;

;

.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
