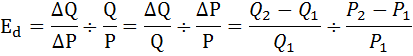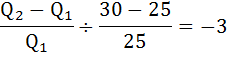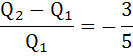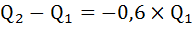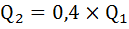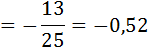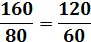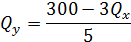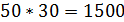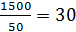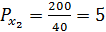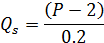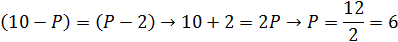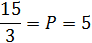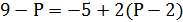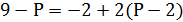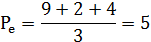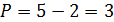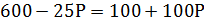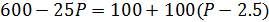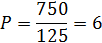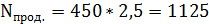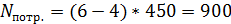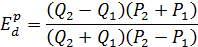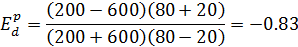Как найти издержки потребителя

Как найти издержки потребителя

Содержание страницы

  1. Что собой представляют издержки обращения?
  2. Состав издержек обращения
  3. Разновидности
  4. От чего зависит уровень издержек обращения?
  5. Для чего требуется определять показатели ИО?
  6. Издержки обращения в бухгалтерском учете
  7. Что делать с полученными значениями?

Деятельность любого предприятия сопровождается издержками. Возникают они как из-за естественных причин, так и вследствие нарушений дисциплины труда. Издержки подразделяются на несколько категорий. Классификация имеет значение при внесении изменений в бухгалтерскую документацию. Издержки обращения – одна из форм подобных затрат.

Вопрос: Как отражаются в учете торговой организации расходы на доставку товара от поставщика до склада организации, если стоимость доставки, согласно договору поставки, оплачивается поставщику сверх цены товара? В соответствии с учетной политикой организации расходы на доставку приобретенного товара включаются в издержки обращения в бухгалтерском и налоговом учете.
Организация приобрела товары на сумму 180 000 руб., в том числе НДС 30 000 руб. Стоимость доставки составила 6 000 руб., в том числе НДС 1 000 руб. На конец месяца товары не проданы.
Посмотреть ответ

Что собой представляют издержки обращения?

Продукция не сразу попадает на прилавки магазинов. До этого она проходит длительный путь, включающий следующие этапы:

  1. поставка комплектующих производителю;
  2. изготовление продукта;
  3. его транспортировка;
  4. реализация.

Как ведется учет издержек обращения в общественном питании?

Данная цепочка зависит от деятельности предприятия. Издержки обращения (ИО) – это те траты, которые возникают при прохождении товара через рассматриваемую цепочку, при его доведении до потребителя. ИО выражаются через денежные средства. Включаются в состав текущих затрат компании. То есть, издержки обращения вызываются различными производственными факторами.

ПРИМЕР 1. Деятельность торговой фирмы включает в себя обслуживание обращения товаров. Поэтому издержки компании также относятся к расходам обращения.

Затраты – это широкое понятие, а издержки – узкое. Затраты могут включать в себя оплату комплектующих, покупку оборудования.

Как ведется управленческий учет издержек обращения на предприятиях оптовой торговли?

Издержки обращения представляют собой только те расходы, которые связаны с рыночным оборотом продукции.

Состав издержек обращения

Издержки обращения могут включать в себя следующие показатели:

  • Затраты на обслуживание оборудования, на котором изготавливается товар.
  • Затраты на содержание производственных пространств.
  • Оплата транспортировочных услуг.
  • Выплата заработной платы.
  • Выплата процентов по взятым кредитам.

В состав издержек входят только те расходы, которые прямо или косвенно связаны с обращением. Если проценты возникли по задолженности, взятой на иные нужды, они не могут быть отнесены к ИО.

Разновидности

Издержки обращения подразделяются на два вида:

  • Дополнительные. Повышают стоимость реализуемой продукции вследствие того, что производитель тратит средства на перевозку, аренду и обслуживание складов, упаковочные услуги.
  • Чистые. Не оказывают прямого влияния на ценообразование. Относятся непосредственно к процессу производства. Данные издержки обращения направляются на повышение качества товаров и услуг.

Также можно выделить следующие категории ИО:

  • Добавочные издержки. Возникают вследствие промежуточной фазы между производством и реализацией продукта. Расходы могут появиться вследствие хранения товара, его транспортировки, фасовки, упаковки, исправления браков.
  • ИО производителя. Это расходы, которые берет на себя производитель товара. Они могут включать в себя траты на рекламу, анализ рыночной сферы, содержание отделов сбыта.
  • Потребительские издержки. Это расходы потребителя. Они могут появляться вследствие уплаты таможенных сборов, транспортировки продукции.

Существует еще множество классификаций по различным признакам.

От чего зависит уровень издержек обращения?

Уменьшение или увеличение издержек обращения может определяться следующими факторами:

  • Объем оборота товаров. ИО находится в прямой зависимости от объема товарооборота. Чем большим будет объем оборота, тем большими будут и ИО. Связано это с тем, что повышение объема потребует дополнительных ресурсов.
  • Вид выпускаемой продукции. От вида товара зависят издержки по его хранению, транспортировке. Наибольшие расходы связаны с реализацией продовольственной продукции.
  • Производительность труда. Здесь наблюдается обратная зависимость. Увеличение трудовой производительности позволяет сократить уровень издержек.
  • Оптимизация транспортировки. Улучшение системы перевозок, сокращение нерациональных решений по доставке, обращение к другим контрагентам для получения транспортных услуг – все это обеспечивает сокращение издержек.

Изменение всех перечисленных факторов приводит к изменению размера издержек. Всесторонняя оптимизация процессов производства обеспечивает сокращение расходов предприятия, увеличивает выручку от производства и реализации.

Для чего требуется определять показатели ИО?

У предприятия есть определенный торговый план. Менеджер должен знать объем расходов, которые требуются для реализации этого плана. Издержки обращения помогают определить, сколько затрат потребуется для нормальных показателей прибыли.

ВАЖНО! Учет издержек позволяет подсчитать чистую прибыль, спланировать деятельность предприятия. Это знание о приблизительных расходах при реализации продукта.

Издержки обращения в бухгалтерском учете

ИО фиксируются на дебете счета 44 «Расходы на продажи». Бухгалтер должен также создать субсчет «Издержки обращения». Данный субсчет может находиться в корреспонденции с другими счетами. Точное отображение проводки будет зависеть от проведенной торговой операции. Субсчет счета 44 может быть поставлен в одну колонку со следующими счетами:

  • КТ 02 «Амортизация базовых средств».
  • КТ 05 «Амортизация нематериальных объектов».
  • КТ 10 «Материалы».
  • КТ 60 «Проведение расчетов с поставщиками» и прочее.

Проводки по кредиту обозначают производственные расходы. К примеру, в кредите 10 обозначается расход средств по оплате материалов. Перечень расходов является весьма значительным, и все они указываются в бухгалтерской отчетности под определенными номерами.

Что делать с полученными значениями?

Цель менеджера – не полное сокращение издержек, а их оптимизация. Сокращение расходов даже на 10% может быть нецелесообразным, так как данная операция сопровождается большими затратами. Не всякое снижение трат можно считать рациональным. Сокращение показателей может привести к снижению качества обращения.

ПРИМЕР 2. Менеджер решил снизить издержки обращения. Для этого он сокращает расходы на упаковку и рекламу продукции. В результате уровень спроса на товар снижается. Продукт, из-за отсутствия упаковки, становится менее привлекательным для клиентов, портится. В итоге вся экономия оборачивается для предприятия еще большими затратами.

ПРИМЕР 3. Менеджер сокращает издержки обращения в компании, занимающейся предоставлением юридических услуг. В частности, сотрудники больше не смогут проходить профессиональное обучение. В итоге их квалификация снижается, а потому услуги фирмы становятся все менее популярными.

Издержки обращения входят в основные расходы предприятия. Они связаны с производством, транспортировкой и реализацией продукта. В состав ИО входит оплата транспортировочных услуг, затраты на аренду торговых помещений, складов. Они должны быть отражены в бухгалтерском учете. Фиксируются при помощи специальных проводок. Полученные значения по издержкам обращения позволяют оптимизировать расходы.

Источник

Выбор классификации зависит от специфики предприятия и системы управленческого учета внутри компании. Разберемся, какие виды издержек выделяют чаще всего.

Себестоимость продукта или услуги — это все расходы, понесенные для их создания. Но затраты бывают разные, и каждая компания использует свою группировку. Кто-то считает переменные и постоянные траты, кто-то учитывает только прямые и косвенные и так далее. Выбор классификации зависит от специфики предприятия и системы управленческого учета внутри компании. Разберемся, какие виды издержек выделяют чаще всего.

Переменные и постоянные

Это очень популярная классификация. Издержки распределяются исходя из того, как они связаны с объемом производства.

Переменные затраты

Переменные издержки — это все затраты компании, которые зависят от объема производства. То есть, чем больше вы выпустите продукции, тем больше затрат понесете. Про эти траты мы подробно рассказали в статье «Что такое переменные издержки».

Виды издержек

К переменным издержкам относятся:

  • оплата сырья и материалов;
  • покупка товаров для перепродажи;
  • издержки на доставку готовой продукции;
  • траты на электроэнергию и топливо;
  • услуги сторонних фирм, необходимые для производства;
  • сдельная зарплата производственных рабочих и так далее.

Переменные издержки бывают разные. Часть из них прямо пропорциональна выпуску продукции, их так и называют — переменные пропорциональные. Есть те, которые растут медленнее, чем объем производства — дегрессивные издержки. А есть, наоборот, растущие быстрее выпуска — прогрессивные.

Постоянные затраты

Постоянные издержки противопоставлены переменным. Они никак не зависят от выпуска. Даже если компания не работает и ничего не выпускает, издержки все равно возникают. Например:

  • платежи за аренду;
  • заработная плата административно-управленческого персонала;
  • амортизация имущества;
  • часть коммунальных затрат;
  • затраты на банковское обслуживание, бухгалтерские услуги, аудит, юридические консультации;
  • налоги и взносы с зарплаты;
  • проценты по кредитам;
  • представительские расходы и так далее.

Про эти затраты мы подробно рассказали в статье «Что относится к постоянным издержкам».

Прямые и косвенные издержки

Для распределения на прямые и косвенные затраты компания должна определить, можно ли отнести определенную статью затрат на конкретный продукт или нельзя.

Прямые затраты

Прямые издержки можно прямо относить на себестоимость каждой единицы продукции. Например, затраты на воду, сахар и сироп для изготовления лимонада можно без проблем рассчитать на каждую единицу. К прямым затратам относят:

  • расходы на сырье и материалы;
  • затраты на покупку полуфабрикатов;
  • иногда расходы на электроэнергию;
  • зарплату рабочего персонала и так далее.

Косвенные затраты

Косвенные затраты связаны в целом с производством, отнести их на конкретный продукт нельзя. Например, для изготовления лимонада нужно ремонтировать оборудование, убирать цех и так далее. К косвенным издержкам относят:

  • арендную плату;
  • затраты на ремонт оборудования и зданий;
  • зарплату управленцев;
  • и большую часть постоянных затрат.

Для расчета себестоимости косвенные издержки распределяются относительно какой-то базы. Например, относительно материальных затрат или фонда оплаты труда.

Прямые и косвенные издержки очень тесно переплетены с переменными или постоянными. Во многом они даже похожи, но не всегда. Например, затраты на доставку готовой продукции — это переменная статья затрат. Но если позиций много, распределить затраты на доставку на отдельный продукт нельзя. Поэтому достака — это переменная косвенная затрата.

Производственные и непроизводственные издержки

Затраты группируются в зависимости от того, участвуют ли они в производственном процессе или нет.

Производственные издержки

Это траты, связанные с производством. К ним относятся практически все переменные и прямые затраты:

  • на сырье и материалы;
  • на ремонт производственных площадок;
  • заработная плата работников;
  • коммунальные расходы и так далее.

Непроизводственные издержки

Это расходы, которые прямо с производством не связаны, но без них компания существовать не может. Например:

  • зарплата административно-управленческого персонала;
  • аренда офиса;
  • коммунальные затраты в офисе;
  • ремонт офисного здания;
  • покупка мебели;
  • оплата банковских, бухгалтерских и аудиторских услуг.

Явные и неявные или бухгалтерские и экономические издержки

Эта группировка встречается гораздо реже, чем предыдущие. Тут издержки определяются по принципу их фактического наличия.

Явные бухгалтерские издержки

Это все затраты, которые зафиксированы в бухгалтерском учете. Поэтому они явные, их очень легко определить. К ним относятся все постоянные и переменные издержки: зарплата, расходы на сырье, аренда, амортизация и так далее. С явными издержками проблем не возникает.

Явные издержки на виду. Всегда есть документы, доказывающие их наличие: счета, накладные, акты и так далее.

Неявные экономические издержки

Неявные издержки скрыты, их в бухучете не фиксируют. Это затраты, которые возникают из-за принятия тех или иных управленческих решений. 

Например, компания занимается продажей сахара. Это биржевой продукт, цена на который меняется ежедневно. Руководитель может принять решение не продавать сахар сегодня по 60 руб/кг,а продать через неделю. Если цена упадет, это будут неявные издержки. В учете они не зафиксированы, но по факту они существуют, и их можно избежать, если принять другое решение. Неявные издержки — это упущенная выгода компании.

Предприниматель всегда оценивает каждый свой шаг. С кем подписать договор, в какой пропорции производить продукцию, по какой цене продавать. Он выделяет неявные издержки, чтобы понять, какое решение в итоге принесет больше прибыли.

Неявные издержки несет даже собственник бизнеса. Например, он мог пойти работать по найму, а не заниматься бизнесом. Мог вложить деньги в акции или на банковский депозит и получать процент, а не вкладывать их в дело и так далее.

Возвратные и невозвратные издержки

Затраты группируют в зависимости от того, вернутся ли вложенные деньги обратно или нет.

Возвратные издержки

Предполагается, что эта группа затрат рано или поздно вернется обратно. Например, это большая часть производственных расходов. Ведь сначала компания вкладывает деньги в производство, затем реализует готовую продукцию, тем самым возвращая понесенные затраты и получая прибыль. Примеры таких затрат: расходы на сырье, зарплату и так далее.

Невозвратные издержки

Эти затраты компания несет, но уже никогда не сможет вернуть. То есть они не участвуют в создании прибыли. Например:

  • затраты на создание и регистрацию компании;
  • расходы на страхование;
  • расходы на банковские услуги и так далее;
  • расходы на неудавшиеся научно-исследовательские работы.

Релевантные и нерелевантные издержки

Размер релевантных затрат зависит от принимаемого решения. Нерелевантные издержки компания несёт в любом случае.

Например, поехать в командировку можно на корпоративной машине или поезде. Релевантные затраты — это расходы на бензин или на билет. А вот транспортный налог — это нерелевантная затрата, так как его нужно платить при любом исходе. 

Контролируемые и неконтролируемые издержки

Если издержки зависят от предприятия, их называют контролируемыми. Например, это затраты на сырье. Фирма сама устанавливает объем производства, а значит заранее определяет размер затрат на материалы, зарплату и так далее.

Неконтролируемые затраты компания несет независимо от того, хочет она этого или нет. Самый яркий пример — налоги.

Рекомендуем вам облачный сервис Контур.Бухгалтерия. В нем можно вести учет затрат по подразделениям и номенклатуре, строить другие управленческие отчеты. Всем новичкам мы дарим бесплатный пробный период на 14 дней.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 февраля 2021 года; проверки требуют 8 правок.

Задача потребителя — формализованная модель потребительского выбора между различными альтернативами (наборами благ) при заданных ограничениях[1]. Задача потребителя наряду с задачей фирмы является основополагающей при построении моделей частичного и общего равновесия, а также для макроэкономических моделей, которые основываются на идее общего равновесия. Задача потребителя позволяет строить функции спроса, а задача фирмы функции предложения. Модели общего равновесия позволяют анализировать эффект от воздействия различных шоков, включая политику государства.

Множество, в котором осуществляется выбор, называется множеством допустимых альтернатив. При этом выбор потребителя может быть дополнительно ограничен тем, что блага являются товарами и имеют цену, а доход потребителя фиксирован. Тогда в задачу вводят бюджетное ограничение и рассматривают выбор в пределах бюджетного множества. Предполагается также, что на множестве допустимых альтернатив задано отношение предпочтения, которым руководствуется потребитель при осуществлении выбора. В частности, предпочтения могут быть представлены функцией полезности, которая позволяет ранжировать альтернативы.

Чаще всего считают, что отношения предпочтения являются рациональными, а потребитель стремится выбрать наиболее предпочтительную альтернативу из множества доступных. Если существует функция полезности и задано бюджетное ограничение, то задача выбора сводится к максимизации полезности при заданных ценах и доходе, либо к минимизации затрат на приобретение благ при заданных ценах и заданном (минимально приемлемом) уровне полезности.

Задачи максимизации полезности и минимизации затрат являются двойственными, а их решение приводит к одному и тому же оптимальному результату.

Решением задачи потребителя является функция (отображение) спроса. В случае задачи максимизации полезности решением является функция маршалловского (вальрасовского спроса), а случае задачи минимизации издержек — функция хиксовского спроса.

Формализация[править | править код]

В терминах предпочтений[править | править код]

Постановка задачи в терминах предпочтений является наиболее общей, так как не всегда предпочтения могут быть представлены функцией полезности.

Если на множестве допустимых альтернатив X задано отношение предпочтения {displaystyle {succeq }}, то задача потребителя сводится к поиску наиболее предпочтительной альтернативы из множества доступных. Формально это означает, что оптимальный выбор не хуже, чем любой другой:

{displaystyle x^{*}succeq x,,forall xin X}.

Если дополнительно предполагается, что блага являются товарами и имеют цену, а доход потребителя ограничен, то поиск осуществляется внутри бюджетного множества. Тогда оптимальность выбора означает, что любой другой допустимый набор, который строго лучше (в смысле этого отношения предпочтения) данного, не принадлежит бюджетному множеству:

{displaystyle xsucc x^{*}implies pcdot x>R}

Решение задачи потребителя не всегда является единственным. В общем случае критерию оптимальности могут удовлетворять сразу несколько равноценных альтернатив.

Решение задачи с использованием предпочтений в общем случае является затруднительным. Поэтому чаще всего делают предположение о том, что предпочтения могут быть представлены функцией полезности, а на выбор потребителя накладывается бюджетное ограничение. Использование функции полезности означает, что потребитель ведет себя рационально.

Если функция полезности является непрерывной и дифференцируемой, то появляется возможность использования методов теории оптимизации. Тогда задача потребителя может быть поставлена в одной из двух форм: в форме максимизации полезности (прямая задача) или минимизации издержек (двойственная).

Задача максимизации полезности[править | править код]

Задача максимизации полезности является прямой (маршаллианской) задачей потребителя при заданной функции полезности и заданном бюджетном ограничении.

Пусть u(x) — функция полезности потребителя, где x — вектор альтернатив (потребительских наборов), являющийся элементом допустимого множества X. Пусть также p — вектор цен, а R — располагаемый доход потребителя. Прямая задача потребителя заключается в максимизации полезности на допустимом бюджетном множестве, задаваемом бюджетным ограничением pxleqslant R:

{begin{cases}u(x)rightarrow max _{x}\pxleqslant R\xin Xend{cases}}

При достаточно слабых предположениях функция полезности непрерывна, а бюджетное множество ограничено и замкнуто, поэтому такая задача всегда имеет решение (теорема Вейерштрасса).

При дифференцируемости функции полезности условия первого порядка для решения задачи имеют вид:

{displaystyle {frac {partial u(x)}{partial x_{l}}}leq lambda p_{l},,l=1,2,...L}

где lambda  — множитель Лагранжа. Знак равенства соответствует внутреннему решению задачи (в оптимальном решении объем товара строго больше нуля), а знак неравенства — угловому (товар не входит в оптимальную корзину). Решением этой задачи является маршаллианский (вальрасовский) спрос {displaystyle x(p,R)}.

Если подставить маршалловский спрос в целевую функцию (полезности), то получится косвенная функция полезности {displaystyle v(p,w)}.

Задача минимизации расходов[править | править код]

Задача минимизации расходов является двойственной (хиксианской) задаче потребителя формулируется как задача минимизации затрат потребителя на приобретение набора благ при условии, что их полезность будет не меньше некоторой величины (выбираемые альтернативы будут не хуже некоторого фиксированного набора благ):

{displaystyle {begin{cases}phrightarrow min _{h}\u(h)geqslant u(x)\hin Xend{cases}}}

где x — некоторый базовый набор, а h — набор не хуже x из множества допустимых альтернатив.

Условия первого порядка:

{displaystyle lambda {frac {partial u(x)}{partial x_{l}}}leq p_{l},,l=1,2,...L}

где lambda  — множитель Лагранжа. Знак равенства соответствует внутреннему решению задачи, а знак неравенства угловому. Решением этой задачи является хиксианский спрос {displaystyle h(p,x)}.

Если подставить хискианский спрос в целевую функцию то получится функция расходов {displaystyle e(p,{bar {u}})}.

Двойственность[править | править код]

Задачи максимизации полезности и минимизации издержек являются двойственными, то есть они приводят к одному и тому же оптимальному решению. Кроме того, зная оптимум в одной задаче, всегда можно найти оптимум в другой, не решая ее.

В точке оптимума маршаллианский и хиксианский спрос совпадают:

{displaystyle x^{*}(p,R)equiv h(p,{bar {u}})}

При этом полезность в задаче минимизации равна максимуму функции полезности в задаче максимизации {displaystyle v(p,e(p,{bar {u}}))={bar {u}}}, и наоборот: минимум затрат в двойственной задаче равен фиксированному доходу в прямой {displaystyle e(p,v(p,R))=R}.

Свойства решений задачи потребителя[править | править код]

Если предпочтения локально ненасыщаемы, функция полезности дважды непрерывно дифференцируема и сильно квазивогнута, то функция маршаллианского спроса непрерывно дифференцируема по ценам и доходу, а функция хиксианского спроса — по ценам.

Можно показать, что решение прямой задачи потребителя удовлетворяет следующему условию:

{displaystyle MU(x)=lambda p}

где {displaystyle MU(x)} — вектор предельных полезностей (градиент функции полезности).

то есть вектор предельных полезностей пропорционален вектору цен. Это означает, что в оптимальном выборе отношение предельных полезностей отдельных благ (предельная норма замещения) равно отношению их цен:

{displaystyle MRS_{ij}={frac {MU_{i}(x)}{MU_{j}(x)}}={frac {p_{i}}{p_{j}}}}

См. также[править | править код]

  • Отношение предпочтения
  • Множество допустимых альтернатив
  • Бюджетное множество
  • Бюджетное ограничение
  • Маршалловский спрос
  • Спрос Хикса
  • Косвенная функция полезности
  • Функция расходов

Примечания[править | править код]

  1. ↑ Бусыгин В. П., Желободько Е. В., Цыплаков А. Микроэкономика-третий уровень: Учебное пособие //Новосибирск: Издательство СО РАН. — 2005. — c. 103

Литература[править | править код]

  • Бусыгин В.П., Е.В. Желободько, А.А. Цыплаков. Микроэкономика – третий уровень. — Новосибирск, 2003.
  • Черемных Ю.Н. Микроэкономика. Продвинутый уровень. — М.: ИНФРА-М, 2008. — 844 с.
  • Фридман А. А. Лекции по курсу микроэкономики продвинутого уровня. — М.: Издательский дом ГУ ВШЭ, 2007. — ISBN 978-5-7598-0335-5.
Источник

Цена на гуталин выросла с 25 до 30 руб. за тюбик. Эластичность спроса на гуталин равна (-3). Как изменятся расходы потребителей на приобретение гуталина?

Решение:

Эластичность спроса рассчитывается по формуле:

Формула точечной эластичности

Подставив известные значения получим:

Расчёт эластичности

Изменение величины спроса

Абсолютное изменение величины спрса

Величина спроса после повышения цены

Далее рассчитаем, как изменятся расходы потребителей на приобретение гуталина:

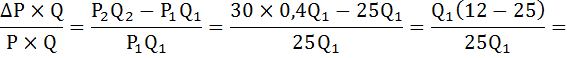
Расчёт изменения расходов1 

Расчёт изменения расходов2

Расходы потребителей на приобретение гуталина снизятся на 52%.

Источник

Увеличением дохода потребителя или пропорциональным снижением цен на товары Х и Y.

Задача 6в. Чем вызван сдвиг бюджетной линии?

Снижением цены товара Y.

Задача 7а. Дана бюджетная линия потребителя.

Цена товара Y – 10. Каков доход потребителя?

Решение: Если Х = 0, то весь доход тратится на товар Y, количество которого равно 15. Отсюда доход равен 15 • 10 = 150.

Задача 7б. Дана бюджетная линия потребителя.

Цена товара Х – 100. Каков доход потребителя? 1000

Задача 7в. Дана бюджетная линия потребителя.

Цена товара Y – 50. Каков доход потребителя? 1500

Задача 8а. Дана бюджетная линия потребителя с доходом 120 ед.

Найти уравнение бюджетной линии.

Решение:Если Х = 0, то весь доход тратится на товар Y, количество которого равно 10. Отсюда цена товара Y = 120 / 10 = 12. Если Y = 0, то весь доход тратится на товар Х, количество которого равно 20. Отсюда цена товара Х = 120 / 20 = 6.

Уравнение бюджетной линии 12Y + 6Х = 120.

Задача 8б.Дана бюджетная линия потребителя с доходом 200 ед.

Найти уравнение бюджетной линии. 20Y + 20Х = 200.

Задача 8в.Дана бюджетная линия потребителя с доходом 500 ед.

Найти уравнение бюджетной линии.5Y + 10Х = 500.

Задача 9а.Даны кривая безразличия и бюджетная линия потребителя. Цена товара Y равна 5 рублей. Найти уравнение бюджетной линии.

Решение:Как в задаче 7а находим доход потребителя – 30 • 5 = 150. Как в задаче 8а находим уравнение бюджетной линии: 5Y + 10Х = 150, или иначе Y = (150 – 10Х) / 5 = 30 – 2Х.

Задача 9б.Даны кривая безразличия и бюджетная линия потребителя. Цена товара Х равна 10 рублей. Найти уравнение бюджетной линии. 30Y + 10Х = 300, или Y = 10 – 1/3Х.

Задача 9в.Даны кривая безразличия и бюджетная линия потребителя. Цена товара Y равна 2 рубля. Найти уравнение бюджетной линии.2Y + 3Х = 120, или Y = 60 – 1,5Х.

Тема: Теория производства

Задача 1а. Затраты фирмы на производство 10 тыс. единиц продукции в течение года составили: заработная плата – 25 млн. руб.; сырье и материалы – 9 млн. руб. Кроме того, фирма арендовала производственные помещения за 48 млн. руб. в год и использовала собственное оборудование, стоимость которого составляла 300 млн. руб., а срок окупаемости – 10 лет. В конце года все затраты были произведены и учтены. Удалось реализовать 100% выпущенных изделий по цене 12 тыс. руб. за штуку. Определите прибыль, накопленную к концу года.

Решение: Затраты фирмы составляют: 25 млн. руб. (заработная плата) + 9 млн. руб. (сырье и материалы) + 48 млн. руб. (аренда) + 30 млн. руб. (300/10 – амортизация оборудования) = 112 млн. руб.

Доход составил 10 тыс. единиц • 12 тыс. руб. за штуку = 120 млн. руб.

Прибыль равна 120 – 112 = 8 млн. руб.

Задача 1б. Затраты фирмы на производство 15 тыс. единиц продукции в течение года составили: заработная плата – 50 млн. руб.; сырье и материалы – 18 млн. руб. Кроме того, фирма арендовала производственные помещения за 96 млн. руб. в год и использовала собственное оборудование, стоимость которого составляла 600 млн. руб., а срок окупаемости – 10 лет. В конце года все затраты были произведены и учтены. Удалось реализовать 100% выпущенных изделий по цене 16 тыс. руб. за штуку. Определите прибыль, накопленную к концу года.

Млн. руб.

Задача 1в.Затраты фирмы на производство 12 тыс. единиц продукции в течение года составили: заработная плата – 5 млн. руб.; сырье и материалы – 2 млн. руб. Кроме того, фирма арендовала производственные помещения за 9 млн. руб. в год и использовала собственное оборудование, стоимость которого составляла 60 млн. руб., а срок окупаемости – 6 лет. В конце года все затраты были произведены и учтены. Удалось реализовать 80% выпущенных изделий по цене 3 тыс. руб. за штуку. Определите прибыль, накопленную к концу года. 2,8 млн. руб.

Задача 2а. Открыв новое дело, бизнесмен вложил в него собственный капитал 80 000. Он мог взять эту сумму в банке под 10 % годовых. Когда после полутора лет работы бизнесмен будет подсчитывать свой доход, какие неявные издержки он вычтет из общей выручки?

Решение: Неявные издержки равны процентам, которые бизнесмен заплатил бы, если бы взял деньги в банке. 1,5 года • (80 000 • 0,1) = 12 000.

Задача 2б. Открыв новое дело, бизнесмен вложил в него собственный капитал 20 000. Он мог взять эту сумму в банке под 5 % годовых. Когда после двух лет работы бизнесмен будет подсчитывать свой доход, какие неявные издержки он вычтет из общей выручки? 2000

Задача 2в. Открыв новое дело, бизнесмен вложил в него собственный капитал 100 000. Он мог взять эту сумму в банке под 20 % годовых. Когда после полугода работы бизнесмен будет подсчитывать свой доход, какие неявные издержки он вычтет из общей выручки? 10000

Задача 3а. Фирма увеличивает применяемый капитал со 12 до 15 ед., используемый труд с 50 до 62,5 ед. Выпуск продукции при этом увеличился с 20 до 22 ед. Какой эффект роста масштаба производства имеет место в данной ситуации?

Решение: Фирма увеличила ресурсы в 1,25 раз (15/12 и 62,5/50), а выпуск увеличился в 1,1 раз (22/20). Это убывающий эффект масштаба производства.

Задача 3б. Фирма увеличивает применяемый капитал с 240 до 300 ед., используемый труд с 1000 до 1250 ед. Выпуск продукции при этом увеличился с 400 до 440 ед. Какой эффект роста масштаба производства имеет место в данной ситуации? Убывающий эффект масштаба производства

Задача 3в. Фирма увеличивает применяемый капитал со 160 до 320 ед., используемый труд с 50 до 100 ед. Выпуск продукции при этом увеличился с 300 до 700 ед. Какой эффект роста масштаба производства имеет место в данной ситуации? Возрастающий эффект масштаба производства

Задача 4а. Функция предельных затрат фирмы МС = 10 + Q (руб.). Цена единицы продукции постоянна и равна 60 руб./шт. Определите объем выпуска, который позволит фирме максимизировать прибыль.

Решение: Фирма максимизирует прибыль при МС = МR, который в условиях совершенной конкуренции равен цене единицы продукции, т.е. 60 руб. Поэтому МR = 60. Откуда МС = 60, а Q = 50.

Задача 4б. Функция предельных затрат фирмы МС = 60 + 2Q (руб.). Цена единицы продукции постоянна и равна 100 руб./шт. Определите объем выпуска, который позволит фирме максимизировать прибыль. 20

Задача 5а. Заполнить таблицу.

Кол-во труда Общий продукт, ТР Средний продукт, АР Предельный продукт, МР

Решение:

Кол-во труда Общий продукт, ТР Средний продукт, АР Предельный продукт, МР
ТР = АР•L= 20•3 = 60 – (найти по этим данным нельзя)
АР = ТР/L=80/4=20 ΔТР / Δ L = 20 / 1 = 20
ТР5 = ТР4 + МР = 80+10=90 АР = ТР/L = 90/5 = 18
АР = ТР/L = 96/6 = 16 ΔТР / Δ L = 6 / 1 = 6

Задача 5б. Заполнить таблицу.

Кол-во труда Общий продукт, ТР Средний продукт, АР Предельный продукт, МР
Кол-во труда Общий продукт, ТР Средний продукт, АР Предельный продукт, МР
–

Задача 5в. Заполнить таблицу.

Кол-во труда Общий продукт, ТР Средний продукт, АР Предельный продукт, МР
Кол-во труда Общий продукт, ТР Средний продукт, АР Предельный продукт, МР
–

Задача 6а. В краткосрочном периоде фирма не может влиять на величину используемого капитала. Определите предельный МР и средний АР продукты труда, исходя из данных таблицы.

Количество используемого труда, L
Совокупный продукт, ТР
Средний продукт, АР
Предельный продукт, МР

Решение:

Количество используемого труда, L
Совокупный продукт, ТР
Средний продукт, АР = ТР / L 35/1=35 80/2=40 123/3=41 156/4=39 177/5=35,4 180/6=30
Предельный продукт, МР = ΔТР / Δ L 35-0=35 80-35=45 123-80=43 156-123=33 177-156=21 180-177=3

Задача 6б. В краткосрочном периоде фирма не может влиять на величину используемого капитала. Определите предельный МР и средний АР продукты труда, исходя из данных таблицы.

Количество используемого труда, L
Совокупный продукт, ТР
Средний продукт, АР
Предельный продукт, МР
Количество используемого труда, L
Совокупный продукт, ТР
Средний продукт, АР
Предельный продукт, МР

Задача 6в. В краткосрочном периоде фирма не может влиять на величину используемого капитала. Определите предельный МР и средний АР продукты труда, исходя из данных таблицы.

Количество используемого труда, L
Совокупный продукт, ТР
Средний продукт, АР
Предельный продукт, МР
Количество используемого труда, L
Совокупный продукт, ТР
Средний продукт, АР
Предельный продукт, МР

Задача 7а.Производственная функция Q = 5L 0,5 • К 0,5 , L – кол-во ч труда, К – кол-во ч работы машины. В день затрачивается 9 ч труда и 9 ч работы машин. Найти количество выпущенной продукции. Определить, каков будет этот объем, если цех удвоил затраты обоих ресурсов.

Решение: Если в день затрачивается 9 ч труда и 9 ч работы машин, то L = К = 9. Тогда выпуск продукции составит Q = 5L 0,5 х К 0,5 =5 х 9 0,5 х 9 0,5 =45единиц.

Если цех удвоил затраты обоих ресурсов, то L = К = 9 • 2 = 18, а выпуск составит Q = 5 • 18 0,5 • 18 0,5 =90 единиц.

Задача 7б.Производственная функция Q = 4L 0,5 • К , L – кол-во ч труда, К – кол-во ч работы машины. В день затрачивается 4 ч труда и 4 ч работы машин. Найти количество выпущенной продукции. Определить, каков будет этот объем, если цех удвоил затраты обоих ресурсов. 32; 90,5

Задача 7в.Производственная функция Q = 25L 0,25 • К 0,25 , L – кол-во ч труда, К – кол-во ч работы машины. В день затрачивается 16 ч труда и 16 ч работы машин. Найти количество выпущенной продукции. Определить, каков будет этот объем, если цех в 4 раза увеличил затраты обоих ресурсов. 100, 200

Задача 8а.Фирма работает по технологии с производственной функцией Q = L 0,5 • К 0,25 . Во сколько раз увеличится выпуск продукции фирмой, если она в 2 раза увеличит использование обоих ресурсов?

Решение:Еслифирма в 2 раза увеличит использование обоих ресурсов, то выпуск составит Q = (2L) 0,5 х (2К) 0,25 = 2 0,5 х L 0,5 х 2 0,25 х К 0,25 = 2 0,5 х 2 0,25 х (L 0,5 х К 0,25 ), т.е. увеличится в 2 0,5 х 2 0,25 или в 2 0,75 ≈ 1,68 раз.

Задача 8б.Фирма работает по технологии с производственной функцией Q = 4 L 0,5 х К 0,5 . Во сколько раз увеличится выпуск продукции фирмой, если она в 4 раза увеличит использование обоих ресурсов? 4

Задача 8в.Фирма работает по технологии с производственной функцией Q = 5 L 0,25 • К 0,5 . Во сколько раз увеличится выпуск продукции фирмой, если она в 16 раз увеличит использование обоих ресурсов? 8

Задача 9а.Производственная функция: Q = L 0,5 • К 0,5 . В день затрачивается 4 ч труда и 4 ч работы машин.

Определить: а) количество выпускаемой продукции; б) средний продукт труда.

Решение: Количество выпускаемой продукции Q = L 0,5 • К 0,5 = 4 0,5 • 4 0,5 = 4 единицы.

Средний продукт труда равен Q / L = 4 /4 = 1.

Задача 9б.Производственная функция: Q = 4 L 0,25 • К 0,25 . В день затрачивается 16 ч труда и 9 ч работы машин.

Определить: а) количество выпускаемой продукции; б) средний продукт капитала. 13,86; 1,54.

Задача 9в.Производственная функция: Q = 2 L 0,25 • К 0,5 . В день затрачивается 256 ч труда и 225 ч работы машин. 120, 0,47.

Определить: а) количество выпускаемой продукции; б) средний продукт труда.

Задача 10а.Процесс производства на предприятии описывается функцией Q = 80 + 10К 2 + 10L, где К – количество капитала, а L – количество труда. Найти предельный продукт труда.

Решение: Необходимо найти производную для L, принимая, что К = const. Тогда (10L)’ = 10.

Задача 10б.Производственная функция определяется уравнением Q = 100 + 12К 2 + 15L, где К – количество капитала, а L – количество труда. Найти предельный продукт капитала. 24К

Задача 10в.Производственная функция определяется уравнением Q = 20 + 6К + 20L 2 , где К – количество капитала, а L – количество труда. Найти предельный продукт труда. 40L

Задача 11а. Два работника вместе производят 80 ед. продукции, а три работника – 100 ед. продукции. Найти предельный продукт третьего работника.

Решение: 100 – 80 = 20 ед.

Задача 11б. Четыре работника вместе производят 120 ед. продукции, а пять работников – 128 ед. продукции. Найти предельный продукт пятого работника. 8

Задача 12а. Совокупный доход фирмы, производящей радиоприемники, составляет 1000 ден. единиц в месяц при объеме выпуска 500 штук в месяц, постоянные издержки равны 800 ден. единиц в месяц, а переменные – 100 ден. единиц в месяц. Чему равна средняя прибыль фирмы?

Решение: Средняя прибыль равна отношению общей прибыли к объему выпуска продукции: АРr = Рr / Q = (1000 – (800+100)) / 500 = 0,2 ден. единиц.

Задача 12б. Совокупный доход фирмы составляет 2000 ден. единиц в месяц при объеме выпуска 800 штук в месяц, постоянные издержки равны 400 ден. единиц в месяц, а переменные – 1200 ден. единиц в месяц. Чему равна средняя прибыль фирмы? 0,5

Тема: Издержки производства

Задача 1а. Заполните таблицу и определите оптимальный объем производства.

Q TC FC VC AC AFC AVC MC

Решение: Т.к. при Q = 0,VC = 0, поэтому FC = 50.

VC = TC – FC. АС = ТС / Q. АFС = FС / Q. AVC = VС / Q. МС = ∆ TC

Q TC FC VC AC AFC AVC MC
– – – –
12,5 37,5

Задача 1б. Заполните таблицу и определите оптимальный объем производства.

Q TC FC VC AC AFC AVC MC
Q TC FC VC AC AFC AVC MC
– – – –
37,5 107,5

Задача 1в. Заполните таблицу и определите оптимальный объем производства.

Q TC FC VC AC AFC AVC MC
Q TC FC VC AC AFC AVC MC
– – – –
3,33
2,5 7,5

Задача 2а. Функция общих затрат фирмы имеет вид ТС = 10Q – Q 2 + 0,05Q 3 . Определить величину предельных затрат фирмы при Q = 4.

Решение: Находим производную функции общих издержек. Получаем (ТС)’ = 10 – 2Q + 0, 15Q 2 . При Q = 4 значение равно 4,4.

Задача 2б. Функция общих затрат фирмы имеет вид ТС = 20Q – 2Q 2 + 0,1Q 3 . Определить величину предельных затрат фирмы при Q = 3. 10,7

Задача 2в.Функция общих затрат фирмы имеет вид ТС = 60Q – 4Q 2 + 0,2Q 3 . Определить величину предельных затрат фирмы при Q = 6. 33,6

Задача 3а. Функция средних переменных затрат имеет вид: AVС = 100 + 20Q. Постоянные затраты равны 120. Найти алгебраическое выражение для функций общих затрат.

Решение: ТС = FC + VС, а VС = AVС • Q, поэтому ТС = 120 + 100Q + 20Q 2 .

Задача 3б.Функция средних переменных затрат имеет вид: AVС = 200 + 50Q. Постоянные затраты равны 400. Найти алгебраическое выражение для функций общих затрат. 400 + 200Q + 50Q 2 .

Задача 3в.Функция средних переменных затрат имеет вид: AVС = 400 + 60 Q. Постоянные затраты равны 500. Найти алгебраическое выражение для функций общих затрат. 500 + 400Q + 60Q 2 .

Задача 4а. При производстве 40 шт. деталей АVС = 20 руб. При выпуске 20 шт. АFС = 10 руб. При выпуске 50 шт. АС = 60 руб. Определите АС при производстве 40 шт. и АVС при 50 шт. деталей.

Решение:Дано

Составим таблицу, дополним и заполним ее.

Q ТС АС = АFС+АVС FС АFС = FС / Q VС АVС
200 = 20•10 10 (по условию)
1000 = 40 • 25 25 = 5 + 20 5 = 200/40 800 = 1000 – 200 (по условию)
60 (по условию) 4 = 200/50 56 = 60 – 4

АС при производстве 40 шт. равна 25, АVС при 50 шт. деталей равна 56.

Задача 4б. При производстве 20 шт. деталей АVС = 10 руб. При выпуске 10 шт. АFС = 5 руб. При выпуске 25 шт. АС = 30 руб. Определите АС при производстве 20 шт. и АVС при 25 шт. деталей. 12,5; 28

Задача 5а. Функция издержек конкурентной фирмы ТС = Q 2 + 5Q + 25. Определите функции переменных, постоянных, средних переменных, средних постоянных, средних общих и предельных затрат.

Решение:

переменные издержки – VС = ТС-FС = Q 2 + 5Q;

постоянные издержки – FС = const = 25;

средние переменные издержки – АVС = VС/ Q = (Q 2 + 5Q / Q = Q + 5;

средние постоянные издержки – FС / Q = 25 / Q

средние общие издержки – АС = ТС/ Q = (Q 2 + 5Q + 25) / Q = Q + 5 + 25 / Q;

предельные издержки – МС = (Q 2 + 5Q + 25)’ = 2Q + 5.

Задача 6а. Средние издержки фирмы составляют 10 и с ростом объема выпуска не изменяются. Насколько увеличатся издержки фирмы при увеличении выпуска с 1000 до 1500 ед. продукции.

Решение: Т.к. средние издержки неизменны, ∆ТС = АС • ∆Q = 10 • (1500 – 1000) = 5000.

Задача 6б. Средние издержки фирмы составляют 20 и с ростом объема выпуска не изменяются. Насколько увеличатся издержки фирмы при увеличении выпуска с 60 до 80 ед. продукции. 400

Задача 7а.Даны объем производства, валовые постоянные и средние переменные издержки. Найти средние валовые издержки при производстве двух единиц продукции.

Объем производства, ед.
Валовые постоянные издержки, руб.
Средние переменные издержки, руб.

Решение: Средние валовые издержки АС = АFС + АVС. АFС = FС / Q = 30 / 2 = 15. АVС по условию 55. Итого ответ 70. Задачу можно решить другим способом. АС = ТС / Q. ТС = VС + FС. VС = АVС • Q = 55 • 2 = 110. FС по условию 30. Ответ: (110 + 30) / 2 = 70.

Задача 7б.Даны объем производства, средние постоянные и средние переменные издержки. Найти валовые издержки при производстве трех единиц продукции. 240

Объем производства, ед.
Средние постоянные издержки, руб.
Средние переменные издержки, руб.

Задача 8а. Q = 100, FC = 250; AVC = 35. Найти общие издержки.

Решение:ТС = FC + VC = FC + АVC • Q = 250 + 35 • 100 = 3750

Задача 8б. Q = 20, АFC = 5; AVC = 25. Найти общие издержки. 600

Последнее изменение этой страницы: 2016-07-22; просмотров: 1779

Теория поведение потребителей (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3

Для данного случая:

Предельные полезности должны относиться как 2:1. Таких сочетаний несколько:

I сочетание: 1 литр молока (MUм=10) и 3 буханки хлеба (MUх=5), т. е. 1-я и 3-я позиции.

II сочетание: 2 литра молока (MUм=8) и 4 буханки хлеба.

Проверим эти сочетания на бюджетное ограничение (2,5 д. ед.).

I сочетание: 1 литр молока ´ 1д. ед. + 3 буханки хлеба ´ 0,5 = 2,5 д. ед.

II сочетание: 2 литра молока ´ 1д. ед + 4 буханки хлеба ´ 0,5 = 4 д. ед.

Бюджетное ограничение позволяет уравновесить только первое сочетание

Вывод: Q М опт. =1 литр; Q м опт. = Q Хопт. = 3 буханки.

Задача №6 на количественный подход к анализу полезности и определение оптимума потребителя: Марина получает от родителей 6 д. е. в неделю на карманные расходы. Эти деньги она тратит на покупку жвачки и конфет. Каждая жвачка стоит 2 д. е., а каждая конфета – 1 д. е. Полезность для Марины каждую неделю складывается из полезности жвачки и полезности конфет. Две составляющие функции полезности представлены табличным способом:

Взвешенная предельная полезность

Взвешенная предельная полезность

1) Заполните пропуски в таблице. 2) Какой потребительский набор выберет Марина?

1) Заполним таблицу

Ответы получены из простых формул:

Предельная полезность: MU = ∆TU / ∆Q = TUn – TUn – 1 / Qn – Qn – 1;

Взвешенная предельная полезность: MUЖ1/РА; MUК1/РВ и т. д.

2) Марина получит максимум полезности, если распределит свой бюджет:

I = PХ*QХ+ PY*QY так, что МUж/Pж = MUк/Pк, при этом бюджет Марины ограничен 6 д. е.

С учетом бюджетных ограничений оптимальная структура покупки для Марины – это 2 жвачки и 2 конфеты, при этом весь бюджет потребителя истрачен, а структура покупки максимально удовлетворит потребности Марины.

Задача №7 на построение кривых безразличия: Постройте кривые безразличия полезности: 1) для двух взаимодополняющих товаров в пропорции 3 : 1; 2) для двух абсолютно взаимозаменяемых товаров пропорции 3 : 1.

Задача №8 на определение предельной нормы замещения: Найти предельную норму замещения товара У товаром Х при переходе от набора В к набору С.

Предельная норма замещения представляет собой то количество одного товара Y, которое потребитель готов заменить единицей другого товара X:

MRS x/y = – Qy/ Qx.

Предельная норма замещения товара У товаром Х при переходе от набора В к набору С равна:

MRS x/y = – Qy/ Qx = – (8-10) / (12-8) = 2 / 4 = 0,5.

Задача №9 на порядковый подход к определению количества благ в оптимальном наборе потребителя: Предельная полезность X для индивида отображается функцией MUХ = 40 – 5*Х, а предельная полезность Y: MUY = 20 – 3*Y. Известны цены благ и доход индивида: PХ = 5; PY=1; I=20. Какое количество каждого из благ должен купить индивид для максимизации общей полезности?

Потребитель получит максимум полезности, если распределит свой бюджет:

I = PХ*QХ+ PY*QY так, что MUХ/PХ = MUY/PY.

Получаем систему из двух уравнений:

Задача №10 на порядковый подход к анализу полезности и определение цены благ в оптимальном наборе потребителя: Функция полезности для данного потребителя U = 4xy, а доход, выделенный им для покупки данных товаров, равен 24 д. е. В оптимальный набор вошли 2 единицы первого блага (Х) и 3 – второго блага (Y). Чему в этом случае равны цены первого и второго благ?

Оптимальный набор должен соответствовать условию бюджетного ограничения:

I = PХ*QХ+ PY*QY 2*Рх + 3*Ру = 24.

Одновременно соотношение цен двух товаров в оптимальм наборе равно соотношению их предельных полезностей: MUx / MUy = Px / Py.

Предельная полезность определяется как первая производная функции полезности:

МUx = dTU / dQХ = 4y; МUy = dTU / dQy = 4x.

Отсюда, МUx = 4*3= 12, МUy = 4*2 = 8.

Поэтому Рх / Ру = 12 / 8 = 3/2.

Можно выразить Рх = 3/2 Ру.

Затем, подставив это выражение в уравнение бюджетного ограничения, получим:

2 * 3/2 Ру + 3Ру = 24

Тогда Рх = 3/2 * Ру = 3/2 * 4=6.

Задача №11 на определение уравнения бюджетной линии: Недельный доход Петрова 40 ден. ед. Он расходует его на хлеб и молоко. Вопрос: а) Если цена буханки хлеба 4, а цена литра молока 10, то каково уравнение бюджетной линии; б) как изменится уравнение бюджетной линии, если доход Петрова уменьшится до 20; в) сколько буханок хлеба смог бы купить Петров, если бы отказался от молока.

А) Подставим данные из условия задачи в уравнение бюджетной линии:.

4 • Qх + 10 • Qм = 40.

Б) Если доход Петрова уменьшится до 20, то уравнение будет выглядеть:

4 • Qх + 10 • Qм = 20.

В) Если бы Петров отказался от молока, то уравнение будет выглядеть:

4 • Qх + 10 • 0 = 40.

Откуда Qх = 10 буханок.

Задача №12 на анализ бюджетной линии и определение дохода потребителя: На рисунке дана бюджетная линия потребителя. Цена товара Y – 10. Каков доход потребителя?

Подставим данные из условия задачи в уравнение бюджетной линии: .

Если Х = 0, то весь доход тратится на товар У, количество которого равно 15.

Отсюда доход равен 15 • 10 = 150.

Задача №13 на анализ бюджетной линии и определение функции бюджетного ограничения: На рисунке дана бюджетная линия потребителя с доходом 120 ед. Найти уравнение бюджетной линии.

Если Х = 0, то весь доход тратится на товар У, количество которого равно 10.

Отсюда цена товара У = 120 / 10 = 12.

Если У = 0, то весь доход тратится на товар Х, количество которого равно 20.

Отсюда цена товара Х = 120 / 20 = 6.

Подставим полученные данные в уравнение бюджетной линии: .

Уравнение бюджетной линии 12 У + 6 Х = 120.

Задача №14 на анализ сдвига бюджетной линии: 1) Чем вызван сдвиг бюджетной линии на рисунке?

2) Допустим, потребитель имеет доход 1000 д. е. в месяц и весь он должен быть израсходован на покупку двух товаров А и Б. Товар А стоит 25 д. е., а товар Б — 50 д. е. Нарисуйте бюджетную линию (2).

3) Какой будет бюджетная линия (3), если доход потребителя вырастает до 1200 д. е.?

4) Какой будет бюджетная линия (4)при доходе 1000, но снижении цены товара А до 20 д. е.

1) Из условия бюджетного ограничения I = PА*QА+ PБ*QБ следует, что сдвиг бюджетной линии (1) на рисунке вызван увеличением цены товара, ведь в этом случае его можно будет купить меньше.

2) Уравнение бюджетной линии (2): 1000 = 25*QА+ 50*QБ.

Бюджетную линию (2) строим по двум точкам:

Если QБ=0, то QА=40;

Если QА=0, то QБ=20.

3) Уравнение бюджетной линии (3): 1200 = 25*QА+ 50*QБ.

Бюджетную линию (3) строим по двум точкам:

Если QБ=0, то QА=48;

Если QА=0, то QБ=24.

4) Уравнение бюджетной линии (4): 1000 = 20*QА+ 50*QБ.

Бюджетную линию строим по двум точкам:

Если QБ=0, то QА=50;

Если QА=0, то QБ=20.

А А А

40 48 50

Задача №15 на порядковый подход к анализу полезности и оптимума потребителя: Предпочтения потребителя заданы в виде функции полезности U(x, y) = xy. Доход равен 800 ден. ед. Цены благ соответственно равны РX = 20, РY= 40. Чему будет равен набор для потребителя? Представьте решение и аналитически, и графически.

Запишем задачу в общем виде:

Поскольку оптимум в этом примере является внутренним, то должно выполняться условие

Таким образом, оптимальный набор должен находиться на прямой х = 2у и в то же время удовлетворять бюджетному ограничению.

Получаем систему из 2-х линейных уравнений:

Ее решение дает оптимальный набор:

Графическая интерпретация этой задачи:

Задача №16 на анализ и построение линии «цена–потребление»: Бюджет индивида равен 200 ден. ед. При цене блага его линия «цена–потребление» отображается формулой 1) На сколько единиц индивид изменит потребление каждого блага при снижении цены блага X с 5 до 4 ден. ед.? 2) Используя данные задачи, постройте кривую спроса.

1) Ассортимент потребляемых благ определяется точкой пересечения бюджетной линии с линией «цена–потребление» (точкой касания бюджетной линии с кривой безразличия).

Системы уравнений при PX = 5 и PX = 4 соответственно:

Тогда ΔX = 20-18 = 2 ед., ΔY = 24-22 = 2 ед.

2) Пункт 2 выполните самостоятельно.

Задача №17 на анализ линии «доход–потребление» и построение кривой Энгеля: При ценах РX = 4; Рy = 5 линия «доход–потребление» индивида имеет вид: 1) На сколько единиц индивид увеличит потребление каждого блага при увеличении его бюджета с 333 до 375 ден. ед? 2) Постройте кривую Энгеля.

1) Ассортимент потребляемых благ определяется точкой пересечения бюджетной линии с линией «доход–потребление» (точкой касания бюджетной линии с кривой безразличия).

Системы уравнений при бюджетах 333 и 375 ден. ед. соответственно:

Тогда потребление блага X изменится на 25-22 = 3 ед., потребление блага Y изменится на 55-49 = 6 ед.

Рис. 1.2. Линия «доход–потребление»

2) Пункт 2 выполните самостоятельно.

3.7. Примеры ответов на тесты

Тест 3.1

Среди следующих утверждений одно является неправильным. Укажите на него:

а) Каждая точка на кривой безразличия означает разную комбинацию двух товаров;

б) Каждая точка на бюджетной линии означает различную комбинацию двух товаров;

в) Все точки на кривой безразличия означают одинаковый уровень удовлетворения потребностей;

г) Все точки на бюджетной линии означают одинаковый уровень денежного дохода;

д) Все точки на кривой безразличия означают одинаковый уровень денежного дохода.

Правильный ответ д).

Данное утверждение является неверным, так как по определению все точки на кривой безразличия означают различные комбинации двух товаров (а), соответствующие одинаковому уровню удовлетворения потребностей (в). Ответы б) и г) относятся к характеристике бюджетной линии и являются верными.

Тест 3.2

Увеличение дохода потребителя графически выражается в:

а) изменении наклона бюджетной линии;

б) параллельном сдвиге бюджетной линии вправо;

в) параллельном сдвиге бюджетной линии влево;

г) уменьшении наклона бюджетной линии;

д) увеличении наклона бюджетной линии.

Правильный ответ б).

Увеличение дохода потребителя означает расширение его возможностей. То есть потребитель получает возможность приобретать большие количества товаров при большем доходе и неизменном уровне цен или при неизменном доходе и снижении цен. Параллельный сдвиг бюджетной линии влево означает уменьшение дохода (в). Изменение наклона бюджетной линии (а): как уменьшение (г), так и увеличение (д) означает изменение в соотношении цен потребляемых благ.

Тест 3.3

Эффект дохода имеет место в следующем случае:

а) Если доходы людей падают, они покупают меньше данного товара;

б) Удешевление товаров приводит к тому, что потребитель может купить больше данного товара, не сокращая объем приобретения других товаров.

В) Объем покупок некоторых товаров сокращается по мере увеличения доходов людей.

Г) По мере того, как доходы людей растут, они сберегают увеличивающуюся часть дохода.

д) Во всех перечисленных случаях.

Правильный ответ б).

Эффект дохода состоит в увеличении возможности удовлетворения потребностей от приобретения товаров либо за счет увеличения дохода при неизменном уровне цен, либо за счет снижения цен при неизменном уровне дохода. Ответ а) и б) определяют сокращение возможностей удовлетворения потребностей. Ответ г) связан с проблемой распределения дохода и характеристикой динамики функции сбережения.

Тема 3.4

Цена товара Х составляет 1,5 руб. Цена товара У составляет 1 руб. Если потребитель оценивает предельную полезность товара У в 30 ютил. И желает максимизировать удовлетворение от покупки товаров Х и У, тогда он должен принять предельную полезность товара Х за:

д) В условии не содержится достаточной информации для ответа на вопрос.

Правильный ответ г).

Соотношение цен товаров равно соотношению их предельных полезностей: Mux / Muy = Px / Py. Поэтому Mux = Muy * Px / Py = 30*1,5 / 1 = 45 (ютил).

Тест 3.5

Предположим, что потребитель имеет доход в 8 долл. Цена товара А равна 1 долл., а цена товара В – 0,5 долл. Какая из следующих комбинаций товаров находится на бюджетной линии?

Правильный ответ г).

Следует исходить из условия бюджетного ограничения: Ра*А + Рв*В = Y. Таким образом, 1* 5 + 0,5* 6 = 8.

Тест 3.6

Общая полезность растет, когда предельная полезность:

в) увеличивается в медленном темпе;

г) увеличивается или уменьшается, но является величиной положительной;
д) является величиной отрицательной.

Правильный ответ г).

Предельная полезность – это прирост общей полезности в расчете на единицу прироста потребления продукта. Общая величина будет увеличиваться до тех пор, пока предельная (прирост) будет иметь положительное значение: если она уменьшается (а) и если она растет (б), даже если растет в медленном темпе (в). Но если предельная величина является отрицательной, общая величина начинает уменьшаться (д).

Тест 3.7

Потребительское равновесие на карте безразличия – это:

а) любое пересечение бюджетной линии и кривой безразличия;

б) любая точка на самой высокой из кривых безразличия;

в) та точка, в которой наклон бюджетной линии равен наклону касательной к ней кривой безразличия;

г) любая точка, расположенная на бюджетной линии;

д) любая точка, расположенная на пространстве, ограниченном бюджетной линией.

Правильный ответ в).

Равновесием потребителя в условиях бюджетных ограничений на графике является точка касания бюджетной линии самой высокой кривой безразличия. Это означает, что в данной точке наклон бюджетной линии и наклон кривой безразличия совпадают. Любое пересечение бюджетной линии и кривой безразличия (а) не может быть равновесием хотя бы потому, что неясно, какую именно кривую безразличия из всей совокупности на карте иметь в виду. Любая точка на самой высокой кривой безразличия (б) может не соответствовать величине бюджета потребителя, а любая точка на бюджетной линии (г) может не являться наилучшей с точки зрения оптимизации потребительских предпочтений.

3.8. Вопросы для самоконтроля

1. Охарактеризуйте общую и предельную полезность: их функции и взаимосвязь. Дайте графическую интерпретацию.

2. Ответьте на вопрос (парадокс А. Смита): “Почему вода, которая настолько необходима, что без нее невозможно жить, имеет такую низкую цену, в то время как у не столь необходимых алмазов такая высокая цена?”

3. Почему предельная полезность снижается?

4. Является ли рациональность естественным свойством человека? Привести примеры нерационального поведения потребителя?

5. Кардинализм и ординализм — два направления в теории потребительского выбора. Сформулировать их общие черты и различия.

6. Что мы понимаем под кривой безразличия? Какую информацию несет в себе кривая безразличия? Почему такие кривые являются: а) нисходящими; б) выпуклыми по отношению к началу координат?

7. Какие факторы определяют бюджетное ограничение потребителя? Какую информацию несет бюджетная линия? Как изменится положение бюджетной линии потребителя при уменьшении потребительского дохода? При удорожании блага X? Удешевлении блага У?

8. Проанализировать, как повлияет на решения потребителей о количестве приобретаемых благ введение Правительством более высоких ставок подоходного налога? Налога с продаж на продукты питания и предметы потребления?

9. Как можно определить (измерить) общую полезность, если известна предельная

10. полезность товара?

11. Каковы условия максимизации общей полезности?

12. В чем проявляется ограниченность теории предельной полезности?

13. Как проявляется эффект замещения в случае с гиффеновским товаром?

14. В чем заключается эффект Веблена?

15. «Эффект дохода» и «эффект замещения». Возможно ли их действие в противоположных направлениях?

1. Микроэкономика. Теория и российская практика: Учебник / Под ред. ­
вой, . М., КНОРУС, 2004. — Гл. 5.

2. Вэриан X. Микроэкономика. Промежуточный уровень. Современный подход. —

М.: Юнити, 1997. — Гл. 2—5.

3. , Игнатьев СМ., Микроэкономика. В 2-х т. — СПб.:
Экономическая школа, 2003. — Т. 1 — Гл. 5.

4. Курс экономической теории: Учебник / Под общей ред. , ­
левой. — Киров: «АСА», 2002. — Гл.5, §9.

5. , Экономикс: Принципы, проблемы и политика: в 2-х
томах / Пер. с англ. 13-го изд. — М.: ИНФРА-М, 2001. — Т.2. —Гл.22— 23.

6. Нуреев P.M. Курс микроэкономики. — М.: Норма-Инфра-М, 2002. — Гл.4.

7. Общая экономическая теория (политэкономия): Учебник / Под общей ред. В. И.
Видяпина и . — М.: ПРОМО-Медия, 1995. — Гл. 17—18.

1. Алчиан Ар. А. Значение измерения полезности // Теория потребительского поведе­
ния и спроса. — СПб.: Экономическая школа, 1993.

2. БлаугМ. Экономическая мысль в ретроспективе. — М., 1994. — С.306—343.

3. Дж., Рынок. Микроэкономическая модель. — СПб., 1992.

4. , Микроэкономика. — М.: ДИС, 1997. — Гл. 5—7.

5. Микроэкономика. — М.: Дело, 1992. — Гл. 3—4.

6. Розанова К, Основы экономического выбора. — М.: ТЕИС, 1996.

7. Суверенитет и рациональность потребителя // Теория потребитель­
ского поведения и спроса. — СПб.: Экономическая школа, 1993.

8. Франк и поведение. — М.: ИНФРА-М, 2000. — Гл. 3—8.

9. Хайман микроэкономика: анализ и применение. В 2-х т. — М.:
Финансы и статистика, 1992. — Т.1. — Гл. 3—4.

10. ХиксДж. Р., Д. Пересмотр теории ценности // Теория потребительского
поведения и спроса. — СПб.: Экономическая школа, 1993.

Оптимальный объем достигается когда отношение предельных полезностей равно отношению цен.

Если 160/80 = 2, то ищем такое же соотношение:

150/2=75 (нет такой предельной полезности конфет);

120/2=60 (Есть такое значение);

90/2=45 (нет такой предельной полезности конфет);

Проверяем бюджет:

Ответ: 1 кг. Конфет и 2 кг. Винограда.

Задание 6.Допустим, потребитель имеет доход 300 ден. ед. в месяц и он весь должен быть израсходован на покупку двух товаров: товара Х ценой 3 ден. ед. за штуку и товара Y ценой 5 ден. ед. за штуку.

Напишите уравнение бюджетной линии и отобразите в виде графика.

Задание 7. На рисунке показана одна из кривых безразличия некоего потребителя и его бюджетная линия.

а) Если цена товара Y равна 50 ден. ед. за единицу, то какой доход имеет потребитель?

б) Какова цена товара Х?

в) Написать уравнение бюджетной линии.

г) Написать уравнение бюджетной линии при условии, что цена товара Y составляет 60 ден. ед. за единицу.

Задание 12. Допустим, потребитель имеет доход 200 ден. ед. На рисунке показаны две бюджетные линии и соответствующие им кривые безразличия.

Определить координаты двух точек линии спроса данного потребителя на товар Х.

– цена товара х.

– цена товара y.

1. Что является предметом изучения теории полезности?

Степень полезности с увеличением количества потребления.

2. Какие факторы влияют на изменение положения и угла наклона бюджетной линии?

Изменение соотношения цен на блага.

Изменения дохода с учетом налоговых отчислений. Следовательно, изменение налогов тоже влияет на доход.

3. В каком случае достигается потребительское равновесие?

Потребитель получает максимальную полезность.

Практическое занятие 3. Спрос, предложение, цена, эластичность

Практическая часть 1

Задание 1.Построить модель частичного рыночного равновесия на рынке зерна, используя данные табл.1, характеризующие общий объем спроса на пшеницу и общий объем предложения пшеницы на зерновой бирже в Канзас-Сити в месяц. Обозначьте равновесную цену буквой «РЕ», а равновесное количество – буквой «QЕ».

Таблица 1. Ситуация на зерновой бирже

Спрос, тыс.бушелей Цена за бушель*, (дол.) Предложение, тыс.бушелей
3,40
3,70
4,00
4,30
4,60
4,90

*Бушель – (англ. bushel) — единица объёма, используемая в английской системе мер. Применяется для измерения сыпучих товаров, в основном сельскохозяйственных (ёмкость примерно на 36 л)

Проанализировав данные табл.1 и построенной модели, ответьте на следующие вопросы:

а) какова будет рыночная или равновесная цена? Каково равновесное количество пшеницы?

Равновесная цена 4,00 доллара за бушель, равновесное количество 75 т.бушелей.

б) почему цена 3,4 дол. не станет на этом рынке равновесной? Почему не станет ею и цена 4,9 дол.?

Объем спроса не равен объему предложения.

в) «Излишки повышают цены, а нехватки их понижают». Вы с этим согласны? Поясните свой ответ.

Не верно. Дефицит увеличивает цену, излишки снижают цену.

г) предположим, что правительство установило потолок цены на пшеницу в размере 3,7 дол. за бушель. Подробно объясните, какие последствия повлечет за собой такая цена? Представьте ваш ответ в графическом изображении на построенной модели. Что могло заставить правительство установить максимальный предел цены?

Избыточный спрос и недостаточное предложение приведет к перераспределению рынка альтернативных продуктов в связи с дефицитом товара. Целью правительства может служить как раз перераспределение рынка, позиционирования альтернативного продукта или снижение нагрузки на население в кризис, для получения политических выгод в ущерб рыночным.

д) допустим, что правительство установило предел цены на пшеницу – 4,6 дол. за бушель. Объясните подробно, какие последствия повлечет за собой эта гарантированная цена. Изобразите ваш ответ на графике. Что могло побудить правительство установить эту гарантированную цену?

Перераспределение рынка на более дешевую альтернативу. Увеличение предложений на начальном этапе и уменьшение поставщиков ввиду падения возможного спроса в будущем.

Задание 2.Поясните с помощью модели рыночного равновесия (графического изображения), как повлияет каждое из перечисленных ниже изменений в спросе и (или) предложении на равновесную цену и равновесное количество продукта на конкурентном рынке:

1) предложение сокращается, а спрос остается неизменным;

Увеличится равновесная цена.

2) спрос сокращается, а предложение остается неизменным;

Уменьшится равновесная цена.

3) предложение увеличивается, а спрос остается неизменным;

Уменьшится равновесная цена.

4) спрос повышается, и предложение повышается;

Равновесная цена не изменится.

5) спрос повышается, а предложение остается неизменным;

Увеличится равновесная цена.

6) предложение увеличивается, а спрос сокращается;

Резко уменьшится равновесная цена.

7) спрос сокращается, и предложение сокращается;

Равновесная цена не изменится.

8) спрос повышается, а предложение сокращается.

Резко увеличится равновесная цена.

Задание3. Предположим, что спрос на товар представлен в виде уравнения РD = 10 – 0,2Q, а предложение – уравнением РS = 2 + 0,2Q , где Q – величины спроса и предложения, а РD и РS – цена соответственно спроса и предложения. Используя условие равновесия PD = PS, определите равновесное количество. Затем определите равновесную цену. В подтверждение ваших ответов дайте графическое изображение двух уравнений.

Приравниваем и решаем:

Отбрасываем знаменатель как не имеющий значения в данном случае.

Задание 4. Функция спроса на мясо имеет следующий вид: QD = 30 – Р, а функция предложения описывается следующим уравнением: QS = 15 + 2Р, где QD и QS – величины соответственно спроса и предложения, а Р – цена. Используя условие равновесия QD = QS, найдите равновесный объем и равновесную цену на мясо и покажите графически. Какая ситуация сложится на рынке мяса (избыток товара или дефицит), если цена упадет до 3 рублей или вырастет до 20 рублей? Сложившуюся ситуацию изобразите на графике.

Равновесная цена 5 ед.денег Равновесный объем 25 ед.мяса

Теоретическая часть 2

Практическая часть 2

Задание 1

Функция спроса населения на данный товар QD = 9 – P, функция предложения данного товара QS = – 5 + 2P.

Предположим, что на данный товар введен налог, уплачиваемый продавцом в размере 2 ден. ед. на единицу товара.

Определите общую сумму налога, поступающего в бюджет (в ден. ед.):

1) 6; 2) 8 2 /3; 3) 10; 4) 12 2 /3; 5) 14; 6) 16 2 /3.

Задание 2

Функции спроса и предложения для конкретного товара имеют вид: QD = 9 – P и QS = – 2 + 2P.

Предположим, что на данный товар введен налог, уплачиваемый продавцом, в размере 2 ден. ед.

Определите, какую цену за единицу продукции реально получает продавец данного товара (в ден. ед.):

1) 3; 2) 5; 3) 7; 4) 9; 5) 1.

Задание 3

Спрос и предложение некоторого товара описываются уравнениями: QD = 600 – 25P и QS = 100 + 100P.

где Р – цена за единицу товара, ден. ед.

Государство установило налог с продажи на единицу данного товара в размере 2,5 ден. ед.

Определите, какую часть налоговых поступлений (в абсолютном измерении) вносят в госбюджет покупатели этого товара ( ден. ед.):

1) 800; 2) 900; 3) 1000; 4) 1100; 5) 1200; 6) 1300.

Ответ №2=900 ден.ед.

Задание 4

Функция спроса на штучный товар имеет вид: QD = 2220 – P, функция предложения: QS = 3P – 300.

Правительство ввело дотацию в 100 ден. ед., получаемую продавцом за каждую единицу продукции. Равновесная цена и равновесный объем продаж после этого составили (в ден. ед.):

1) 480; 2) 500; 3) 555; 4) 600; 5) 645.

Ответ №3=555 ден.ед.

Практическая часть 3

Задание 1.Определить коэффициент прямой эластичности спроса по цене, если известно, что при цене 20 ден. ед. объём спроса на товар 600 штук, а при цене 80 ден. ед. – 200 штук.

Задание 2.За определенный период времени потребитель покупает 12 кг говядины по цене 16 ден. ед. за 1 кг, а по цене 14 ден. ед. – 13 кг. Определите коэффициент эластичности и с какого рода ценовой эластичностью мы имеем дело:

[spoiler title=”источники:”]

http://pandia.ru/text/78/452/39181-3.php

http://poisk-ru.ru/s42415t3.html

[/spoiler]

Источник

Добавить комментарий