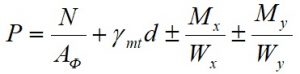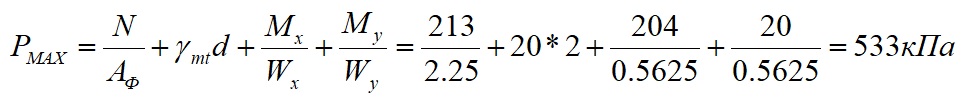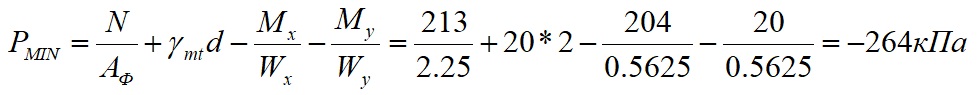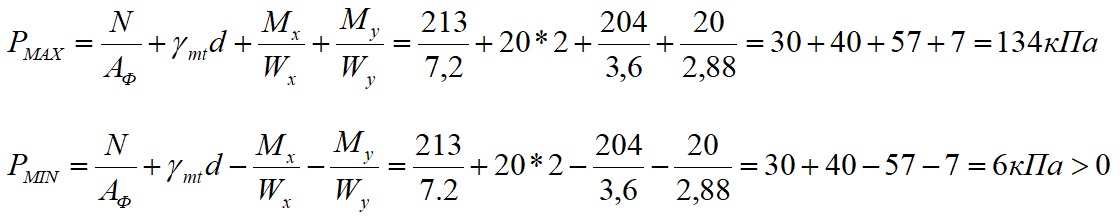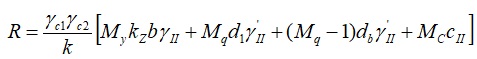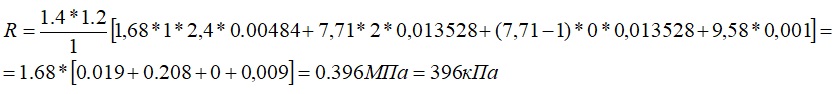5.1 Определение продольных сил от расчетных нагрузок
Грузовая площадь
средней колонны при сетке колонн 5.1х6.5
= 33.15 м2.
Постоянная нагрузка
от перекрытий одного этажа с учетом
коэффициента надежности по назначению
здания n
= 0.95:
;
от ригеля: 4.1х5.4
= 22.14кН;
от
стойки: (0.3х0.3; l
= 3.8м;
= 2500 кг/м3;
f
= 1.15;n
= 0.95):
Временная нагрузка
от перекрытия одного этажа с учетом n
= 0.95:
,
в том числе длительная:
кратковременная
Постоянная нагрузка
от покрытия при весе кровли и плит 5
кН/м2
составит
от ригеля – 22.14 кН; от стойки – 9.34 кН.
Итого:
G
= 188.83
кН.
Временная нагрузка
– снег для III
снегового района при коэффициентах
надежности по нагрузке f
= 1.5 и по назначению здания n
= 0.95:
,
в том числе длительная нагрузка:
,
кратковременная V
= 23.62
кН.
Продольная сила
колонны первого этажа рамы от длительной
нагрузки:
N
= 23.62+188.83+(168.78+261.23)х2 = 1072.47
кН,
то же от полной
нагрузки:
N
= 1072.47 + 23.62 + 111.96х2 = 1320.01
кН.
5.2 Определение изгибающих моментов колонны от расчетных нагрузок
Вычисляют опорные
моменты ригеля перекрытия первого
этажа. Отношение погонных жесткостей,
вводимых в расчет согласно прил.111,
k1
= 1.2k
= 1.2х3.9 = 4.7
Определяем
максимальный момент колонн при загружении
1 + 2 без перераспределения моментов. При
действии длительных нагрузок:
При действии полной
нагрузки:
Разность абсолютных
значений опорных моментов в узле рамы:
При длительных
нагрузках:
При полной нагрузке:
Изгибающий момент
колонны первого этажа от длительной
нагрузки:
От полной нагрузки:
.
Вычисляем изгибающие
моменты колонны, соответствующие
максимальным продольным силам. От
длительных нагрузок:
Изгибающие моменты
колонн первого этажа :
От полных нагрузок:
Изгибающий момент
колонн первого этажа:
5.3 Расчет прочности средней колонны
5.3.1 Характеристики прочности бетона и арматуры
Класс тяжелого
бетона C
20/25 и класс арматуры S400
принимают такими же, как и для ригеля.
Комбинация расчетных
усилий : max
N
= 1320.01 кН, в том числе от длительных
нагрузок Nl
= 1072.47 кН и соответствующий момент M
= 29.33 кНм, в том числе от длительных
нагрузок Ml
= 23.22 кНм и соответствующее загружению
1 + 2 значение N
= 1320.01– 221.53/2 = 1209.3 кН; в том числе Nl
= 1072.47-155.071/2 = 994.93
кН.
5.3.2 Подбор сечений симметричной арматуры
AS1
= AS2
Рабочая высота
сечения d
= h
– c
= 30 – 4 = 26см, ширина b
= 30см.
Эксцентриситет
силы: еo
= M/N
= 29.33/1320.01 = 0.022 м = 2.2см.
Случайный
эксцентриситет: еo
= h/30
= 30/30 = 1см, или еo
= lcol/600
= 380/600 = 0.63 см, но не менее 1см.
Так как эксцентриситет
силы еo
= 2.2см, больше
случайного эксцентриситета еo
= 1 см, то
принимаем для расчета статически
неопределимой системы е=2.2.
Найдем значение
моментов в сечении относительно оси,
проходящей через центр тяжести наименее
сжатой (растянутой) арматуры. При
длительной
нагрузке:
При полной нагрузке:
Отношение l0/r
= 380/8.6 = 44.2
14, где
– радиус ядра сечения.
Выражение для
критической продольной силы при
прямоугольном сечении с симметричным
армированием AS1
= AS2
с учетом, что Ib
= r2A,
IS
= 1A(h/2-a)2,
= 2AS/A
принимает
вид:

Расчетную длину
колонн многоэтажных зданий при жестком
соединении с колоннами в сборных
перекрытиях принимают равной высоте
этажа lo
= l
=4,9м.
Для тяжелого бетона
;
,
принимаем
= 0.24.
Отношение модулей
упругости
= Es/Eb
= 200000/39000 = 5.128.
Задаемся коэффициентом
армирования
и вычисляем критическую силу:
Вычисляем коэффициент
:
Значение е равно:
Определяем граничную
относительную высоту сжатой зоны:
ξlim=
;
Вычисляем:
,
где
.
Определяем площадь
арматуры:

Принимаем 220
S400
с As
= 6.28 см2.
Проектируем консоль
колонны:
Опорное давление
ригеля: V
= 221.53 кН, бетон класса C20/25,
fcd
= 13.33 МПа, b2
= 0.9 МПа, fctd
= 2.755 МПа;
S400,
fyd=
365 МПа, fywd
= 290 МПа.
l
= 20см, lbm
= 25см.
Проверяем условие:
.
Вылет консоли с
учетом зазора 5 см составляет: l1
= l
+ c
= 20 + 5 = 25см,
при
этом
.
Высота сечения
консоли у грани колонны
.
При угле наклона сжатой грани
= 45,
высота консоли у свободного края
,
при этом
.
Рабочая высота
сечения консоли
.
Поскольку
,
консоль короткая.
Консоль армируют
горизонтальными хомутами 26
S240
с АSW
= 0.564 см2
с шагом S
= 10см (при этом S
< 40/4 =10 см и S
< 15 см) и отгибами 216
S400
АS
= 4.02 см2.
Проверяем прочность
сечения консоли:
;
;
;
,
при
этом
.
Правая часть
условия принимается не более:
.
Следовательно,
– прочность обеспечена.
Изгибающий момент
консоли у грани колонны:
.
Площадь сечения
продольной арматуры при
= 0,9:
– принимаем 216
S400
с As
= 4.02 см2.
Колонна
армируется пространственными каркасами,
образованными из плоских сварных
каркасов. Диаметр поперечных стержней
при диаметре продольной арматуры 20
принимают 5
S400
с шагом S
= 300 мм по размеру стороны сечения колонны
b
= 300 мм, что менее 20d
= 500 мм.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчет металлической колонны

Колонны передают нагрузку от выше лежащей конструкции на фундамент. Расчетная схема одноярусной колонны определяется с учетом способа закрепления ее в фундамент, а также способа прикрепления балок, передающих нагрузку на колонну.
Расчетная длина колонны определяется по формуле:
lef = μ*l
где, μ — коэффициент расчетной длины, применяемый в зависимости от закрепления стержня.
При шарнирном креплении колонны сверху и внизу μ = 1.
Колонны могут быть два типа: сплошные и сквозные.
Максимально возможная расчетная нагрузка для сквозных колонн из двух швеллеров достигает 2700…3600 кН, для колонн из двутавров — 5500…6000 кН.
При значительных нагрузках сквозные колонны получаются сложными в изготовлении, более рациональными оказываются сплошные колонны, которые проектируются в виде широкополочного двутавра (прокатного или сварного).
В данном примере рассмотрим расчет сквозной колонны, сечение которого составлено из двух швеллеров.
Расчет металлической колонны относительно оси Х-Х
Подбор сечения колонны начинаем с определения требуемой площади поперечного сечения колонны по формуле:
где, N — расчетная нагрузка на колонну, передаваемая балками;
φ — коэффициент продольного изгиба;
Ry = 24 кН/см2 — расчетное сопротивление стали;
γc — коэффициент условной работы, принимается по табл.1
Табл. 1 Коэффициент условной работы γc
Так как на колонну опирается две главные балки, то N = 2Qmax
где, Qmax — реакция главной балки.
Коэф. φ принимаем по табл.2 в зависимости от предварительно заданной гибкости стержня колонны λs, которая назначается для сквозные колонн с нагрузкой:
- до 1500 кН — λs = 90…60;
- с нагрузкой до 3000 кН — λs = 60…40;
- для сплошных колонн с нагрузкой до 2500 кН — λs = 100…70;
- с нагрузкой до 4000 кН — λs = 70…50
Табл. 2 Коэффициенты устойчивости при центральном сжатии φ
Задаемся гибкостью λs = 70, при этом φ = 0,754
Требуемая площадь сечения:
Требуемый радиус инерции сечения:
По требуемой площади сечения и радиусу инерции подбиаем по сортаменту соответствующий прокатный профиль, выписываем действительные характеристики принятого сечения h, Jx, Jy0, ix, iy, z0 для сечения, составленного из двух швеллеров (Рис.3 а) или для двух двутавров (Рис.3 б).
Рис. 1 Типы сечения сквозных колонн а — сечение из двух швеллеров б — сечение из двух двутавров
По Aтр = 57,37 см2 и ix,тр = 11,3 см по сортаменту принимаем два швеллера №27
Тогда А = 2*35,2 = 70,4 см2, ix = 10.9 см
Рассчитываем гибкость колонны:
По табл. 2 в зависимости от λx = 72.48 определяем коэффициент продольного изгиба φ = 0,737
Проверяем устойчивость стержня колонны по формуле:
Перенапряжение не допускается, недонапряжение допускается не более 5 %.
Принимаем сечение. составленное из двух швеллеров №27 на планках.
Расчет металлической колонны относительно оси Y-Y
Определяем расстояние между ветвями колонны из условия равноустойчивости:
λпр = λх
где, λпр — приведенная гибкость относительно оси Y-Y; λх — гибкость относительно оси Х-Х.
Задаемся гибкостью ветви на участке между планками от 30 до 40. Для рядовых планок равна:
ls = (0.5…0.8)b
где b — ширина сечения сквозной колонны;
Концевые планки принимаются длиной, равной примерно 1,5ls.
Толщина планок назначается из конструктивны условий ts = (1/10…1/25) ls в пределах 6…12 мм. Рис. 2
Рис. 2 Схема расположения планок в колонне
Ширина сечения сквозной колонны равна:
b ≥ 2*bшв + a
где bшв — ширина пояса швеллера, а — 100…150 мм из конструктивных соображений.
b ≥ 2*95 + 100 ≈ 300 мм
Тогда
ls = 0.7*b = 0.7*300 ≈ 200 мм, ts = 8 мм.
Максимальное расстояние между планками l0 определяется по принятой гибкости λ1:
l0 = λ1 * i1
где λ1 = 30 — гибкость на участке между планками; i = 2,73 см — радиус инерции швеллера №27, i1 = iy;
l0 = 30*2.73 = 82 см
Тогда, расчетная длина ветви равна:
lв = l0 + ls
lв = 82+20 = 102 см
Значение lв принимаем кратным высоте колонны.
Вычисляем соотношение:
где Jпл — момент инерции площади поперечного сечения планки;
J1 = 262 см4 — момент инерции сечения швеллера №27;
J1 = Jy
Вычисляем гибкость стержня колонны λy. При n > 5 имеем:
В колоннах с раскосной решеткой (рис.3) имеем:
где 
A – площадь сечения всего стержня колонны;
Ap – площадь сечения раскосов в двух плоскостях.
Рис. 3 Схема узла раскосной решетки
При n < 5 имеем:
При λ1 = 30 — гибкость ветви (задаем в пределах 30…40);
n — соотношение жесткостей;
γ1 — угол перекоса;
Угол перекоса γ1 определяем по формуле:
где Δp — удлинение раскоса (Рис.3).
При λy определяется радиус инерции сечения стержня колонны
где Jy — момент инерции сечения стержня колонны;
Требуемая ширина сечения равна:
Полученное значение меньше b = 300 мм, следовательно, принимаем b = 30 см.
Определяем гибкость стержня колонны относительно свободной оси:
Тогда получаем:
Если λпр = λх, то напряжение можно не проверять, колонна устойчива в двух плоскостях.
Если значение λпр отличается от λх, то необходима проверка устойчивости стержня колонны по формуле:
где φy — коэф. принимаем по табл.2 в зависимости от λy.
Расчет планок
Расчет планок сквозной колонны сводится к назначению их размеров и расчету их прикрепления к ветвям.
Расчет планок проводится на условную поперечную силу Qусл:
Qусл = 0,26 A
где А — площадь поперечного сечения стержня колонны.
Qусл = 0,26*70,4 = 18,3 кН
Поперечная сила, приходящаяся на планку одной грани, равна:
Qпл = Qусл / 2
Qпл = 18,3 / 2 = 9,15 кН
Определяем изгибающий момент и поперечную силу в месте прикрепления планки:
Принимается приварка планок к полкам швеллера угловыми швами с катетом шва kш = 0,7 см.
Тогда прочность по металлу шва, равна:
меньше прочности по металлу границы сплавления, равной
Следовательно, необходима проверка по металлу шва.
Для проверки определяется площадь сварного шва:
где, lш = ls = 20 см — момент сопротивления шва.
Определяем напряжение в шве от момента и поперечной силы:
Прочность шва определяем по равнодействующему напряжению:
Если проверка не выполняется, необходимо увеличить катет шва kш и сделать перерасчет.
Смотрите также: Расчет крепления консоли к металлической колонне
p.s.: Если у вас есть знакомые которые ищут расчет строительных конструкций в программе Lira (Лира), Мономах, SCad поделитесь этой статьей в социальных сетях и тем самым поможете им.
Заказать расчет конструкций
Ранее мы рассматривали расчёт столбчатого фундамента при действии только вертикальной нагрузки и при действии изгибающего момента в одной плоскости.
В этой статье рассмотрим расчёт фундамента под колонну по 1-му предельному состоянию при нагружении фундамента вертикальной нагрузкой и горизонтальной нагрузкой с изгибающими моментами, действующими в двух плоскости.
Как правило, колонну здания закрепляют жёстко только в одном направлении, а в другом закрепляют шарнирно обеспечивая жёсткость каркаса установкой связей, однако даже на фундамент не прилагается изгибающий момент от колонны, он всё равно может появиться из-за действия поперечной нагрузки на уровне закрепления фундамента.
Исходные данные
Исходными данными для расчёта фундамента будут нагрузки, приходящие на фундамент от колонны и инженерно-геологические изыскания.
В результате расчёта рамы в расчётной программе получили следующие нагрузки на фундамент:
N=21.3 т (вертикальная нагрузка)
Mx=14.8 т*м (изгибающий момент)
My=1 т*м (изгибающий момент)
Qx=2.8 т (поперечная нагрузка)
Qy=0,5 т (поперечная нагрузка)
Хочу отметить, что лучше всего проверить 2-а расчётных сочетания:
- Полная ветровая, снеговая, вес конструкций, равномерно-распределённая
- Полная ветровая и вес конструкций
Дело в том, что одно из условий расчёта является недопущение отрыва края фундамента от земли и при отсутствии снеговой нагрузки вертикальная нагрузка будет меньше и соответственно меньше сопортивления изгибающему моменту.
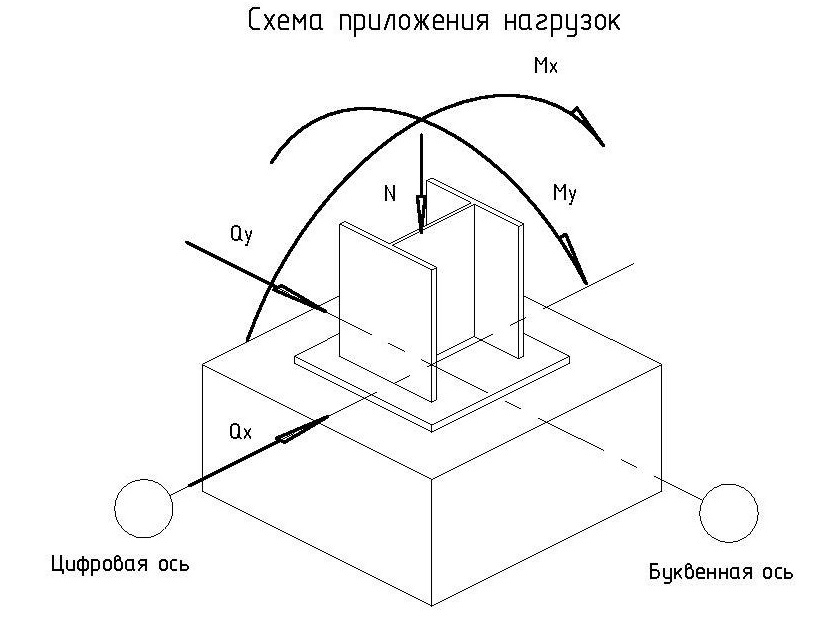
Также нужно отметить, что при расчёте изгибающего момента от действия ветра нужно брать отдельно изгибающий момент в 2-х плоскостях. Т.е. когда изгибающий момент от действия ветра в одной оси даёт положительное значение, в другой оно равно нулю. В этом случае нужно также считать 2-а отдельных сочетания: при действии ветровой нагрузки вдоль оси Х и при действии ветровой нагрузки вдоль оси Y.
Схему приложения нагрузок см. на рисунке ниже.
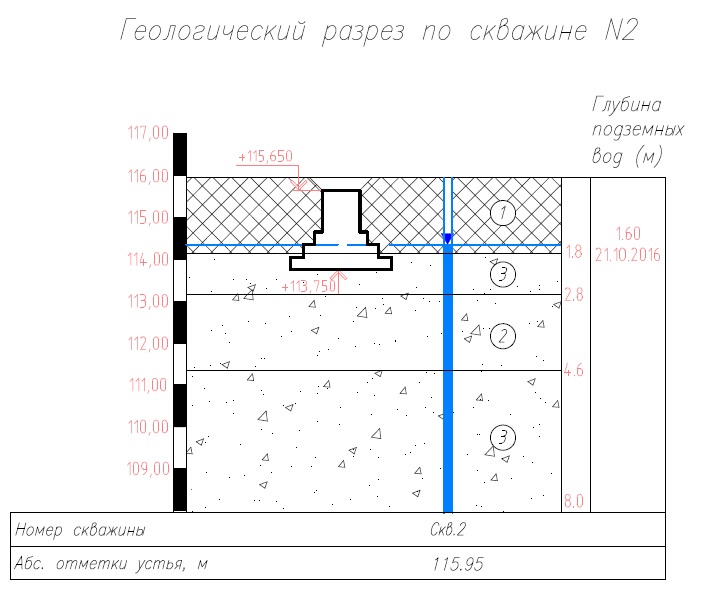
Инженерно-геологические изыскания:
Глубина сезонного промерзания – 1,79 м;
Уровень грунтовых вод 1,6 м;
Свойства грунтов:
Прочностные свойства грунтов определяются по инженерно-геологическим изысканиям. Для этого ищем инженерно-геологический разрез под нужный фундамент и таблицу с нормативными и расчётными характеристиками грунтов. Для расчёта по 1-му предельному состоянию (расчёту на прочность) необходимы расчётные характеристики при α=0.95 (доверительная вероятность расчётных значений), согласно п.5.3.17 СП 22.13330.2016.
ИГЭ-1 — насыпной грунт — песок разной крупности c вкл. строительного мусора до 15-20%, комки суглика, обломки ж.д. плит (в расчёте не участвует т.к. отметка низа фундамента находится ниже этого слоя грунта);
ИГЭ-2 — песок средней крупности, средней плотности, водонасыщенный: (e=0.65, ρ=1,8 т/м³, Е=30 МПа, ϕ=35°, С=1 кПа).
ИГЭ-3 — песок средней крупности, с редкими прослоями текучей супеси, суглинка, глиниcтый средней плотности, водонасыщенный: (e=0.6, ρ=1,82 т/м³, Е=35 МПа, ϕ=36°, С=1,5 кПа).
Уровень грунтовых вод 1,8 м от уровня земли.
Расчёт фундамента
Схема приложения нагрузок на фундамент выглядит следующим образом:
Глубина заложения фундамента
Глубину заложения фундамента определяем в зависимости от максимальной глубины сезонного промерзания, которая дана в отчёте по инженерно-геологическим изысканиям. В моём случае нормативная глубина сезонного промерзания равна dfn=1,79м.
Расчётная глубина сезонного промерзания вычисляется по формуле 5.4 СП 22.13330.2016
df=kh*dfn
где kh — коэффициент, учитывающий влияние теплового режима сооружения, принимаемый для наружных фундаментов отапливаемых сооружений — по таблице 5.2 СП 22.13330.2016; для наружных и внутренних фундаментов неотапливаемых сооружений kh=1,1, кроме районов с отрицательной среднегодовой температурой;
В нашем случае здание неотапливаемое, поэтому
df=1.1*1.79=1.969≈2 м
Глубина заложения фундамента должна быть не выше расчётной глубины промерзания (согласно таблице 5.3 СП 22.13330.2016). Для отапливаемых зданий допускается устраивать фундаменты внутри здания (не под наружными стенами) выше глубины промерзания, но должно быть гарантировано, что в холодное время года будет отопление здания. Если же допускается, что здание могут подвергнуть консервации или отключить отопление, тогда и внутренние фундаменты также должны быть заложены на расчётную глубину промерзания.
Предварительные размеры фундамента
Определяем предварительно площадь основания фундамента.
Предварительные размеры фундамента определяем по формуле:
А=N/(R0-ȳd)
N — вертикальная нагрузка от колонны, которую мы получили при расчёте каркаса здания (N=21,3 т=213 кН);
R0 – расчётное сопротивление грунта, предназначенное для предварительного расчёта приведены в Приложении Б СП 22.13330.2016 (в нашем случае Таблица Б.2 для песка средней крупности и средней плотности R0 = 400кПа, для глины и других грунтов см. другие таблицы в приложении Б);
Таблица Б.2 — Расчетные сопротивления R0 песков
| Пески | Значения R0, кПа, в зависимости от плотности сложения песков | |
| плотные | средней плотности | |
| Крупные | 600 | 500 |
| Средней крупности | 500 | 400 |
| Мелкие: | ||
| маловлажные | 400 | 300 |
| влажные и насыщенные водой | 300 | 200 |
| Пылеватые: | ||
| маловлажные | 300 | 250 |
| влажные | 200 | 150 |
| насыщенные водой | 150 | 100 |
ȳ — среднее значение удельного веса фундамента и грунта на его обрезах, предварительно принимаемое ȳ=20 кН/м³;
d – глубина заложения фундамента (в нашем случае d=2 м)
А=N/(R0-ȳd)=213,246/(400-20*2)=0,6 м²
+20% т.к. фундамент внецентренно сжатый 0,72 м²
Размеры подошвы фундамента назначаются с шагом 0,3 м, размером не менее 1,5х1,5м (Таблица 4 Пособия по проектированию фундаментов на естественном основании)
Таблица 4 Пособия по проектированию фундаментов на естественном основании
| Эскиз фундамента | Модульные размеры фундамента, м, при модуле, равном 0,3 | ||||||||
| h | hpl | соответственно hpl | подошвы | подколонника | |||||
| h1 | h2 | h3 | квадратной b ´ l | прямоугольной b ´ l | под рядовые колонны bcf ´ lcf | под колонны в температурных швах bcf ´lcf | |||
| 1,5 | 0,3 | 0,3 | — | — | 1,5´1,5 | 1,5´1,8 | 0,6´0,6 | 0,6´1,8 | |
| 1,8 | 0,6 | 0,3 | 0,3 | — | 1,8´1,8 | 1,8´2,1 | 0,6´0,9 | 0,9´2,1 | |
| 2,1 | 0,9 | 0,3 | 0,3 | 0,3 | 2,1´2,1 | 1,8´2,4 | 0,9´0,9 | 1,2´2,1 | |
| 2,4 | 1,2 | 0,3 | 0,3 | 0,6 | 2,4´2,4 | 2,1´2,7 | 0,9´1,2 | 1,5´2,1 | |
| 2,7 | 1,5 | 0,3 | 0,6 | 0,6 | 2,7´2,7 | 2,4´3,0 | 0,9´1,5 | 1,8´2,1 | |
| 3,0 | 1,8 | 0,6 | 0,6 | 0,6 | 3,0´3,0 | 2,7´3,3 | 1,2´1,2 | 2,1´2,1 | |
| 3,6 | — | — | — | — | 3,6´3,6 | 3,0´3,6 | 1,2´1,5 | 2,1´2,4 | |
| 4,2 | — | — | — | — | 4,2´4,2 | 3,3´3,9 | 1,2´1,8 | 2,1´2,7 | |
| Далее с шагом | — | — | — | — | 4,8´4,8 | 3,6´4,2 | 1,2´2,1 | — | |
| 5,4´5,4 | 3,9´4,5 | 1,2´2,4 | — | ||||||
| 0,3 м | — | — | — | — | — | 4,2´4,8 | 1,2´2,7 | — | |
| или | — | — | — | — | — | 4,5´5,1 | — | — | |
| 0,6 | — | — | — | — | — | 4,8´5,4 | — | — | |
| — | — | — | — | — | 5,1´5,7 | — | — | ||
| — | — | — | — | — | 5,4´6,0 | — | — |
Предварительно назначаем фундамент 1,5х1,5=2,25 м², что больше предварительного минимума 0,72 м².
Расчёт максимального и минимального краевого давления
Максимальное и минимальное краевое давление находим по формуле 5.11 СП 22.13330.2016 (в формуле момент разложен на 2-е составляющие)
Где N=21,3т=213 кН вертикальная нагрузка от колонны в кН;
Аф=2,25 м² – площадь фундамента, м²;
γmt – средневзвешенное значение удельных весов тела фундамента, грунтов и полов, принимаемое 20 кН/м³;
d=2 – глубина заложения фундамента, м;
Mx-момент от равнодействующей всех нагрузок, действующий по подошве фундамента в кН*м, находим по формуле:
Мx=Mx+Qx*d=14,8+2.8*2=20.4т*м=204кН*м
Мy=My+Qy*d=1+0.5*2=2т*м=20кН*м
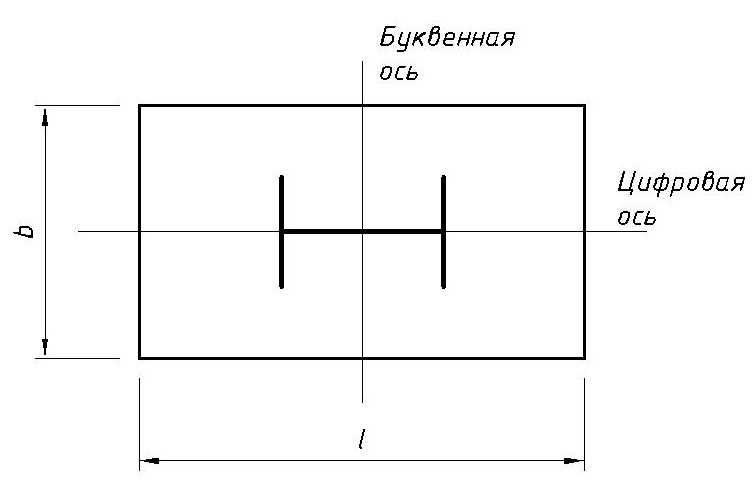
W – момент сопротивления подошвы фундамента, м³. Для прямоугольного сечения находится по формуле W=bl²/6 где в нашем случае b – это сторона подошвы фундамента вдоль буквенной оси, l – длина стороны подошвы фундамента вдоль цифровой оси (см. картинку ниже).
Т.к. предварительно мы приняли фундамент с размерами 1,5х1,5 м, то
Wx= bl²/6=1.5*1.5²/6=0.5625 м³
Wy= lb²/6=1.5*1.5²/6=0.5625 м³
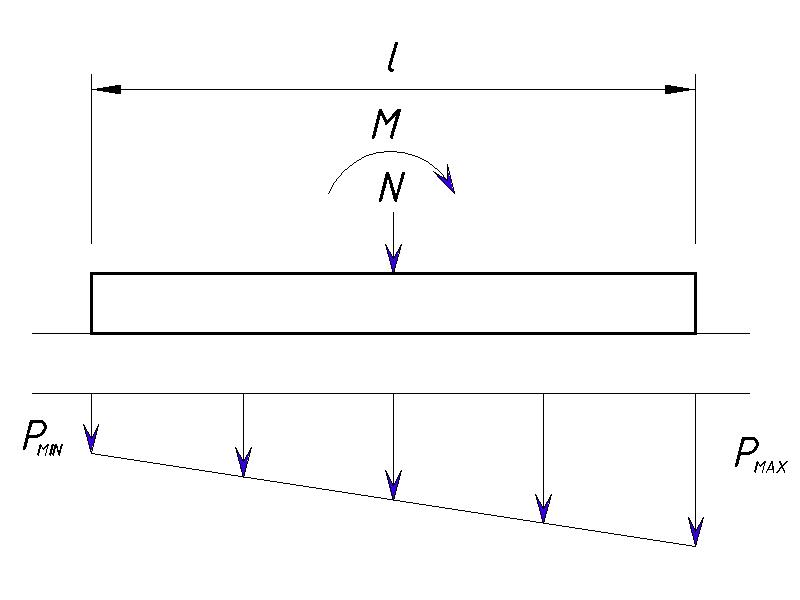
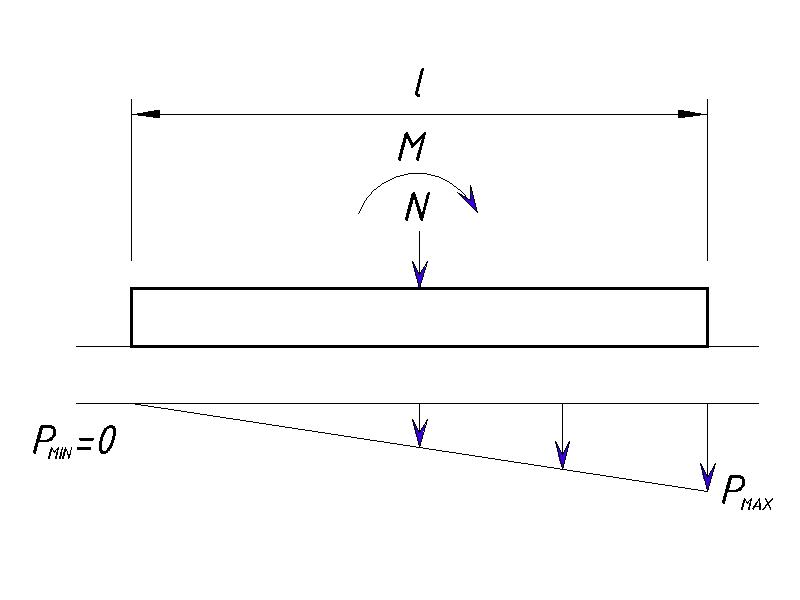
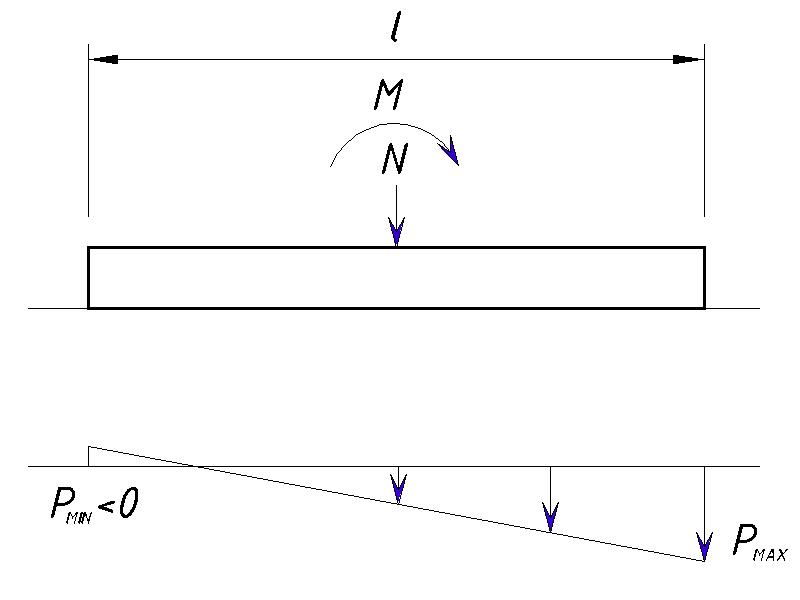
При действии вертикальной нагрузки на фундамент совместно с изгибающим моментом у нас может быть 3 варианта эпюр давления на грунты:
- Трапециевидная
- Треугольная
- Треугольная с отрывом края фундамента
Нельзя допускать, чтобы происходил отрыв фундамента, т.е. Pmin всегда должен быть ≥0.
В нашем случае Pmin<0, поэтому нужно увеличить ширину фундамента таким образом, чтобы Pmin стал больше или равен нулю. Далее увеличиваем размеры фундамента методом подбора. При этом шаг изменения размера фундамента равен 300 мм.
Назначаем фундамент согласно модульным размерам с шагом 0,3 м. Лучше использовать фундамент прямоугольной формы с длинной стороной по оси наибольшего изгибающего момента. Увеличиваем размеры фундамента до тех пор, пока Pmin не станет больше нуля
В результате подбора мы получили, что фундамент должен иметь размеры 3,0х2,4 м (l=3.0м, b=2.4м)
Аф=3,0*2,4=7,2 м² – площадь фундамента, м²;
Wx= bl²/6=2.4*3.0²/6=3.6 м³
Wy= lb²/6=3.0*2.4²/6=2.88 м³
Для фундаментов колонн зданий, оборудованных мостовыми кранами грузоподъёмностью выше 75 т и выше, а также для фундаментов колонн открытых крановых эстакад грузоподъёмностью выше 15 т, для сооружений башенного типа, а также для всех типов сооружений при расчётном сопротивлении грунта основания R<150кПа размеры фундамента нужно назначать такими, чтобы эпюра давлений была трапециевидной и Pmin/Pmax≥0.25 (п.5.6.27 СП 22.13330.2016). В нашем случае мы должны проверить расчётное сопротивление грунта, и если оно будет меньше 150кПа, то нужно ещё увеличить размеры фундамента.
Расчёт сопротивления грунта
Расчётное сопротивление грунта основания рассчитываем по формуле 5.7 СП 22.13330.2016
γс1=1,4 (таблица 5.4 СП 22.13330.2016)
γс2=1,2 (таблица 5.4 СП 22.13330.2016)
Таблица 5.4 СП 22.13330.2016
| Грунты | Коэффициент γс1 | Коэффициент γс2 для сооружений с жесткой конструктивной схемой при отношении длины сооружения или его отсека к высоте L/H, равном | |
| 4 и более | 1,5 и менее | ||
| Крупнообломочные с песчаным заполнителем и пески, кроме мелких и пылеватых | 1,4 | 1,2 | 1,4 |
| Пески мелкие | 1,3 | 1,1 | 1,3 |
| Пески пылеватые: маловлажные | 1,25 | 1,0 | 1,2 |
| и влажные, насыщенные водой | 1,1 | 1,0 | 1,2 |
| Глинистые, а также крупнообломочные с глинистым заполнителем с показателем текучести грунта или заполнителя IL≤0,25 | 1,25 | 1,0 | 1,1 |
| То же, при 0,25< IL ≤0,5 | 1,2 | 1,0 | 1,1 |
| То же, при IL >0,5 | 1,1 | 1,0 | 1,0 |
| Примечания
1 К сооружениям с жесткой конструктивной схемой относят сооружения, конструкции которых специально приспособлены к восприятию усилий от деформации оснований, в том числе за счет мероприятий, указанных в 5.9. 2 Для зданий с гибкой конструктивной схемой значение коэффициента γс2 принимают равным единице. 3 При промежуточных значениях L/H коэффициент γс2 определяют интерполяцией. 4 Для рыхлых песков γс1 и γс2 , принимают равными единице. |
k=1 (п.5.6.7 СП 22.13330.2016 коэффициент, принимаемый равным единице, если прочностные характеристики грунта (φII и СII ) определены непосредственными испытаниями, и k=1,1, если они приняты по таблицам приложения А).
My=1,68 (таблица 5.5 СП 22.13330.2016)
Mq=7,71 (таблица 5.5 СП 22.13330.2016)
Mc=9,58 (таблица 5.5 СП 22.13330.2016)
Тут хочу обратить внимание, несмотря на то, что мы опираемся на грунт ИГЭ-3, грунт ИГЭ-2 имеет более низкие прочностные характеристики и он заложен ниже грунта ИГЭ-3, поэтому мы принимаем считаем несущую способность основания по ИГЭ-2.
Таблица 5.5 СП 22.13330.2016
| Угол внутреннего трения φII, град. | Коэффициенты | ||
| My | Mq | Mc | |
| 0 | 0 | 1,00 | 3,14 |
| 1 | 0,01 | 1,06 | 3,23 |
| 2 | 0,03 | 1,12 | 3,32 |
| 3 | 0,04 | 1,18 | 3,41 |
| 4 | 0,06 | 1,25 | 3,51 |
| 5 | 0,08 | 1,32 | 3,61 |
| 6 | 0,10 | 1,39 | 3,71 |
| 7 | 0,12 | 1,47 | 3,82 |
| 8 | 0,14 | 1,55 | 3,93 |
| 9 | 0,16 | 1,64 | 4,05 |
| 10 | 0,18 | 1,73 | 4,17 |
| 11 | 0,21 | 1,83 | 4,29 |
| 12 | 0,23 | 1,94 | 4,42 |
| 13 | 0,26 | 2,05 | 4,55 |
| 14 | 0,29 | 2,17 | 4,69 |
| 15 | 0,32 | 2,30 | 4,84 |
| 16 | 0,36 | 2,43 | 4,99 |
| 17 | 0,39 | 2,57 | 5,15 |
| 18 | 0,43 | 2,73 | 5,31 |
| 19 | 0,47 | 2,89 | 5,48 |
| 20 | 0,51 | 3,06 | 5,66 |
| 21 | 0,56 | 3,24 | 5,84 |
| 22 | 0,61 | 3,44 | 6,04 |
| 23 | 0,66 | 3,65 | 6,24 |
| 24 | 0,72 | 3,87 | 6,45 |
| 25 | 0,78 | 4,11 | 6,67 |
| 26 | 0,84 | 4,37 | 6,90 |
| 27 | 0,91 | 4,64 | 7,14 |
| 28 | 0,98 | 4,93 | 7,40 |
| 29 | 1,06 | 5,25 | 7,67 |
| 30 | 1,15 | 5,59 | 7,95 |
| 31 | 1,24 | 5,95 | 8,24 |
| 32 | 1,34 | 6,34 | 8,55 |
| 33 | 1,44 | 6,76 | 8,88 |
| 34 | 1,55 | 7,22 | 9,22 |
| 35 | 1,68 | 7,71 | 9,58 |
| 36 | 1,81 | 8,24 | 9,97 |
| 37 | 1,95 | 8,81 | 10,37 |
| 38 | 2,11 | 9,44 | 10,80 |
| 39 | 2,28 | 10,11 | 11,25 |
| 40 | 2,46 | 10,85 | 11,73 |
| 41 | 2,66 | 11,64 | 12,24 |
| 42 | 2,88 | 12,51 | 12,79 |
| 43 | 3,12 | 13,46 | 13,37 |
| 44 | 3,38 | 14,50 | 13,98 |
| 45 | 3,66 | 15,64 | 14,64 |
kz=1 (п.5.6.7 СП 22.13330.2016 коэффициент, принимаемый равным единице при b<10 м);
b=2.4 (ширина фундамента);
γII — (осредненное (см. 5.6.10) расчетное значение удельного веса грунтов, залегающих ниже подошвы фундамента (при наличии подземных вод определяется с учетом взвешивающего действия воды), кН/м³) на глубину, равную z=b/2=0.75м. Если быть проще, удельный вес грунта – это плотность грунта в кН/м³. Чтобы перевести плотность грунта в т/м³ в кН/м³ значение умножают на 10 (1,8т/м³=18 кН/м³).
Т.к. у нас грунты водонасыщенные, то в нашем случае определяем с учётом взвешивающего действия воды по формуле 36 Пособия по проектированию оснований зданий и сооружений
γsb = (γs – γw)/(1 + e))
где γw – удельный вес воды, равный 10 кН/м³,
e=0.65 — коэффициент пористости, принимаемый по данным инженерно-геологических изысканий,
γII = (γs – γw)/(1 + e)) =(18-10)/(1+0.65)=4.84 кН/ м³;
γ’II — (расчетное значение удельного веса грунтов, залегающих выше подошвы фундамента). В нашем случае это будет обратная засыпка, поэтому удельный вес грунта без учёта взвешивающего действия воды 16 кН/м³.
Коэффициент пористости задаётся не менее 0,65. Глубина грунтовых вод 1.6 м от поверхности земли. Поэтому удельный вес грунта с учётом взвешивающего действия воды
γsb = (γs – γw)/(1 + e)) =(16-10)/(1+0,65)=3,64 кН/м³ (на глубине от 2 до 1,6 м, т.е. мощность слоя 0,4 м);
Расчётное значение вычисляем как осреднённое значение удельного веса грунта по формуле
γ’II=Σ γ’i*h/Σhi=(3.64*0,4+16*1,6)/2=13,528 кН/м³;
d1=2.0м (глубина заложения фундамента от уровня планировки);
db=0 (глубина подвала, при его отсутствии равно нулю согласно примечанию 5 к п.5.6.7 СП 22.13330.2016);
СII=1кПа (расчётное значение удельного сцепления грунта, залегающего непосредственно под фундаментом, принимаемое по данным изысканий, либо согласно Приложению А СП 22.13330.2016);
Рассчитываем расчётное сопротивление грунта под основанием:
При действии изгибающего момента на фундамент краевое давление Rmax=R/1.2=0.330 МПа (п.5.6.26 СП 22.13330.2016).
Pmax=134кПа < R=330кПа
Также мы видим, что R>150 кПа, поэтому увеличивать размеры фундамента нет необходимости.
Следовательно, фундамент удовлетворяет требованиям по несущей способности основания.
После этого нужно сконструировать фундамент, назначить размеры, арматуру, бетон, что обязательно рассмотрю в следующих статьях.
Расчётную программу в Excel можно скачать по ссылке