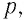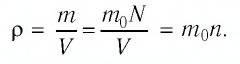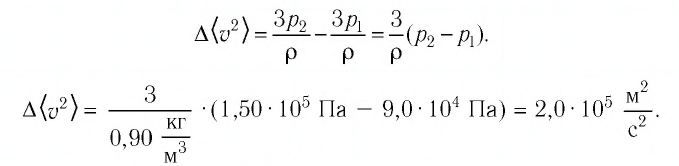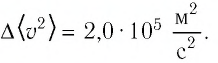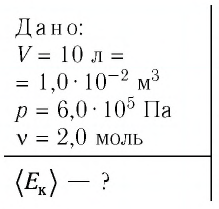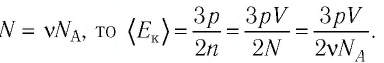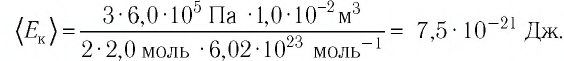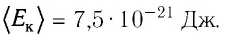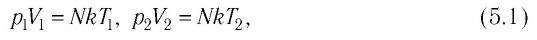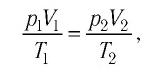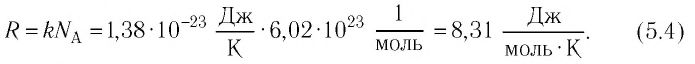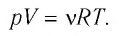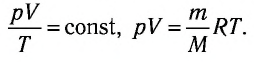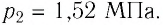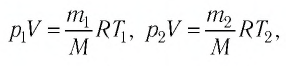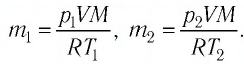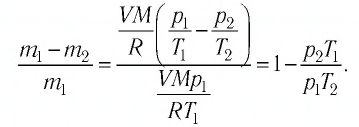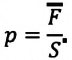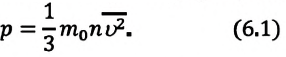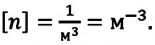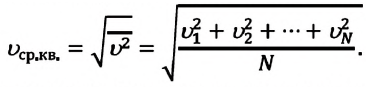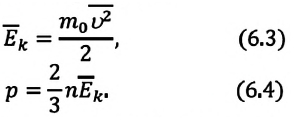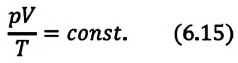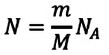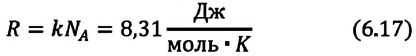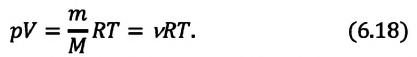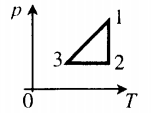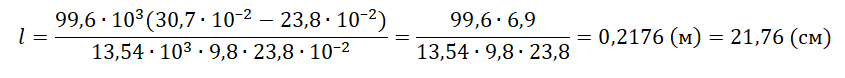Уравне́ние состоя́ния идеа́льного га́за (иногда уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
,
где
Уравнение состояния идеального газа можно записать в виде:
,
где 


или в виде
,
где 


Эта форма записи носит имя уравнения (закона) Клапейрона — Менделеева.
Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную 
Менделеев обнаружил, что 


Связь с другими законами состояния идеального газа[править | править код]
В случае постоянной массы газа уравнение можно записать в виде:
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
— закон Бойля — Мариотта — Изотермический процесс.
— Закон Гей-Люссака — Изобарный процесс.
— закон Шарля (второй закон Гей-Люссака, 1808 г.) — Изохорный процесс
В форме пропорции 
С точки зрения химика этот закон может звучать несколько иначе: объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:
.
1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:
.
- Закон Бойля — Мариотта
Закон Бойля — Мариотта
назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.
В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
где 

Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. Это обстоятельство может быть прояснено на основании молекулярных представлений.
С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.
С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение 

См. также[править | править код]
- Совершенный газ
- Реальный газ
- Уравнение состояния реального газа
Примечания[править | править код]
Литература[править | править код]
- Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высшая школа, 2009. — 527 с. — ISBN 978-5-06-006161-1.
Онлайн калькулятор поможет рассчитать какое будет конечное давления идеального газа от изменения температуры, при условии, что объем газа остается постоянным. Зависимость давления от температуры в этом случае описывается законом Гей-Люссака (законом Шарля).
Формула: P2 = P1×T2/T1
Где:
P1 – начальное давление;
P2 – конечное давление;
T1 – начальная температура (в Кельвинах);
T2 – конечная температура (в Кельвинах).
Например, данный калькулятор поможет приблизительно определить зависимость давления в шинах от температуры.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также
Давление идеального газа, теория и онлайн калькуляторы
Давление идеального газа
Определение давления идеального газа
Определение
Давление идеального газа – это один из самых важных макроскопических параметров, при помощи которого характеризуют состояние
системы в молекулярной физике.
Обозначают давление буквой $p$. Если для известной массы идеального газа определены давление и температура (или объем), то полагают, что состояние термодинамической системы в состоянии равновесия определяется однозначно, так как существующие законы и уравнения молекулярно кинетической теории (МКТ) позволяют все остальные параметры вычислить.
В общем случае давление определяют как:
[p={mathop{lim }_{Delta Sto 0} frac{Delta F_n}{Delta S} }left(1right),]
где $F_n$ проекция силы на нормаль к поверхности S данная сила оказывает воздействие, $Delta S$- площадь поверхности.
Идеальный газ оказывает давление на стенки сосуда, в котором он находится, за счет того, что молекулы этого газа движутся и ударяются о стенки сосуда. Давление идеального газа можно найти, применяя основные положение МКТ. При этом получают, что давление идеального газа равно:
[p=frac{1}{3}nm_0{leftlangle v_{kv}rightrangle }^2left(2right),]
где $m_0$ – масса одной молекулы газа; $n$- концентрация молекул газа; $leftlangle v_{kv}rightrangle =sqrt{frac{1}{N}sumlimits^N_{i=1}{v^2_i}}, N $- количество молекул в объеме газа равном $V$. Уравнение (2) называют основным уравнением МКТ. Его можно записать в другом виде, используя среднюю кинетическую энергию молекул ($leftlangle E_krightrangle $):
[p=frac{2}{3}nleftlangle E_krightrangle left(3right).]
С таким важным термодинамическим параметром как термодинамическая температура давление связывает формула:
[p=nkT left(4right),]
где $k$ – постоянная Больцмана. Уравнение (4) называют уравнением состояния идеального газа.
Если проводить изохорный процесс ($V=const$) с некоторой массой идеального газа, то давление его будет подчинено закону Шарля:
[p_2=p_1frac{T_2}{T_1}left(5right),]
где $p_1$- давление газа имеющего температуру $T_1$.
При проведении изотермического процесса ($T=const$) c постоянной массой некоторого газа поведение давления можно характеризовать, используя уравнение:
[p_1V_1=p_2V_2left(6right).]
В соответствии с законом Дальтона давление смеси газов можно найти как сумму давлений каждого газа:
[p=sumlimits^N_{i=1}{p_i} left(7right),]
где $p_i$ – давление каждого газа в отдельности.
Уравнения МКТ, содержащие давление идеального газа
Уравнение Менделеева – Клапейрона (еще один вариант уравнения состояния):
$pV=frac{m}{mu }RT$(8),
где $frac{m}{mu }=nu $ -количество вещества; $m$ – масса газа; $mu $- молярная масса газа; $R$ – универсальная газовая постоянная.textit{}
Определение работы газа в термодинамике:
[A=intlimits^{V_2}_{V_1}{pdV}left(9right).]
Соответственно, первое начало термодинамики для идеального газа в дифференциальном виде запишем как:
[delta Q=pdV+frac{i}{2}nu RdTleft(10right),]
где $i$ – число степеней свободы молекулы газа; $delta Q$ – элементарное количество теплоты, которое получает идеальный газ; $frac{i}{2}nu RdT=dU$ – изменение внутренней энергии термодинамической системы.textit{}
Примеры задач с решением
Пример 1
Задание. В идеальном газе проводят процесс, при котором $p=frac{AU}{V},$ где $U$ – внутренняя энергия газа; $A=const$ для определенного газа. Сравните коэффициенты пропорциональности $A$, если в первом случае газ одноатомный, во втором двух атомный. textit{}
Решение. Внутренняя энергия идеального газа для любого процесса равна:
[U=frac{i}{2}nu RT left(1.1right).]
Состояние идеального газа описывает уравнение Менделеева – Клайперона:
[pV=nu RT left(1.2right).]
Подставим правую часть уравнения, которое описывает заданный в условиях задачи процесс ($p=frac{AU}{V}$) вместо давления в (1.2), имеем:
[frac{AU}{V}V=nu RT left(1.3right).]
Получим из (1.3), что внутренняя энергия вычисляется как:
[U=frac{1}{A}nu RTleft(1.4right).]
Сравним выражения для внутренней энергии (1.1) и (1.4), имеем:
[frac{i}{2}=frac{1}{A}left(1.5right).]
Для одноатомного газа $i=3$; для двухатомного газа (без учета колебаний молекул) $i=5$.
[frac{3}{2}=frac{1}{A_1};; frac{5}{2}=frac{1}{A_2}to frac{A_2}{A_1}=frac{3}{2}cdot frac{2}{5}=frac{3}{5}.]
Ответ. $frac{A_2}{A_1}=frac{3}{5}$
Пример 2
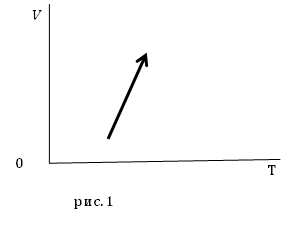
Задание. На рис.1 представлены процессы, проводимые с постоянной массой идеального газа, укажите, как изменяются давления в процессах?
Решение. Уравнение процесса можно аналитически описать уравнением:
[V(T)=AT-B left(2.1right),]
где $A$ и $B$ положительные постоянные величины.
Состояние газа определим при помощи уравнения Менделеева – Клапейрона:
[pV=nu RT left(2.2right).]
Вместо объема подставим уравнение процесса в (2.2):
[pleft(AT-Bright)=nu RTleft(2.3right).]
Раздели обе части (2.3) на температуру:
[frac{pleft(AT-Bright)}{T}=nu Rto pleft(A-frac{B}{T}right)=nu Rto p=frac{nu R}{A-frac{B}{T}} left(2.4right).]
Из уравнения (2.4) следует, что при увеличении температуры $frac{B}{T}$ уменьшается, следовательно, знаменатель дроби правой части выражения (2.4) увеличивается, значит, давление уменьшается.
Ответ. Давление в заданном процессе уменьшается.
Читать дальше: диэлектрический гистерезис.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Содержание:
Идеальный газ:
Наиболее простым из всех агрегатных состояний вещества является газообразное. Поэтому изучение свойств веществ начинают с газов. Газ (греч. chaos — хаос) — такое агрегатное состояние вещества, когда составляющие его частицы почти свободно и хаотически движутся между соударениями, во время которых происходит резкое изменение их скорости. Термин «газ» предложил в начале XVII в. нидерландский химик Ян Батист ван Гельмонт (1579— 1644).
Макро- и микропараметры:
При изучении механики в 9-м классе вы познакомились с понятием «состояние механической системы тел». Параметрами этого состояния являются координаты, скорости или импульсы тел. В тепловых процессах основными физическими величинами, характеризующими состояние макроскопических тел без учёта их молекулярного строения, являются давление
Одна из важнейших задач молекулярно-кпнетической теории состоит в установлении связи между макроскопическими и микроскопическими параметрами.
Идеальный газ
Для теоретического объяснения свойств газов используют их упрощённую модель — идеальный газ.
Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия их взаимодействия равна нулю); силы действуют только во время столкновений молекул, причём это силы отталкивания.
Поведение молекул идеального газа можно описать, используя законы Ньютона и учитывая, что между соударениями молекулы движутся практически равномерно и прямолинейно.
Модель идеального газа можно использовать в ограниченном диапазоне температур и при достаточно малых давлениях. Так, например, свойства водорода и гелия при нормальном атмосферном давлении и комнатной температуре близки к свойствам идеального газа.
Изучая физику в 7-м классе, вы узнали, что давление газа на стенки сосуда, в котором он находится, как и на любое тело, помещённое внутрь сосуда, создаётся в результате ударов частиц, образующих газ (рис. 14). Вследствие хаотичности их движения усреднённое по времени давление газа в любой части сосуда одинаково, и его можно определить по формуле
Выражение (3.1) называют основным уравнением молекулярно-кинетической теории идеального газа. Это уравнение позволяет рассчитать макроскопический параметр давление р идеального газа через массу 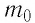
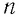
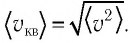
Зависимость давления газа от среднего значения квадрата скорости 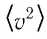
Обозначим через 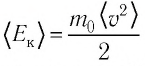
Из выражения (3.2) следует, что давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации.
Пример №1
Баллон электрической лампы наполнен газом, плотность которого 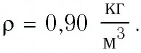
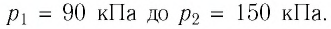
Решение. Покажем, что между плотностью р газа и концентрацией 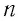
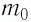
Тогда основное уравнение молекулярно-кинетической теории можно записать в виде: 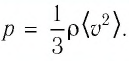
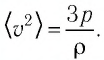
Ответ:
Пример №2
В сосуде вместимостью 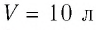
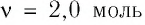
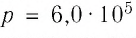
Решение. Из основного уравнения молекулярно-кинетической теории, записанного в виде 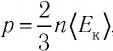
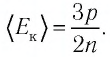
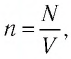
Ответ:
Уравнение состояния идеального газа
Выясним, как связаны между собой макроскопические параметры идеального газа, которые характеризуют его равновесное состояние: давление, масса всего газа, объём, предоставленный ему, и температура.
Состояние макроскопической системы полностью определено, если известны её макроскопические параметры — давление р, масса 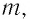
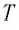
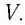
Если при переходе идеального газа из одного состояния в другое число его т
молекул 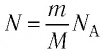
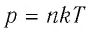
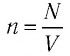
где 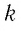
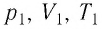
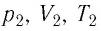
или
При неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной.
Уравнение (5.2) связывает два рассматриваемых состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.
Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799—1864), поэтому его называют уравнением Клапейрона.
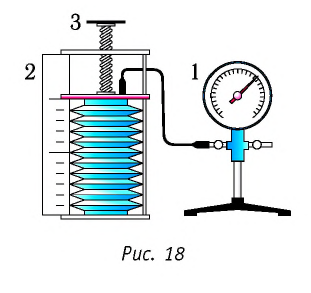
В справедливости уравнения состояния можно убедиться, воспользовавшись установкой, изображённой на рисунке 18. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно рассчитать, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.
Измерив параметры газа 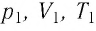
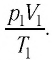
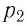
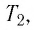
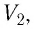
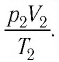
Уравнение состояния (5.2) можно применять для газов при следующих условиях:
- не очень большие давления (пока собственный объём всех молекул газа пренебрежимо мал по сравнению с предоставленным ему объёмом);
- не слишком низкие или же высокие температуры (пока абсолютное значение потенциальной энергии межмолекулярного взаимодействия пренебрежимо мало по сравнению с кинетической энергией теплового движения молекул).
Поскольку число частиц 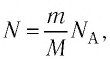
Величину, равную произведению постоянной Больцмана 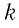
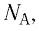
С учётом выражения (5.4) уравнение (5.3) примет вид:
Поскольку количество вещества 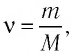
Уравнение состояния в виде (5.5) впервые получил русский учёный Д. И. Менделеев (1834—1907) в 1874 г., поэтому его называют уравнением Клапейрона—Менделеева.
Отметим, что уравнение Клапейрона—Менделеева связывает между собой макроскопические параметры конкретного состояния идеального газа. Используя уравнение Клапейрона-Менделеева, можно описать различные процессы, происходящие в идеальном газе.
Давление смеси газов
В повседневной жизни часто приходится иметь дело не с газом, состоящим из одинаковых молекул, а со смесью нескольких разнородных газов, не вступающих в химические реакции при рассматриваемых условиях. Например, воздух в комнате является смесью азота, кислорода, инертных газов и водорода, а также некоторых других газов.
Вследствие теплового движения частиц каждого газа, входящего в состав газовой смеси, они равномерно распределяются по всему предоставленному смеси объёму. Столкновения частиц обеспечивают в смеси тепловое равновесие.
Каждый газ вносит свой вклад в суммарное давление, производимое газовой смесью, создавая давление, называемое парциальным.
Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
Смесь идеальных газов принимают за идеальный газ.
Из истории физики:
Фундаментальные исследования газовых смесей провёл английский учёный Джон Дальтон (1766-1844). Им сформулирован закон независимости парциальных давлений компонентов смеси (1801-1802). В 1802 г. на несколько месяцев раньше французского учёного Жозефа Гей-Люссака (1778-1850) Дальтон установил закон теплового расширения газов, а также ввёл понятие атомного веса.
При постоянных массе и молярной массе отношение произведения давления идеального газа и его объёма к абсолютной температуре является величиной постоянной (уравнение состояния идеального газа):
Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
Пример №3
Баллон с газом, давление которого 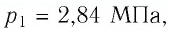
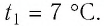
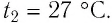
Решение. Если пренебречь тепловым расширением баллона, то его вместимость не изменяется. Запишем уравнение Клапейрона—Менделеева для начального и конечного состоянии газа, считая его идеальным:
откуда
Тогда
Ответ:
Основное уравнение молекулярно-кинетической теории идеального газа
В молекулярной физике изучаются свойства вещества во всех агрегатных состояниях, в том числе и газообразном. В природе почти нет отдельно взятого газа, реальный газ атмосферы представляют собой сложную систему разных газов.
Основная задача молекулярно-кинетической теории – установление связи между макроскопическими и микроскопическими параметрами, характеризующими свойства этой сложной системы. С этой целью реальный газ сложного состава заменяется упрощенной, идеализированной моделью.
Идеальный газ:
Первый шаг в создании любой физической теории состоит в построении идеализированной модели реального объекта. Такая модель всегда имеет упрощенный вид действительности, и с ее помощью изучаются количественные и качественные закономерности и свойства реального объекта с учетом определенных ограничений.
Для изучения свойств газов в молекулярно-кинетической теории применяется идеализированная модель – “идеальный газ”.
Идеальный газ – это газ, удовлетворяющий следующим условиям:
- — линейные размеры молекул во много раз меньше расстояний между ними и не принимаются во внимание. Поэтому можно сказать, что молекулы идеального газа не взаимодействуют друг с другом, то есть потенциальная энергия взаимодействия молекул идеального газа равна нулю:
Поэтому идеальный газ можно сколько угодно сжимать; —только при соударении молекул друг с другом или со стенками сосуда между ними возникают силы отталкивания;
- — соударения молекул абсолютно упругие;
- — скорость молекул может иметь произвольные значения, движение каждой молекулы подчиняется законам классической механики.
Свойства идеального газа характеризуются микроскопическими и макроскопическими параметрами и связями между ними.
Микроскопические параметры газа – это параметры, характеризующие движение молекул газа. К ним относятся масса молекулы, его скорость, импульс и кинетическая энергия поступательного движения молекулы.
Макроскопическими являются такие параметры газа, как ее давление, объем и температура, определяющие свойства газа в целом.
Основной задачей молекулярно-кинетической теории является установление взаимной связи между микроскопическими параметрами, характеризующими молекулы газа, и макроскопическими (измеряемыми) величинами, характеризующими газ.
Основное уравнение молекулярно-кинетической теории идеального газа:
Известно, что давление газа возникает в результате многочисленных непрерывных и беспорядочных соударений молекул газа о стенки сосуда, в котором он находится. Это давление равно среднему значению модуля равнодействующей силы, приходящейся на единицу площади:
В 1857 г. немецкий физик Рудольф Клаузиус (1822-1888), используя модель идеального газа, определил уравнение для давления газа, называемое основным уравнением молекулярно-кинетической теории идеального газа.
Основное уравнение молекулярно-кинетической теории идеального газа — это уравнение, связывающее макроскопический параметр газа – его давление, с микроскопическими параметрами, характеризующими молекулы газа:
Где 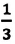
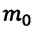
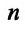
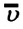
Концентрация молекул — это число молекул в единице объема:
Единица концентрации в СИ:
Средняя квадратичная скорость молекул равна корню квадратному из средней арифметической величины квадратов скоростей отдельных молекул:
Так как среднее значение квадрата скорости молекул связано со средним значением кинетической энергии их поступательного движения, то, следовательно, и давление идеального газа зависит от среднего значения кинетической энергии молекул:
Давление идеального газа прямо пропорционально концентрации молекул и среднему значению кинетической энергии молекул.
Если принять во внимание, что плотность газа 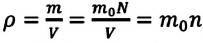
Вы исследовали идеальный газ с позиций MKT и определили связь между его макроскопическими и микроскопическими параметрами.
Уравнение Клапейрона
Связь между тремя макроскопическими параметрами (давление, объем и температура), характеризующими состояние идеального газа, определяет уравнение состояние идеального газа.
Уравнение состояния идеального газа – это уравнение, описывающее состояние газа и устанавливающее связь между параметрами его начального и конечного состояний.
Если число молекул идеального газа остается постоянным, то есть масса и молярная масса не меняются, то при переходе идеального газа из одного состояния в другое, из формул (6.2) и (6.9) имеем для этих состояний:
Где 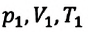
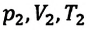
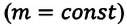
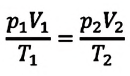
Это уравнение (6.15), характеризующее состояние идеального газа, впервые в 1834 году получил французский физик Бенуа Клапейрон (1799-1864), поэтому его назвали уравнением Клапейрона.
Отношение произведения давления идеального газа данной массы на его объем к абсолютной температуре является постоянной величиной.
Уравнение Менделеева-Клапейрона:
Приняв во внимание формулу, связывающую число частичек вещества, общую массу вещества, молярную массу и число Авогадро,
в формуле (6.14), получим:
Произведение постоянной Больцмана на постоянную Авогадро также является постоянной величиной. Оно называется универсальной газовой постоянной, обозначается буквой 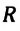
Приняв во внимание выражение (6.17) в (6.16), получаем выражение, характеризующее состояние идеального газа и называемое уравнением Менделеева-Клапейрона.
Физический смысл универсальной газовой постоянной определяется из последнего выражения.
Универсальная газовая постоянная равна отношению произведения давления и объема к абсолютной температуре одного моля любого газа.
Уравнение Менделеева-Клапейрона можно записать и в таком виде:
Где 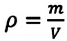
- Уравнение МКТ идеального газа
- Уравнение состояния идеального газа
- Температура в физике
- Парообразование и конденсация
- Зависимость веса тела от вида движения
- Движение тел под воздействием нескольких сил
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
Объединенный газовый закон был открыт экспериментально. Он также является следствием основного уравнения состояния идеального газа. Согласно ему:
Определение
При постоянной массе газа и его неизменной молярной массе отношение произведения давления на объем к его абсолютной температуре остается величиной постоянной:
pVT=const или p1V1T1=p2V2T2
Объединенный газовый закон применительно к изопроцессам
Объединенный газовый закон объединяет три независимых газовых закона: Бойля — Мариотта, Шарля и Гей-Люссака. Газовые законы действуют в частных случаях — изопроцессах.
Определение
Изопроцессы — термодинамические процессы, во время которых количество вещества и один из параметров состояния: давление, объём, температура или энтропия — остаётся неизменным.
Изотермический процесс. Закон Бойля — Мариотта.
Изотермический процесс — термодинамический процесс, происходящий в системе при постоянной температуре и массе:
m = const (m1 = m2)
T = const (T1 = T2)
Для изотермического процесса действует закон Бойля — Мариотта:
Закон Бойля — Мариотта
Для газа данной массы произведение газа на его объем постоянно, если температура газа не меняется.
pV = const (p1V1 = p2V2)
Изохорный процесс. Закон Шарля.
Изохорный процесс — термодинамический процесс, происходящий в системе при постоянном объеме и массе:
m = const (m1 = m2)
V = const (V1 = V2)
Для изохорного процесса действует закон Шарля:
Закон Шарля
Для газа данной массы отношение давления к температуре постоянно, если объем не меняется.
pT=const (p1T1=p2T2)
Изобарный процесс. Закон Гей-Люссака.
Изобарный процесс — термодинамический процесс, происходящий в системе при постоянном давлении и массе:
m = const (m1 = m2)
p = const (p1 = p2)
Закон Гей-Люссака
Для газа данной массы отношение объема к температуре постоянно, если давление газа не меняется.
VT=const (V1T1=V2T2)
Пример №1. Идеальный газ изобарно нагревают так, что его температура изменяется на ∆T = 240 К, а давление — в 1,6 раза. Масса газа постоянна. Найдите начальную температуру газа по шкале Кельвина.
Так как газ нагревают, то:
T2 – T1 = 240 (К)
Отсюда:
T2 = 240 + T1 (К)
p1 = p
p2 = 1,6p
Запишем закон Шарля применительно к данному случаю:
pT1=1,6p240+ T1
Сделаем некоторые преобразования и вычислим начальную температуру:
pT1=1,6p240+ T1
240+ T1=1,6T1
0,6T1=240
T1=2400,6=400 (К)
Подсказки к задачам на газовые законы
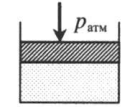 |
Газ под невесомым поршнем: p = pатм p — давление газа; pатм — давление, оказываемое на газ со стороны поршня. |
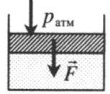 |
На невесомый поршень действует сила: p=pатм+FS F — сила, действующая на поршень; S — площадь поршня. |
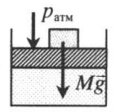 |
На невесомый поршень поставили груз. В данном случае на поршень дополнительно будет действовать сила тяжести: p=pатм+FтяжS=pатм+MgS Fтяж — сила тяжести, действующая на поршень со стороны груза; M — масса груза; g — ускорение свободного падения. |
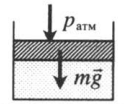 |
Газ под массивным поршнем. В данном случае на него дополнительно будет действовать сила тяжести поршня: p=pатм+mgS m — масса поршня. |
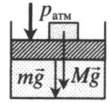 |
На массивный поршень поставили груз. В данном случае на поршень дополнительно будут действовать силы тяжести со стороны поршня и груза: p=pатм+MgS+mgS |
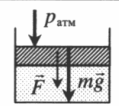 |
На массивный поршень действует сила. В данном случае газ сдавливается как атмосферным давлением, так и силой тяжести поршня, а также силой, которая на него действует: p=pатм+mgS+FS |
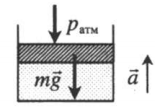 |
Газ, находящийся в цилиндре под массивным поршнем, находится в лифте, ускорение которого направлено вверх. Когда ускорение движения лифта противоположно направлено ускорению свободного падения, вес тел увеличивается. Поэтому: p=pатм+mgS+maS a — модуль ускорения, с которым движется лифт. |
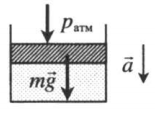 |
Газ, находящийся в цилиндре под массивным поршнем, находится в лифте, ускорение которого направлено вниз. Когда ускорение движения лифта направлено в сторону вектора ускорения свободного падения, вес тел уменьшается. Поэтому: p=pатм+mgS−maS |
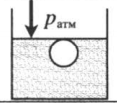 |
«Пузырек у поверхности воды» — на пузырек действует только атмосферное давоение: p = pатм |
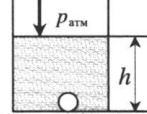 |
«Пузырек на глубине» — на пузырек действует атмосферное давление и давление столба жидкости: p = pатм + ρgh ρ — плотность жидкости; h — глубина, на которой находится пузырек. |
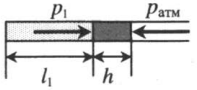 |
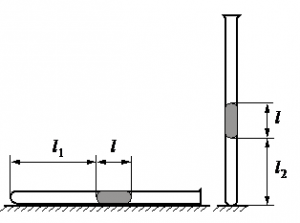
Газ, находящийся в горизонтальной пробирке, отделен от атмосферы столбиком ртути. Объем газа можно вычислить, используя параметры пробирки: V1 = l1S V1 — объем газа; l1 — длина части пробирки, которую занимает газ; S — площадь поперечного сечения пробирки. Давление газа равно атмосферному давлению: p1 = pатм |
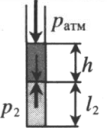 |
Пробирку поворачивают открытым концом вверх. В этом случае кроме атмосферного давления на газ давит давление со стороны ртути: P2 = pатм + ρgh Объем газа можно вычислить, используя параметры пробирки: V2 = l2S |
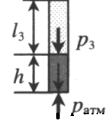 |
Пробирку поворачивают открытым концом вниз. В этом случае сумма давлений газа и ртути в пробирке равна атмосферному давлению. Отсюда давление газа равно: P3 = pатм – ρgh Объем газа можно вычислить, используя параметры пробирки: V3 = l3S |
| Шар или понтон поднимается вверх в воздухе или жидкости | Архимедова сила больше силы тяжести:
FA > Fтяж |
Пример №2. Поршень площадью 10 см2 массой 5 кг может без трения перемещаться в вертикальном цилиндрическом сосуде, обеспечивая при этом герметичность. Сосуд с поршнем, заполненный газом, покоится на полу неподвижного лифта при атмосферном давлении 100 кПа, при этом расстояние от нижнего края поршня до дна сосуда 20 см. Каким станет это расстояние, когда лифт поедет вверх с ускорением, равным 2 м/с2? Изменение температуры газа не учитывать.
10 см2 = 10–3 м2
20 см = 0,2 м
100 кПа = 105 Па
Составим уравнения для 1 и 2 случая. Когда лифт находится в покое, давление газа равно сумме атмосферного давления и давления, оказываемое массивным поршнем:
p1=pатм+mgS
Когда лифт начал двигаться, появилось дополнительное давление, связанное с увеличением веса поршня при ускоренном движении вверх:
p2=pатм+mgS+maS
Так как изменением температуры можно пренебречь, можно считать, что это процесс изотермический. Следовательно:
p1V1 = p2V2
Объемы в 1 и 2 случае будут определяться формулами:
V1 = Sh1
V2 = Sh2
h1 — расстояние от нижнего края поршня до дна сосуда в первом случае. h2 — та же самая величина, но во втором случае (искомая величина).
Запишем закон Бойля — Мариотта для обоих случаев с учетом объемов:
p1V1=Sh1(pатм+mgS)
p2V2=Sh2(pатм+mgS+maS)
Так как это изотермический процесс, правые части уравнений можно приравнять:
Sh1(pатм+mgS)= Sh2(p
атм+mgS+maS)
Отсюда:
Графики изопроцессов
Изопроцессы можно изобразить графически в координатах (p;V), (V;T) и (p;T). Рассмотрим все виды графиком для каждого из процессов.
| Изопроцесс | График в координатах (p;V) | График в координатах (V;T) | График в координатах (p;T) |
| Изотермический (график — изотерма) | 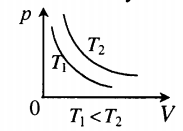
Изотерма в координатах (p;V) — гипербола. Чем ближе изотерма к началу координат и осям, тем меньшей температуре она соответствует. Характер изменения переменных величин хорошо виден на графике. |
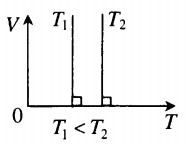
Изотерма в координатах (V;T) — прямая, перпендикулярная оси OT и параллельная оси OV. Чем ближе изотерма к оси OV, тем меньшей температуре она соответствует. С увеличением объема давление уменьшается. |
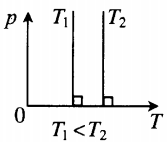
Изотерма в координатах (p;T) — прямая, перпендикулярная оси OT и параллельная оси Op. Чем ближе изотерма к оси Op, тем меньшей температуре она соответствует. С увеличением давления объем уменьшается. |
| Изохорный (график — изохора) | 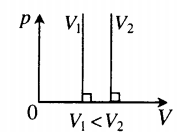
Изохора в координатах (p;V) — прямая, перпендикулярная оси OV и параллельная оси Op. Чем ближе изохора к оси Op, тем меньшему объему она соответствует. С увеличением давления увеличивается температура. |
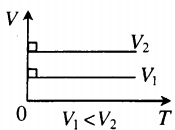
Изохора в координатах (V;T) — прямая, перпендикулярная оси OV и параллельная оси OT. Чем ближе изохора к оси OT, тем меньшему объему она соответствует. С увеличением температуры увеличивается давление. |
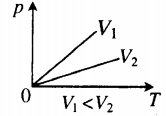
Изохора в координатах (p;T) — прямая, исходящая из начала координат. Чем меньше угол наклона изохоры к оси OT, тем меньшему объему она соответствует. Характер изменения переменных величин хорошо виден на графике. |
| Изобарный (график — изобара) | 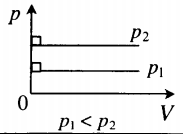
Изобара в координатах (p;V) — прямая, перпендикулярная оси Op и параллельная оси OV. Чем ближе изобара к оси OV, тем меньшему давлению она соответствует. С увеличением объема температура растет. |
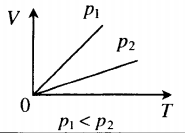
Изобара в координатах (V;T) — прямая, исходящая из начала координат. Чем меньше угол наклона изобары к оси OT, тем меньшему давлению она соответствует. Характер изменения переменных величин хорошо виден на графике. |

Изобара в координатах (p;T) — прямая, перпендикулярная оси Op и параллельная оси OT. Чем ближе изобара к оси OT, тем меньшему давлению она соответствует. С увеличением температуры объем растет. |
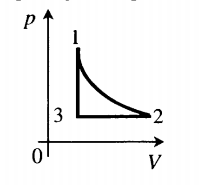
Пример №3. На рисунке представлен график циклического процесса. Вычертить его в координатах (p;T).
Определим характер изменения величин:
- Процесс 1–2. Гипербола — это изотерма. Следовательно T12 = const. В координатах (p;T) изотерма будет выглядеть как прямая, перпендикулярная оси OT.
- Процесс 2–3. Прямая линия, перпендикулярная оси Op — это изобара. Следовательно p23 = const. В координатах (p;T) изобара будет выглядеть как прямая, перпендикулярная оси Op.
- Процесс 3–1. Прямая линия, перпендикулярная оси OV — это изохора. Следовательно V31 = const. В координатах (p;T) изохора будет выглядеть как прямая, выходящая из начала координат.
Теперь, зная, какими будут графики всех величин в координатах (p;T), можно построить сам график. Он примет следующий вид:
Задание EF19012

Алгоритм решения
1.Указать, в каких координатах построен график.
2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
T=2−Ek3
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
νR=p1V1T1=p2V2T2
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
Ответ:
• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.
• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17615
1 моль идеального газа изохорно охлаждают на 200 К, при этом его давление уменьшается в 2 раза. Какова первоначальная абсолютная температура газа?
Ответ:
а) 600 К
б) 400 К
в) 350 К
г) 300 К
Алгоритм решения
1.Записать исходные данные.
2.Определить вид изопроцесса.
3.Выбрать и записать подходящий для данного изопроцесса газовый закон.
4.Выполнить решение в общем виде.
5.Вычислить искомую величину.
Решение
Запишем исходные данные:
• Изменение температуры ∆T = 200 К.
• Первоначальный объем p1 = 2p.
По условию задачи это изохорный процесс, следовательно он происходит в соответствии с законом Шарля:
p1T1=p2T2
Выразим конечную температуру и получим:
T2 = T1 – ∆T
Перепишем закон Шарля применительно к задаче и выразим первоначальную температуру:
2pT1=pT1−ΔT
2(T1−ΔT)=T1
2T1−T1=2ΔT
T1=2ΔT=2·200=400 (К)
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18859
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения физических величин в СИ.
2.Определить вид изопроцесса и записать для него газовый закон.
3.Выполнить решение в общем виде.
4.Вычислить искомую величину.
Решение
Запишем исходные данные:
• Длина столбика воздуха под столбиком ртути в первоначальном состоянии: l1 = 30,7 см.
• Длина столбика воздуха под столбиком ртути в конечном состоянии: l2 = 23,8 см.
• Атмосферное давление: pатм = 747 мм рт. ст.
30,7 см = 30,7∙10–2 м
23,8 см = 23,8∙10–2 м
1 мм рт. ст. = 133,322 Па
747 мм рт. ст. = 99,6∙103 Па
Плотность ртути равна: ρрт = 13,54∙103 кг/м3.
Так как процесс изменения состояния газа происходит при постоянной температуре, процесс можно считать изотермическим. Для него действует газовый закон Бойля — Мариотта:
p1V1 = p2V2
Первоначальное давление на столбик воздуха равно атмосферному давлению:
p1 = pатм
Конечное давление на столбик воздуха равно сумме атмосферного давления и давления, оказываемое силой тяжести столбика ртути:
p2=pатм+mртgS
S —площадь поперечного сечения трубки.
Масса ртути равна произведению плотности на объем столбика металла. Объем в свою очередь равен произведению длины столбика ртути на площадь поперечного сечения трубки. Поэтому:
p2=pатм+ρртVртgS=pатм+ρртlSgS=pатм+ρртlg
Первоначальный объем столбика воздуха равен произведению площади поперечного сечения трубки на высоту этого столбика:
V1 = Sl1
Конечный объем столбика воздуха равен произведению площади поперечного сечения трубки на высоту этого столбика:
V2 = Sl2
Выразив первоначальные и конечный величины, можем записать закон Бойля — Мариотта применительно к данной задаче:
pатмSl1=(pатм+ρртlg)Sl2
Преобразуем уравнение, выразим искомую величину и произведем вычисления:
pатмl1=pатмl2+ρртlgl2
ρртlgl2=pатмl1−pатмl2
l=pатм(l1−l2)ρртgl2
Ответ: 21,76
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18139
Паук-серебрянка медленно спускается на дно равномерно прогретого озера, неся между волосками брюшка пузырьки воздуха для своего подводного жилища. Какой процесс происходит с воздухом в пузырьках по мере погружения паука?
Ответ:
а) изобарное сжатие
б) изохорное нагревание
в) изотермическое сжатие
г) адиабатное сжатие
Алгоритм решения
- Установить, какие величины меняются по мере погружения пузырьков воздуха на глубину.
- Выяснить, какие величины сохраняются постоянными.
- Установить вид изопроцесса.
Решение
Когда паук спускается в воде на глубину, давление постепенно увеличивается. На пузырьки воздуха будет действовать сумма атмосферного давления и давления столба воды. Под действием этого давления пузырек будет сжиматься. То есть, давление будет уменьшаться. Но само давление воздуха в пузырьке при этом будет равно давлению, оказываемому на него со стороны внешней среды. Следовательно, давление в пузырьке будет увеличиваться. При условии, что количество вещества в пузырьке при этом не меняется, величина температуры также должна оставаться постоянной. Это следует из уравнения состояния идеального газа. Следовательно, воздух в пузырьках претерпевает изотермическое сжатие.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 11.6k