Добрый день наш уважаемый читатель. Получая часто вопросы от наших клиентов в 90% процентов из всех случаев, мы даем быстрые, четкие и грамотные ответы нашему собеседнику. Дело в том, что нашего богатого опыта работа отлично хватает чтобы закрыть потребности среднестатистического клиента или спикера.
Развернуто и не очень мы уже отвечали в нашем блоге людям на следующие вопросы:
Поставленная задача
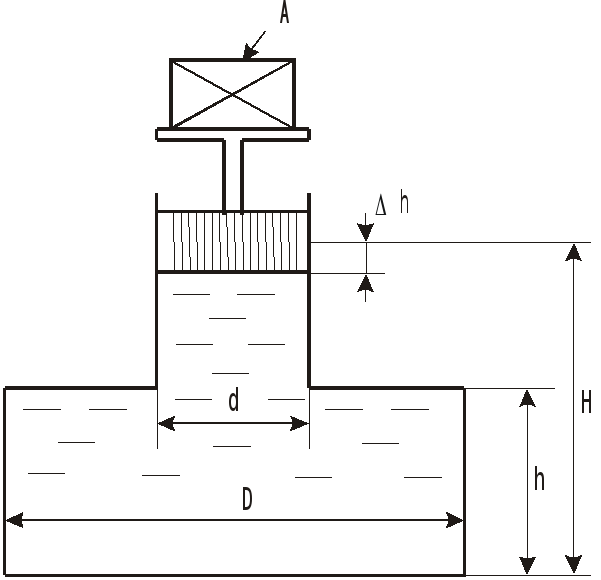
Сейчас перед нами встала следующая задача вот такого содержания: есть сосуд с неизменяемым объемом жидкости внутри него. Предположим, что сосуд состоит из обыкновенного железа, например, возьмем простой накопительный бойлер (V = 50 литров). Начальное давление в системе 2 атмосферы, начальная температура воды Т1 = 17 градусов цельсия, конечная температура после нагрева Т2 = 57 градусов цельсия. Исходные параметры могут быть разные, но конечная задача, на которую нужно получить ответ будет следующая: какое давление будет в закрытом сосуде при нагреве воды до указанной температуры Т2, если учесть, что краны на сосуде (вход и выход) находятся в положении закрыто, и начальный объем не изменяется??? Давление можно снимать (измерять) при помощи встроенного или выносного трубного манометра. Расширительного бака нет. Все для эксперимента.
Закон и формула Шарля
Начав решать эту задачу, каждый может прибегнуть к такому ответу: «да ладно, это же задачка за 7 класс, тут нужно применять формулу известного физика Шарля, Вы что учебник физики не читали?». Далее следует решение:
Формула: (273+t2)/(273+t1)=коэффициент увеличения давления от исходного.
(273+57)/(273+17)=330/290=1.13.
1.13 умножаем на 2 получаем что давление будет равно 2.26 после нагрева жидкости с 17 до 57 на 40 единиц.
Ну дела, вот же решение, зачем страдать дальше? Но нет друзья, это решение конечно же хорошее – но применимо только для изохорных идеальных газов, но не в коем случае не для жидкости, представленной у нас на примере воды.
Едем дальше изучая попутно других известных святил физики, и воуля мы натыкаемся на еще одно решение.
Для расчетов берем исходные данные из чего изготовлен сосуд, у нас это железо. Коэффициент объёмного расширения железа стабильно одинаковый, берем за основу среднее значение 0,000036, а вот коэффициент объема воды изменяется в зависимости от ее нагрева. Примерно 0,00015 при 20 градусах цельсия и 0,00045 при 60 градусах цельсия. Среднее значение путем сложения из двух данных получаем 0,00030.
Чтобы посчитать объем во сколько увеличиться объем в сосуде воспользуемся формулой: 1 + коэффициент расширения железа * (t2-t1).
В цифрах будет выглядеть так: 1 + 0,000036 * (57 – 17) = 1.002;
В качестве информационной нагрузки узнаем еще на сколько бы увеличился V воды если бы она была вне сосуда: 1 + 0,0003 * (57 – 17) = 1,012. Далее все упирается на сколько же прочный Ваш сосуд и не раздует ли его при повышении давления.
Чтобы узнать процентное увеличение объема воды с воздействием на сосуд воспользуемся следующей формулой подставим все цифры: 1,012 / 1,002 * 100 – 100 = 1 %.
Обратившись к учебнику физики, мы узнаем, что при давлении каждой атмосферы объем воды уменьшается на 0,000006. Например, 50 литров, при одной атмосфере сожмется на 0,001 и будет 49.999. Зато по сравнению с газами сжимаемость жидкостей действительно ничтожна: в десятки тысяч раз меньше.
Если объём воды при 2 атм = 50 литров, то при 500 атм объём станет примерно на 1 литр меньше. (разница в двух числах 2%).
1%/2% * 500 = 250 атмосфер, то значение при котором по идее должно разорвать Ваш бак и то давление которое будет у вас при нагреве. Честно, считаем это какой-то бред и не он никак не сочетается с реальными жизненными показателями, полученными в ходе эксперимента.
Изучав дальше интернет и опираясь на наши знания всех из коллег нашего отдела было перепробовано масса различных вариантов и изучено мнений других людей, которые потом можно было бы использоваться для выявления формулы по нашей задаче:
Вода при нагревании увеличивается в объеме до 4%, т.е. 50 наших литров должны превратиться в 52 литра за счет ее расширения, но применить данную теорию в нашем вопросе нам пока не удалось. Мы даже изучили соотношение плотности льда к плотности воды и поняли объем в этом случае увеличивается на 11 процентов.
Есть мнение (алгоритм) с нашей стороны что ни одну из формул применить тут нельзя, так как в баке или бойлере представленным нами невозможно заполнить его на все 100% жидкостью, какую часть в одной жидкости все равно будет составлять воздух, который в этом случае будет работать как расширительный бак и возможно поэтому те 800 атмосфер которые получаются у разных людей нормализуются тем количеством воздуха который содержаться в сосуде.
Если Вы физик или технически подкованный человек, разбираетесь в данном вопросе и готовы разрешить наш спор и получить ответ на поставленную задачу – ждем Ваших решений под этой записью в комментариях.
Со своей стороны хотим так же сказать, что при проведении реального эксперимента и нагрева воды в бойлере с 18-20 градусов до 50, давление поднялось по манометру с 1.5 очков (бар, атмосфер) примерно и до 5 бар.
Спасибо за проявленный труд, терпение и прочтение данной статьи. Надеемся что этот вопрос решится в ближайшее время и мы найдем грамотный ответ.
Всего Вам доброго и приятного дня.
Другие полезные записи в блоге – только для Вас!
- Котел КСУВ наружного размещения. Почему он является лучшим из всех? Технические особенности, выбор большинства организаций. Котельная больше не нужна. Устанавливай прямо со зданием.
- История на “миллион”, как мы помогли ДОЛ “Лесное озеро”. Крупный DIY проект России, сделай сам!
- Тепловой пункт: какой промышленный котел выбрать?
- Наглядный ремонт КЧМ руками наших специалистов.
- ОАО “Кировский завод” банкрот. Какая судьба ожидает котлы КЧМ-5, КЧМ-5К, КЧМ-7 Гном?
- Почему в котлах КЧМ-5К не используются колосники? Техническая информация и не только.
- Все основные запасные части к котлу КЧМ, артикулы, описание и много полезной информации.
- Лемакс – лучшее соотношение цена/качество в бытовых котлах.
- 1000 колосников на складе компании МОНТАЖНИК – новый завоз.
- Что такое колосник? Расскажем все очень подробно.
- Почему котлы ИШМА покупают 90 из 100 клиентов. Лучшее соотношение цены-качества.
- Лучший конкурент котла Buderus, Valliant, Protherm – это Кентатсу (Kentatsu) – или как мы его называем один в поле ВОИН! А так же там мы ответили на вопрос, что лучше русский КЧМ или Турецкояпонский гигант?
- Полная подробная инструкция по монтажу промышленных котлов
- Посмотреть все статьи и новости
Наши отправки (отгрузки), услуги и выполненные работы:
Статьи посвященные нашим отгрузкам не только поднимают наш авторитет как считаем мы, но они направлены на увеличение доверия со стороны потенциальных клиентов. Нам нечего скрывать – мы делимся с Вами своими продажами и успехами. У нас нет скрытых продаж и ухода от налогов. Мы стараемся делать наше с Вами сотрудничество и работу максимально прозрачными. Мы хотим чтобы Вы доверяли нашей команде!
Если у Вас есть идеи о том, о том что Вы бы хотели увидеть на нашем канале. То присылайте их на нашу легкую почту: 426909@bk.ru. Если Вам понравилась статья оцените ее, поставьте палец вверх слева экрана (если Вы читаете ее с компьютера), а также подпишитесь на наш блог, Вас ждет много полезной и интересной информации.
С вами на связи была компания ООО “Монтажник” – официальный дистрибьютор нескольких заводов изготовителей по всей стране. По вопросам приобретения котлов, насосов и другого сопутствующего оборудования (запчасти, дымоходы, автоматика) можете обращаться по телефонам: 8(47354) 2-55-25; 2-69-09 или на электронную почту: 426909@bk.ru или montagnikvrn@yandex.ru.
Отзывы о нашей компании:
Посмотреть все отзывы.
СПАСИБО ЧТО ОСТАЕТЕСЬ С НАМИ! Рассказывайте друзьям, делитесь материалом со своими знакомыми. Нам важен каждый.
Компания которая относится к своему клиенту с ДУШОЙ!
Понятие жидкости включает все тела,
обладающие текучестью, т.е. способностью
сколь угодно сильно изменять свою форму
под действием незначительных сил (т.е.
как капельные жидкости, так и газы).
Жидкость характеризуется:
массовой плотностью
![]() ,
,
где
![]()
– масса,
![]()
– объем,
и удельным весом
![]() ,
,
где
![]()
– вес.
Если жидкость однородна, то можно
определять
![]()
и
![]()
из соотношений:
![]()
т.к.
![]() ,
,
где
![]() –
–
ускорение свободного падения.
Из-за текучести жидкости в ней могут
действовать только распределенные по
поверхности или по объему силы. Нормальная
составляющая поверхностной силы
называется силой давления
![]() .
.
Напряжение силы давления
![]()
называется давлением
![]()
где
![]() –
–
площадь.
Свойства давления.
Давление всегда направлено по нормали
внутрь объема жидкости, в любой точке
жидкости одинаково по всем направлениям,
т.е. не зависит от угла наклона площадки,
на которую действует.
B системе СИ давление
измеряется в паскалях
![]() .
.
Кроме принятой международной системы
единиц СИ применяются системы единиц
МКГСС и СГС. Размерность величин в
различных системах приведена в таблице.
Более удобными для практического
использования являются кратные единицы:
-
гектопаскаль
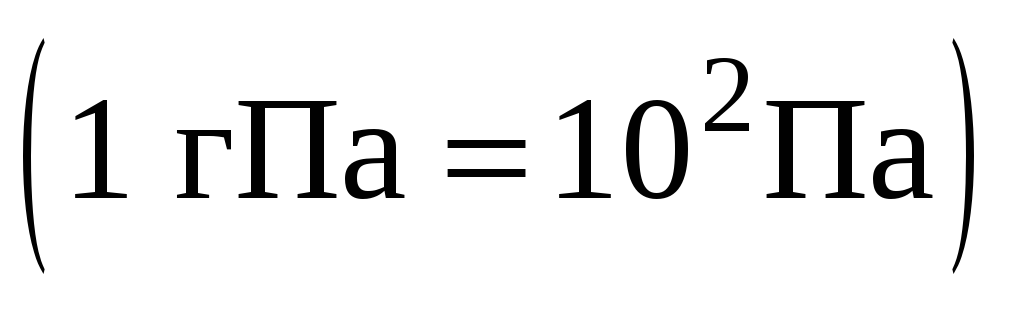 ,
, -
килопаскаль
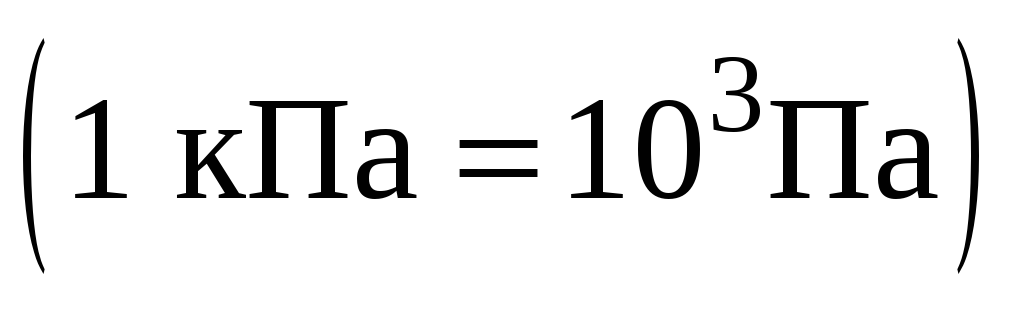 ,
, -
мегапаскаль
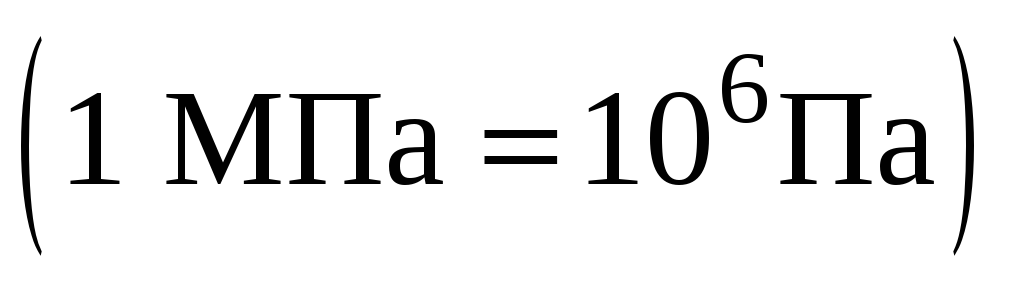 .
.
Таблица. Системы единиц.
|
Величина |
Размерность |
СИ |
МКГСС |
СГС |
|
Длина |
|
|
|
|
|
Время |
|
|
|
|
|
Масса |
|
|
|
|
|
Сила |
|
|
|
|
|
Плотность |
|
|
|
|
|
Удельный вес |
|
|
|
|
|
Давление |
|
|
|
|
Кроме единицы давления Па допускается
применение и внесистемных единиц –
технической атмосферы
![]()
и высот, на которые поднимется рабочая
жидкость в пьезометре, чтобы уравновесить
давление – мм ртутного столба – и мм и м
водяного столба.
Соотношения между различными единицами
измерения давления приведены в таблице.
Таблица. Соотношение между единицами
давления в разных системах.
|
СИ |
Паскаль |
|
|
|
МКГСС |
|
|
|
|
внесистемные |
техническая |
|
|
|
|
|
760 мм 736 мм рт.ст. соответствуют |
|
|
|
|
|
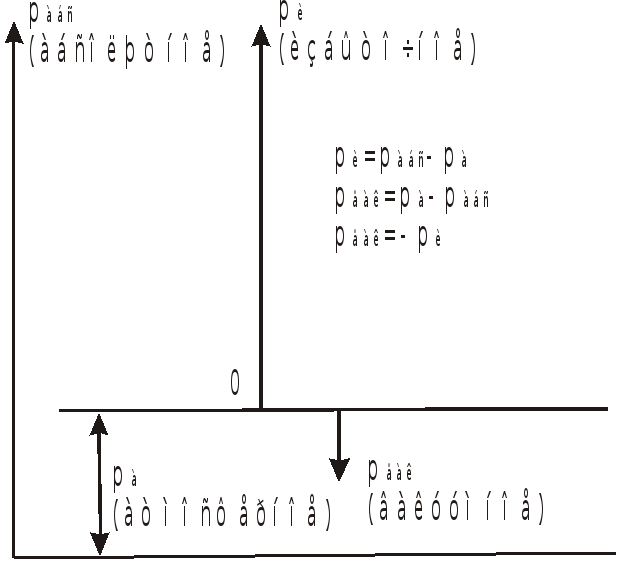
Полное напряжение сжатия от действия
всех внешних сил (поверхностных и
массовых), приложенных к жидкости,
называется абсолютным давлением.
В технике удобно за начало отсчета
принимать давление атмосферного воздуха.
В этом случае превышение
![]()
(абсолютного давления) над атмосферным
![]() –
–
называется избыточным давлением
![]() .
.
Отрицательное избыточное давление
называется вакуумом.
Схематически шкалы измерения давления
показаны на рисунке.
Сжимаемость жидкости.
Способность жидкости изменять объем
под действием давления характеризуется
коэффициентом сжимаемости
![]() ,
,
определяемого из соотношения:
![]()
![]()
где
![]()
– модуль упругости жидкости.
Для характеристики газов
![]()
не пригоден.
Коэффициент температурного расширения
![]()
определяется из соотношения:
![]() .
.
При изменении температуры жидкости в
герметически закрытой емкости происходит
изменение давления, которое можно
определить из соотношения:
![]() ,
,
где
![]()
и
![]()
– коэффициенты температурного расширения
жидкости и материала, из которого
изготовлена емкость.
Задача 1.1 Сосуд объемом
![]()
заполнен водой. Чему будет равен объем
при увеличении давления на
![]() ?
?
Дано:
![]() ;
;
![]() ;
;
![]() .
.
Найти
![]() .
.
Решение:
![]() ,
,
откуда уменьшение объема
![]() .
.
Окончательный объем
![]() ;
;
![]() ;
;
![]()
![]() .
.
Ответ:
![]() .
.
Задача 1.2 Объем жидкости
гидросистемы самолета
![]() литров.
литров.
Определить запас емкости бака, необходимый
для компенсации температурного
расширения, если
![]()
Диапазон рабочих температур
![]()
Дано:
![]() ;
;
![]() ;
;
![]() .
.
Найти:
![]()
Решение:
![]() .
.
![]()
Ответ:
![]() .
.
Задача 1.3 Бак, заполненный
жидкостью с модулем упругости
![]() ,
,
нагревается от
![]()
до
![]() .
.
Определить давление в баке, считая, что
бак герметичен и заполнен полностью,
стенки бака абсолютно жесткие. Начальное
избыточное давление
![]()
Ответ дать в атмосферах.
Дано:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Найти:
![]()
Решение:
Т.к. стенки абсолютно жесткие, то объем
жидкости не изменится
![]() ,и
,и
температурное расширение компенсируется
повышением давления при сжатии, т.е.
![]() ;
;
![]() ;
; ![]() ;
;
![]()
![]() ;
;
![]()
откуда
![]() .
.
![]()
Ответ:
![]() .
.
З
адача 1.4 Определить объемный
модуль упругости жидкости, если под
действием груза А, массой 250 кг, поршень
прошел расстояние
![]() .
.
Начальная высота положения поршня (без
груза)
![]() ,
,
диаметры поршня
![]() ,
,
резервуара
![]() ,
,
высота резервуара
![]() .
.
Весом поршня пренебречь. Резервуар
считать абсолютно жестким.
Дано:
![]()
![]()
![]()
![]()
![]()
![]()
Найти:
![]()
Решение:
![]()
![]() –
–
объем жидкости до сжатия:
![]() .
.
Уменьшение объема
![]() .
.
![]() –
–
давление, создаваемое грузом массой
![]()
на площади поршня S:
![]() ;
;
![]() .
.
![]() .
.
Ответ:
![]() .
.
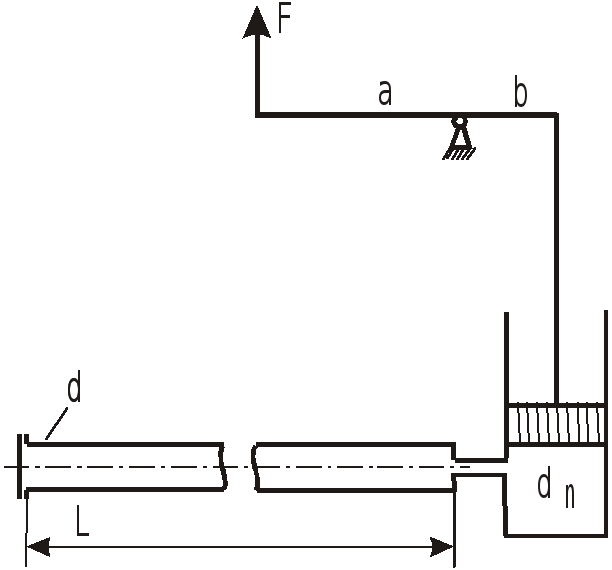
Задача 1.5 Для опрессовки
трубопровода применяется ручной насос.
1. Определить объем воды, который нужно
накачать в трубопровод для повышения
в нем избыточного давления от 0 до 1 МПа.
(Модуль упругости воды
![]()
трубопровод считать абсолютно жестким.
Размеры трубопровода:
![]() ).
).
2. Чему равно усилие
![]()
на рукоятке насоса в последний момент
опрессовки, если диаметр поршня насоса
![]()
Соотношение плеч рычажного механизма
![]() .
.
Д
ано:
![]()
![]()
![]()
![]()
![]()
![]()
Найти:
![]()
Решение:
1. Т.к. объем воды в насосе несоизмерим
с объемом воды в трубе, считаем объем
сжимаемой воды равным объему трубы.
![]()
из зависимости
![]()
находим значение
![]()
(знак минус означает, что объем воды при
опрессовке (сжатии) уменьшился).
![]() .
.
2. Из условия равновесия сил на рычаге
имеем
![]() ,
,
где
![]()
– сила, действующая на поршень в конце
опрессовки.
![]() ,
,
тогда
![]() .
.
Ответ:![]() .
.
Задача 1.6 В вертикальном
цилиндрическом резервуаре диаметром
4 м хранится 100 т нефти, плотность которой
при
![]()
![]() .
.
Определить изменение уровня в резервуаре
при изменении температуры нефти от 0 до
![]() .
.
Расширение резервуара не учитывать.
Коэффициент теплового расширения нефти
принять равным
![]() .
.
Ответ: 0,203 м.
Задача 1.7 Трубопровод диаметром
![]() ,
,
длиной
![]() ,
,
подготовленный к гидравлическому
испытанию, заполнен водой при атмосферном
давлении.
Какое количество воды необходимо
дополнительно подать в трубопровод,
чтобы давление в нем поднялось до 5 МПа?
Коэффициент сжимаемости воды принять
равным
![]() .
.
Деформацией трубопровода пренебречь.
Ответ:
![]() .
.
Задача 1.8
В
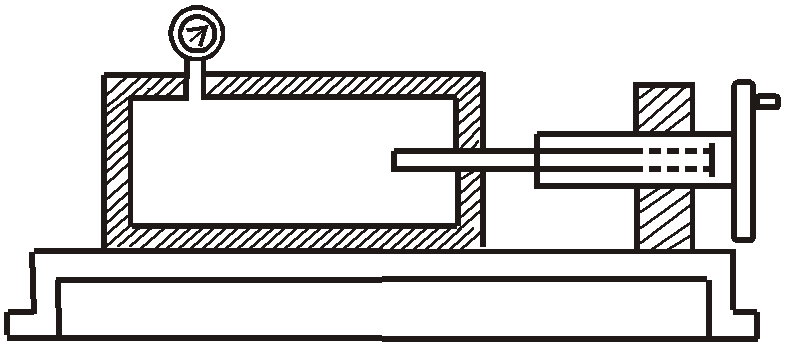
интовой пресс для тарировки манометров
работает на масле с коэффициентом
сжимаемости
![]() .
.
Определить, на сколько оборотов надо
повернуть маховик винта, чтобы поднять
давление на
![]() ,
,
если начальный объем рабочей жидкости
камеры пресса
![]() ,
,
диаметр плунжера 20 мм, шаг винта 2 мм.
Стенки рабочей камеры считать
недеформируемыми.
Ответ: 1/16 оборота.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
План урока:
Можно ли бежать по снегу?
Способы изменения давления
Давление газа
Закон Паскаля
Давление жидкости
Сообщающиеся сосуды
Можно ли бежать по снегу?
В соревнованиях, когда одна команда бежит на лыжах по рыхлому снегу, а другая без лыж победит, конечно же, команда с лыжами. Все дело в лыжах. Когда человек стоит на лыжах, его вес равномерно распределяется по всей площади лыж. Нетрудно сравнить площадь двух лыж и площадь подошв обуви.

Площадь лыж больше площади подошв. Если одинаковый вес человека распределить на разные площади, получится, что каждой единице площади лыж достанется веса меньше, чем такой же единице площади подошв. (Чтобы лучше понять это, надо представить простую ситуацию: на разные по размерам куски хлеба намазать по одинаковому количеству сливочного масла. На маленьком куске хлеба получится толстый слой масла, а на большом – масло размажется очень тонко).
Сила, которая давит на длинные лыжи и небольшие подошвы – это вес человека. А вот сила, которая приходится на единицу площади лыжи или подошвы – это уже не полный вес человека, а лишь маленькая часть этого веса. Эту силу в физике называют давлением.
Значит, команда на лыжах выиграла, так как оказывала на снег меньшее давление, и передвигаться ей, не проваливаясь, было легче.
Нужно отличать давление от силы давления. В примере в роли силы давления выступает вес человека, а давление – это часть веса, которая достается единице площади.
Давление принято обозначать буквой p (маленькая латинская буква) и находить по правилу:
p = F/S.
Достаточно понятная формула: «силу давления F разделить (распределить) на площадь S».

Источник
Давление измеряют и другими единицами:

Источник
Давление оказывают тела не только своим весом. Когда, например, режут хлеб или сыр на части, то нож разрезает продукты под действием мышечной силы руки.
Зная давление, можно найти силу, которая действует на поверхность:
F = p ∙ S
Способы изменения давления
Жарким летним днем, когда асфальт будто плавится, на нем остаются следы.
Какая обувь оставляет самые заметные, глубокие следы? Несомненно, ответ прост: это шпильки женских туфель. Маленькая площадь, следовательно, большое давление – и видимый результат.
Иногда давление необходимо сделать большим, иногда – маленьким.
Большое давление нужно там, где имеют дело с режущими и колющими инструментами. Необходимо, чтобы они были остро заточены, чтобы площадь соприкосновения была минимальной. Если нажать посильнее, то можно получить огромные давления. Резец токарного станка срезает стружку, оказывая давление на деталь 2,45 ∙ 109 Па.

Источник
В рукопашном бое востока преобладают колющие и рубящие удары пальцами рук, ног и ребром ладони. Обладая маленькой массой, можно нанести резкий болевой удар, ведь площадь кончиков пальцев или ребра ладони значительно меньше площади всей ладони или кулака. А значит, при одинаковой силе можно оказать большее давление на место удара.
А какое давление оказывает лезвие из дамасской стали, если легкая шелковая лента, упав на саблю, перерезается пополам!
В тех случаях, когда давление должно быть маленьким, сила должна быть тоже небольшой, а это в современных технологиях встречается редко. Тогда для уменьшения давления нужно увеличить площадь опоры.
Гусеницы тракторов, вездеходов значительно уменьшают давление на почву (всего 40 – 50 кПа), поэтому этот вид транспорта хорошо проходим даже в условиях болота. Для сравнения давление, которое оказывают колеса легкового автомобиля на дорогу равно 200 – 300 кПа, причем вес автомобиля значительно меньше, чем у трактора. Человек для прохождения по болотистой почве применяет специальные болотоходы, а по снегу – снегоходы.

Для того, чтобы дома и другие строения не давали осадку, необходимо под них подводить широкий фундамент (увеличение площади). Известная всему миру Останкинская башня, высотой 533 м, давит своим фундаментом на землю всего в 270 кПа (как легковой автомобиль). Таким же фундаментом для железнодорожных рельсов являются шпалы, уменьшающие давление вагонов на рельсы.
Для похода лучше выбирать рюкзак с широкими лямками, даже не нужно объяснять, почему.
Животным природа подарила возможность учитывать и использовать давление:
- клыки (хищники легко разрывают ими мясо);
- когти (кошки свободно забираются на дерево, спасаясь от собаки);
- острые зубы (пираньи – хищные рыбы пресных вод в считанные секунды обгладывают свои жертвы):
- клювы (дятел быстро долбит кору деревьев, находя там жучков для еды);
- острые носы (комар мгновенно протыкает кожу людей и животных и высасывает кровь);

Приведенные примеры говорят о том, как животные приспособились к борьбе за существование.
Итак, давление учитывает и человек, и природа, стремясь держать его большим или маленьким в нужных случаях.
Давление газа
Воздушные шары и мыльные пузыри знакомы всем взрослым и детям. Это обязательный атрибут игр или праздников. А как получить такой шарик? Он наполняется воздухом, который человек вдувает в шарик при выдохе. С каждым выдохом шарик растет все больше, и делается все более упругим. На резину шарика воздух давит, стараясь растянуть его в разные стороны. Силе давления противостоит сила упругости деформированного шарика, и нужно вовремя остановиться, иначе сила давления перерастет силу упругости, произойдет громкий хлопок – шарик лопнет.

Твердое тело весом давит на часть поверхности, на которой стоит (если ведро стоит на полу, то оно и давит только на пол), а газ действует во всех направлениях одинаково, поэтому мыльные пузыри имеют форму шара. Форму воздушного шара определяет резина, из которой он изготовлен. Если резина везде одинакова, то шар будет круглым. Если резина имеет в разных частях шара разную упругость, то и шар надуется по-разному, и будет иметь заданную форму.
Молекулы газообразного вещества мечутся беспорядочно и хаотично, но такой хаос большого количества частиц обеспечивает некий порядок: в любых направлениях зигзагообразными траекториями движется примерно одинаковое количество молекул. Суммарная сила удара сразу всех молекул, действующая на единицу площади, и образует давление газа.

Источник
Если накачивать насосом камеру велосипеда или мяча, то с каждым качком камера становится будто бы более твердой, потому что молекулы воздуха все прибывают и прибывают, сила суммарного удара по стенкам камеры становится все больше и больше. А значит, давление растет. Если воздух выходит, то камера на глазах «худеет», давление уменьшается. С ростом числа молекул связано увеличение массы газа, а уменьшение числа молекул ведет к уменьшению массы. Поэтому давление газа зависит от его массы, которую опытным путем гораздо легче определить, чем само давление.

С повышением температуры тела молекулы перемещаются быстрее. Чем выше скорость, тем сильнее молекулы ударяются о сосуд, в котором газ находится. Значит, чем температура выше, тем значительнее давление, оказываемое газом.
Еще интересный пример изменения давления. Надо взять бумажный пакет, надуть его и резко ударить по нему ладонью. Хлопок, и пакет разорван. Все очень быстро и просто, а ведь здесь произошли вполне объяснимые физические процессы. Кулек под ударом ладони сжимается, объем газа в нем становится меньше, количество молекул не увеличивается, но так как молекулы расположены плотнее, на единицу площади стенок их количество растет, что приводит к росту давления. Давление разрывает бумагу, резко вырвавшийся воздух является причиной звука в виде хлопка. Получается, давление газа связано и с объемом: давление становится больше с уменьшением объема газа, а если объем газа увеличивается, то давление его уменьшается.
И следующее. У разных газов молекулы различны по массе. С ростом молекулярной массы увеличивается ударная сила молекулы о поверхность, что приводит к росту давления. Поэтому различные газы в одном объеме, с одной и той же температурой оказывают неодинаковые давления.
Итак:
- давление газа определяется общими ударами большого числа молекул о поверхности, окружающие газ;
- если изменить количество молекул газа, его температуру или объем сосуда, в котором газ находится, то можно изменить давление этого газа;
- в одинаковых прочих условиях (число молекул, объем, температура) у различных газов давление неодинаково.
Закон Паскаля
Твердые тела, соприкасаясь с поверхностью, давят на нее перпендикулярно. Газы давят в различных направлениях. А как давят жидкости?
Молекулы жидкости, перемещаясь, долго не задерживаются на месте. Здесь они подобны молекулам газов. Различие лишь состоит в расстояниях между молекулами. Поэтому в жидкостях, как и газах, есть давление, которое действует в любых направлениях одинаково. Почему в ванной вода из крана течет одной струей, а эта же самая вода из душа течет большим количеством одинаковых струек? Если бы вместо душевого сита был шар с дырками, то вода лилась бы во все стороны, и даже вверх. Объясняет эти явления знаменитый закон Паскаля:

Источник
Закон Паскаля справедлив для газов тоже. Примером из жизни служит уже рассмотренное надувание воздушного шарика. Струю воздуха человек направляет прямо перед собой (он же не крутит головой, чтобы заполнить шар), а шар заполняется везде, во всех направлениях. Накачивая резиновую лодку ручным насосом, рыбак нажимает сверху вниз на насос, воздух же наполняет полностью всю форму лодки.
Этот закон давления нашел широчайшее применение в механизмах, использующих принцип работы гидравлического пресса (изобретен Б. Паскалем). Если нажать на маленький поршень S1 силой F1, давление получится p1 = F1/ S1. Это давление без изменения (по закону Паскаля) будет передаваться во всех направлениях и дойдет до поршня S2. Значит, там давление p2 = F2/S2 такое же. p1 = p2, то есть F1/ S1 = F2/S2.
Используя математику, из этого равенства можно получить следующее: F1/F2 = S1/S2. Это равенство выражает закон гидравлического пресса (гидравлический – водяной или жидкостный). Оно означает: действуя маленькой силой на небольшую площадь можно получить большую силу, действующую на большую площадь. Силы будут отличаться во столько же раз, во сколько отличаются площади. Если действовать на малую площадь маленькой силой, используя площадь в несколько раз большую, можно получить силу во столько же раз большую.

Источник
Само слово «пресс» обозначает: механизм для обработки материалов давлением.
С помощью пресса макулатуре, металлолому, сену придают формы удобные для транспортировки.
Методом прессования изготовляют детали сложнейших приборов и машин.
В водяных насосах, отбойных молотках, также используется закон Паскаля и закон гидравлического пресса. Нажимая на тормоз, шофер останавливает автомобиль. Усиленное давление по этим законам передается на тормозные колодки, которые не дают вращаться колесам. Но это, конечно, далеко не весь перечень примеров проявления и использования свойств давления.
Давление жидкости
Можно ли численно рассчитать давление жидкости? Ответ получается, если применить нетрудные математические преобразования.
По определению p = F/S. F – сила, с которой жидкость (ведь она обладает весом P) давит на дно. Дальше, вспомнив формулы веса (P = mg), массы (m = ρV), объема (V = Sh), можно получить:
p = P/S = mg/S = ρVg/S = ρShg/S. Сократить полученную дробь на S, и результат готов:
p = ρgh
Изначально в формуле была задействована площадь дна, а в результате получилось выражение, в котором давление жидкости зависит ни от формы сосуда, ни от площади его стенок и дна, а от плотности ρ и глубины h жидкости (физики называют глубину высотой столба жидкости). Число g ≈ 10 Н/кг осталось от формулы веса.
 Источник Источник
Источник Источник
А теперь самое интересное. Можно ли водой из кружки разрушить большую бочку? Тот факт, что высота столба определяет давление жидкости, позволяет ответить на этот вопрос: « Да, можно!»
Если взять несколько сосудов различной формы, одинаковой высоты и с одинаковой площадью дна, которое затянуто эластичной пленкой, наполнить сосуды водой, то дно прогнется одинаково во всех трех случаях. Хотя вес жидкости разный, сила давления возникает одинаковая (но ведь силой давления является вес!). Что происходит? А вот что:
F = p ∙ S, а p = ρgh и F = ρgh ∙ S
Одна жидкость, плотность ρ, высота h и площадь S дна – одинаковы. Значит, и сила давления одинаковая. Это явление «гидростатического парадокса».

Источник
Первое объяснение этому парадоксу (противоречие с общепринятым утверждением; перевод с греческого «докса» – «мнение», «пара» – «против») дано опять же Б.Паскалем.
 Источник
Источник
Явления, связанные со стоячей жидкостью (в сосуде, в луже, в пруду) и давлением называют гидростатическими.
Сообщающиеся сосуды
Красивое зрелище – действующие фонтаны. Они всегда привлекают к себе внимание детей и взрослых. А каков же их принцип действия?
Первый человек, который это объяснил, опять был Блез Паскаль. Если взять две стеклянные трубочки и соединить их трубкой резиновой, и через воронку наливать воду в одну трубочку, то при любом положении трубочек вода в них будет на одинаковом уровне.
Эти трубочки, а на их месте могут быть любые сосуды, соединяются (сообщаются) друг с другом. Давление в обеих трубочках одинаково (по закону Паскаля), значит, и высота столбиков жидкости в этих соединенных, сообщающихся сосудах – одинакова.

Источник
Если один сосудов поднять на большую высоту, то из второго сосуда жидкость будет стремиться подняться до уровня первого сосуда, но сила тяжести, возвращает ее обратно на землю. Таков основной принцип работы фонтана. Вот его примерная схема:

Фонтан соединяется с большой башней, в которую закачивается вода с помощью насосов. Такую башню называют водонапорной. А если водонапорную башню соединить с водопроводной сетью, то вода поступит в любую квартиру, в любое здание. Водопровод – это пример применения в жизни сообщающихся сосудов.

Источник
К сообщающимся сосудам относятся насосы со шлангами, лейки, чайники, кофейники. В них по два сосуда: емкость под жидкость и носик. Звучит непривычно, но это так.
При помощи сообщающихся сосудов измеряют небольшое давление. Прибор называется жидкостным манометром. Один сосуд закрыт, а ко второму эластичной трубкой присоединена пластмассовая коробочка, затянутая пленкой. Если на пленку нажать, по закону Паскаля давление передастся на жидкость. В одном колене такого манометра жидкость опускается, а в другом поднимается. Давление тем больше, чем больше разница уровней жидкости.
 Источник
Источник
Принцип сообщающихся сосудов используется в шлюзах – устройствах, пропускающих речные корабли через плотины, перегораживающие реки. Плотины обычно устраивают там, где работают гидроэлектростанции. Плотины разделяют течение реки на части: верхнее течение (там накапливается вода) и нижнее. Там, где проходят корабли, сделаны специальные огромные ворота, которые удерживают воду. Получается, что большие сообщающиеся сосуды между собой перекрыты.
Пусть корабль идет по течению реки вниз. Он попадает в верхнюю часть шлюза, где уровень воды высокий. Ворота открываются, и вода начинает перетекать в нижнюю часть, уровень воды снижается, а вместе с ним опускается и корабль (в нижней части наоборот уровень повышается). Снижение происходит до тех пор, пока не произойдет выравнивание (закон сообщающихся сосудов) верхнего и нижнего течений. Корабль может дальше двигаться по реке. Если корабль движется вверх по течению, он вначале попадает в нижнюю часть шлюза. Ворота открываются, вода из верхней части поступает в нижнюю до выравнивания уровней. В нижней части вода поднимается, и вместе с ней поднимается корабль. После выравнивания уровней корабль может двигаться дальше. Шлюзы очень больших плотин могут иметь не одни ворота, а сразу несколько. Ворота могут открываться, как обычные двери (по течению реки) или вертикально.

Источник
Если дно непрозрачного бака соединить с тонкой стеклянной трубкой снизу, расположенной вертикально ему, то можно увидеть высоту воды в баке (см. рисунок). Так устроены водомерные стекла в паровых котлах.
Важный момент. В данных примерах используется одна жидкость. А если в разные сосуды налить разные жидкости, например, воду и керосин. Что будет наблюдаться?
Давление в обоих сосудах одинаково (закон Паскаля). Но ведь плотность воды 1000 кг/м3, а керосина – 800 кг/м3, тогда столб керосина с меньшей плотностью должен быть выше, чем столб воды в 1,25 раза, т. к. плотности отличаются тоже в 1,25 раза.
Наблюдается обратно пропорциональная зависимость:
h1/h2 = ρ2/ρ1
 Источник
Источник
Значит, в сообщающихся сосудах уровни одинаковы для однородной жидкости, а для разных жидкостей уровни различны.
Жидкости. В природе различают четыре вида состояния вещества: твердое, жидкое, газообразное и плазменное. Основное отличие жидкостей от твердых тел заключается в их текучести, т.е. способности легко принимать форму сосуда, в который жидкость поместили, при этом объем жидкости не изменяется. Газ тоже обладает текучестью, но при этом занимает любой предоставленный ему объем. В сосудах жидкость образует свободную поверхность, а газ аналогичной поверхностью не обладает. Однако с точки зрения механики и жидкость, и газ подчиняются одним и тем же закономерностям в случае, если сжимаемостью газа можно пренебречь. Поэтому в гидравлике под термином «жидкость» понимаются и собственно жидкости (которые часто называют капельными жидкостями), и газы (газообразные жидкости).
Основные свойства жидкости (при рассмотрении задач механики жидкости) — это плотность, способность изменять свой объем при нагревании (охлаждении) и изменениях давления, вязкость жидкости. Рассмотрим каждое из свойств жидкости подробнее.
Плотность жидкости. Плотностью жидкости ρ называется ее масса, заключенная в единице объема:


где m — масса жидкости; W — объем жидкости.
Единица измерения плотности — кг/м 3 .
Так как вода является наиболее распространенной в природе жидкостью, в качестве примера количественного значения параметра, определяющего то или иное свойство жидкости, будем приводить значение рассматриваемого параметра для воды.
Плотность воды при 4 °С ρв = 1000 кг/м 3 . Плотность жидкости уменьшается при увеличении температуры. Однако для воды эта закономерность справедлива только с 4 °С, в чем проявляется одно из аномальных свойств воды.
Удельный вес. Удельный вес γ — это вес жидкости, приходящийся на единицу объема:

где G — вес жидкости в объеме W.
Единица измерения удельного веса — Н/м 3 .
Удельный вес воды при температуре 4 °С γв= 9810 Н/м 3 .
Плотность и удельный вес связаны между собой соотношением


где g — ускорение свободного падения (g=9,81 м/с 2 ).
Температурное расширение. Это свойство жидкости характеризуется изменением объема при изменении температуры, которое определяется температурным коэффициентом объемного расширения жидкости βt:

где W — начальный объем жидкости; ΔW — Изменение объема после уменьшения или увеличения температуры; Δt — изменение температуры.
Знак Δ означает разницу между начальной величиной и конечной величиной.
То есть ΔW=Wконечный-Wначальный
Единица измерения βt; — град -1 ,
для воды,при t=20 °С βt = 0,00015 [1/°С].
Сжимаемость. Это свойство жидкости менять свой объем при изменении давления, которое характеризуется коэффициентом объемного сжатия βp :

где W — начальный объем жидкости; ΔW — изменение объема после изменения давления; ΔP — изменение давления.
Единица измерения βp — Па -1 Коэффициент объемного сжатия капельных жидкостей мало меняется в зависимости от давления и температуры.
Для воды βp = 5×10 -10 Па -1
Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкости Е и определяется по формуле:

для воды E=2×10 9 Па.
Вязкость жидкости — свойство жидкостей оказывать сопротивление сдвигу. Это свойство проявляется только при движении жидкостей. Вязкость характеризует степень текучести жидкости. Наряду с легко подвижными жидкостями (вода, спирт, воздух и др.) существуют очень вязкие жидкости (глицерин, машинные масла и др.).
Вязкость жидкости характеризуется динамической вязкостью μ.
И. Ньютон выдвинул гипотезу о силе трения F, возникающей между двумя слоями жидкости на поверхности их раздела площадью ω, согласно которой сила внутреннего трения в жидкости не зависит от давления, прямо пропорциональна площади соприкосновения слоев ω и быстроте изменения скорости в направлении, перпендикулярном направлению движения слоев, и зависит от рода жидкости.
Пусть жидкость течет по плоскому дну параллельными ему слоями

Вследствие тормозящего влияния дна слои жидкости будут двигаться с разными скоростями. Скорости слоев Показаны стрелками. Рассмотрим два слоя жидкости, середины которых расположены на расстоянии Δу друг от друга. Слой А движется со скоростью u, а слой В со скоростью u + Δu.
На площадке ω вследствие вязкости возникает сила сопротивления F. Согласно гипотезе Ньютона эта сила

коэффициент пропорциональности μ, в этой формуле и является динамической вязкостью, отношение Δu/Δy называется градиентом скорости.
Таким образом, динамическая вязкость является силой трения, приходящейся на единицу площади соприкосновения слоев жидкости при градиенте скорости, равном единице.
Размерность μ — Па • с.
Гипотеза И. Ньютона, представленная в формуле, экспериментально подтверждена и математически оформлена в дифференциальном виде

основоположником гидравлической теории смазки Н.П. Петровым и в настоящее время носит название закона внутреннего трения Ньютона.
В гидравлических расчетах часто удобнее пользоваться другой величиной, характеризующей вязкость жидкости, — ν:

Эта величина называется кинематической вязкостью. Размерность v — м 2 /с
Название «кинематическая вязкость» не несет особого физического смысла, так как название было предложено потому, что размерность v похожа на размерность скорости.
Вязкость жидкости зависит как от температуры, так и от давления. Кинематическая вязкость капельных жидкостей уменьшается с увеличением температуры, а вот вязкость газов, наоборот, возрастает с увеличением температуры. Кинематическая вязкость жидкостей при давлениях, встречающихся в большинстве случаев на практике, мало зависит от давления, а вязкость газов с возрастанием давления уменьшается.
Вязкость жидкости измеряют с помощью вискозиметров различных конструкций.
Жидкости, для которых справедлив закон внутреннего тяготения Ньютона, называют ньютоновскими. Существуют жидкости, которые не подчиняются закономерности формулам, к ним относятся растворы полимеров, гидросмеси из цемента, глины, мела и др. Такие жидкости относятся к неньютоновским.
Я кстати уже нашел формулы которые нужны сантехникам и инженерам, опишу их в других статьях. Пишите коментарии, я обязательно отвечу на ваши вопросы и постараюсь подкорректировать статьи под вашы нужды.
Основные понятия гидропневмоавтоматики

Схема гидравлического привода с дроссельным регулированием
Основные свойства рабочих жидкостей и газов
Плотность – количество массы в единице объема: 
Вязкость
Свойство жидкости сопротивляться сдвигу или скольжению ее слоев.
 ,
, 
где:  — напряжение сдвига;
— напряжение сдвига;
 — динамический коэффициент вязкости;
— динамический коэффициент вязкости;
 — скорость течения жидкости;
— скорость течения жидкости;
 — расстояние между слоями жидкости.
— расстояние между слоями жидкости.
 — кинематический коэффициент вязкости
— кинематический коэффициент вязкости
Сжимаемость
Свойство жидкости изменять свой объем под действием давления.  ,
,
где:  — адиабатический модуль объемной упругости жидкости;
— адиабатический модуль объемной упругости жидкости;
 — объем рабочей жидкости;
— объем рабочей жидкости;
 — давление рабочей жидкости.
— давление рабочей жидкости.
Для газов:  или
или  — закон Бойля-Мариотта.
— закон Бойля-Мариотта.
Облитерация
Свойство жидкости заращивать (засорять) узкие каналы и капиллярные щели при ее течении под действием перепада давления.
Кавитация
Разрыв рабочей жидкости под действием высокого давления при наличии большого количества растворенного воздуха.
Для идеального газа
Зависимость давления и объема
Изотермный процесс – процесс, проходящий при постоянной температуре

Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8464 —  | 7349 —
| 7349 —  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Жидкость в гидравлике рассматривают как сплошную среду без пустот и промежутков. Кроме того, не учитывают влияние отдельных молекул, то есть даже бесконечно малые частицы жидкости считают состоящими из весьма большого количества молекул.
Из курса физики известно, что вследствие текучести жидкости, т.е. подвижности ее частиц, она не воспринимает сосредоточенные силы. Поэтому в жидкости действуют только распределенные силы, причем эти силы могут распределяться по объему жидкости(массовые или объемные силы) или по поверхности (поверхностные силы).
Объемные (массовые) силы
К объемным (массовым) силам относятся силы тяжести и силы инерции. Они пропорциональны массе и подчиняются второму закону Ньютона.
К поверхностным силам следует отнести силы, с которыми воздействуют на жидкость соседние объемы жидкости или тела, так как это воздействие осуществляется через поверхности. Рассмотрим их подробнее.
Пусть на плоскую поверхность площадью S под произвольным углом действует сила R
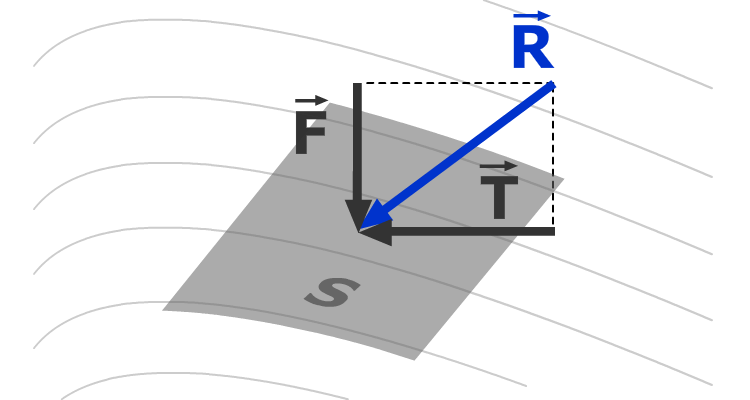
Силу R можно разложить на тангенциальную Т и нормальную F составляющие.
Тангенциальная составляющая называется силой трения Т и вызывает в жидкости касательные напряжения (или напряжения трения):
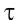 = T / S
= T / S
Единицей измерения касательных напряжений в системе СИ является Паскаль (Па) — ньютон, отнесенный к квадратному метру (1 Па = 1 Н/м 2 ).
Давление в жидкости
Нормальная сила F называется силой давления и вызывает в жидкости нормальные напряжения сжатия, которые определяются отношением:
Нормальные напряжения, возникающие в жидкости под действием внешних сил, называются гидромеханическим давлением или просто давлением.
Системы отсчета давления
Рассмотрим системы отсчета давления. Важным при решении практических задач является выбор системы отсчета давления (шкалы давления). За начало шкалы может быть принят абсолютный нуль давления. При отсчете давлений от этого нуля их называют абсолютными — Pабс.
Однако, как показывает практика, технические задачи удобнее решать, используя избыточные давления Pизб, т.е. когда за начало шкалы принимается атмосферное давление.
Давление, которое отсчитывается “вниз” от атмосферного нуля, называется давлением вакуума Pвак, или вакуумом.
где Pатм — атмосферное давление, измеренное барометром.
Связь между абсолютным давлением Pабс и давлением вакуума Pвак можно установить аналогичным путем:
И избыточное давление, и вакуум отсчитываются от одного нуля (Pатм), но в разные стороны.
Таким образом, абсолютное, избыточное и вакуумное давления связаны и позволяют пересчитать одно в другое.
Единицы измерения давления
Практика показала, что для решения технических (прикладных) задач наиболее удобно использовать избыточные давления. Основной единицей измерения давления в системе СИ является паскаль (Па), который равен давлению, возникающему при действии силы в 1 Н на площадь размером 1 м2 (1 Па = 1 Н/м2).
Однако чаще используются более крупные единицы: килопаскаль (1 кПа = 10 3 Па) и мегапаскаль (1 МПа = 10 6 Па).
В технике широкое распространение получила внесистемная единица — техническая атмосфера (ат), которая равна давлению, возникающему при действии силы в 1 кгс на площадь размером 1 см 2 (1 ат = 1 кгс/см 2 ).
Соотношения между наиболее используемыми единицами следующие:
10 ат = 0,981 МПа ≈ 1 МПа или 1 ат = 98,1 кПа ≈ 100 кПа.
В зарубежной литературе используется также единица измерения давления бар
В каких ещё единицах измеряется давление, можно посмотреть здесь
Рассмотрим некоторые свойства жидкостей, которые оказывают наиболее существенное влияние на происходящие в них процессы и поэтому учитываются при расчетах гидравлических систем.
Плотность и удельный вес
Важнейшими характеристиками механических свойств жидкости являются ее плотность и удельный вес. Они определяют “весомость” жидкости.
Под плотностью ρ (кг/м 3 ) понимают массу жидкости m, заключенную в единице ее объема V, т.е.
Вместо плотности в формулах может быть использован также удельный вес γ (Н/м 3 ), т.е. вес G = m⋅g, приходящийся на единицу объема V:
γ = G / V = m⋅g / V = ρ⋅g
Изменения плотности и удельного веса жидкости при изменении температуры и давления незначительны, и в большинстве случаев их не учитывают.
Плотности наиболее употребляемых жидкостей и газов (кг/м 3 ):
| бензин | 710. 780 |
| керосин | 790. 860 |
| вода | 1000 |
| ртуть | 13600 |
| масло гидросистем (АМГ-10) | 850 |
| масло веретенное | 890. 900 |
| масло индустриальное | 880. 920 |
| масло турбинное | 900 |
| метан | 0,7 |
| воздух | 1,3 |
| углекислый газ | 2,0 |
| пропан | 2,0 |
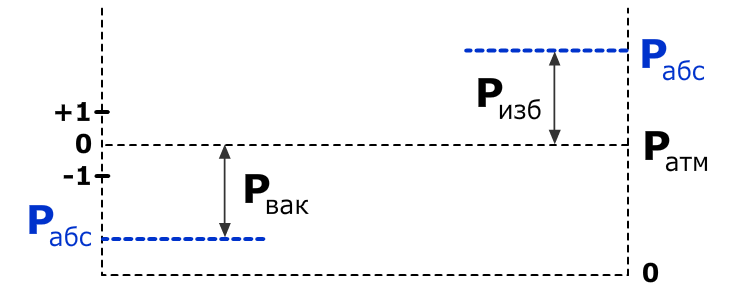
Вязкость
Вязкость — это способность жидкости сопротивляться сдвигу, т. е. свойство, обратное текучести (более вязкие жидкости являются менее текучими). Вязкость проявляется в возникновении касательных напряжений (напряжений трения).
Рассмотрим слоистое течение жидкости вдоль стенки (рисунок)
В этом случае происходит торможение потока жидкости, обусловленное ее вязкостью. Причем скорость движения жидкости в слое тем ниже, чем ближе он расположен к стенке. Согласно гипотезе Ньютона касательное напряжение, возникающее в слое жидкости на расстоянии у от стенки, определяется зависимостью:
Закон трения Ньютона
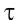 = = |
μ⋅ | dv |
| dy |
где dv/dy — градиент скорости, характеризующий интенсивность нарастания скорости v при удалении от стенки (по оси у), μ ‑ динамическая вязкость жидкости.
Течения большинства жидкостей, используемых в гидравлических системах, подчиняются закону трения Ньютона, и их называют ньютоновскими жидкостями.
Однако следует иметь в виду, что существуют жидкости, в которых закон Ньютона в той или иной степени нарушается. Такие жидкости называют неньютоновскими.
Величина μ, входящая в формулу (динамическая вязкость жидкости), измеряется в Па⋅с либо в пуазах 1 П = 0.1 Па⋅с. Пуа́з (обозначение: П, до 1978 года пз; международное — P; от фр. poise) — единица динамической вязкости в системе единиц СГС. Один пуаз равен вязкости жидкости, оказывающей сопротивление силой в 1 дину взаимному перемещению двух слоев жидкости площадью 1 см², находящихся на расстоянии 1 см друг от друга и взаимно перемещающихся с относительной скоростью 1 см/с.
1 П = 1 г / (см·с) = 0,1 Н·с/м²
Единица названа в честь Ж. Л. М. Пуазёйля. Пуаз имеет аналог в системе СИ — паскаль-секунда (Па·c).
Вода при температуре 20 °C имеет вязкость 0,01002 П, или около 1 сантипуаза.
Однако на практике более широкое применение нашла
Единицей измерения последней в системе СИ является м 2 /с или более мелкая единица — см 2 /с, которую принято называть стоксом, 1 Ст = 1 см 2 /с. Для измерения вязкости также используются сантистоксы: 1 сСт = 0,01 Ст.
Вязкость жидкостей существенно зависит от температуры, причем вязкость капельных жидкостей с повышением температуры падает, а вязкость газов — растет (см. рисунок).
Это объясняется тем, что в капельных жидкостях, где молекулы расположены близко друг к другу, вязкость обусловлена силами молекулярного сцепления. Эти силы с ростом температуры ослабевают, и вязкость падает. В газах молекулы располагаются значительно дальше друг от друга. Вязкость газа зависит от интенсивности хаотичного движения молекул. С ростом температуры эта интенсивность растет и вязкость газа увеличивается.
Вязкость жидкостей зависит также от давления, но это изменение незначительно, и в большинстве случаев его не учитывают.
Сжимаемость
Сжимаемость — это способность жидкости изменять свой объем под действием давления. Сжимаемость капельных жидкостей и газов существенно различается. Так, капельные жидкости при изменении давления изменяют свой объем крайне незначительно. Газы, наоборот, могут значительно сжиматься под действием давления и неограниченно расширяться при его отсутствии.
Для учета сжимаемости газов при различных условиях могут быть использованы уравнения состояния газа или зависимости для политропных процессов.
Сжимаемость капельных жидкостей характеризуется коэффициентом объемного сжатия βр (Па -1 ):
где dV — изменение объема под действием давления; dр — изменение давления; V — объем жидкости.
Знак “минус” в формуле обусловлен тем, что при увеличении давления объем жидкости уменьшается, т.е. положительное приращение давления вызывает отрицательное приращение объема.
При конечных приращениях давления и известном начальном объеме V можно определить конечный объем жидкости:
а также ее плотность
Величина, обратная коэффициенту объемного сжатия βр, называется объемным модулем упругости жидкости (или модулем упругости) К = 1/ βр (Па).
Эта величина входит в обобщенный закон Гука, связывающий изменение давления с изменением объема
Модуль упругости капельных жидкостей изменяется при изменении температуры и давления. Однако в большинстве случаев K считают постоянной величиной, принимая за нее среднее значение в данном диапазоне температур или давлений.
Модули упругости некоторых жидкостей (МПа):
| бензин | 1300 |
| керосин | 1280 |
| вода | 2000 |
| ртуть | 32400 |
| масло гидросистем (АМГ-10) | 1300 |
| масло индустриальное 20 | 1360 |
| масло индустриальное 50 | 1470 |
| масло турбинное | 1700 |
Температурное расширение
Способность жидкости изменять свой объем при изменении температуры называется температурным расширением. Оно характеризуется коэффициентом температурного расширения βt:
где dT- изменение температуры; dV- изменение объема под действием температуры; V — объем жидкости.
При конечных приращениях температуры:
Как видно из формул, с увеличением температуры объем жидкости возрастает, а плотность уменьшается.
Коэффициент температурного расширения жидкостей зависит от давления и температуры:
| Т, °C | p, МПа | βt, 1/град |
| 0,1 | 14·10 -6 | |
| 100 | 10 | 700·10 -6 |
То есть при разных условиях коэффициент температурного расширения изменился в 50 раз. Однако на практике обычно принимают среднее значение в данном диапазоне температур и давления.Например, для минеральных масел βt ≈ 800·10 -6 1/град.
Газы весьма значительно изменяют свой объем при изменении температуры. Для учета этого изменения используют уравнения состояния газов или формулы политропных процессов.
Испаряемость
Любая капельная жидкость способна изменять свое агрегатное состояние, в частности превращаться в пар. Это свойство капельных жидкостей называют испаряемостью. В гидравлике наибольшее значение имеет условие, при котором начинается интенсивное парообразование по всему объему — кипение жидкости.
Для начала процесса кипения должны быть созданы определенные условия (температура и давление). Например, дистиллированная вода закипает при нормальном атмосферном давлении и температуре 100°С. Однако это является частным случаем кипения воды. Та же вода может закипеть при другой температуре, если она будет находиться под воздействием другого давления, т. е. для каждого значения температуры жидкости, используемой в гидросистеме, существует свое давление, при котором она закипает.
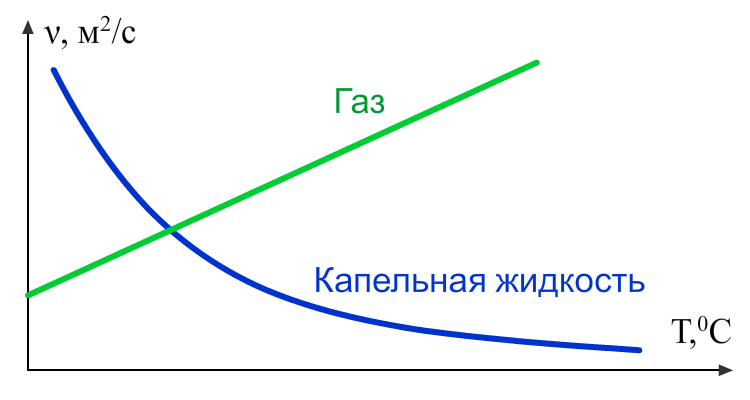
Давление при котором жидкость закипает, называют давлением насыщенных паров (pн.п.).
Величина pн.п. всегда приводится как абсолютное давление и зависит от температуры.
Для примера на рисунке приведена зависимость давления насыщенных паров воды от температуры.
На графике выделена точка А, соответствующая температуре 100°С и нормальному атмосферному давлению ра. Если на свободной поверхности воды создать более высокое давление р1, то она закипит при более высокой температуре Т1 (точка В на рисунке). И наоборот, при малом давлении р2 вода закипает при более низкой температуре Т2 (точка С).
Растворимость газов
Многие жидкости способны растворять в себе газы. Эта способность характеризуется количеством растворенного газа в единице объема жидкости, различается для разных жидкостей и изменяется с увеличением давления.
Относительный объем газа, растворенного в жидкости до ее полного насыщения, можно считать по закону Генри прямо пропорциональным давлению, то есть:
где Vг — объем растворенного газа, приведенный к нормальным условиям (p, Т);
Vж — объем жидкости;
k — коэффициент растворимости;
р — давление жидкости.
Коэффициент k имеет следующие значения при 20°С:
| вода | 0,016 |
| керосин | 0,13 |
| минеральные масла | 0,08 |
| жидкость АМГ-10 | 0,1 |
При понижении давления выделяется растворенный в жидкости газ, причем интенсивнее, чем растворяется в ней. Это явление может отрицательно сказывается на работе гидросистем.

Давление — физическая величина, численно равная силе, действующей на единицу площади поверхности перпендикулярно этой поверхности. Для обозначения давления обычно используется символ p — от лат.pressura (давление).
Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.
Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.
Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.
Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.
Главная страница
Содержание
Введение
Основы гидростатики
Основы гидродинамики
Гидравлические сопротивления
Истечние жидкости из отверстий, насадков и из-под затворов
Гидравлический расчет простых трубопроводов
Гидравлические машины
Лекция 2. ОСНОВЫ ГИДРОСТАТИКИ
Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидродинамика является более обширным
разделом и будет рассмотрена в последующих лекциях. В этой лекции будет рассмотрена гидростатика.
Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости
и их практическое применение.
В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением.
Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних
слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.
Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рис.2.1, а). На дно
резервуара действует сила P равная весу налитой жидкости G = γ V, т.е. P = G.
Если эту силу P разделить на площадь дна Sabcd, то мы получим среднее гидростатическое
давление, действующее на дно резервуара.
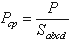
Гидростатическое давление обладает свойствами.
Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке
касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.
Для доказательства этого утверждения вернемся к рис.2.1, а. Выделим на боковой стенке резервуара
площадку Sбок (заштриховано). Гидростатическое давление действует на эту площадку в виде
распределенной силы, которую можно заменить одной равнодействующей, которую обозначим P. Предположим,
что равнодействующая гидростатического давления P, действующая на эту площадку, приложена в точке
А и направлена к ней под углом φ (на рис. 2.1 обозначена штриховым отрезком со
стрелкой). Тогда сила реакции стенки R на жидкость будет иметь ту же самую величину, но
противоположное направление (сплошной отрезок со стрелкой). Указанный вектор R можно разложить на
два составляющих вектора: нормальный Rn (перпендикулярный к заштрихованной площадке) и
касательный Rτ к стенке.
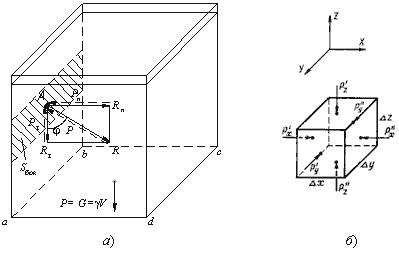
Рис. 2.1. Схема, иллюстрирующая свойства гидростатического давления
а – первое свойство; б – второе свойство
Сила нормального давления Rn вызывает в жидкости напряжения сжатия. Этим напряжениям
жидкость легко противостоит. Сила Rτ действующая на жидкость вдоль
стенки, должна была бы вызвать в жидкости касательные напряжения вдоль стенки и частицы должны были бы
перемещаться вниз. Но так как жидкость в резервуаре находится в состоянии покоя, то составляющая
Rτ отсутствует. Отсюда можно сделать вывод первого свойства
гидростатического давления.
Свойство 2. Гидростатическое давление неизменно во всех направлениях.
В жидкости, заполняющей какой-то резервуар, выделим элементарный кубик с очень малыми сторонами
Δx, Δy, Δz (рис.2.1, б). На каждую из боковых поверхностей будет
давить сила гидростатического давления, равная произведению соответствующего давления Px,
Py , Pz на элементарные площади. Обозначим вектора давлений,
действующие в положительном направлении (согласно указанным координатам) как P’x,
P’y, P’z, а вектора давлений, действующие в обратном направлении
соответственно P”x, P”y, P”z. Поскольку кубик
находится в равновесии, то можно записать равенства
P’xΔyΔz=P”xΔyΔz
P’yΔxΔz = P”yΔxΔz
P’zΔxΔy + γΔx, Δy, Δz = P”zΔxΔy
где γ – удельный вес жидкости;
Δx, Δy, Δz – объем кубика.
Сократив полученные равенства, найдем, что
P’x = P”x; P’y = P”y; P’z + γΔz = P”z
Членом третьего уравнения γΔz, как бесконечно малым по сравнению с P’z
и P”z, можно пренебречь и тогда окончательно
P’x = P”x; P’y = P”y; P’z=P”z
Вследствие того, что кубик не деформируется (не вытягивается вдоль одной из осей), надо полагать, что
давления по различным осям одинаковы, т.е.
P’x = P”x = P’y = P”y = P’z=P”z
Это доказывает второй свойство гидростатического давления.
Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.
Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки
давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. Третье свойство гидростатического
давления может быть записано в виде
P=f(x, y, z)
Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила –
сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке
рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.
Пусть жидкость содержится в сосуде (рис.2.2) и на ее свободную поверхность действует давление P0
. Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на
глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на
ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного
объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь
будет внешним и направлено по нормали внутрь объема, т.е. вверх.
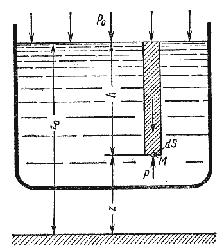
Рис. 2.2. Схема для вывода основного уравнения гидростатики
Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:
PdS – P0 dS – ρghdS = 0
Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре
объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они
перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на
dS и перегруппировав члены, найдем
P = P0 + ρgh = P0 + hγ
Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой
точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления
P0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев
жидкости.
Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее
всегда будет действовать давление, приложенное к внешней поверхности P0. Другими словами
давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем
направлениям одинаково. Это положение известно под названием закона Паскаля.
Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня (подробно рассмотрим
в п.2.6). В обычных условиях поверхности уровня представляют собой горизонтальные плоскости.
Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина
стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b
(рис.2.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим
график изменения избыточного гидростатического давления на стенку АВ.
Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh,
то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например
А и B.
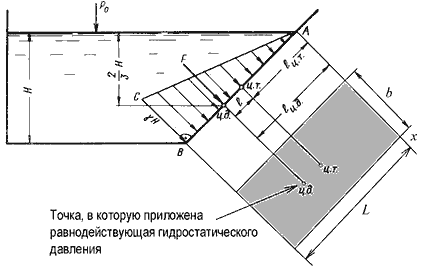
Рис. 2.3. Схема к определению равнодействующей гидростатического давления на плоскую
поверхность
Избыточное гидростатическое давление в точке А будет равно
PA = γh = γ·0 = 0
Соответственно давление в точке В:
PB = γh = γH
где H – глубина жидкости в резервуаре.
Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей
поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH,
надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом
отрезка γH, получим треугольную эпюру распределения давления АВС с прямым
углом в точке В. Среднее значение давления будет равно
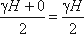
Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна
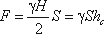
где hc = Н/2 – глубина погружения центра тяжести плоской поверхности под уровень жидкости.
Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать
с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна
отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.
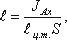
где JАx – момент инерции площади S относительно центральной оси, параллельной
Аx.
В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит
на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3
от нижней стороны.
Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную
поверхность АВС (рис.2.4), простирающуюся в направлении читателя на ширину b. Восстановим из
точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсеке АОСВ
находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и
силы веса взаимно уравновешиваются.
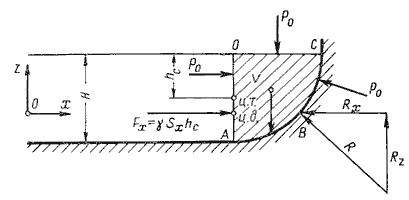
Рис. 2.4. Схема к определению равнодействующей гидростатического давления на
цилиндрическую поверхность
Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и
жидкость (этот объем на рис.2.4 заштрихован). Левая поверхность этого объема (на чертеже вертикальная
стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на
плоскость yOz.
Cила гидростатического давления на площадь Sx равна Fx = γ
Sxhc.
С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка
приложения и направление этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим на
две составляющие Rx и Rz.
Из действующих поверхностных сил осталось учесть только давление на свободной поверхности
Р0. Если резервуар открыт, то естественно, что давление Р0 одинаково
со всех сторон и поэтому взаимно уравновешивается.
На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.
Спроецируем все силы на ось Ох:
Fx – Rx = 0 откуда Fx = Rx = γSxhc
Теперь спроецируем все силы на ось Оz:
Rx – G = 0 откуда Rx = G = γV
Составляющая силы гидростатического давления по оси Oy обращается в нуль, значит Ry = Fy = 0.
Таким образом, реакция цилиндрической поверхности в общем случае равна
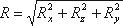
а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давления R=F,
то делаем вывод, что
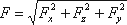
Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление,
направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.
Pвыт = ρжgVпогр
Для однородного тела плавающего на поверхности справедливо соотношение
где: V – объем плавающего тела;
ρm – плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь
гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние
называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют
водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) – центром
водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат
на одной вертикальной прямой O’-O”, представляющей ось симметрии судна и называемой осью плавания
(рис.2.5).
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна
KLM вышла из жидкости, а часть K’L’M’, наоборот, погрузилось в нее. При этом получили новое
положении центра водоизмещения d’. Приложим к точке d’ подъемную силу R и линию ее
действия продолжим до пересечения с осью симметрии O’-O”. Полученная точка m называется
метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h
положительным, если точка m лежит выше точки C, и отрицательным – в противном случае.
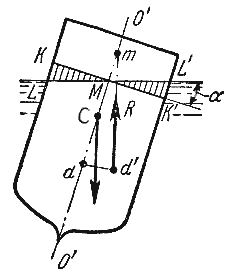
Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h<0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее
опрокидывание судна.
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше
будет остойчивость судна.
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью
уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы
жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость
принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого относительного покоя.
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна
движется по горизонтальному пути с постоянным ускорением a (рис.2.6).
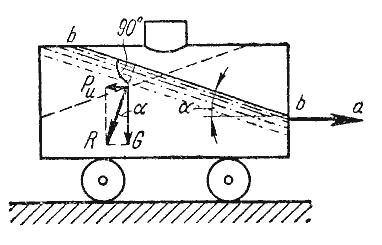
Рис. 2.6. Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила
инерции Pu, равная по величине ma. Равнодействующая 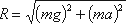
этих сил направлена к вертикали под углом α, тангенс которого равен
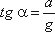
Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной
равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную,
составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от
ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в
цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту
под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным,
направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону
(см. рис.2.6, пунктир).
В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости
во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом
случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила
тяжести G = mg и центробежная сила Pu = mω2r, где r
– расстояние частицы от оси вращения, а ω – угловая скорость вращения сосуда.
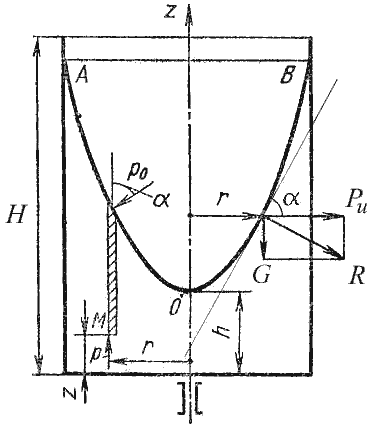
Рис. 2.7. Вращение сосуда с жидкостью
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и
представит собой параболоид вращения. Из чертежа находим
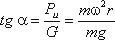
С другой стороны:
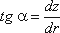
где z – координата рассматриваемой точки. Таким образом, получаем:
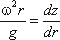
откуда
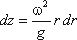
или после интегрирования
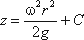
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем
иметь
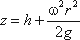
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму
имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим
вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS
(точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в
вертикальном направлении. С учетом уравнения (2.11) будем иметь
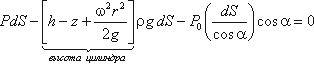
После сокращений получим
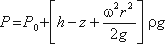
Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально
высоте z.
Проверить себя ( Тест )
Наверх страницы

