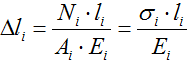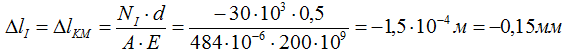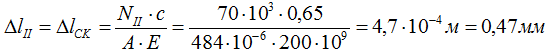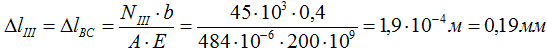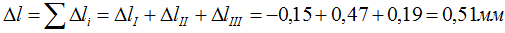Пример решения задачи на расчет деформаций участков и изменение общей длины стального стержня при его растяжении-сжатии.
Задача
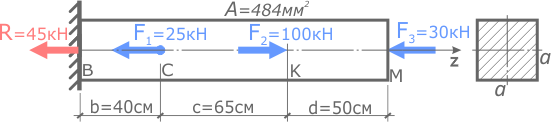
Рассчитать деформации участков и общее изменение длины прямого стержня постоянного сечения.
Другие примеры решений >
Помощь с решением задач >
Модуль продольной упругости стали E=200ГПа.
Пример решения
Предыдущие пункты решения задачи
- Определение опорных реакций,
- Построение эпюр внутренних продольных сил,
- Подбор размеров поперечного сечения стержня,
- Построение эпюр нормальных напряжений.
Стержень имеет три силовых участка, на которых площадь сечения одинакова, но внутренние силы и нормальные напряжения отличаются, поэтому определим абсолютные деформации всех участков в отдельности, после чего сложив их, получим изменение длины всего стержня в целом.
Изменение длины участков стержня при растяжении-сжатии рассчитывается по формуле:
где N – величина внутренней продольной силы,
l – длина рассматриваемого участка,
A – площадь его поперечного сечения,
E – модуль Юнга (продольной упругости) для материала стержня,
σ — значение нормальных напряжений на рассматриваемом участке.
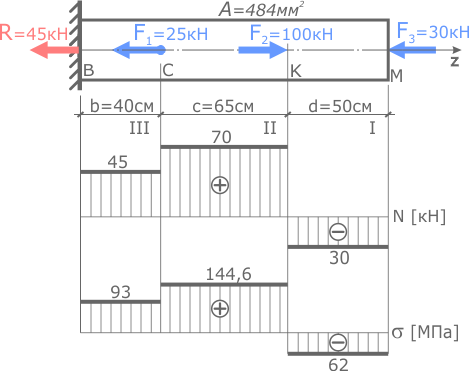
Значения внутренних сил и напряжений принимаются с построенных эпюр N (σ).
По эпюрам видно, что первый участок сжимается, а участки II и III растягиваются, следовательно, деформации Δl второго и третьего участков будут положительны (их длина увеличивается), а первого отрицательны (продольный размер уменьшается).
Рассчитаем их:
Деформация I участка (KM)
II участок (CK)
Удлинение третьего участка BC
Сложив (с учетом их знака) деформации всех участков получим величину изменения длины всего стержня в целом:
В результате деформации общая длина стержня увеличится на 0,51мм.
Расчет и построение эпюры перемещения сечений >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Добавил:
Uman
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
575
Добавлен:
04.03.2014
Размер:
1.33 Mб
Скачать
С учетом того что ε =N/EF, вторая формула (3.13) принимает вид:
|
∆ l = |
N l |
, |
(3.14) |
|
|
E F |
||||
где EF – жёсткость при растяжении-сжатии (этот параметр зависит от свойств материала (Е) стержня и площади его поперечного сечения).
Формула (3.14) может быть получена непосредственно из закона Гука (3.5) с учетом формул (3.9) и (2.1). Поэтому выражение (3.14) определяют как закон Гука для участка бруса при постоянной деформации на участке.
Если на участке бруса действует распределенная нагрузка постоянной интенсивности q (рис. 3.5,б), то нормальная сила в произвольном сечении при известном значении в начальном сечении (Nн ) рав-
|
на: |
||||||
|
N = Nн – qz . |
(3.15) |
|||||
|
При z = l |
Nк = Nн |
– q l. |
||||
|
Подставляя выражение (3.15) в формулу (3.10), после интегриро- |
||||||
|
вания при wo = wн получаем: |
||||||
|
w = wн + |
N н z |
− |
qz2 |
. |
(3.16) |
|
|
EF |
2EF |
|||||
|
Следовательно, эпюра w (см. рис. 3.5,б) ограничена параболой |
||||||
|
выпуклостью вверх (d2w/dz2< 0). Если на участке эпюра N |
пересекает |
ось, то в этом сечении функция w имеет экстремум (dw/dz = 0). Этот случай на рис. 3.5,б показан штриховыми линиями. При z = l перемещение концевого сечения участка равно:
|
wк = wн + |
N |
н |
l |
− |
q l2 |
. |
|
|
EF |
2EF |
||||||
Изменение длины стержня может вызываться различными причинами: силовым воздействием, изменением температуры, отклонением от номинальной длины стержня.
Если на стержень действуют заданные нагрузки, то изменение длины любого его участка с постоянной деформацией (рис. 3.6,а) определяется по формуле (3.14).
40

Рис 3.6
При изменении температуры стержня на ∆ T° (температурное воздействие) любой его участок изменяет длину (рис. 3.6,б) на величину
|
∆ lT = α T ∆ T l , |
(3.17) |
где α T – температурный коэффициент линейного расширения мате-
риала. (Например, для стали α T =1,25 10-5 1/град.) Соответственно возникают температурные деформации:
|
ε ò = |
∆ lT |
= |
α T ∆ T . |
(3.18) |
|
l |
Если силовое и температурное воздействия осуществляются одновременно, то изменение длины и деформация определяются с использованием принципа суперпозиции:
|
∆ l = |
N l |
+ |
α T ∆ T l ; |
ε |
= |
σ + |
αα Τ ∆ Τ . |
(3.19) |
|
|
EF |
|||||||||
|
E |
Использование принципа суперпозиции, при котором силовая и температурная деформации рассматриваются как независимые, справедливо в том случае, когда модуль упругости Е и температурный коэффициент α T не зависят от температуры. Практически это имеет место при умеренном температурном воздействии. Например, для малоуглеродистой стали при Т < 300° C (cм. рис. 2.10).
Кроме того, изменение длины стержня или его участка может быть связано и с тем, что он изготовлен длиннее или короче своей номинальной длины на величину ∆ o= l – lo (рис. 3.6,в). Отклонение от номинального размера положительно (∆ o> 0), если стержень длиннее,
иотрицательно (∆ o< 0), если – короче.
Сучетом всех перечисленных факторов изменение длины участка стержня определяется выражением
|
∆ l = |
N l |
+ |
α Τ ∆Τ∆Τ l+ |
∆ 0 . |
(3.20) |
|
|
EF |
||||||
Полное изменение длины стержня равно сумме изменений длин его участков.
41
3.5. Расчет стержня на прочность
Прочностной анализ стержня заключается в определении напряжений для стержня в целом, выявлении максимальных напряжений и сопоставлении их с допускаемыми или предельными напряжениями.
Сечение стержня, в котором возникают максимальные напряжения, называется опасным. Если максимальные напряжения действуют на всем участке стержня, то такой участок также называется опасным. При расчете на прочность стержня из пластичного материала ис-
пользуется условие прочности:
|
σ max ≤ [σ ]; [σ ] = σ т / nт или [σ ] = σ 0,2 / nт . |
(3.21) |
Максимальные напряжения σ max = (N/F)max в опасном сечении могут быть как растягивающими (положительными), так и сжимающими (отрицательными). В последнем случае величина напряжения берется по модулю. Допускаемые напряжения [σ ] либо заданы, либо вычисляются по второй формуле (3.21) при известном пределе текучести σ т (или σ 0,2) и коэффициенте запаса nт.
При расчете на прочность стержня из хрупкого материала используется система условий прочности:
|
σ |
р,max ≤ |
[σ ]р; |
[σ ]р = σ вр / nв, |
|
|
σ |
с,max ≤ |
[σ ]с; |
[σ ]с = σ вс / nв. |
(3.22) |
Расчет ведется как для опасного сечения, в котором возникают максимальные растягивающие напряжения σ р,max, так и для опасного сечения с максимальными сжимающими напряжениями σ с,max.
Условия прочности (3.21), (3.22) подробно рассмотрены в разде-
ле 2.5.
При известных допускаемых напряжениях для материала стержня могут проводиться три варианта расчетов.
1. Если заданы нагрузки и размеры сечений стержня, то проводится поверочный расчет.
2.Если заданы нагрузки, то могут быть определены размеры сечений стержня (проектировочный расчет).
3.Если заданы размеры сечений, то могут быть определены допускаемые нагрузки.
Эти варианты расчета на конкретном примере рассмотрены в следующем разделе.
42

3.6. Расчёт статически определимого стержня
Для статически определимого стержня (рис. 3.7) реакция в за-
делке (или нормальная сила в любом сечении) может быть определена с использованием уравнений статики. Если реакция в заделке предварительно не определена, то построение эпюры N рациональнее начинать со свободного конца стержня. При этом, используя метод сечений, необходимо отбрасывать часть стержня с заделкой. Последовательно применяя метод сечений на каждом участке (i =1, 2, 3, 4), определяются нормальные силы на участках. По полученным значениям строится эпюра N. Скачки на эпюре N по величине равны силам, приложенным в соответствующих сечениях. Участок АВ не деформируется, участки ВС и DM растягиваются, а участок СD сжимается.
Рис. 3.7
Для построения эпюры σ определяются нормальные напряжения на каждом участке по формуле (3.9)
|
σ ( i) = |
Ni |
; |
i = 1, 2, 3, 4 |
(3.23) |
|
Fi |
с учётом того, что F1=F2=F3=F и F4=2F.
Если стержень изготовлен из пластичного материала, то участки 3 и 4 равноопасны. Если стержень изготовлен из хрупкого материала, то более опасным может оказаться участок 4 (как правило, хрупкий материал хуже работает на растяжение).
Линейные деформации на участках определяются из закона Гука
|
(3.5): |
σ ( i) |
|||
|
ε (i) = |
; |
i = 1, 2, 3, 4. |
(3.24) |
|
|
E( i) |
43
Если стержень выполнен из одного материала (E(i) = E), то эпюра ε имеет такой же вид, как и эпюра σ .
Эпюра осевых перемещений w строится, начиная с сечения, где известно перемещение. Для рассматриваемого стержня – от сечения
М, так как wМ= 0.
В соответствии с формулами (3.13), (3.14) и учитывая, что wн = wМ= 0, а wк = wD, получим перемещение сечения D:
|
w |
= ∆ l = |
4Pl |
= |
2Pl |
. |
|
|
D |
||||||
|
4 |
E 2F |
EF |
||||
Если на i-ом участке стержня определена деформация ε (i) = const, то проще вычислять ∆ li по второй формуле (3.13):
Аналогично определяем перемещения других сечений по участ-
кам:
|
wC = wD +∆ l3 |
= 2 |
P l |
+ (−− 2 |
P |
) 1,5l== −− |
Pl |
; |
||||||
|
EF |
EF |
EF |
|||||||||||
|
wB = wC + ∆ l2 |
= − |
P l |
+ ( |
P |
) 1,5l= |
0,5 |
P l |
; wA = wB. |
|||||
|
EF |
EF |
EF |
Участок АВ перемещается как жесткое тело, не деформируясь. Поэтому перемещения всех сечений на этом участке одинаковы. Сечение А перемещается вверх. Направления перемещения просто определить по участку 4. Так как этот участок растягивается (N4 > 0), то при wD > 0 сечение D перемещается вверх. Отсюда следует, что сечения, у которых w > 0, перемещаются вверх, и наоборот.
Полное изменение длины стержня (удлинение или укорочение), а значит и перемещение его концевого сечения относительно начального сечения, может быть определено суммированием изменений длин участков:
|
∆ l = ∑m |
∆∆ l |
i |
, |
(3.26) |
|
i = |
1 |
|||
|
где m – число участков. |
В данном случае ∆ l = wA = ∆ l1 +∆ l2 + ∆ l3 + ∆ l4.
Из построенной эпюры w видно, что наибольшее перемещение
имеет сечение D (wmax = wD).
Отметим, что в соответствии с формулой (3.4) значение деформации ε является производной от функции перемещений w. Двигаясь в положительном направлении оси z (вверх) от сечения М (см. рис.3.7), значения на эпюре ε определяют возрастание или убывание
44

функции перемещений w. И наоборот, перемещения являются интегральной функцией от деформаций ε формула (3.11). Например, перемещение произвольного сечения w(z) на участке 4 равно площади прямоугольника длиной z на эпюре ε (w(z) = ε 4 z).
Рассмотрим различные варианты расчета стержня на прочность.
Вариант 1. Проверить прочность стержня при заданных параметрах:
F = 2 см2, Р=10 кН, σ T = 320 МПа, nТ = 2.
Определяем максимальные напряжения σ max (см. эпюру σ на рис. 3.7) и допускаемые напряжения (3.21):
|
3 |
||||||
|
σ max= σ |
(2) |
=σ (3)=2 |
P |
, σ max=2 |
10 10 |
=108 Па = 100 МПа; |
|
F |
− 4 |
|||||
|
2 10 |
[σ ]= 320 = 160 МПа. 2
Сравнивая максимальные напряжения с допускаемыми, делаем заключение, что условие прочности (3.21) для стержня удовлетворяется. Вариант 2. Определить параметр F при следующих исходных дан-
ных:
Р = 20 кН; [σ
Учитывая что σ
2FP ≤ [σ ] .
] = 160 MПа.
mах = 2P/F, условие прочности (3.21) примет вид:
Решая это неравенство относительно параметра F, находим:
|
F ≥ |
2P |
; |
Fmin = 2 |
2 20 103 |
= 2,5 10− 4м2=2,5 см2. |
|
160 106 |
|||||
|
[σ ] |
Вариант 3. Определить максимально допустимое значение параметра нагрузкиРдлястержняизхрупкогоматериала, используятакиеданные:
F = 2 см2; σ вр =240 МПа; σ вс = 960 МПа; nв = 4 .
Материал стержня хуже работает при растяжении, поэтому наиболее опасным является участок 3 (см. эпюру σ на рис. 3.7). Подставляя σ p,max= 2P/F в первое неравенство (3.22), получим:
|
2 |
P |
≤ [σ ]р; [σ ]р = 240/4 = 60 МПа. |
|
|
F |
|||
Решая это неравенство, находим:
Р ≤ [σ ]р F/ 2; Pдоп = 60 106 2 10 –4/2 = 6 кН.
Определимизменениедлиныстержняпризначенияхпараметров:
F = 2 см2; P = 20 кН ; l = 1м; E = 2 105 МПа.
45

Как следует из эпюры w (см. рис. 3.7,б), стержень удлиняется, так как wA > 0 (сечение А перемещается вверх):
|
wA = |
0,5 |
20 10− 4 1 |
= 2,5 10− 3 |
м= 2,5 ìì . |
|
|
2 1011 |
2 10− 4 |
||||
При расчете стержня не учитывался его собственный вес. Считается, что им можно пренебречь по сравнению с действующими силами. Но в ряде практических случаев необходимо учитывать напряжения от собственного веса.
Рассмотрим стержень постоянного сечения (рис. 3.8,а), нагруженный собственным весом. Следует отметить, что расчетная схема стержня с сосредоточенной силой, равной силе веса стержня и приложенной в его центре тяжести (рис. 3.8,б), является весьма приближённой, так как нагруженной является половина стержня (см эпюру N на рис. 3.8,б). Тогда как очевидно, что в произвольном сечении 1-1 нормальная сила равна силе веса отсеченной части.
Рис. 3.8
Для расчётной схемы стержня (рис. 3.8,в) объемную нагрузку, определяемую собственным весом стержня P, заменим погонной нагрузкой интенсивности q = P/l. С учетом соотношения P = γ Fl, где γ – удельный вес материала стержня, получим q = γ F. Тогда N и σ в произвольном сечении стержня (рис. 3.8,в) определяются выражениями:
N = q (l – z) = γ F (l – z); σ = N/F = γ (l – z).
Соответствующие эпюры N и σ представлены наэтом жерисунке. Найдем предельную длину стержня lпр, при которой максимальные напряжения в стержне у заделки достигнут предела прочности и
стержень разрушится:
σ max = σ вр; γ lпр = σ вр; lпр = σ вр/γ .
46
Как видим, предельная длина стержня постоянного сечения не зависит от его площади поперечного сечения. Например, для стального стержня с γ = 7,8 104 Н/м3 и σ вр= 780 МПа получим lпр= 104м.
Более эффективно применять материал, у которого высокие прочностные характеристики (σ вр) и/или наименьший удельный вес (γ ), т.е. материал, имеющий большее значение lпр=σ вр/γ . В наибольшей степени таким условиям удовлетворяют волокнистые композитные материалы (углепластик, органопластик и др.).
Осевые перемещения сечений стержня определяются по формуле (3.18) при wн = 0 (в заделке):
|
w (z) = − |
q z2 |
+ |
Níz |
= − |
q z2 |
++ |
ql z |
. |
|
2EF |
||||||||
|
2EF |
EF |
EF |
Функция w(z) является квадратичной параболой. Перемещение концевого сечения стержня (при z = l и c учетом ql = P) равно:
w = Pl/2EF.
Отметим, что этот же результат получается и с использованием приближённой расчетной схемы на рис. 3.8,б. Следует также отметить, что при использовании этой схемы правильно определяются максимальные напряжения в стержне у заделки, однако распределение N , σ и w по длине стержня описываются неверно.
3.7. Расчёт статически неопределимого стержня
Статически неопределимым является стержень с двумя заделками (рис. 3.9). Две реакции не могут быть определены из одного уравне-
|
ния статики: |
|
|
Σ Fz = 0; RA + P – 5P + RD = 0. |
(3.27) |
Второе уравнение должно быть получено из рассмотрения деформирования стержня. Для этого условно сделаем стержень статически определимым, удалив одну из заделок, например правую. Вместо удаленной заделки приложим неизвестную реакцию X1=RA. Получим
стержень, аналогичный (статически эквивалентный) заданному. При этом нужно учитывать, что из-за наличия двух заделок изменение полной длины стержня равно нулю (деформационное условие). В со-
|
ответствии с формулой (3.26) запишем: |
|
|
∆ l1 +∆ l2 +∆ l3 = 0. |
(3.28) |
|
Для определения ∆ li (3.14) получим нормальные силы Ni в сече- |
|
|
ниях каждого участка: |
|
|
N1 = X1; N2 = X1 + P ; N3 = X1 + P – 5P = X1 – 4P . |
(3.29) |
47

Используя формулу (3.14), значения Ni (3.29) и физико-геомет- рические параметры участков (Ei, Fi, li), уравнение (3.28) запишем в виде:
|
X1l |
+ |
( X1 + P) l |
+ |
( X1 − 4P) l |
|
EF |
E2F |
E2F |
||
Это уравнение является дополнительным к уравнению статики
(3.27).
Уравнение (3.30) может быть преобразовано к виду :
Первое слагаемое в этом уравнении определяет для эквивалентного стержня перемещение концевого сечения А от неизвестной реакции Х1, а второе слагаемое – перемещение от заданных сил. При этом коэффициент при Х1 численно равен перемещению сечения А от силы
Х1=1.
Решая уравнение (3.31), находим Х1 = RA = 3/4P, а затем из (3.29) – усилия на участках. После чего строятся эпюры N, σ и w, которые представлены на рис. 3.9. Эпюра w построена, начиная с сечения D. Правильность решения контролируется равенством нулю перемещения сечения А.
Для статически неопределимого стержня практическое значение имеет вычисление температурных и монтажных напряжений.
48
При изменении температуры статически определимого стержня в нем не возникают усилия и напряжения. Стержень просто удлиняется или укорачивается. Если же нагревать или охлаждать статически неопределимый стержень, то в нем возникают температурные усилия и напряжения. Это объясняется тем, что жесткие заделки не позволяют изменяться длине стержня. В результате при нагреве возникают сжимающие усилия и напряжения, а при охлаждении стержня – растягивающие усилия и напряжения.
Если длина стержня имеет отклонение от номинального размера (например, стержень выполнен длиннее на величину ∆ 0 = l – l0), то после принудительной установки такого стержня между жесткими опорами в нем возникают так называемые монтажные усилия и на-
пряжения.
Учет вышеуказанных факторов покажем для стержня, рассмотренного в предыдущем примере (см. рис.3.9). Предположим, что стержень нагрет на ∆ T° C и выполнен короче своей номинальной длины на ∆ 0 (рис. 3.10). При нагреве стержень получил бы удлинение ∆ T=α T∆ T.3l при отсутствии правой заделки. Если ∆ 0 ≥ ∆ T, то усилия и напряжения в стержне не возникают. Если же ∆ 0 < ∆ T, то в заделках возникают реакции RA и RD, которые не могут быть определены из одного уравнения статики:
|
RD – RA = 0; RD= RA. |
(3.32) |
Отметим, что возникающие реакции самоуравновешены.
Удалим правую заделку и вместо неё в сечении А приложим неизвестную реакцию X1 = RA. Учитывая, что изменение длины стержня (или перемещение сечения А) равно ∆ 0, запишем:
|
∆ l1 + ∆ l2 = ∆ 0. |
(3.33) |
Нормальные силы на участках стержня равны:
Используя первую формулу (3.19) для определения ∆ li и значения Ni , уравнение (3.33) запишем в виде:
|
( |
− |
X1l |
+ α |
T |
∆ Tl)++ |
(− |
− |
X1 2l |
++ αα |
∆ |
∆ T2l)== ∆ |
0 |
. |
(3.35) |
||
|
EF |
EF |
T |
||||||||||||||
|
Решая это уравнение, получим: |
||||||||||||||||
|
X1 |
= |
EF |
( ∆ |
Τ − ∆∆ |
0 ) ; |
∆ 0 ≤ ∆ |
T, |
(3.36) |
||||||||
|
2l |
где ∆ T = 3α T∆ Tl – температурное удлинение стержня.
49
Если ∆ T = ∆ 0, то X1 = 0. На рис. 3.10 представлены эпюры N, σ и w. Эпюра w построена от сечения D (wD = 0). При этом получим:
|
w |
B |
= ∆ l |
== |
− X1 2l |
+ α |
∆∆ T2l |
; w |
A |
= |
w |
B |
++ |
∆ l |
== |
w |
B |
+ |
− X1l |
+ α |
∆∆ Tl . |
|
|
2 |
E2F |
T |
1 |
EF |
T |
||||||||||||||||
|
С учетом формулы(3.36) получим: |
|||||||||||||||||||||
|
wВ = (∆ |
О + α T∆ T l)/2 ; |
wA = ∆ |
0. |
Последнее равенство является проверкой расчёта. Из этого условия исходили, решая задачу.
При одновременном воздействии на стержень нагрузки, температуры и наличии монтажных отклонений в соответствии с принципом суперпозиции усилия, напряжения и перемещения, полученные при соответствующем расчете стержня (см. рис. 3.9) и (см. рис. 3.10), суммируются.
50
Соседние файлы в папке Книги и методические указания
- #
04.03.201414.07 Mб252Кочетов Сопротивление материалов.pdf
- #
5. Деформации при растяжении и сжатии. Закон Гука. Коэффициент поперечной деформации
Некоторые элементы конструкций и элементов подвергаются только продольным нагрузкам, что вызывает в них деформацию растяжения или сжатия. Длина стержня, подвергнутого растяжению, увеличивается, а площадь его поперечного сечения уменьшается. При сжатии наоборот — длина уменьшается, а площадь сечения увеличивается. При этом изменение длины называют линейной продольной деформацией, а изменение площади поперечного сечения — поперечной линейной деформацией. Для оценки интенсивности деформации применяют такие понятия, как относительная продольная ε и относительная поперечная ε’ — деформации, приходящиеся на единицу длины или пощади сечения стержня.
где Δl — изменение длины стержня;
Δa — изменение площади сечения.
Продольную деформацию растяжения обычно считают положительной, деформацию сжатия — отрицательной. Продольная и поперечная деформации связаны соотношением
μ — коэффициент поперечной деформации, который имеет свое значение для разных тел (в пределах упругого деформирования). Этот коэффициент называют коэффициентом Пуассона.
В пределах упругого деформирования экспериментально была установлена прямая зависимость между нормальным напряжением σ и относительной деформацией ε.
σ = Eε
Это соотношение носит название закона Гука, а коэффициент пропорциональности E называется модулем упругости первого рода. Модуль упругости — это величина, постоянная для каждого материала. Из соотношения видно, что при постоянном напряжении деформация меньше при большем модуле упругости.
Если рассматривать участок длиной l, на котором продольная сила и площадь поперечного сечения постоянны, закон Гука можно представить в виде:
Произведение EA называется жесткостью сечения.
При растяжении или сжатии стержня его сечения перемещаются. Осевое перемещение сечений друг относительно друга равно изменению длины стержня между этими сечениями. График, на котором изображены перемещения всех сечений относительно одного, принятого за неподвижное, называется эпюром перемещений.
В общей физике и теоретической механике мы предполагали, что тело абсолютно твердое. То есть расстояние между любыми точками равно вне зависимости от ситуации. Однако в самом фундаменте курса сопромата мы уже выяснили, что материалы выдерживают внешние (и внутренние, но об этом позже) воздействия именно за счет изменения расстояния между молекулами: химические связи стремятся вернуть самое оптимальное для них расстояние. Это стремление материала к занятию определенной формы называется напряжением, и в прошлой статье мы поговорили о том, как его искать. Пора нам научиться численно оценивать, чему равна деформация продольного растяжения.
Деформация продольного растяжения
Как мы уже говорили, то, с какой силой атомы конкретного материала будут притягиваться друг к другу зависит от расстояния между атомами. Вопрос силы связи с точки зрения химии мы рассматривать не будем и возьмём силы противодействия внешним усилиям как данность, экспериментальные данные которые мы будем использовать при расчётах, а не пытаться их интерпретировать.
Если мы измерим силу взаимодействия между атомами в зависимости от расстояния между ними, то мы получим следующую картину:
По графику видно, что есть достаточно существенный отрезок, на котором сила изменяется линейно. Более того, забегая вперёд скажу также что именно этот участок для нас наиболее интересен, так как на нем не происходят неупругие (т.е. когда после снижения нагрузки материал не возвращается в первоначальное положение) деформации. И очень велик соблазн попытаться найти формулу, по которой изменяется сила в зависимости от изменения расстояния.
И именно это и сделал Гук, обобщив интуитивное предположение «это должна описывать какая-то формула», имеющуюся теорию и экспериментальные данные.
Продольные деформации: закон Гука
Итак, действие равно противодействию, а противодействие зависит от изменения формы. А как вычислить силу сопротивления материала имея только измененный размер? Или, наоборот, увидев насколько велика будет деформация продольного растяжения, сказать через сколько он порвётся?
Разумеется, провести эксперимент! Возьмём цилиндрический предмет из некоторого материала (условная сталь). С одной стороны его закрепим, а с другой приложим усилие. Разумеется, перед проведением эксперимента, мы измерим изначальную длину образца. Затем посмотрим, насколько образец увеличится в длину. Или, как это принято обозначать в сопромате, «измерим длину образца под нагрузкой».
Обычно этих данных достаточно, но могут быть особые случаи, когда нам необходимо знать и то, как изменяется брусок в диаметре, поэтому эти данные мы тоже померим.
Соответственно, под нагрузкой наш цилиндр становится на какие-то доли миллиметра длиннее (dl). И отношение этого приращения к изначальной длине (l) называется относительной продольной деформацией (общается ε, эпсилон): ε=dl/l. Иными словами, если умножить длину бруска до нагрузки на относительную продольную деформацию (ε), мы получим его длину под нагрузкой.
Для чего это нужно?
Представим себе железную дорогу Санкт-Петербург–Москва. Это 634 км. по прямой. И вот случается перепад температур, зима сменилась летом, сталь расширилась. И, казалось бы, что эта пара миллиметров на несколько километров сделают. А потом считаем все как следует и оказывается, что увеличение длины в сумме составляет около 100 метров. И все, вокзал переезжает два раза в год на олимпийскую дистанцию. Разумеется, рельсы закреплены жёстко и двигаться никуда не будут. Однако очевидно, что такие нагрузки (представьте равномерно распределенную между Санкт-Петербургом и Москвой нагрузку и какое суммарное продольное напряжение получится) не способствуют долговечности конструкций.
Температурное расширение мы будем разбирать позже, но от того, внутренние ли силы или внешние силы воздействуют на материал, суть разговора не меняется. Просто если мы сейчас разбираем случаи, когда мы приложили усилия к бруску и начали менять в нем расстояния между молекулами, то сейчас, наоборот, идеальное расстояние между молекулами изменилось, и оно оказывает влияние на внешний мир.
История, между прочим, абсолютно реальная. И для решения этой проблемы между рельсами могут оставлять небольшой зазор, чтобы при температурных перепадах рельсы не находились под нагрузкой и не теряли микроструктуру.
Гораздо очевиднее будет пример монтажа конструкций: пока все детали изделия находятся на бумаге, они взаимодействуют правильно. Однако когда на объект начинает действовать сила тяжести, из-за расстяжения отверстие и заклепка могут оказаться на совершенно разных высотах. И несмотря на то, что нагрузки конструкция выдерживает, за счет изменения ее габаритов смонтировать ее становится на порядок сложнее. Если изменения не учитывать при проектировании, будет увеличена трудоемкость монтажа.
Точно также можно найти относительную поперечную (в ширину) деформацию: εп=Δd/d
Отношение продольной и поперечной деформации обычно одинаково под любой нагрузкой и оно уже давно экспериментально установлено для каждого конкретного материала. В справочниках искать коэффициент Пуассона:
μ=|εп/ε|
Остается только выяснить, насколько удлинится конкретный стержень при определенной нагрузке.
И, как ни странно, все необходимое для таких вычислений у нас уже есть. А именно, у нас есть некоторая нагрузка, длина и ширина стержня. Логично предположить, что чем больше сила (P), тем больше растяжение. Также логично предположить, что чем больше длина (l), тем легче растягивать: вспомните, ведь более длинную пружину проще растянуть, нежели короткую. В то же время, чем больше площадь, тем сложнее нечто растягивать: чем больше площадь, тем больше в ней связей между атомами. Помимо прочего для связей каждого материала должна быть своя константа, которая будет обозначать силу сопротивления на единицу материала. Называется она модулем Юнга (E) и для большинства материалов уже найдена.
Итого, изменение длины (dl) стержня длиной l, площадью сечения F, с модулем Юнга этого материала E под воздействием силы P:
dl=Nl/EF
Это выражение называется Законом Гука.

На практике для расчетов используется напряжение, которое можно из этой формулы вывести. σ=N/F. следовательно, dl=σl/E. ε=dl/l. Следовательно:
σ=εE
Деформация продольного растяжения под нагрузкой
Какая техническая наука возможна без экспериментов? Я лично таких не припомню.
Попробуем экспериментально проверить, насколько будет удлиняться образец под нагрузкой.
Так как оборудования у меня под рукой нет, я предоставлю перерисованный график без численных значений оставшийся у меня с лабораторных работ в Санкт-Петербургском Политехническом Университете.
Жёстко закрепляем стальной стержень и пытаемся его растянуть:
До определенной точки график действительно линеен и деформация продольного растяжения полностью отвечает теоретическим значениям. Однако в точке А график «скругляется» и значения начинают отличаться от полученных через формулу закона Гука. При этом, если нагрузку убрать до того, как удлинение достигнет точки B, образец вернётся в первоначальное состояние. Однако точка B (предел упругости) является граничной: все что будет после неё – это неупругие, пластичные деформации, которые для конструкций недопустимым.
Затем при увеличении нагрузки происходит резкий скачок удлинения. На графике это практически плоская линия BC, а называется площадкой текучести (напряжение же возникающее на площадке: предел текучести).
Если мы снимем нагрузку, то образец будет иметь не первоначальную длину, а изменится на определённую величину (её можно приблизительно найти проведя из нашей точки на графике линию параллельную линии AB до нуля нагрузки).
Затем на промежутке упрочнения CD деформация продольного растяжения требует увеличения усилия: под нагрузкой кристалическая решётка перестроилась, избавилась от микродефектов, повысилась прочность стержня.
Затем (на промежутке DE) нагрузку необходимо снижать, так как из-за уменьшения площади сечения образец в состоянии выдерживать все меньшие усилия.
Однако, по мере удлинения стержня, он, со временем, всё-таки порвётся.
График напряжения в зависимости от относительного продольного удлинения можно увидеть ниже:
Резюмируем. Деформация продольного растяжения под нагрузкой делится на основных этапов:
- Упругое пропорциональное растяжение OA (σ_у)
- Упругое непропорциональное растяжение AB (или предел упругости σ_п.у.)
- Скачок растяжения BC (напряжение – предел текучести (σ_т), отрезок – площадка текучести)
- Упрочнение CD (напряжение максимальное временное в точке D σ_в)
- Снижение несущей способности из-за уменьшения поперечного сечения DE (разрыв в точке E (σ_р))
Изменение длины под воздействием внешних сил
Возвращаемся от стержня конкретного к стержню абстрактному и попробуем рассчитать его удлинение при разных приложенных нагрузках.
Самый простой способ мы, по сути, уже разобрали. К некоторому невесомому стержню диаметра F и длины l жёстко закрепленному одним концом приложили силу P. Из таблицы мы знаем Модуль Юнга E.
Для удобства мы строим эпюру, из которой становится понятно, что продольные напряжения в каждом из сечений равны, а значит и изменяться длина будет достаточно равномерно:

По сути, теперь нам остаётся только подставить в закон Гука все значения и получить удлинение стержня:
dl=Pl/EF
При необходимости мы также можем найти и изменение диаметра, так как коэффициент Пуассона (μ=|ε_п/ε|) никто у нас не забирал из справочной литературы. Необходимо только рассчитать относительное продольное удлинение, домножить на константу материала и получить относительное поперечное сужение.
Также возможны ситуации, когда конструкция будет составной и (или) к ней будут приложены разные силы в разных точках. Тогда потребуется точно также построить эпюры и вычислить требуемые значения для каждого участка.
В случае с распределенными нагрузками ситуация сложнее, но не сильно.
Фактически вся проблема сводится к тому, что мы ищем функцию распределения нагрузки, её подставляем в формулу и таким образом получаем функцию распределения удлинения по всему стержню. При необходимости интегрируем и получаем суммарное удлинение стержня.
dl= ₀∫lNdx/EF
Опасное напряжение и коэффициент запаса
Ширина и длина у образцов может быть разная, а нам бы хотелось вычислить заранее, достаточно ли прочный для данной нагрузки у нас стержень.
Экспериментально мы уже померили относительные продольные деформации и знаем, при каких значениях материал испытывает упругие деформации, а когда его структура меняется навсегда. Компетентные органы тоже испытания провели и в соответствующей документации уже отсортировали напряжения, которые приняты опасными и их и следует использовать как граничных.
Вообще, “опасные” напряжения определяются прежде всего нормативной документацией и справочной информацией. И считать их самостоятельно не только не надо, но и нельзя (главные друзья инженера — это не умение считать в уме и идеальная память, а калькулятор и справочник).
Методика расчета мне не известна, но могу предположить, что она учитывает в себе как экспериментальные данные по исследованию материалов (в частности, предел текучести обычно понимается под опасным напряжением), так и статистику по практике эксплуатации (аварии и т.д.).
Примечание: в науках изучающих материалы принято разделение на пластичные и хрупкие материалы. Пластичные одинаково хорошо выдерживают как растяжение, так и сжатие, хрупкие нет. Надо понимать, что разделение довольно условно, так как “степень пластичности”, если можно так назвать соотношение предельных нагрузок перед необратимой деформацией для сжатия и растяжения различается не только для материалов, но и для разных условий. Например сталь, пластичная в нормальных условиях, при низких температурах будет становиться более хрупкой. Среди влияний можно выделить как температуру, так и радиационное излучение, если мы говорим о проектировании конструкций ядерных реакторов, сталкивающихся с большим нейтронным потоком, или космических аппаратов, бомбардируемых космическим излучением.
Для пластичных материалов опасное напряжение примерно равно как на сжатие (σ_оп.сж.), так и на растяжение (σ_оп.рас.). Однако в ряде материалов опасное напряжение для сжатия и разрыва будет разным.
Помимо прочего, предельные нагрузки будут отличаться в зависимости от условий, таких как температура.
Во время проектирования конструкций важны две вещи:
- Надежность
- Экономичность
Ни у кого нет желания рассчитывать конструкцию «впритирку», так как возможны и брак и нецелевое использование и просто непредвиденные ситуации. Но и материал надо беречь, всё-таки это ваши деньги и труд других людей.
По этой причине используются коэффициенты запаса прочности (k). Разделив на некоторую величину опасное напряжение можно найти предельно допустимое напряжение в конструкции, которое можно оставлять в материале:
[σ]=σ/k
Находить коэффициенты необходимо в справочной и нормативной документации.
Нормативная и справочная документация специфична для разных отраслей. Например, в строительстве искать значения опасных напряжений следует в СП, а коэффициенты запаса прочности в СНиП-ах.
Автор: Овчинников К.А.
Фактчекер и редактор: Сабуров Д.А.
- Лекции по сопротивлению материалов в СПбПУ им. Петра Великого
- Лекции по сопротивлению материалов в БГТУ “ВОЕНМЕХ” им. Устинова
4 307
|
|
Макеты страниц
Размеры растянутого стержня меняются в зависимости от величины приложенных сил. Если до нагружения стержня его длина была равна 



Рис. 1.8
Будем считать, что абсолютное удлинение и деформации связаны только с напряжениями, возникающими в стержне. В действительности имеются и другие факторы, влияющие на деформации. Так, деформации зависят от температуры и времени действия нагрузки. Неупругие деформации зависят от “истории” нагружения, т.е. от порядка возрастания и убывания внешних сил. Пока, однако, этих вопросов мы касаться не будем.
Если стержень нагружен только силой Р, то напряженное состояние является однородным и все участки растянутого стержня находятся в одинаковых условиях; деформация 


Эта величина называется относительным удлинением стержня.
Если стержень нагружен сосредоточенной силой Р и распределенными силами 



до и после нагружения (см. рис. 1.6). Если обозначить перемещение плоскости АА элемента стержня через и, то плоскость 




Заметим, что вследствие равномерного распределения напряжений по сечению удлинения для всех элементарных отрезков (см. рис. 1.6), взятых на участке 
В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность между напряжениями и деформациями:

Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости первого рода. Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и а, т.е. в мегапаскалях. Вместе с тем, поскольку модуль упругости может иметь довольно большие числовые значения, его предпочтительнее измерять не в мега-, а в гигапаскалях: 
Для наиболее часто применяемых материалов модуль упругости Е имеет следующие значения, 

Закон Гука представляет собой простейшую и очевидную аппроксимацию наблюдаемой в опытах зависимости удлинения от напряжения. Естественно, что точность этой аппроксимации определяется в первую очередь тем, сколь широкий диапазон изменения напряжения имеется в виду. Всегда можно подобрать достаточно малый интервал напряжений, чтобы в его пределах функцию 

Вернемся к выражению (1.4) и заменим в нем а на 


или

В результате получаем систему, состоящую из двух уравнений: первого уравнения системы 


Из первого уравнения системы (1.6) находим осевое усилие 



Абсолютное удлинение стержня переменного сечения на длине 

В том случае, когда стержень нагружен только по концам, нормальная сила 



При решении многих практических задач возникает необходимость наряду с удлинениями, обусловленными напряжением 
наложения и деформацию с рассматривают как сумму силовой и чисто температурной деформации:

где а – коэффициент температурного расширения материала.
Для однородного стержня, нагруженного по концам и равномерно нагретого, получаем

Таким образом, силовая и температурная деформации рассматриваются как независимые. Основанием этому служит экспериментально установленный факт, что модуль упругости Е при умеренном нагреве слабо меняется с температурой, точно так же как и а практически не зависит от 


Рассмотрим примеры определения напряжений и перемещений в некоторых простейших случаях растяжения и сжатия.
Пример 1.1. Требуется выявить закон изменения нормальных сил, напряжений и перемещений по длине ступенчатого стержня, нагруженного на конце силой Р (рис. 1.7, а), определить числовые значения наибольшего напряжения и наибольшего перемещения, если 


Рис. 1.7
Из условий равновесия любой отсеченной части стержня вытекает, что нормальная сила 





Для того чтобы получить эпюру напряжений а, надо ординаты эпюры 


Определим перемещение и 







Пример 1.2. Построить эпюры нормальных сил, напряжений и перемещений для свободно подвешенного цилиндрического стержня, нагруженного силами собственного веса (рис. 1.8, о). Длина стержня 


Рис. 1.8
Нормальная сила в сечении z равна весу нижележащей части стержня: 

значения 

Перемещение и в сечении z равно удлинению верхнего участка стержня. Согласно формуле (1.5),

Таким образом, закон изменения и изображается квадратичной функцией 2. Наибольшее перемещение «шах имеет нижнее торцевое сечение (рис. 1.8, г):

Пример 1.3. Колонна (рис. 1.9, а) нагружена силой Р и силами собственного веса. Требуется подобрать такой закон изменения площади поперечного сечения 


Рис. 1.9
На расстоянии 


По условию задачи

откуда

Дифференцируя обе части этого равенства по z, получим 



При 



Построение эпюр удобнее всего начинать с эпюры напряжения 
Нормальная сила в сечении z равна 

Рассмотренная задача относится к числу часто встречающихся в сопротивлении материалов задач на отыскание условий равнопрочности. Если напряжение в некотором теле (в данном случае в колонне) будет постоянно для всех точек объема, такую конструкцию называют равнопрочной. В подобных конструкциях материал используется наиболее эффективно.
Пример 1.4. Кронштейн 


Из условий равновесия узла В (рис. 1.10, б) находим нормальные силы в стержнях: 
Далее определяем площади поперечного сечения стержней по величине заданного напряжения и:


Рис. 1.10
Вес конструкции кронштейна пропорционален объему: 

Величина V имеет минимум при 
Оглавление
- Предисловие
- Введение
- В2. Реальный объект и расчетная схема
- В3. Силы внешние и внутренние. Уравнения равновесия стержня
- В4. Напряжения
- В5. Перемещения и деформации
- В6. Закон Гука и принцип независимости действия сил
- В7. Общие принципы расчета элементов конструкции
- Глава 1. РАСТЯЖЕНИЕ И СЖАТИЕ
- 1.1. Внутренние силы и напряжения, возникающие в поперечных сечениях стержня при растяжении – сжатии
- 1.2. Удлинения стержня и закон Гука. Уравнения равновесия
- 1.3. Потенциальная энергия деформации при растяжении – сжатии стержня
- 1.4. Статически определимые и статически неопределимые стержневые системы
- 1.5. Напряженное и деформированное состояния при растяжении — сжатии
- 1.6. Испытание материалов на растяжение – сжатие
- 1.7. Диаграмма растяжения
- 1.8. Механизм образования деформации
- 1.9. Основные механические характеристики материала
- 1.10. Пластичность и хрупкость. Твердость
- 1.11. Влияние температуры и фактора времени на механические характеристики материала
- 1.12. Коэффициент запаса
- Глава 2. КРУЧЕНИЕ
- 2.1. Чистый сдвиг и его особенности
- 2.2. Кручение стержня с круглым поперечным сечением. Уравнения равновесия
- 2.3. Кручение стержня с некруглым поперечным сечением
- 2.4. Краткие сведения о пленочной (мембранной) аналогии
- 2.5. Кручение тонкостенного стержня
- Глава 3. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ СТЕРЖНЯ
- 3.2. Моменты инерции сечения
- 3.3. Главные оси и главные моменты инерции
- Глава 4. ИЗГИБ СТЕРЖНЕЙ
- 4.1. Внутренние силовые факторы, возникающие в поперечных сечениях стержня при изгибе
- 4.2. Напряжения при чистом изгибе
- 4.3. Напряжения при поперечном изгибе
- 4.4. Касательные напряжения при поперечном изгибе тонкостенных стержней
- 4.5. Центр изгиба
- 4.6. Дифференциальные уравнения равновесия стержня. Перемещения при изгибе
- 4.7. Стержень на упругом основании
- 4.8. Косой изгиб
- 4.9. Внецентренное растяжение – сжатие
- 4.10. Изгиб бруса большой кривизны
- Глава 5. ПЕРЕМЕЩЕНИЯ В СТЕРЖНЕВОЙ СИСТЕМЕ ПРИ ПРОИЗВОЛЬНОЙ НАГРУЗКЕ
- 5.2. Теорема Кастилиано
- 5.3. Интеграл Мора
- 5.4. Способ Верещагина
- 5.5. Определение перемещений и напряжений в витых пружинах
- 5.6. Теорема взаимности работ
- Глава 6. РАСКРЫТИЕ СТАТИЧЕСКОЙ НЕОПРЕДЕЛИМОСТИ СТЕРЖНЕВЫХ СИСТЕМ МЕТОДОМ СИЛ
- 6.2. Метод сил. Выбор основной системы
- 6.3. Канонические уравнения метода сил
- 6.4. Использование свойств симметрии при раскрытии статической неопределимости
- 6.5. Плоскопространственные и пространственные системы
- 6.6. Определение перемещений в статически неопределимых системах
- 6.7. О методе перемещений
- Глава 7. ОСНОВЫ ТЕОРИИ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЙ
- 7.2. Определение напряжений в произвольно ориентированной площадке
- 7.3. Главные оси и главные напряжения
- 7.4. Круговая диаграмма напряженного состояния
- 7.5. Обзор различных типов напряженных состояний
- 7.6. Деформированное состояние
- 7.7. Обобщенный закон Гука и потенциальная энергия деформации в общем случае напряженного состояния
- 7.8. Анизотропия
- Глава 8. КРИТЕРИИ ПЛАСТИЧНОСТИ И РАЗРУШЕНИЯ
- 8.2. Гипотезы (критерии) появления пластических деформаций
- 8.3. Теория Мора и ее применение
- 8.4. О хрупком разрушении и вязкости
- 8.5. О новых материалах
- Глава 9. ТОЛСТОСТЕННЫЕ ТРУБЫ
- 9.2. Определение перемещений и напряжений в толстостенном цилиндре
- 9.3. Определение напряжений в составных трубах
- Глава 10. ПЛАСТИНЫ И ОБОЛОЧКИ
- 10.1. Основные особенности пластин и оболочек
- 10.2. Определение напряжений в симметричных оболочках по беэмоментной теории
- 10.3. Изгиб круглых симметрично нагруженных пластин
- 10.4. Определение напряжений и перемещений в круглых пластинах
- 10.5. Изгиб прямоугольных пластин
- 10.6. Изгиб цилиндрической оболочки при симметричном нагружении
- Глава 11. ОСНОВЫ РАСЧЕТА ЭЛЕМЕНТОВ КОНСТРУКЦИЙ, РАБОТАЮЩИХ ЗА ПРЕДЕЛАМИ УПРУГОСТИ
- 11.2. Напряжения и перемещения в простейших стержневых системах при наличии пластических деформаций
- 11.3. Упругопластический изгиб стержня
- 11.4. Кручение стержня круглого поперечного сечения при наличии пластических деформаций
- 11.5. Основы расчета по предельным нагрузкам
- 11.6. Основы теории пластичности
- Глава 12. ПРОЧНОСТЬ ПРИ ЦИКЛИЧЕСКИ ИЗМЕНЯЮЩИХСЯ НАПРЯЖЕНИЯХ
- 12.2. Основные характеристики цикла и предел выносливости
- 12.3. Влияние концентрации напряжений на прочность при циклическом нагружении
- 12.4. Масштабный эффект
- 12.5. Влияние качества обработки поверхности
- 12.6. Коэффициент запаса при циклическом нагружении и его определение
- Глава 13. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ДЕФОРМИРУЕМЫХ СИСТЕМ
- 13.2. Определение критических нагрузок
- 13.3. Задача Эйлера
- 13.4. Зависимость критической силы от условий закрепления стержня
- 13.5. Устойчивость плоской формы изгиба прямолинейного стержня
- 13.6. Энергетический метод определения критических нагрузок
- 13.7. Продольно-поперечный изгиб
- Глава 14. МЕТОДЫ ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ ДЕФОРМИРОВАННОГО И НАПРЯЖЕННОГО СОСТОЯНИЙ
- 14.2. Определение деформаций при помощи механических тензометров
- 14.3. Применение датчиков сопротивления
- 14.4. Оптический метод определения напряжений при помощи прозрачных моделей
- ПРИЛОЖЕНИЕ