Как найти изменение энтальпии при нагревании

Расчеты изменений
энтропии в различных процессах основаны
на использовании неравенства Клаузиуса,
которое связывает изменение энтропии
с количеством теплоты,
которым система обменивается с окружающей
средой при температуре

.

(3.1)

В данном случае
знак равенства имеет место при обратимых,
а неравенства – при необратимых
процессах.

Величину энтропии
данной системы нельзя измерить
непосредственно на опыте, но ее можно
вычислить, пользуясь формулой

.

(3.2)

Эта формула
позволяет найти не абсолютную величину
энтропии, а разности энтропий в двух
состояниях системы, т.е. изменение
энтропии при переходе системы из
состояния 1 в состояние 2.

Изменение энтропии
при постоянном давлении можно найти
интегрированием частной производной
энтропии по температуре при постоянном
давлении

,

(3.3)

где

изобарная теплоемкость системы, Дж/К.

.
(3.4)

При решении
уравнения (3.4) возможно два случая.

Случай 1.
Теплоемкость вещества в интервале
температур
−не зависит от температуры. Тогда после
интегрирования (3.4) имеем:

.
(3.5)

Случай 2.
Теплоемкость является некоторой
функцией температуры, например для
мольной изобарной теплоемкости известны
так называемые температурные ряды

,

(3.6)

где

эмпирически найденные коэффициенты.
Их значения приводятся в справочной
литературе.

Подстановка
выражения (3.6) в (3.4) позволяет после
интегрирования получить следующее
выражение

.
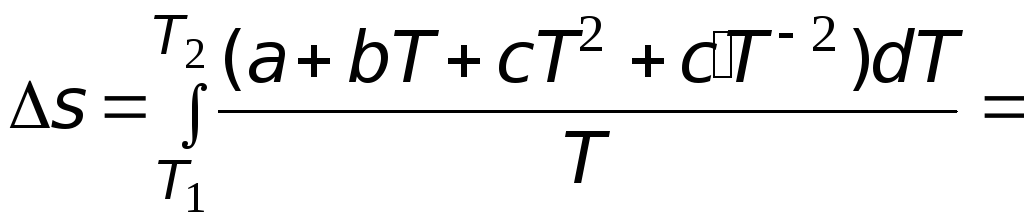
(3.7)

Разность энтропий
в двух состояниях вычисляется просто,
если обратимый переход из одного
состояния в другое происходит при
постоянной температуре. Это имеет
место, например, при переходах из одного
агрегатного состояния в другое, при
фазовых переходах. Равновесные фазовые
превращения (испарение, плавление,
возгонка и т.д.) происходят в условиях
постоянства температуры и давления.
Они возможны только при подведении
(или отводе) теплоты, затрачиваемой на
проведения фазового превращения. Тогда
формула (3.4) принимает вид

,

(3.8)

где

скрытая теплота фазового превращения.

При постоянном
давлении скрытая теплота превращения
равна изменению энтальпии, т.е. например,
для фазового превращения 
испарения − формула (3.8) примет вид

,

(3.9)

где

энтальпия испарения, Дж;

температура
кипения, К.

Если вещество в
указанном диапазоне температур
претерпевает фазовое превращение, то
общее изменение энтропии будет
складываться из нескольких слагаемых.
Например, пусть некое условное вещество
А
переходит из твердого состояния при
температуре
в жидкое состояние при температуре.
Из условия задачи видно, что при
определенной температуре имеет место
фазовое превращение (фазовый переход)
плавление. Находим в справочнике эту
температуру, обозначим ее в общем виде
.
Общее изменение энтропии будет равно
сумме трех слагаемых (так называемых
вкладов).

.

(3.10)

Первый вклад в
общее изменение энтропии 
это изменение энтропии при нагреве
твердого вещества от температуры
до температуры плавления

.

(3.11)

При температуре
плавления твердое состояние переходит
в жидкое, при этом наблюдается изменение
энтропии. Изменение энтропии при
фазовом превращении:

.

(3.12)

И, наконец,
последний вклад в общее изменение
энтропии внесет изменение энтропии
при дальнейшем нагреве уже образовавшейся
жидкости от температуры плавления до
температуры

.

(3.13)

Абсолютная мольная
энтропия газообразного вещества в
стандартном
состоянии при температуре Т
может быть найдена как сумма изменений
мольной энтропии в следующих процессах:
нагрев исследуемого вещества в твердом
состоянии от нуля до температуры
плавления; процесс плавления; нагрев
жидкого вещества до температуры кипения;
испарение жидкости; нагрев полученного
газообразного вещества до нужной
температуры.

+.
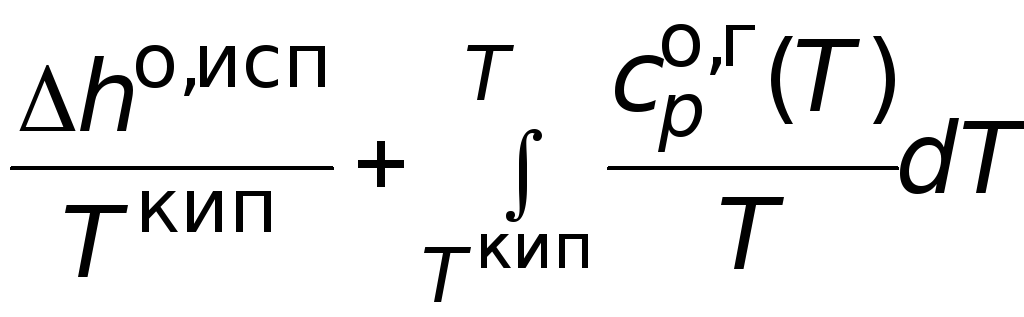(3.14)

В справочных
термодинамических таблицах обычно
приводят значения абсолютной энтропии
в стандартном состоянии при температуре
298 К
.
Тогда расчет абсолютного значения
энтропии при какой-либо другой температуре
можно произвести исходя из значения
энтропии при 298 К, используя формулу
(3.14) и учитывая агрегатное состояние
исследуемого вещества при 298 К.

Для расчета
изменения энтальпии системы, в которой
нет химической реакции, а только
происходит изменение температуры,
например, при постоянном давлении,
воспользуемся определительным
выражением изобарной теплоемкости

,
отсюда
.
(3.15)

Так же как и при
расчете энтропии, тут возможно два
случая.

Случай 1.
Теплоемкость
вещества в интервале температур
−
не
зависит от температуры. Тогда после
интегрирования (3.15) имеем:

.
(3.16)

Случай 2.
Теплоемкость является некоторой
функцией температуры. Подстановка
выражения (3.6) в (3.16) позволяет после
интегрирования получить следующее
выражение

.
(3.17)

Если в указанном
диапазоне температур возможно фазовое
превращение, как это было рассмотрено
в вышеприведенном примере с нагревом
твердого вещества А,
то все изменение энтальпии
будет равно сумме

,
(3.18)

где

вклад в общее изменение энтальпии за
счет процесса нагрева
твердого вещества от температуры
до температуры плавления

,

(3.19)

изменение
энтальпии за счет фазового превращения,
это энтальпия фазового перехода,
находится в справочниках;

изменение энтальпии
за счет дальнейшего нагрева системы
от температуры фазового перехода до
нужной температуры. Очевидно, что форма
уравнения для расчета
будет аналогичной (3.19), только
коэффициенты температурного ряда
теплоемкости нужно брать для жидкого
вещества А.

.

Для расчета
изменения энергии Гиббса чистого
вещества при переходе его из состояния
I
в состояние II
удобно использовать расчетную формулу:

.

(3.20)

Более подробно
расчет изменения энергии Гиббса будет
рассмотрен при решении задачи.

Примеры задач

Пример 1.
Вычислите
изменение энтропии 1 кг этиленгликоля
при его нагреве от температуры 100 до
300 ^оС.

Решение. Используя
справочную литературу,
определим
коэффициенты температурных зависимостей
теплоемкостей жидкого и газообразного
этиленгликоля, температуру фазового
превращения
и величину мольной энтропии фазового
превращения.

=
151,0 Дж/(мольК).

=

=
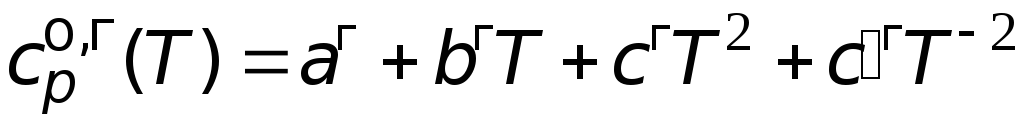46,26 + 0,2005T

77,9010^6
T
²
Дж/(мольК).

=
479,4 К.

Мольная энтропии
испарения

= 103,4 Дж/(моль·К).

Производим расчеты.

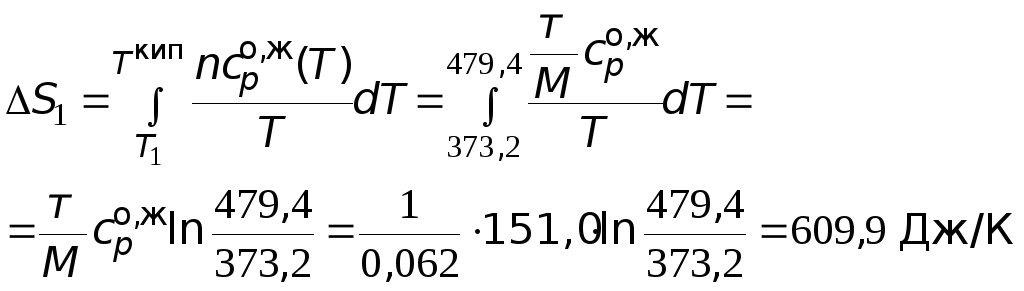
=1667,7Дж/К.

=

= 2652,2 Дж/К = 2,65
кДж/К.

Пример
2.
Чему
равна мольная энтропия этиленгликоля
при температуре 350 К?

Решение.
Формула
(3.14) для расчета абсолютного значения
энтропии при определенной температуре
в рассматриваемом примере упрощается.
В качестве
нижнего уровня отсчета можно использовать
абсолютное значение энтропии при 298 К
и давлении 1 атм. Это справочная величина,
она равна
= 167,32 Дж/(мольК).
Выражение для расчета абсолютного
значения мольной энтропии этиленгликоля
при 350 К будет иметь вид

.

И при 298 К, и при
350 К этиленгликоль находится в одинаковом
фазовом состоянии − жидком − т.е. в
температурном интервале 298−350 К нет
фазовых превращений. Мольная изобарная
теплоемкость жидкого этиленгликоля в
исследуемом температурном интервале
постоянна и равна
=
151,0 Дж/(мольК).

191,6
Дж/(мольК).

Пример
3. Чему
равно изменение энтальпии при нагреве
1 моля этиленгликоля от 350 К до 500 К?

Решение.
В
указанный в условии диапазон температур
попадает температура фазового превращения
479,4 К, следовательно, до этой температуры
изменение энтальпии происходит за счет
нагревания жидкости, затем следует
изменение энтальпии при фазовом
превращении, а далее изменение энтальпии
связано с нагреванием газа. Расчет
проводим по формуле (3.18), перейдя к
мольным величинам, температурные
зависимости теплоемкости нам известны.
Мольную энтальпию фазового перехода
находим в справочной литературе, она
равна
48,610³
Дж/моль.

;

=

= 19 539,4 Дж/моль;

48,610³
Дж/моль;

=

70
702,2 Дж/моль = 70,7 кДж/моль.

Пример 4.
Вывести уравнение зависимости мольной
энтропии от температуры для газообразного
бензола при давлении 1 атм. Определить
величину стандартной мольной изобарной
теплоемкости бензола при 500 К двумя
способами.

Решение.
Зависимость мольной энтропии вещества
от температуры можно найти после
интегрирования выражений

.
(3.21)

Слева в уравнении
(3.21) стоит разность
.
Если в качестве первого состояния
вещества выбрать его состояние при 298
К и 1 атм, то величину мольной энтропии
()
этого вещества легко найти в справочнике.

Тогда из уравнения
(3.21) имеем

.
(3.22)

Уравнения (3.22) −
это уже зависимость мольной энтропии
от температуры, но её нужно обязательно
преобразовать, учитывая, что известно
числовое значение
,
а также значениеТ₁
= 298 К.
Необходимо учитывать, что уравнение
(3.22) написано в общем виде, поэтому
включает и эмпирический коэффициент

,
и эмпирический коэффициент .
Когда уравнение будет записано для
конкретного вещества, тогда в зависимости
от природы этого вещества в уравнении
будет слагаемое или с коэффициентом

(для органических веществ), или с
коэффициентом
(для
неорганических веществ).

В рамках данной
задачи имеем следующие данные:

Вещество	, кДж / моль	, Дж/(моль∙К)	Коэффициенты уравнения
а	103	106	10−5
C6H6 (г) бензол	82,93	269,2	21,09	400,12	169,87	

Следовательно,
энтропия газообразного бензола при
любой произвольной температуре Т

.

После подстановки
числовых значений и преобразований
имеем выражение температурной зависимости
мольной энтропии газообразного бензола

.
(3.23)

Используя уравнение
(3.23), можно графически изобразить
зависимость мольной энтропии газообразного
бензола от температуры (рис. 3.1), а далее
по этой зависимости определить величину
изобарной теплоемкости бензола при
температуре 500 К. Мольная изобарная
теплоемкость связана с частной
производной энтропии по температуре

.

С

1

ледовательно,
для того чтобы графически найти
теплоемкость, нужно определить частную
производнуюзависимости
энтропии от температуры в точке,
соответствующей 500 К. Графически
производную находят, проводя к
интересующей нас точке на кривой
касательную, а затем определяя угловой
коэффициента
этой касательной. Чтобы
найти угловой коэффициент касательной,
нужно взять на прямой две достаточно
удаленные друг от друга точки и определить
их координаты. Угловой коэффициент
численно равен тангенсу угла наклона
прямой (для рассматриваемого случая):

.

Затем находим
изобарную теплоемкость
.

Из анализа рис.
3.1 видно, что зависимость энтропии от
температуры имеет слабо выраженную
кривизну, и если точек для построения
кривой мало, то кажется, что такую
зависимость можно описать прямой
линией. Однако зависимость мольной
энтропии от температуры − это все-таки
кривая линия, и к ней можно провести
касательную. Рекомендованный шаг по
температуре для построения зависимости
составляет 50 К. В случае если какой-то
участок зависимости носит явно линейный
характер, угловой коэффициент касательной
будет совпадать с угловым коэффициентом
самой линии.

Следующий способ
определения мольной изобарной
теплоемкости газообразного бензола
расчетный, по формуле температурной
зависимости изобарной теплоемкости,
которая имеет вид:

= −21,09 +
0,4T
− 0,000 169Т
²
.

По этому способу
мольная изобарная теплоемкость бензола
при 500 К равна 136,66 Дж/(моль∙К). Значения
теплоемкости,
вычисленные разными способами, должны
быть близки.

Пример 5.
Углекислый
газ массой 200 г находится в состоянии
1 при температуре 600 К и давлении 2,5 атм.
Его перевели в состояние 2, при котором
температура равна 298 К, а давление 1 атм.

Принимая
свойства углекислого газа близкими к
свойствам идеального газа, найти
изменения мольных и полных 1) объема;
2) энтропии; 3) энтальпии; 4) внутренней
энергии и 5) энергии Гиббса системы
при этом переходе.

Решение.
Из
справочных таблиц определяем форму
уравнения и значения коэффициентов
температурной зависимости мольной
изобарной теплоемкости углекислого
газа

Вещество	кДж / моль	Дж/(моль∙К)	Коэффициенты уравнения
а	103		10−5
CО2 (г)	−393,51	213,66	44,14	9,04	−	−8,54

= a
+ bT
+ c’T
⁻²

= 44,14 + 9,04∙10⁻³
T

8,54∙10⁵
T
⁻²
.

1. Используя
уравнение состояния идеального газа,
находим изменение мольного объема
следующим образом:

=

= 4,74 ∙10⁻³
м³/моль.

Полное изменение
объёма углекислого газа при рассматриваемом
переходе составит
.

Число молей находим
по формуле
4,55
моль.

4,55∙4,74∙10⁻³
= 2,16∙10⁻²
м³.

2. Расчет мольного
изменения энтропии углекислого газа
при переходе из состояния 1 в состояние
2 производится по формуле

=

=

=
−46,89 Дж/(мольК).

Полное изменение
энтропии равно

−213,32 Дж/К.

3. Для идеального
газа изменение энтальпии не зависит
от давления, поэтому формула для расчета
мольного изменения энтальпии имеет
вид:

=
Дж/моль.

Полное изменение
энтальпии равно

=
4,55∙(−15998,5) = −72793,18 Дж.

4. Для идеального
газа мольное изменение внутренней
энергии связано с мольным изменением
энтальпии

Следовательно,

= −15998,5−8,314(298−600)=
−13487,7 Дж/моль.

Полное изменение
внутренней энергии найдем как

=4,55(−13487,7)
= − 61369 Дж.

5. Мольное изменение
энергии Гиббса при переходе углекислого
газа из состояния 1 в состояние 2 определим
как
.

Но известно, что

,
а.
Кроме того,.

Тогда

=

=
=.

Мольные изменения
энтальпии и энтропии определены ранее,
значение мольной энтропии в состоянии
2 можно найти по справочнику, т.к. это
состояние 298 К и 1 атм:
213,66
Дж/(моль∙К).

−15998,5
−213,66(298−600)−600∙(−46,89) =76660,8 Дж/моль.

4.
ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА РАСТВОРОВ

Для характеристики
раствора применяют следующие виды
концентраций.

−мольная
доля компонента k
(часто – молярная доля),

.

−массовая
доля компонента,

.

−молярная
концентрация (c),
другое название − плотность числа
молей,

. [c
] = моль/м³
.

−массовая
концентрация, другое название –
плотность массы компонента k,

.
[]
= кг/м³.

−моляльная
концентрация раствора, или мольно-массовая
концентрация, другое название –
мольно-массовое отношение,

. [ d
] = моль/кг.

Состояние компонента
k
в растворе нельзя описать функциями,
отвечающими чистому компоненту k.
Для описания свойств компонента в
растворе вводится понятие
парциальных
мольных свойств
компонента.
Если обозначить полное экстенсивное
свойство раствора, образованного
компонентами в общем виде, как
,
то мольное экстенсивное свойство
раствора, состоящего из компонентовk,
будет
обозначаться как
,
причем.
Вклад компонентаk
в любое экстенсивное свойство E
раствора определяется его парциальной
мольной (ПМ) величиной
,
которая равна

.

(4.1)

Следует отметить,
что парциальные мольные величины
отражают изменение
свойств и их нельзя уподоблять
соответствующим мольным величинам.
Парциальные мольные величины могут
принимать значения, которые немыслимы
для мольных величин; например, парциальный
мольный объем может быть отрицательным.
Парциальные мольные величины могут
быть образованы от любой экстенсивной
величины. В общем случае экстенсивное
свойство Е
однородной системы, состоящей из k
компонентов,
можно представить в виде функции
температуры, давления и чисел молей
компонентов, т.е.
.
Если зафиксировать постоянными давление
и температуру, то получим.

Образуем полный
дифференциал этого выражения:

.
(4.2)

С учетом (4.1) из
уравнения (4.2) можно получить

или
.
(4.3)

Учитывая, что E
− однородная
функция первой степени от независимых
аргументов n_k,
и
привлекая теорему Эйлера об однородных
функциях, получаем из (4.3) выражение

.

(4.4)

Если раствор
двухкомпонентный, или как еще говорят,
бинарный, т.е. число компонентов k
= 2, то соотношения, получающиеся в этом
случае, имеют вид:

.

(4.5)

При делении
выражения (4.5) на общее число молей
получим

,

(4.6)

с учетом
определительного выражения для мольной
доли компонента k
(4.6) можно записать как

.

(4.7)

Используем эти
же выражения для объема
.

,

,

где V
– полный объем раствора;
₁
и
₂

парциальные мольные объемы 1 и 2
компонентов раствора; n₁
и n₂
– числа молей компонентов 1 и 2; N₁
и N₂
– мольные доли компонентов 1 и 2 в
растворе;
– мольный объем раствора.

Способы определения
парциальных мольных величин рассмотрим
на примере определения парциальных
мольных объемов в бинарном растворе.

Первый способ.
Определение парциального мольного
объема по зависимости полного объема
раствора от числа молей одного из
компонентов.

Согласно
определительному выражению для
парциальной мольной величины (4.1),
парциальный мольный (ПМ) объем второго
компонента − это величина₂
=,
а ПМ объем первого компонента − это
₁
=.
Если известно уравнение зависимости,
например
,
то для получения₂
=
нужно продифференцировать его.
Если
зависимость дана в форме таблицы или
в виде графика, то нужно определить
угловой коэффициент касательной к
кривой зависимости

в той точке, в которой нам требуется
определить ПМ объем. При графическом
определении частной производной нужно
найти угловой коэффициент касательной,
проведенной к кривой зависимости в
определенной точке (рис. 4.1).

Рис. 4.1. Зависимость
полного

объема раствора
от числа молей

второго компонента
(p,T,
n₁
– const)

Частная производная
полного объема по числу молей второго
компонента в условиях постоянства
давления, температуры и остального
состава равна

.

Угловой коэффициент
касательной находится

Второй способ.
Определение
ПМ объемов по зависимости мольного
объема раствора от состава.

Парциальные
мольные объемы компонентов бинарной
смеси следующим образом связаны с
мольным объемом смеси

₁
=

N₂

.
(4.8)

₂
=

+ (1 N₂).


(4.9)

Из данных выражений
следует, что для вычисления парциальных
мольных объемов по этому методу
необходимо по зависимости мольного
объема от мольной доли второго компонента
определить частную производную мольного
объема раствора по мольной доле второго
компонента при постоянных давлении и
температуре
в
интересующем нас растворе. Для
определения производной, например,
графическим способом, нужно к зависимости
мольного объема раствора от состава
(см. рис. 4.2, линия ВАС)
в соответствующей точке провести
касательную и определить угловой
коэффициент этой касательной по
координатам двух достаточно удаленных
друг от друга точек, лежащих на
касательной

.

Далее по уравнениям
(4.8) и (4.9) вычислить парциальные мольные
объемы обоих компонентов.

Рис. 4.2. Зависимость
мольного объема раствора от состава
раствора

Третий способ.
Определение
ПМ объемов по методу Розебома

(метод отрезков).

Из анализа рис.
4.2 и уравнений (4.8−4.9) видно, что
касательная к зависимости
=f
(N₂)
отсекает на левой оси ординат отрезок,
равный парциальному мольному объему
первого компонента в растворе концентрации
N₂,
а на правой оси 
отрезок, равный парциальному мольному
объему второго компонента в растворе
той же концентрации.

Примеры
задач

Пример 1

Жидкий бензол
массой 500 г занимает объем 568,8 см³
(293 К, 1 атм). Вычислить его мольный и
удельный объемы и плотность массы.

Дано:

Чистое вещество
– бензол

M
= 0,078 кг/моль

m
= 500 г = 0,5 кг

V
= 568,8 см³ =
5,688∙10⁻⁴
м³.

Найти:
.

Решение

= 8,887∙10⁻⁵
м³/моль

=
1,138∙10^-4
м³/кг

==8,787∙10²
кг/м³.

Пример
2.
Общее
число молей в водно-ацетоновом растворе
составляет 12,58 моль. Плотность массы
раствора и плотность числа молей ацетона
в нем равны соответственно 916 кг/м³
и 7897 моль/м³
при 298 К и 1 атм. Определить массу и объем
раствора, его мольную массу и удельное
число молей.

Дано:
двухкомпонентный раствор. Компонент
1 – вода, H₂O.
Компонент 2 – ацетон, (CH₃)₂CO.
M₁ = 0,018
кг/моль; M₂ = 0,058
кг/моль; n₂
=
12,58 моль; ρ = 918 кг/м³;
c₂ = 7897
моль/м³.

Найти:
m,
V,
M,
n_уд.

Решение. Решение
основано на взаимосвязи между
концентрационными шкалами.

Масса раствора:
=

=.

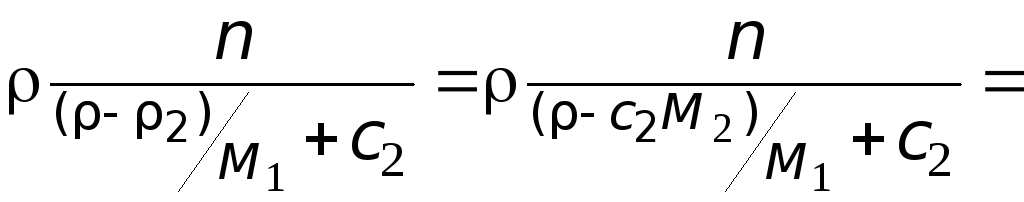
Объем раствора:

=

=м³.

Мольная масса
раствора:

=

=
кг/моль.

Удельное число
молей раствора:

=

=
моль/кг.

Пример 3. Для
двухкомпонентного водно-аммиачного
раствора приведена в табличной форме
зависимость объема раствора от числа
молей аммиака при постоянных параметрах:
температуре 293 К, давлении 1 атм и числе
молей воды 5,556 моль.

, моль	0	0,392	0,682	1,498	2,521
·104, м3	1,00	1,10	1,17	1,34	1,48

Вычислите
парциальные мольные объемы обоих
компонентов при мольной доле аммиака,
равной 0,15.

Дано: двухкомпонентный
раствор. Компонент 1 − вода, H₂O.

M₁
= 0,018 кг/моль.
Компонент 2 – аммиак, NH₃.
M₂
= 0,017 кг/моль. n₁=
5,556 моль. N₂
= 0,15. Найти:
.

Решение. Изобразим
графически данную в условии задачи
зависимость объема системы от числа
молей второго компонента.

По
определению парциальный мольный объем
компонента 2 – это частная производная
полного объема по числу молей второго
компонента в условиях постоянства
температуры, давления и числа молей
первого компонента, т.е.=.

Полный объем
бинарного раствора может быть найден
как
.

По рис. 4.3 найдем
частную производную объема по числу
молей второго компонента
.
Для этого определим угловой коэффициент
касательной, проведенной к нашей
зависимости в определенной точке.
Данная точка должна показывать число
молей второго компонента в растворе
при мольной доле его, равной 0,15. Найдем
значение
n₂
из
соотношения

.

=
моль.

При числе молей
второго компонента 0,98 восстанавливаем
перпендикуляр к кривой и проводим к
точке пересечения перпендикуляра с
кривой касательную. Затем находим
угловой коэффициент касательной

м³/моль,

= 2,210
⁻⁵ м³/моль.

Примечание.
Если зависимость полного объема от
числа молей второго компонента
представляет собой прямую линию, то
касательная будет совпадать с ходом
этой прямой.

Чтобы найти
,
воспользуемся соотношением,
причем значение полного объема системы
при числе молей второго компонента,
которое соответствует мольной доле
его 0,15, определим по графику.V
= 1,2510
⁻⁴
м³.

=
= 1,8610⁻⁵
м³/моль.

N2	0,0	0,255	0,424	0,617	0,870	1,000
∙105, м3/моль	7,600	7,982	8,359	8,790	9,378	9,800

Пример
4.
Для
двухкомпонентного жидкого раствора
ацетон (1-й компонент) 
трихлорметан (2-й компонент) представлена
в табличной форме (Т
= 298 К, р
= 1 атм) зависимость мольного объема
раствора

от мольной доли второго компонента
N₂
.

Определите
для обоих компонентов парциальные
мольные объемы
₁

и

₂
при мольной доле второго компонента
N₂
= 0,6.

Решение.
Изображаем
данные, приведенные в условии задачи,
в виде графической зависимости мольного
объема от состава (мольная доля второго
компонента). Проводим касательную к
точке на кривой, при которой
мольная доля трихлорметана (компонент
2) равна 0,6. Касательную проводим до
пересечения с осями ординат и по
величине, отсекаемой на каждой из осей,
находим значения парциальных мольных
объемов.

₁
= 7,3∙10⁻⁵
м³/моль;

₂
= 9,6∙10⁻⁵
м³/моль.

Пример
5.
Для
двухкомпонентного жидкого раствора
вода Н₂О
(1-й компонент) 
уксусная кислота С₂Н₄О₂
(2-й компонент) имеется полученная на
опыте в табличной форме зависимость
изобарной теплоемкости С_р
от массы кислоты m₂
(Т
= 298 К, р
= 1 атм) при постоянной массе воды m₁
=
0,5 кг:

m2	0,0	0,057	0,088	0, 103	0,161	0,260
Сp, Дж/К	2090	2238	2314	2352	2476	2682

Удельные
изобарные теплоемкости чистых компонентов
1 и 2 ()равны
4180 и 2056 Дж/(Кмоль).

Требуется
1) построить график зависимости изобарной
теплоемкости смешения раствора С_р^m
от числа молей кислоты n₂;
2) определить для обоих компонентов их
парциальные мольные изобарные
теплоемкости смешения с_р1^m
и
с_р2^m
при мольной доле второго компонента
N₂
= 0,05; 3) вычислить для тех же компонентов
при той же N₂
парциальные мольные изобарные
теплоемкости с_р1
и с_р2.

Решение

1. Для
получения зависимости изобарной
теплоемкости смешения раствора С_р^m
от числа молей кислоты n₂
(С_р^m
= f(n₂))
в табличной и графической формах
необходимо преобразовать
табличные данные по зависимости
изобарной
теплоемкости С_р
от массы второго компонента
(С_р=
f
(m₂))
. Используя определительные выражения
для понятий число молей и функция
смешения, получим:

;

.

Пример расчета:

моль;

2238
− (4180∙0,5 +
2056∙0,057)
= 30,81 Дж/К.

n2	0	0,95	1,47	1,72	2,68	4,33
Срm, Дж/К	0	30,81	43,07	50,23	54,98	57,44

Данные расчетов
приведены ниже

Графический
образ зависимостиС_р^m
= f
(n₂)
приведен на рис.4.5.

Рис.
4.5. Зависимость изобарной теплоемкости
смешения раствора С_р^m
от числа молей кислоты n₂

2. В
основе определения

и

лежит система вида

,

.

По
заданной мольной доле найдем координаты
точки на кривой С_р^m
=f(n₂)
(рис.4.5),
к которой нужно проводить касательную):

и
(А)
в точке А
на кривой :

==1,46
моль.

(А)
= 43 Дж/К (определили по графику при n₂
=1,46 моль).

Примечание.
Следует отметить, что числовые значения,
которые в этой задаче определяются по
графику, при приближенном построении
графика, конечно, не являются точными.
При графических решениях нужно
использовать миллиметровую бумагу и
достаточно крупный масштаб, тогда
значения получатся более точными.

Определим по
угловому коэффициенту касательной 
тангенсу угла наклона касательной tg
₂
в точке А величину парциальной мольной
изобарной теплоемкости смешения второго
компонента
=Дж/(моль∙К).

Затем
можно найти
:

==0,496Дж/(моль∙К).

3).
Каждую из величин с_р1
и с_р2
находим
с помощью выражения для
:;

= 0,496 +4180∙ 0,018
=75,736 Дж/(моль∙К).

= 20+ 2056∙ 0,060= 143,36Дж/(моль∙К).

В уроке 19 «Изменение энтальпии» из курса «Химия для чайников» рассмотрим понятие теплоты реакции и ее единицу измерения; выясним, что происходит при экзотермических и эндотермических реакциях, а также познакомимся с законом Гесса. Данный урок потребует от вас знания химических основ из прошлых уроков. Обязательно прочитайте о составлении химических реакций и формулировку законов сохранения массы и энергии, чтобы не возникало лишних вопросов.

Хоть данная глава и называется «Законы сохранения массы и энергии«, однако пока мы ничего не говорили о законе сохранения энергии. Для тех, кто забыл: закон сохранения энергии гласит, что теплОты реакций аддитивны и энергия процесса не зависит от того, проводится ли он в одну или несколько стадий.

Единица измерения теплоты

Так как это курс химии, а не физики, то совсем мельком напомню, что теплота и работа являются хоть и различными, но формами энергии, поэтому измеряются в одинаковых единицах (в Дж). Если вы совершаете работу над каким-либо телом или совокупностью тел, можно повысить энергию этой системы или нагреть ее в зависимости от того, каким образом совершается работа. К примеру, когда мы поднимает какой-либо предмет, работа превращается в потенциальную энергию, а если потереть этот предмет, то работа (трение) переходит в теплоту. И наоборот, при падении тяжелого предмета энергия превращается в теплоту, а при работе двигателя внутреннего сгорания выделяемая в нем теплота переходит в работу. Химиков, в отличии от физиков, занимает не работа, а теплота, которая может поглощаться и выделяться при протекании химической реакции.

Единицей измерения теплоты служит — Джоуль (Дж). 1 Джоуль можно определить как количество теплоты, необходимое для повышения температуры 1 г чистой воды на 1/4 градуса. В повседневной жизни 1 джоуль энергии требуется для поднятия небольшого яблока (102 г) строго вертикально на высоту один метр.

Теплота реакции

Представление о законе сохранения энергии можно получить на примере разложения пероксида водорода, H₂O₂. Когда водный раствор H₂O₂ реагирует с образованием газообразного кислорода и жидкой воды, происходит заметное выделение тепла: разложение 1 моля H₂O₂ при 25°С (комнатная температура) сопровождается выделением 94,7 кДж (94700 Дж) тепла.

Теплоту химической реакции, проводимой при постоянном давлении, принято называть изменением энтальпии реагирующей системы, ΔH (читается «дельта-аш»). Если в процессе реакции выделяется теплота, то энтальпия реагирующей системы убывает и ΔH отрицательно, а сами реакции называются экзотермическими. Напротив, эндотермические реакции протекают с поглощением теплоты и сопровождаются возрастанием энтальпии реакционной смеси. Для реакции разложения пероксида водорода можно записать:

• H₂O₂(водн.) → H₂O(ж.) + ½O₂(г.)  ΔH = -94,7 кДж (1)

Это количество теплоты, которое выделяется при разложении 1 моля пероксида водорода на 1 моль воды и 1/2 моля газообразного кислорода, т.е. в расчете на 1 моль реагента. Если удвоить все коэффициенты в уравнении реакции, то придется удвоить и теплоту реакции, поскольку она будет относиться теперь к вдвое большему количеству реагента:

• 2H₂O₂(водн.) → 2H₂O(ж.) + O₂(г.)  ΔH = -189,4 кДж (2)

Физическое состояние реагентов и продуктов также оказывает влияние на теплоту реакции (изменение энтальпии). Если H₂O₂ заставить разлагаться на газообразный кислород и водяной пар, а не жидкую воду, часть молярной теплоты разложения H₂O₂ (94,7 кДж) затратится на испарение H₂O, которое описывается уравнением:

• H₂O(водн.) → H₂O(г.)  ΔH = +44,0 кДж (3)

и поэтому при таком разложении пероксида водорода будет выделяться меньше теплоты:

• H₂O₂(водн.) → H₂O(г.) + ½O₂(г.)  ΔH = -50,7 кДж (4)

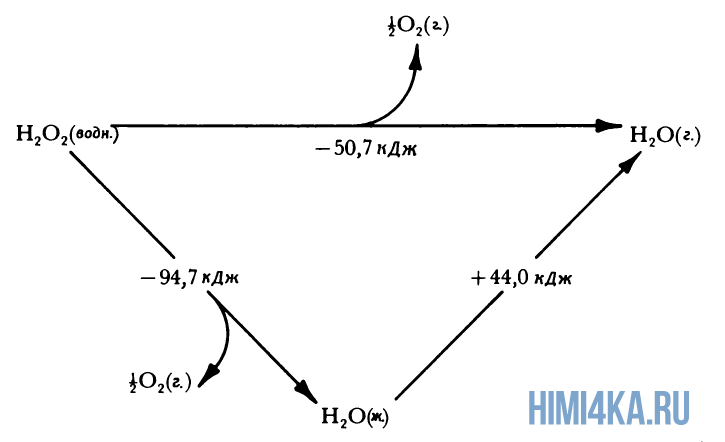
Здесь мы молчаливо воспользовались очень важным предположением, что теплоты реакций аддитивны. Уравнение (1) в сумме с уравнением (3) дает уравнение (4), и поэтому мы предположили, что теплота третьей из этих реакций должна быть равна сумме первых двух:

• ΔH = -94,7 кДж + 44,0 кДж = -50,7 кДж (5)

Закон Гесса

Аддитивность теплот реакций вытекает непосредственно из первого закона термодинамики: изменение энергии или энтальпии между двумя состояниями системы зависит только от самих этих состояний, а не от того, каким образом осуществляется переход между ними. Следовательно, разность между энтальпиями реагентов и продуктов, т.е теплота реакции, должна зависеть только от исходного и конечного состояний, а не от того конкретного пути, по которому следует реакция. Это утверждение носит название закон аддитивности теплот реакций (закон Гесса).

Благодаря закону Гесса совсем не обязательно измерять изменение энтальпии каждой возможной химической реакции. Например, если известны теплота испарения жидкой воды (3), то совсем не обязательно измерять теплоту разложения пероксида водорода с образованием водяного пара; эту величину гораздо проще получить путем вычислений. Если какую-либо реакцию трудно провести в лабораторных условиях, можно попытаться подобрать последовательность легче осуществляемых реакций, сумма которых дает необходимую реакцию. После измерения изменений энтальпии для всех индивидуальных реакций в такой последовательности можно просуммировать соответствующие изменения энтальпии подобно самим химическим уравнениям и найти теплоту трудно проводимой реакции.

Урок 19 «Изменение энтальпии» бесспорно был сложным, но чрезвычайно важным. Скорее всего у вас сейчас каша в голове, но не пугайтесь, ведь в следующем уроке все встанет на свои места. Если у вас возникли вопросы по данному уроку, то пишите их в комментарии.

Была ли эта статья полезной?

The enthalpy change of a reaction is the amount of heat absorbed or released as the reaction takes place, if it happens at a constant pressure. You complete the calculation in different ways depending on the specific situation and what information you have available. For many calculations, Hess’s law is the key piece of information you need to use, but if you know the enthalpy of the products and the reactants, the calculation is much simpler.

Definition of Enthalpy

The precise definition of enthalpy (H) is the sum of the internal energy (U) plus the product of pressure (P) and volume (V). In symbols, this is:

H = U + PV

A change in enthalpy (∆H) is therefore:

∆H = ∆U + ∆P∆V

Where the delta symbol (∆) means “change in.” In practice, the pressure is held constant and the above equation is better shown as:

∆H = ∆U + P∆V

However, for a constant pressure, the change in enthalpy is simply the heat (q) transferred:

∆H = q

If (q) is positive, the reaction is endothermic (i.e., absorbs heat from its surroundings), and if it is negative, the reaction is exothermic (i.e., releases heat into its surroundings). Enthalpy has units of kJ/mol or J/mol, or in general, energy/mass. The equations above are really related to the physics of heat flow and energy: thermodynamics.

Simple Enthalpy Change Calculation

The most basic way to calculate enthalpy change uses the enthalpy of the products and the reactants. If you know these quantities, use the following formula to work out the overall change:

∆H = H_products − H_reactants

The addition of a sodium ion to a chloride ion to form sodium chloride is an example of a reaction you can calculate this way. Ionic sodium has an enthalpy of −239.7 kJ/mol, and chloride ion has enthalpy −167.4 kJ/mol. Sodium chloride (table salt) has an enthalpy of −411 kJ/mol. Inserting these values gives:

∆H = −411 kJ/mol – (−239.7 kJ/mol −167.4 kJ/mol)

= −411 kJ/mol – (−407.1 kJ/mol)

= −411 kJ/mol + 407.1 kJ/mol = −3.9 kJ/mol

So the formation of salt releases almost 4 kJ of energy per mole.

Enthalpy of Phase Transitions

When a substance changes from solid to liquid, liquid to gas or solid to gas, there are specific enthalpies involved in these changes. The enthalpy (or latent heat) of melting describes the transition from solid to liquid (the reverse is minus this value and called the enthalpy of fusion), the enthalpy of vaporization describes the transition from liquid to gas (and the opposite is condensation) and the enthalpy of sublimation describes the transition from solid to gas (the reverse is again called the enthalpy of condensation).

For water, the enthalpy of melting is ∆H_melting = 6.007 kJ/mol. Imagine that you heat ice from 250 Kelvin until it melts, and then heat the water to 300 K. The enthalpy change for the heating parts is just the heat required, so you can find it using:

∆H = nC∆T

Where (n) is the number of moles, (∆T) is the change in temperatue and (C) is the specific heat. The specific heat of ice is 38.1 J/K mol and the specific heat of water is 75.4 J/K mol. So the calculation takes place in a few parts. First, the ice has to be heated from 250 K to 273 K (i.e., −23 °C to 0°C). For 5 moles of ice, this is:

∆H = nC∆T

= 5 mol × 38.1 J/K mol × 23 K

= 4.382 kJ

Now multiply the enthalpy of melting by the number of moles:

∆H = n ∆H_melting

= 5 mol × 6.007 kJ/mol

= 30.035 kJ

Calculations for vaporization are the same, except with the vaporization enthalpy in place of the melting one. Finally, calculate the final heating phase (from 273 to 300 K) in the same way as the first:

∆H = nC∆T

= 5 mol × 75.4 J/K mol × 27 K

= 10.179 kJ

Sum these parts to find the total change in enthalpy for the reaction:

∆H_total = 10.179 kJ + 30.035 kJ + 4.382 kJ

= 44.596 kJ

Hess’s Law

Hess’s law is useful for when the reaction you’re considering has two or more parts and you want to find the overall change in enthalpy. It states that the enthalpy change for a reaction or process is independent of the route through which it occurs. This means that if reaction transforms on substance into another, it doesn’t matter if the reaction occurs in one step (reactants become products immediately) or whether it goes through many steps (reactants become intermediaries and then become products), the resulting enthalpy change is the same in both cases.

It usually helps to draw a diagram (see Resources) to help you use this law. One example is if you start with six moles of carbon combined with three of hydrogen, they combust to combine with oxygen as an intermediary step and then form benzene as an end-product.

Hess’ law states that the change in enthalpy of the reaction is the sum of the changes in enthalpy of both parts. In this case, the combustion of one mole of carbon has ∆H = −394 kJ/mol (this happens six times in the reaction), the change in enthalpy for the combustion of one mole of hydrogen gas is ∆H = −286 kJ/mol (this happens three times) and the carbon dioxide and water intermediaries become benzene with an enthalpy change of ∆H = +3,267 kJ/mol.

Take the sum of these changes to find the total enthalpy change, remembering to multiply each by the number of moles needed in the first stage of the reaction:

∆H_total = 6×(−394) + 3×(−286) +3,267

= 3,267 − 2,364 – 858

= 45 kJ/mol

Тепловой эффект химической реакции — изменение внутренней энергии или энтальпии системы вследствие протекания химической реакции и превращения исходных веществ (реактантов) в продукты реакции в количествах, соответствующих уравнению химической реакции (стехиометрии реакции^[1]) при следующих условиях:

• единственно возможной работой при этом является работа против внешнего давления,
• как исходные вещества, так и продукты реакции имеют одинаковую температуру^[2][3].

Теплота термохимического процесса и тепловой эффект химической реакции[править | править код]

Поясним приведённое выше определение теплового эффекта химической реакции^{[K 1]}. Для этого запишем фундаментальные уравнения Гиббса для внутренней энергии и энтальпии простой^[10] открытой однородной термодинамической системы^[11][12]:

(Фундаментальное уравнение Гиббса для внутренней энергии)

(Фундаментальное уравнение Гиббса для энтальпии)

Здесь  — абсолютная температура,  — энтропия,  — давление,  — объём,  — количество (или масса) -го составляющего систему вещества,  — химический потенциал этого вещества (см. Энтропия открытой системы).

Для бесконечно малого^[13] квазистатического изохорного процесса ()

(Изменение внутренней энергии в бесконечно малом квазистатическом изохорном процессе)

для бесконечно малого квазистатического изобарного процесса ()

(Изменение энтальпии в бесконечно малом квазистатическом изобарном процессе)

Важно понимать, что представление о теплоте химической реакции при сохранении исторически сложившегося названия (восходящего ко временам, когда любое изменение температуры связывали с поглощением или выделением теплоты) уже не имеет прямого отношения к общефизическому понятию количества теплоты. Действительно, при химической реакции в изолированной системе (например, инициируемом электрической искрой взрыве гремучего газа в герметически закрытом термосе) может иметь место изменение температуры (за счёт выделения теплоты), но не происходит обмена с окружающей средой(так как попросту это термос — изолированная система), ни изменения внутренней энергии системы. Наконец, традиционная трактовка теплоты, основанная на представлении об адиабатической изоляции системы от окружающей среды^[14] (см. Неоднозначность понятий «теплота» и «работа») к открытым системам не применима, и для них теплоту бесконечно малого квазистатического процесса полагают равной^[15][16]

(Дефиниция теплоты для любого бесконечно малого квазистатического процесса)

Таким образом, теплота бесконечно малого квазистатического изохорного процесса равна

(Теплота бесконечно малого квазистатического изохорного процесса)

а теплота бесконечно малого квазистатического изобарного процесса равна

(Теплота бесконечно малого квазистатического изобарного процесса)

Для закрытых систем изменение энергии системы за счёт изменения масс составляющих систему веществ (химическую работу^{[17][18][19][20][21]}, работу перераспределения масс составляющих систему веществ^[22]) учитывать не требуется^[23][24], и выражения для теплот ещё более упрощаются:

(Теплота бесконечно малого квазистатического изохорного процесса в простой закрытой системе)

(Теплота бесконечно малого квазистатического изобарного процесса в простой закрытой системе)

Из сказанного ясно, почему в дефиниции теплового эффекта химической реакции фигурируют внутренняя энергия, энтальпия и запрет на любые виды работ в системе, кроме работы расширения/сжатия. Уточним, что в понятии «химическая работа» термин «работа» не имеет отношения к понятию «термодинамическая работа» и использован просто как синоним словосочетания «изменение энергии». Наконец, подчеркнём, что когда речь идёт о тепловом эффекте химической реакции, то, как и во многих других случаях, касающихся термохимии, подразумевается, что речь идёт о закрытой системе и полномасштабное применение мощного, но громоздкого математического аппарата термодинамики систем переменного состава не требуется^[23][24][25].

Энергетический эффект химической реакции всегда рассматривают применительно к конкретному термохимическому уравнению, которое может не иметь отношения к реальному химическому процессу. Термохимическое уравнение лишь показывает, какие наборы начальных и конечных индивидуальных веществ, находящихся в определённых состояниях и количественных соотношениях, исчезают и образуются. В начальном состоянии должны присутствовать только исходные вещества (реактанты), а в конечном — только продукты химической реакции. Единственным условием при записи термохимического уравнения является соблюдение материального и зарядового баланса. Вещества в растворённом или адсорбированном состоянии тоже считаются индивидуальными соединениями; если растворитель или адсорбент не участвует непосредственно в химической реакции и не реагирует с растворённым веществом, то он рассматривается просто как фактор, влияющий на термодинамические свойства рассматриваемого вещества. Наконец, в термохимическом уравнении могут фигурировать частицы, не способные к самостоятельному существованию (электроны, протоны, ионы, радикалы, атомарные простые вещества)^[26].

Энергетический эффект реального процесса с химической реакцией зависит от условий проведения процесса и не может служить стандартной характеристикой конкретной химической реакции^[3]. Химическая же термодинамика нуждается в показателе, связанном с энергетикой химической реакции, но не зависящем от условий её проведения. Покажем, как может быть получен интересующий нас показатель. Для этого рассмотрим следующий мысленный эксперимент. Возьмем чистые индивидуальные исходные вещества в мольных количествах, соответствующих стехиометрическим коэффициентам интересующего нас термохимического уравнения, и находящиеся при определённых температуре и давлении. Если привести эти вещества в контакт, то энтальпия образовавшейся неравновесной системы в начальный момент времени будет равна сумме энтальпий исходных веществ. Теперь рассмотрим конечное состояние изучаемой системы в предположении, что реактанты прореагировали полностью^[27] и продукты реакции находятся при той же температуре и том же давлении, что и реактанты. Энтальпия системы (в общем случае неравновесной) из продуктов химической реакции будет равна сумме энтальпий этих веществ. Поскольку энтальпия — функция состояния, то разность энтальпий системы в конце и начале рассмотренного мысленного эксперимента не зависит от условий проведения химической реакции. Эту разность энтальпий и называют изобарным тепловым эффектом (термохимической теплотой) химической реакции, соответствующей определённому термохимическому уравнению^[28][29]. Важно, что реальная осуществимость рассмотренного мысленного эксперимента, гипотетические условия его проведения и неравновесность исходного и конечного состояний термохимической системы не сказываются на дефиниции теплового эффекта химической реакции.

Часто тепловой эффект химической реакции относят к 1 молю одного из продуктов реакции^[30].

Резюмируем сказанное: теплота процесса, связанного с фактическим протеканием химической реакции, и энергетический эффект химической реакции отнюдь не одно и то же, а дефиниция теплового эффекта химической реакции вообще не предполагает действительного осуществления реакции, соответствующей рассматриваемому термохимическому уравнению^[31].

И внутренняя энергия, и энтальпия представляют собой функции состояния, поэтому тепловой эффект химической реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, то есть от числа и характера промежуточных стадий (закон Гесса)^{[32][33][34][35]}.

Тепловой эффект химической реакции, протекающей при постоянном давлении, и равный изменению энтальпии системы в процессе, соответствующем термохимическому уравнению, называется изобарным тепловым эффектом или энтальпией химической реакции. Тепловой эффект химической реакции, протекающей при постоянном объёме, и равный изменению внутренней энергии системы в процессе, соответствующем термохимическому уравнению, называют изохорным тепловым эффектом^[2].

Для отдельных типов химических реакций вместо общего термина «тепловой эффект химической реакции» используют специальные (сокращённые) термины: теплота образования, теплота сгорания и т. п.^[1]

Дефиниции тепловых эффектов должны быть дополнены указанием на начальные точки отсчёта значений энергии и энтальпии. Для сравнения тепловых эффектов и упрощения термодинамических расчётов все величины тепловых эффектов реакций относят к стандартным условиям (все вещества находятся в стандартных состояниях)^[1]. Если реакцию — реально или гипотетически — проводят при стандартных условиях (T = 298,15 К = 25 °С и P = 1 бар = 100 кПа)^[36], то тепловой эффект называют стандартным тепловым эффектом реакции или стандартной энтальпией реакции ΔHo
r.

Химические реакции, сопровождающиеся повышением температуры, называют экзотермическими, понижением температуры — эндотермическими. В термодинамической системе знаков тепловой эффект экзотермической реакции ( или ) считают отрицательным, эндотермической ( или ) — положительным. В устаревшей и не рекомендуемой к употреблению термохимической системе знаков положительным, наоборот, считается тепловой эффект экзотермической реакции, а отрицательным — эндотермической^[37].

Тепловые эффекты химических реакций важны для теоретической химии и необходимы при расчётах равновесных составов смесей, выхода продуктов реакций, удельной тяги топлив реактивных двигателей и для решения многих других прикладных задач^[1].

Изучение тепловых эффектов химических реакций составляет важнейшую задачу термохимии^[3]. Для расчёта стандартных тепловых эффектов химических реакций используют таблицы стандартных теплот образования или сгорания^[37].

Стандартная энтальпия образования (стандартная теплота образования)[править | править код]

Под стандартной теплотой образования понимают тепловой эффект реакции образования одного моля вещества из простых веществ, его составляющих, находящихся в устойчивых стандартных состояниях.

Например, стандартная энтальпия образования 1 моля метана из углерода и водорода равна тепловому эффекту реакции:

С(тв) + 2H₂(г) = CH₄(г) + 74,9 кДж/моль.

Стандартная энтальпия образования обозначается ΔHo
f. Здесь индекс f означает formation (образование), а знак «O» в верхнем индексе указывает, что величина относится к стандартному состоянию вещества: один моль индивидуального химического соединения, взятого в чистом виде при стандартных условиях в том агрегатном состоянии, которое устойчиво в этих условиях (если нет специальной оговорки)^[38]. Иногда для обозначения стандартного состояния используют перечёркнутый символ «O» в верхнем индексе; согласно рекомендациям ИЮПАК по использованию обозначений в физической химии^[39], перечёркнутый и неперечёркнутый символ «O», используемые для обозначения стандартного состояния, одинаково приемлемы. В литературе часто встречается другое обозначение стандартной энтальпии — ΔHo
298,15, где знак «O» указывает на равенство давления одной атмосфере^[40] (или, несколько более точно, на стандартные условия^[41]), а 298,15 — температура. Иногда индекс «O» используют для величин, относящихся к чистому веществу, оговаривая, что обозначать им стандартные термодинамические величины можно только тогда, когда в качестве стандартного состояния выбрано именно чистое вещество^[42]. Стандартным также может быть принято, например, состояние вещества в предельно разбавленном растворе.

Энтальпия образования простых веществ принимается равной нулю, причем нулевое значение энтальпии образования относится к агрегатному состоянию, устойчивому при T = 298,15 K. Например, для иода в кристаллическом состоянии ΔH^o(I₂, тв) = 0 кДж/моль, а для жидкого иода ΔH^o(I₂, ж) = 22 кДж/моль. Энтальпии образования простых веществ при стандартных условиях являются их основными энергетическими характеристиками.

Тепловой эффект любой реакции находится как разность между суммой теплот образования всех продуктов и суммой теплот образования всех реагентов в данной реакции (следствие закона Гесса):

ΔH^o_{реакции} = ΣΔHo
f (продукты) — ΣΔHo
f (реагенты).

Термохимические эффекты можно включать в химические реакции. Химические уравнения в которых указано количество выделившейся или поглощенной теплоты, называются термохимическими уравнениями. Реакции, сопровождающиеся выделением тепла в окружающую среду имеют отрицательный тепловой эффект и называются экзотермическими. Реакции, сопровождающиеся поглощением тепла имеют положительный тепловой эффект и называются эндотермическими. Тепловой эффект обычно относится к одному молю прореагировавшего исходного вещества, стехиометрический коэффициент которого максимален.

Температурная зависимость теплового эффекта (энтальпии) реакции[править | править код]

Чтобы рассчитать температурную зависимость энтальпии реакции, необходимо знать мольные теплоемкости веществ, участвующих в реакции. Изменение энтальпии реакции при увеличении температуры от Т₁ до Т₂ рассчитывают по закону Кирхгофа (предполагается, что в данном интервале температур мольные теплоемкости не зависят от температуры и нет фазовых превращений):

Если в данном интервале температур происходят фазовые превращения, то при расчёте необходимо учесть теплоты соответствующих превращений, а также изменение температурной зависимости теплоемкости веществ, претерпевших такие превращения:

где ΔC_p(T₁, T_φ) — изменение теплоемкости в интервале температур от Т₁ до температуры фазового перехода;  — тепловой эффект фазового перехода; ΔC_p(T_φ, T₂) — изменение теплоемкости в интервале температур от температуры фазового перехода до конечной температуры, и T_φ — температура фазового перехода.

Стандартная энтальпия сгорания[править | править код]

Стандартная энтальпия сгорания — ΔHо
гор., тепловой эффект реакции сгорания одного моля вещества в кислороде до образования оксидов в высшей степени окисления. Теплота сгорания негорючих веществ принимается равной нулю.

Стандартная энтальпия растворения[править | править код]

Стандартная энтальпия растворения — ΔHо
раств., тепловой эффект процесса растворения 1 моля вещества в бесконечно большом количестве растворителя. Складывается из теплоты разрушения кристаллической решётки и теплоты гидратации (или теплоты сольватации для неводных растворов), выделяющейся в результате взаимодействия молекул растворителя с молекулами или ионами растворяемого вещества с образованием соединений переменного состава — гидратов (сольватов). Разрушение кристаллической решетки, как правило, эндотермический процесс — ΔH_реш. > 0, а гидратация ионов — экзотермический, ΔH_гидр. < 0. В зависимости от соотношения значений ΔH_реш. и ΔH_гидр. энтальпия растворения может иметь как положительное, так и отрицательное значение. Так растворение кристаллического гидроксида калия сопровождается выделением тепла:

ΔHо
раств.KOH = ΔHо
реш. + ΔHо
гидр.К⁺ + ΔHо
гидр.OH⁻ = −59 кДж/моль.

Под энтальпией гидратации ΔH_гидр. понимается теплота, которая выделяется при переходе 1 моля ионов из вакуума в раствор.

Стандартная энтальпия нейтрализации[править | править код]

Стандартная энтальпия нейтрализации ΔHо
нейтр. — энтальпия реакции взаимодействия сильных кислот и оснований с образованием 1 моля воды при стандартных условиях:

HCl + NaOH = NaCl + H₂O

H⁺ + OH⁻ = H₂O, ΔHо
нейтр. = −55,9 кДж/моль

Стандартная энтальпия нейтрализации для концентрированных растворов сильных электролитов зависит от концентрации ионов, вследствие изменения значения ΔHо
гидратации ионов при разбавлении.

См. также[править | править код]

• Термохимия
• Химическая термодинамика

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

• Callen H. B. Thermodynamics and an Introduction to Thermostatistics. — 2nd ed. — N. Y. e. a.: John Wiley, 1985. — XVI + 493 p. — ISBN 0471862568, 9780471862567.
• Lebon G., Jou D., Casas-Vázquez J. Understanding Non-equilibrium Thermodynamics: Foundations, Applications, Frontiers. — Berlin — Heidelberg: Springer, 2008. — XIII + 325 p. — ISBN 978-3-540-74251-7, 978-3-540-74252-4. — doi:10.1007/978-3-540-74252-4.
• Александров Н. Е., Богданов А. И., Костин К. И. и др. Основы теории тепловых процессов и машин. Часть II / Под ред. Н. И. Прокопенко. — 5-е изд. (электронное). — М.: Бином. Лаборатория знаний, 2015. — 572 с. — ISBN 978-5-9963-2613-6. (недоступная ссылка)
• Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
• Большая Советская Энциклопедия / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: Советская Энциклопедия, 1976. — Т. 25: Струнино — Тихорецк. — 600 с. Архивная копия от 5 августа 2017 на Wayback Machine
• Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М.: Инфра-М, 2017. — 868 с. — ISBN 978-5-16-104227-4.
• Бурдаков В. П., Дзюбенко Б. В., Меснянкин С. Ю., Михайлова Т. В. Термодинамика. Часть 2. Специальный курс. — М.: Дрофа, 2009. — 362 с. — (Высшее образование. Современный учебник). — ISBN 978-5-358-06140-8.
• Жариков В. А. Основы физической геохимии. — М.: Наука; Изд-во МГУ, 2005. — 656 с. — (Классический университетский учебник). — ISBN 5-211-04849-0, 5-02-035302-7.
• Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с.
• Карякин Н. В. Основы химической термодинамики. — М.: Академия, 2003. — 463 с. — (Высшее профессиональное образование). — ISBN 5-7695-1596-1. (недоступная ссылка)
• Кнорре Д. Г., Крылова Л. Ф., Музыкантов В. С. Физическая химия. — 2. — М.: Высшая школа, 1990. — 416 с. — ISBN 5-06-000655-7.
• Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
• Ляшков В. И. Теоретические основы теплотехники. — М.: Курс; Инфра-М, 2015. — 328 с. — ISBN 978-5-905554-85-8, 978-5-16-0І0639-7.
• Морачевский А. Г., Кохацкая М. С. Прикладная химическая термодинамика. — СПб.: Изд-во Политехн. ун-та, 2008. — 254 с. — ISBN 978-5-7422-2006-0.
• Морачевский А. Г., Фирсова Е. Г. Физическая химия. Термодинамика химических реакций. — 2-е изд., испр. — СПб.: Лань, 2015. — 101 с. — (Учебники

для вузов. Специальная литература). — ISBN 978-5-8114-1858-9. (недоступная ссылка)

• Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — М.: Мир, 1971. — 296 с.
• Нараев В. Н. Физическая химия. Часть 1. Химическая термодинамика. Фазовые равновесия и учение о растворах. Электрохимия. — СПб.: Санкт-Петербургский государственный технологический институт (Технический университет), 2007. — 262 с. (недоступная ссылка)
• Никольский Б. П., Смирнова Н. А., Панов М. Ю. и др. Физическая химия. Теоретическое и практическое руководство / Под ред. Б. П. Никольского. — 2-е изд., перераб. и доп. — Л.: Химия, 1987. — 880 с. — (Для высшей школы).
• Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М.: Наука, 1971. — 376 с.
• Степановских Е. И., Брусницына Л. А., Маскаева Л. Н. Химическая термодинамика в вопросах и ответах. — Екатеринбург: УИПЦ, 2014. — 221 с. — ISBN 978-5-4430-0061-9.
• Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
• Тамм М. Е., Третьяков Ю. Д. Неорганическая химия. Том 1. Физико-химические основы неорганической химии / Под. ред. акад. Ю. Д. Третьякова. — М.: Академия, 2004. — 240 с. — (Высшее профессиональное образование). — ISBN 5-7695-1446-9.
• Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.
• Химическая энциклопедия / Гл. ред. Н. С. Зефиров. — М.: Большая Российская энциклопедия, 1995. — Т. 4: Пол — Три. — 640 с. — ISBN 5-85270-092-4.
• Химический энциклопедический словарь / Гл. ред. И. Л. Кнунянц. — М.: Советская энциклопедия, 1983. — 792 с.
• Шмидт Э. Введение в техническую термодинамику / Пер. с нем. — М.—Л.: Энергия, 1965. — 392 с.
• Эткинс П. Физическая химия. — М.: Мир, 1980.